Practical Use of Starlink Downlink Tones for Positioning
Abstract
:1. Introduction
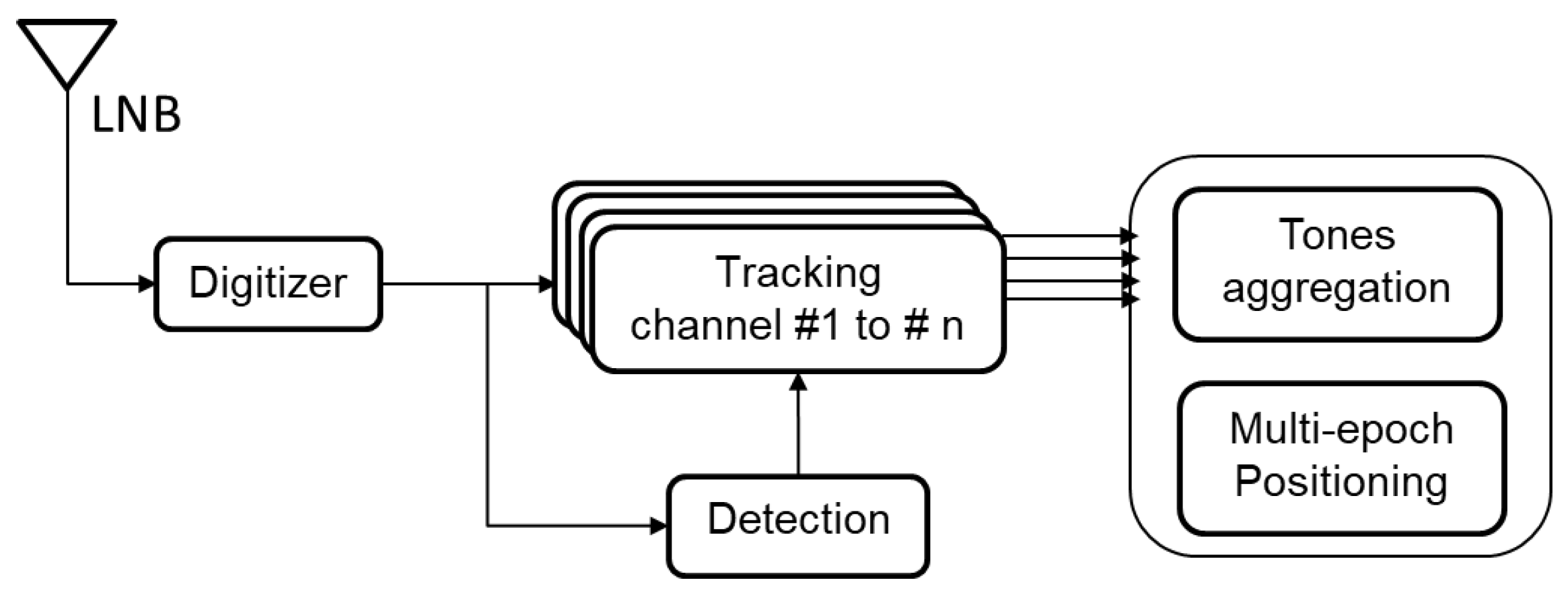
2. Signal Detection and Tracking
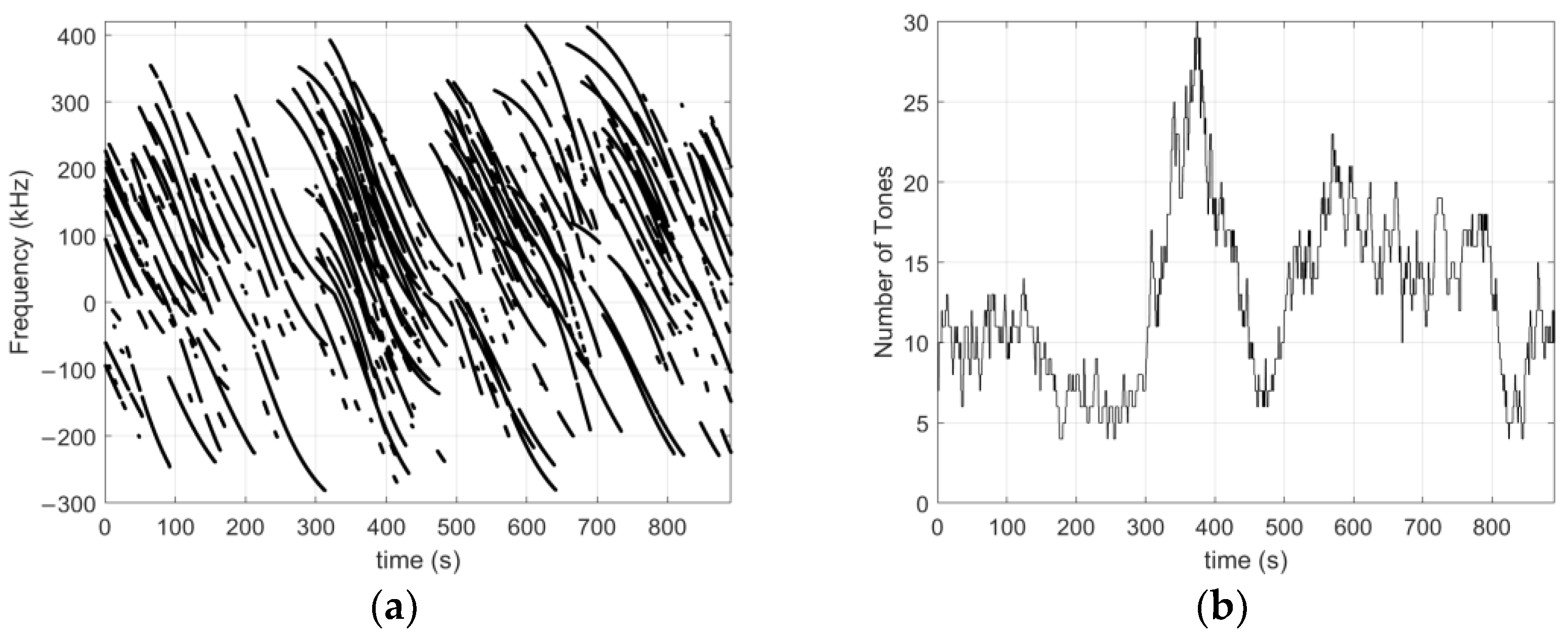
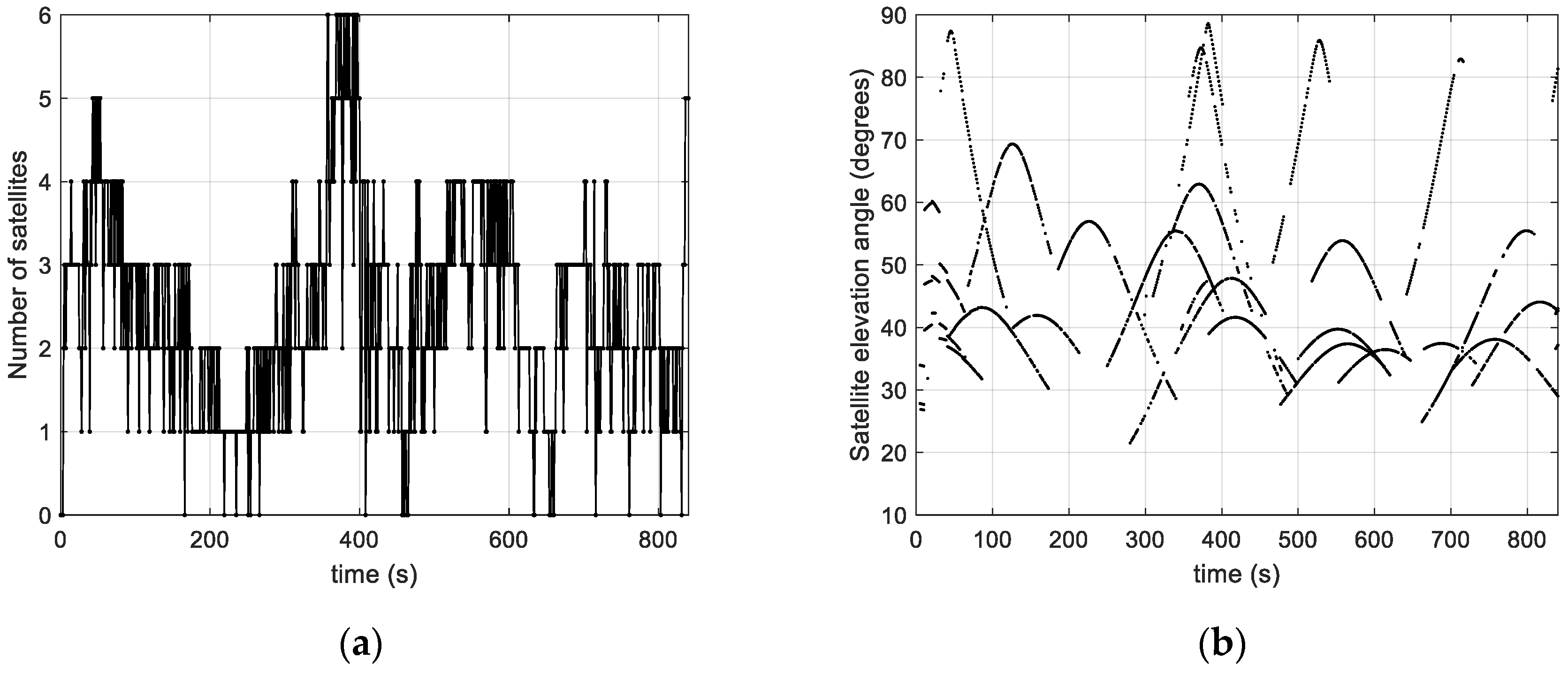
2.1. Range Dynamics and Visibility
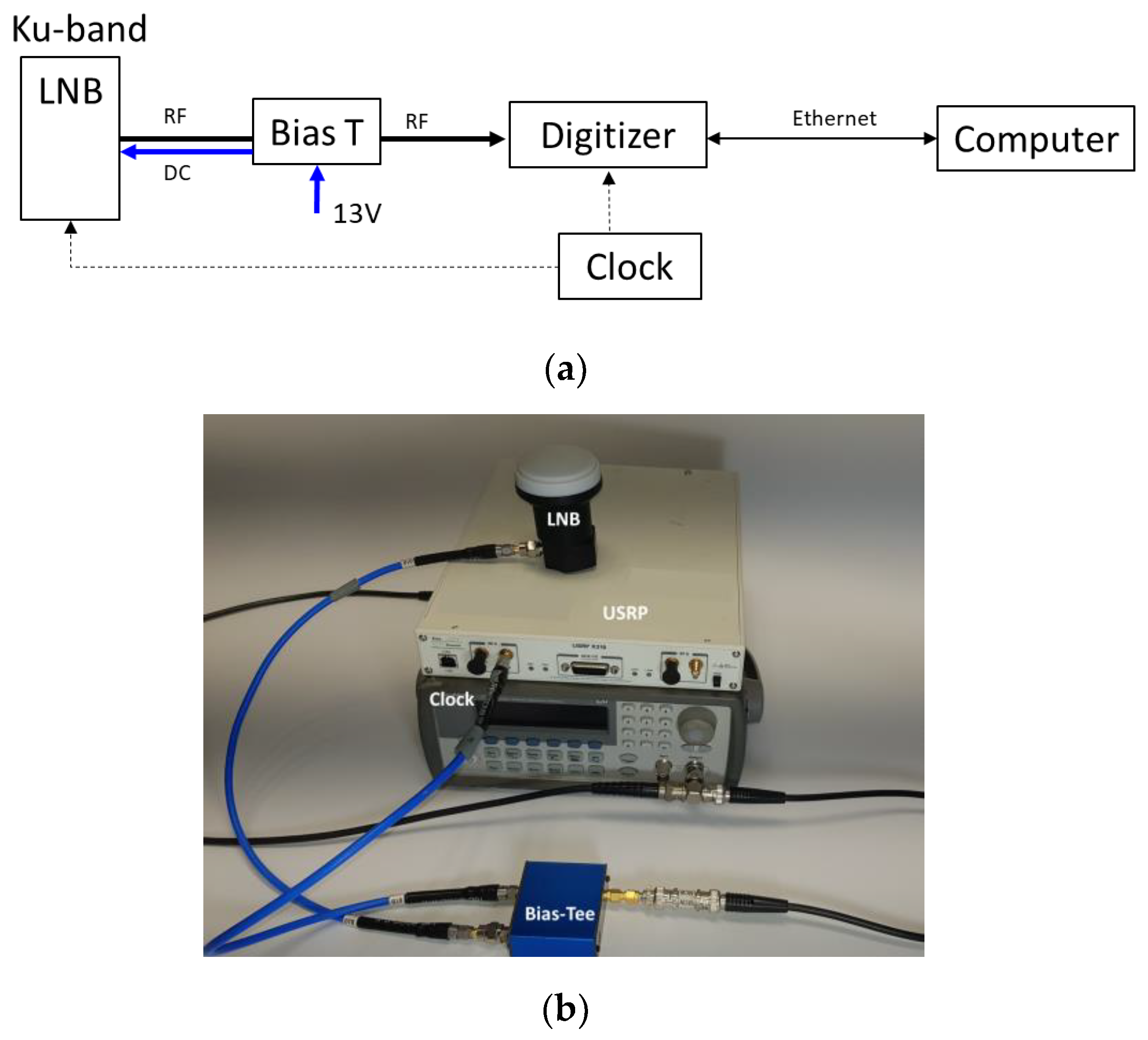
2.2. Signal Recording
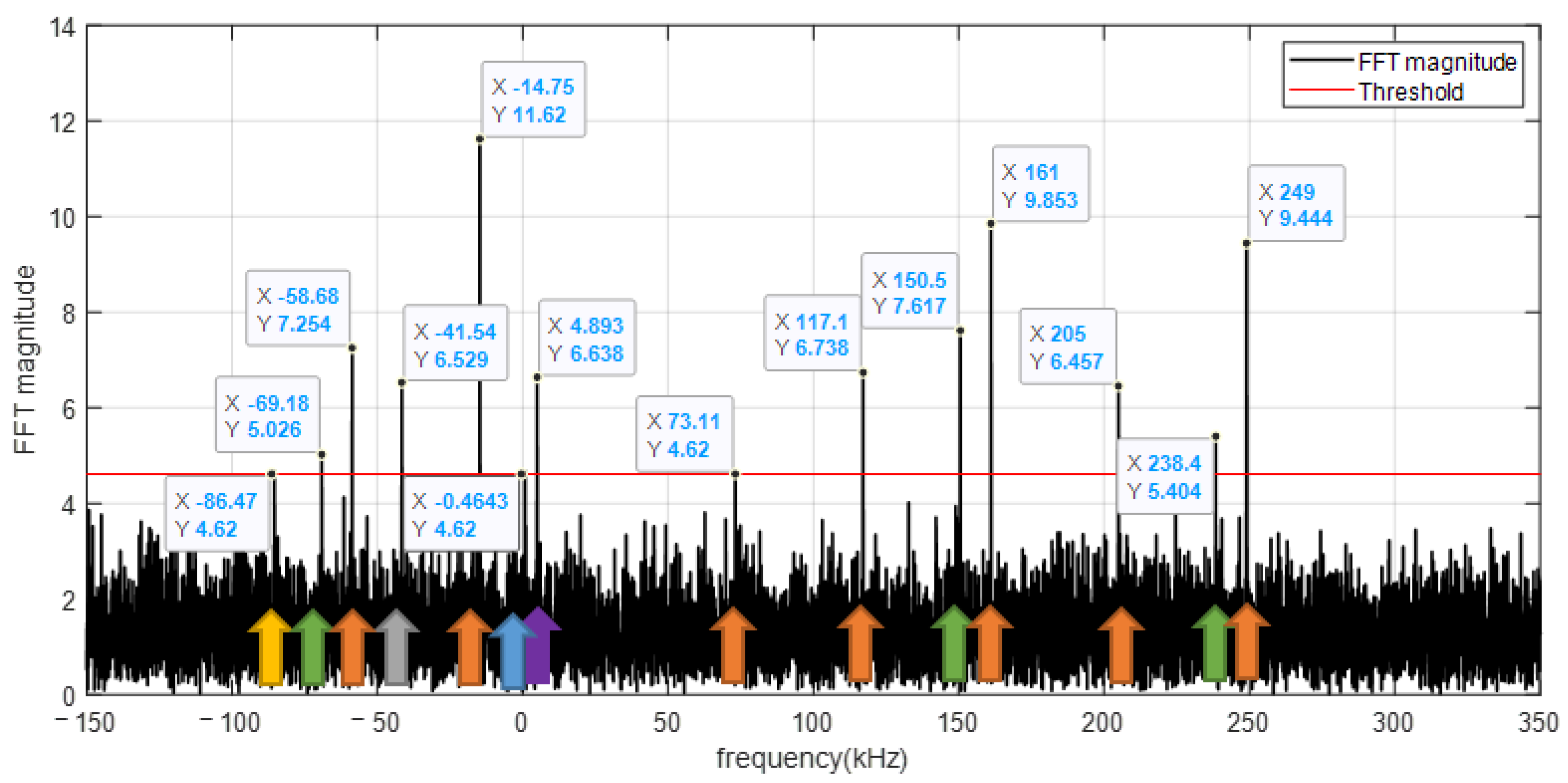
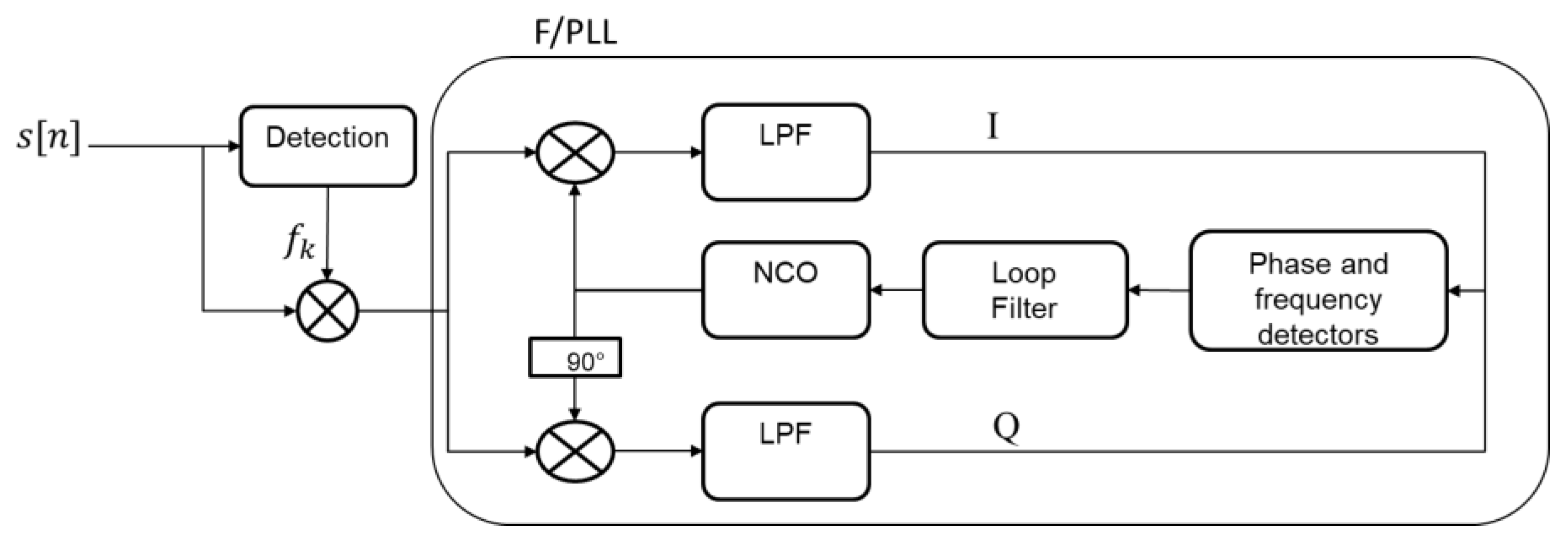
2.3. Tones Detection and Tracking
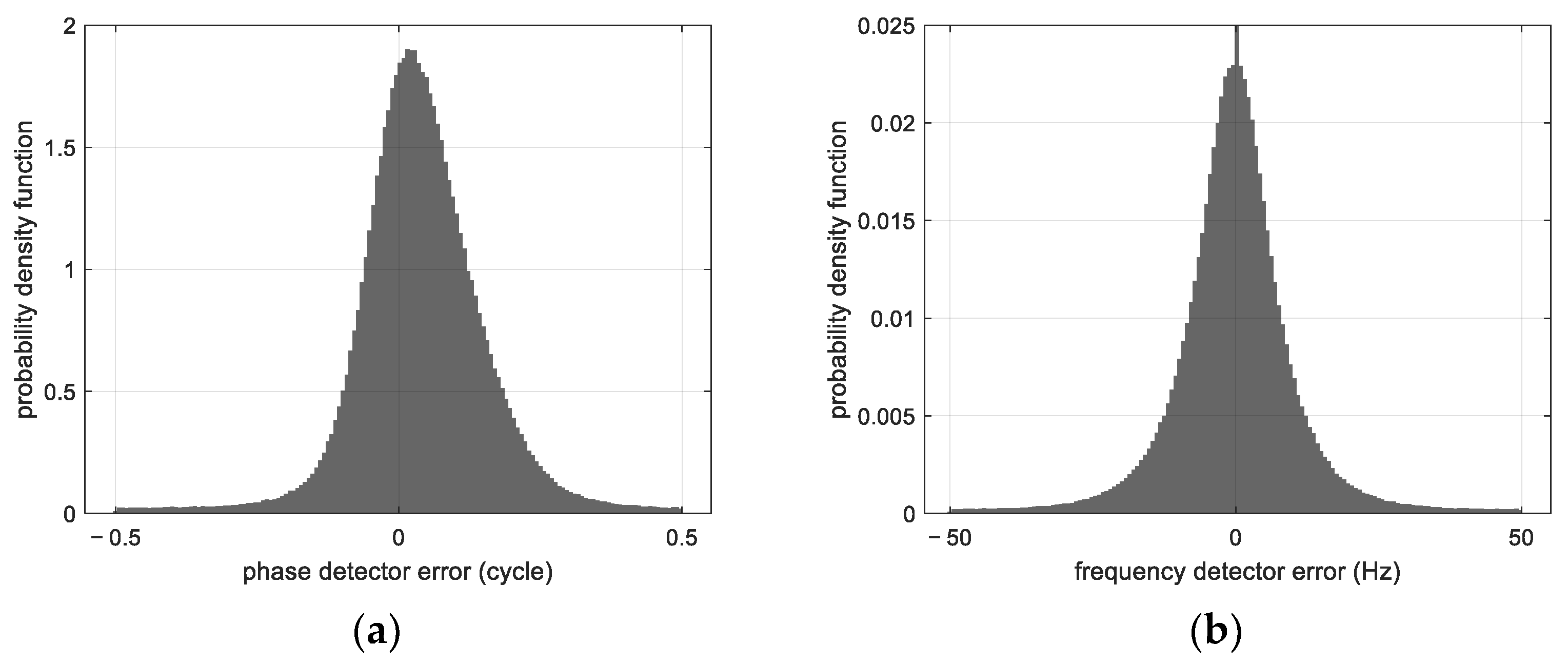
2.4. Tones Frequency Shift
3. Tones Frequencies Aggregation
- -
- is the kth-satellite Doppler shift (Hz)
- -
- is the frequency shift induced by the orbit error for the kth-satellite (Hz). A rough approximation is
- -
- is the frequency shift induced by the user position and velocity error for the kth-satellite. A rough approximation is
- -
- is the frequency shift induced by the timing error for the kth-satellite (Hz)
4. Multi-Epoch Positioning
4.1. A Simplified Frequency Error Model
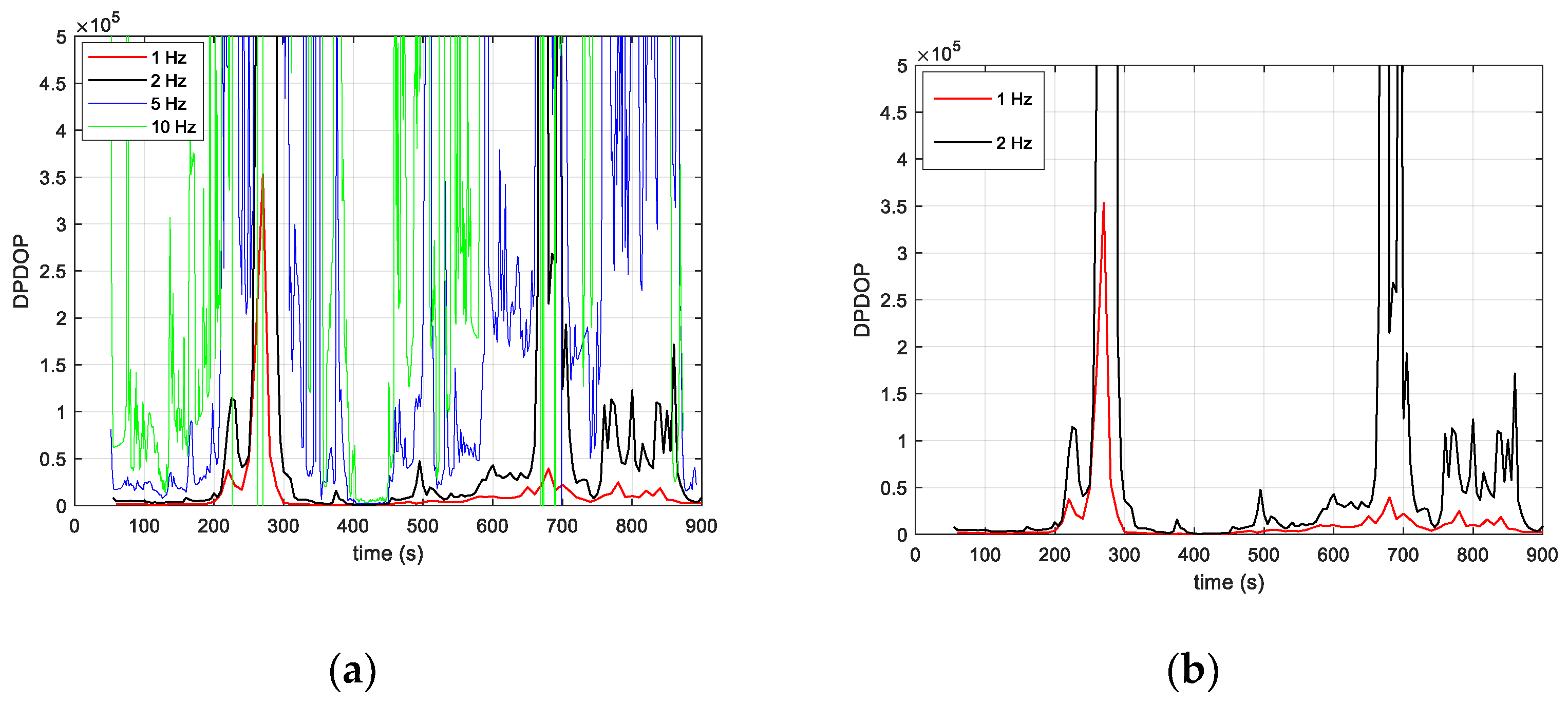
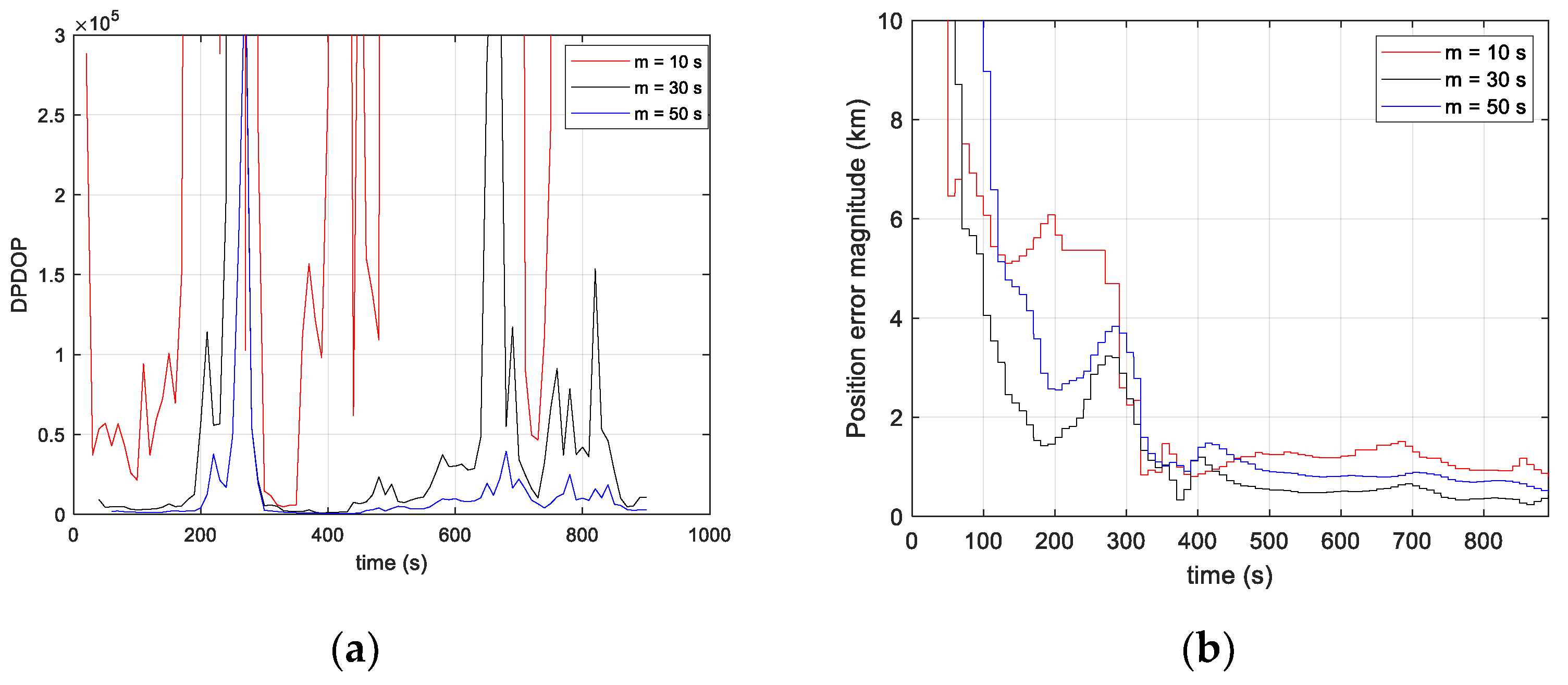
4.2. Positioning Algorithm
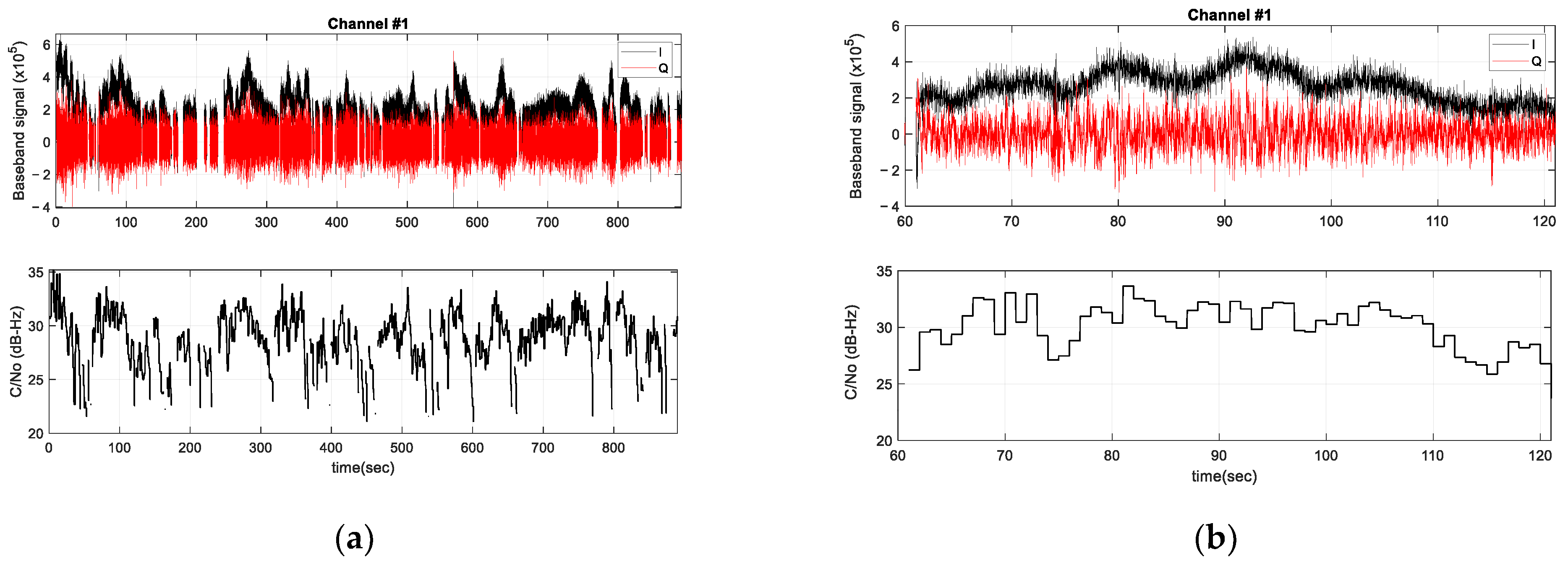
4.3. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morales-Ferre, R.; Richter, P.; Falletti, E.; de la Fuente, A.; Lohan, E.S. A Survey on Coping With Intentional Interference in Satellite Navigation for Manned and Unmanned Aircraft. IEEE Commun. Surv. Tutor. 2019, 22, 249–291. [Google Scholar] [CrossRef]
- Iridium and Qualcomm Collaborate to Support Satellite Messaging in Smartphones. Available online: https://investor.iridium.com/2023-01-05-Iridium-and-Qualcomm-Collaborate-to-Support-Satellite-Messaging-in-Smartphones (accessed on 9 February 2023).
- Prol, F.; Ferre, R.; Saleem, Z.; Välisuo, P.; Pinell, C.; Lohan, E.; Elsanhoury, M.; Elmusrati, M.; Islam, S.; Celikbilek, K.; et al. Position, Navigation, and Timing (PNT) Through Low Earth Orbit (LEO) Satellites: A Survey on Current Status, Challenges, and Opportunities. IEEE Access 2022, 10, 83971–84002. [Google Scholar] [CrossRef]
- Ferre, R.M.; Praks, J.; Seco-Granados, G.; Lohan, E.S. A Feasibility Study for Signal-in-Space Design for LEO-PNT Solutions with Miniaturized Satellites. IEEE J. Miniat. Air Space Syst. 2022, 3, 171–183. [Google Scholar] [CrossRef]
- Ren, J.; Sun, D.; Pan, D.; Li, M.; Zheng, J. Cost-Efficient LEO Navigation Augmentation Constellation Design under a Constrained Deployment Approach. Int. J. Aerosp. Eng. 2021, 2021, 5042650. [Google Scholar] [CrossRef]
- Egea-Roca, D.; López-Salcedo, J.A.; Seco-Granados, G.; Falletti, E. Comparison of Several Signal Designs Based on Chirp Spread Spectrum (CSS) Modulation for a LEO PNT System. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+), St. Louis, MO, USA, 20–24 September 2021; pp. 2804–2818. [Google Scholar]
- Reid, T.G.R.; Chan, B.; Goel, A.; Gunning, K.; Manning, B.; Martin, J.; Neish, A.; Perkins, A.; Tarantino, P. Satellite Navigation for the Age of Autonomy. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 342–352. [Google Scholar] [CrossRef]
- Gutt, G.; Lawrence, D.; Cobb, S.; O’Connor, M. Recent PNT improvements and test results based on low earth orbit satellites. In Proceedings of the 49th Annual Precise Time and Time Interval Systems and Applications Meeting, Reston, VR, USA, 29 January–1 February 2018; pp. 72–79. [Google Scholar]
- Psiaki, M.L. Navigation using carrier Doppler shift from a LEO constellation: TRANSIT on steroids. J. Inst. Navig. 2021, 68, 621–641. [Google Scholar] [CrossRef]
- Reid, S. ORBCOMM System Overview, ORBCOMM LLC, Document No. A80TD0008-Revision G. 18 December 2001. Available online: https://www.ctu.cz/sites/default/files/cs/download/oznamene_typy_rozhrani/orbcomm-rozhrani_02_06_2010.pdf (accessed on 15 March 2023).
- Dietrich, F.J.; Metzen, P.; Monte, P. The Globalstar cellular satellite system. IEEE Trans. Antennas Propag. 1998, 46, 935–942. [Google Scholar] [CrossRef]
- Ardito, C.; Morales, J.; Khalife, J.; Abdallah, A.A.; Kassas, Z.M. Performance Evaluation of Navigation Using LEO Satellite Signals with Periodically Transmitted Satellite Positions. In Proceedings of the 2019 International Technical Meeting of The Institute of Navigation, Reston, VA, USA, 28–31 January 2019; pp. 306–318. [CrossRef] [Green Version]
- Khalife, J.; Kassas, Z.M. Receiver design for doppler positioning with LEO satellites. In Proceedings of the ICASSP 2019—2019 IEEE ICASSP, Brighton, UK, 12–17 May 2019; pp. 5506–5510. [Google Scholar]
- Leng, M.; Lei, L.; Razul, S.G.; See, C.M. Joint Synchronization and Localization Using Iridium Ring Alert Signal; ICICS: Vancouver, BC, Canada, 2015; pp. 1–5. [Google Scholar]
- Tan, Z.; Qin, H.; Cong, L.; Zhao, C. Positioning Using IRIDIUM Satellite Signals of Opportunity in Weak Signal Environment. Electronics 2020, 9, 37. [Google Scholar] [CrossRef] [Green Version]
- Benzerrouk, H. Iridium Next LEO Satellites as an Alternative PNT in GNSS Denied Environments. Inside GNSS 2019, 14, 56–64. [Google Scholar]
- Khalife, J.; Neinavaie, M.; Kassas, Z.M. Navigation with Differential Carrier Phase Measurements From Megaconstellation LEO Satellites. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1393–1404. [Google Scholar] [CrossRef]
- Joerger, M.; Gratton, L.; Pervan, B.; Cohen, C.E. Analysis of Iridium-Augmented GPS for Floating Carrier Phase Positioning. Navigation 2010, 57, 137–160. [Google Scholar] [CrossRef]
- Morales, J.; Roysdon, P.F.; Kassas, Z.M. Signals of opportunity aided inertial navigation. In Proceedings of the 2016 ITM of the Institute of Navigation, Portland, OR, USA, 21–24 September 2016; pp. 1492–1501. [Google Scholar]
- Benzerrouk, H.; Nguyen, Q.; Xiaoxing, F.; Amrhar, A.; Nebylov, A.V.; Landry, R. Alternative PNT based on Iridium Next LEO Satellites Doppler/INS Integrated Navigation System. In Proceedings of the 2019 26th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), St. Petersburg, Russia, 27–29 May 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Jardak, N.; Jault, Q. The Potential of LEO Satellite-Based Opportunistic Navigation for High Dynamic Applications. Sensors 2022, 22, 2541. [Google Scholar] [CrossRef] [PubMed]
- Farhangian, F.; Landry, R., Jr. Multi-Constellation Software-Defined Receiver for Doppler Positioning with LEO Satellites. Sensors 2020, 20, 5866. [Google Scholar] [CrossRef] [PubMed]
- Khalife, J.; Neinavaie, M.; Kassas, Z.M. The First Carrier Phase Tracking and Positioning Results with Starlink LEO Satellite Signals. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1487–1491. [Google Scholar] [CrossRef]
- Neinavaie, M.; Khalife, J.; Kassas, Z.M. Acquisition, Doppler Tracking, and Positioning with Starlink LEO Satellites: First Results. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2606–2610. [Google Scholar] [CrossRef]
- Humphreys, T.E.; Iannucci, P.A.; Komodromos, Z.M.; Graff, A.M. Signal Structure of the Starlink Ku-Band Downlink. arXiv 2022. [Google Scholar] [CrossRef]
- FCC Report (2018, November). Spacex Non-geostationary Satellite System, Attachment A, Technical Information to Supplement Schedule, S. Available online: https://fcc.report/IBFS/SAT-MOD-20181108-00083/1569860.pdf (accessed on 9 February 2023).
- NORAD General Perturbations (GP) Element Sets. Available online: https://www.celestrak.com/NORAD/elements/ (accessed on 9 February 2023).
- Vallado, D.; Crawford, P. SGP4 Orbit Determination. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, Hawaii, 18–21 August 2008. [Google Scholar] [CrossRef]
- Vallado, D.A.; Crawford, P.; Hujsak, R.; Kelso, T.S. Revisiting Spacetrack Report #3. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; ISBN 978-1-62410-048-2. [Google Scholar] [CrossRef] [Green Version]
- Milroy, D.; Belden, S. Antenna apparatus having adhesive coupling. US Patent US20200381831A1, 3 December 2020. [Google Scholar]
- Kaplan, E.; Hegarty, C. Understanding GPS Principles and Applications, 2nd ed.; Artech House Inc.: Norwood, OH, USA, 2006; pp. 164–173. [Google Scholar]
- Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment. Radio Transmission Commission for Aeronautics, 2006. RTCA DO-229D. Available online: https://www.rtca.org (accessed on 9 February 2023).




| Unit | A Typical Range Limit | |
|---|---|---|
| Range | km | 400 to 1150 |
| Doppler shift | kHz | −230 to 230 |
| Doppler shift rate | kHz/s | <5 |
| Rate of the Doppler shift rate | Hz/s2 | <70 |
| Number of satellites in view | - | 16–35 |
| Satellite visibility time | minutes | <4 |
| Frequency Error Source | Assumption | Frequency Error |
|---|---|---|
| Receiver clock drift | 1 ppm | 11.345 kHz |
| Satellite clock drift | 0.01 ppm | 0.11345 kHz |
| Troposphere | Elevation mask < 25° | <a few Hz |
| Time error | , | <5 kHz |
| Satellite and user position errors | | <6.2 kHz |
| Satellite and user velocity errors | <150 Hz | |
| Noise | 24–36 dB-Hz | <10 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jardak, N.; Adam, R. Practical Use of Starlink Downlink Tones for Positioning. Sensors 2023, 23, 3234. https://doi.org/10.3390/s23063234
Jardak N, Adam R. Practical Use of Starlink Downlink Tones for Positioning. Sensors. 2023; 23(6):3234. https://doi.org/10.3390/s23063234
Chicago/Turabian StyleJardak, Nabil, and Ronan Adam. 2023. "Practical Use of Starlink Downlink Tones for Positioning" Sensors 23, no. 6: 3234. https://doi.org/10.3390/s23063234






