Interferometric Fiber Optic Probe for Measurements of Cavitation Bubble Expansion Velocity and Bubble Oscillation Time
Abstract
:1. Introduction
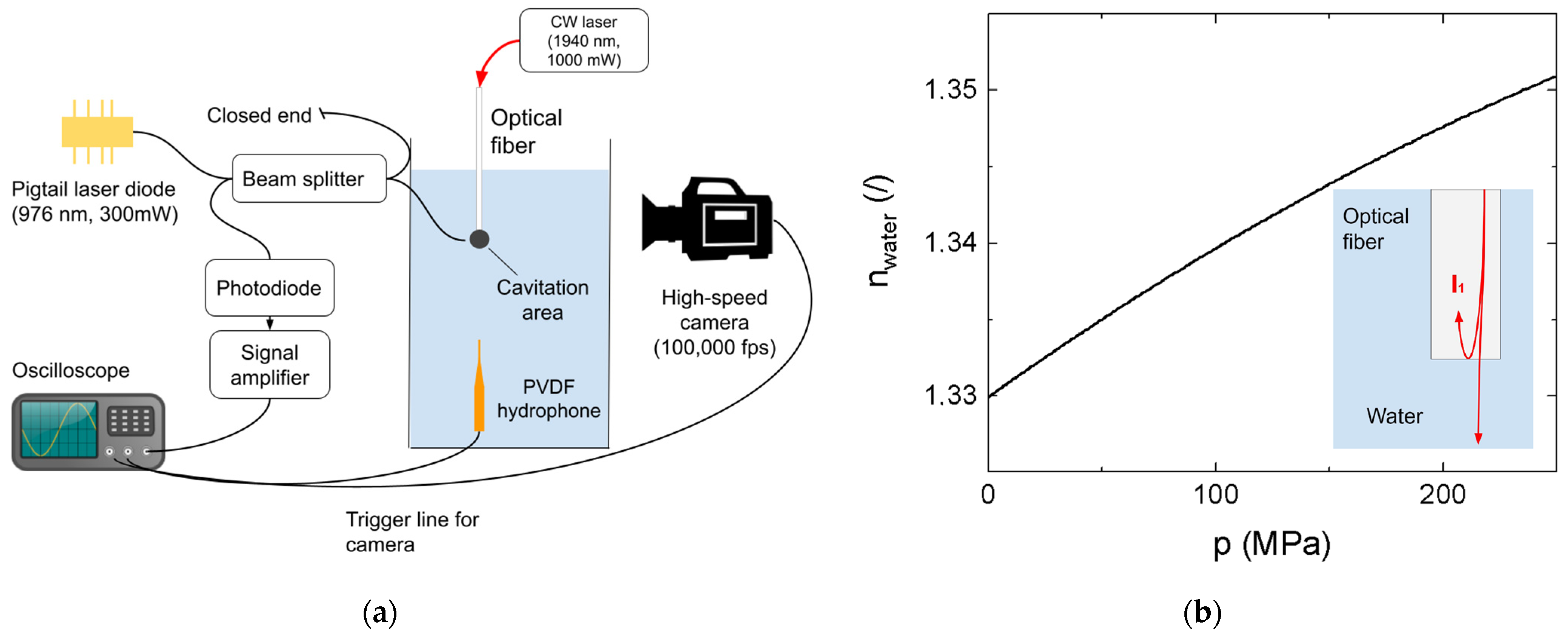
2. Materials and Methods
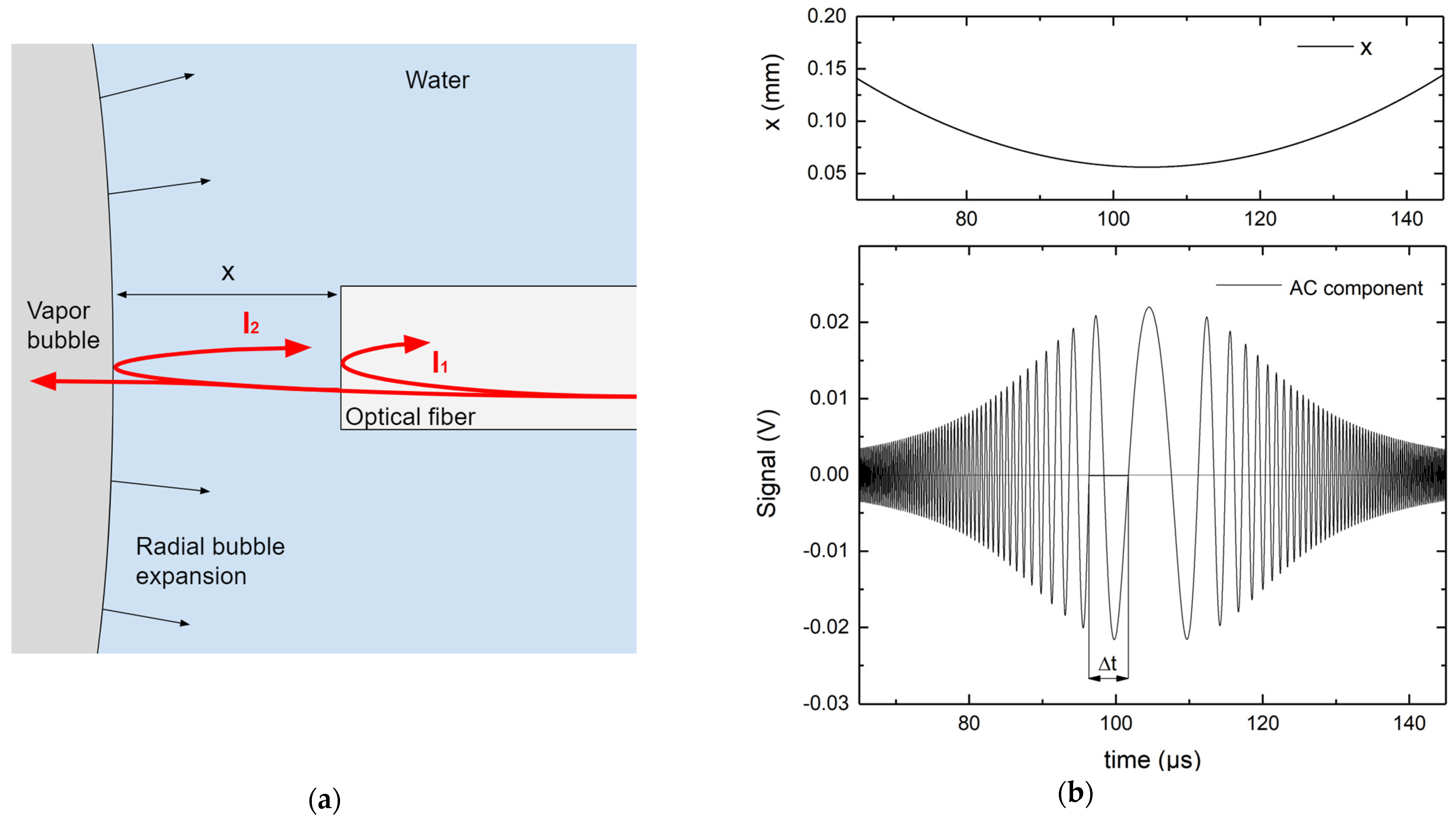
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hurrell, A.; Beard, P. Piezoelectric and Fibre-Optic Hydrophones. Ultrason. Transducers Mater. Des. Sens. Actuators Med. Appl. 2012, 619–676. [Google Scholar] [CrossRef]
- Parsons, J.E.; Cain, C.A.; Fowlkes, J.B. Cost-Effective Assembly of a Basic Fiber-Optic Hydrophone for Measurement of High-Amplitude Therapeutic Ultrasound Fields. J. Acoust. Soc. Am. 2006, 119, 1432. [Google Scholar] [CrossRef] [PubMed]
- De Paula, R.P.; Cole, J.H.; Bucaro, J.A.; Flax, L. Single-Mode Fiber Ultrasonic Sensor. IEEE J. Quantum Electron. 1982, 18, 680–683. [Google Scholar] [CrossRef] [Green Version]
- Wurster, C.; Staudenraus, J.; Eisenmenger, W. Fiber Optic Probe Hydrophone. In Proceedings of the IEEE Ultrasonics Symposium, Cannes, France, 31 October–3 November 1994; Volume 2. [Google Scholar]
- Petelin, J.; Lokar, Z.; Horvat, D.; Petkovsek, R. Localized Measurement of a Sub-Nanosecond Shockwave Pressure Rise Time. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Vogel, A.; Busch, S.; Parlitz, U. Shock Wave Emission and Cavitation Bubble Generation by Picosecond and Nanosecond Optical Breakdown in Water. J. Acoust. Soc. Am. 1996, 100, 148–165. [Google Scholar] [CrossRef]
- Močnik, G.; Petkovšek, R.; Možina, J. Optodynamic Characterization of the Shock Waves after Laser-Induced Breakdown in Water. Opt. Express 2005, 13, 4107–4112. [Google Scholar] [CrossRef]
- Huber, P.; Debus, J.; Peschke, P.; Hahn, E.W.; Lorenz, W.J. In Vivo Detection of Ultrasonically Induced Cavitation by a Fibre-Optic Technique. Ultrasound Med. Biol. 1994, 20, 811–825. [Google Scholar] [CrossRef]
- Vogel, A.; Hentschel, W.; Holzfuss, J.; Lauterborn, W. Cavitation Bubble Dynamics and Acoustic Transient Generation in Ocular Surgery with Pulsed Neodymium:YAG Lasers. Ophthalmology 1986, 93, 1259–1269. [Google Scholar] [CrossRef]
- Lukač, M.; Olivi, G.; Constantin, M.; Lukač, N.; Jezeršek, M. Determination of Optimal Separation Times for Dual-Pulse SWEEPS Laser-Assisted Irrigation in Different Endodontic Access Cavities. Lasers Surg. Med. 2021, 53, 998–1004. [Google Scholar] [CrossRef] [PubMed]
- Brennen, C.E. Cavitation in Medicine. Interface Focus 2015, 5, 1–12. [Google Scholar] [CrossRef]
- Thiel, M.; Nieswand, M.; Dörffel, M. Review: The Use of Shock Waves in Medicine—A Tool of the Modern OR: An Overview of Basic Physical Principles, History and Research. Minim. Invasive Ther. Allied Technol. 2000, 9, 247–253. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, S.K. Kailash Shock Wave Treatment in Medicine. J. Biosci. 2005, 30, 269–275. [Google Scholar] [CrossRef] [PubMed]
- Sinibaldi, G.; Occhicone, A.; Alves Pereira, F.; Caprini, D.; Marino, L.; Michelotti, F.; Casciola, C.M. Laser Induced Cavitation: Plasma Generation and Breakdown Shockwave. Phys. Fluids 2019, 31, 103302. [Google Scholar] [CrossRef] [Green Version]
- Muller, M.; Garen, W.; Koch, S.; Marsik, F.; Neu, W.; Saburov, E. Shock Waves and Cavitation Bubbles in Water and Isooctane Generated by Nd:YAG Laser: Experimental and Theoretical Results. In Laser-Assisted Micro-and Nanotechnologies 2003; Society of Photo Optical: Bellingham, WA, USA, 2004; pp. 275–282. [Google Scholar] [CrossRef]
- Zhong, X.; Eshraghi, J.; Vlachos, P.; Dabiri, S.; Ardekani, A.M. A Model for a Laser-Induced Cavitation Bubble. Int. J. Multiph. Flow 2020, 132, 103433. [Google Scholar] [CrossRef]
- Akhatov, I.; Lindau, O.; Topolnikov, A.; Mettin, R.; Vakhitova, N.; Lauterborn, W. Collapse and Rebound of a Laser-Induced Cavitation Bubble. Phys. Fluids 2001, 13, 2805. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.-X.; Linz, N.; Freidank, S.; Paltauf, G.; Vogel, A. Comprehensive Analysis of Spherical Bubble Oscillations and Shock Wave Emission in Laser-Induced Cavitation. J. Fluid Mech. 2021, 940, A5. [Google Scholar] [CrossRef]
- Supponen, O.; Akimura, T.; Minami, T.; Nakajima, T.; Uehara, S.; Ohtani, K.; Kaneko, T.; Farhat, M.; Sato, T. Jetting from Cavitation Bubbles Due to Multiple Shockwaves. Appl. Phys. Lett. 2018, 113, 193703. [Google Scholar] [CrossRef]
- Li, H.; Huang, J.; Wu, X.; Zhang, J.; Wang, J.; Wang, Y.; Huang, C. Dynamic Behaviors of a Laser-Induced Bubble and Transition Mechanism of Collapse Patterns in a Tube. AIP Adv. 2020, 10, 035210. [Google Scholar] [CrossRef]
- Kobayashi, T.; Ohtani, K.; Takayama, K.; Umezu, S.; Okatsu, K. Underwater Rock Drilling by CO2 Laser. In Proceedings of the 26th International Congress on Applications of Lasers and Electro-Optics, ICALEO 2007—Congress Proceedings, Orlando, FL, USA, 29 October–1 November 2007. [Google Scholar]
- Lakshmi, B.S.; Leela, C.; Bagchi, S.; Kiran, P.P.; Prashant, T.S.; Tewari, S.P.; Ashoka, V.S. Interferometric and Shadowgraphic Studies of Shock Wave and Cavitation Bubble Generated with Nd:YAG Nano Second Laser Pulses Induced Breakdown in Water. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2011; Volume 1391. [Google Scholar]
- Ward, B.; Emmony, D.C. Direct Observation of the Pressure Developed in a Liquid during Cavitation-Bubble Collapse. Appl. Phys. Lett. 1991, 59, 2228–2230. [Google Scholar] [CrossRef]
- Hupfeld, T.; Laurens, G.; Merabia, S.; Barcikowski, S.; Gökce, B.; Amans, D. Dynamics of Laser-Induced Cavitation Bubbles at a Solid-Liquid Interface in High Viscosity and High Capillary Number Regimes. J. Appl. Phys. 2020, 127, 044306. [Google Scholar] [CrossRef]
- Gregorčič, P.; Jezeršek, M.; Možina, J. Optodynamic Energy-Conversion Efficiency during an Er:YAG-Laser-Pulse Delivery into a Liquid through Different Fiber-Tip Geometries. J. Biomed. Opt. 2012, 17, 075006. [Google Scholar] [CrossRef] [Green Version]
- Sakka, T.; Tamura, A.; Matsumoto, A.; Fukami, K.; Nishi, N.; Thornton, B. Effects of Pulse Width on Nascent Laser-Induced Bubbles for Underwater Laser-Induced Breakdown Spectroscopy. Spectrochim. Acta Part B At. Spectrosc. Spectrochim. 2014, 97, 94–98. [Google Scholar] [CrossRef] [Green Version]
- Lai, G.; Geng, S.; Zheng, H.; Yao, Z.; Zhong, Q.; Wang, F. Early Dynamics of a Laser-Induced Underwater Shock Wave. J. Fluids Eng. Trans. ASME 2022, 144, 011501. [Google Scholar] [CrossRef]
- Wilson, B.G.; Fan, Z.; Sreedasyam, R.; Botvinick, E.L.; Venugopalan, V. Single-Shot Interferometric Measurement of Cavitation Bubble Dynamics. Opt. Lett. 2021, 46, 1409–1412. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-San-Juan, J.C.; Rodriguez-Aboytes, E.; Korneev, N.; Baldovinos-Pantaleon, O.; Chiu-Zarate, R.; Gutiérrez-Juárez, G.; Dominguez-Cruz, R.; Ramos-García, R. Cavitation Induced by Continuous Wave Lasers. In Optical Trapping and Optical Micromanipulation IV; Society of Photo Optical: Bellingham, WA, USA, 2007; Volume 6644. [Google Scholar]
- Korneev, N.; Rodríguez-Montero, P.; Durán Sánchez, M.; Ibarra Escamilla, B.; Kuzin, A.E. Thermoactivated Cavitation Induced in Water by Low Power, Continuous Wave Thulium-Doped Fiber Laser. Rev. Mex. Física 2019, 65, 185–189. [Google Scholar] [CrossRef] [Green Version]
- Padilla-Martinez, J.P.; Berrospe-Rodriguez, C.; Aguilar, G.; Ramirez-San-Juan, J.C.; Ramos-Garcia, R. Optic Cavitation with CW Lasers: A Review. Phys. Fluids 2014, 26, 122007. [Google Scholar] [CrossRef] [Green Version]
- Korneev, N.; Montero, P.R.; Ramos-García, R.; Ramirez-San-Juan, J.C.; Padilla-Martinez, J.P. Ultrasound Induced by CW Laser Cavitation Bubbles. J. Phys. Conf. Ser. 2011, 278, 012029. [Google Scholar] [CrossRef]
- Chudnovskii, V.M.; Yusupov, V.I.; Dydykin, A.V.; Nevozhai, V.I.; Kisilev, A.Y.; Zhukov, S.A.; Bagratashvili, V.N. Laser-Induced Boiling of Biological Liquids in Medical Technologies. Quantum Electron. 2017, 47, 361. [Google Scholar] [CrossRef]
- Lum, P.; Greenstein, M.; Grossman, C.; Szabo, T.L. High-Frequency Membrane Hydrophone. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 536–544. [Google Scholar] [CrossRef]
- Kendir, E.; Yaltkaya, Ş. Effect of Temperature and Wavelength on the Refractive Index of Water: A Fiber-Optic Sensor Application. Indian J. Phys. 2022, 96, 1247–1252. [Google Scholar] [CrossRef]
- Kimura, K.; Takeuchi, S.; Koike, Y. Investigation of Cavitation Bubble Influence on Frequency Spectrum of Fiber Optic Probe Hydrophone Output. In Proceedings of the IEEE International Ultrasonics Symposium, IUS, IEEE Computer Society, Las Vegas, NV, USA, 7 September 2020; Volume 2020. [Google Scholar]
- Horiba, T.; Ogasawara, T.; Takahira, H. Cavitation Inception Pressure and Bubble Cloud Formation Due to the Backscattering of High-Intensity Focused Ultrasound from a Laser-Induced Bubble. J. Acoust. Soc. Am. 2020, 147, 1207–1217. [Google Scholar] [CrossRef] [PubMed]
- Weiss, L.; Tazibt, A.; Tidu, A.; Aillerie, M. Water Density and Polarizability Deduced from the Refractive Index Determined by Interferometric Measurements up to 250 MPa. J. Chem. Phys. 2012, 136, 124201. [Google Scholar] [CrossRef] [PubMed]
- Irvine, W.M.; Pollack, J.B. Infrared Optical Properties of Water and Ice Spheres. Icarus 1968, 8, 324–360. [Google Scholar] [CrossRef]
- Petkovsek, R.; Gregorcic, P.; Mozina, J. A Beam-Deflection Probe as a Method for Optodynamic Measurements of Cavitation Bubble Oscillations. Meas. Sci. Technol. 2007, 18, 2972. [Google Scholar] [CrossRef]
- Matsumoto, A.; Tamura, A.; Kawasaki, A.; Honda, T.; Gregorčič, P.; Nishi, N.; Amano, K.I.; Fukami, K.; Sakka, T. Comparison of the Overall Temporal Behavior of the Bubbles Produced by Short- and Long-Pulse Nanosecond Laser Ablations in Water Using a Laser-Beam-Transmission Probe. Appl. Phys. A Mater. Sci. Process. 2016, 122, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Lee, J.; Kim, Y.; Lee, B.H. Nanometer-Scale Vibration Measurement Using an Optical Quadrature Interferometer Based on 3 × 3 Fiber-Optic Coupler. Sensors 2020, 20, 2665. [Google Scholar] [CrossRef]
- Steinegger, A.; Wolfbeis, O.S.; Borisov, S.M. Optical Sensing and Imaging of PH Values: Spectroscopies, Materials, and Applications. Chem. Rev. 2020, 120, 12357–12489. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubalic, E.; Vella, D.; Babnik, A.; Jezeršek, M. Interferometric Fiber Optic Probe for Measurements of Cavitation Bubble Expansion Velocity and Bubble Oscillation Time. Sensors 2023, 23, 771. https://doi.org/10.3390/s23020771
Zubalic E, Vella D, Babnik A, Jezeršek M. Interferometric Fiber Optic Probe for Measurements of Cavitation Bubble Expansion Velocity and Bubble Oscillation Time. Sensors. 2023; 23(2):771. https://doi.org/10.3390/s23020771
Chicago/Turabian StyleZubalic, Emil, Daniele Vella, Aleš Babnik, and Matija Jezeršek. 2023. "Interferometric Fiber Optic Probe for Measurements of Cavitation Bubble Expansion Velocity and Bubble Oscillation Time" Sensors 23, no. 2: 771. https://doi.org/10.3390/s23020771





