How Good Is a Tactical-Grade GNSS + INS (MEMS and FOG) in a 20-m Bathymetric Survey?
Abstract
:1. Introduction
- How close or far is the tactical-grade GNSS + INS positioning performance from the survey-grade systems on a hydrographic survey platform in calm weather?
- Will the tactical-grade sensor meet the International Hydrographic Organization’s (IHO) Standard for Hydrographic Survey (S-44 6th ed.) in shallow water?
- Can we use those sensor grades for navigation chart production?
2. Methods
2.1. MBES Georeferencing Overview
- Compute beams footprints’ coordinates () in the transducer frame, , using the respective acoustic steering angle (θ) and measured range () from two-way travel time in Equation (1):
- Compute the coordinates of the vessel reference point from translation vector , and determine the vessel’s attitude from ; where are heading with respect to north, pitch, and roll (“angles measured in a rotated coordinate frame as defined by the Tate–Bryant convention [16]”)
- Transform the coordinates in to using Equation (2);where is the rotation matrix.
- 4.
- Compute refraction corrections, , relative to measured ranges, as a function of the sound speed profile (SSP) and acoustic steering angles using the geometric raytracing algorithm discussed in [17] (pp. 47–52);
- 5.
- Apply refraction corrections to sounding positions: +
- 6.
- Account for small angular misalignments, , between the transducer and the INS frame; the so-called patch test/ boresight calibration offset:
- 7.
- In Equation (3), calculate the final multibeam-sounding coordinates () in the vessel frame, , with boresight calibration, refraction corrections, and the separation model (SEP) applied, such that the final depths are reduced to a chart datum:
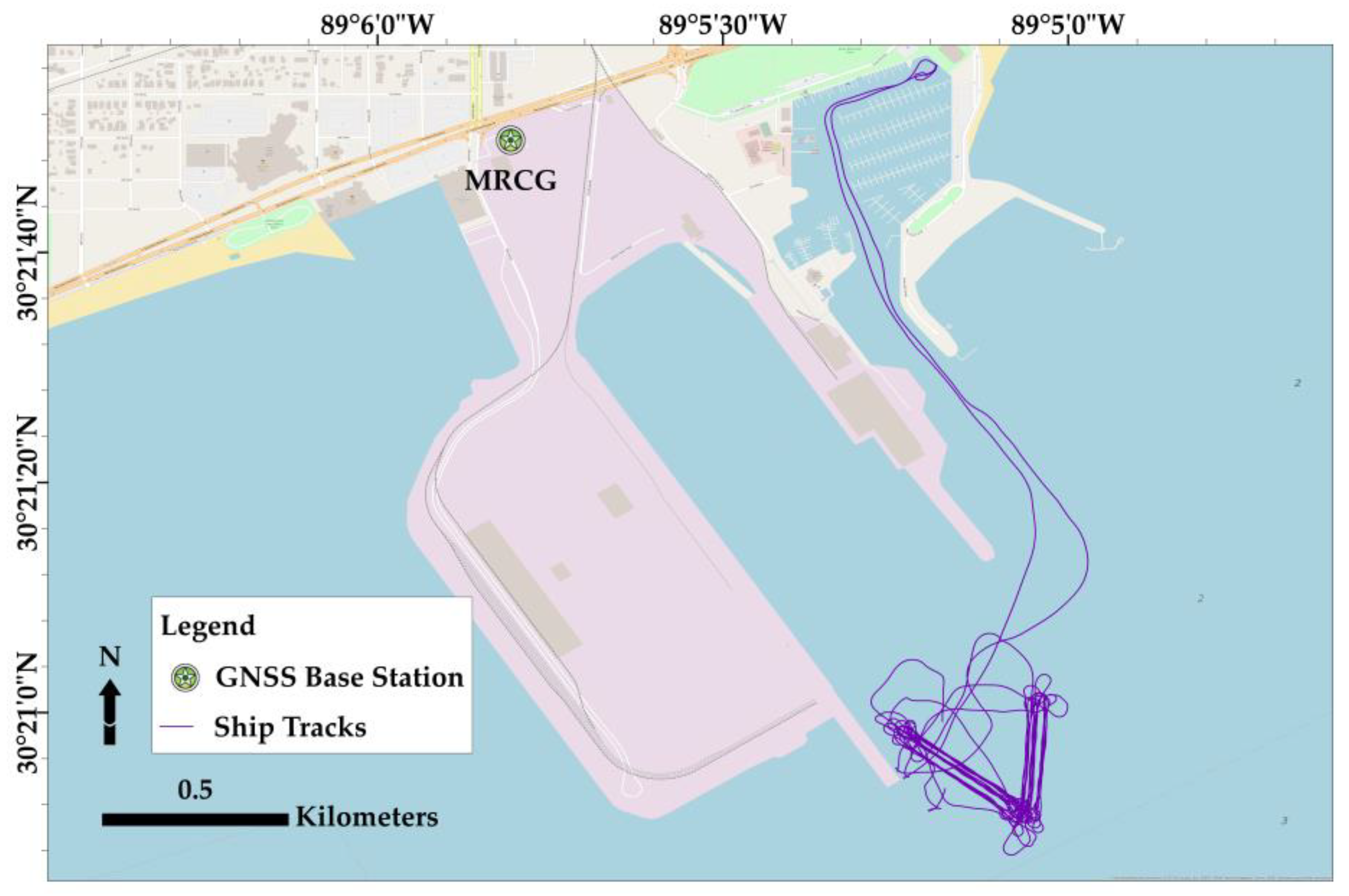
2.2. Experiment Design
2.3. Processing and Analysis Strategy
3. Results
- Formal errors (uncertainties) from software’s GNSS + INS stochastic and noise models;
- Direct comparisons of roll, pitch, and heights between systems;
- CARIS’s boresight calibration results (patch test) from a multibeam dataset georeferenced with system-specific SBET;
- Bathymetric surface and beam analysis.
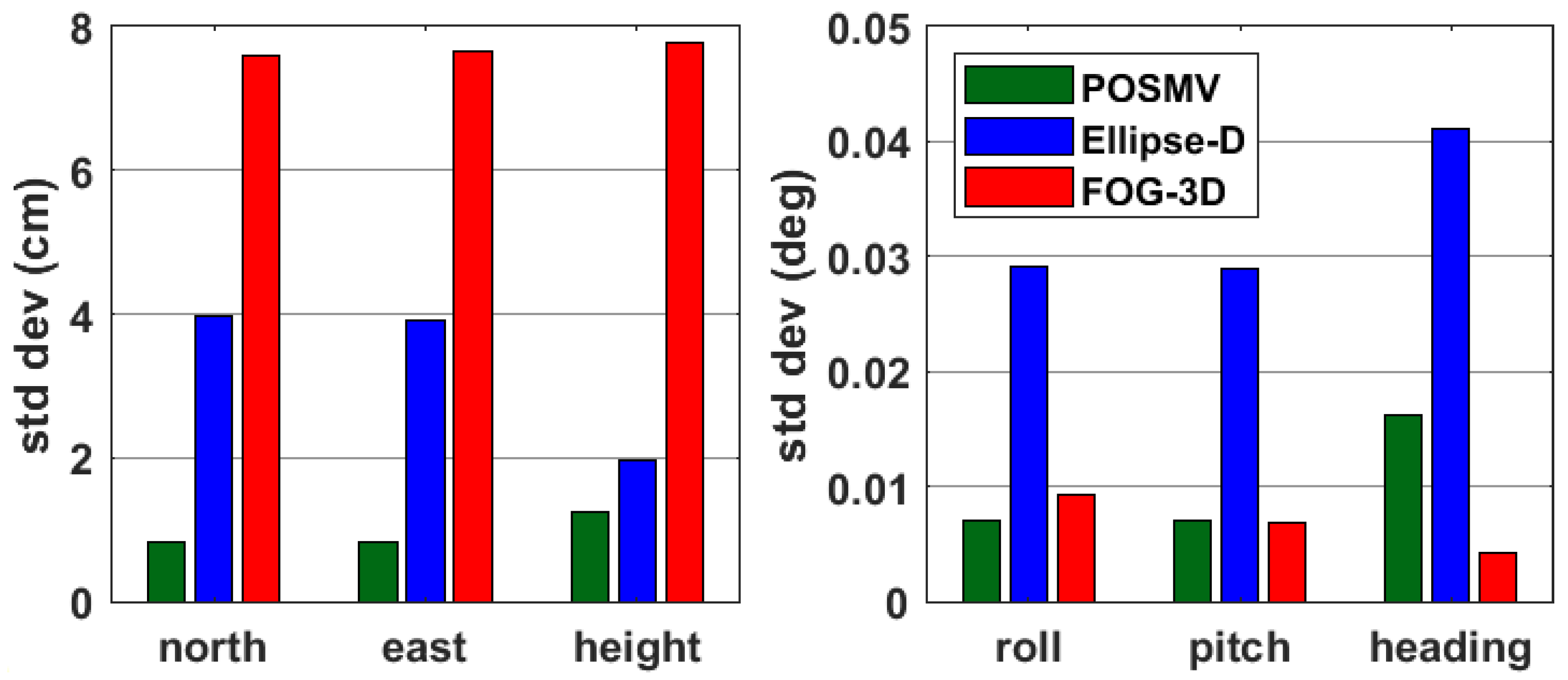
3.1. Formal Errors
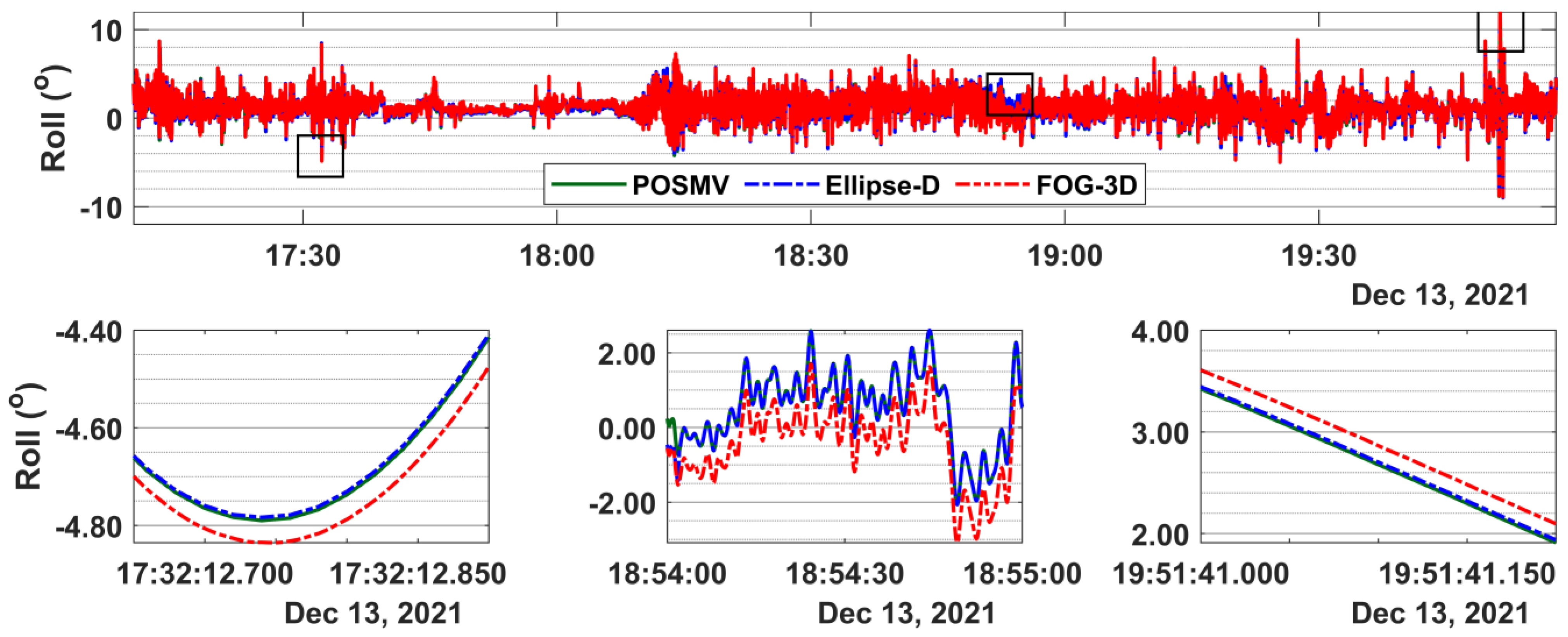
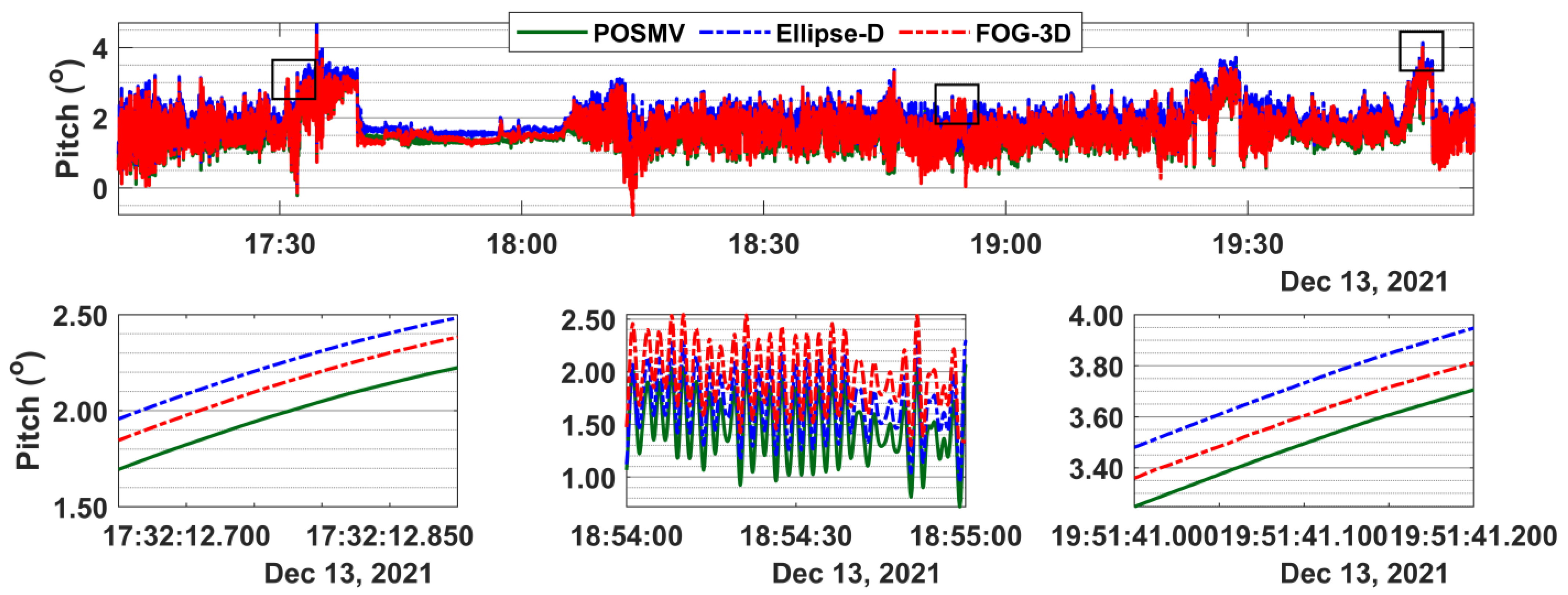
3.2. Attitude Results
3.3. Ellipsoidal Height Time Series
3.4. Boresight Calibration
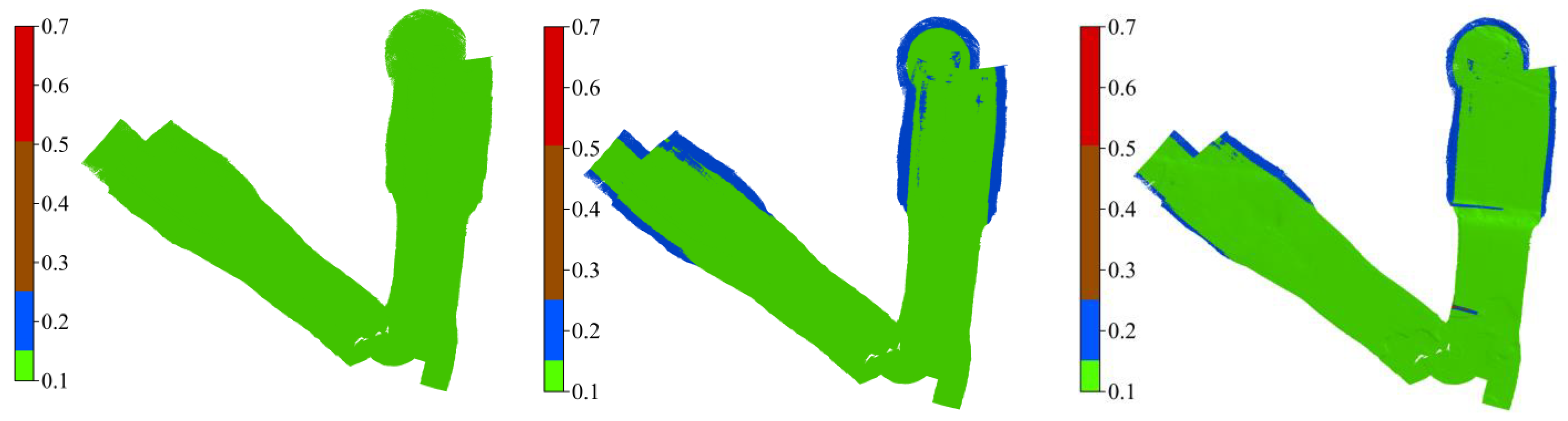
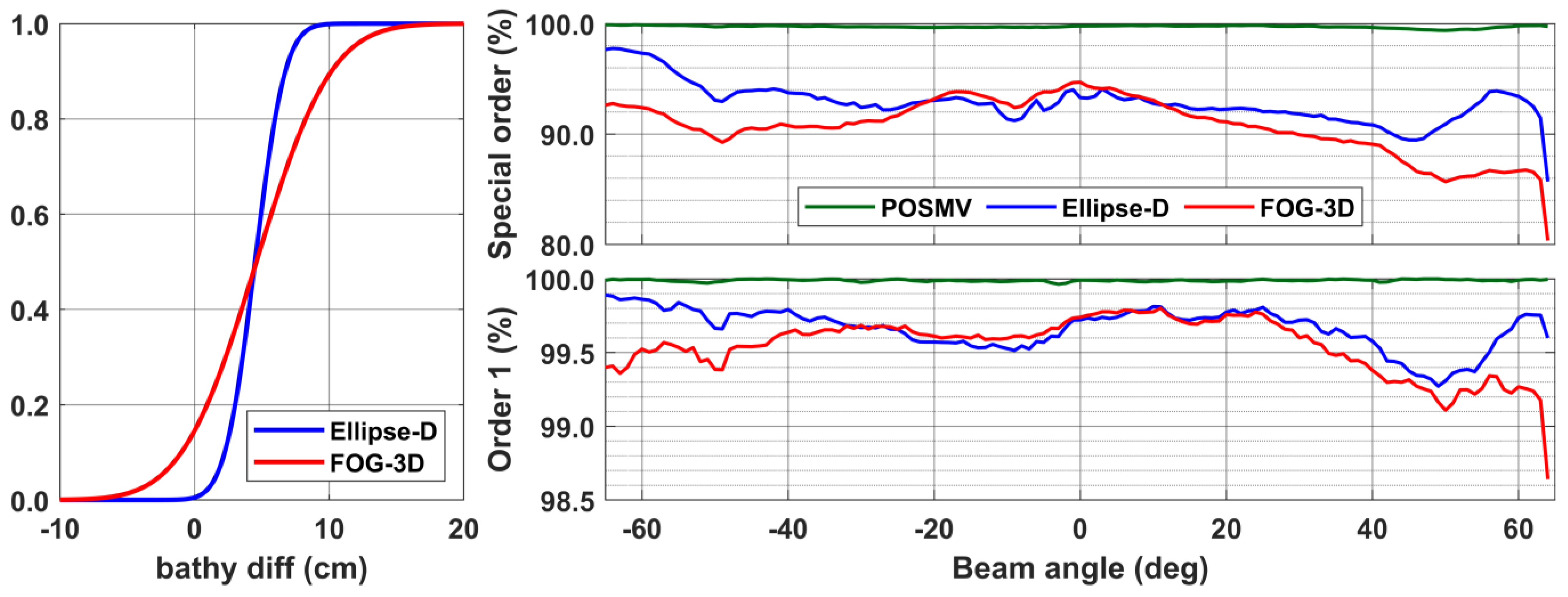
3.5. Bathymetry and Beams Uncertainty
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barbour, N.; Schmidt, G. Inertial sensor technology trends. IEEE Sens. J. 2001, 1, 332–339. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Vana, S.; Naciri, N.; Bisnath, S. Low-cost, dual-frequency PPP GNSS and MEMS-IMU integration performance in obstructed environments. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 3005–3018. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, T.; Lin, T.; Tang, H.; Niu, X. Implementation and performance of a deeply-coupled GNSS receiver with low-cost MEMS inertial sensors for vehicle urban navigation. Sensors 2020, 20, 3397. [Google Scholar] [CrossRef] [PubMed]
- Sirikonda, S.; Parayitam, L. Integration of low-cost IMU with MEMS and NAVIC/IRNSS receiver for land vehicle navigation. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021; pp. 2705–2717. [Google Scholar] [CrossRef]
- Deppe, O.; Dorner, G.; König, S.; Martin, T.; Voigt, S.; Zimmermann, S. MEMS and FOG technologies for tactical and navigation grade inertial sensors—Recent improvements and comparison. Sensors 2017, 17, 567. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of multi-GNSS PPP and MEMS inertial measurement unit data. GPS Solut. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J. GPS+BDS RTK: A low-cost single-frequency positioning approach. GPS World 2017, 50–54. Available online: https://www.researchgate.net/publication/320087686_GPSBDS_RTK_A_low-cost_single-frequency_positioning_approach (accessed on 5 October 2022).
- Odolinski, R.; Teunissen, P.J.G. Single-frequency, dual-GNSS versus dual-frequency, single-GNSS: A low-cost and high-grade receivers GPS-BDS RTK analysis. J. Geod. 2016, 90, 1255–1278. [Google Scholar] [CrossRef]
- Gao, W.; Meng, X.; Gao, C.; Pan, S.; Wang, D. Combined GPS and BDS for single-frequency continuous RTK positioning through real-time estimation of differential inter-system biases. GPS Solut. 2018, 22, 20. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Low-cost, high-precision, single-frequency GPS–BDS RTK positioning. GPS Solut. 2017, 21, 1315–1330. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined BDS, Galileo, QZSS and GPS single-frequency RTK. GPS Solut. 2015, 19, 151–163. [Google Scholar] [CrossRef]
- Cécile, D.; René, W. GPS+ Galileo single-frequency relative positioning with low-cost receivers. In Proceedings of the 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 3956–3966. [Google Scholar]
- Oguntuase, J.O.; Wells, D.; Bisnath, S. Vertical Accuracies of Mass-Market GNSS Receivers and Antennas in Ellipsoid Reference Survey Strategy for Marine Applications. In Proceedings of the Global Oceans 2020: Singapore—U.S. Gulf Coast, Biloxi, MS, USA, 5–30 October 2020. [Google Scholar] [CrossRef]
- Oguntuase, J.O. Cost-Effective GNSS Hardware for High-Accuracy Surveys and Its Prospects for Post-Processed Kinematic (PPK) and Precise Point Positioning (PPP) Strategies. Ph.D. Thesis, The University of Southern Mississippi, Hattiesburg, MS, USA, 2020. Available online: https://aquila.usm.edu/dissertations/1846 (accessed on 5 October 2022).
- Hare, R.; Godin, A.; Mayer, L. Accuracy Estimation of Canadian Swath and Sweep Sounding Systems; Canada Hydrographic Service: Ottawa, ON, Canada, 1995. [Google Scholar]
- Lurton, X. An Introduction to Underwater Acoustics. Principles and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 9783540784807. [Google Scholar]
- SBG Systems. Ellipse Series. Datasheet. 2016, pp. 1–9. Available online: http://www.sbg-systems.com/docs/Ellipse_Series_Leaflet.pdf (accessed on 8 November 2022).
- KVH. GEO-FOG 3D Dual INS. Available online: http://www.canalgeomatics.com/wp-content/uploads/2022/07/kvh-geo-fog-3d-dual-ins-datasheet.pdf (accessed on 8 November 2022).
- KVH. KVH GEO-FOG 3D Dual Reference Manual; KVH: Middletown, RL, USA, 2022; Available online: https://www.advancednavigation.com/wp-content/uploads/2021/08/Spatial-FOG-Dual-Reference-Manual.pdf (accessed on 17 October 2022).
- Applanix Corporation. POS AV V5 Installation and Operation Guide; Applanix Corporation: Richmond Hill, OT, Canada, 2022. [Google Scholar]
- Applanix Corporation. POS MV Datasheet; Applanix Corporation: Richmond Hill, OT, Canada, 2019. [Google Scholar]
- SBG Systems. Ellipse Series, High Performance, Miniature Inertial Sensors; SBG Systems: Carrières-sur-Seine, France, 2020. [Google Scholar]
- Mills, J.; Dodd, D. Ellipsoidally Referenced Surveying for Hydrography; International Federation of Surveyors (FIG): Copenhagen, Denmark, 2014; ISBN 9788792853097. [Google Scholar]
- Dodd, D.; Mills, J. Ellipsoidally Referenced Surveys Separation Models. In Proceedings of the FIG Working Week 2012. Knowing to Manage the Territory, Protect the Environment, Evaluate the Cultural Heritage, Rome, Italy, 6–10 May 2012; pp. 1–20. [Google Scholar]
- Hutton, J.; Ip, A.; Bourke, T.; Scherzinger, B.; Gopaul, N.; Canter, P.; Oveland, I.; Blankenberg, L. Tight Integration of GNSS Post-Processed Virtual Reference Station with Inertial Data for Increased Accuracy and Productivity of Airborne Mapping. 2008. Available online: https://isprs.org/proceedings/XXXVII/congress/5_pdf/146.pdf (accessed on 17 September 2022).
- Wanninger, L. The Performance of Virtual Reference Stations in Active Geodetic GPS-Networks under Solar Maximum Conditions. In Proceedings of the 12th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1999), Nashville, TN, USA, 14–17 September 1999; pp. 14–17. Available online: https://www.ion.org/publications/abstract.cfm?articleID=3291 (accessed on 21 September 2022).
- Vollath, U.; Buecherl, A.; Landau, H.; Pagels, C.; Wagner, B. Multi-Base RTK Positioning Using Virtual Reference Stations. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000; pp. 123–131. [Google Scholar]
- Vollath, U.; Landau, H.; Chen, X. Network RTK—Concept and Performance. In Proceedings of the GNSS Workshop-2002 International Symposium on GPS/GNSS, Wuhan, China, 6–8 November 2002; Available online: https://www.researchgate.net/publication/266041935_Network_RTK_-_Concept_and_Performance (accessed on 23 September 2022).
- Wanninger, L. Virtual reference stations (VRS). GPS Solut. 2003, 7, 143–144. [Google Scholar] [CrossRef]
- Landau, H.; Vollath, U.; Chen, X. Virtual Reference Station Systems. J. Glob. Position. Syst. 2010, 1, 137–143. [Google Scholar] [CrossRef] [Green Version]
- Calder, B.; Wells, D. CUBE User’s Manual. 2004, pp. 1–54. Available online: https://scholars.unh.edu/cgi/viewcontent.cgi?article=2217&context=ccom (accessed on 14 October 2022).
- Hiroji, A.; Oguntuase, J.O. Challenges and Possible Solutions with Multibeam Calibration Surveys in Very Shallow Waters. In Proceedings of the OCEANS 2021: San Diego—Porto, San Diego, CA, USA, 20–23 September 2021. [Google Scholar] [CrossRef]
- Keyetieu, R.; Seube, N.; Djine, V.; Roue, G.; Clement, B.; Bosser, P. Multi-Beam Echo Sounders–INS Automatic Latency Calibration. Mar. Geod. 2018, 41, 477–493. [Google Scholar] [CrossRef]
- Seube, N.; Keyetieu, R. Multibeam Echo Sounders-IMU Automatic Boresight Calibration on Natural Surfaces. Mar. Geod. 2017, 40, 172–186. [Google Scholar] [CrossRef]
- IHO. International Hydrographic Organization Standards for Hydrographic Surveys (S-44), 6th ed.; International Hydrographic Organization: Monte Carlo, Monaco, 2020. [Google Scholar]





| Manufacturer/GNSS + INS Brand | Grade | GNSS Model/ INS Data Rate | GNSS Antenna |
|---|---|---|---|
| Applanix/Wave Master II | Survey | */ 200 Hz | Zephyr Model 2 |
| SBG Systems/Ellipse-D (MEM-based accelerometers) | Tactical | Ublox ZED-F9P/ 50 Hz | Omnister G5Ant-53A4T1 |
| KVH/FOG 3D (MEMS-based accelerometers and FOG-based gyros) | Tactical | Trimble MB-Two/ 200 Hz | Omnister G5Ant-53A4T1 |
| Wave Master II | Ellipse-D | FOG-3D | ||
|---|---|---|---|---|
| Group Number (Rate = 200 Hz) | Binary Log | Rate (Hz) | Packet ID | Rate (Hz) |
| 1–5 | System status, UTC | 1 | 20 System state | 200 |
| 9–11 | EKF Euler | 50 | 28 Raw sensors | 200 |
| 99, 102 | EKF navigation | 50 | 29 Raw GNSS | 20 |
| 110–114 | Ship navigation | 50 | 60 Raw satellite data | 20 |
| 10,001, 10,007–10,009, 10,011–10,012 | IMU Short, GPS1 velocity, GPS1 position, GPS1 true heading GPS1 raw data | On new demand | ||
| Parameters | Wave Master II | Ellipse-D | FOG 3D | |
|---|---|---|---|---|
| Accelerometer * | Input rate (g) | * | * | 10 (max) |
| In-run bias instability (μg|mg) | * | 14|0.014 | <50|0.05 | |
| Random walk (μg/√Hz|mg/√Hz) | * | 57|0.057 | ≤120|0.12 | |
| Bandwidth (Hz) | * | 390 | ≥200 | |
| Gyroscope | Input rate (°/s) | * | * | 490 (max) |
| In-run bias instability (°/h) | * | 8 | 0.05 | |
| Random walk (°/h/√Hz) | * | * | 0.7 | |
| Bandwidth (Hz) | 200 | 133 | ≥440 | |
| Magnetometer | Range (G) | * | * | 8 |
| Bias instability (mG) | * | 1 | * | |
| Random walk (μG/√Hz|mg/√Hz) | * | * | 210|0.21 | |
| Bandwidth (Hz) | * | 22 | 110 | |
| Pressure | Range (KPa) | * | 0.05–0.35 | 10 to 120 |
| Bias instability (Pa/yr) | * | <100 | 100 | |
| Random walk (Pa/√Hz) | * | * | 0.56 | |
| Bandwidth (Hz) | * | 100 | 50 | |
| GNSS aiding | Heading accuracy (1-m baseline, °) | 0.015–0.03 | 0.4 | 0.01 |
| Velocity accuracy (m/s) | 0.05 | 0.05 | 0.005 | |
| Navigation | Roll and pitch accuracy (°) | 0.02–0.03 | <0.1 | 0.01 |
| Roll | Pitch | Heading | Elev | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | 95% | Mean | 95% | Mean | 95% | Mean | 95% | |
| POSMV/Ellipse-D | 0.005 | 0.012 | 0.233 | 0.247 | 0.694 | 0.430 | 0.048 | 0.082 |
| POSMV/FOG-3D | 0.194 | 0.505 | 0.094 | 0.234 | 0.087 | 0.159 | 0.046 | 0.084 |
| Exclusive | Special | Order-1 | |
|---|---|---|---|
| a | 0.15 | 0.25 | 0.5 |
| b | 0.0075 | 0.0075 | 0.013 |
| min depth (m) | 5 | 5 | 5 |
| max depth (m) | 11 | 11 | 11 |
| TVU (min {m}) | 0.15 | 0.25 | 0.50 |
| TVU (max {m}) | 0.17 | 0.26 | 0.52 |
| POSMV | Ellipse-D | FOG 3D | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Calibration (roll, pitch, heading {°}) | 0.564 ± 0.040 | −0.752 ± 0.210 | 0.356 ± 0.261 | 0.720 ± 0.044 | −0.869 ± 0.138 | 0.007 ± 0.251 | 0.634 ± 0.070 | −0.832 ± 0.487 | 0.860 ± 0.610 |
| Ellipsoidal heights with respect to POSMV | - | ±11 cm | ±10 cm | ||||||
| Bathymetry with respect to POSMV | - | ±14 cm | ±18 cm | ||||||
| Beams within 130-degree swaths passing IHO Special Order | 99.4–99.9% | 85.7–97.7% | 80.3–94.7% | ||||||
| Beams within 130-degree swaths passing IHO Order-1 | 99.6–100% | 99.3–99.9% | 98.6–99.8% | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oguntuase, J.O.; Hiroji, A.; Komolafe, P. How Good Is a Tactical-Grade GNSS + INS (MEMS and FOG) in a 20-m Bathymetric Survey? Sensors 2023, 23, 754. https://doi.org/10.3390/s23020754
Oguntuase JO, Hiroji A, Komolafe P. How Good Is a Tactical-Grade GNSS + INS (MEMS and FOG) in a 20-m Bathymetric Survey? Sensors. 2023; 23(2):754. https://doi.org/10.3390/s23020754
Chicago/Turabian StyleOguntuase, Johnson O., Anand Hiroji, and Peter Komolafe. 2023. "How Good Is a Tactical-Grade GNSS + INS (MEMS and FOG) in a 20-m Bathymetric Survey?" Sensors 23, no. 2: 754. https://doi.org/10.3390/s23020754





