Using DWS Optical Readout to Improve the Sensitivity of Torsion Pendulum
Abstract
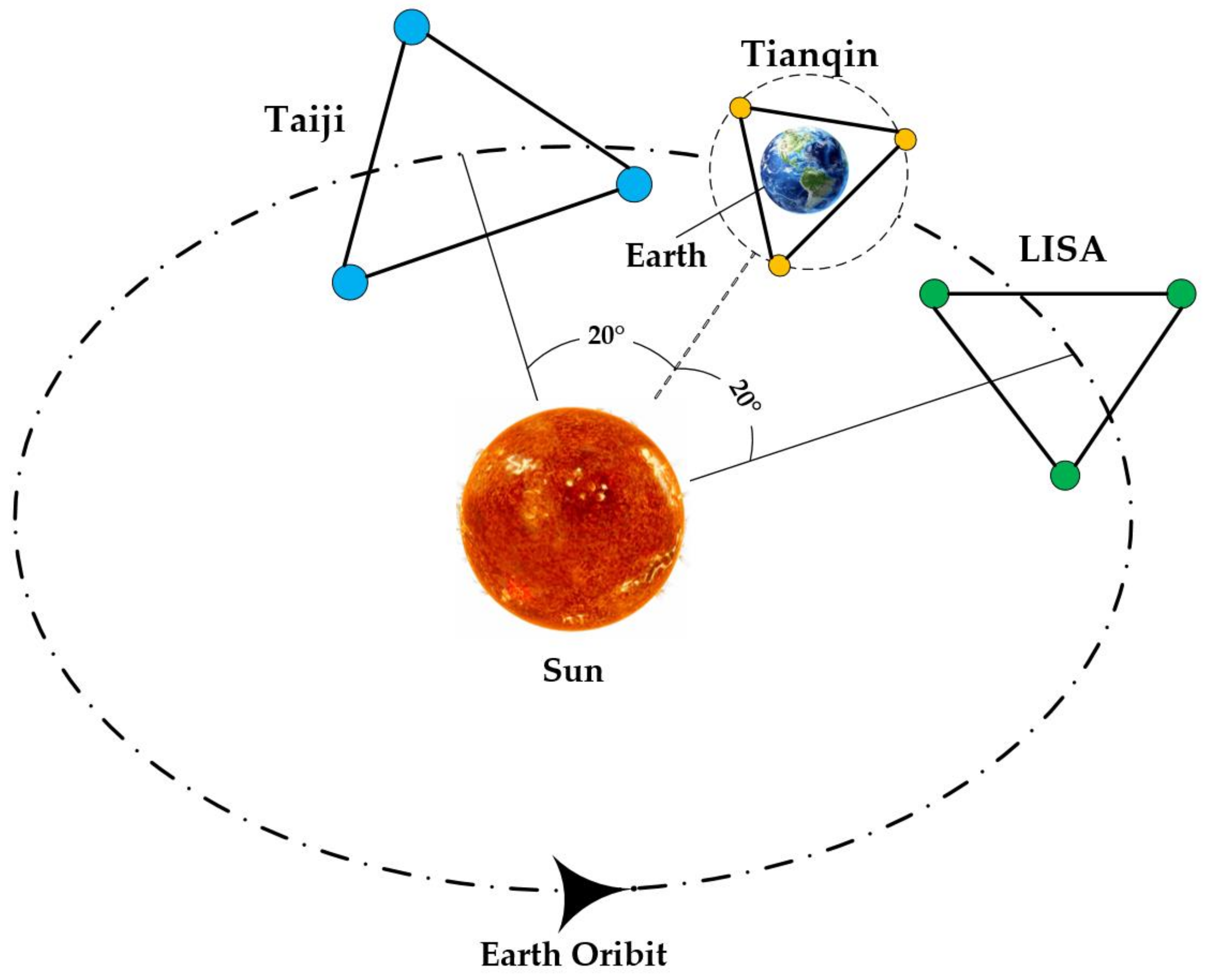
:1. Introduction
2. Torsion Pendulum Design
2.1. The Basic Principle of the Torsion Pendulum
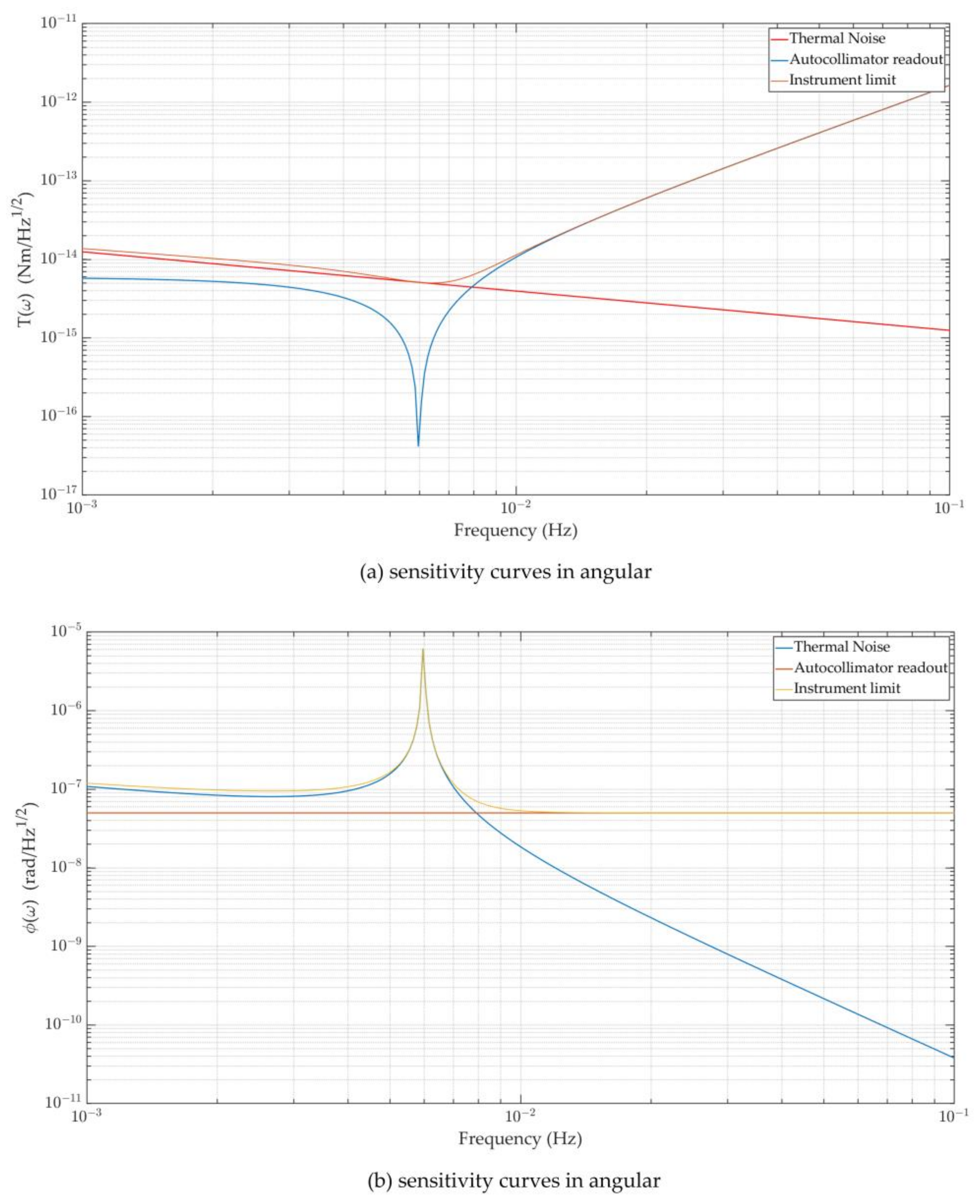
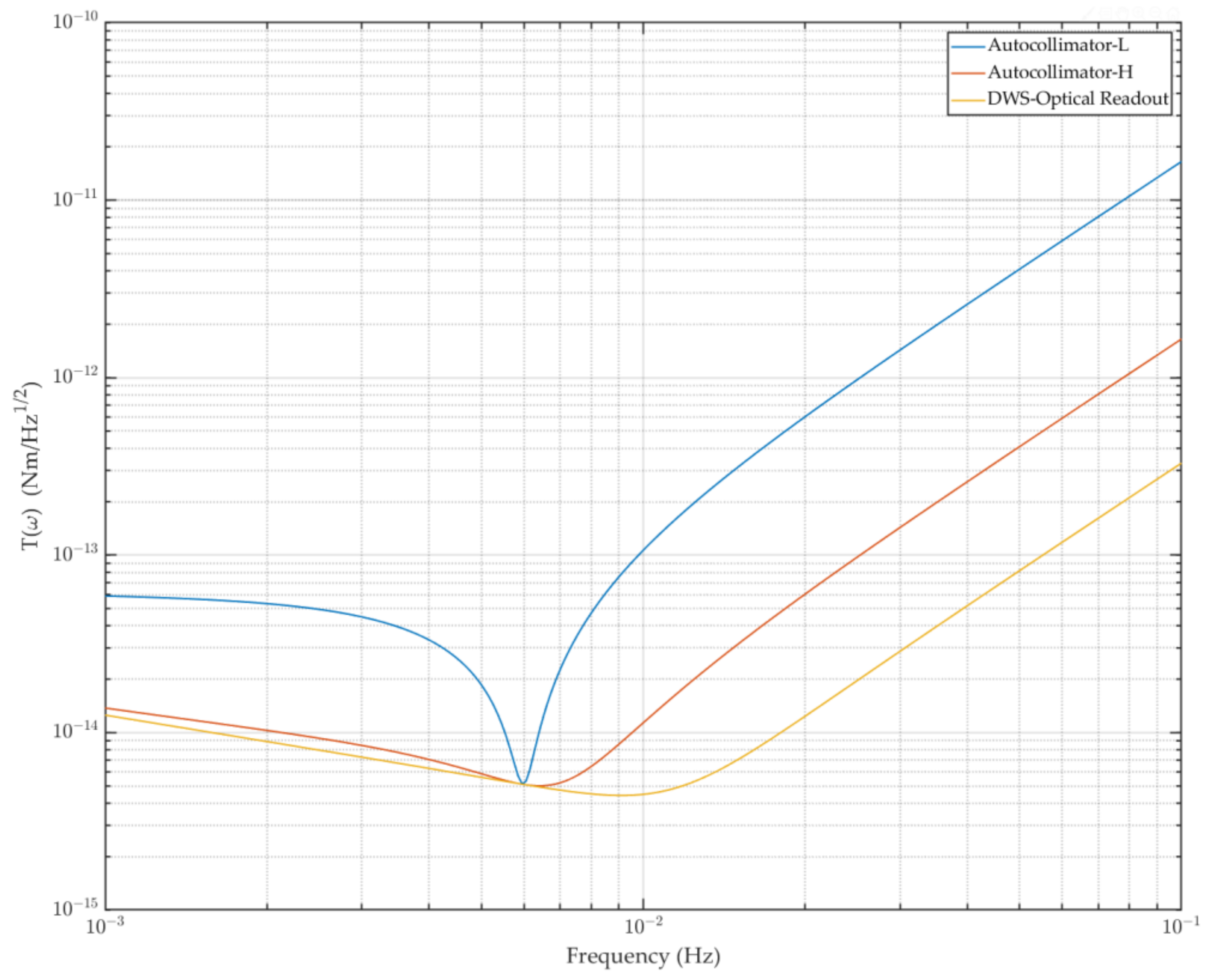
2.2. Initial Structural Design and Performance Evaluation
3. DWS Interferometer Optical Readout System
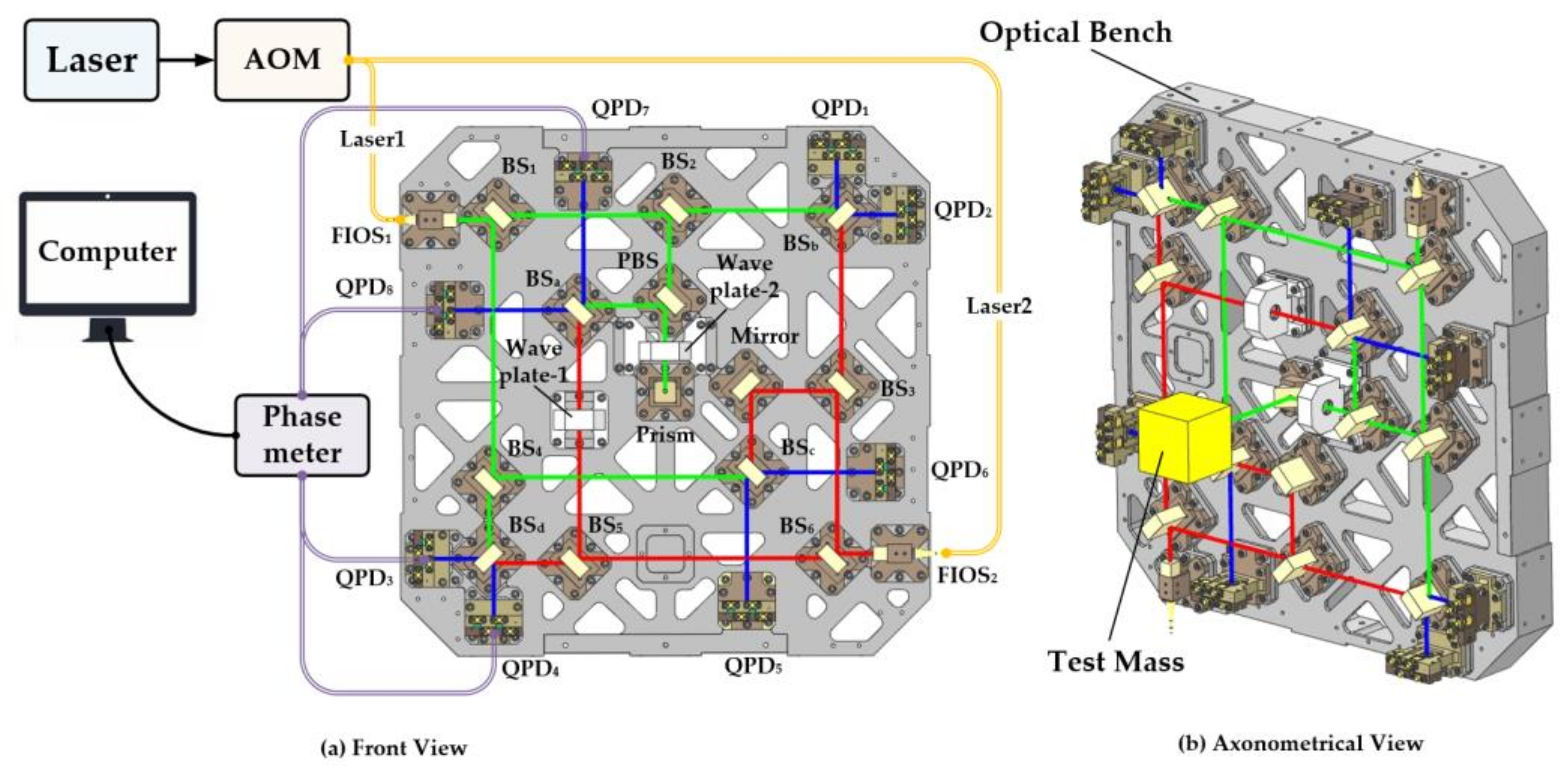
3.1. Design of the Interferometer
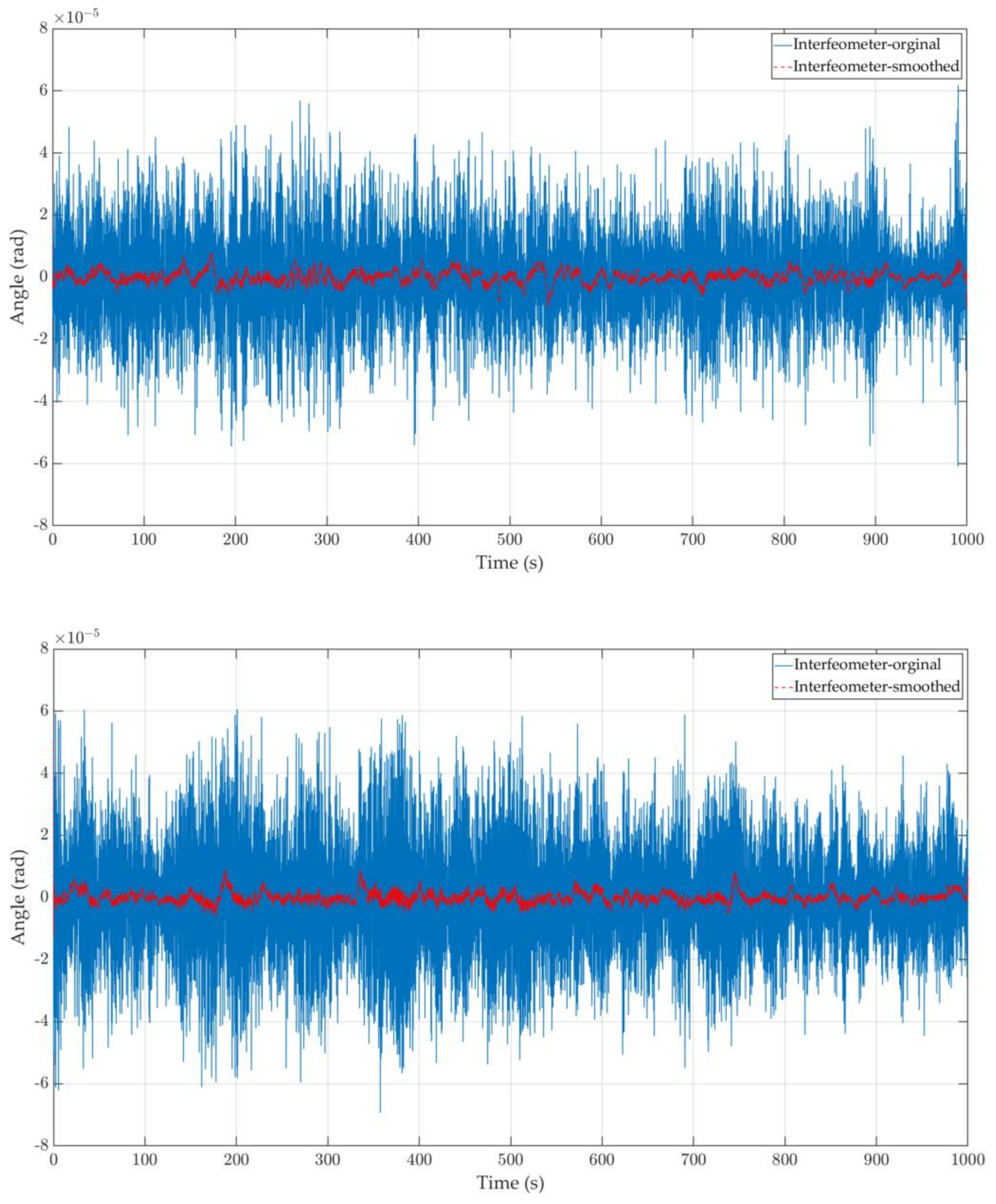
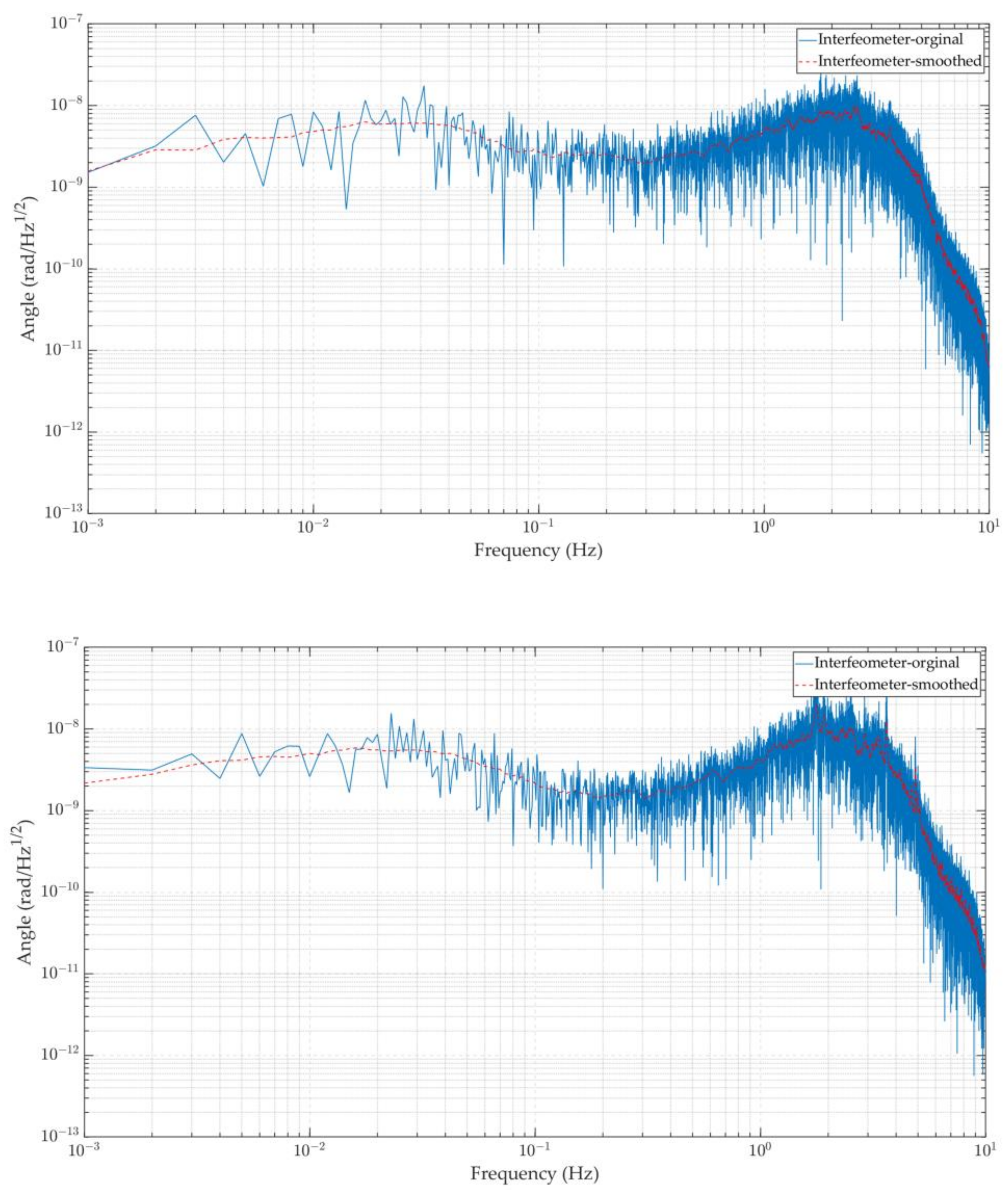
3.2. Resolution Test of the Laser Interferometer Measurement System
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW150914: The Advanced LIGO detectors in the era of first discoveries. Phys. Rev. Lett. 2016, 116, 131103. [Google Scholar] [CrossRef] [PubMed]
- Schutz, B.F. Gravitational wave astronomy. Class. Quantum Gravity 1999, 16, A131. [Google Scholar] [CrossRef]
- eLISA Consortium. The Gravitational Universe: A White Paper on the Gravitationnal Waves Detection and Characterization in Space Using Million Kilometers Laser Interferometry; ESA: Paris, Freance, 2013; Volume 2013.
- Joffre, E.; Wealthy, D.; Fernandez, I.; Trenkel, C.; Voigt, P.; Ziegler, T.; Martens, W. LISA: Heliocentric formation design for the laser interferometer space antenna mission. Adv. Space Res. 2021, 67, 3868–3879. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser interferometer space antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Danzmann, K. LISA: Laser Interferometer Space Antenna for Gravitational Wave Measurements; Blackwell Publishing Ltd.: Oxford, UK, 1995; Volume 759, pp. 481–484. [Google Scholar]
- Armano, M.; Audley, H.; Auger, G.; Baird, J.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Brandt, N.; Bursi, A.; Caleno, M.; et al. The LISA pathfinder mission. J. Phys. Conf. Ser. 2015, 610, 012005. [Google Scholar] [CrossRef]
- Armano, M.; Audley, H.; Auger, G.; Baird, J.T.; Bassan, M.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Brandt, N.; Caleno, M.; et al. Sub-femto-g free fall for space-based gravitational wave observatories: LISA pathfinder results. Phys. Rev. Lett. 2016, 116, 231101. [Google Scholar] [CrossRef]
- Armano, M.; Audley, H.; Baird, J.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Castelli, E.; Cavalleri, A.; Cesarini, A.; Cruise, A.M.; et al. Beyond the required lisa free-fall performance: New lisa pathfinder results down to 20 μHz. Phys. Rev. Lett. 2018, 120, 061101. [Google Scholar] [CrossRef]
- Wanner, G. Space-based gravitational wave detection and how LISA Pathfinder successfully paved the way. Nat. Phys. 2019, 15, 200–202. [Google Scholar] [CrossRef]
- Ni, W.T.; Shiomi, S.; Liao, A.C. ASTROD, ASTROD I and their gravitational-wave sensitivities. Class. Quantum Gravity 2004, 21, S641. [Google Scholar] [CrossRef]
- Ni, W.T. ASTROD-GW: Overview and progress. Int. J. Mod. Phys. D 2013, 22, 1341004. [Google Scholar] [CrossRef]
- Kawamura, S.; Nakamura, T.; Ando, M.; Seto, N.; Tsubono, K.; Numata, K.; Takahashi, R.; Nagano, S.; Ishikawa, T.; Musha, M.; et al. The Japanese space gravitational wave antenna—DECIGO. Class. Quantum Gravity 2006, 23, S125. [Google Scholar] [CrossRef]
- Musha, M. Space gravitational wave detector DECIGO/pre-DECIGO. In Proceedings of the International Conference on Space Optics—ICSO 2016, Biarritz, France, 18–21 October 2016; SPIE: Washington, DC, USA, 2017; Volume 10562, pp. 1119–1123. [Google Scholar]
- Crowder, J.; Cornish, N.J. Beyond LISA: Exploring future gravitational wave missions. Phys. Rev. D 2005, 72, 083005. [Google Scholar] [CrossRef]
- Harry, G.M.; Fritschel, P.; Shaddock, D.A.; Folkner, W.; Phinney, E.S. Laser interferometry for the big bang observer. Class. Quantum Gravity 2006, 23, 4887. [Google Scholar] [CrossRef]
- Hu, W.R.; Wu, Y.L. The Taiji Program in Space for gravitational wave physics and the nature of gravity. Natl. Sci. Rev. 2017, 4, 685–686. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.S.; Duan, H.Z.; Gong, Y.G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quantum Gravity 2016, 33, 035010. [Google Scholar] [CrossRef]
- Gong, Y.; Luo, J.; Wang, B. Concepts and status of Chinese space gravitational wave detection projects. Nat. Astron. 2021, 5, 881–889. [Google Scholar] [CrossRef]
- Jin, G. Program in space detection of gravitational wave in Chinese Academy of Sciences. J. Phys. Conf. Ser. 2017, 840, 012009. [Google Scholar] [CrossRef]
- Ruan, W.H.; Guo, Z.K.; Cai, R.G.; Zhang, Y.Z. Taiji program: Gravitational-wave sources. Int. J. Mod. Phys. A 2020, 35, 2050075. [Google Scholar] [CrossRef]
- Luo, Z.; Guo, Z.; Jin, G.; Wu, Y.; Hu, W. A brief analysis to Taiji: Science and technology. Results Phys. 2020, 16, 102918. [Google Scholar] [CrossRef]
- Wang, S.; Chen, L.; Wang, Y.; Zhou, Z.; Qi, K.; Wang, Z. A Space Inertial Sensor Ground Evaluation System for Non-Sensitive Axis Based on Torsion Pendulum. Appl. Sci. 2020, 10, 3090. [Google Scholar] [CrossRef]
- Liu, H.S.; Luo, Z.R.; Sha, W.; Taiji Scientific Collaboration. In-orbit performance of the laser interferometer of Taiji-1 experimental satellite. Int. J. Mod. Phys. A 2021, 36, 2140004. [Google Scholar] [CrossRef]
- He, J.W.; Duan, L.; Kang, Q.; Taiji Scientific Collaboration. Ground performance tests and evaluation of RF ion microthrusters for Taiji-1 satellite. Int. J. Mod. Phys. A 2021, 36, 2140014. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, Y.; Wu, Y.; Hu, W.; Jin, G. The Taiji program: A concise overview. Prog. Theor. Exp. Phys. 2021, 2021, 05A108. [Google Scholar] [CrossRef]
- Martínez, A.A. Replication of Coulomb’s torsion balance experiment. Arch. Hist. Exact Sci. 2006, 60, 517–563. [Google Scholar] [CrossRef]
- Clotfelter, B.E. The Cavendish experiment as Cavendish knew it. Am. J. Phys. 1987, 55, 210–213. [Google Scholar] [CrossRef]
- Andrews, J.J.; Bobowski, J.S. Automation of the Cavendish torsion-balance experiment to measure G. Eur. J. Phys. 2019, 40, 035001. [Google Scholar] [CrossRef]
- Szabó, Z. The history of the 125 year old Eötvös torsion balance. Acta Geod. Geophys. 2016, 51, 273–293. [Google Scholar] [CrossRef]
- Chen, S.J.; Pan, S.S. Nanonewton force generation and detection based on a sensitive torsion pendulum. IEEE Trans. Instrum. Meas. 2009, 58, 897–901. [Google Scholar] [CrossRef]
- Willemenot, E.; Touboul, P. On-ground investigation of space accelerometers noise with an electrostatic torsion pendulum. Rev. Sci. Instrum. 2000, 71, 302–309. [Google Scholar] [CrossRef]
- Cavalleri, A.; Ciani, G.; Dolesi, R.; Heptonstall, A.; Hueller, M.; Nicolodi, D.; Rowan, S.; Tombolato, D.; Vitale, S.; Wass, P.J.; et al. A new torsion pendulum for testing the limits of free-fall for LISA test masses. Class. Quantum Gravity 2009, 26, 094017. [Google Scholar] [CrossRef]
- Bassan, M.; Cavalleri, A.; De Laurentis, M.; De Marchi, F.; De Rosa, R.; Di Fiore, L.; Dolesi, R.; Finetti, N.; Garufi, F.; Grado, A.; et al. Actuation crosstalk in free-falling systems: Torsion pendulum results for the engineering model of the LISA pathfinder gravitational reference sensor. Astropart. Phys. 2018, 97, 19–26. [Google Scholar] [CrossRef]
- Russano, G.; Cavalleri, A.; Cesarini, A.; Dolesi, R.; Ferroni, V.; Gibert, F.; Giusteri, R.; Hueller, M.; Liu, L.; Pivato, P.; et al. Measuring fN force variations in the presence of constant nN forces: A torsion pendulum ground test of the LISA Pathfinder free-fall mode. Class. Quantum Gravity 2017, 35, 035017. [Google Scholar] [CrossRef]
- Yang, F.; Bai, Y.; Hong, W.; Li, H.; Liu, L.; Sumner, T.J.; Yang, Q.; Zhao, Y.; Zhou, Z. Investigation of charge management using UV LED device with a torsion pendulum for TianQin. Class. Quantum Gravity 2020, 37, 115005. [Google Scholar] [CrossRef]
- Bai, Y.; Li, Z.; Hu, M.; Liu, L.; Qu, S.; Tan, D.; Tu, H.; Wu, S.; Yin, H.; Li, H.; et al. Research and Development of Electrostatic Accelerometers for Space Science Missions at HUST. Sensors 2017, 17, 1943. [Google Scholar] [CrossRef] [PubMed]
- Apple, S.M.; Chilton, A.; Olatunde, T.; Bickerstaff, B.; Hillsberry, D.; Parry, S.; Ciani, G.; Mueller, G.; Conklin, J. University of Florida Torsion Pendulum for Testing Key LISA Technology. In Proceedings of the AIAA SPACE and Astronautics Forum and Exposition, Orlando, FL, USA, 12–14 September 2017; p. 5138. [Google Scholar]
- Chilton, A.; Shelley, R.; Olatunde, T.; Ciani, G.; Conklin, J.W.; Mueller, G. The UF Torsion Pendulum, a LISA Technology Testbed: Sensing System and Initial Results. J. Phys. Conf. Ser. 2015, 610, 012038. [Google Scholar] [CrossRef]
- Pollack, S.E.; Schlamminger, S.; Gundlach, J.H. Outgassing, temperature gradients and the radiometer effect in LISA: A torsion pendulum investigation. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2006; Volume 873, pp. 158–164. [Google Scholar]
- Hueller, M.; Armano, M.; Carbone, L.; Cavalleri, A.; Dolesi, R.; Hoyle, C.D.; Vitale, S.; Weber, W.J. Measuring the LISA test mass magnetic properties with a torsion pendulum. Class. Quantum Gravity 2005, 22, S521. [Google Scholar] [CrossRef]
- González, G.I.; Saulson, P.R. Brownian motion of a torsion pendulum with internal friction. Phys. Lett. A 1995, 201, 12–18. [Google Scholar] [CrossRef]
- Ikram, M.; Hussain, G. Michelson interferometer for precision angle measurement. Appl. Opt. 1999, 38, 113–120. [Google Scholar] [CrossRef]
- Audley, H.; Danzmann, K.; Marín, A.G.; Heinzel, G.; Monsky, A.; Nofrarias, M.; Steier, F.; Gerardi, D.; Gerndt, R.; Hechenblaikner, G.; et al. The LISA Pathfinder interferometry—Hardware and system testing. Class. Quantum Gravity 2011, 28, 094003. [Google Scholar] [CrossRef]
- Liu, H.; Luo, Z.; Jin, G. The development of phasemeter for Taiji space gravitational wave detection. Microgravity Sci. Technol. 2018, 30, 775–781. [Google Scholar] [CrossRef]
- Sha, W.; Fang, C.; Niu, Y.; Taiji Scientific Collaboration. Successful application of optical bench in Taiji-1 laser interferometer. Int. J. Mod. Phys. A 2021, 36, 2140001. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.; Zhao, Y.; Sha, W.; Wang, Z.; Luo, Z.; Jin, G. Demonstration of an ultraprecise optical bench for the Taiji space gravitational wave detection pathfinder mission. Appl. Sci. 2019, 9, 2087. [Google Scholar] [CrossRef]
- Taiji Scientific Collaboration; Wu, Y.-L.; Luo, Z.-R.; Wang, J.-Y.; Bai, M.; Bian, W.; Cai, H.-W.; Cai, R.-G.; Cai, Z.-M.; Cao, J.; et al. Taiji program in space for gravitational universe with the first run key technologies test in Taiji-1. Int. J. Mod. Phys. A 2021, 36, 2102002. [Google Scholar]





| Parameters | Symbol | Values | Units | |
|---|---|---|---|---|
| Test mass | Length of sides | d | 46 | mm |
| Mass | mtotal | 0.238 | kg | |
| Tungsten wire | Length | L | 0.841 | m |
| Shear elasticity | G | 161 | GPa | |
| Radius | r | 25 | μm | |
| Quality factor | Q | 2000 | / | |
| Environment conditions | Gravitational acceleration | g | 9.801 | m/s2 |
| Temperature | T | 300 | K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Liu, H.; Dai, L.; Luo, Z.; Xu, P.; Li, P.; Gao, R.; Li, D.; Qi, K. Using DWS Optical Readout to Improve the Sensitivity of Torsion Pendulum. Sensors 2023, 23, 8087. https://doi.org/10.3390/s23198087
Wang S, Liu H, Dai L, Luo Z, Xu P, Li P, Gao R, Li D, Qi K. Using DWS Optical Readout to Improve the Sensitivity of Torsion Pendulum. Sensors. 2023; 23(19):8087. https://doi.org/10.3390/s23198087
Chicago/Turabian StyleWang, Shaoxin, Heshan Liu, Lei Dai, Ziren Luo, Peng Xu, Pan Li, Ruihong Gao, Dayu Li, and Keqi Qi. 2023. "Using DWS Optical Readout to Improve the Sensitivity of Torsion Pendulum" Sensors 23, no. 19: 8087. https://doi.org/10.3390/s23198087





