Miniaturization and Model-Integration of the Optical Measurement System for Temperature-Sensitive Paint Investigations
Abstract
:1. Introduction
2. Methods
2.1. 1-m Wind Tunnel Göttingen
2.2. SPECTRA-A Configuration
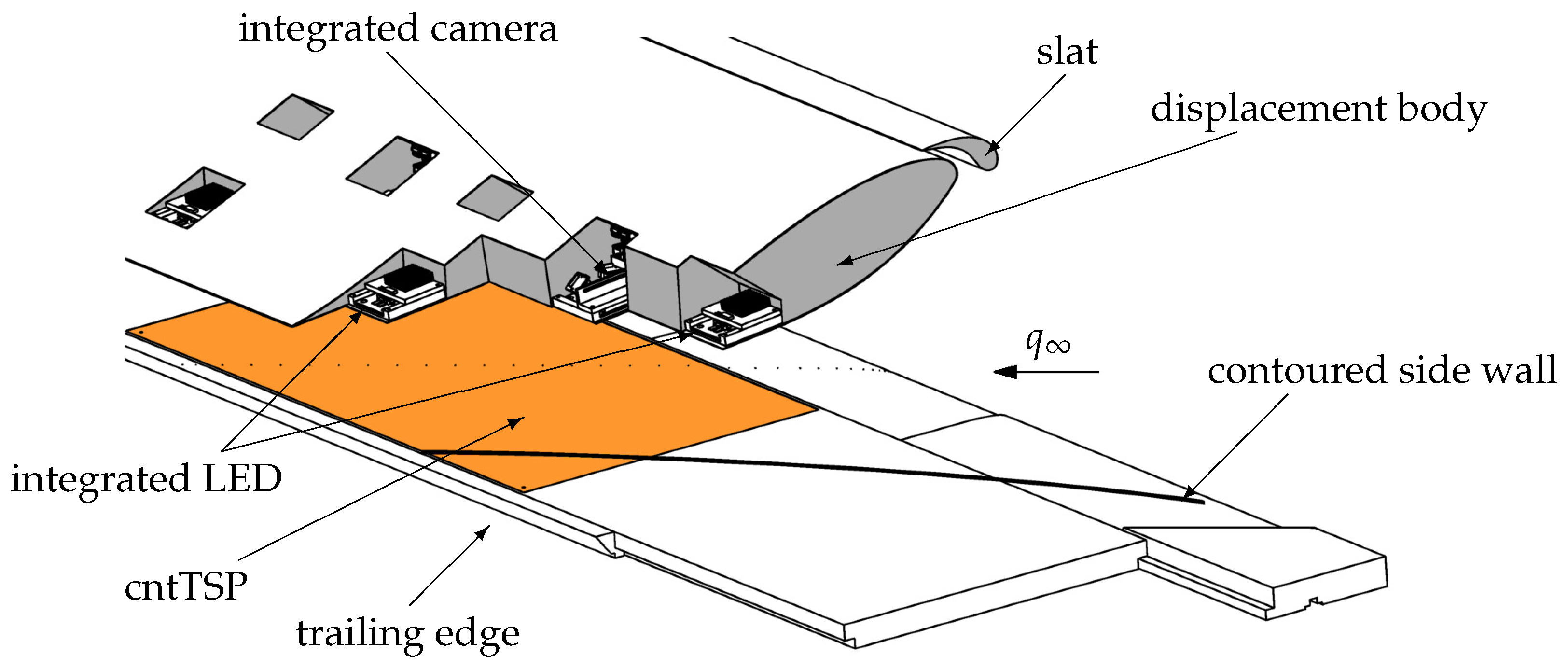
Model Integration of the TSP Measurement System
2.3. TSP Method
Evaluation
3. Qualification of the Miniaturized Camera for TSP Acquisition
3.1. Linearity
3.2. Flat Field
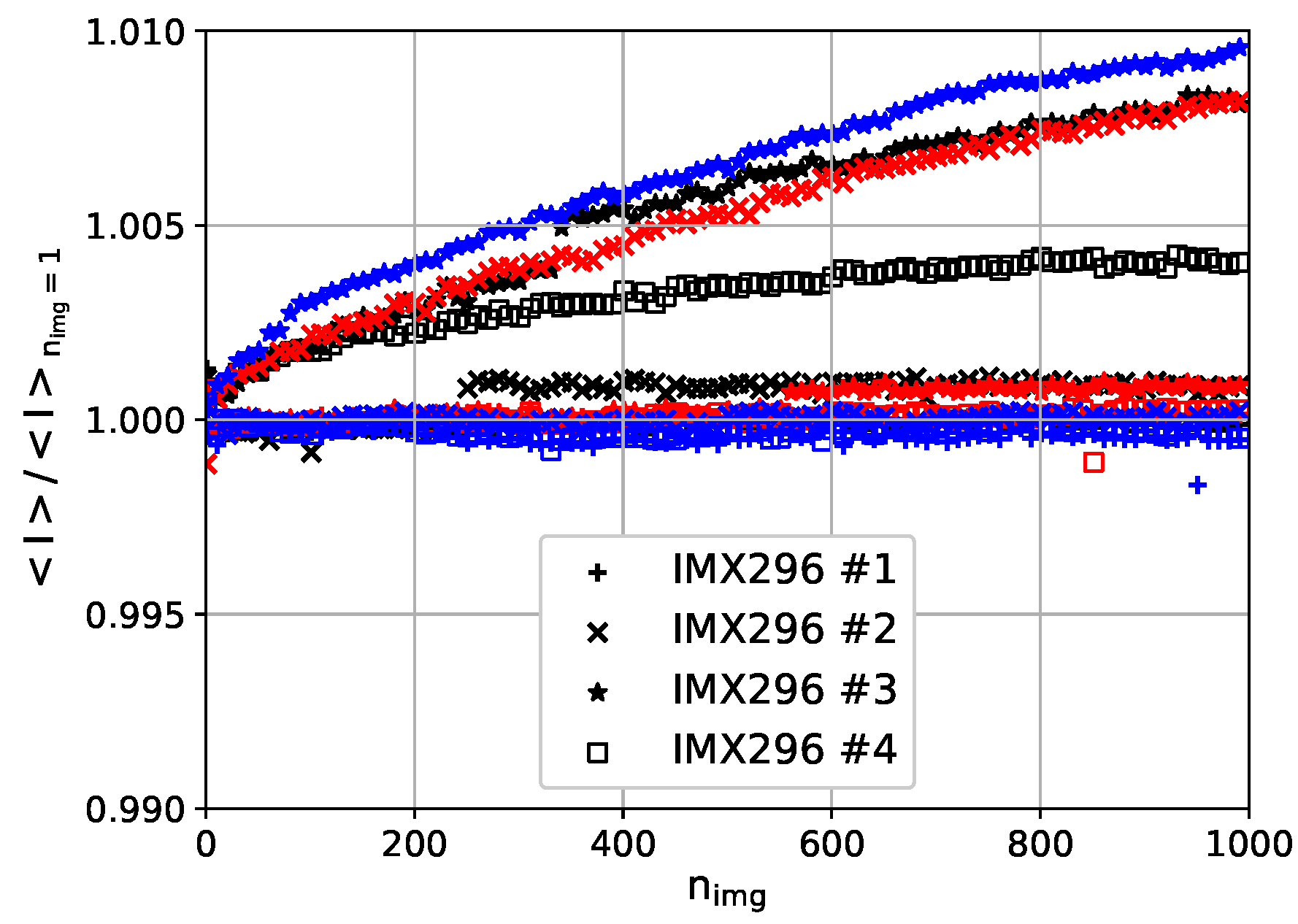
3.3. Temporal Signal Drift
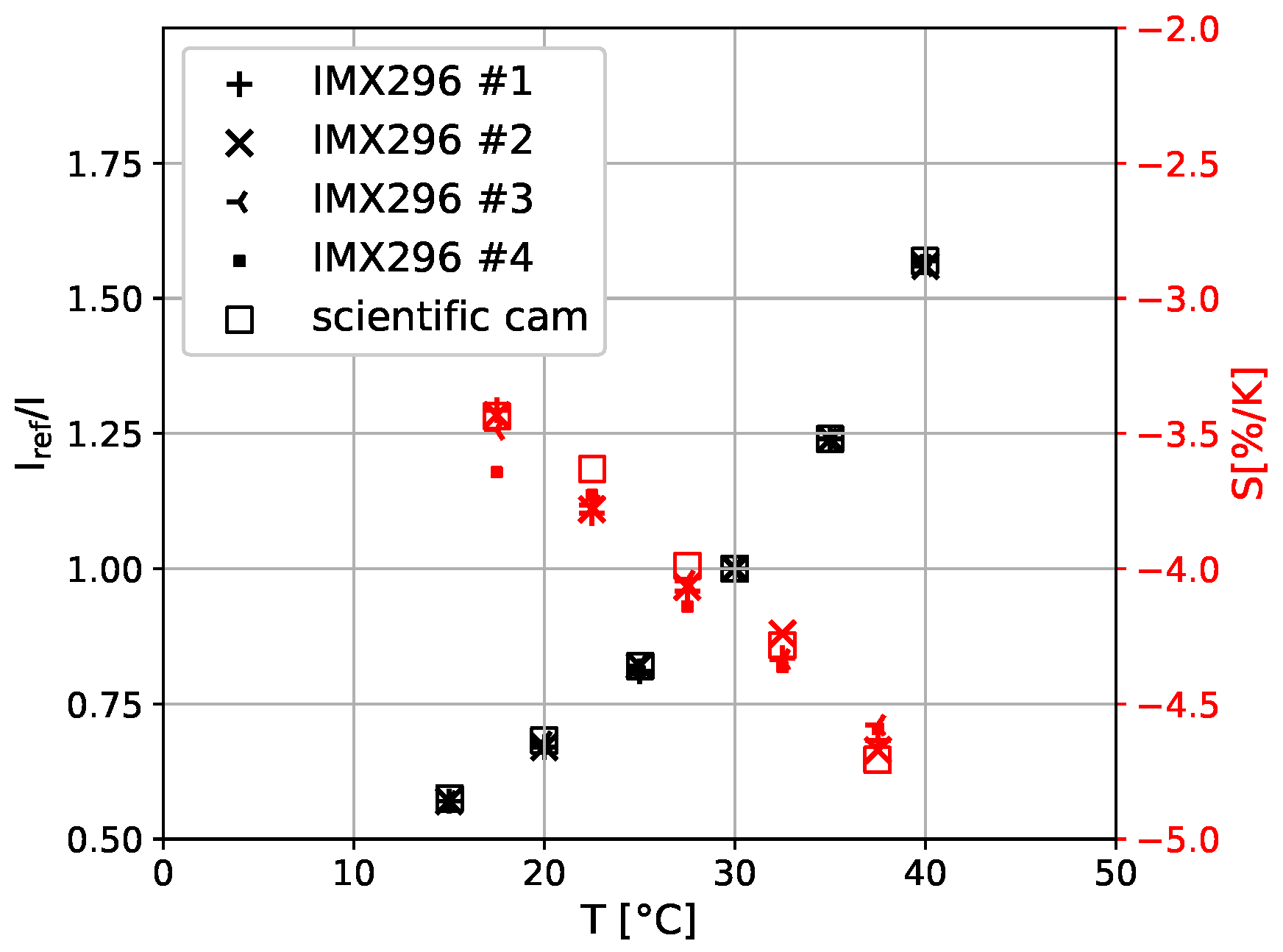
3.4. TSP Calibration
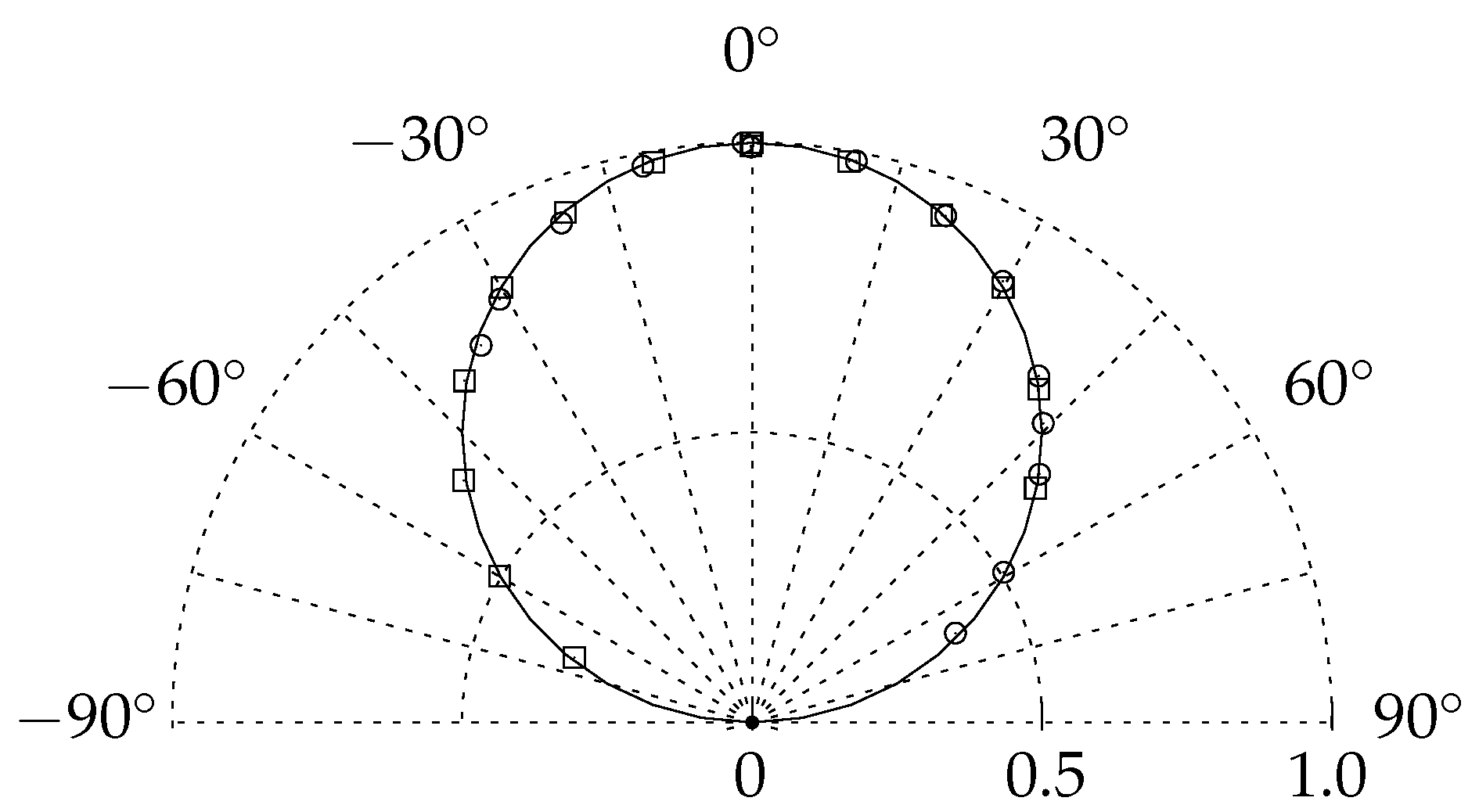
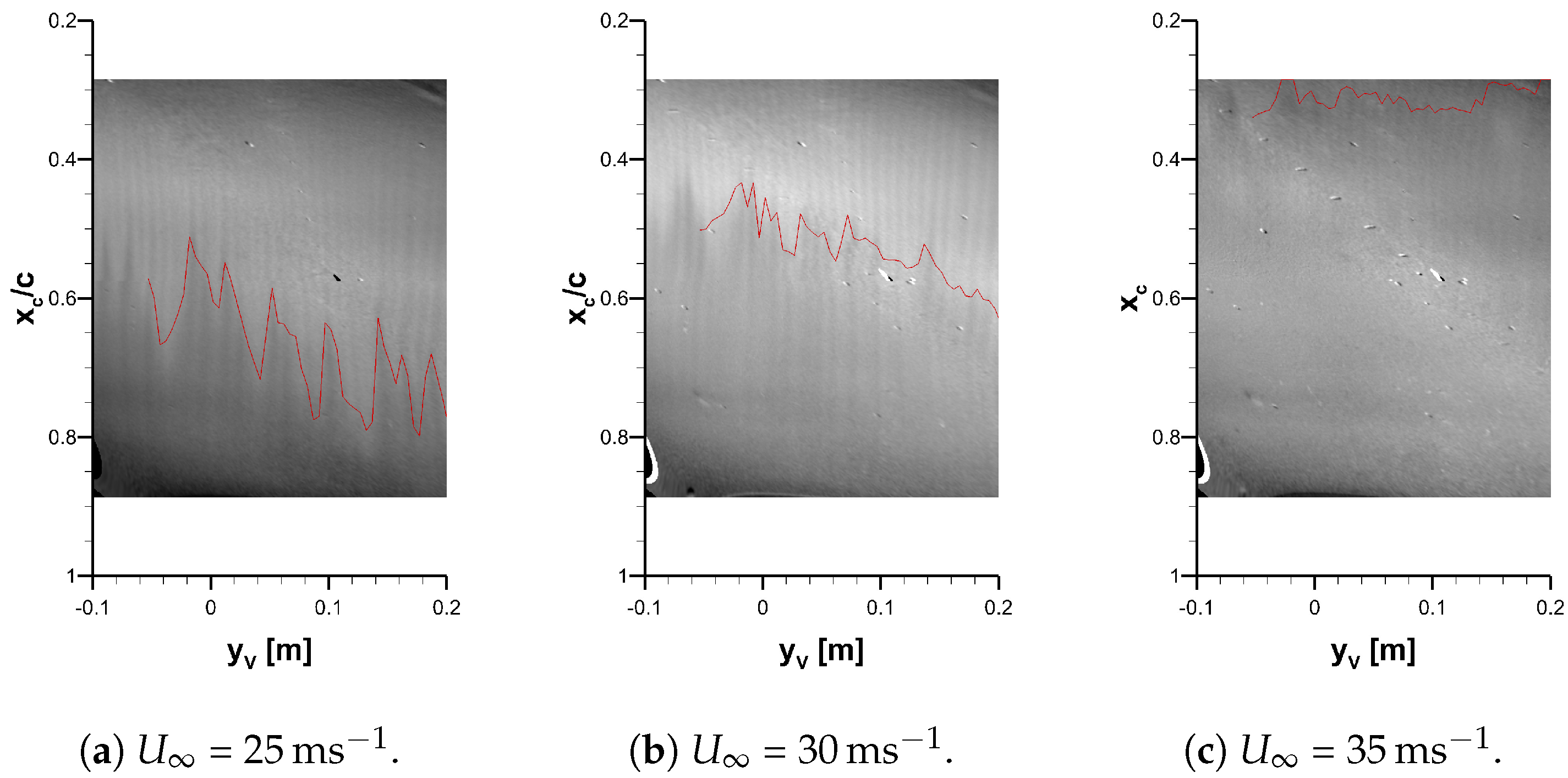
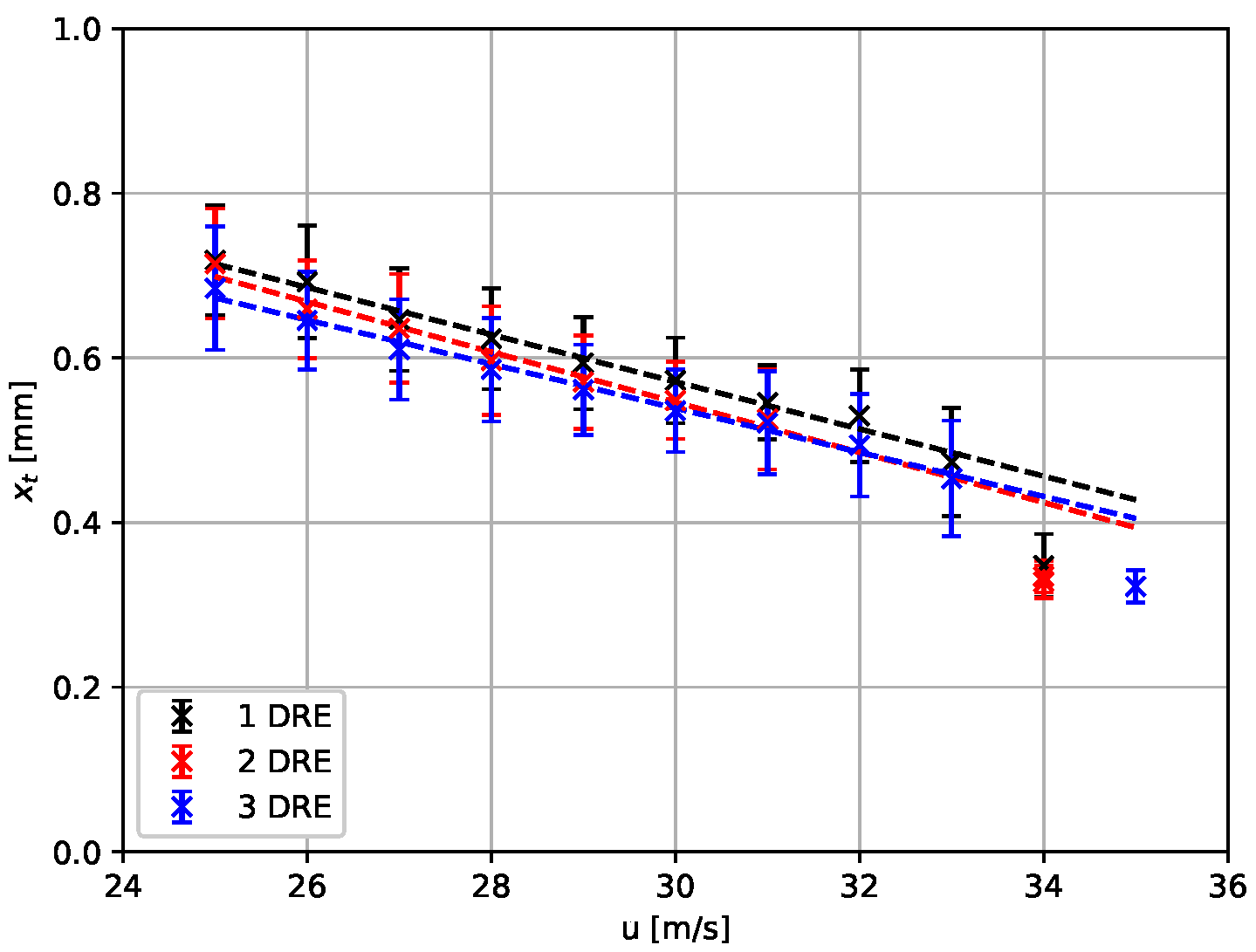
4. Visualization of Laminar–Turbulent Transition
5. Discussion
6. Conclusions
- Laboratory investigations revealed that the camera offers commendable linearity and a tolerable temporal drift. However, unpredictable fluctuations in the intensity signal and inconsistent behaviors across different cameras and measurements were observed.
- The integration of the cameras and LEDs into the SPECTRA-A configuration could be achieved easily due to the small dimensions.
- The achieved TSP visualization quality is good because small changes of the transition location and differences in the footprints of cross-flow vortices are resolved.
- The low price of under EUR 1000 for each camera, including all accessories, provides an inexpensive optical acquisition system for TSP measurements, thereby reducing the initial system costs for new groups of TSP-users.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, T.; Campbell, B.; Sullivan, J. Accuracy of Temperature-Sensitive Fluorescent Paint for Heat Transfer Measurements. In Proceedings of the 30th AIAA Thermophysics Conference, San Diego, CA, USA, 19–22 June 1995. [Google Scholar] [CrossRef]
- Cattafesta, L.; Liu, T.; Sullivan, J. Uncertainty Estimates for Temperature-Sensitive Paint Measurements with Charge-Coupled Device Cameras. AIAA J. 1998, 36, 2102–2108. [Google Scholar] [CrossRef]
- Nakakita, K.; Osafune, T.; Asai, K. Global heat transfer measurement in a hypersonic shock tunnel using temperature sensitive paint. In Proceedings of the 41’st AIAA Aerospace Sciences Meeting, Reno, NV, USA, 6–9 January 2003. AIAA 2003-0743. [Google Scholar] [CrossRef]
- Ozawa, H.; Laurence, S.; Martinez Schramm, J.; Wagner, A.; Hannemann, K. Fast-response temperature-sensitive-paint measurements on a hypersonic transition cone. Exp. Fluids 2014, 56, 1853. [Google Scholar] [CrossRef]
- Liu, T. Global skin friction measurements and interpretation. Prog. Aerosp. Sci. 2019, 111, 100584. [Google Scholar] [CrossRef]
- Fey, U.; Egami, Y. Transition-Detection by Temperature-Sensitive Paint. In Springer Handbook of Experimental Fluid Mechanics; Tropea, C., Yarin, A., Foss, J., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007; pp. 537–552. [Google Scholar]
- Liu, T.; Sullivan, J.P.; Asai, K.; Klein, C.; Egami, Y. Pressure And Temperature Sensitive Paints; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Costantini, M. Experimental Analysis of Geometric, Pressure Gradient and Surface Temperature Effects on Boundary-Layer Transition in Compressible High Reynolds Number Flows. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 2016. [Google Scholar]
- Fey, U.; Egami, Y.; Engler, R. High Reynolds Number Transition Detection by Means of Temperature Sensitive Paint. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar] [CrossRef]
- Barth, H.P.; Hein, S. Experimental Investigation of Spanwise-Periodic Surface Heating for Control of Crossflow-Dominated Laminar-Turbulent Transition. In IUTAM Laminar-Turbulent Transition, Proceedings of the 9th IUTAM Symposium, London, UK, 2–6 September 2019; Springer International Publishing: Cham, Switzerland, 2021; pp. 267–278. [Google Scholar] [CrossRef]
- Krueger, W.; Boden, F.; Kirmse, T.; Lemarechal, J.; Schroeder, A.; Barth, H.P.; Oertwig, S.; Siller, H.; Delfs, J.; Moreau, A.; et al. Common numerical methods & common experimental means for the demonstrators of the large passenger aircraft platforms. In Proceedings of the Aerospace Europe Conference, Aerospace Europe Conference 2020, Bordeaux, France, 25–28 February 2020. [Google Scholar]
- Saric, W.; Reed, H.; White, E. Stability and Transition of Three-Dimensional Boundary Layers. Annu. Rev. Fluid Mech. 2003, 35, 413–440. [Google Scholar] [CrossRef] [Green Version]
- Nitschke-Kowsky, P.; Bippes, H. Instability and transition of a three-dimensional boundary layer on a swept flat plate. Phys. Fluids 1988, 31, 786–795. [Google Scholar] [CrossRef]
- Müller, B.; Bippes, H. Experimental Study of Instability Modes in a Three-Dimensional Boundary Layer. In Proceedings of the Fluid Dynamics of Three-Dimensional Turbulent Shear Flows and Transition, Cesme, Turkey, 3–6 October 1988. AGARD CONFERENCE PROCEEDINGS No. 438. [Google Scholar]
- Deyhle, H.; Bippes, H. Disturbance growth in an unstable three-dimensional boundary layer and its dependence on environmental conditions. J. Fluid Mech. 1996, 316, 73–113. [Google Scholar] [CrossRef]
- Lerche, T. Experimental investigation of nonlinear wave interactions and secondary instability in three-dimensional boundary-layer flow. In Proceedings of the Advances in Turbulence IV, 6th European Turbulence Conf, Lausanne, Switzerland, 2–5 July 1996; Kluwer Academic: Dordrecht, The Netherlands, 1996; pp. 357–360. [Google Scholar]
- Bippes, H. Basic experiments on transition in three-dimensional boundary layers dominated by crossflow instability. Prog. Aerosp. Sci. 1999, 35, 363–412. [Google Scholar] [CrossRef]
- Perraud, J.; Séraudie, A. Effects of steps and gaps on 2D and 3D transition In Proceedings of the ECCOMAS 2000, Barcelona, Spain, 11–14 September 2000.
- Duncan, G.; Crawford, B.; Tufts, M.; Saric, W.; Reed, H. Effects of Step Excrescences on Swept-Wing Transition. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013; AIAA 2013-2412. [Google Scholar] [CrossRef]
- Eppink, J.; Wlezien, R.; King, R.; Choudhari, M. The Interaction of a Backward-Facing Step and Crossflow Instabilities in Boundary-Layer Transition. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; AIAA 2015-0273. [Google Scholar] [CrossRef]
- Rius-Vidales, A.F.; Kotsonis, M. Unsteady interaction of crossflow instability with a forward-facing step. J. Fluid Mech. 2022, 939, 32. [Google Scholar] [CrossRef]
- Quinn, M.K.; Spinosa, E.; Roberts, D.A. Miniaturisation of Pressure-Sensitive Paint Measurement Systems Using Low-Cost, Miniaturised Machine Vision Cameras. Sensors 2017, 17, 1708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brinkema, R. Experimentelle und Numerische Untersuchung der Strömungsbedingungen in Einem Windkanal. Master’s Thesis, RWTH Aachen, Aachen, Germany, 2015. [Google Scholar]
- Barth, H.P. Beeinflussung des Laminar-Turbulenten Grenzschichtumschlags Durch Kontrollierte Anregung stationäRer Querströmungsinstabilitäten. Ph.D. Thesis, Georg-August-Universität Göttingen, Göttingen, Germany, 2021. [Google Scholar]
- Wassermann, P.; Kloker, M. Mechanisms and passive control of crossflow-vortex-induced transition in a three-dimensional boundary layer. J. Fluid Mech. 2002, 456, 49–84. [Google Scholar] [CrossRef] [Green Version]
- Radetzsky, R.; Reibert, M.; Saric, W. Effect of isolated micron-sized roughness on transition in swept-wing flows. AIAA J. 1999, 37, 1370–1377. [Google Scholar] [CrossRef] [Green Version]
- Kurz, H.; Kloker, M. Receptivity of a sept-wing boundary layer to micron-sized discrete roughness elements. J. Fluid Mech. 2014, 755, 62–82. [Google Scholar] [CrossRef]
- Klein, C.; Henne, U.; Sachs, W.; Beifuß, U.; Ondrus, V.; Bruse, M.; Lesjak, R.; Löhr, M. Application of Carbon Nanotubes (CNT) and Temperature-Sensitive Paint (TSP) for the Detection of Boundary Layer Transition. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- Ondrus, V.; Meier, R.J.; Klein, C.; Henne, U.; Schäferling, M.; Beifuß, U. Europium 1,3-di(thienyl)propane-1,3-diones with outstanding properties for temperature sensing. Sens. Actuators A Phys. 2015, 233, 434–441. [Google Scholar] [CrossRef]
- Crawford, B.; Duncan, G., Jr.; West, D.; Saric, W. Laminar-Turbulent Boundary Layer Transition Imaging Using IR Thermography. Opt. Photonics J. 2013, 3, 233–239. [Google Scholar] [CrossRef]
- Lemarechal, J.; Costantini, M.; Klein, C.; Kloker, M.; Wuerz, W.; Kurz, H.; Streit, T.; Schaber, S. Investigation of stationary-crossflow-instability induced transition with the temperature-sensitive paint method. Exp. Therm. Fluid Sci. 2019, 109, 109848. [Google Scholar] [CrossRef]
- Klein, C.; Engler, R.; Henne, U.; Sachs, W. Application of pressure-sensitive paint for determination of the pressure field and calculation of the forces and moments of models in a wind tunnel. Exp. Fluids 2005, 39, 475–483. [Google Scholar] [CrossRef]
- Dagenhart, J. Crossflow Stability and Transition Experiments in a Swept-Wing Flow. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1992. [Google Scholar]
- White, E.; Saric, W.; Gladden, R.; Gabet, P. Stages of Swept-Wing Transition. In Proceedings of the 39th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 8–11 January 2001; AIAA 2001-0271. [Google Scholar]
- Tufts, M.W.; Reed, H.L.; Crawford, B.K.; Duncan, G.T.; Saric, W.S. Computational Investigation of Step Excrescence Sensitivity in a Swept-wing Boundary Layer. J. Aircr. 2017, 54, 602–626. [Google Scholar] [CrossRef]






| IMX296 | PCO.4000 | |
|---|---|---|
| resolution [px] | ||
| dynamic [bit] | 10 | 14 |
| full-well capacity [] | 11,000 | 60,000 |
| [] | ||
| [] | 0.42 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lemarechal, J.; Dimond, B.D.; Barth, H.P.; Hilfer, M.; Klein, C. Miniaturization and Model-Integration of the Optical Measurement System for Temperature-Sensitive Paint Investigations. Sensors 2023, 23, 7075. https://doi.org/10.3390/s23167075
Lemarechal J, Dimond BD, Barth HP, Hilfer M, Klein C. Miniaturization and Model-Integration of the Optical Measurement System for Temperature-Sensitive Paint Investigations. Sensors. 2023; 23(16):7075. https://doi.org/10.3390/s23167075
Chicago/Turabian StyleLemarechal, Jonathan, Benjamin Daniel Dimond, Hans Peter Barth, Michael Hilfer, and Christian Klein. 2023. "Miniaturization and Model-Integration of the Optical Measurement System for Temperature-Sensitive Paint Investigations" Sensors 23, no. 16: 7075. https://doi.org/10.3390/s23167075





