Efficient Sensor Scheduling Strategy Based on Spatio-Temporal Scope Information Model
Abstract
1. Introduction
1.1. Contributions and Paper Outline
- Utilizing the spatio-temporal correlation of sensor nodes, a SSIM is proposed to quantify the valuable information of sensor data, which decays with space and time.
- A single-step optimal decision-making mechanism is proposed. The possible scheduling results under different node layouts are analyzed, and a method to solve the boundary node distribution among various scheduling situations is provided.
- A long-term optimal decision-making mechanism is proposed, which is modeled as a Markov decision process, and the Q-learning algorithm is utilized to solve the optimal scheduling results.
- With a single-step mechanism, the approximate bounds for the node layout between partial scheduling results are obtained from the theoretical analysis and numerical calculation, which match with the simulation results. The optimal scheduling results with a long-term mechanism corresponding to different node layouts are obtained. Finally, the different performances of the two mechanisms are experimentally verified, and the advantages and limitations of each are summarized.
1.2. Related Work
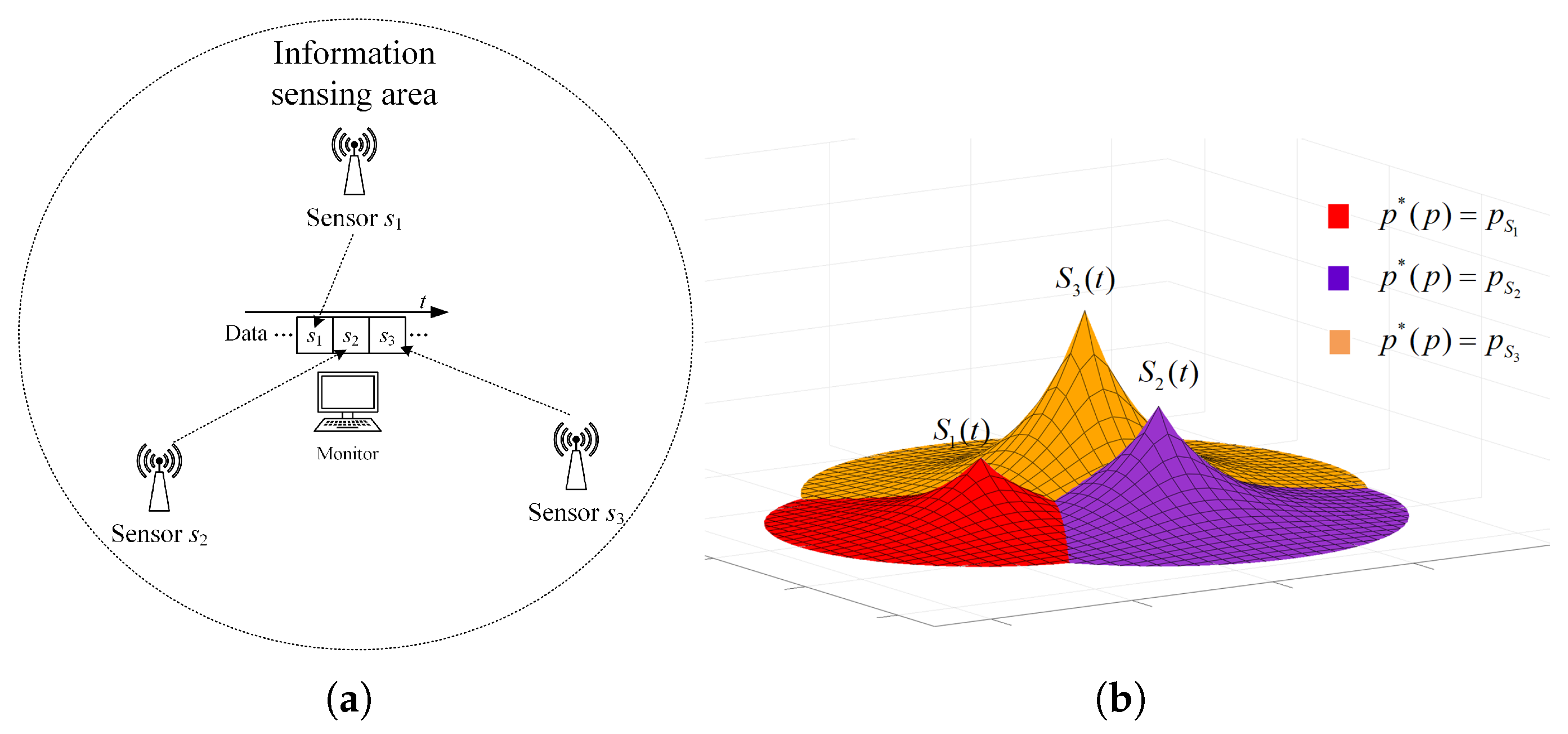
2. System Model and Problem Formulation
2.1. System Model
2.2. Spatio-Temporal Scope Information Model
2.3. Problem Formulation
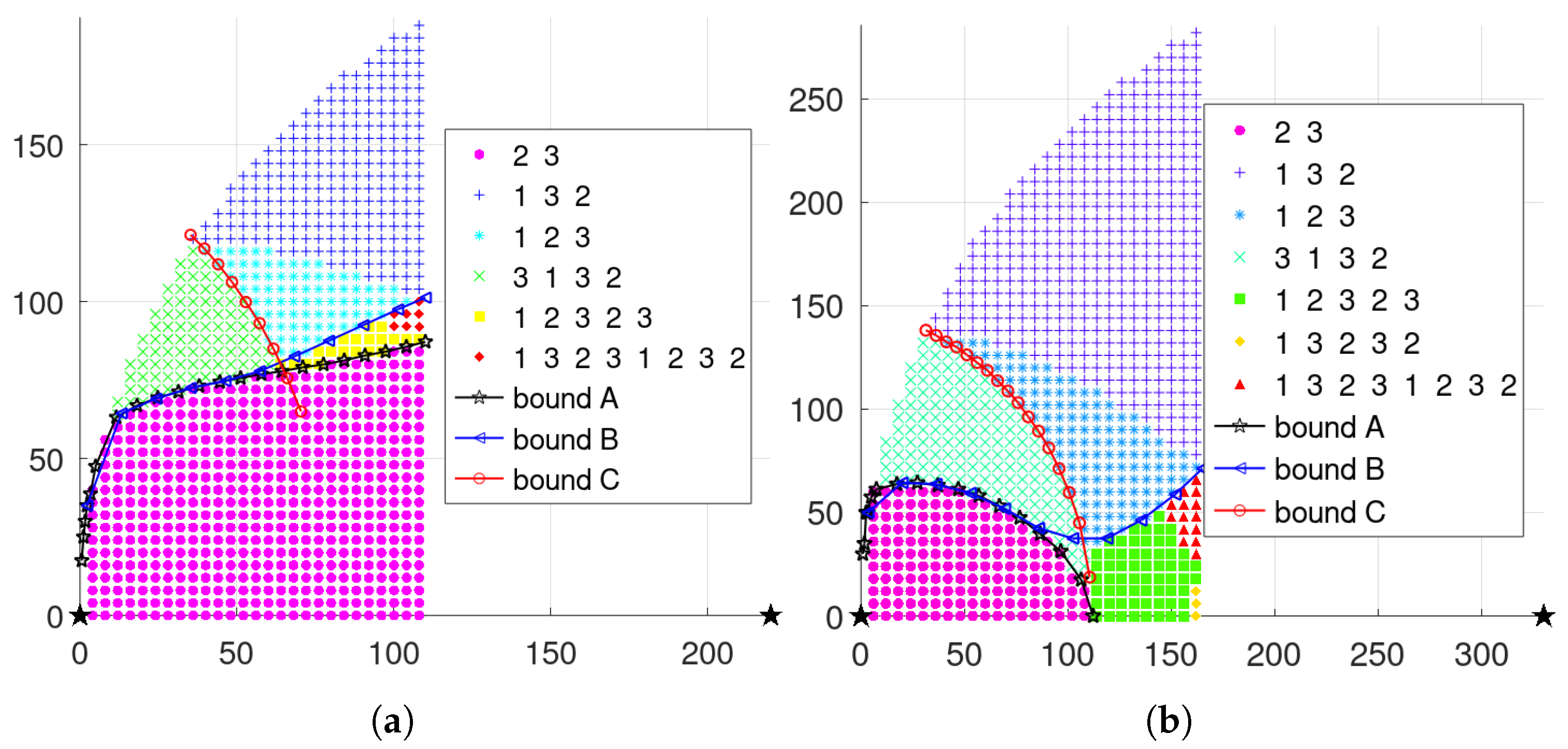
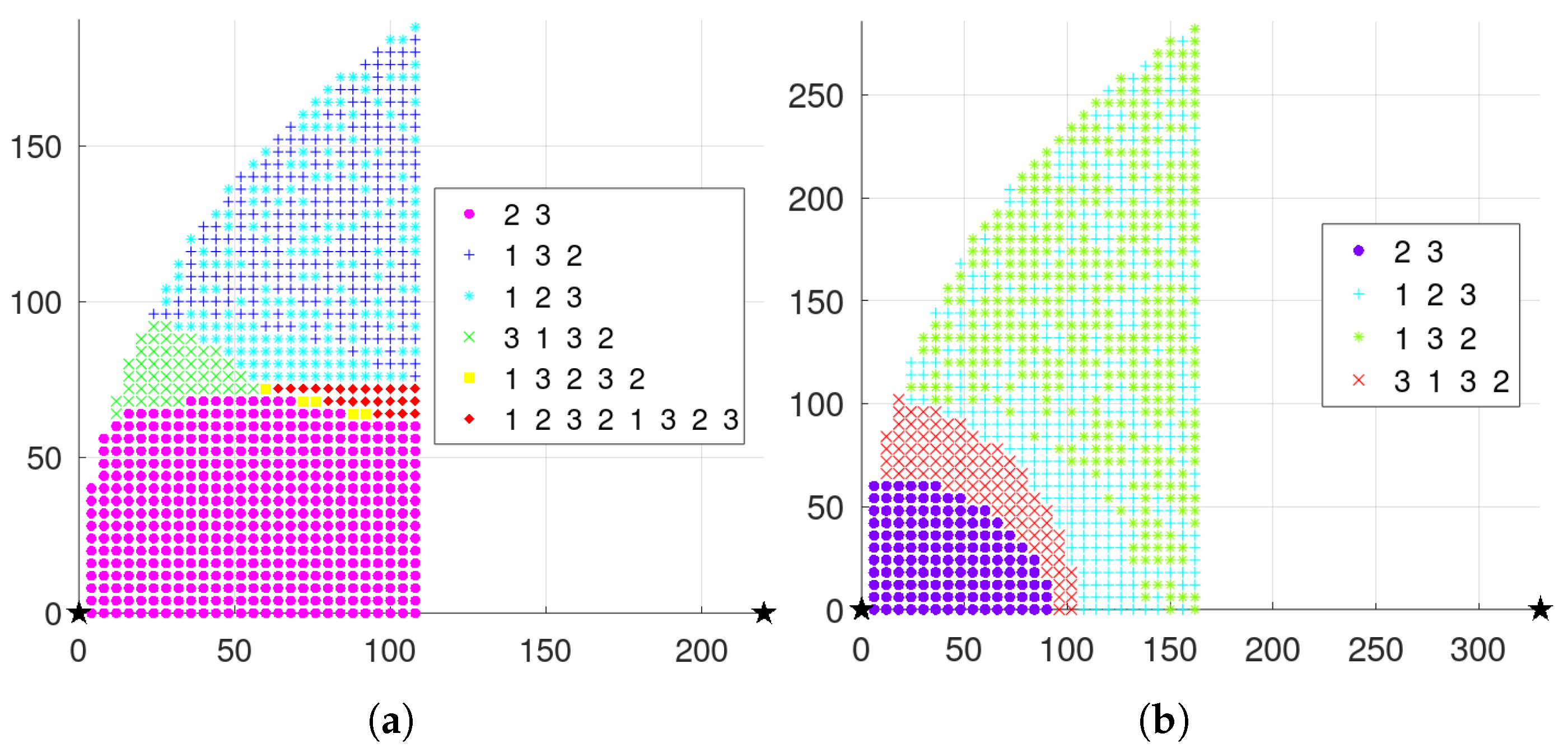
3. Single-Step Optimal Mechanism
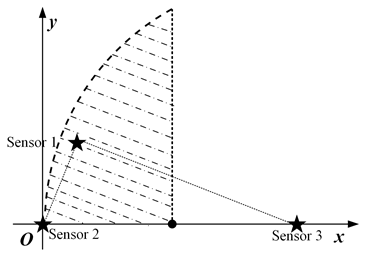
3.1. Three-Node Isosceles Triangle Layout
3.2. Three-Node General Triangular Layout
4. Long-Term Optimal Mechanism
4.1. States, Actions, and Rewards
4.2. Q Learning Algorithm
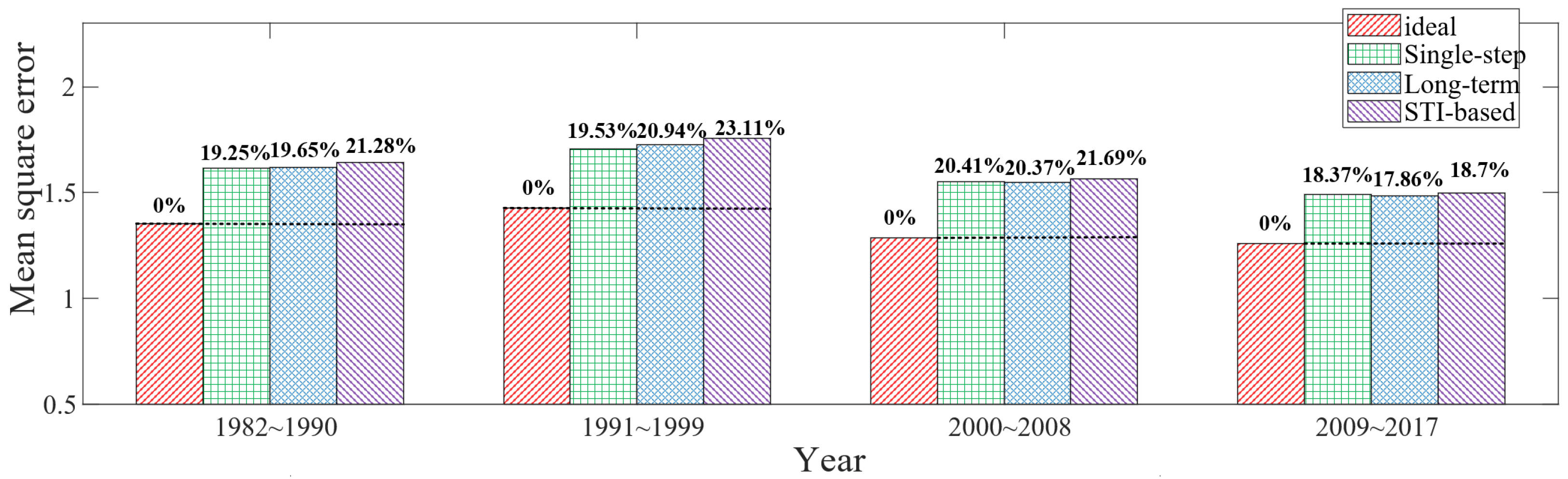
5. Numerical and Simulation Results
5.1. Scheduling Results with Single-Step Optimal Mechanism
5.1.1. Three-Node Isosceles Triangle Layout
5.1.2. Three-Node General Triangular Layout
5.2. Scheduling Results with Long-Term Optimal Mechanism
5.3. Performance Comparison of Two Mechanisms
5.4. Complexity Analysis
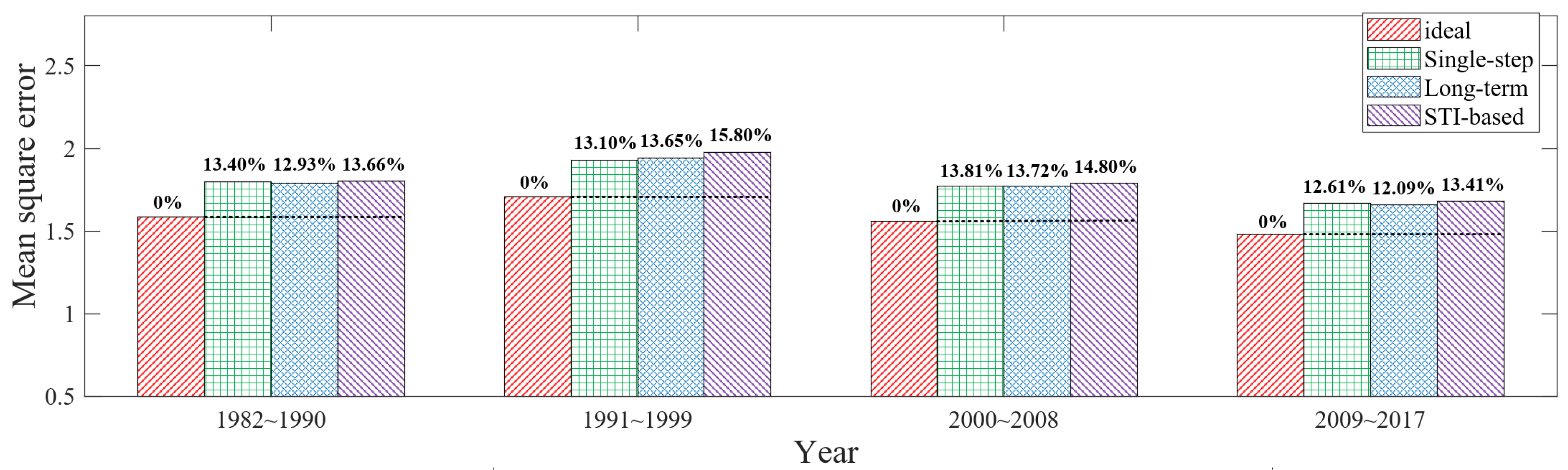
6. Experimental Evaluation
6.1. Data Analysis
6.2. Performance Comparison
6.3. Summary and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of Things: A Survey on Enabling Technologies, Protocols, and Applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Villa, T.; Salimi, F.; Morton, K.; Morawska, L.; Gonzalez, F. Development and validation of a UAV based system for air pollution measurements. Sensors 2016, 16, 2202. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, L.F.P.; Manera, L.T.; Luz, P.D.G.D. Development of a Smart Traffic Light Control System with Real-Time Monitoring. IEEE Internet Things J. 2021, 8, 3384–3393. [Google Scholar] [CrossRef]
- Friha, O.; Ferrag, M.A.; Shu, L.; Maglaras, L.; Wang, X. Internet of Things for the Future of Smart Agriculture: A Comprehensive Survey of Emerging Technologies. IEEE/CAA J. Autom. Sin. 2021, 8, 718–752. [Google Scholar] [CrossRef]
- Fascista, A.; Coluccia, A.; Ravazzi, C. A Unified Bayesian Framework for Joint Estimation and Anomaly Detection in Environmental Sensor Networks. IEEE Access 2023, 11, 227–248. [Google Scholar] [CrossRef]
- Kaul, S.; Yates, R.; Gruteser, M. Real-time status: How often should one update? In Proceedings of the 2012 Proceedings IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 2731–2735. [Google Scholar]
- Kadota, I.; Sinha, A.; Modiano, E. Scheduling Algorithms for Optimizing Age of Information in Wireless Networks with Throughput Constraints. IEEE/ACM Trans. Netw. 2019, 27, 1359–1372. [Google Scholar] [CrossRef]
- Talak, R.; Karaman, S.; Modiano, E. Optimizing Information Freshness in Wireless Networks under General Interference Constraints. IEEE/ACM Trans. Netw. 2020, 28, 15–28. [Google Scholar] [CrossRef]
- Akar, N.; Dogan, O. Discrete-Time Queueing Model of Age of Information with Multiple Information Sources. IEEE Internet Things J. 2021, 8, 14531–14542. [Google Scholar] [CrossRef]
- Sun, Y.; Uysal-Biyikoglu, E.; Yates, R.D.; Koksal, C.E.; Shroff, N.B. Update or Wait: How to Keep Your Data Fresh. IEEE Trans. Inf. Theory 2017, 63, 7492–7508. [Google Scholar] [CrossRef]
- Kosta, A.; Pappas, N.; Ephremides, A.; Angelakis, V. The Age of Information in a Discrete Time Queue: Stationary Distribution and Non-Linear Age Mean Analysis. IEEE J. Sel. Areas Commun. 2021, 39, 1352–1364. [Google Scholar] [CrossRef]
- Poojary, S.; Bhambay, S.; Parag, P. Real-Time Status Updates for Markov Source. IEEE Trans. Inf. Theory 2019, 65, 5737–5749. [Google Scholar] [CrossRef]
- Chamberland, J.-F.; Veeravalli, V.V. How Dense Should a Sensor Network Be for Detection with Correlated Observations? IEEE Trans. Inf. Theory 2006, 52, 5099–5106. [Google Scholar] [CrossRef]
- Vuran, M.C.; Akan, O.B. Spatio-temporal Characteristics of Point and Field Sources in Wireless Sensor Networks. In Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; pp. 234–239. [Google Scholar]
- Wang, B.; Zhu, J.; Yang, L.T.; Mo, Y. Sensor Density for Confident Information Coverage in Randomly Deployed Sensor Networks. IEEE Trans. Wirel. Commun. 2016, 15, 3238–3250. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, B. The Optimal Placement Pattern for Confident Information Coverage in Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2016, 15, 1022–1032. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Yang, L.T.; Deng, X.; Yi, L. A Nature-Inspired Node Deployment Strategy for Connected Confident Information Coverage in Industrial Internet of Things. IEEE Internet Things J. 2019, 6, 9217–9225. [Google Scholar] [CrossRef]
- Hribar, J.; Costa, M.; Kaminski, N.; DaSilva, L.A. Using Correlated Information to Extend Device Lifetime. IEEE Internet Things J. 2019, 6, 2439–2448. [Google Scholar] [CrossRef]
- Hribar, J.; Marinescu, A.; Ropokis, G.A.; DaSilva, L.A. Using Deep Q-Learning to Prolong the Lifetime of Correlated Internet of Things Devices. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Hribar, J.; Marinescu, A.; Chiumento, A.; Dasilva, L.A. Energy-Aware Deep Reinforcement Learning Scheduling for Sensors Correlated in Time and Space. IEEE Internet Things J. 2022, 9, 6732–6744. [Google Scholar] [CrossRef]
- Sun, Y.; Cyr, B. Information Aging Through Queues: A Mutual Information Perspective. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]
- Wang, Z.; Badiu, M.-A.; Coon, J.P. A Value of Information Framework for Latent Variable Models. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Wang, Z.; Badiu, M.-A.; Coon, J.P. A Framework for Characterizing the Value of Information in Hidden Markov Models. IEEE Trans. Inf. Theory 2022, 68, 5203–5216. [Google Scholar] [CrossRef]
- Kim, J.; Kim, M.; Lee, J. Sensing and Transmission Design for AoI-Sensitive Wireless Sensor Networks. In Proceedings of the 2020 IEEE Globecom Workshops (GC Wkshps), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Kim, J.; Kim, M.; Lee, J. Securing fresh data in wireless monitoring networks: Age-of-information sensitive coverage perspective. arXiv 2021, arXiv:2103.07149. [Google Scholar]
- Jiang, Z.; Zhou, S. Status from a Random Field: How Densely Should One Update? In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 1037–1041. [Google Scholar]
- Zhang, H.; Jiang, Z.; Xu, S.; Zhou, S. Error Analysis for Status Update From Sensors with Temporally and Spatially Correlated Observations. IEEE Trans. Wirel. Commun. 2021, 20, 2136–2149. [Google Scholar] [CrossRef]
- Håkansson, V.W.; Venkategowda, N.K.D.; Werner, S.; Varshney, P.K. Optimal Scheduling of Multiple Spatio-temporally Dependent Observations for Remote Estimation using Age-of-Information. IEEE Internet Things J. 2022, 9, 20308–20321. [Google Scholar] [CrossRef]
- Håkansson, V.W.; Venkategowda, N.K.D.; Werner, S.; Varshney, P.K. Optimal Transmission-Constrained Scheduling of Spatio-Temporally Dependent Observations Using Age-of-Information. IEEE Sens. J. 2022, 22, 15596–15606. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Y.; Zhang, Q.; Yang, Z. Age-Driven Spatially Temporally Correlative Updating in the Satellite-Integrated Internet of Things via Markov Decision Process. IEEE Internet Things J. 2022, 9, 13612–13625. [Google Scholar] [CrossRef]
- Pan, W.; Deng, Z.; Wang, X.; Zhou, P.; Wu, W. Optimizing the Age of Information for Multi-Source Information Update in Internet of Things. IEEE Trans. Netw. Sci. Eng. 2022, 9, 904–917. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, C.; Qin, X.; Xu, X. Efficient Sensor Scheduling Strategy Based on Spatio-temporal Scope Information Model. arXiv 2022, arXiv:2212.07008. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Feng, F.; Wang, K.C. Merging satellite retrievals and reanalyses to produce global long-term and consistent surface incident solar radiation datasets. Remote Sens. 2018, 10, 115. [Google Scholar] [CrossRef]
- Feng, F.; Wang, K.C. Merging ground-based sunshine duration observations with satellite cloud and aerosol retrievals to produce high-resolution long-term surface solar radiation over China. Earth Syst. Sci. Data 2021, 13, 907–922. [Google Scholar] [CrossRef]
- Mao, Y.N.; Wang, K.C.; Liu, X.M.; Liu, C.M. Water storage in reservoirs built from 1997 to 2014 significantly altered the calculated evapotranspiration trends over China. J. Geophys. Res.-Atmos. 2016, 121, 10097–10112. [Google Scholar] [CrossRef]
- Mao, Y.N.; Wang, K.C. Comparison of Evapotranspiration Estimates based on the Surface Water Balance, Modified Penman-Monteith Model, and Reanalysis Datasets for Continental China. J. Geophys. Res. Atmos. 2017, 122, 3228–3244. [Google Scholar] [CrossRef]
- Wang, K. Homogeneous Grid Dataset of Chinaese Land Surface Observation (Surface Solar Radiation, Surface Wind Speed, Relative Humidity and Land Surface Evapotranspiration); National Tibetan Plateau Data Center: Beijing, China, 2022. [Google Scholar]





| References | Information Source | Sensors | Metrics | Research Results |
|---|---|---|---|---|
| [18] | Single-point | Two | Estimation Error | Optimal time shift between two sensors |
| [19,20] | Multi-point | Multiple | Estimation Error | DRL-based scheduling mechanism |
| [22,23] | Single-point (Noisy Ornstein-Uhlenbeck process) | Single | Mutual information | Closed-form VoI expressions |
| [24,25] | Regional | Multiple | Error-tolerable sensing (ETS) coverage | AoI violation probability, Optimal sensors’ transmission power |
| [26,27] | Time-varying Gauss–Markov Random Field (GMRF) | Multiple | Mean squared Estimation error | Closed-form expressions for estimation error, optimal spatial-temporal Sampling rates |
| [28,29] | N Gaussian process | Multiple | Mean squared error (MSE) | Optimal scheduling policy |
| [30] | Single-point | Multiple | Spatial-temporal mutual information | Optimal update interval |
| [31] | Multi-point | Multiple | Overall utility of information update | Status update node set |
| This work | Regional | Three | Spatial-temporal Scope information | Node activation strategy in any layout |
| Typical Layout | Scheduling Results | Conditions |
|---|---|---|
 | ||
| Boundary | ||
| ⋮ | ⋮ | |
| Boundary | ||
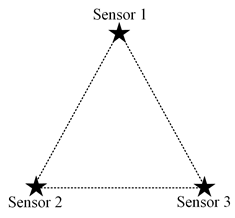 | ||
| Boundary | ||
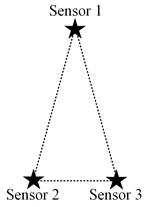 |
| Typical Layout | Scheduling Results | Conditions |
|---|---|---|
 | ||
| Boundary A | ||
| ⋮ | ⋮ | |
| Boundary B | ||
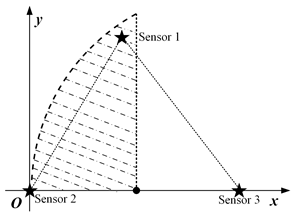 | ||
| Boundary C | ||
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Dong, C.; Qin, X.; Xu, X. Efficient Sensor Scheduling Strategy Based on Spatio-Temporal Scope Information Model. Sensors 2023, 23, 5437. https://doi.org/10.3390/s23125437
Liu Y, Dong C, Qin X, Xu X. Efficient Sensor Scheduling Strategy Based on Spatio-Temporal Scope Information Model. Sensors. 2023; 23(12):5437. https://doi.org/10.3390/s23125437
Chicago/Turabian StyleLiu, Yang, Chen Dong, Xiaoqi Qin, and Xiaodong Xu. 2023. "Efficient Sensor Scheduling Strategy Based on Spatio-Temporal Scope Information Model" Sensors 23, no. 12: 5437. https://doi.org/10.3390/s23125437
APA StyleLiu, Y., Dong, C., Qin, X., & Xu, X. (2023). Efficient Sensor Scheduling Strategy Based on Spatio-Temporal Scope Information Model. Sensors, 23(12), 5437. https://doi.org/10.3390/s23125437






