A New Weak-Coupling Method with Eccentric Dual Bucking Coils Applied to the PRBS Helicopter TEM System
Abstract
:1. Introduction
2. PRBS Helicopter TEM System
2.1. Transmitter–Receiver Configuration
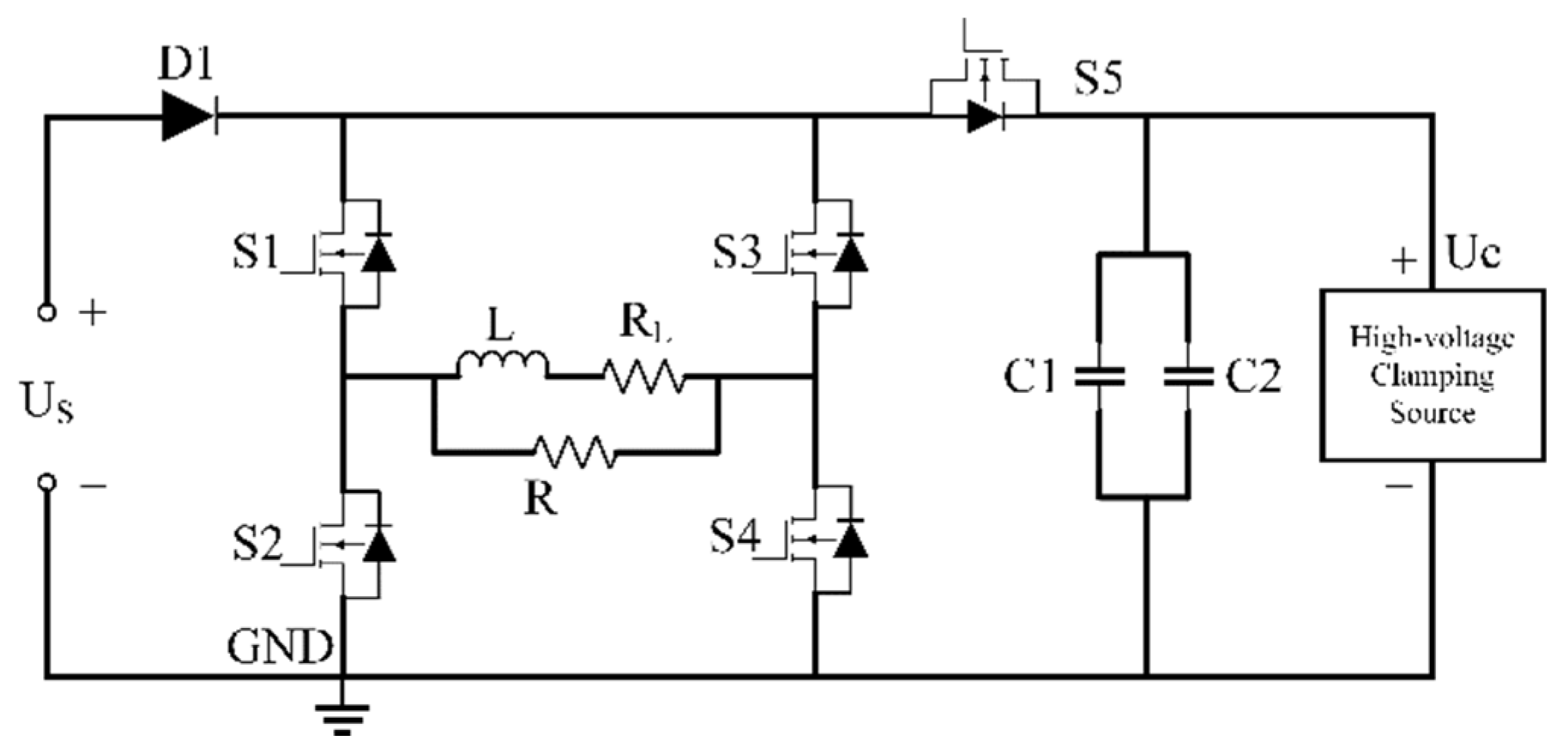
2.2. Transmitter Circuit
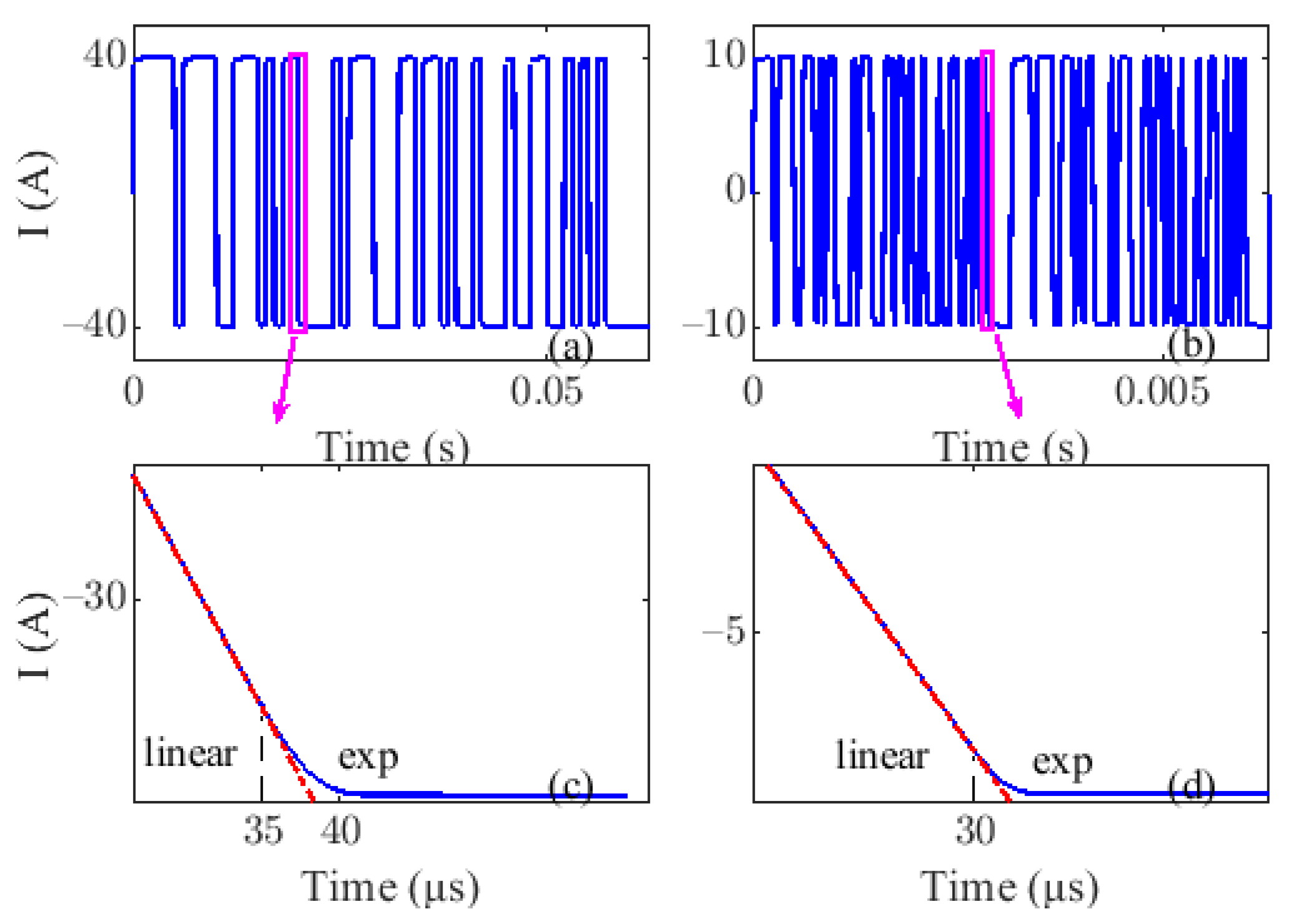
2.3. Waveform Analysis
3. Designment and Optimization of Eccentric Dual Bucking Modeling
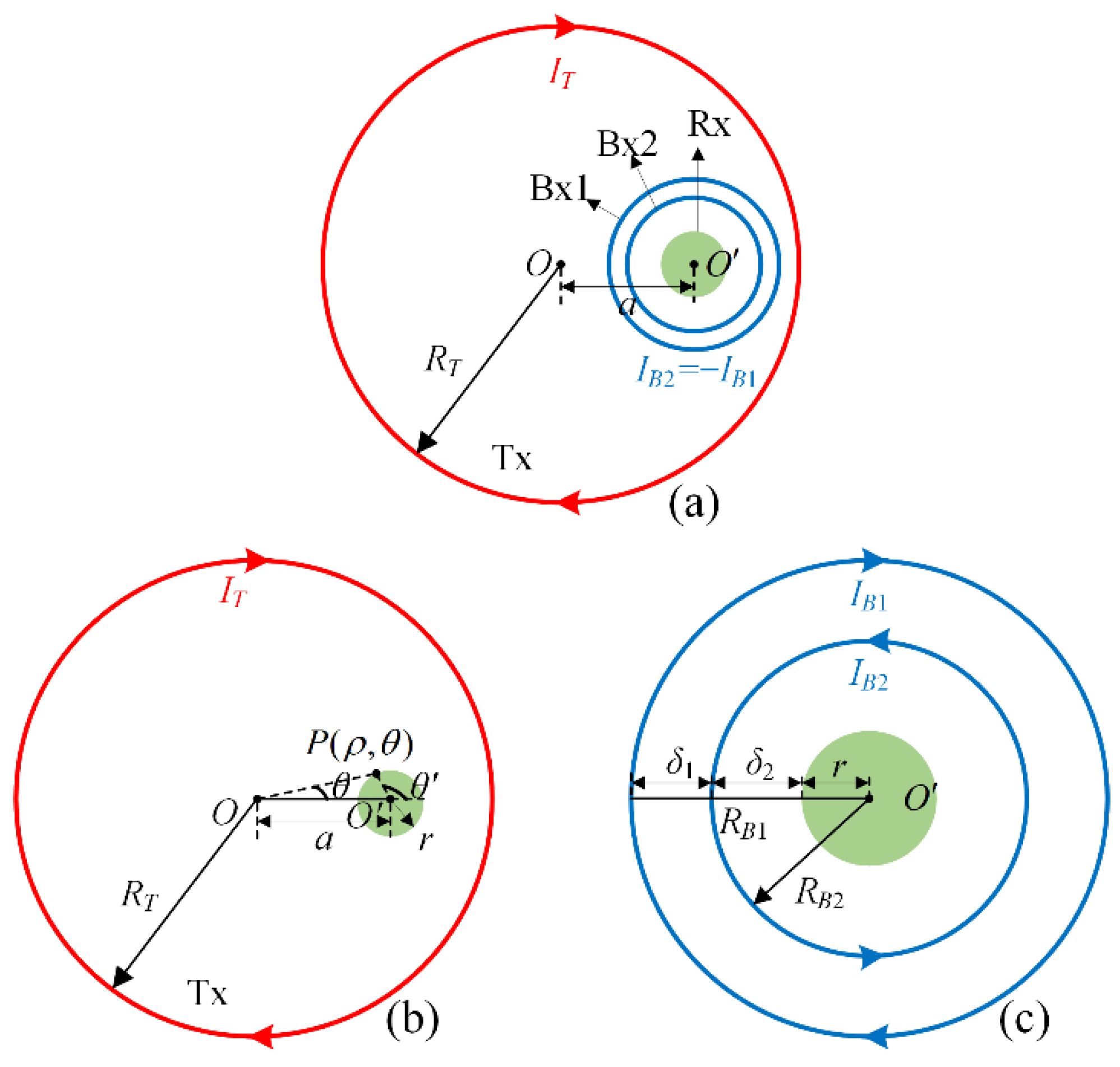
3.1. Calculation of Electromagnetic Field
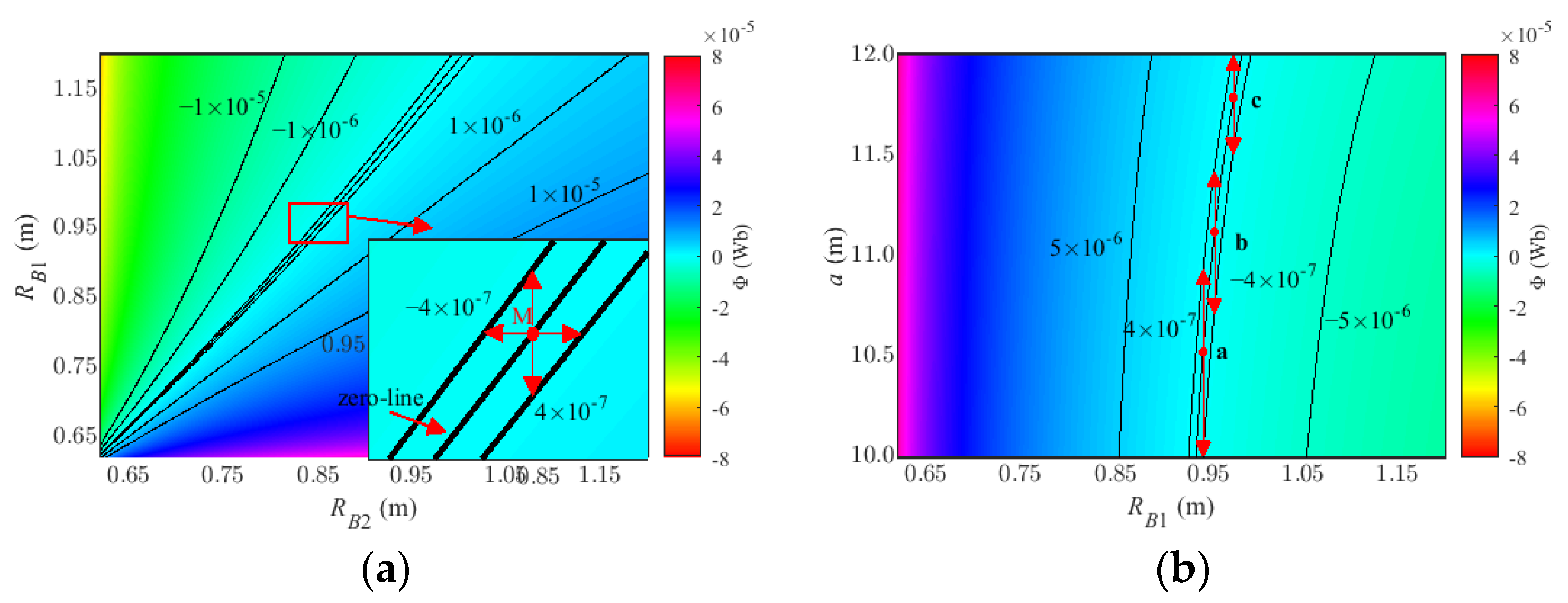
3.2. Determination of Bucking Parameters
4. Simulation Results
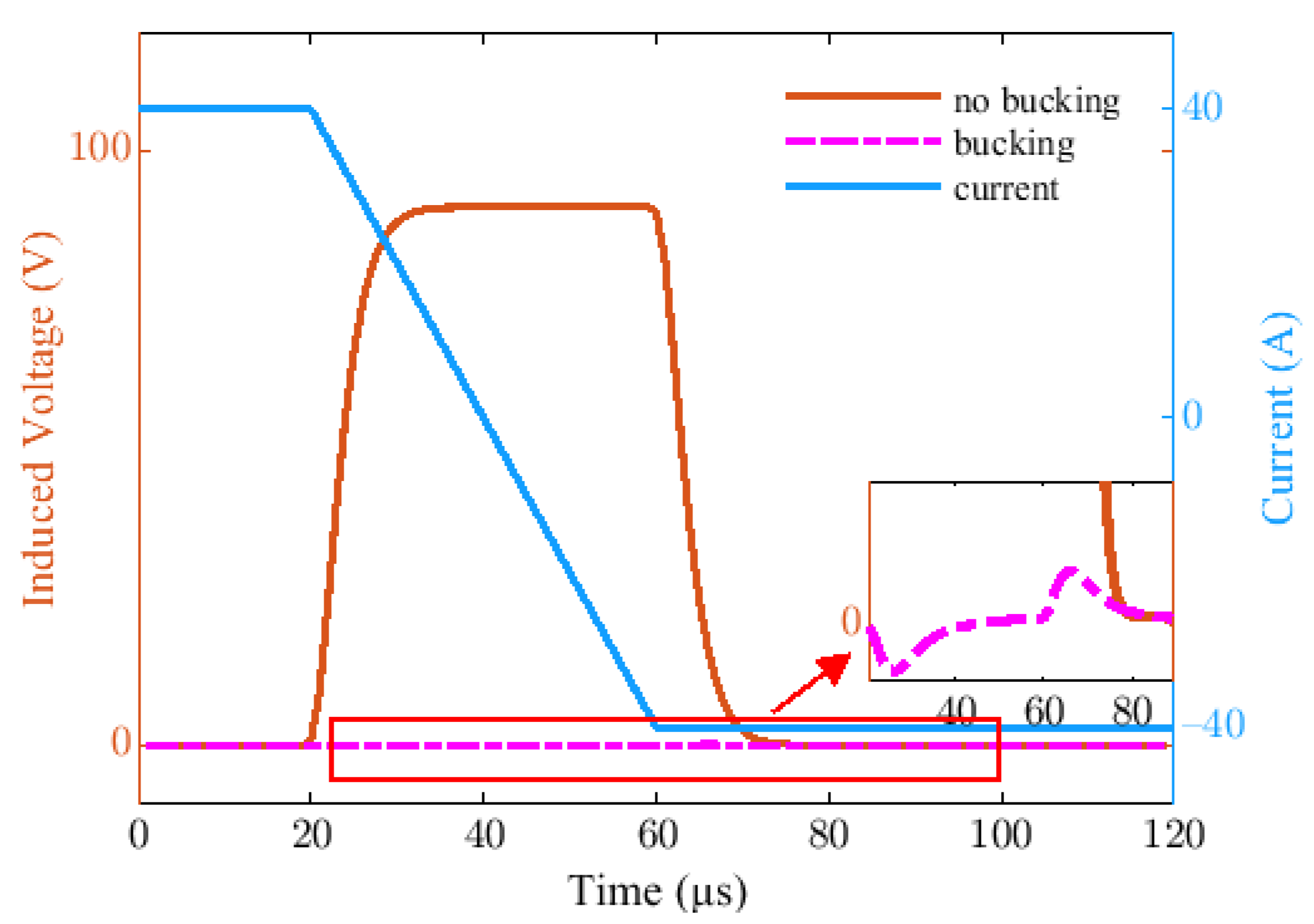
4.1. Simulation of Bucking Model
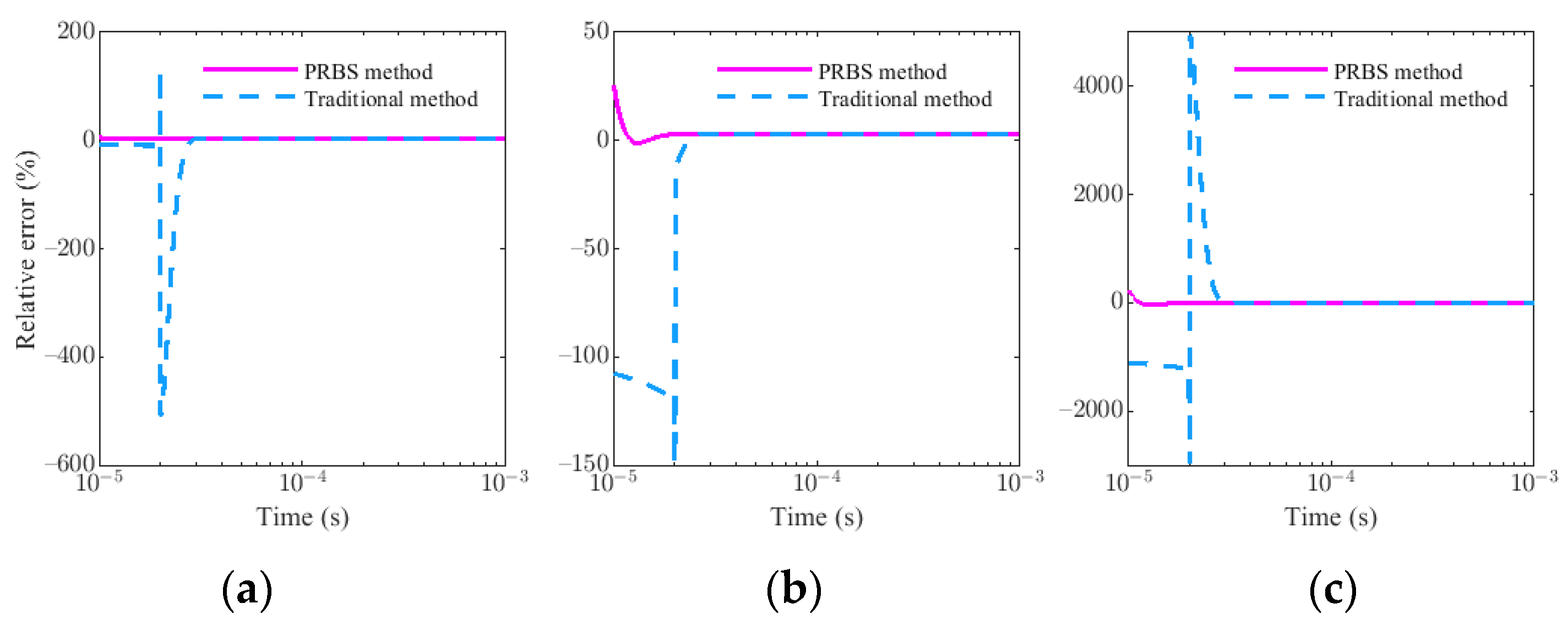
4.2. Quantitatively Analysis of the Difference betweeen PRBS Method and Traditional Method
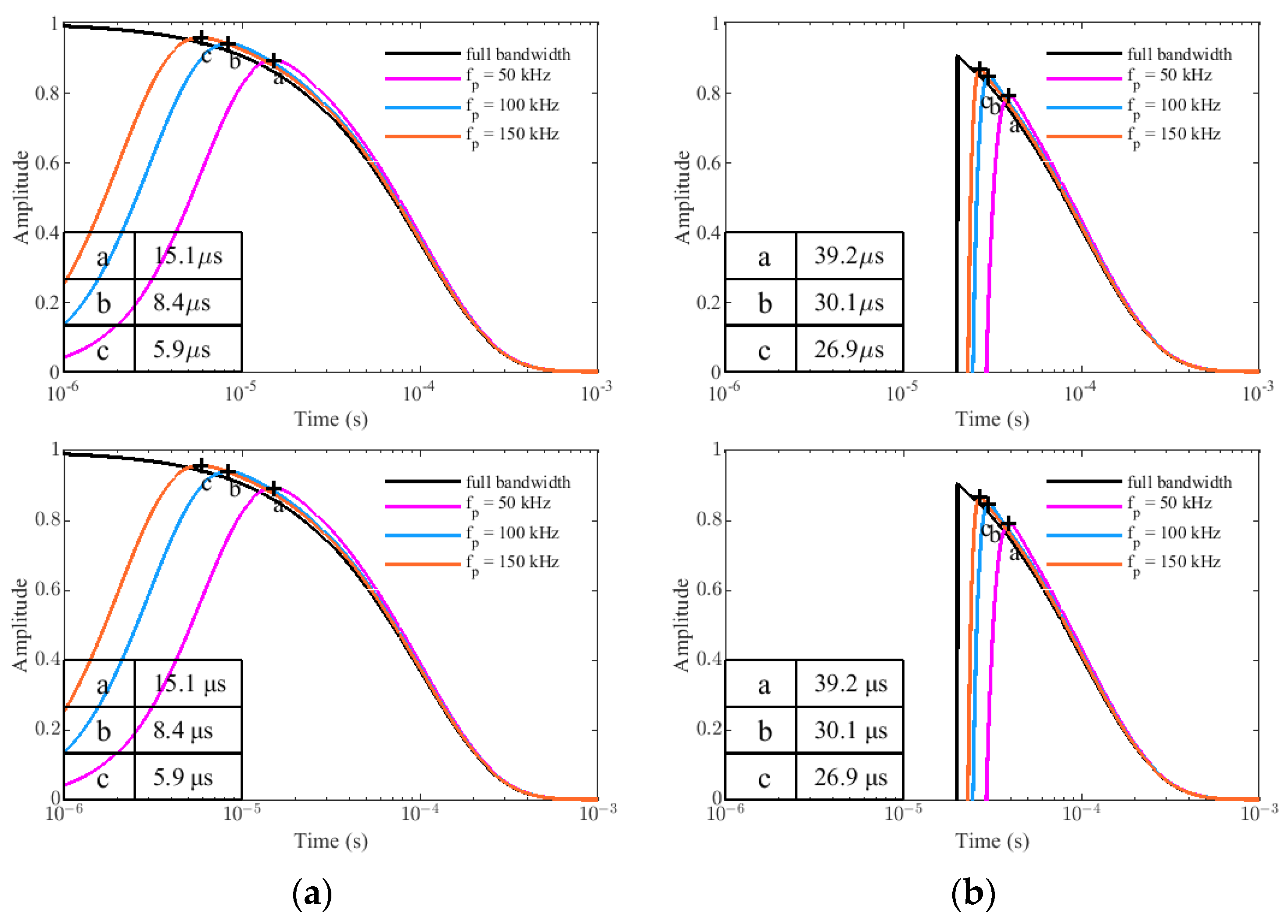
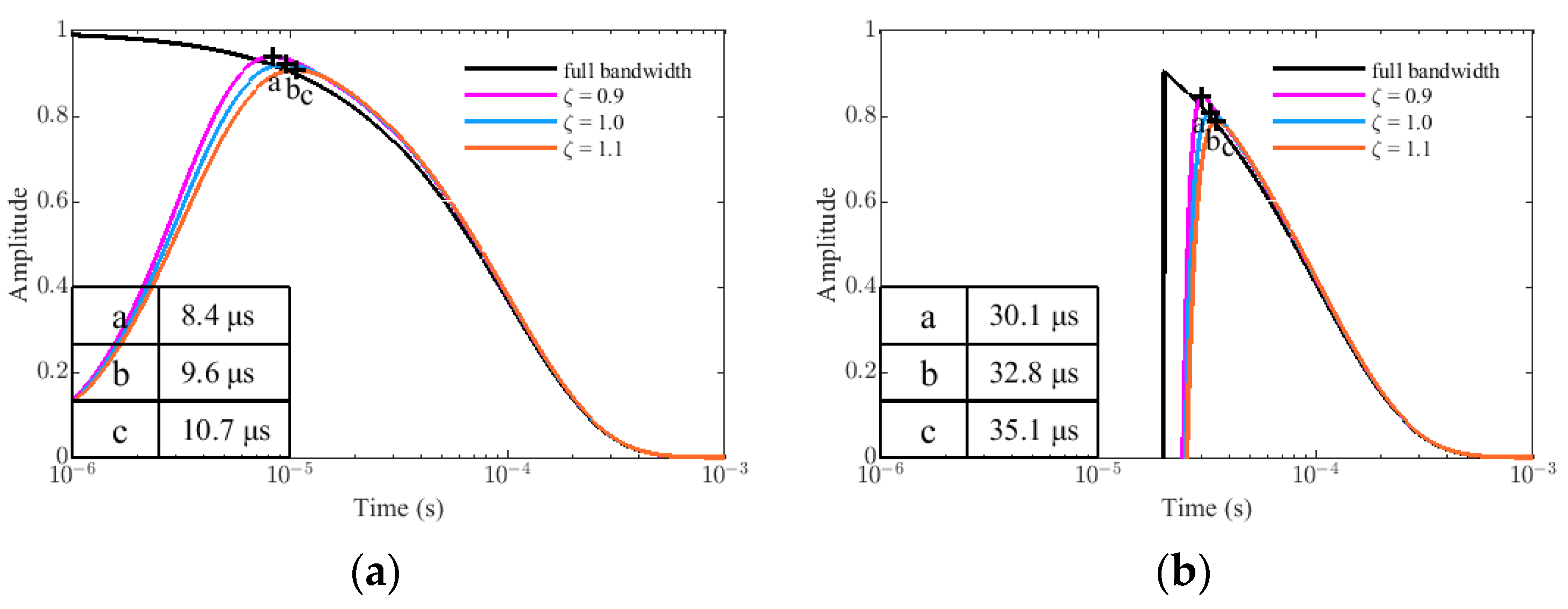
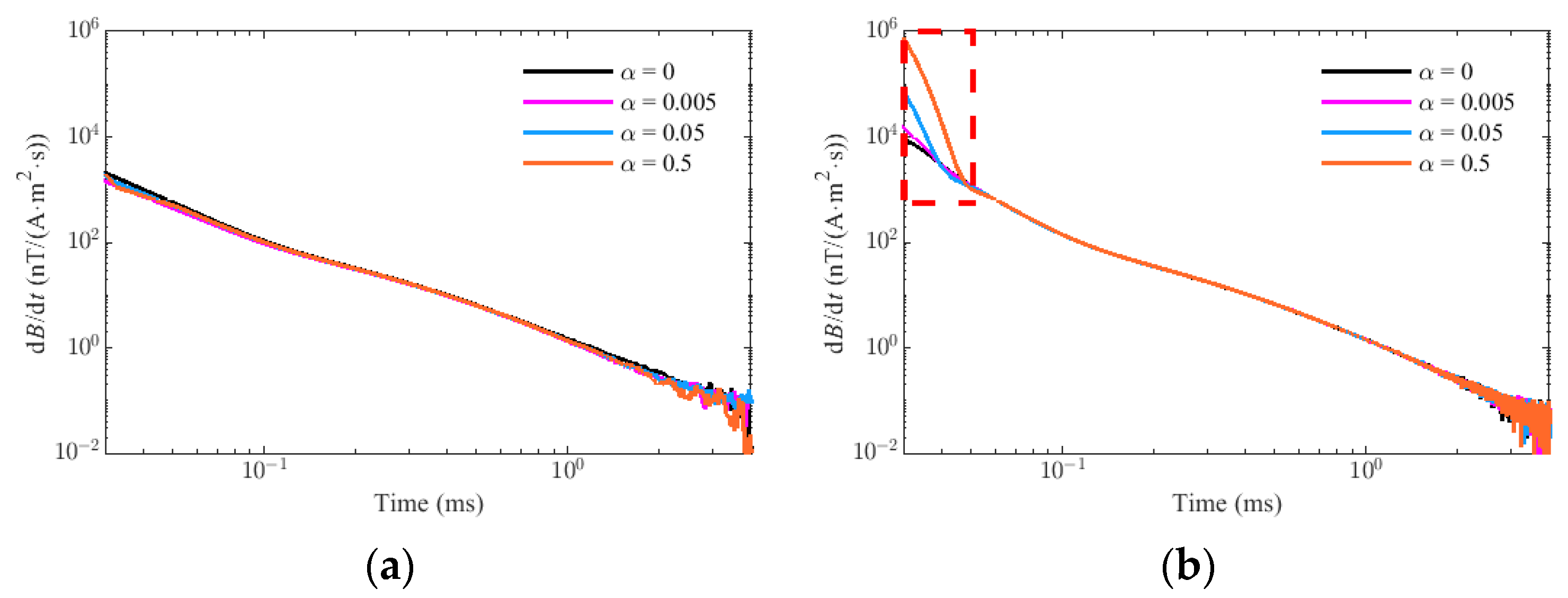
4.2.1. Different Resonant Frequency wp and Damping Coefficient ζ
4.2.2. Different Primary Field Coefficient K
4.3. Data Sysnthesis and Preprocessing of PRBS HTEM System
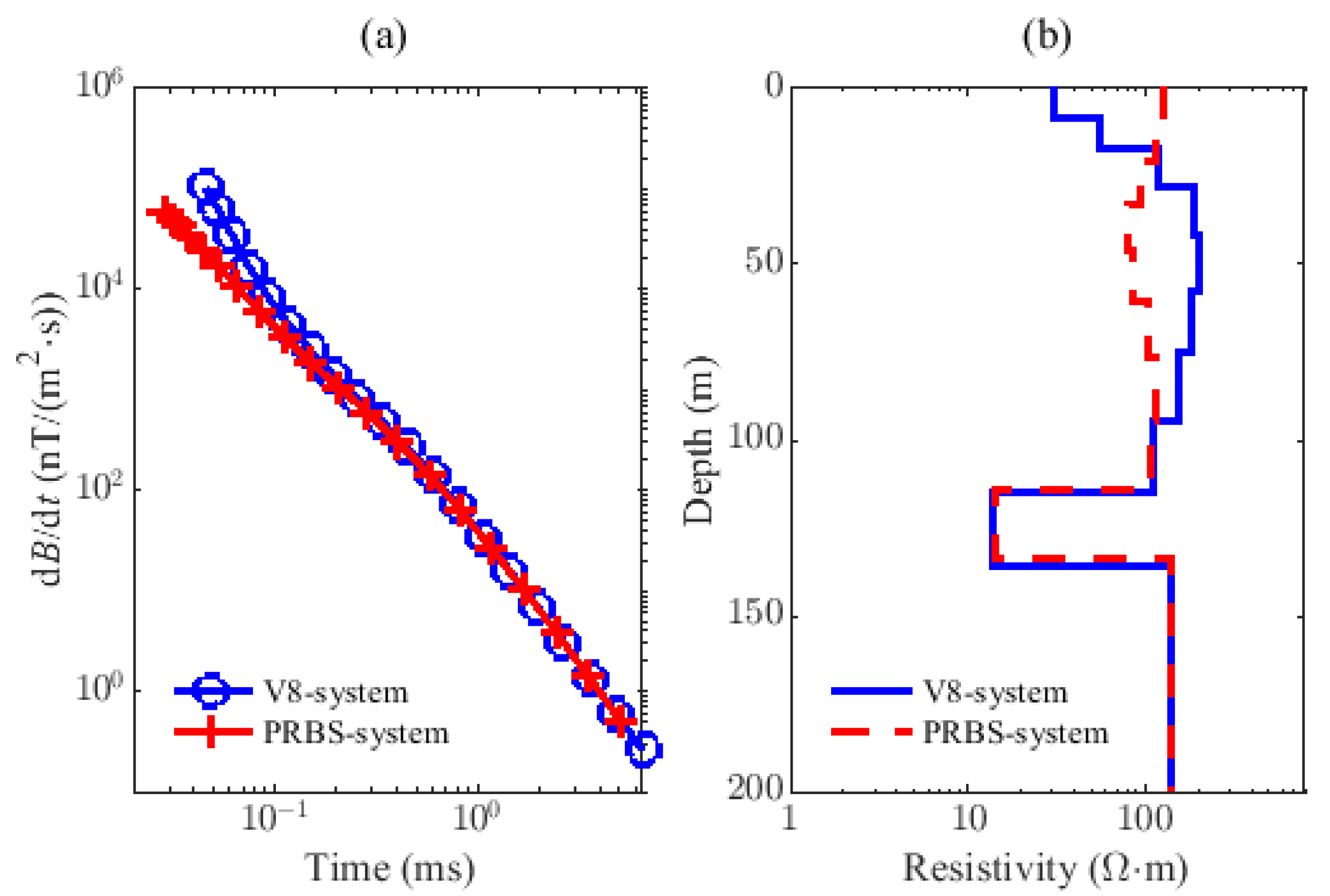
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Time Domain Correlation Identification Algorithm
References
- Allard, M.; Milkereit, B. On the origin of the HTEM species. Proc. Explor. 2007, 7, 355–374. [Google Scholar]
- Mulè, S.; Carter, S.; Wolfgram, P. Advances in Helicopter Airborne Electromagnetics. ASEG Ext. Abstr. 2019, 2012, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Legault, J.M. Airborne electromagnetic systems–state of the art and future directions. CSEG Rec. 2015, 40, 38–49. [Google Scholar]
- Liang, B.; Qiu, C.; Han, F.; Zhu, C.; Liu, N.; Liu, H.; Liu, F.; Fang, G.; Liu, Q.H. A New Inversion Method Based on Distorted Born Iterative Method for Grounded Electrical Source Airborne Transient Electromagnetics. IEEE Trans. Geosci. Remote Sens. 2018, 56, 877–887. [Google Scholar] [CrossRef]
- Liu, L.; Li, J.; Huang, L.; Liu, X.; Fang, G. Double Clamping Current Inverter with Adjustable Turn-off Time for Bucking Coil Helicopter Transient Electromagnetic Surveying. IEEE Trans. Ind. Electron. 2021, 68, 5405–5414. [Google Scholar] [CrossRef]
- Fu, Z.; Wang, H.; Wang, Y.; Fu, N.; Tai, H.M.; Qin, S. Elimination of mutual inductance effect for small-loop transient electromagnetic devices. Geophysics 2019, 84, E143–E154. [Google Scholar] [CrossRef]
- Auken, E.; Boesen, T.; Christiansen, A.V. A Review of Airborne Electromagnetic Methods with Focus on Geotechnical and Hydrological Applications From 2007 to 2017. Adv. Geophys. 2017, 2017, 47–93. [Google Scholar]
- Sorensen, K.I.; Auken, E. SkyTEM–a New High-resolution Helicopter Transient Electromagnetic System. Explor. Geophys. 2018, 35, 194–202. [Google Scholar] [CrossRef]
- Hodges, G.; Chen, T.; Van Buren, R. HELITEM detects the Lalor VMS deposit. Explor. Geophys. 2018, 47, 285–289. [Google Scholar] [CrossRef]
- Witherly, K.; Irvine, R. The VTEM heli-time domain EM system-Four Case Studies. ASEG Ext. Abstr. 2019, 2006, 1–4. [Google Scholar] [CrossRef]
- Combrinck, M.; Wright, R. XciteTM: Great Results Require more than Good Data; ASEG-PESA: Adelaide, Australia, 2016. [Google Scholar]
- Wu, X.; Fang, G.; Xue, G.; Liu, L.; Liu, L.; Li, J. The Development and Applications of the Helicopter-borne Transient Electromagnetic System CAS-HTEM. J. Environ. Eng. Geophys. 2019, 24, 653–663. [Google Scholar] [CrossRef]
- Rudd, J.; Walker, S. The AeroTEM system in Africa. ASEG Ext. Abstr. 2009, 2009, 1–4. [Google Scholar] [CrossRef]
- Chen, C.; Liu, F.; Lin, J.; Zhu, K.; Wang, Y. An Optimized Air-Core Coil Sensor with a Magnetic Flux Compensation Structure Suitable to the Helicopter TEM System. Sensors 2016, 16, 508. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Lin, J.; Wang, Y.; Wang, S.; Xu, Q.; Cao, X.; Li, Z.; Chen, B. Reducing Motion-Induced Noise with Mechanically Resonant Coil Sensor in a Rigid Helicopter Transient Electromagnetic System. IEEE Trans. Ind. Electron. 2020, 67, 2391–2401. [Google Scholar] [CrossRef]
- Li, M.; Wei, W.; Luo, W.; Xu, Q. Time-Domain Spectral Induced Polarization Based on Pseudo-random Sequence. Pure Appl. Geophys. 2012, 170, 2257–2262. [Google Scholar] [CrossRef]
- Ziolkowski, A.; Hobbs, B.A.; Wright, D. Multitransient electromagnetic demonstration survey in France. Geophysics 2007, 72, F197–F209. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Hao, K.; Li, M. Improved Correlation Identification of Subsurface Using All Phase FFT Algorithm. KSII Trans. Internet Inf. Syst. 2020, 14, 495–513. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Hamilton Printing Company: Castleton, NY, USA, 1998; pp. 180–182. [Google Scholar]
- Xiao, P.; Wu, X.; Shi, Z.; Guo, R.; Pang, Y.; Fang, G. Principal time constant map, a more accurate mapping tool for helicopter TEM data. J. Appl. Geophys. 2018, 159, 260–267. [Google Scholar] [CrossRef]
- Chen, S.; Guo, S.; Wang, H.; He, M.; Liu, X.; Qiu, Y.; Zhang, S.; Yuan, Z.; Zhang, H.; Fang, D.; et al. An Improved High-Sensitivity Airborne Transient Electromagnetic Sensor for Deep Penetration. Sensors 2017, 17, 169. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Wang, H.; Fu, Z.; Fu, W. Analysis of Primary Field Shielding Stability for the Weak Coupling Coil Designs. Sensors 2020, 20, 519. [Google Scholar] [CrossRef] [Green Version]
- Key, K. Is the fast Hankel transform faster than quadrature? Geophysics 2012, 77, F21–F30. [Google Scholar] [CrossRef] [Green Version]







| Items | Low Frequency | High Frequency |
|---|---|---|
| Transmitter area | 1400 m2 | 700 m2 |
| Peak current | 40 A | 10 A |
| Peak moment | 56 kA·m2 | 7 kA·m2 |
| Code frequency | 1–20 kHz | 20–50 kHz |
| Order | 6–8 | 8–10 |
| Sample interval | 5 μs | 1 μs |
| Points | a (m) | RB1 (m) | ΔH (m) |
|---|---|---|---|
| a | 10.50 | 0.943 | 0.93 |
| b | 11.10 | 0.955 | 0.71 |
| c | 11.77 | 0.975 | 0.49 |
| Model Parameters | Value |
|---|---|
| Tx waveform | Step pulse |
| Ramp time | 40 μs |
| Tx current | 40 A |
| Tx coils radius | 15 m |
| Rx coils radius | 0.6 m |
| Bucking coils radius | 0.850 m/0.943 m |
| Terrain clearance | 30 m |
| Earth resistivity | 100 Ω·m |
| Sample interval | 1 μs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, Z.; Liu, L.; Jiang, L.; Yan, S.; Ji, Y.; Liu, X.; Fang, G. A New Weak-Coupling Method with Eccentric Dual Bucking Coils Applied to the PRBS Helicopter TEM System. Sensors 2022, 22, 2675. https://doi.org/10.3390/s22072675
Ke Z, Liu L, Jiang L, Yan S, Ji Y, Liu X, Fang G. A New Weak-Coupling Method with Eccentric Dual Bucking Coils Applied to the PRBS Helicopter TEM System. Sensors. 2022; 22(7):2675. https://doi.org/10.3390/s22072675
Chicago/Turabian StyleKe, Zhen, Lihua Liu, Longbin Jiang, Shichu Yan, Yicai Ji, Xiaojun Liu, and Guangyou Fang. 2022. "A New Weak-Coupling Method with Eccentric Dual Bucking Coils Applied to the PRBS Helicopter TEM System" Sensors 22, no. 7: 2675. https://doi.org/10.3390/s22072675






