A Comprehensive Evaluation of Possible RNSS Signals in the S-Band for the KPS
Abstract
:1. Introduction
2. S-Band and Adjacent Bands Systems
2.1. Navigation with Indian Constellation
2.2. Globalstar
2.3. Other Communication Systems in Adjacent Bands
3. Navigation Signal Design Considerations
3.1. RF Compatibility
3.2. Spectral Efficiency
3.3. Ranging Performance
3.3.1. DLL Error
3.3.2. Gabor Bandwidth
3.3.3. Multipath Error
3.4. Receiver Complexity
4. FoMs Analysis
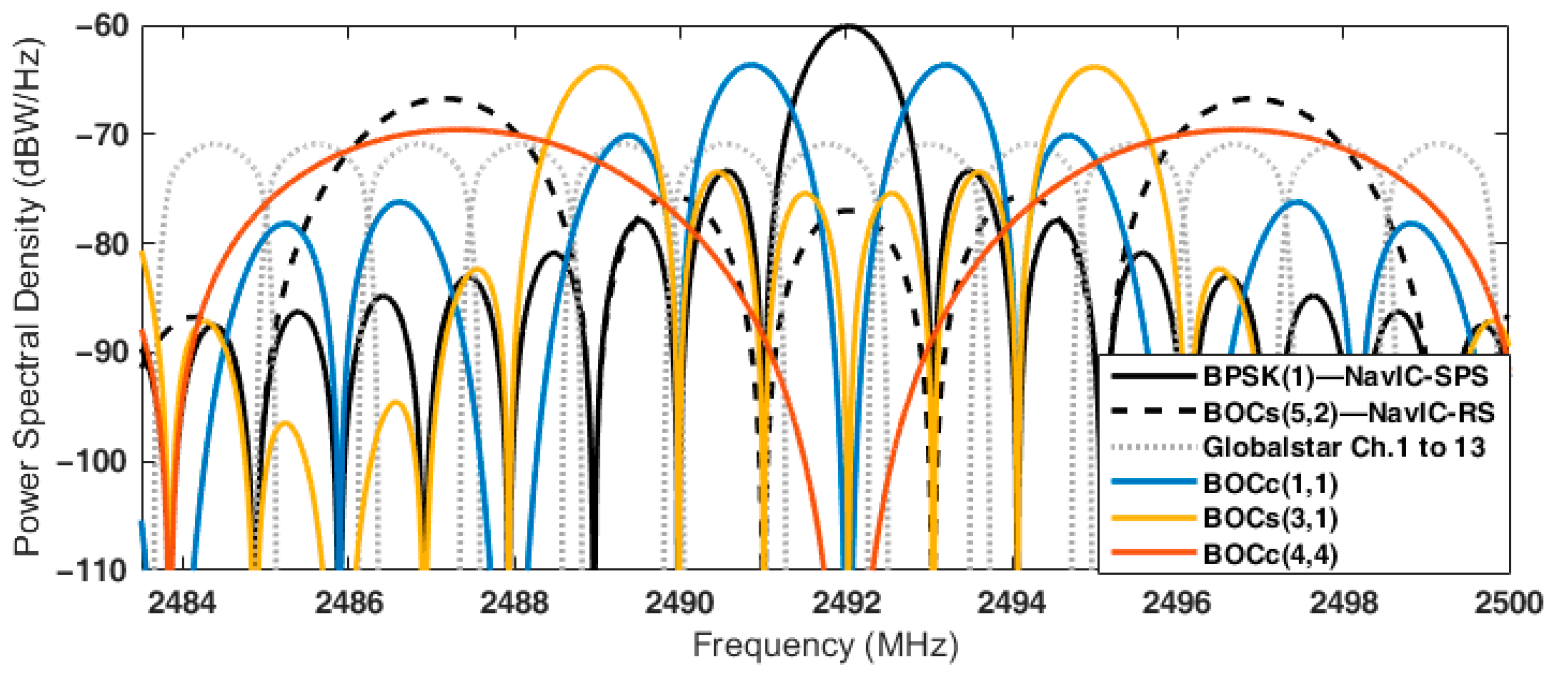
4.1. SSC Analysis Results
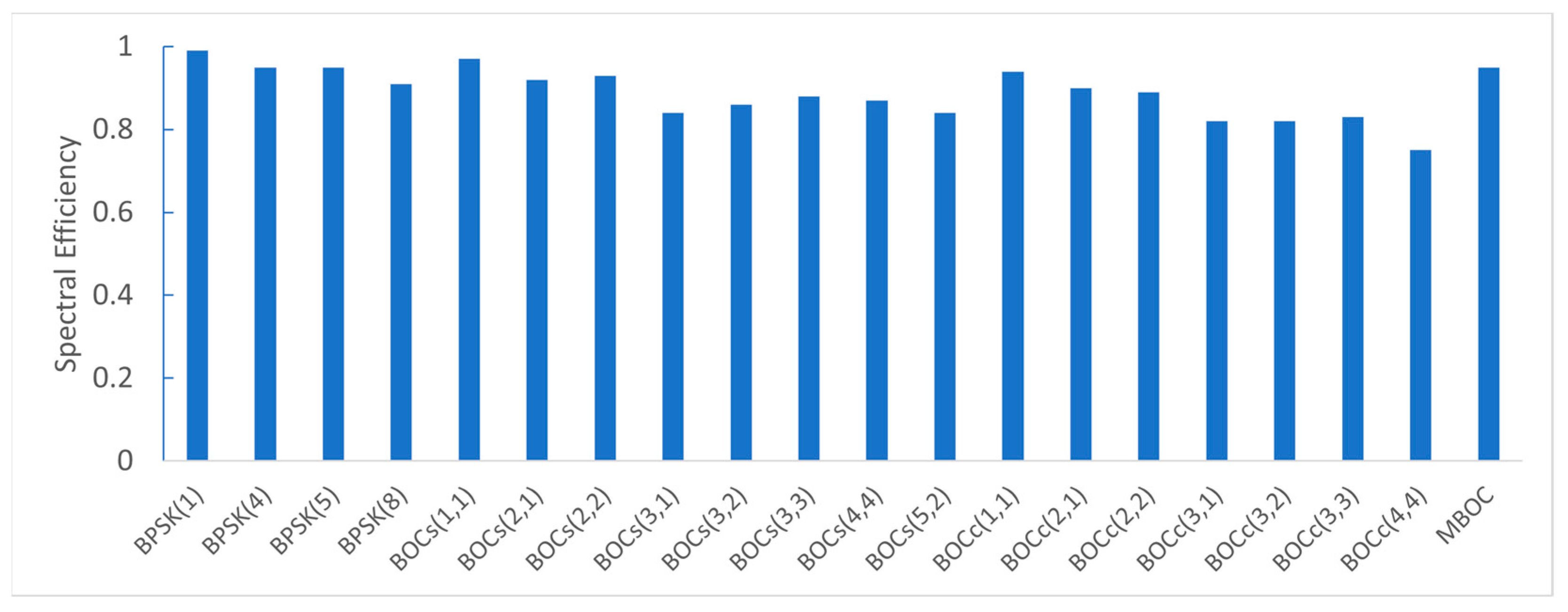
4.2. Spectral Efficiency Analysis Results
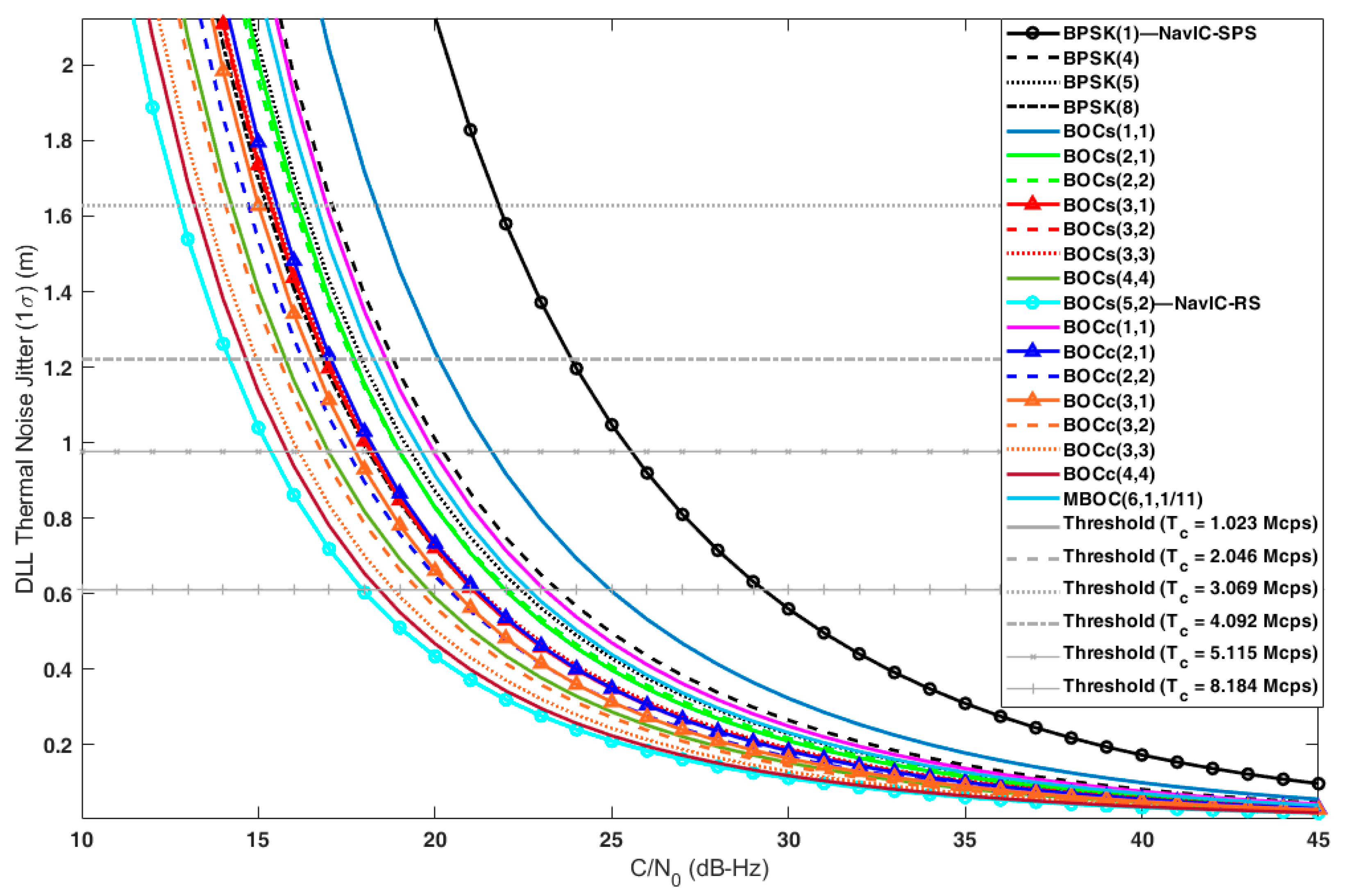
4.3. DLL Error Analysis Results
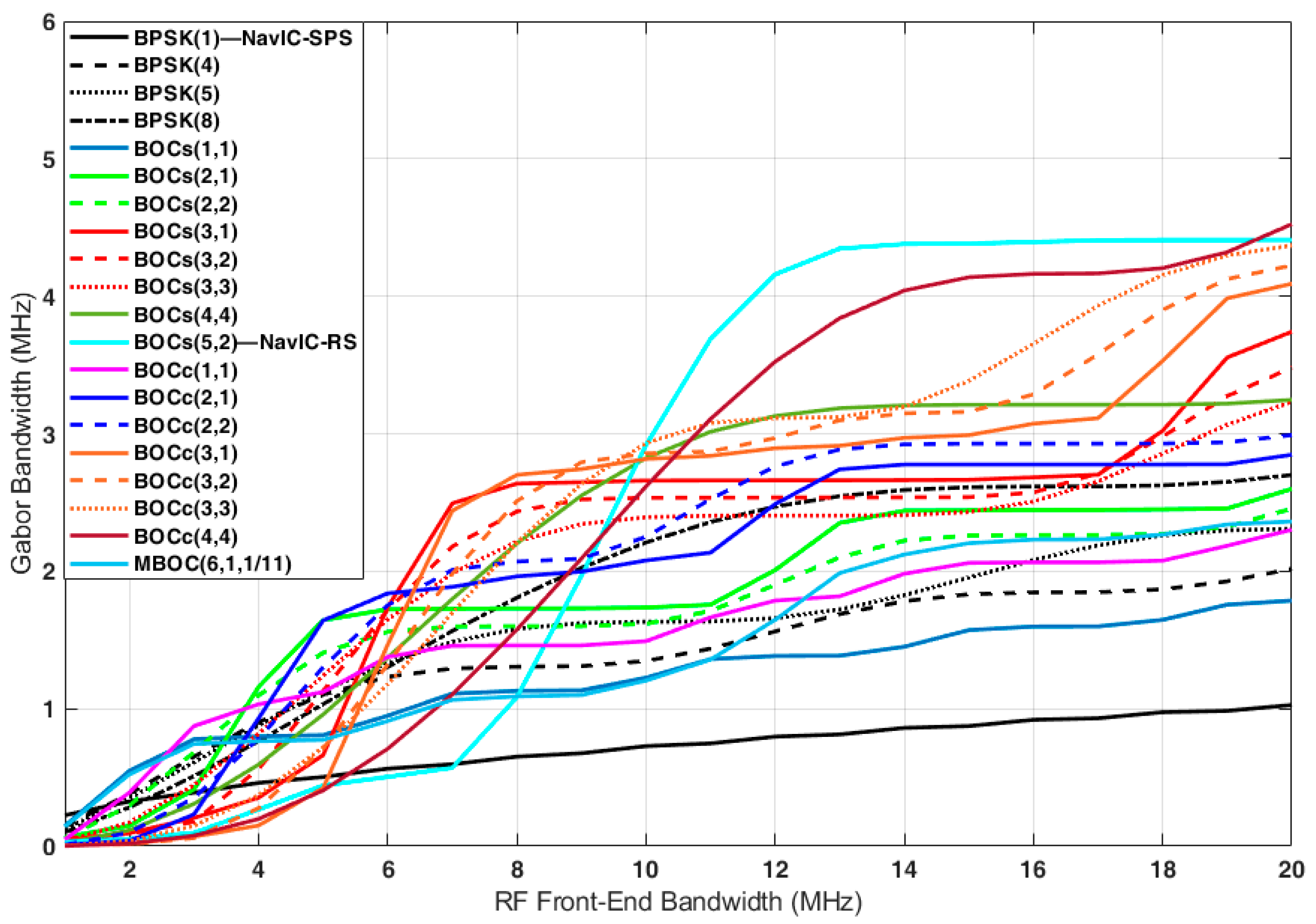
4.4. Gabor Bandwidth Analysis Results
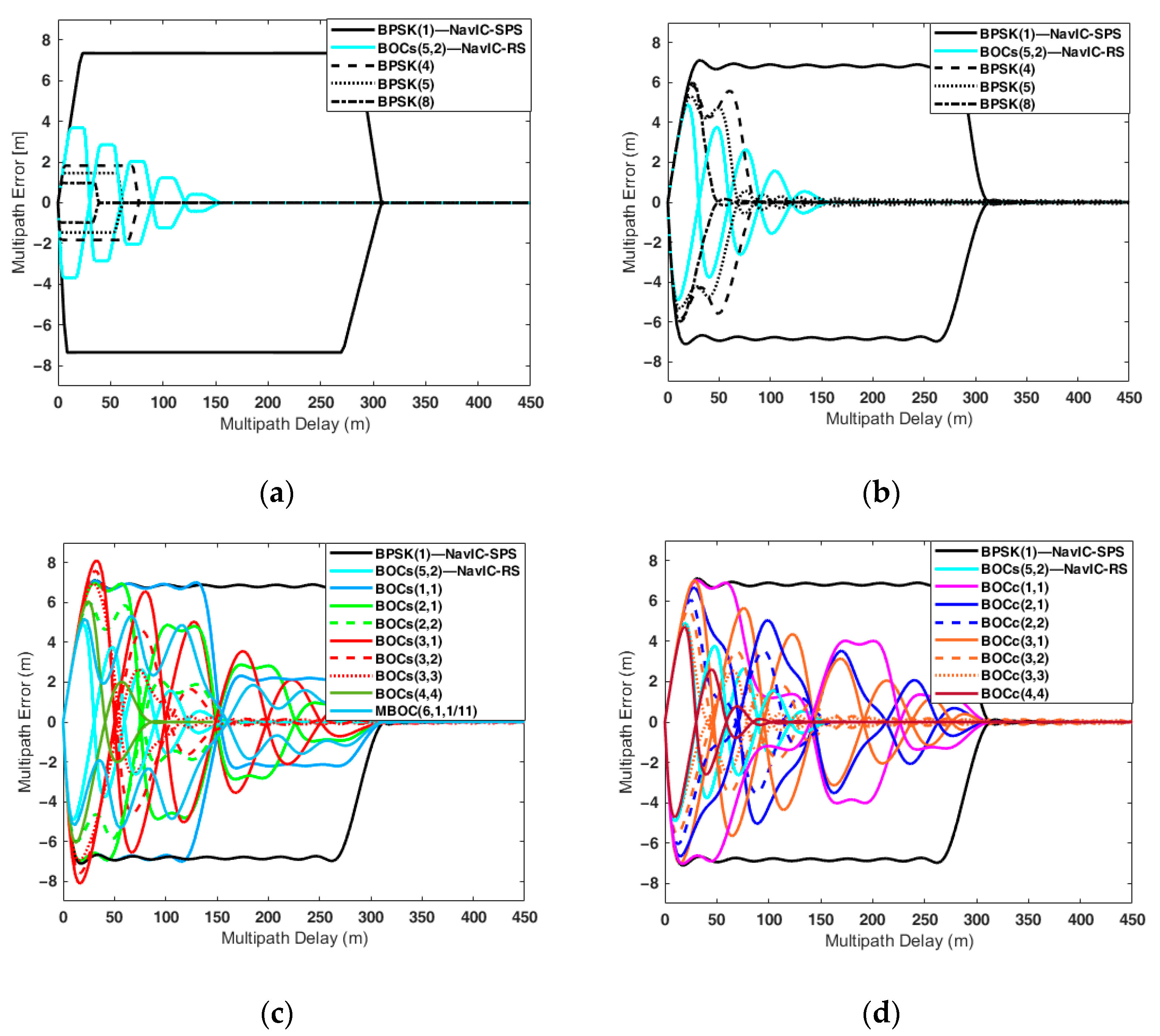
4.5. Multipath Error Analysis Results
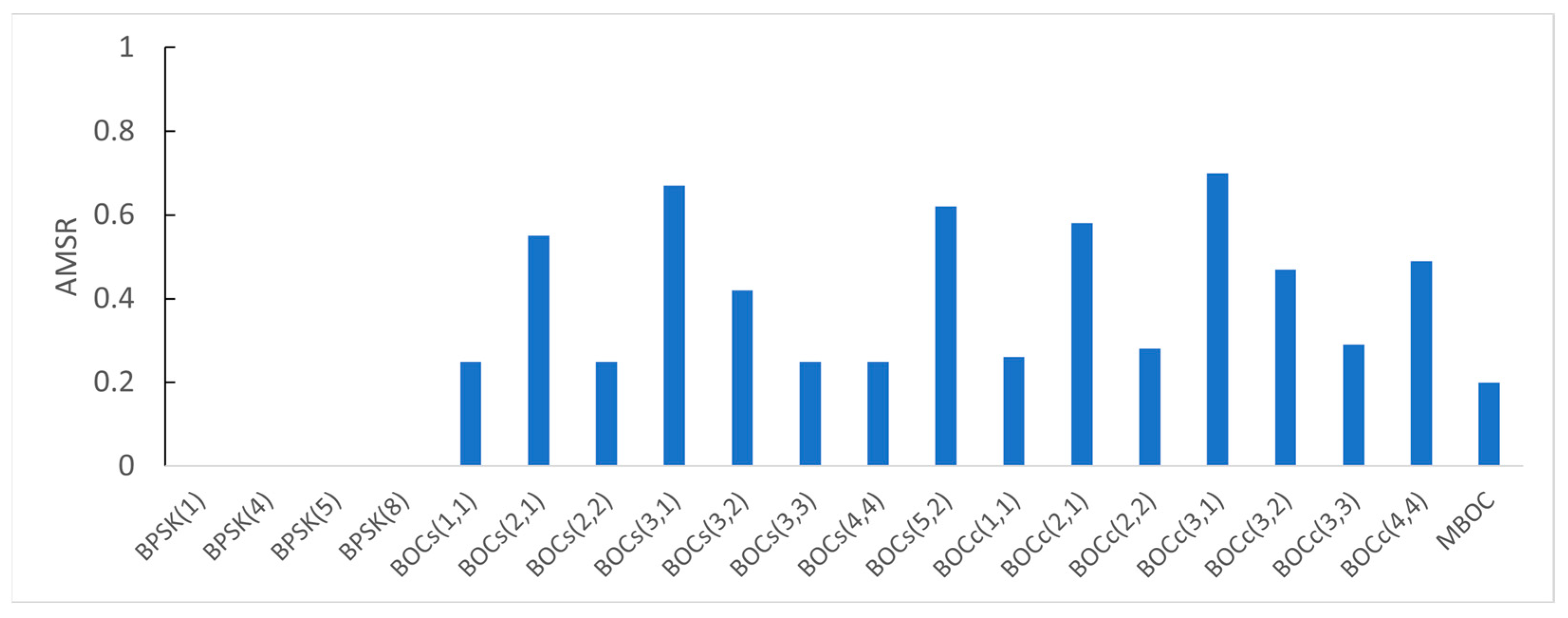
4.6. AMSR Analysis Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Disclaimer
References
- The State Council Information Office of the People’s Republic of China. China’s BeiDou Navigation Satellite System; Foreign Languages Press: Beijing, China, 2016.
- Completion and Commissioning of the BeiDou Navigation Satellite System (BDS-3). Available online: http://en.beidou.gov.cn/WHATSNEWS/202008/t20200803_21013.html (accessed on 1 January 2022).
- Programme. Available online: https://www.gsc-europa.eu/galileo/programme (accessed on 1 January 2022).
- Galileo Next-Gen Satellites on the Horizon. Available online: https://www.esa.int/Applications/Navigation/Galileo_next-gen_satellites_on_the_horizon (accessed on 1 January 2022).
- Nobuo, H. Status Update on the Quasi-Zenith Satellite System (QZSS). In Proceedings of the Fifteenth Meeting of the International Committee on Global Navigation Satellite Systems (ICG-15), Vienna, Austria, 27 September–1 October 2021. [Google Scholar]
- Sura, P.S. NavIC and GAGAN System Update. In Proceedings of the Fifteenth Meeting of the International Committee on Global Navigation Satellite Systems (ICG-15), Vienna, Austria, 27 September–1 October 2021. [Google Scholar]
- Kim, T. Korean Positioning System (KPS) and Korean Augmentation Satellite System (KASS) Update. In Proceedings of the Fifteenth Meeting of the International Committee on Global Navigation Satellite Systems (ICG-15), Vienna, Austria, 27 September–1 October 2021. [Google Scholar]
- Launch to Become the World’s Seventh ‘Space Powerhouse’! Available online: https://www.msit.go.kr/bbs/view.do?sCode=eng&mId=4&mPid=2&bbsSeqNo=42&nttSeqNo=568 (accessed on 1 January 2022).
- Signing Ceremony for Korea-U.S. Joint Statement on Civil Global Navigation Satellite Systems Cooperation. Available online: https://www.msit.go.kr/bbs/view.do?sCode=eng&mId=4&mPid=2&bbsSeqNo=42&nttSeqNo=514 (accessed on 1 January 2022).
- Hein, G.W.; Godet, J.; Issler, J.-L.; Martin, J.-C.; Lucas-Rodriguez, R.; Pratt, T. The GALILEO Frequency Structure and Signal Design. In Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2001), Salt Lake City, UT, USA, 11–14 September 2001. [Google Scholar]
- Irsigler, M.; Hein, G.W.; Schmitz-Peiffer, A. A Use of C-Band frequencies for satellite navigation: Benefits and drawbacks. GPS Solut. 2004, 8, 119–139. [Google Scholar] [CrossRef]
- Avila-Rodriguez, J.-A.; Wallner, S.; Won, J.-H.; Eissfeller, B.; Schmitz-Peiffer, A.; Floch, J.-J.; Colzi, E.; Gerner, J.-L. Study on a Galileo Signal and Service Plan for C-Band. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Schmitz-Peiffer, A.; Stopfkuchen, L.; Soualle, F.; Floch, J.-J.; King, R.; Fernandez, A.; Jorgensen, R.; Eissfeller, B.; Avila Rodriguez, J.-A.; Wallner, S.; et al. Assessment on the use of C-Band for GNSS within the European GNSS Evolution Programme. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Won, J.-H.; Avila-Rodriguez, J.-A.; Wallner, S.; Eissfeller, B.; Floch, J.-J.; Schmitz-Peiffer, A.; Colzi, E. C-Band User Terminal Aspect for Bandwidth Efficient Modulation Schemes in European GNSS Evolution Programme. In Proceedings of the International Symposium on GPS/GNSS 2008, Tokyo, Japan, 11–14 November 2008. [Google Scholar]
- ITU. Final Acts of the WARC MOB-87; ITU: Geneva, Switzerland, 1987; pp. 74–75. ISBN 92-61-03101-3. [Google Scholar]
- ITU. Radio Regulations, 1990 ed.; ITU: Geneva, Switzerland, 1994; Volume 1, pp. RR8-116–RR8-118. ISBN 92-61-05171-5. [Google Scholar]
- Xue, R.; Sun, Y.; Zhao, D. CPM signals for satellite navigation in the S and C bands. Sensors 2015, 15, 13184–13200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mateu, I.; Paonni, M.; Issler, J.-L.; Eissfeller, B.; Ries, L.; Boulanger, C.; Mulassano, P.; Caporale, M.; Germaine, S.; Guyomard, J.-Y.; et al. A search for spectrum: GNSS signals in S-Band part 2. Inside GNSS 2010, 5, 46–53. [Google Scholar]
- Matzner, R.; Englberger, F.; Huber, J. A digital transmission system using quaternary partial response CPM: Principle structure and measurement results. In Proceedings of the ICC’93-IEEE International Conference on Communications, Geneva, Switzerland, 23–26 May 1993. [Google Scholar] [CrossRef]
- Ghassemi, A.; Gulliver, T.A. Carrier Frequency Offset Mitigation in OFDM Systems Using Efficient Tone Reservation. In Proceedings of the Seventh Annual Communication Networks and Services Research Conference, Moncton, NB, Canada, 11–13 May 2009. [Google Scholar] [CrossRef]
- Mateu, I.; Boulanger, C.; Issler, J.-L.; Ries, L.; Avila-Rodriguez, J.-A.; Wallner, S.; Kraus, T.; Eissfeller, B.; Mulassano, P.; Germaine, S.; et al. Exploration of possible GNSS signals in S-band. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009. [Google Scholar]
- Mateu, I.; Paonni, M.; Issler, J.-L.; Hein, G.W. A search for spectrum: GNSS signals in S-Band part 1. Inside GNSS 2010, 5, 65–71. [Google Scholar]
- Sun, Y.; Xue, R.; Zhao, D.; Wang, D. Radio Frequency Compatibility Evaluation of S Band Navigation Signals for Future BeiDou. Sensors 2017, 17, 1039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, K.; Won, J.-H. Investigation on Figures-of-Merit of Signal Performance for Next Generation RNSS Signal Design. JPNT 2020, 9, 191–205. [Google Scholar] [CrossRef]
- Han, K.; Won, J.-H. Investigation on the Relationship between GNSS Signal Design Parameters and its Navigation Performance for the Next Generation GNSS Signal Design. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018. [Google Scholar]
- ITU. Radio Regulations, 2020 ed.; ITU: Geneva, Switzerland, 2020; Volume 1, pp. 114–116. ISBN 978-92-61-30301-3. [Google Scholar]
- Majithiya, P. Enhancements in upcoming NavIC Satellites. In Proceedings of the Fourteenth Meeting of the International Committee on Global Navigation Satellite Systems (ICG-14), Bengaluru, India, 9–13 December 2019. [Google Scholar]
- Indian Space Research Organization. IRNSS Signal-in-Space Interface Control Document (ISRO-IRNSS-ICD-SPS-1.1); Indian Space Research Organization: Bengaluru, India, 2017. [Google Scholar]
- Globalstar Satellites. Available online: https://www.n2yo.com/satellites/?c=17 (accessed on 1 January 2022).
- Globalstar, L.P. Description of the Globalstar System (GS-TR-94-0001); Revision, E; Globalstar, L.P.: San Jose, CA, USA, 2020.
- Mazar, H. Internaltional, regional and national regulation of SRDs. In Proceedings of the ITU Workshop on Short Range Devices (SDRs) and Ultra Wide Band (UWB), Geneva, Switzerland, 3 June 2014; Available online: https://www.itu.int/en/ITU-R/study-groups/workshops/RWP1B-SRD-UWB-14/Presentations/International,%20regional%20and%20national%20regulation%20of%20SRDs.pdf (accessed on 11 February 2022).
- Han, K.; Song, Y.-J.; Won, J.-H. A Study on the Effects of Out-of-Band Interference on RNSS Receivers in S-band. In Proceedings of the 34th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021. [Google Scholar] [CrossRef]
- Grini, D. RF basics, RF for non-RF engineers. In Proceedings of the ATC 2006—MSP430 Advanced Technical Conference 2006, Sonthofen, Germany, 10–11 September 2006; Available online: https://www.ti.com/lit/ml/slap127/slap127.pdf. (accessed on 11 February 2022).
- Baghel, S.K.; Ingale, M.A.; Goyal, G. Coexistence possibilities of LTE with ISM technologies and GNSS. In Proceedings of the 2011 National Conference on Communications (NCC), Bangalore, India, 28–30 January 2011. [Google Scholar] [CrossRef]
- Avila-Rodríguez, J.-A.; Hein, G.H.; Wallner, S.; Issler, J.-L.; Ries, L.; Lestarquit, L.; de Latour, A.; Godet, J.; Bastide, F.; Pratt, T.; et al. The MBOC modulation: The final touch to the Galileo frequency and signal plan. Navigation 2008, 55, 15–28. [Google Scholar] [CrossRef]
- ITU. A Coordination Methodology for Radionavigation-Satellite Service Inter-System Interference Estimation (Recommendation ITU-R M.1831-1); ITU: Geneva, Switzerland, 2015. [Google Scholar]
- Betz, J.W.; Goldstein, D.B. Candidate Designs for an Additional Civil Signal in GPS Spectral Bands. In Proceedings of the 2002 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 28–30 January 2002. [Google Scholar]
- Avila-Rodriguez, J.-A. On Generalized Signal Waveforms for Satellite Navigation. Ph.D. Thesis, Universität der Bundeswehr München, Neubiberg, Germany, 2008. [Google Scholar]
- Hegarty, C.J.; Kaplan, E.D.; de Haag, M.U.; Cosentino, R. GNSS Errors. In Understanding GPS: Principles and Applications, 3rd ed.; Kaplan, E.D., Hegarty, C.J., Eds.; Artech House Inc.: Norwood, MA, USA, 2017; pp. 619–659, ISBN-13: 978-1-63081-058-0. [Google Scholar]
- Ward, P.W. GNSS Receivers. In Understanding GPS: Principles and Applications, 3rd ed.; Kaplan, E.D., Hegarty, C.J., Eds.; Artech House Inc.: Norwood, MA, USA, 2017; pp. 339–548, ISBN-13: 978-1-63081-058-0. [Google Scholar]
- Betz, J.W.; Kolodzieiski, K.R. Generalized Theory of Code Tracking with an Early-Late Discriminator Part I: Lower Bound and Coherent Processing. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1538–1556. [Google Scholar] [CrossRef]
- Betz, J.W.; Kolodzieiski, K.R. Generalized Theory of Code Tracking with an Early-Late Discriminator Part II: Noncoherent Processing and Numerical Results. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1557–1564. [Google Scholar] [CrossRef]
- Zhang, X.; Zhan, X.Q. Joint Determination of Precorrelation Bandwidth, Sampling Frequency and Quantization in Wideband Compass Receivers. Navigation 2012, 59, 195–208. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006; pp. 393–430, ISBN-13:978-0970954411. [Google Scholar]
- Irsigler, M. Multipath Propagation, Mitigation and Monitoring in the Light of Galileo and the Modernized GPS. Ph.D. Thesis, Universität der Bundeswehr München, Neubiberg, Germany, 2008. [Google Scholar]
- Fine, P.; Wilson, W. Tracking Algorithm for GPS Offset Carrier Signals. In Proceedings of the 1999 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 25–27 January 1999. [Google Scholar]
- Hao, F.; Yu, B.; Gan, X.; Jia, R.; Zhang, H.; Huang, L.; Wang, B. Unambiguous Acquisition/Tracking Technique Based on Sub-Correlation Functions for GNSS Sine-BOC Signals. Sensors 2020, 20, 485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Julien, O.; Macabiau, C.; Cannon, M.E.; Lachapelle, G. ASPeCT: Unambiguous sine-BOC(n,n) acquisition/tracking technique for navigation applications. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 150–162. [Google Scholar] [CrossRef] [Green Version]
- Yao, Z.; Lu, M.; Feng, Z. Unambiguous sine-phased binary offset carrier modulated signal acquisition technique. IEEE Trans. Wirel. Commun. 2010, 9, 577–580. [Google Scholar] [CrossRef]
- Dey, A.; Singh, P.; Sharma, N. Performance Evaluation of Tracking Loop under RF Interference using NavIC Software-Receiver. In Proceedings of the 2019 IEEE Asia-Pacific Microwave Conference (APMC), Singapore, 19 March 2019. [Google Scholar] [CrossRef]
- Ghosh, U. An Empirical Performance Study of IRNSS S-band Signals under Bluetooth Interference. In Proceedings of the 2019 URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019. [Google Scholar] [CrossRef]





| Frequency (MHz) | Allocated Services |
|---|---|
| 2450–2483.5 | Fixed Mobile Radiolocation * |
| 2483.5–2500 | Fixed Mobile Mobile satellite (space-to-Earth) Radiolocation * RDSS (space-to-Earth) |
| 2500–2520 | Fixed Fixed satellite (space-to-Earth) ** Mobile (except aeronautical mobile) Mobile satellite (space-to-Earth) *** |
| Service Name | Center Frequency (MHz) | Modulation | Code Length (Family) | Message Type | Data Rate |
|---|---|---|---|---|---|
| SPS-S | 2492.028 | BPSK(1) | 1023 chips (Gold) | IRNSS | 25 bps (50 sps) |
| RS-S | BOCs(5,2) | N/A | N/A | N/A |
| Center Frequency (MHz) | Modulation Type | Chip Rate
(Mcps) | Subcarrier Frequency (MHz) | Remarks |
|---|---|---|---|---|
| 2492.028 | BPSK-R | 1.023 | - | NavIC S-SPS [22] |
| 4.092 | - | [22] | ||
| 5.115 | - | - | ||
| 8.184 | - | [22] [17] | ||
| Sine-BOC (BOCs) | 1.023 | 1.023 | [22] | |
| 1.023 | 2.046 | - | ||
| 2.046 | 2.046 | - | ||
| 1.023 | 3.069 | - | ||
| 2.046 | 3.069 | - | ||
| 3.069 | 3.069 | - | ||
| 4.192 | 4.192 | [23] | ||
| 2.046 | 5.115 | NavIC S-RS | ||
| Cosine-BOC (BOCc) | 1.023 | 1.023 | - | |
| 1.023 | 2.046 | - | ||
| 2.046 | 2.046 | - | ||
| 1.023 | 3.069 | - | ||
| 2.046 | 3.069 | - | ||
| 3.069 | 3.069 | - | ||
| 4.192 | 4.192 | - | ||
| MBOC | 1.023 | 1.023 6.138 | [22] |
| Candidates | (MHz) | SSC (dB/Hz) | (MHz) | SSC (dB/Hz) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BPSK(1) (S-SPS) | BOCs(5,2) (S-RS) | Globalstar (for 1 Ch.) | Self SSC | BPSK(1) (S-SPS) | BOCs(5,2) (S-RS) | Globalstar (for 1 Ch.) | Self SSC | |||
| BPSK(1) | 16.5 | −61.85 | −77.80 | −73.04 | −61.85 | 2.046 | −61.86 | −77.51 | −73.04 | −61.86 |
| BPSK(4) | −66.47 | −78.27 | −77.45 | −67.85 | 8.184 | −66.48 | −79.80 | −77.45 | −67.86 | |
| BPSK(5) | −67.36 | −78.76 | −78.37 | −68.81 | 10.23 | −67.36 | −78.95 | −78.37 | −68.82 | |
| BPSK(8) | −69.27 | −74.86 | −80.34 | −70.83 | 16.368 | −69.27 | −74.86 | −80.34 | −70.83 | |
| BOCs(1,1) | −67.86 | −80.04 | −75.80 | −64.84 | 4.092 | −67.87 | −83.33 | −75.80 | −64.88 | |
| BOCs(2,1) | −73.87 | −76.66 | −76.83 | −66.06 | 6.138 | −73.88 | −77.90 | −76.83 | −66.11 | |
| BOCs(2,2) | −73.87 | −77.81 | −77.48 | −67.83 | 8.184 | −73.88 | −79.67 | −77.48 | −67.86 | |
| BOCs(3,1) | −77.38 | −80.34 | −76.87 | −66.35 | 8.184 | −77.39 | −80.88 | −76.87 | −66.35 | |
| BOCs(3,2) | −73.40 | −77.33 | −78.01 | −68.72 | 10.23 | −73.40 | −77.34 | −78.01 | −68.73 | |
| BOCs(3,3) | −77.39 | −76.83 | −79.03 | −69.59 | 12.276 | −77.39 | −76.83 | −79.03 | −69.59 | |
| BOCs(4,4) | −79.87 | −72.97 | −80.28 | −70.82 | 16.368 | −79.87 | −72.97 | −80.28 | −70.82 | |
| BOCs(5,2) | −77.80 | −69.20 | −78.45 | −69.20 | 14.322 | −77.80 | −69.20 | −78.45 | −69.20 | |
| BOCc(1,1) | −73.88 | −79.37 | −76.52 | −66.08 | 4.092 | −74.03 | −84.27 | −76.52 | −66.28 | |
| BOCc(2,1) | −79.89 | −75.29 | −76.37 | −66.43 | 6.138 | −80.09 | −78.02 | −76.37 | −66.53 | |
| BOCc(2,2) | −79.88 | −74.87 | −78.27 | −69.06 | 8.184 | −80.00 | −79.40 | −78.27 | −69.24 | |
| BOCc(3,1) | −83.44 | −77.85 | −77.18 | −66.53 | 8.184 | −83.62 | −80.68 | −77.18 | −66.54 | |
| BOCc(3,2) | −83.44 | −74.83 | −78.42 | −69.37 | 10.23 | −83.52 | −75.28 | −78.42 | −69.42 | |
| BOCc(3,3) | −83.42 | −72.87 | −79.75 | −70.84 | 12.276 | −83.49 | −72.88 | −79.75 | −70.95 | |
| BOCc(4,4) | −85.97 | −71.17 | −80.89 | −72.16 | 16.368 | −85.97 | −71.17 | −80.89 | −72.16 | |
| MBOC | −68.26 | −78.52 | −76.20 | −65.61 | 14.328 | −68.26 | −78.52 | −76.20 | −65.61 | |
| Candidates | (MHz) | Spectral Efficiency |
|---|---|---|
| BPSK(1) | 16.5 | 0.99 |
| BPSK(4) | 0.95 | |
| BPSK(5) | 0.95 | |
| BPSK(8) | 0.91 | |
| BOCs(1,1) | 0.97 | |
| BOCs(2,1) | 0.92 | |
| BOCs(2,2) | 0.93 | |
| BOCs(3,1) | 0.84 | |
| BOCs(3,2) | 0.86 | |
| BOCs(3,3) | 0.88 | |
| BOCs(4,4) | 0.87 | |
| BOCs(5,2) | 0.84 | |
| BOCc(1,1) | 0.94 | |
| BOCc(2,1) | 0.90 | |
| BOCc(2,2) | 0.89 | |
| BOCc(3,1) | 0.82 | |
| BOCc(3,2) | 0.82 | |
| BOCc(3,3) | 0.83 | |
| BOCc(4,4) | 0.75 | |
| MBOC | 0.95 |
(s) | Tx. Filter | Rx. Filter | Code Tracking Parameters | |||||
|---|---|---|---|---|---|---|---|---|
| Type | BW (MHz) | Type | BW (MHz) | (Hz) | Loop Order | Discriminator Type | EML Spacing (Chips) | |
| 0.02 | - | Brick-wall | 16.5 | 0.1 | 1 | NELP | 0.1 | |
| Candidates | DLL Error (m) | Minimum Required C/N0 (dB-Hz) | |
|---|---|---|---|
| C/N0 = 20 dB-Hz | C/N0 = 40 dB-Hz | ||
| BPSK(1) | 2.13 | 0.17 | 15.12 |
| BPSK(4) | 1.01 | 0.08 | 18.81 |
| BPSK(5) | 0.87 | 0.07 | 19.30 |
| BPSK(8) | 0.66 | 0.05 | 21.06 |
| BOCs(1,1) | 1.24 | 0.10 | 12.43 |
| BOCs(2,1) | 0.83 | 0.06 | 10.65 |
| BOCs(2,2) | 0.83 | 0.07 | 13.86 |
| BOCs(3,1) | 0.72 | 0.06 | 9.94 |
| BOCs(3,2) | 0.72 | 0.06 | 13.25 |
| BOCs(3,3) | 0.74 | 0.06 | 15.40 |
| BOCs(4,4) | 0.59 | 0.05 | 15.77 |
| BOCs(5,2) | 0.43 | 0.03 | 10.79 |
| BOCc(1,1) | 0.97 | 0.08 | 11.31 |
| BOCc(2,1) | 0.73 | 0.06 | 10.16 |
| BOCc(2,2) | 0.65 | 0.05 | 12.66 |
| BOCc(3,1) | 0.66 | 0.05 | 9.73 |
| BOCc(3,2) | 0.56 | 0.04 | 12.06 |
| BOCc(3,3) | 0.50 | 0.04 | 13.50 |
| BOCc(4,4) | 0.47 | 0.04 | 14.65 |
| MBOC | 1.24 | 0.10 | 11.09 |
| Candidates | Gabor Bandwidth (MHz) | ||
|---|---|---|---|
| = 4 MHz | = 16.5 MHz | or 2() | |
| BPSK(1) | 0.46 | 0.93 | 0.33 |
| BPSK(4) | 0.90 | 1.85 | 1.31 |
| BPSK(5) | 0.88 | 2.19 | 1.63 |
| BPSK(8) | 0.76 | 2.62 | 2.62 |
| BOCs(1,1) | 0.80 | 1.60 | 0.80 |
| BOCs(2,1) | 1.16 | 2.45 | 1.72 |
| BOCs(2,2) | 1.10 | 2.26 | 1.60 |
| BOCs(3,1) | 0.35 | 2.70 | 2.64 |
| BOCs(3,2) | 0.56 | 2.71 | 2.53 |
| BOCs(3,3) | 0.82 | 2.65 | 2.40 |
| BOCs(4,4) | 0.59 | 3.21 | 3.21 |
| BOCs(5,2) | 0.27 | 4.41 | 4.38 |
| BOCc(1,1) | 1.03 | 2.06 | 1.03 |
| BOCc(2,1) | 0.93 | 2.78 | 1.84 |
| BOCc(2,2) | 0.78 | 2.93 | 2.07 |
| BOCc(3,1) | 0.15 | 3.11 | 2.70 |
| BOCc(3,2) | 0.28 | 3.58 | 2.86 |
| BOCc(3,3) | 0.37 | 3.93 | 3.11 |
| BOCc(4,4) | 0.20 | 4.17 | 4.16 |
| MBOC | 0.76 | 2.23 | 2.12 |
| Candidates | Max. MP Error (m) | RA of MPEE (m) ( = 16.5 MHz) | |||
|---|---|---|---|---|---|
| = 16.5 MHz | = 26 m | = 51 m | = 400 m | ||
| BPSK(1) | 7.35 | 7.12 | 4.72 | 5.66 | 4.82 |
| BPSK(4) | 1.83 | 5.83 | 4.18 | 4.47 | 0.86 |
| BPSK(5) | 1.46 | 5.31 | 3.89 | 4.16 | 0.73 |
| BPSK(8) | 0.98 | 5.98 | 4.20 | 3.09 | 0.41 |
| BOCs(1,1) | 7.35 | 7.10 | 4.72 | 5.65 | 3.00 |
| BOCs(2,1) | 7.35 | 6.97 | 4.67 | 5.59 | 2.23 |
| BOCs(2,2) | 3.68 | 6.00 | 4.24 | 4.67 | 1.14 |
| BOCs(3,1) | 7.35 | 8.12 | 5.07 | 4.81 | 2.02 |
| BOCs(3,2) | 3.69 | 7.58 | 4.95 | 4.81 | 1.14 |
| BOCs(3,3) | 2.46 | 6.95 | 4.72 | 4.60 | 0.86 |
| BOCs(4,4) | 1.83 | 6.04 | 4.18 | 3.11 | 0.50 |
| BOCs(5,2) | 3.68 | 4.90 | 3.22 | 2.87 | 0.63 |
| BOCc(1,1) | 7.35 | 7.03 | 4.69 | 5.62 | 2.13 |
| BOCc(2,1) | 7.35 | 6.66 | 4.48 | 4.64 | 1.76 |
| BOCc(2,2) | 3.68 | 6.06 | 4.19 | 3.42 | 0.80 |
| BOCc(3,1) | 6.82 | 7.03 | 4.60 | 3.95 | 1.73 |
| BOCc(3,2) | 3.68 | 5.56 | 3.90 | 2.93 | 0.83 |
| BOCc(3,3) | 2.46 | 4.80 | 3.35 | 2.20 | 0.54 |
| BOCc(4,4) | 1.83 | 4.72 | 3.24 | 2.48 | 0.37 |
| MBOC | 6.18 | 5.32 | 3.41 | 3.18 | 1.66 |
| Candidates | AMSR | ||
|---|---|---|---|
| = | or 2() | ||
| BPSK (1) | 0 | 0 | 0 |
| BPSK(4) | 0 | 0 | 0 |
| BPSK(5) | 0 | 0 | 0 |
| BPSK(8) | 0 | 0 | 0 |
| BOCs(1,1) | 0.25 | 0.25 | 0.25 |
| BOCs(2,1) | 0.56 | 0.55 | 0.54 |
| BOCs(2,2) | 0.25 | 0.25 | 0.25 |
| BOCs(3,1) | 0.68 | 0.67 | 0.68 |
| BOCs(3,2) | 0.44 | 0.42 | 0.42 |
| BOCs(3,3) | 0.25 | 0.25 | 0.25 |
| BOCs(4,4) | 0.25 | 0.25 | 0.25 |
| BOCs(5,2) | 0.62 | 0.62 | 0.62 |
| BOCc(1,1) | 0.25 | 0.26 | 0.49 |
| BOCc(2,1) | 0.56 | 0.58 | 0.77 |
| BOCc(2,2) | 0.25 | 0.28 | 0.49 |
| BOCc(3,1) | 0.68 | 0.70 | 0.87 |
| BOCc(3,2) | 0.44 | 0.47 | 0.67 |
| BOCc(3,3) | 0.25 | 0.29 | 0.49 |
| BOCc(4,4) | 0.25 | 0.49 | 0.49 |
| MBOC | 0.18 | 0.20 | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, K.; Lee, S.; You, M.; Won, J.-H. A Comprehensive Evaluation of Possible RNSS Signals in the S-Band for the KPS. Sensors 2022, 22, 2180. https://doi.org/10.3390/s22062180
Han K, Lee S, You M, Won J-H. A Comprehensive Evaluation of Possible RNSS Signals in the S-Band for the KPS. Sensors. 2022; 22(6):2180. https://doi.org/10.3390/s22062180
Chicago/Turabian StyleHan, Kahee, Sanguk Lee, Moonhee You, and Jong-Hoon Won. 2022. "A Comprehensive Evaluation of Possible RNSS Signals in the S-Band for the KPS" Sensors 22, no. 6: 2180. https://doi.org/10.3390/s22062180






