Direct Measurement of the Reduced Scattering Coefficient by a Calibrated Random Laser Sensor
Abstract
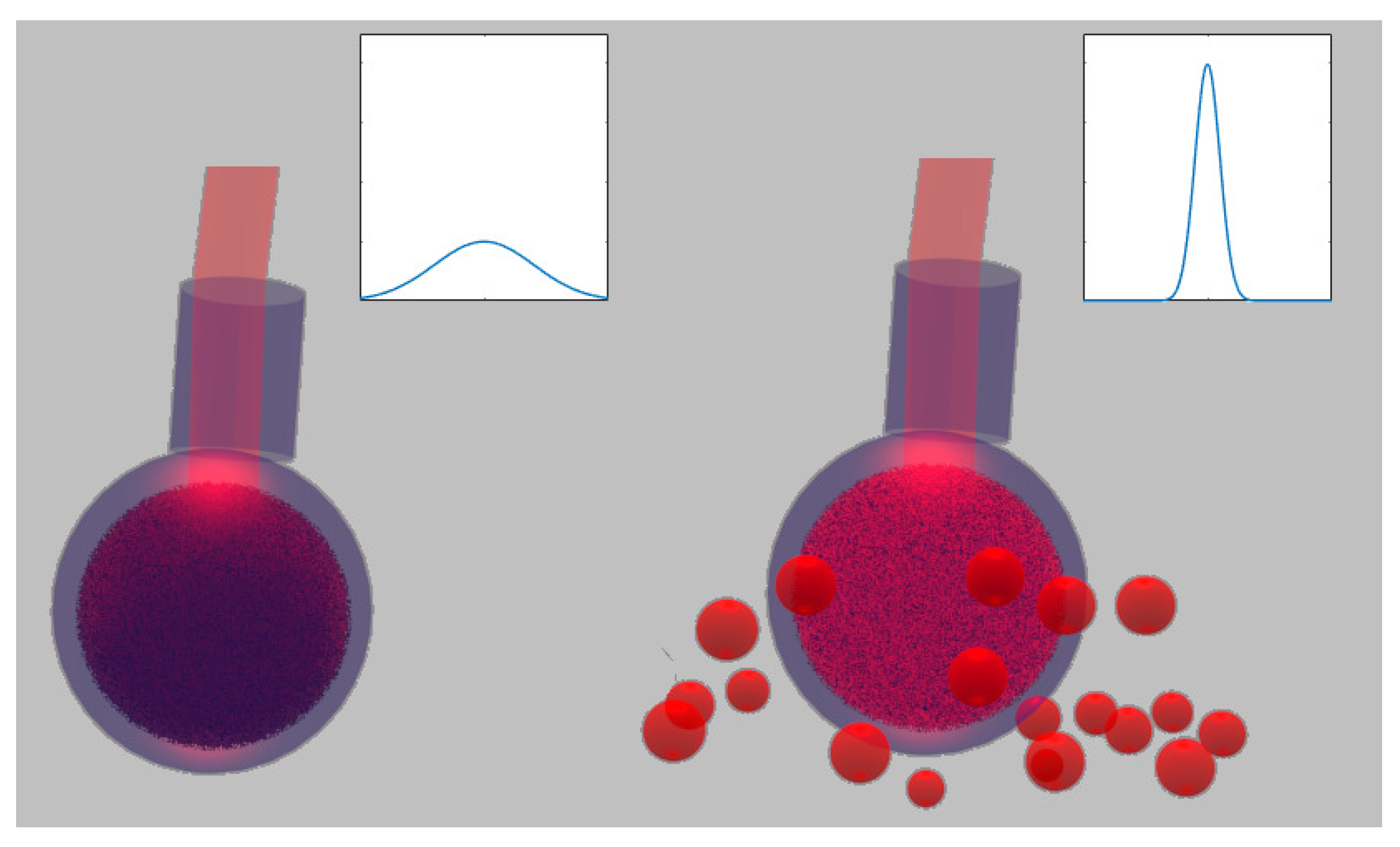
:1. Introduction
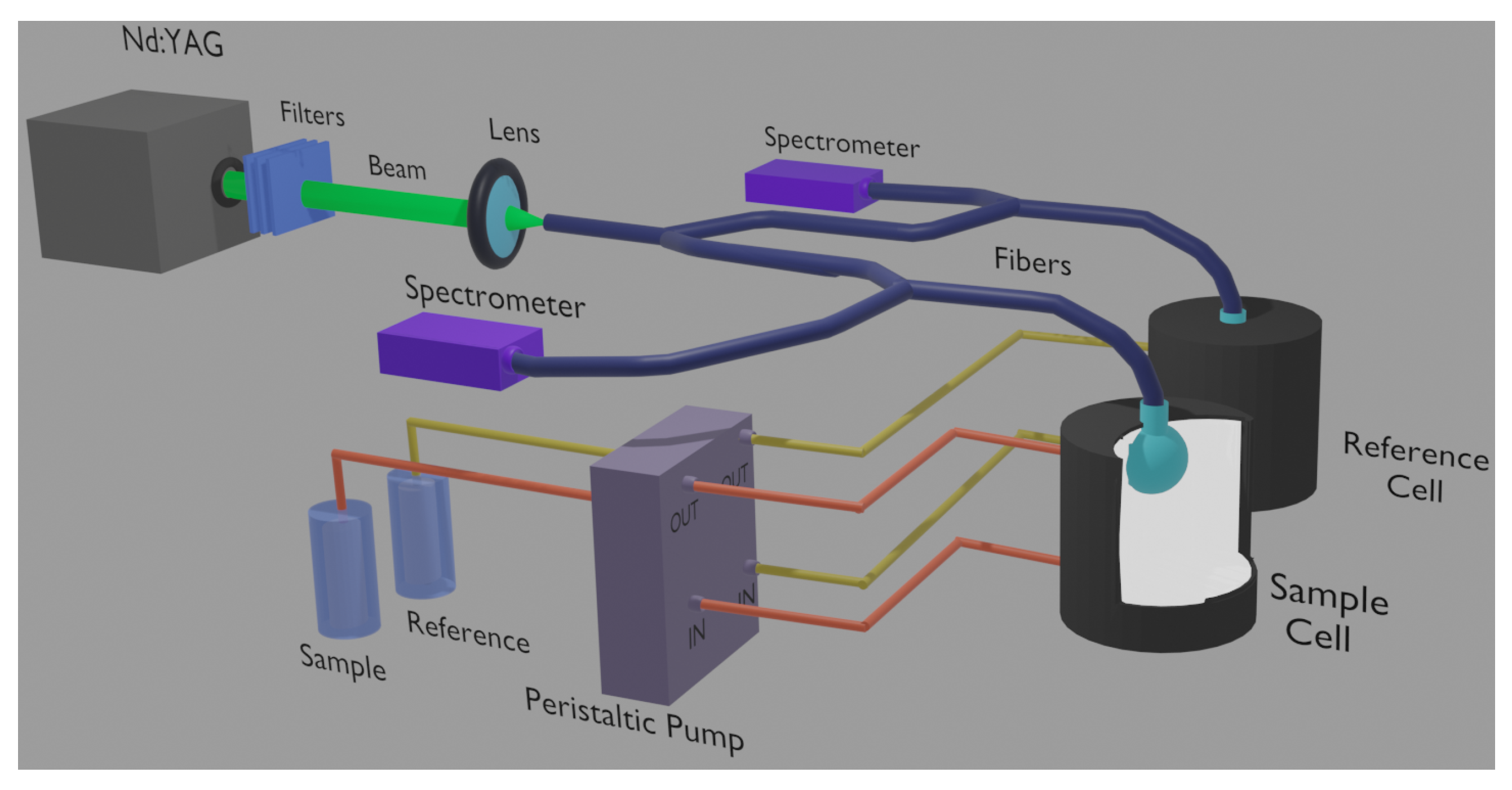
2. Experimental Setup
3. Results
4. Discussion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wiersma, D.S. The physics and applications of random lasers. Nat. Phys. 2008, 4, 359. [Google Scholar] [CrossRef]
- Letokhov, V.S. Generation of Light by a Scattering Medium with Negative Resonance Absorption. Sov. J. Exp. Theor. Phys. 1968, 26, 835. [Google Scholar]
- Lawandy, N.M.; Balachandran, R.M.; Gomes, A.S.L.; Sauvain, E. Laser action in strongly scattering median. Nature 1994, 368, 436. [Google Scholar] [CrossRef]
- Polson, R.C.; Vardeny, Z.V. Organic random lasers in the weak-scattering regime. Phys. Rev. B 2005, 71, 045205. [Google Scholar] [CrossRef]
- Frolov, S.V.; Vardeny, Z.V.; Yoshino, K.; Zakhidov, A.; Baughman, R.H. Stimulated emission in high-gain organic media. Phys. Rev. B 1999, 59, R5284–R5287. [Google Scholar] [CrossRef]
- Noginov, M.A.; Noginova, N.E.; Caulfield, H.J.; Venkateswarlu, P.; Thompson, T.; Mahdi, M.; Ostroumov, V. Short-pulsed stimulated emission in the powders of NdAl3(BO3)4, NdSc3(BO3)4, and Nd:Sr5(PO4)3F laser crystals. J. Opt. Soc. Am. B 1996, 13, 2024–2033. [Google Scholar] [CrossRef]
- Froufe-Pérez, L.S.; Guerin, W.; Carminati, R.; Kaiser, R. Threshold of a Random Laser with Cold Atoms. Phys. Rev. Lett. 2009, 102, 173903. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.; Zhao, Y.G.; Ho, S.T.; Seelig, E.W.; Wang, Q.H.; Chang, R.P.H. Random Laser Action in Semiconductor Powder. Phys. Rev. Lett. 1999, 82, 2278–2281. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Liu, D.; He, N.; Jacques, S.L.; Thomsen, S.L. Biological laser action. Appl. Opt. 1996, 35, 1775–1779. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Babin, S.A.; El-Taher, A.E.; Harper, P.; Churkin, D.V.; Kablukov, S.I.; Ania-Castañón, J.D.; Karalekas, V.; Podivilov, E.V. Random distributed feedback fiber laser. Nat. Photonics 2010, 4, 231. [Google Scholar] [CrossRef]
- Zhai, T.; Niu, L.; Cao, F.; Tong, F.; Li, S.; Wang, M.; Zhang, X. A RGB random laser on an optical fiber facet. RSC Adv. 2017, 7, 45852–45855. [Google Scholar] [CrossRef] [Green Version]
- Churkin, D.V.; Sugavanam, S.; Vatnik, I.D.; Wang, Z.; Podivilov, E.V.; Babin, S.A.; Rao, Y.; Turitsyn, S.K. Recent advances in fundamentals and applications of random fiber lasers. Adv. Opt. Photon. 2015, 7, 516–569. [Google Scholar] [CrossRef]
- Hokr, B.H.; Bixler, J.N.; Cone, M.T.; Mason, J.D.; Beier, H.T.; Noojin, G.D.; Petrov, G.I.; Golovan, L.A.; Thomas, R.J.; Rockwell, B.A.; et al. Bright emission from a random Raman laser. Nat. Commun. 2014, 5, 4356. [Google Scholar] [CrossRef] [PubMed]
- Wiersma, D.S.; Cavalieri, S. A temperature-tunable random laser. Nature 2001, 414, 708–709. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Pattelli, L.; Torre, R.; Wiersma, D.S. Remote control of liquid crystal elastomer random laser using external stimuli. Appl. Phys. Lett. 2018, 113, 013701. [Google Scholar] [CrossRef]
- Sznitko, L.; Kaliciak, K.; Adamow, A.; Mysliwiec, J. A random laser made of nematic liquid crystal doped with a laser dye. Opt. Mater. 2016, 56, 121–128. [Google Scholar] [CrossRef]
- Dice, G.D.; Mujumdar, S.; Elezzabi, A.Y. Plasmonically enhanced diffusive and subdiffusive metal nanoparticle-dye random laser. Appl. Phys. Lett. 2005, 86, 131105. [Google Scholar] [CrossRef]
- Qiao, Q.; Shan, C.X.; Zheng, J.; Zhu, H.; Yu, S.F.; Li, B.H.; Jia, Y.; Shen, D.Z. Surface plasmon enhanced electrically pumped random lasers. Nanoscale 2013, 5, 513–517. [Google Scholar] [CrossRef]
- Frolov, S.V.; Vardeny, Z.V.; Zakhidov, A.A.; Baughman, R.H. Laser-like emission in opal photonic crystals. Opt. Commun. 1999, 162, 241–246. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, X.; Wu, D.; Xu, T.; Tian, Y.T.; Zhang, Y.; Li, X.J.; Du, G. Near-infrared random lasing realized in perovskite CH3NH3PbI3 thin film. J. Mater. Chem. C 2016, 4, 8373–8379. [Google Scholar] [CrossRef]
- Choi, S.H.; Kim, Y.L. The potential of naturally occurring lasing for biological and chemical sensors. Biomed. Eng. Lett. 2014, 4, 201–212. [Google Scholar] [CrossRef]
- Ignesti, E.; Tommasi, F.; Fini, L.; Martelli, F.; Azzali, N.; Cavalieri, S. A new class of optical sensors: A random laser based device. Sci. Rep. 2016, 6, 35225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tommasi, F.; Ignesti, E.; Fini, L.; Martelli, F.; Cavalieri, S. Random laser based method for direct measurement of scattering properties. Opt. Express 2018, 26, 27615–27627. [Google Scholar] [CrossRef]
- Abegão, L.M.G.; Pagani, A.A.C.; Zílio, S.C.; Alencar, M.A.R.C.; Rodrigues, J.J. Measuring milk fat content by random laser emission. Sci. Rep. 2016, 6, 35119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, X.; Ge, K.; Tong, J.H.; Zhai, T. Low-cost biosensors based on a plasmonic random laser on fiber facet. Opt. Express 2020, 28, 12233–12242. [Google Scholar] [CrossRef] [PubMed]
- Hohmann, M.; Späth, M.; Ni, D.; Dörner, D.; Lengenfelder, B.; Klämpfl, F.; Schmidt, M. Random laser as a potential tool for the determination of the scattering coefficient. Biomed. Opt. Express 2021, 12, 5439–5451. [Google Scholar] [CrossRef] [PubMed]
- Redding, B.; Choma, M.A.; Cao, H. Speckle-free laser imaging using random laser illumination. Nat. Photonics 2012, 6, 355–359. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.W.; Liao, W.C.; Liao, Y.M.; Lin, H.I.; Lin, H.Y.; Lin, W.J.; Lin, S.Y.; Perumal, P.; Haider, G.; Tai, C.T.; et al. A White Random Laser. Sci. Rep. 2018, 8, 2720. [Google Scholar] [CrossRef]
- Shojaie, E.; Madanipour, K. Detection of nanoparticle changes in nanocomposite active sample using random laser emission. In Modeling Aspects in Optical Metrology VI; Bodermann, B., Frenner, K., Silver, R.M., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2017; Volume 10330, pp. 363–369. [Google Scholar]
- Xu, Y.; Zhang, M.; Lu, P.; Mihailov, S.; Bao, X. Multi-parameter sensor based on random fiber lasers. AIP Adv. 2016, 6, 095009. [Google Scholar] [CrossRef] [Green Version]
- Boschetti, A.; Taschin, A.; Bartolini, P.; Tiwari, A.K.; Pattelli, L.; Torre, R.; Wiersma, D.S. Spectral super-resolution spectroscopy using a random laser. Nat. Photonics 2020, 14, 177–182. [Google Scholar] [CrossRef]
- Giacomelli, G.; Lepri, S.; Trono, C. Optical networks as complex lasers. Phys. Rev. A 2019, 99, 023841. [Google Scholar] [CrossRef] [Green Version]
- Caselli, N.; Consoli, A.; Sánchez, Á.M.M.; López, C. Networks of mutually coupled random lasers. Optica 2021, 8, 193–201. [Google Scholar] [CrossRef]
- Sharma, D.; Ramachandran, H.; Kumar, N. Lévy statistical fluctuations from a random amplyfyng medium. Fluct. Noise Lett. 2006, 6, L95–L101. [Google Scholar] [CrossRef] [Green Version]
- Mujumdar, S.; Ricci, M.; Torre, R.; Wiersma, D.S. Amplified Extended Modes in Random Lasers. Phys. Rev. Lett. 2004, 93, 053903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lepri, S. Fluctuations in a Diffusive Medium with Gain. Phys. Rev. Lett. 2013, 110, 230603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lepri, S.; Cavalieri, S.; Oppo, G.L.; Wiersma, D.S. Statistical regimes of random laser fluctuations. Phys. Rev. A 2007, 75, 063820. [Google Scholar] [CrossRef] [Green Version]
- Uppu, R.; Tiwari, A.K.; Mujumdar, S. Identification of statistical regimes and crossovers in coherent random laser emission. Opt. Lett. 2012, 37, 662–664. [Google Scholar] [CrossRef] [Green Version]
- Ignesti, E.; Tommasi, F.; Fini, L.; Lepri, S.; Radhalakshmi, V.; Wiersma, D.S.; Cavalieri, S. Experimental and theoretical investigation of statistical regimes in random laser emission. Phys. Rev. A 2013, 88, 033820. [Google Scholar] [CrossRef] [Green Version]
- Tommasi, F.; Ignesti, E.; Fini, L.; Cavalieri, S. Controlling directionality and the statistical regime of the random laser emission. Phys. Rev. A 2015, 91, 033820. [Google Scholar] [CrossRef]
- Tommasi, F.; Fini, L.; Ignesti, E.; Lepri, S.; Martelli, F.; Cavalieri, S. Statistical outliers in random laser emission. Phys. Rev. A 2018, 98, 053816. [Google Scholar] [CrossRef]
- Uppu, R.; Mujumdar, S. Dependence of the Gaussian-Lévy transition on the disorder strength in random lasers. Phys. Rev. A 2013, 87, 013822. [Google Scholar] [CrossRef] [Green Version]
- Lima, B.C.; Pincheira, P.I.R.; Raposo, E.P.; Menezes, L.d.S.; de Araújo, C.B.; Gomes, A.S.L.; Kashyap, R. Extreme-value statistics of intensities in a cw-pumped random fiber laser. Phys. Rev. A 2017, 96, 013834. [Google Scholar] [CrossRef]
- Gofraniha, N.; Viola, I.; Di Maria, F.; Barbarella, G.; Gigli, G.; Leuzzi, L.; Conti, C. Experimental evidence of replica symmetry breaking in random lasers. Nat. Commun. 2015, 6, 6058. [Google Scholar] [CrossRef] [PubMed]
- Antenucci, F.; Crisanti, A.; Leuzzi, L. The glassy random laser: Replica symmetry breaking in the intensity fluctuations of emission spectra. Sci. Rep. 2015, 5, 16792. [Google Scholar] [CrossRef] [Green Version]
- Gomes, A.S.L.; Raposo, E.P.; Moura, A.L.; Fewo, S.I.; Pincheira, P.I.R.; Jerez, V.; Maia, L.J.Q.d.A. Observation of Lévy distribution and replica symmetry breaking in random lasers from a single set of measurements. Sci. Rep. 2016, 5, 27987. [Google Scholar] [CrossRef]
- Tommasi, F.; Ignesti, E.; Lepri, S.; Cavalieri, S. Robustness of replica symmetry breaking phenomenology in random laser. Sci. Rep. 2016, 6, 37113. [Google Scholar] [CrossRef]
- Araújo, C.B.d.; Gomes, A.S.L.; Raposo, E.P. Lévy Statistics and the Glassy Behavior of Light in Random Fiber Lasers. Appl. Sci. 2017, 7, 644. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; He, J.; Xie, K.; Zhang, X.; Hu, L.; Li, Y.; Chen, X.; Ma, J.; Wen, J.; Chen, J.; et al. Replica Symmetry Breaking in FRET-Assisted Random Laser Based on Electrospun Polymer Fiber. Ann. Phys. 2019, 531, 1900066. [Google Scholar] [CrossRef]
- Kong, J.; He, J.; Zhang, J.; Ma, J.; Xie, K.; Chen, J.; Hong, L.; Hu, Z. Replica Symmetry Breaking in Cholesteric Liquid Crystal Bandgap Lasing. Ann. Phys. 2021, 533, 2000328. [Google Scholar] [CrossRef]
- Gradenigo, G.; Antenucci, F.; Leuzzi, L. Glassiness and lack of equipartition in random lasers: The common roots of ergodicity breaking in disordered and nonlinear systems. Phys. Rev. Res. 2020, 2, 023399. [Google Scholar] [CrossRef]
- Chen, Y.; Fiorentino, A.; Dal Negro, L. A fractional diffusion random laser. Sci. Rep. 2019, 9, 8686. [Google Scholar] [CrossRef] [Green Version]
- Tommasi, F.; Fini, L.; Martelli, F.; Cavalieri, S. Superdiffusive random laser. Phys. Rev. A 2019, 99, 063836. [Google Scholar] [CrossRef] [Green Version]
- Roa González, I.; Lima, B.; Pincheira, P.; Brum, A.; Macêdo, A.; Vasconcelos, G.; Menezes, L.; Raposo, E.; Gomes, A.; Kashyap, R. Turbulence Hierarchy in a Random Fibre Laser. Nat. Commun. 2017, 8, 15731. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hokr, B.H.; Bixler, J.N.; Noojin, G.D.; Thomas, R.J.; Rockwell, B.A.; Yakovlev, V.V.; Scully, M.O. Single-shot stand-off chemical identification of powders using random Raman lasing. Proc. Natl. Acad. Sci. USA 2014, 111, 12320–12324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaio, M.; Caixeiro, S.; Marelli, B.; Omenetto, F.G.; Sapienza, R. Gain-Based Mechanism for pH Sensing Based on Random Lasing. Phys. Rev. Appl. 2017, 7, 034005. [Google Scholar] [CrossRef] [Green Version]
- Martelli, F.; Del-Bianco, S.; Zaccanti, G.; Pifferi, A.; Torricelli, A.; Bassi, A.; Taroni, P.; Cubeddu, R. Phantom validation and in vivo application of an inversion procedure for retrieving the optical properties of diffusive layered media from time-resolved reflectance measurements. Opt. Lett. 2004, 29, 2037–2039. [Google Scholar] [CrossRef]
- Farina, A.; Torricelli, A.; Bargigia, I.; Spinelli, L.; Cubeddu, R.; Foschum, F.; Jäger, M.; Simon, E.; Fugger, O.; Kienle, A.; et al. In-vivo multilaboratory investigation of the optical properties of the human head. Biomed. Opt. Express 2015, 6, 2609–2623. [Google Scholar] [CrossRef] [Green Version]
- Siddique, M.; Yang, L.; Wang, Q.; Alfano, R. Mirrorless laser action from optically pumped dye-treated animal tissues. Opt. Commun. 1995, 117, 475–479. [Google Scholar] [CrossRef]
- Song, Q.; Xiao, S.; Xu, Z.; Liu, J.; Sun, X.; Drachev, V.; Shalaev, V.M.; Akkus, O.; Kim, Y.L. Random lasing in bone tissue. Opt. Lett. 2010, 35, 1425–1427. [Google Scholar] [CrossRef]
- Zhang, D.; Kostovski, G.; Karnutsch, C.; Mitchell, A. Random lasing from dye doped polymer within biological source scatters: The pomponia imperatorial cicada wing random nanostructures. Org. Electron. 2012, 13, 2342–2345. [Google Scholar] [CrossRef]
- Wang, C.S.; Chang, T.Y.; Lin, T.Y.; Chen, Y.F. Biologically inspired flexible quasi-single-mode random laser: An integration of Pieris canidia butterfly wing and semiconductors. Sci. Rep. 2014, 4, 6736. [Google Scholar] [CrossRef] [PubMed]
- Polson, R.C.; Vardeny, Z.V. Random lasing in human tissues. Appl. Phys. Lett. 2004, 85, 1289–1291. [Google Scholar] [CrossRef]
- Polson, R.C.; Vardeny, Z.V. Cancerous tissue mapping from random lasing emission spectra. J. Opt. 2010, 12, 024010. [Google Scholar] [CrossRef]
- He, J.; Hu, S.; Ren, J.; Cheng, X.; Hu, Z.; Wang, N.; Zhang, H.; Lam, R.H.W.; Tam, H.Y. Biofluidic Random Laser Cytometer for Biophysical Phenotyping of Cell Suspensions. ACS Sens. 2019, 4, 832–840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lahoz, F.; Martín, I.R.; Urgellés, M.; Marrero-Alonso, J.; Marín, R.; Saavedra, C.J.; Boto, A.; Díaz, M. Random laser in biological tissues impregnated with a fluorescent anticancer drug. Laser Phys. Lett. 2015, 12, 045805. [Google Scholar] [CrossRef]
- Umar, M.; Min, K.; Kim, S.; Kim, S. Random lasing and amplified spontaneous emission from silk inverse opals: Optical gain enhancement via protein scatterers. Sci. Rep. 2019, 9, 16266. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.J.; Liao, Y.M.; Lin, H.Y.; Haider, G.; Lin, S.Y.; Liao, W.C.; Wei, R.T.; Perumal, P.; Chang, T.Y.; Tseng, C.Y.; et al. All-marine based random lasers. Org. Electron. 2018, 62, 209–215. [Google Scholar] [CrossRef]
- Biswas, S.; Kumbhakar, P. Continuous wave random lasing in naturally occurring biocompatible pigments and reduction of lasing threshold using triangular silver nanostructures as scattering media. Nanoscale 2017, 9, 18812–18818. [Google Scholar] [CrossRef] [Green Version]
- Gummaluri, V.S.; Krishnan, S.R.; Vijayan, C. Stokes mode Raman random lasing in a fully biocompatible medium. Opt. Lett. 2018, 43, 5865–5868. [Google Scholar] [CrossRef]
- Martelli, F.; Del Bianco, S.; Ismaelli, A.; Zaccanti, G. Light Propagation through Biological Tissue and Other Diffusive Media: Theory, Solutions, and Software; SPIE Press: Bellingham, WA, USA, 2009. [Google Scholar]
- Brito-Silva, A.M.; Galembeck, A.; Gomes, A.S.L.; Jesus-Silva, A.J.; de Araújo, C.B. Random laser action in dye solutions containing Stöber silica nanoparticles. J. Appl. Phys. 2010, 108, 033508. [Google Scholar] [CrossRef]
- Anderson, B.R.; Gunawidjaja, R.; Eilers, H. Photodegradation and self-healing in a Rhodamine 6G dye and Y2O3 nanoparticle-doped polyurethane random laser. Appl. Phys. B 2015, 120, 1–12. [Google Scholar] [CrossRef] [Green Version]
- van Staveren, H.J.; Moes, C.J.M.; van Marie, J.; Prahl, S.A.; van Gemert, M.J.C. Light scattering in lntralipid-10% in the wavelength range of 400–1100 nm. Appl. Opt. 1991, 30, 4507–4514. [Google Scholar] [CrossRef] [Green Version]
- Spinelli, L.; Botwicz, M.; Zolek, N.; Kacprzak, M.; Milej, D.; Sawosz, P.; Liebert, A.; Weigel, U.; Durduran, T.; Foschum, F.; et al. Determination of reference values for optical properties of liquid phantoms based on Intralipid and India ink. Biomed. Opt. Express 2014, 5, 2037–2053. [Google Scholar] [CrossRef]
- Di Ninni, P.; Martelli, F.; Zaccanti, G. Intralipid: Towards a diffusive reference standard for optical tissue phantoms. Phys. Med. Biol. 2011, 56, N21. [Google Scholar] [CrossRef]
- Aernouts, B.; Zamora-Rojas, E.; Beers, R.V.; Watté, R.; Wang, L.; Tsuta, M.; Lammertyn, J.; Saeys, W. Supercontinuum laser based optical characterization of Intralipid® phantoms in the 500–2250 nm range. Opt. Express 2013, 21, 32450–32467. [Google Scholar] [CrossRef]
- Aernouts, B.; Beers, R.V.; Watté, R.; Lammertyn, J.; Saeys, W. Dependent scattering in Intralipid® phantoms in the 600–1850 nm range. Opt. Express 2014, 22, 6086–6098. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tommasi, F.; Auvity, B.; Fini, L.; Martelli, F.; Cavalieri, S. Direct Measurement of the Reduced Scattering Coefficient by a Calibrated Random Laser Sensor. Sensors 2022, 22, 1401. https://doi.org/10.3390/s22041401
Tommasi F, Auvity B, Fini L, Martelli F, Cavalieri S. Direct Measurement of the Reduced Scattering Coefficient by a Calibrated Random Laser Sensor. Sensors. 2022; 22(4):1401. https://doi.org/10.3390/s22041401
Chicago/Turabian StyleTommasi, Federico, Baptiste Auvity, Lorenzo Fini, Fabrizio Martelli, and Stefano Cavalieri. 2022. "Direct Measurement of the Reduced Scattering Coefficient by a Calibrated Random Laser Sensor" Sensors 22, no. 4: 1401. https://doi.org/10.3390/s22041401





