Experimental Verification of the Impact of Radial Internal Clearance on a Bearing’s Dynamics
Abstract
:1. Introduction
1.1. Background
1.2. State of the Art
1.3. Contribution to the Study
1.4. Remainder
2. Mathematical Model
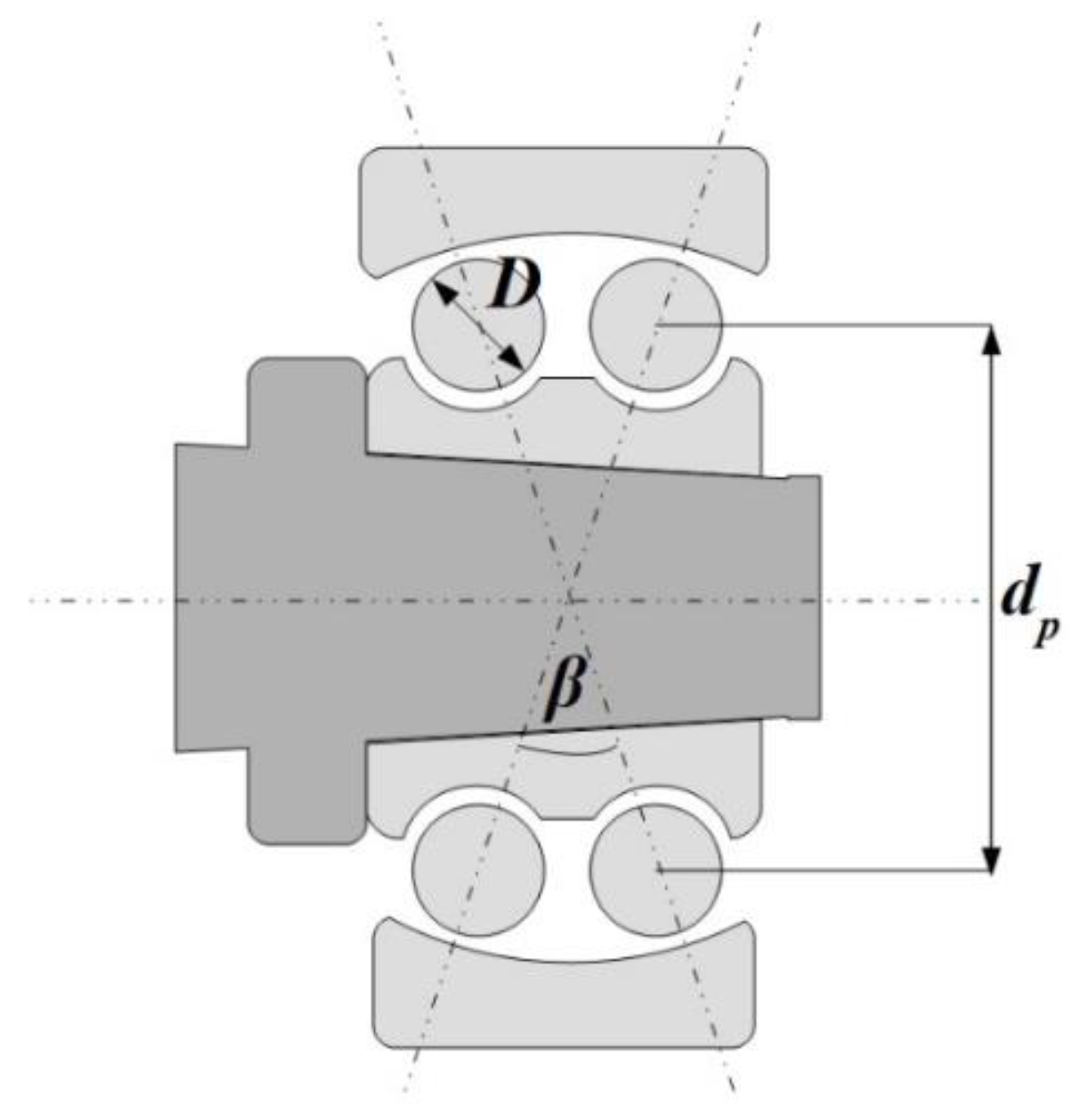
2.1. Description of the 2-DOF Mathematical Model of the Self-Aligning Ball Bearing (SABB)
2.2. Shape Errors
2.3. Eccentricity
2.4. Damping Coefficient
2.5. Hertzian Contact Theory
2.6. Equations of Motion
3. Bifurcation Analysis
4. Test Rigs and Experiment
- Radial internal clearance reduction with axial nut;
- Radial internal clearance measurement;
- Bearing’s mounting in the plummer block with pre-defined clearance;
- Setting operational for one of rotational velocities from 10 to 50 Hz;
- Acceleration measurements for 10 min;
- Signal normalization for time series comparison between cases;
- Signal filtering with frequency range of 0–100 Hz.
5. Recurrence Analysis for the Mathematical Model and Experimental Data
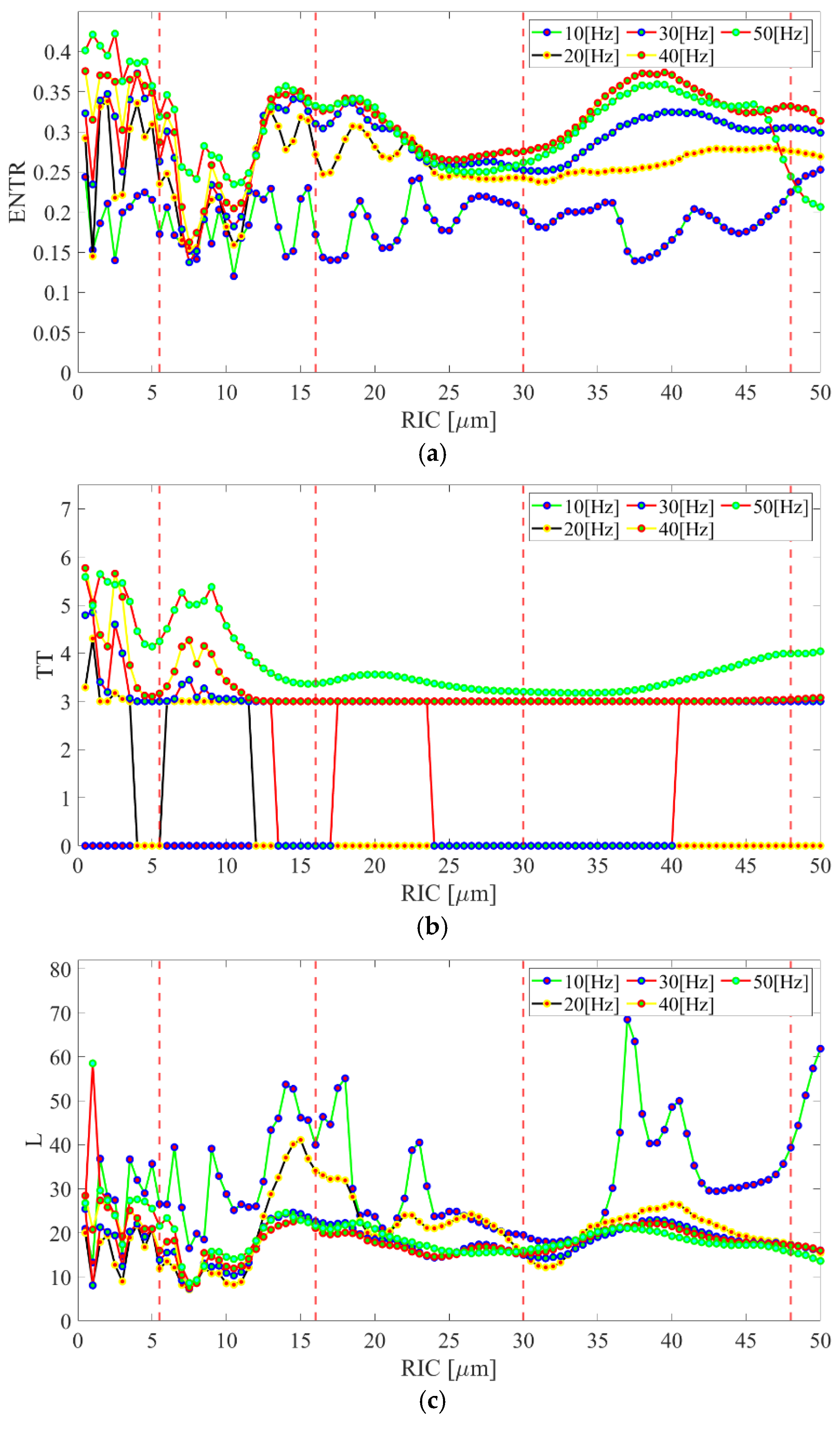
5.1. Recurrence Analysis
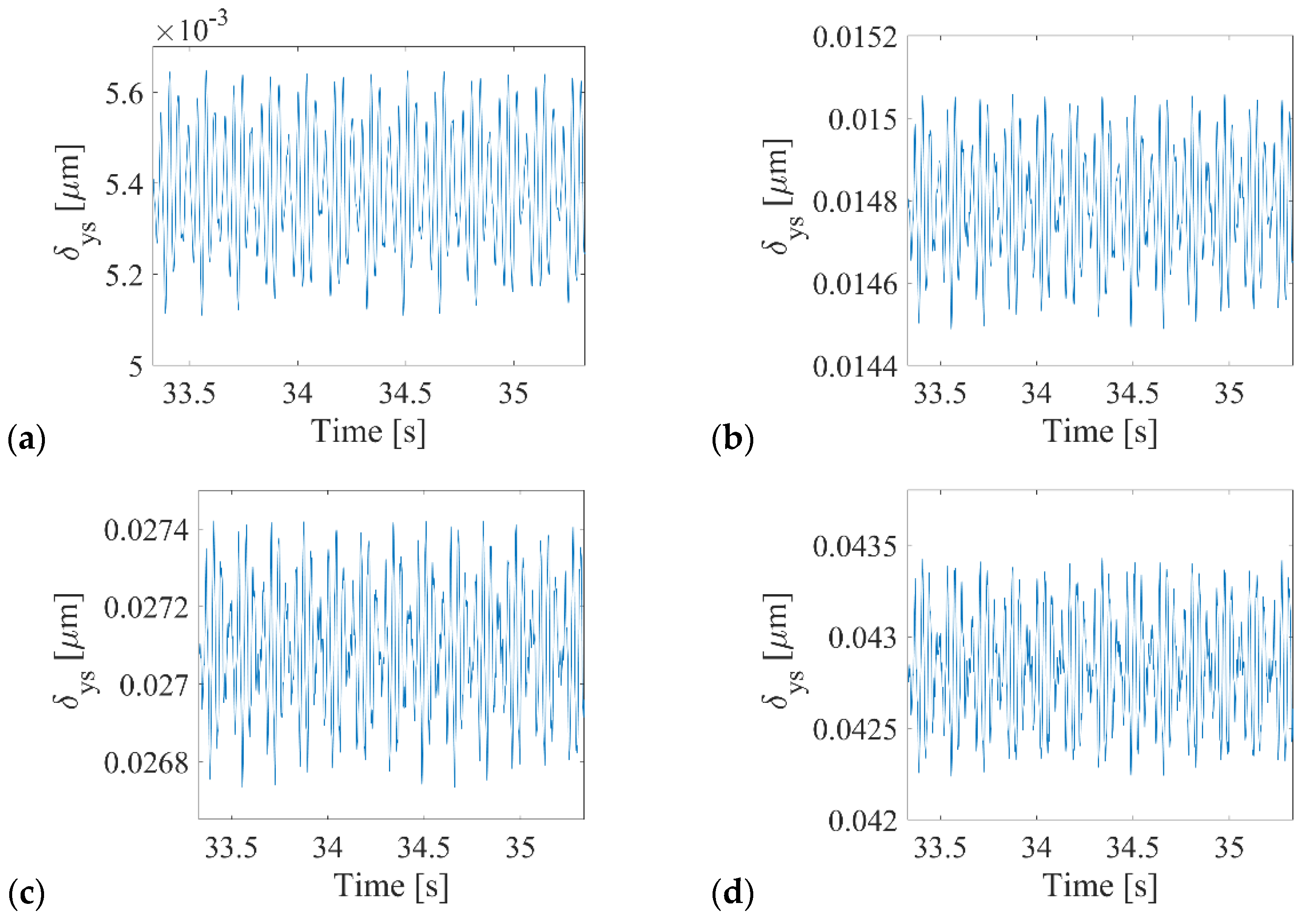
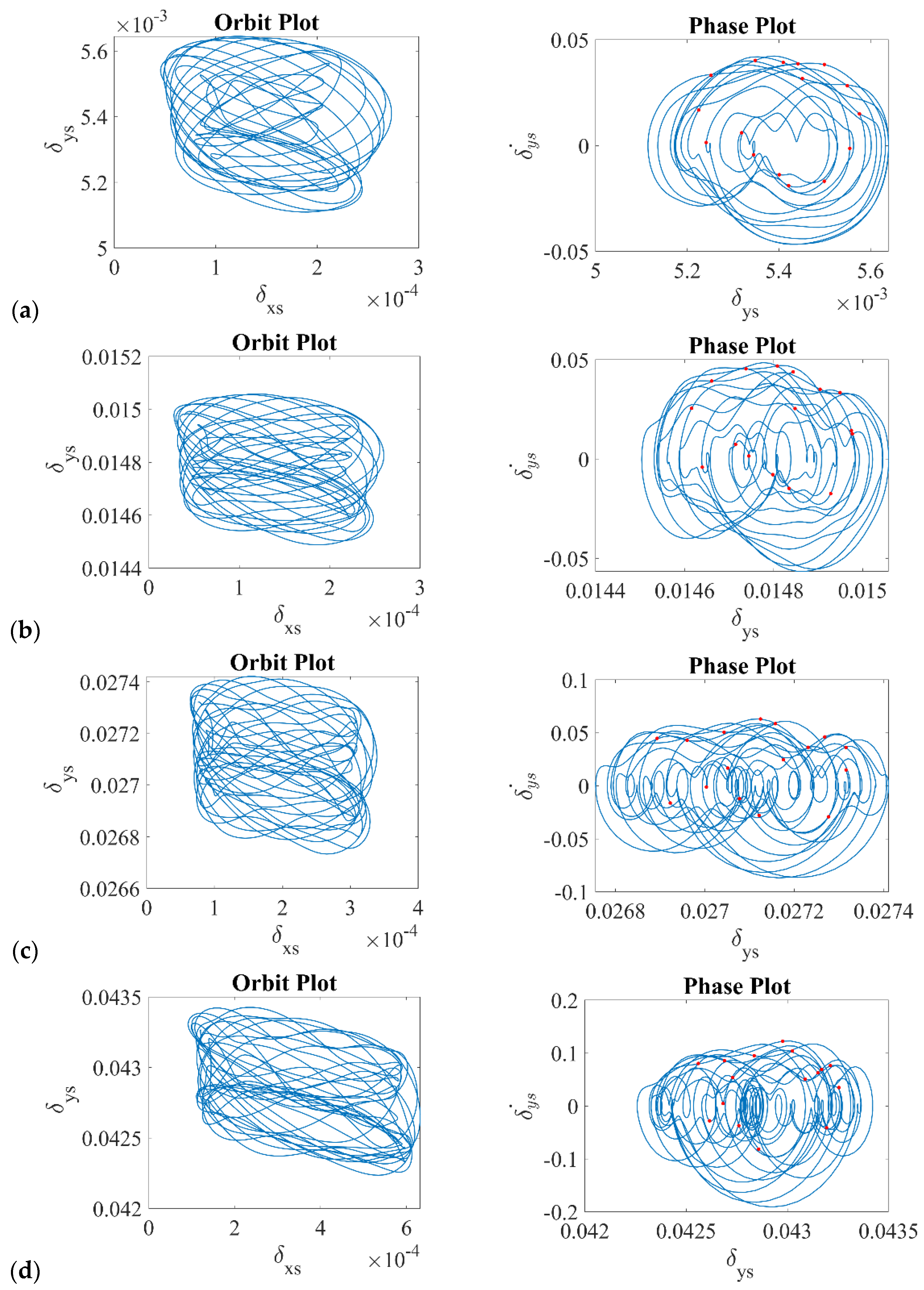
5.2. Phase-Space Reconstruction
5.3. Comparison of the Results and Discussions
- Entropy ENTR—is the measure of the distribution of the diagonal segments. It reflects the complexity of the recurrence plot regarding the diagonal lines:
- Trapping Time TT—denotes the average length of the vertical structures at the recurrence plot:
- Average line length of the diagonal line L—shows that a part of the phase-space trajectory is at a close distance during l time steps to another part of the phase-space trajectory in a different time:
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOF | Degree of Freedom |
| SABB | Self-aligning ball bearing |
| RIC | Radial internal clearance |
| RP | Recurrence plot |
| RQA | Recurrence quantification analysis |
| ODE | Ordinary differential equation |
| CRP | Cross recurrence plot |
| MI | Mutual information |
| FNN | False nearest neighbors |
| RR | Recurrence rate |
| ENTR | Entropy |
| TT | Trapping time |
| L | Average length of the diagonal line |
References
- Fei, C.-W.; Choy, Y.-S.; Bai, G.-C.; Tang, W.-Z. Multi-feature entropy distance approach with vibration and acoustic emission signals for process feature recognition of rolling element bearing faults. Struct. Health Monit. 2018, 17, 156–168. [Google Scholar] [CrossRef]
- Piltan, F.; Kim, J.-M. Bearing fault diagnosis by a robust higher-order super-twisting sliding mode observer. Sensors 2018, 18, 1128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ai, Y.-T.; Guan, J.-Y.; Fei, C.-W.; Tian, J.; Zhang, F.-L. Fusion information entropy method of rolling bearing fault diagnosis based on n-dimensional characteristic parameter distance. Mech. Syst. Signal Process. 2017, 88, 123–136. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Zheng, L.; Gogu, C. An end-to-end fault diagnostics method based on convolutional neural network for rotating machinery with multiple case studies. J. Intell. Manuf. 2022, 33, 809–830. [Google Scholar] [CrossRef]
- Ravikumar, K.N.; Yadav, A.; Kumar, H.; Gangadharan, K.V.; Narasimhadhan, A.V. Gearbox fault diagnosis based on Multi-Scale deep residual learning and stacked LSTM model. Meas. J. Int. Meas. Confed. 2021, 186, 110099. [Google Scholar] [CrossRef]
- Yi, Q.; Li, C.; Folin, C.; Chen, H. A fault dynamic model of high-speed angular contact ball bearings. Mech. Mach. Theory 2020, 143, 103627. [Google Scholar]
- Hammami, M.; Martins, R.; Fernandes, C.; Seabra, J.; Abbes, M.S.; Haddar, M. Friction torque in rolling bearings lubricated with axle gear oils. Tribol. Int. 2018, 119, 419–435. [Google Scholar] [CrossRef]
- Deng, S.-E.; Sun, C.-Y.; Gu, J.-F.; Cui, Y.-C. Vibration chracteristics of low-noise deep groove ball bearings. J. Vib. Shock. 2015, 34, 12–19. [Google Scholar]
- Witkowski, K.; Kudra, G.; Skurativskyi, S.; Wasilewski, G.; Awrejcewicz, J. Modeling and dynamics analysis of a forced two-degree-of-freedom mechanical oscillator with magnetic springs. Mech. Syst. Signal Process. 2021, 148, 107138. [Google Scholar] [CrossRef]
- Amer, T.S.; El-Sabaa, F.M.; Zakria, S.K.; Galal, A.A. The stability of 3-DOF triple-rigid-body pendulum system near resonances. Nonlinear Dyn. 2022. [Google Scholar] [CrossRef]
- Tiwari, M.; Gupta, K.; Prakash, O. Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor. J. Sound Vib. 2000, 238, 723–756. [Google Scholar] [CrossRef]
- Lioulios, A.N.; Antoniadis, I.A. Effect of rotational speed fluctuations on the dynamic behaviour of rolling element bearings with radial clearances. Int. J. Mech. Sci. 2006, 48, 809–829. [Google Scholar] [CrossRef]
- Harsha, S.P. Nonlinear dynamic response of a balanced rotor supported by rolling element bearings due to radial internal clearance effect. Mech. Mach. Theory 2006, 41, 688–706. [Google Scholar] [CrossRef]
- Changqing, B.; Qingyu, X. Dynamic model of ball bearings with internal clearance and waviness. J. Sound Vib. 2006, 294, 23–48. [Google Scholar] [CrossRef]
- Upadhyay, S.H.; Harsha, S.P.; Jain, S.C. Analysis of nonlinear phenomena in high speed bearings due to radial clearance and unbalanced rotor effects. J. Vib. Control 2010, 16, 65–88. [Google Scholar] [CrossRef]
- Zhuo, Y.; Zhou, X.; Yang, C. Dynamic analysis of double-row self-aligning ball bearings due to applied loads, internal clearance, surface waviness and number of balls. J. Sound Vib. 2014, 333, 6170–6189. [Google Scholar] [CrossRef]
- Xu, M.; Feng, G.; He, Q.; Gu, F.; Ball, A. Vibration characterstics of rolling element bearings with different radial clearances for condition monitoring of wind turbine. Appl. Sci. 2020, 10, 4731. [Google Scholar] [CrossRef]
- Xu, M.; Han, Y.; Sun, X.; Shao, Y.; Gu, F.; Ball, A. Vibration characteristics and condition monitoring of internal radial clearance within a ball bearing in a gear-shaft-bearing system. Mech. Syst. Signal Process. 2022, 165, 108280. [Google Scholar] [CrossRef]
- Ambrożkiewicz, B.; Syta, A.; Meier, N.; Litak, G.; Georgiadis, A. Radial internal clearance analysis in ball bearings. Eksploat. I Niezawodn.-Maint. Reliab. 2021, 23, 42–54. [Google Scholar] [CrossRef]
- Ambrożkiewicz, B.; Syta, A.; Gassner, A.; Georgiadis, A.; Litak, G.; Meier, N. The influence of the radial internal clearance on the dynamic response of self-aligning ball bearings. Mech. Syst. Signal Process. 2022, 171, 108954. [Google Scholar] [CrossRef]
- Marwan, N.; Carmen Romano, M.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Kitio Kwuimy, C.A.; Samadani, M.; Nataraj, C. Bifurcation analysis of a nonlinear pendulum using recurrence and statistical methods: Applications to fault diagnostics. Nonlinear Dyn. 2014, 76, 1963–1975. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R.; Hu, S. Bearing degradation evaluation using recurrence quantification analysis and kalman filter. IEEE Trans. Intrumentation Meas. 2014, 63, 2599–2610. [Google Scholar] [CrossRef]
- Joshuva, A.; Sugumaran, V. A comparative study of Bayes classifiers for blade fault diagnosis in wind turbines through vibration signals. SDHM Struct. Durab. Health Monit. 2017, 12, 69–90. [Google Scholar]
- Syta, A.; Bowen, C.R.; Kim, H.A.; Rysak, A.; Litak, G. Responses of bistable piezoelectric-composite energy harvester by means of recurrences. Mech. Syst. Signal Process. 2016, 76–77, 823–832. [Google Scholar] [CrossRef] [Green Version]
- Parmar, V.; Saran, V.H.; Harsha, S.P. Effect of dynamic misalignment on the vibration response, trajectory followed and defect-depth achieved by the rolling-elements in a double-row spherical rolling-element bearing. Mech. Mach. Theory 2021, 162, 104366. [Google Scholar] [CrossRef]
- Ravikumar, S.; Kanagasabapathy, H.; Muralidharan, V. Fault diagnosis of self-aligning troughing rollers in belt conveyor system using k-star algorithm. Measurement 2019, 133, 341–349. [Google Scholar] [CrossRef]
- Liu, J.; Pang, R.; Xu, Y.; Ding, S.; He, Q. Vibration analysis of a single row angular contact ball bearing with the coupling errors including the surface roundness and waviness. Sci. China Technol. Sci. 2020, 63, 943–952. [Google Scholar] [CrossRef]
- Yakout, M.; Nassef, M.; Backar, S. Effect of clearances in rolling element bearings on their dynamic performance, quality and operating life. J. Mech. Sci. Technol. 2019, 33, 2037–2042. [Google Scholar] [CrossRef]
- Martowicz, A.; Roemer, J.; Lubieniecki, M.; Żywica, G.; Bagiński, P. Experimental and numerical study on the thermal control strategy for a gas foil bearing enhanced with thermoelectric modules. Mech. Syst. Signal Process. 2020, 138, 106581. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Y.; Wang, M. Analysis of contact stress distribution between rolling element and variable diameter raceway of cageless bearing. Appl. Sci. 2022, 12, 5764. [Google Scholar] [CrossRef]
- Damping in a Rolling Bearing Arrangement. Available online: https://evolution.skf.com/damping-in-a-rolling-bearing-arrangement/ (accessed on 18 July 2022).
- Sharma, S.; Coetzee, E.B.; Lowenberg, M.H.; Neild, S.A.; Krauskopf, B. Numerical continuation and bifurcation analysis in aircraft design: An industrial perspective. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 2051. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Litak, G.; Borowiec, M.; Syta, A. Vibration of generalized double well oscillators. ZAMM Z. Fur Angew. Math. Und Mech. 2007, 32, 694–701. [Google Scholar] [CrossRef] [Green Version]
- Meier, N.; Georgiadis, A. Automatic assembling of bearings including clearance measurement. Procedia CIRP 2016, 41, 242–246. [Google Scholar] [CrossRef] [Green Version]
- Meier, N.; Ambrożkiewicz, B.; Georgiadis, A.; Litak, G. Verification of measuring the bearing clearance using kurtosis, recurrences and neural networks and comparison of these approaches. 2019 IEEE SENSORS, 2019, pp. 1–4. Available online: https://ieeexplore.ieee.org/document/8956597 (accessed on 1 August 2022). [CrossRef]
- Donner, R.V.; Zou, Y.; Donges, J.F.; Marwan, N.; Kurths, J. Recurrence networks—A novel paradigm for nonlinear time series analysis. New J. Phys. 2010, 12, 033025. [Google Scholar] [CrossRef] [Green Version]
- Cross Recurrence Plot Toolbox 5.24 (R34). Available online: https://tocsy.pik-potsdam.de/CRPtoolbox/ (accessed on 28 July 2022).
- Eckmann, J.P.; Olifsson Kamphorst, O.; Ruelle, D. Recurrence plots of dynamical systems. Eur. Phys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef] [Green Version]
- Zbilut, J.P.; Webber, C. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 1992, 171, 199–203. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Giuliani, A.; Webber, C. Recurrence quantification analysis and principal components in the detection of short complex signals. Phys. Lett. A 1998, 237, 131–135. [Google Scholar] [CrossRef] [Green Version]
- Takens, F. Detecting strange attractors in turbulence. Lect. Notes Math. 1981, 898, 366–381. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2003; pp. 30–47. [Google Scholar]
- Wallot, S.; Mønster, D. Calculation of Average Mutual Information (AMI) and False-Nearest Neighbours (FNN) for the estimation of embedding parameters of multidimensional time series in Matlab. Front. Psychol. 2018, 9, 1679. [Google Scholar] [CrossRef] [Green Version]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marwan, N. How to avoid potential pitfalls in recurrence plot based data analysis. Int. J. Bifurc. Chaos 2010, 21, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Oswald, F.B.; Zaretsky, E.V.; Poplawski, J.V. Effect of internal clearance on load distribution and life of radially loaded ball and roller bearings. Tribol. Trans. 2012, 55, 245–265. [Google Scholar] [CrossRef]








| Term | Symbol | Unit | Value |
|---|---|---|---|
| Rotational velocity | ωs | Hz | 10; 20; 30; 40; 50 |
| Ball diameter | D | mm | 15.875 |
| Pitch diameter | dp | mm | 71.810 |
| Pressure angle | β | ° | 15.520 |
| Radial Internal Clearance | rc | μm | 0.5:0.5:50 |
| Load deflection factor | K | N/mm | 1,874,580 |
| Damping factor in the vertical/horizontal direction | cx, cy | Ns/mm | 725.2–2029.3 (10 Hz) 625.2–1929.3 (20 Hz) 525.2–1829.3 (30 Hz) 425.2–1729.3 (40 Hz) 325.2–1629.3 (50 Hz) |
| Mass of the inner ring and shaft | m | kg | 1 |
| Amplitude of the biggest undulation on the inner ring | Uin | mm | 0.0004 |
| Amplitude of the biggest undulation on the outer ring | Uout | mm | 0.00028 |
| Number of undulations on the perimeter of the inner ring | Nin | - | 28 |
| Number of undulations on the perimeter of the outer ring | Nout | - | 19 |
| Number of rolling elements | n | - | 26 |
| Eccentricity | e | μm | 0.35–(10 Hz) 0.80–(20 Hz) 0.71–(30 Hz) 0.59–(40 Hz) 0.65–(50 Hz) |
| External vertical force | Fy | N | 50 |
| External horizontal force | Fx | N | 0 |
| Term | Time Delay (τ) | Embedding Dimension (m) | Threshold (ε) |
|---|---|---|---|
| Mathematical model | 5 | 5 | Based on the constant RR |
| Experimental data | 7–10 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambrożkiewicz, B.; Syta, A.; Georgiadis, A.; Gassner, A.; Meier, N. Experimental Verification of the Impact of Radial Internal Clearance on a Bearing’s Dynamics. Sensors 2022, 22, 6366. https://doi.org/10.3390/s22176366
Ambrożkiewicz B, Syta A, Georgiadis A, Gassner A, Meier N. Experimental Verification of the Impact of Radial Internal Clearance on a Bearing’s Dynamics. Sensors. 2022; 22(17):6366. https://doi.org/10.3390/s22176366
Chicago/Turabian StyleAmbrożkiewicz, Bartłomiej, Arkadiusz Syta, Anthimos Georgiadis, Alexander Gassner, and Nicolas Meier. 2022. "Experimental Verification of the Impact of Radial Internal Clearance on a Bearing’s Dynamics" Sensors 22, no. 17: 6366. https://doi.org/10.3390/s22176366






