Intelligent Smart Marine Autonomous Surface Ship Decision System Based on Improved PPO Algorithm
Abstract
:1. Introduction and Background
- An intelligent SMASS decision-making system based on the Proximal Policy Optimization (PPO) algorithm was proposed in this paper, which could make the critic network and action network converge faster.
- Through the Gazebo simulation environment, sensors such as laser radar and navigation radar were used to obtain external environmental information. Intelligent SMASS could make complex path planning decisions in different environments. After the training, if unknown obstacles are placed on the map, the intelligent ship could still successfully avoid obstacles.
- The Nomoto model was brought into the training of this experiment. Training the model could meet the needs of practical engineering.
2. Intelligent Ship Decision System and Ship Mathematical Model
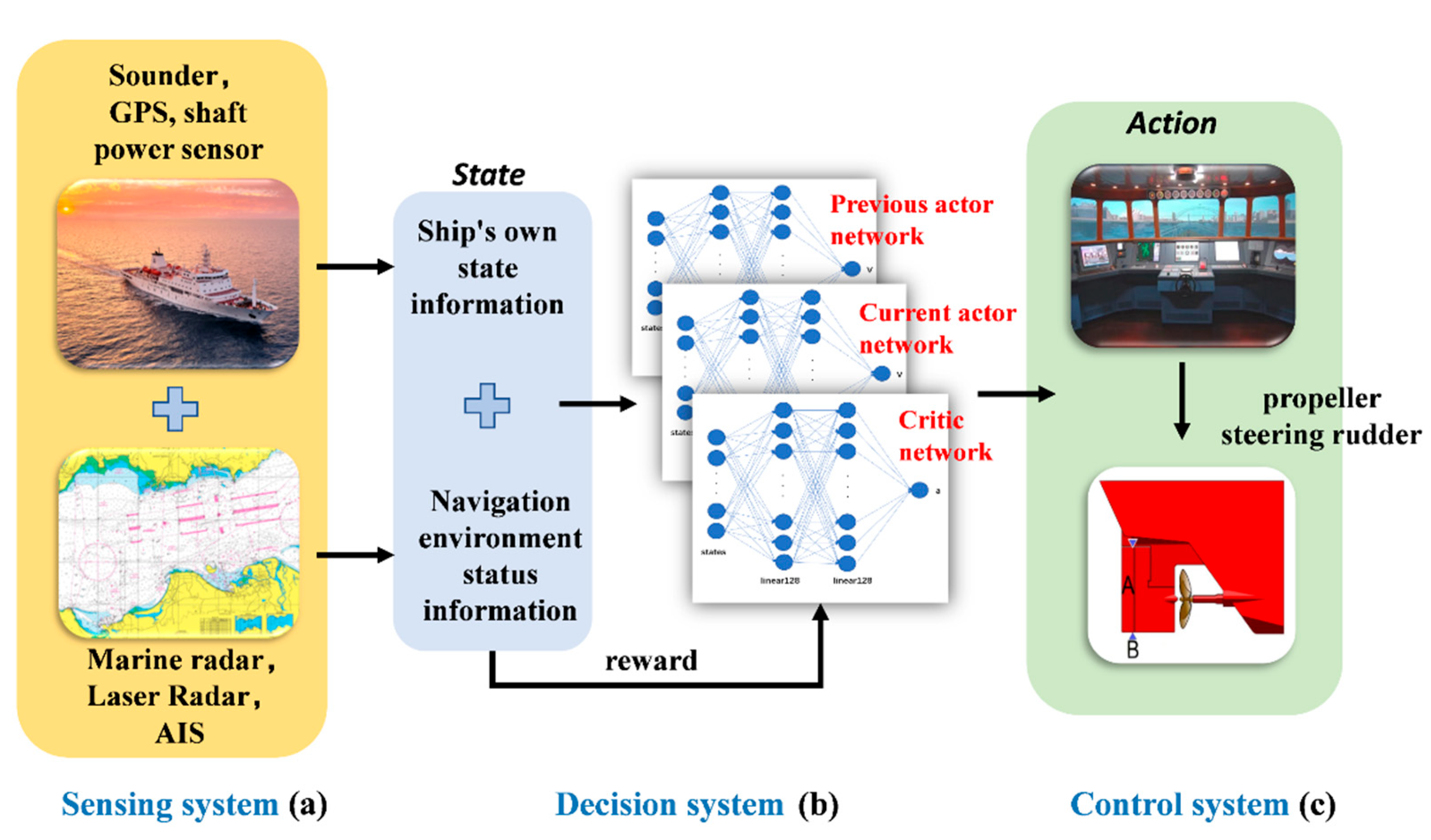
2.1. Intelligent Ship Decision System
- With autonomous learning ability, the convergence rate was faster than the common calculation method.
- The trained intelligent SMASS navigation system could obtain strong generalization, which would solve different scene problems. For example, it can solve the problem of path planning for SMASS sailing in broad waters, narrow waters, and restricted waters. In local path planning, it could successfully avoid unknown obstacles that do not appear on the electronic chart.
- The path planning problem and SMASS decision problem could be solved simultaneously. SMASS could find the optimal path to the target point through known obstacle information. Under the unknown environment, the SMASS could detect the position of obstacles by laser radar and accurately avoid the obstacles.
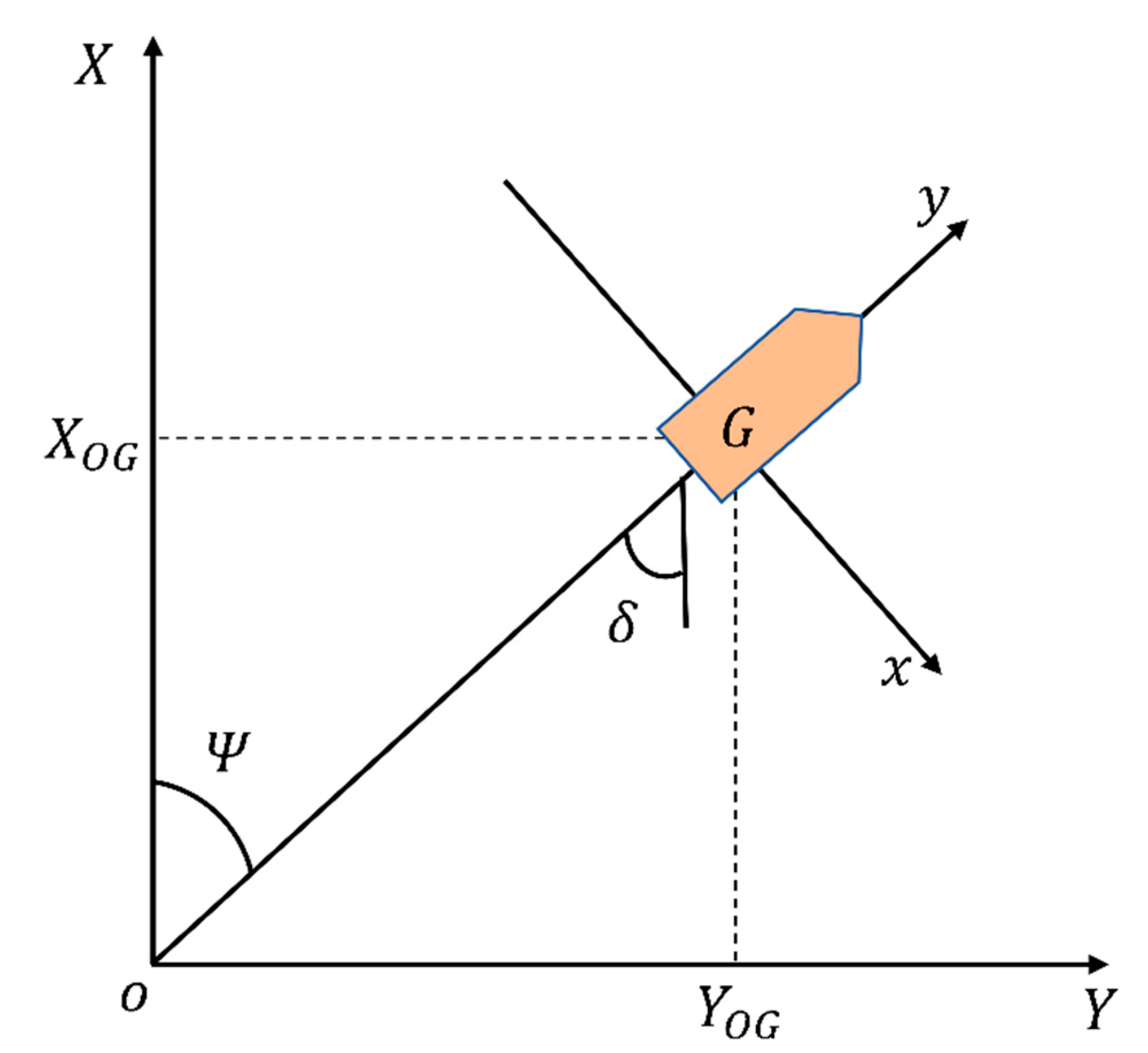
2.2. Ship Mathematical Model
- In the low-frequency range, the spectrum of the Nomoto model is very close to that of the high order model.
- The designed controller has low order and is easy to implement.
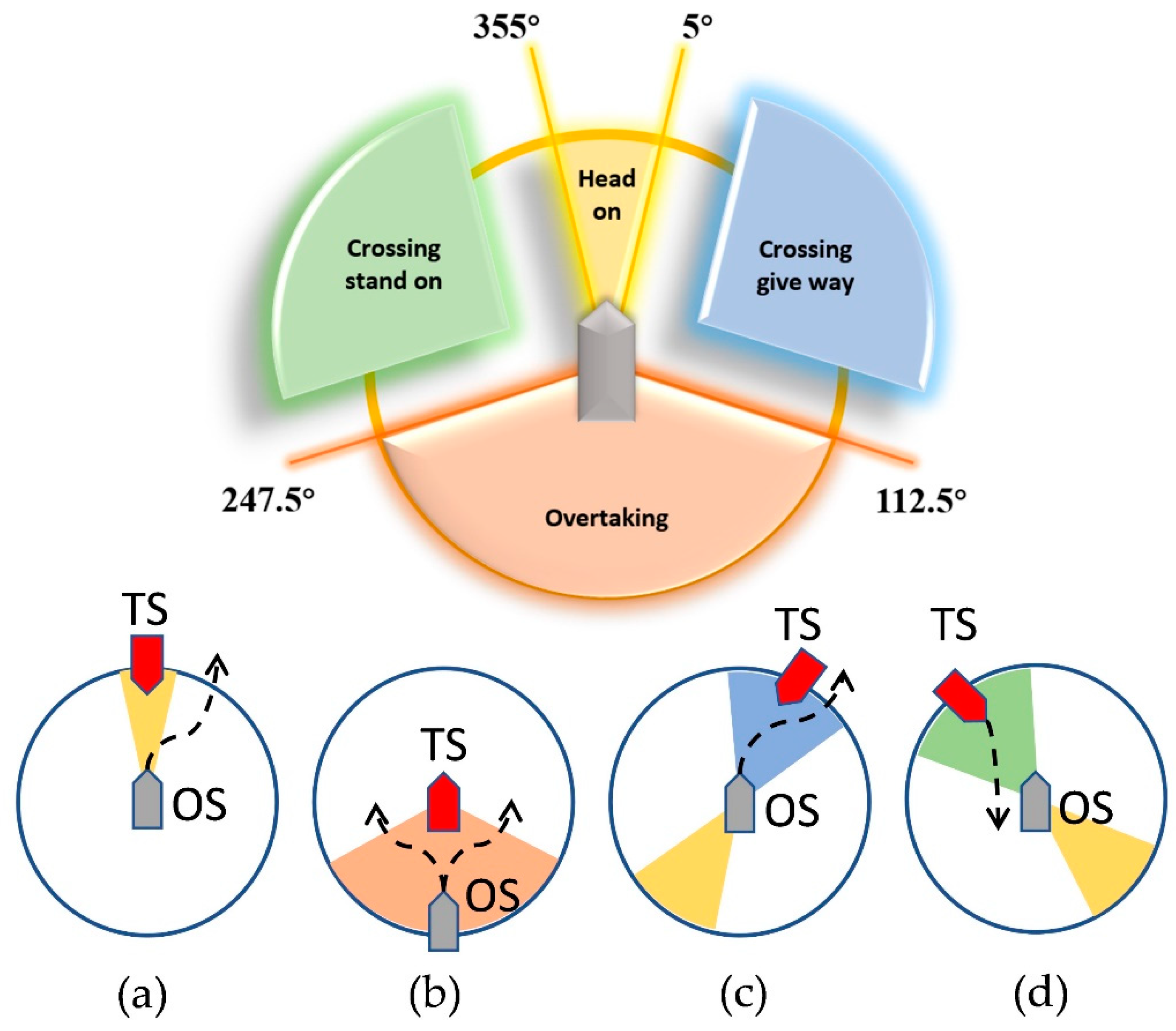
2.3. COLREGs
- (1)
- Head-on
- (2)
- Overtaking
- (3)
- Crossing give-way
- (4)
- Crossing stand-on
3. Improved PPO Algorithm
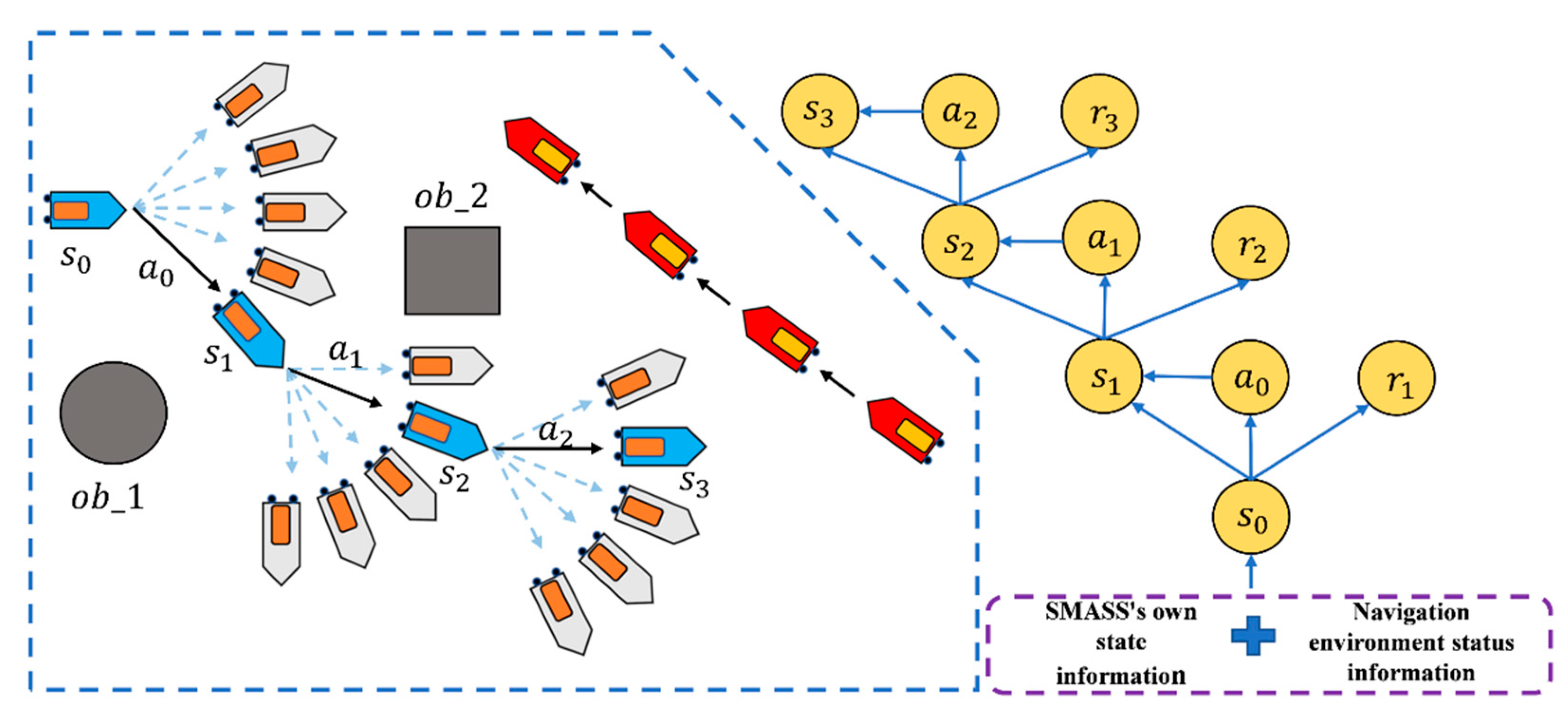
3.1. Deep Reinforcement Learning
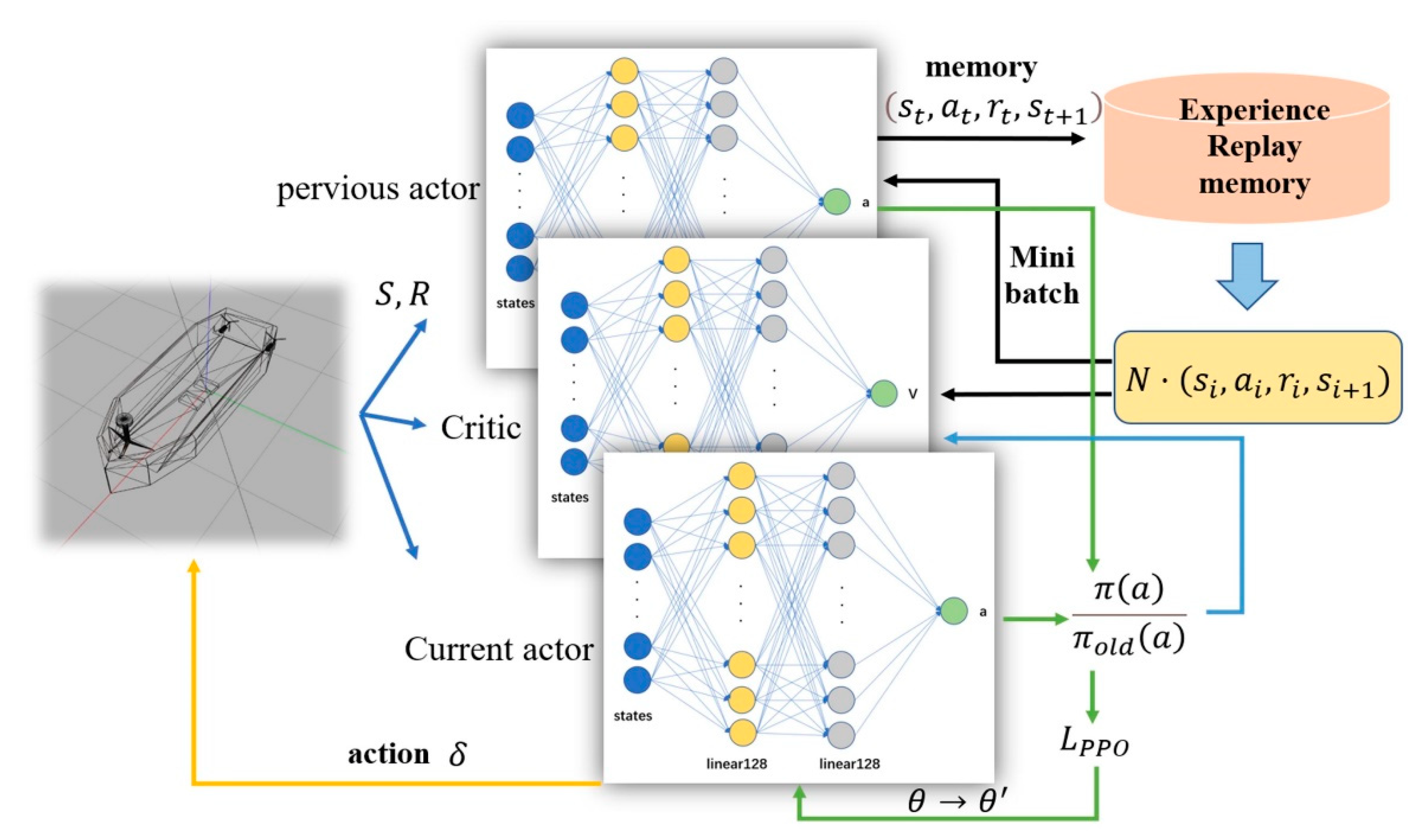
3.2. Improved PPO Algorithm
4. Neural Network Design and Reward Function
4.1. Network Construction and Input and Output Information
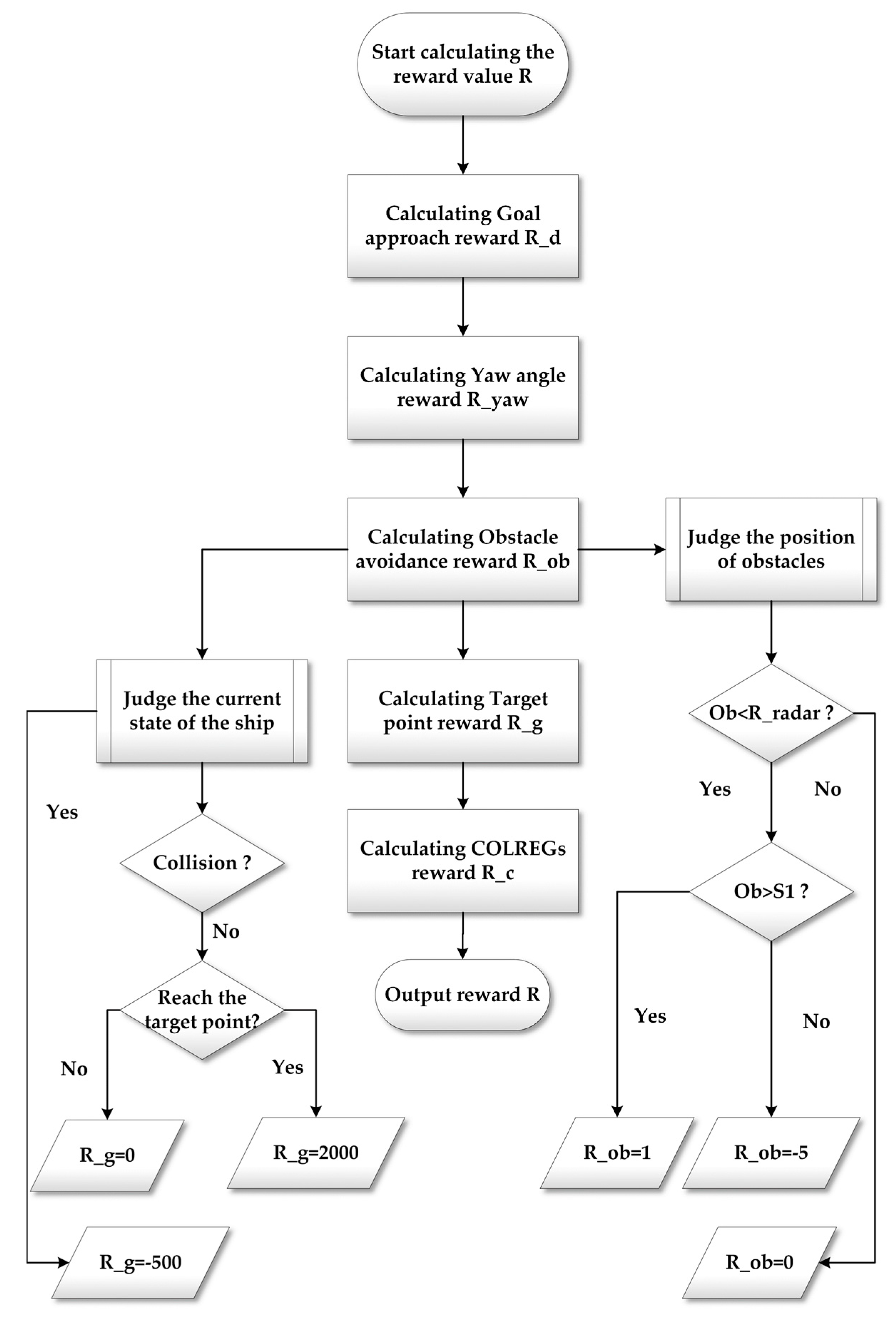
4.2. Reward Function
- (1)
- Goal approach reward
- (2)
- Yaw angle reward
- (3)
- Target point reward
- (4)
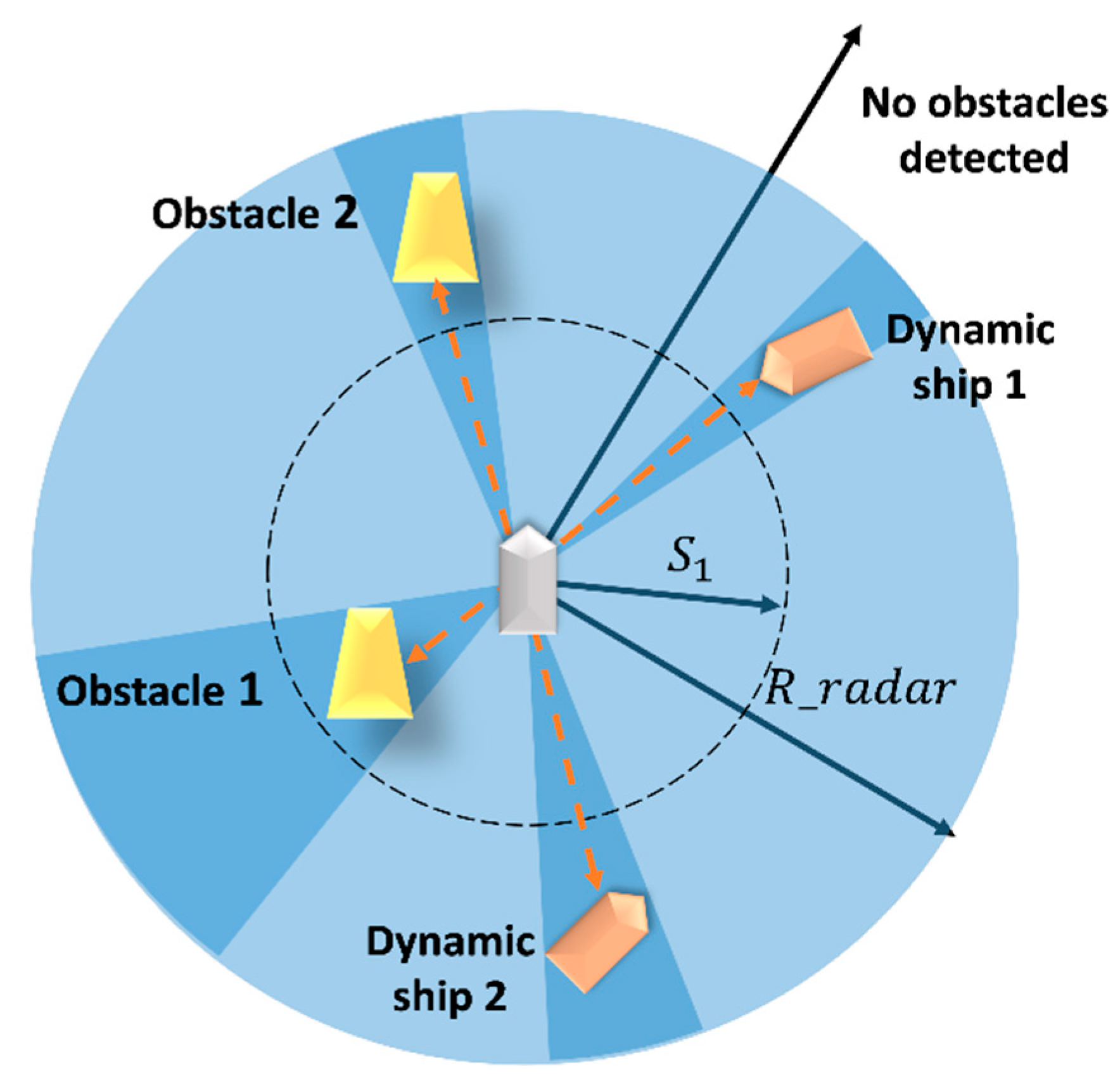
- Obstacle avoidance reward
- (5)
- COLREGs reward
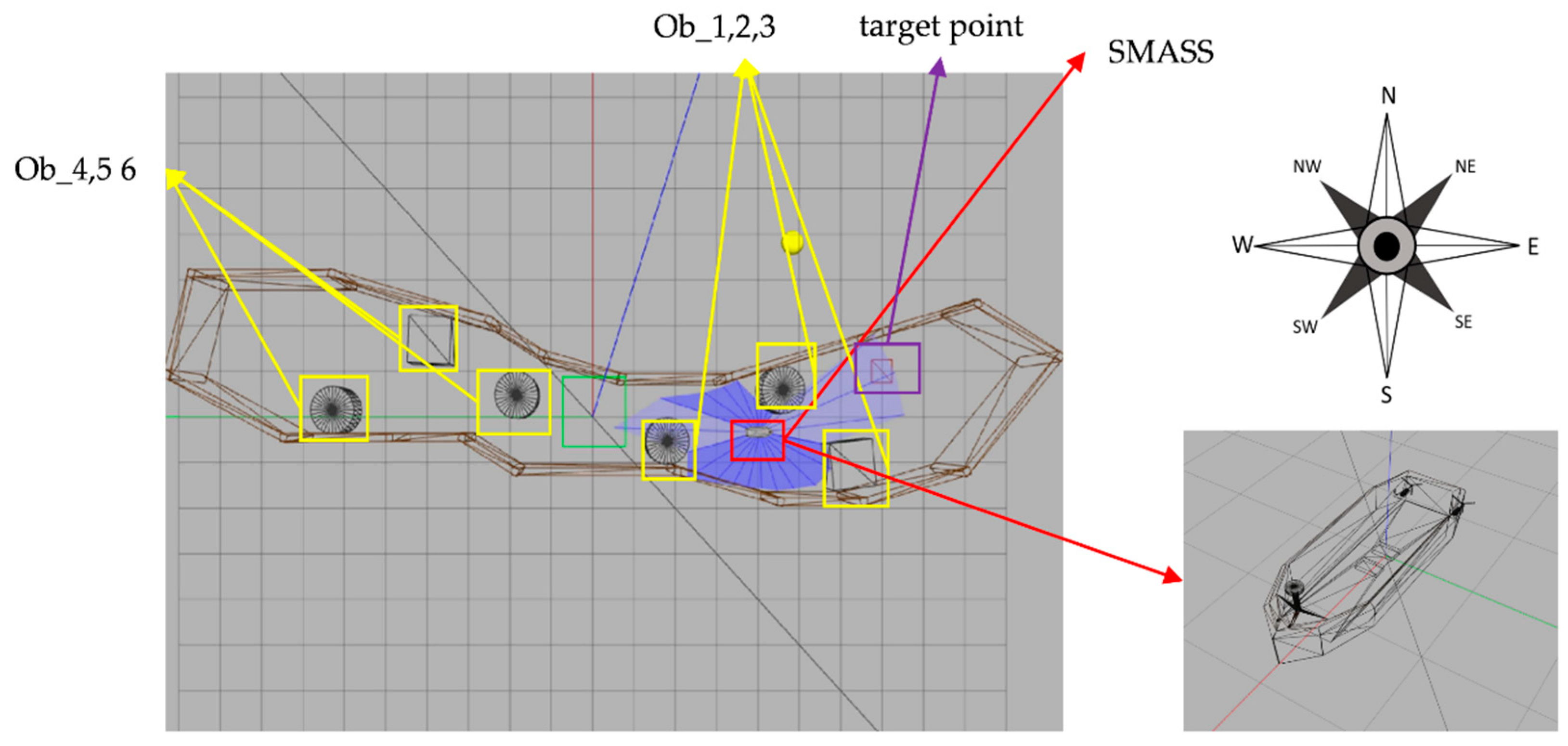
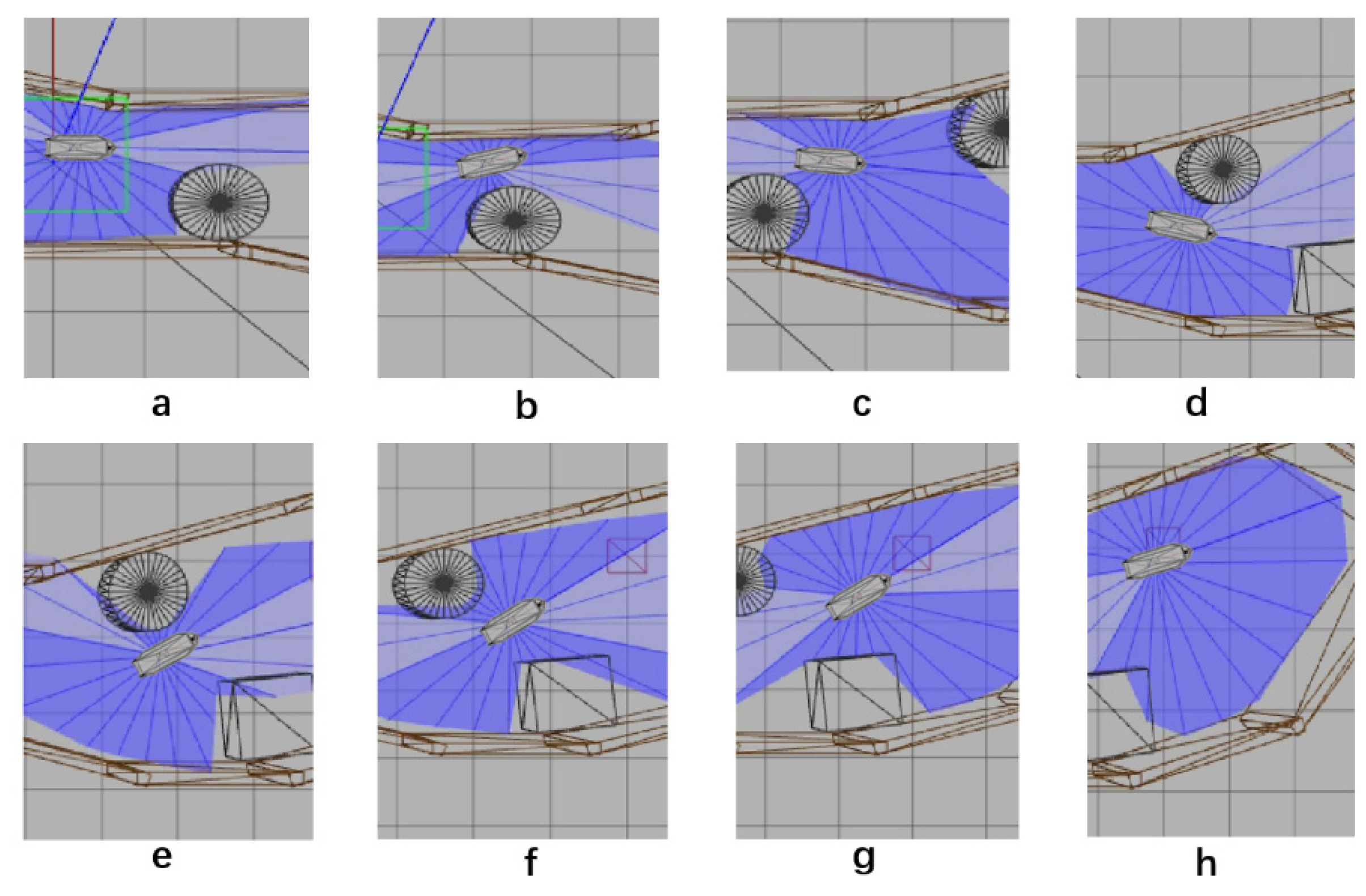
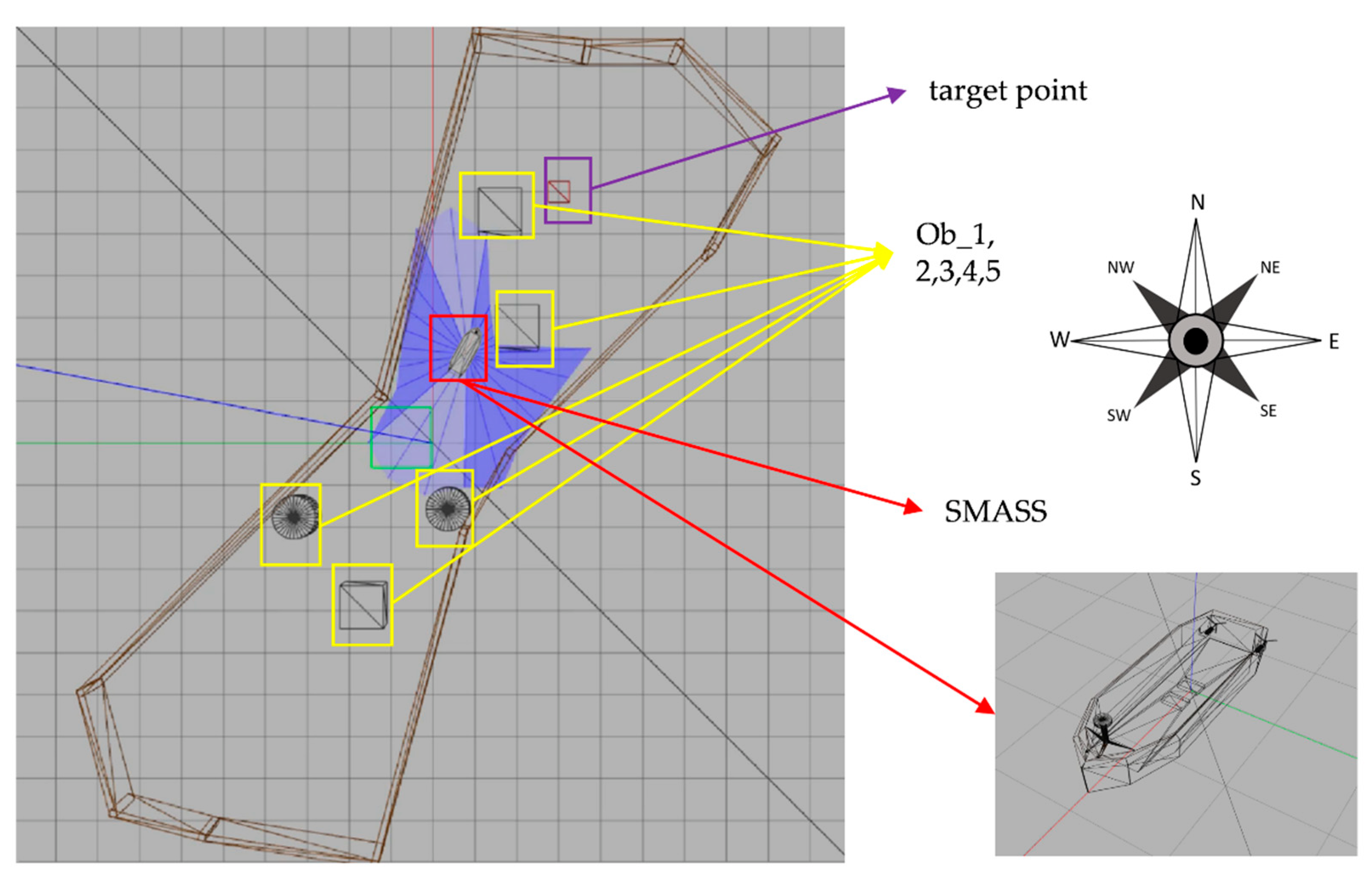
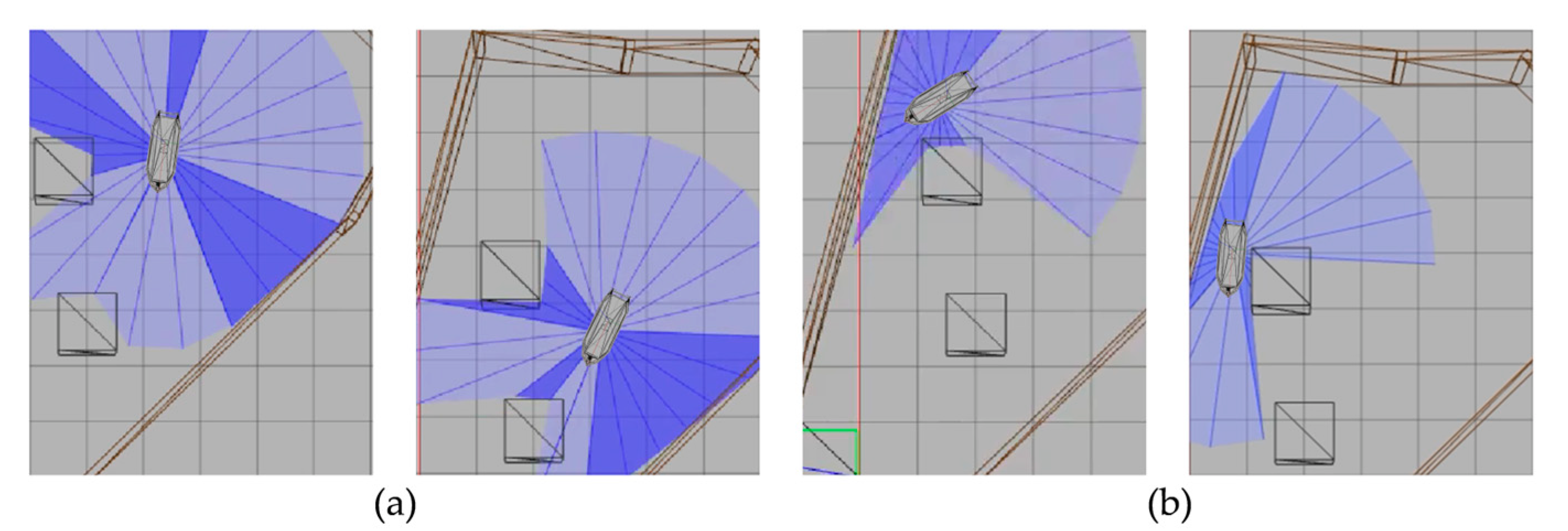
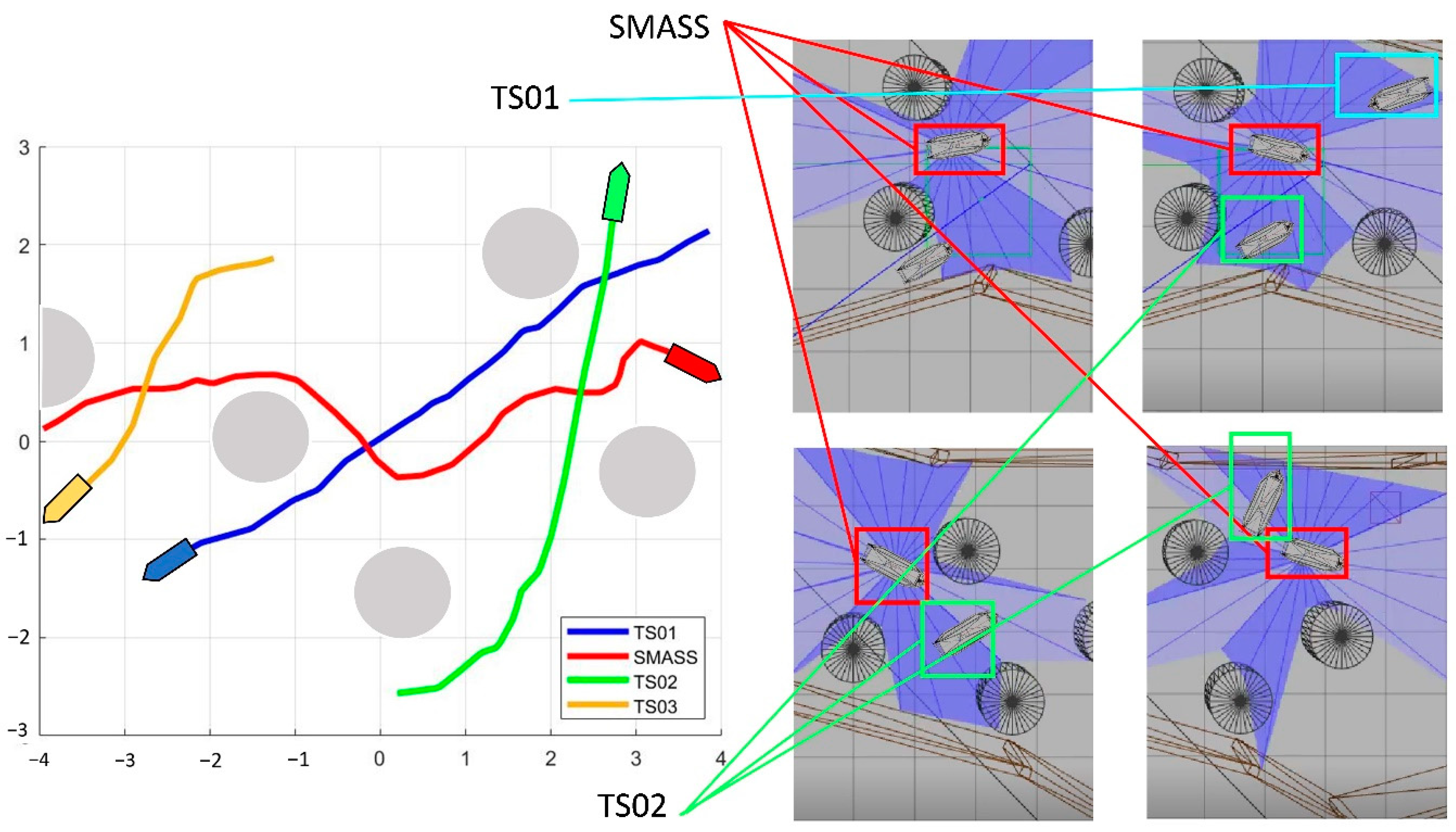
5. Simulation
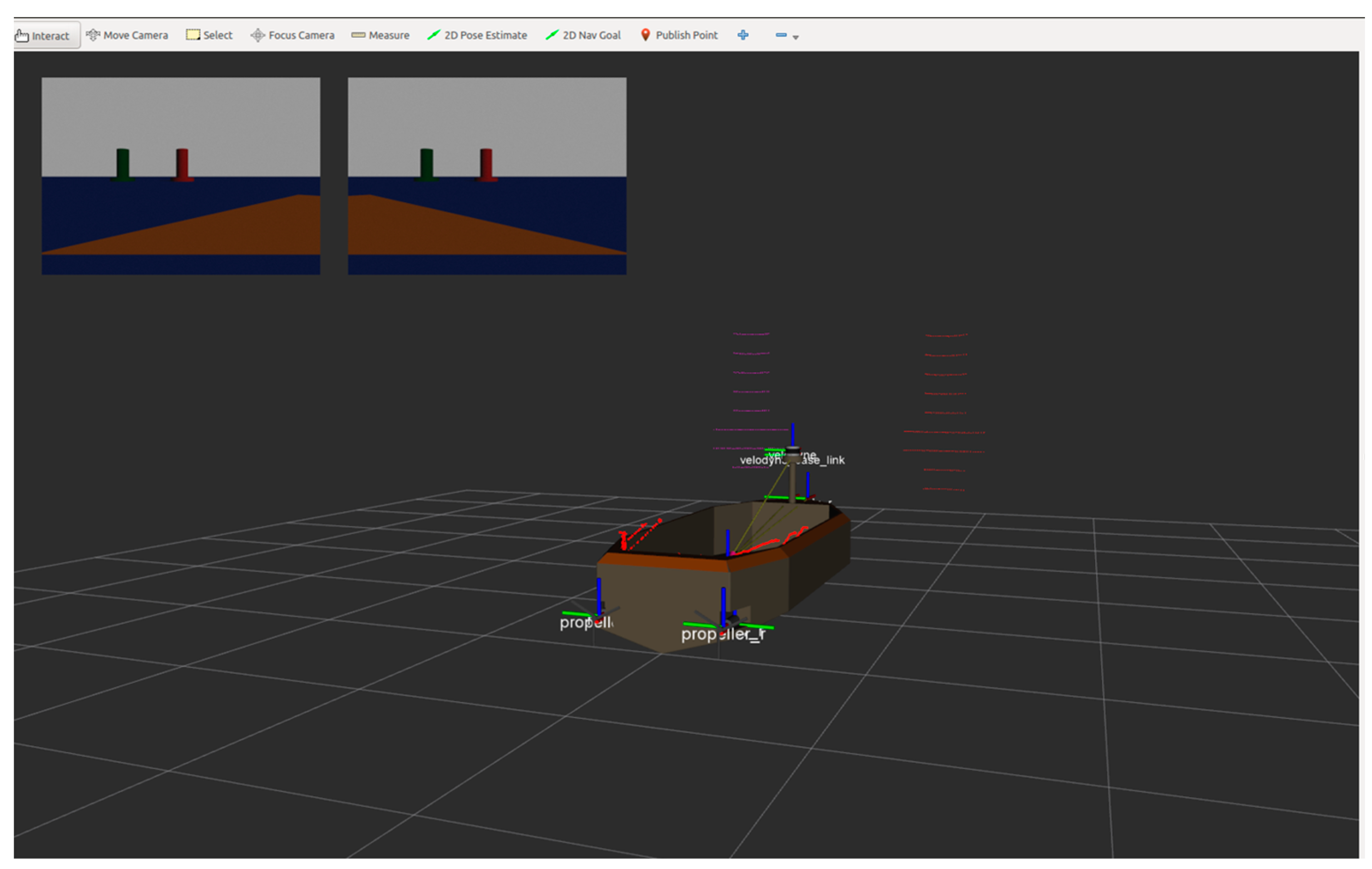
5.1. Design of Simulation
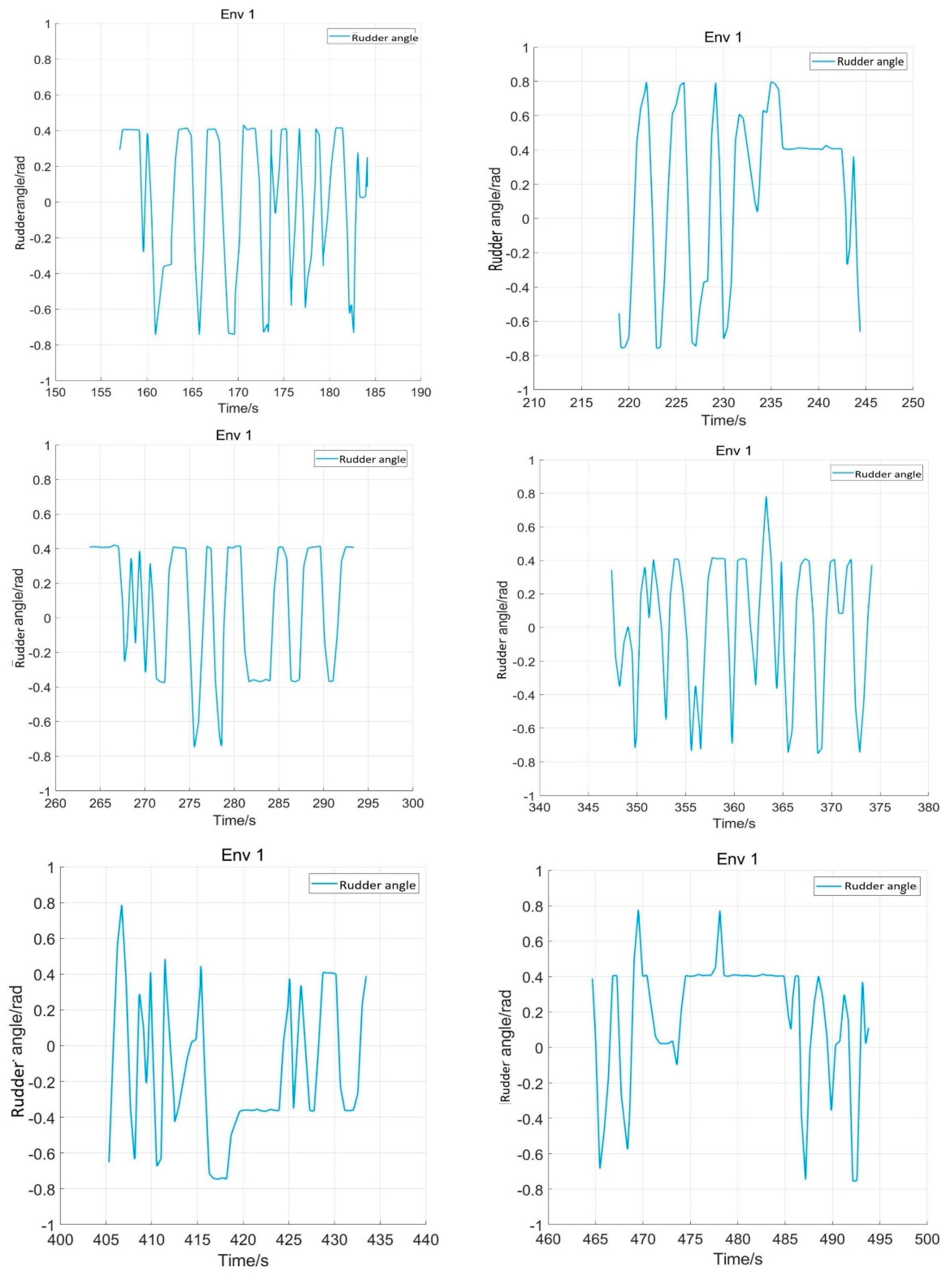
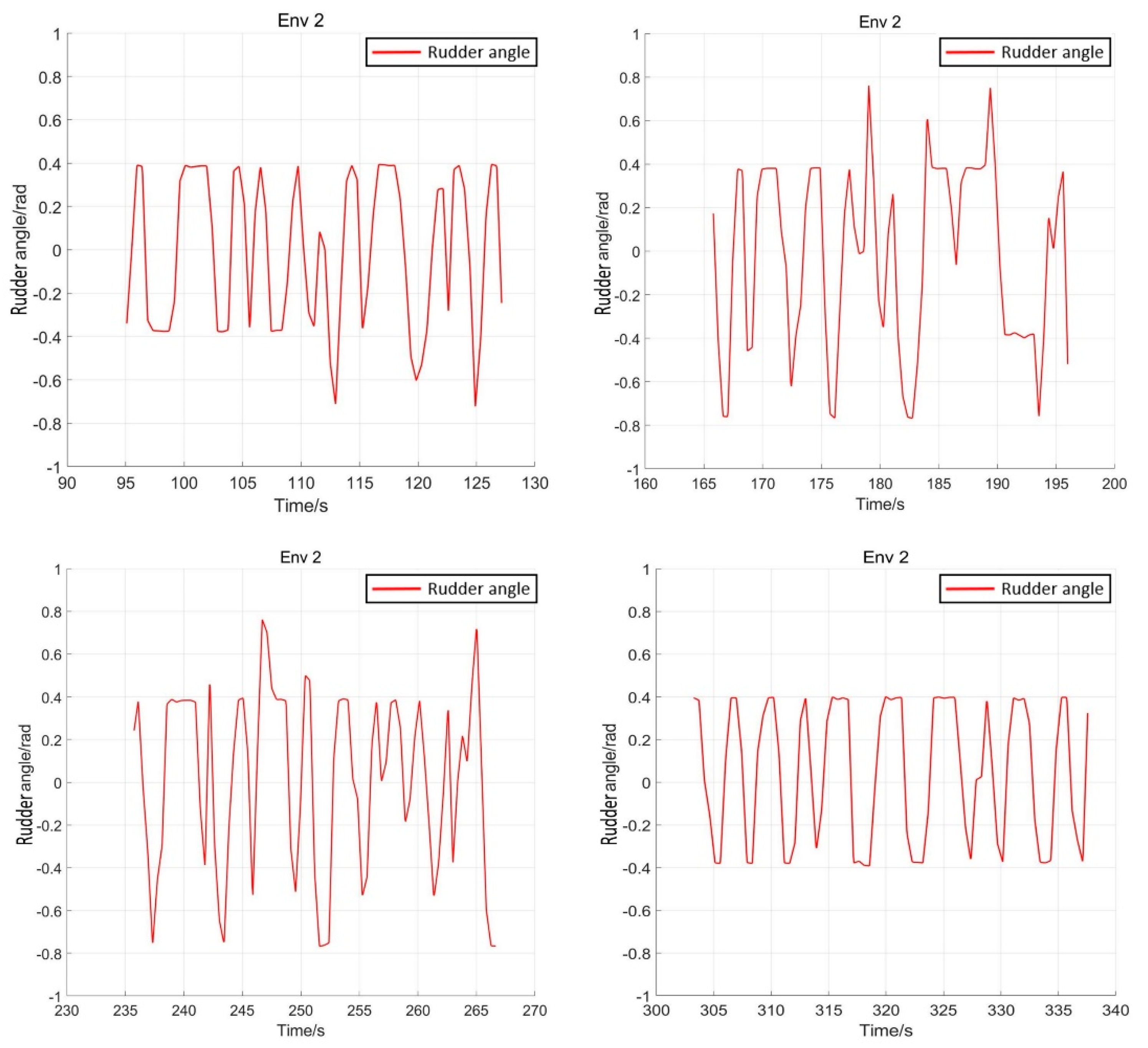
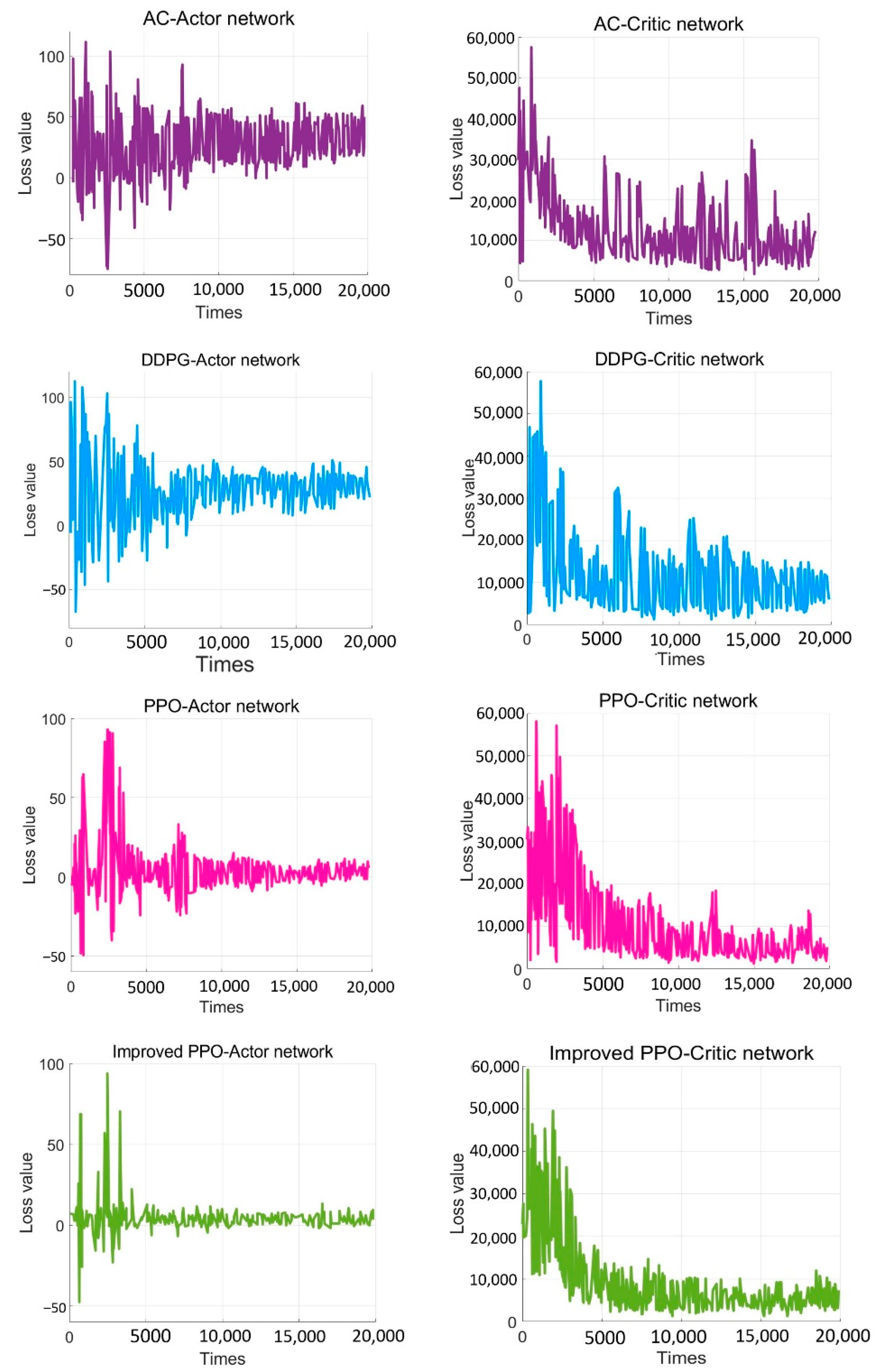
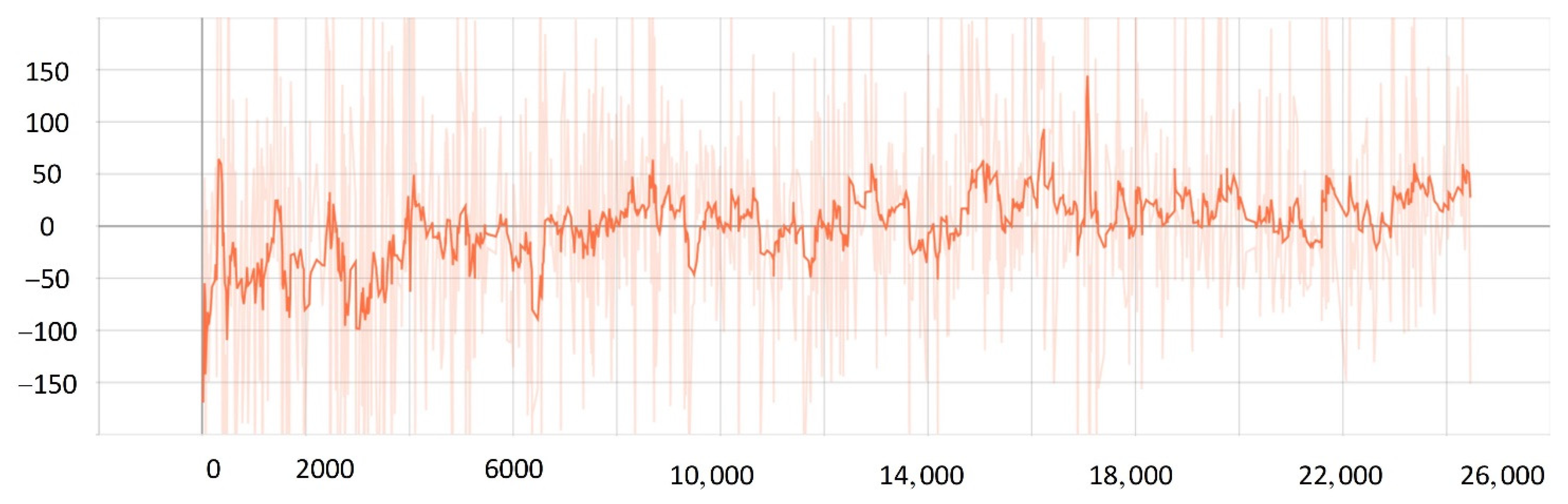
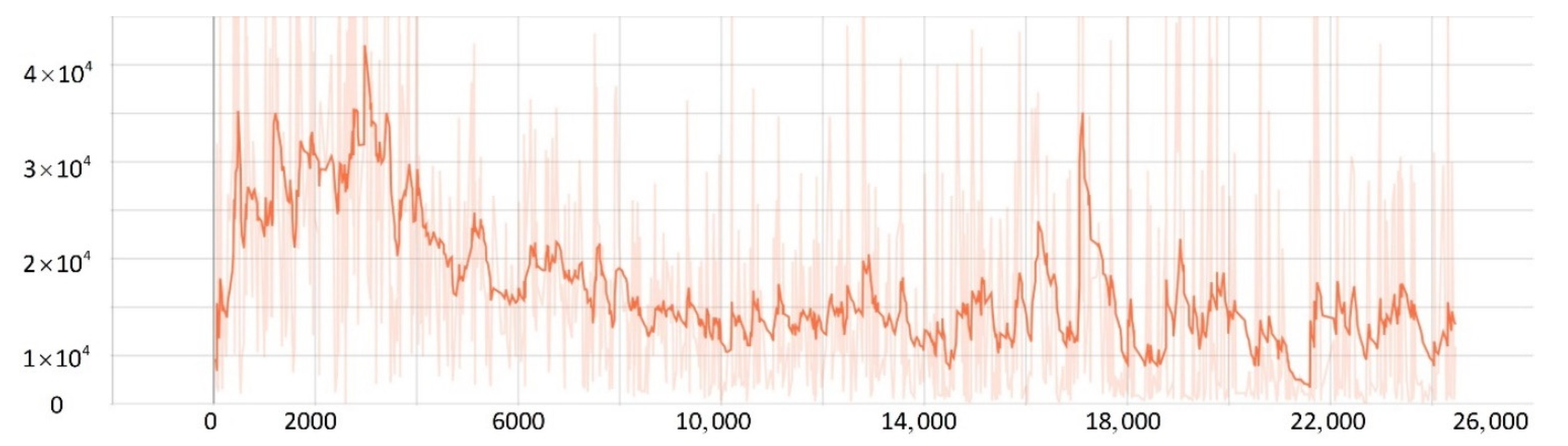
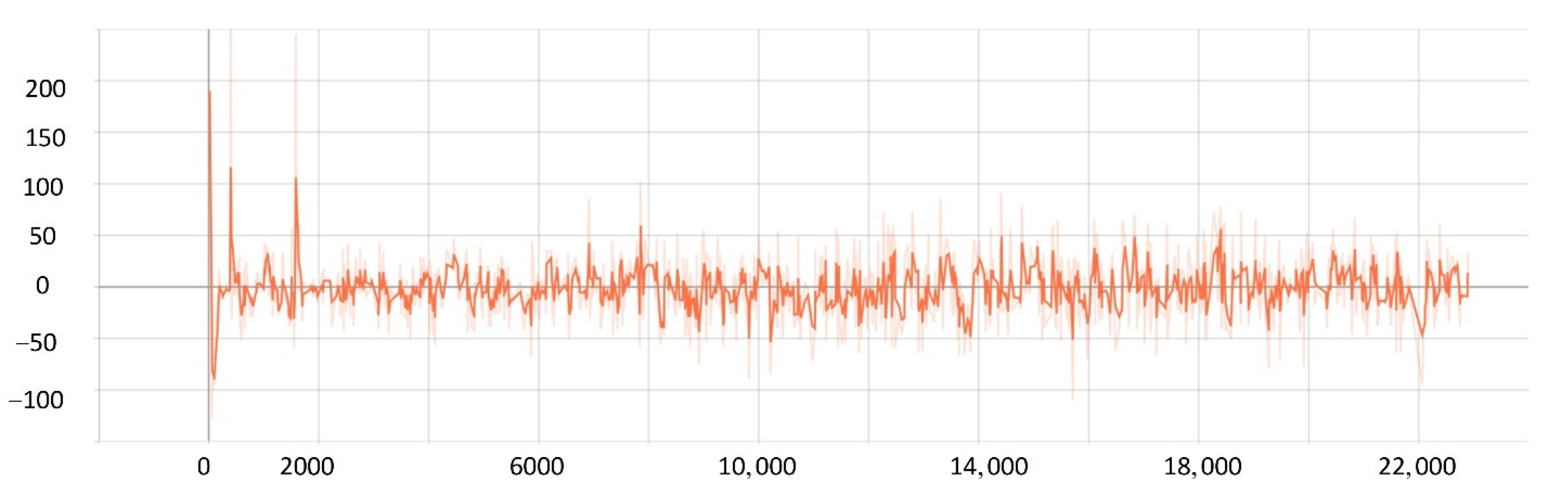
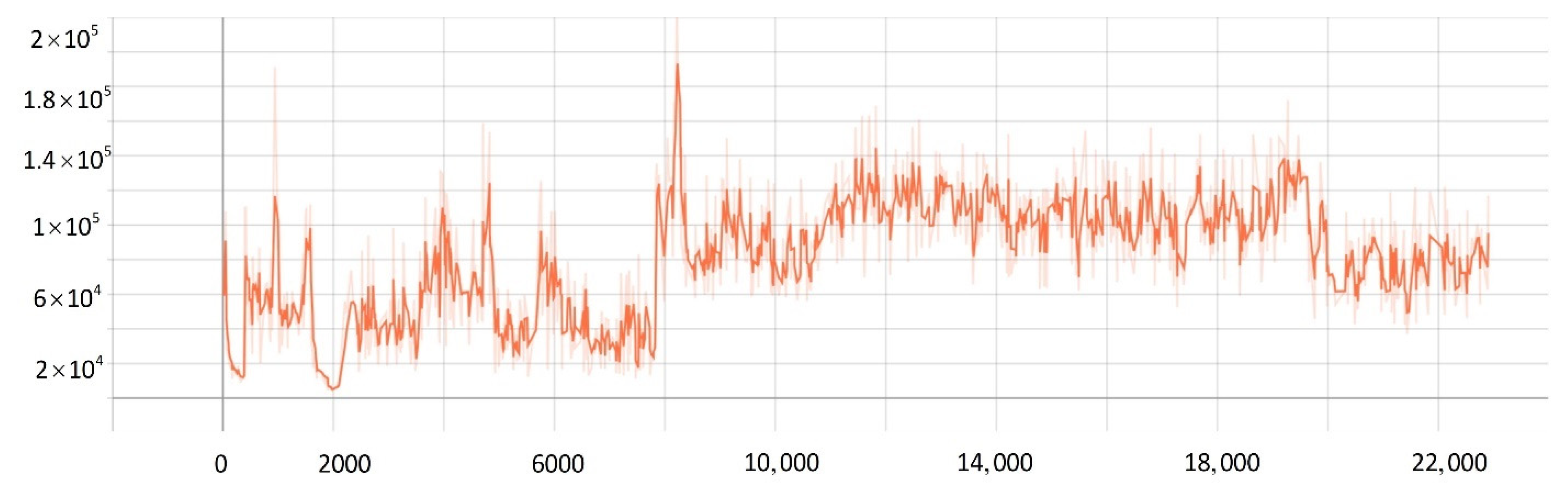
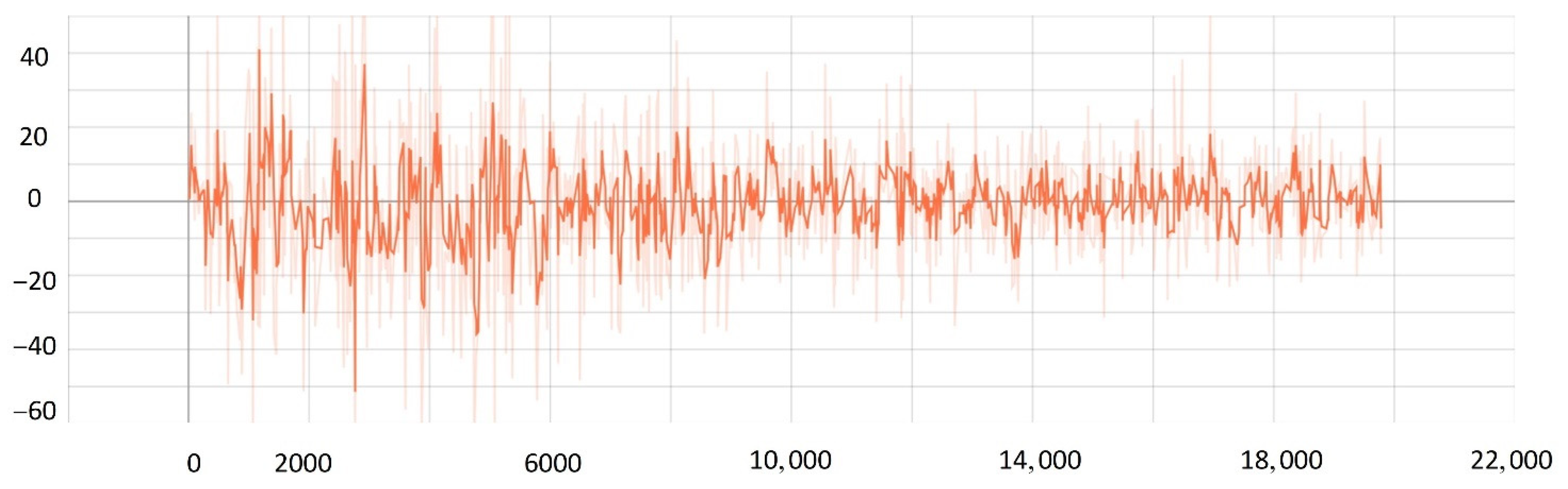
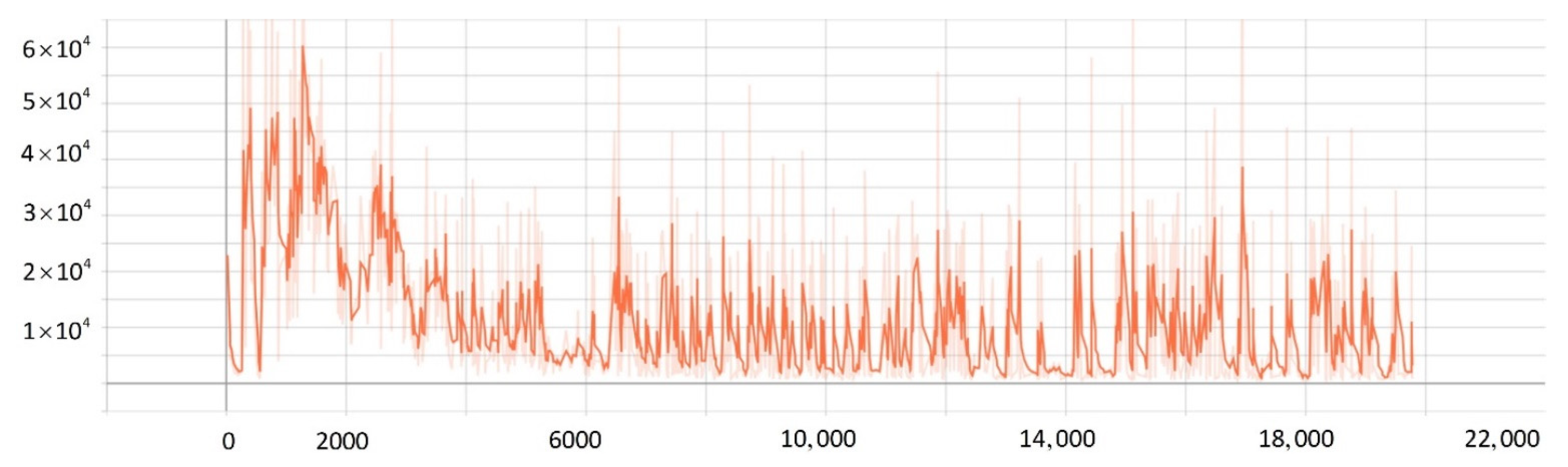
5.2. Network Training Process
5.3. Comparison Experiment
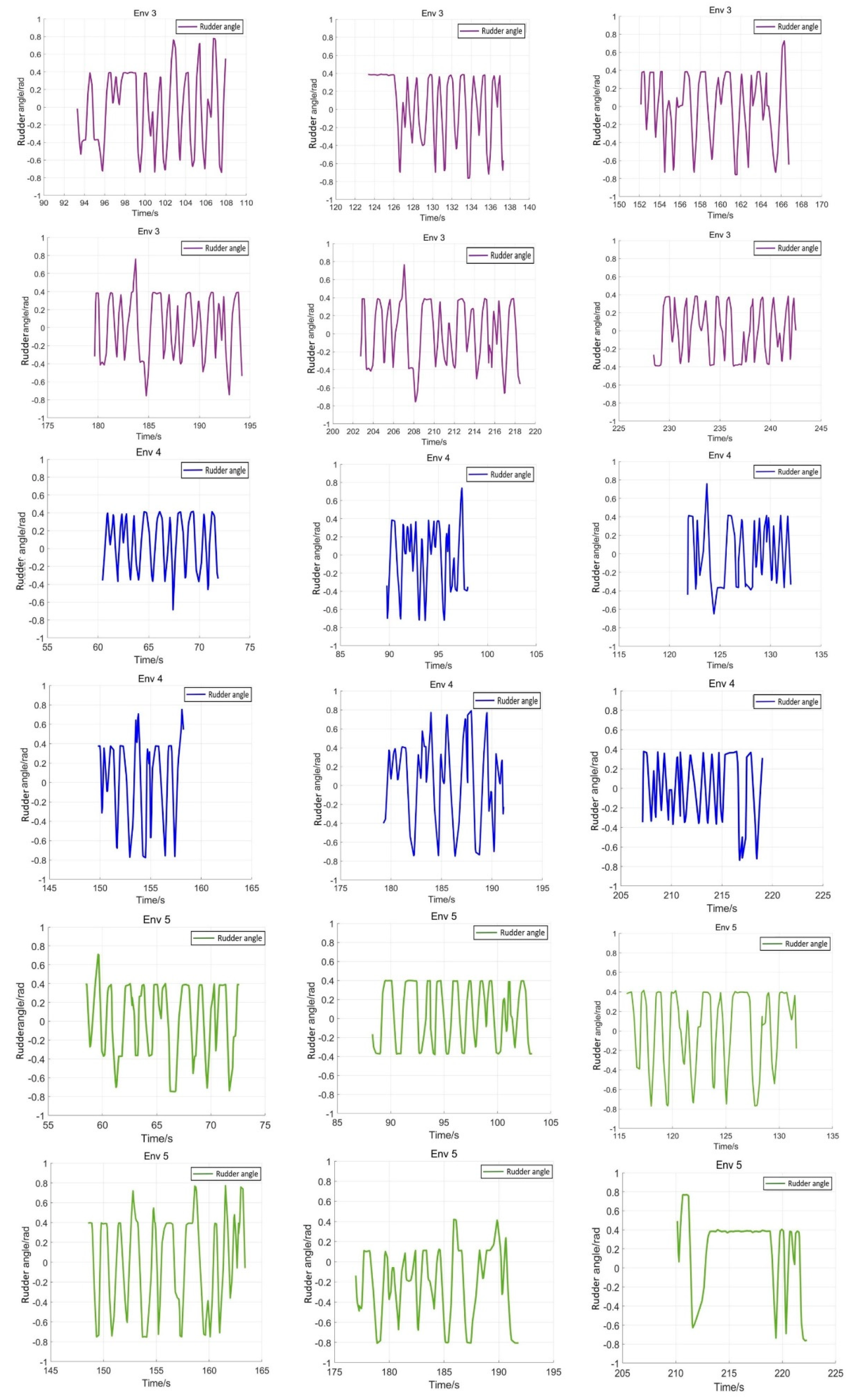
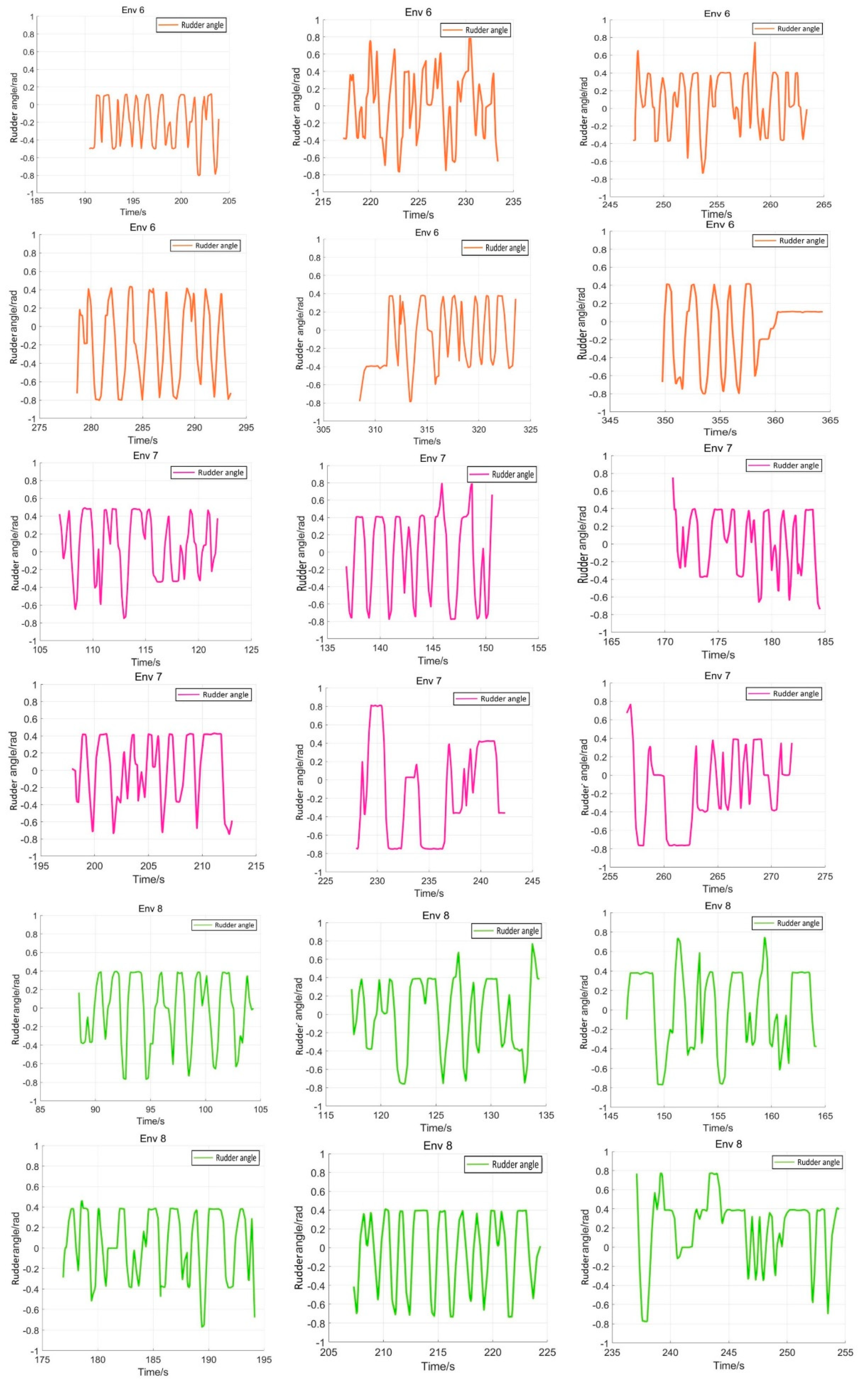
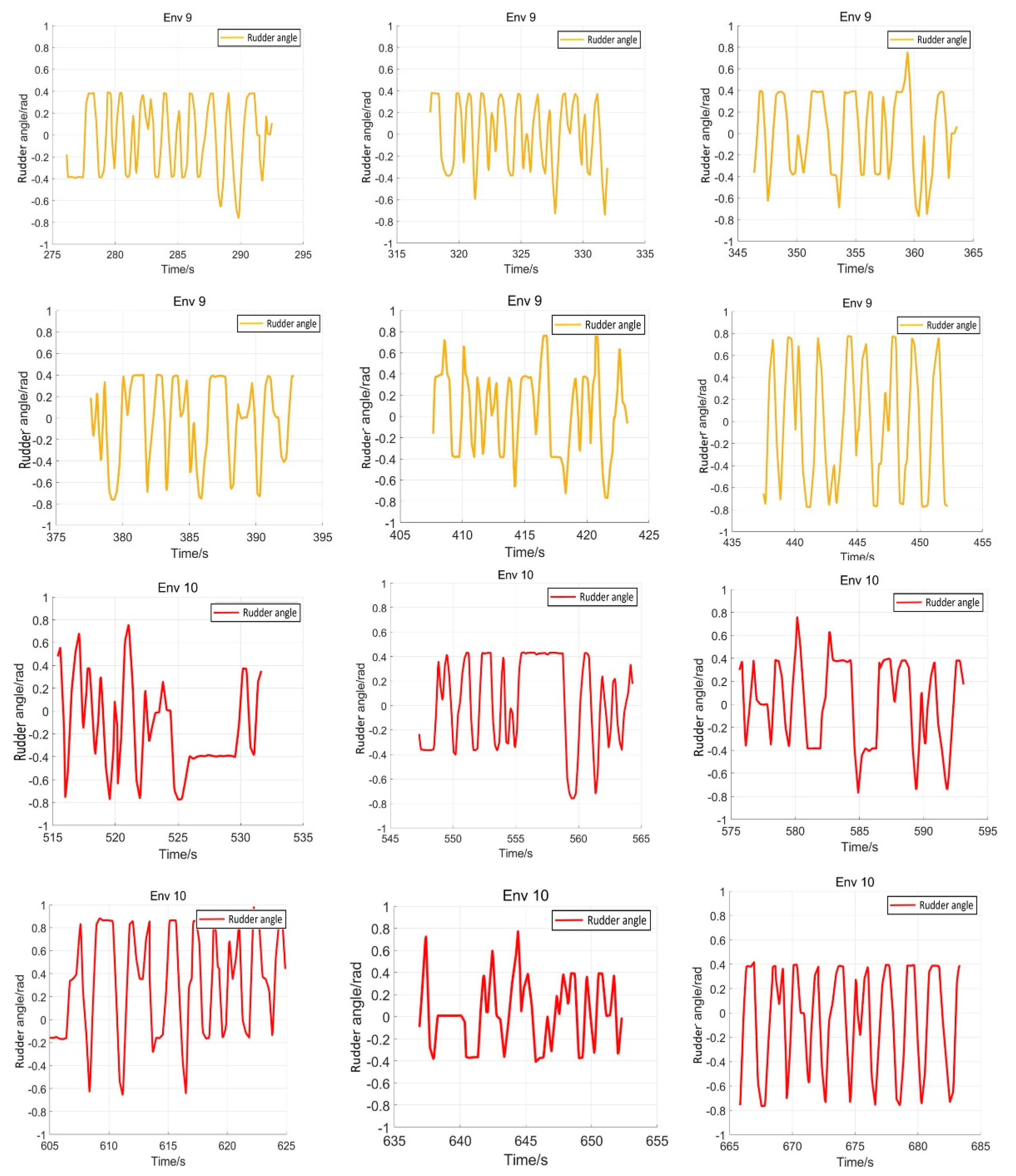
5.4. Verification Simulation
6. Conclusions
- The improved PPO algorithm is superior to other traditional model-free reinforcement learning algorithms based on strategy learning in solving ship decision-making and local path planning problems. The improved PPO algorithm has the advantages of fast convergence and low loss value.
- The improved PPO algorithm has a strong self-learning ability and strong generalization, which could be used to solve the SMASS local path planning and collision avoidance decision-making simultaneously in different complex navigation environments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seuwou, P.; Banissi, E.; Ubakanma, G.; Sharif, M.S.; Healey, A. Actor-Network Theory as a Framework to Analyse Technology Acceptance Model’s External Variables: The Case of Autonomous Vehicles. In International Conference on Global Security, Safety, and Sustainability; Springer: Berlin/Heidelberg, Germany, 2017; pp. 305–320. [Google Scholar]
- Erckens, H.; Busser, G.A.; Pradalier, C.; Siegwart, R.Y. Avalon Navigation Strategy and Trajectory Following Controller for an Autonomous Sailing Vessel. IEEE Robot. Autom. Mag. 2010, 17, 45–54. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, D.F.; Gu, J.D.; Li, F.S. A Path-Planning Strategy for Unmanned Surface Vehicles Based on an Adaptive Hybrid Dynamic Stepsize and Target Attractive Force-RRT Algorithm. J. Mar. Sci. Eng. 2019, 7, 132. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.Y.; Li, Y.; Zhang, J.; Zheng, J.; Yang, C.X. Self-Adaptive Dynamic Obstacle Avoidance and Path Planning for USV Under Complex Maritime Environment. IEEE Access 2019, 7, 114945–114954. [Google Scholar] [CrossRef]
- Xie, S.R.; Wu, P.; Peng, Y.; Luo, J.; Qu, D.; Li, Q.M.; Gu, J. The Obstacle Avoidance Planning of USV Based on Improved Artificial Potential Field. In Proceedings of the IEEE International Conference on Information and Automation (ICIA), Hailar, China, 28–30 July 2014; pp. 746–751. [Google Scholar]
- Lyu, H.; Yin, Y. COLREGS-Constrained Real-time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2019, 72, 588–608. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.Q.; Ma, F.; Zeng, X.J.; Wang, J. A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean. Eng. 2019, 189, 106299. [Google Scholar] [CrossRef]
- Everett, M.; Chen, Y.F.; How, J.P. Motion Planning Among Dynamic, Decision-Making Agents with Deep Reinforcement Learning. In Proceedings of the 25th IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3052–3059. [Google Scholar]
- Zhang, J.; Springenberg, J.T.; Boedecker, J.; Burgard, W. Deep Reinforcement Learning with Successor Features for Navigation across Similar Environments. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Shen, H.; Hashimoto, H.; Matsuda, A.; Taniguchi, Y.; Terada, D.; Guo, C. Automatic collision avoidance of multiple ships based on deep Q-learning. Appl. Ocean. Res. 2019, 86, 268–288. [Google Scholar] [CrossRef]
- Li, L.; Wu, D.; Huang, Y.; Yuan, Z.-M. A path planning strategy unified with a COLREGS collision avoidance function based on deep reinforcement learning and artificial potential field. Appl. Ocean. Res. 2021, 113, 102759. [Google Scholar] [CrossRef]
- Hu, Z.; Wan, K.; Gao, X.; Zhai, Y.; Wang, Q. Deep Reinforcement Learning Approach with Multiple Experience Pools for UAV’s Autonomous Motion Planning in Complex Unknown Environments. Sensors 2020, 20, 1890. [Google Scholar] [CrossRef] [Green Version]
- Chun, D.-H.; Roh, M.-I.; Lee, H.-W.; Ha, J.; Yu, D. Deep reinforcement learning-based collision avoidance for an autonomous ship. Ocean. Eng. 2021, 234, 109216. [Google Scholar] [CrossRef]
- Zhao, L.; Roh, M.-I.; Lee, S.-J. Control method for path following and collision avoidance of autonomous ship based on deep reinforcement learning. J. Mar. Sci. Technol.-Taiwan 2019, 27, 293–310. [Google Scholar]
- Xu, X.L.; Lu, Y.; Liu, X.C.; Zhang, W.D. Intelligent collision avoidance algorithms for USVs via deep reinforcement learning under COLREGs. Ocean. Eng. 2020, 217, 107704. [Google Scholar] [CrossRef]
- Long, P.; Fan, T.; Liao, X.; Liu, W.; Zhang, H.; Pan, J. Towards Optimally Decentralized Multi-Robot Collision Avoidance via Deep Reinforcement Learning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 6252–6259. [Google Scholar]
- Guan, W.; Peng, H.W.; Zhang, X.K.; Sun, H. Ship Steering Adaptive CGS Control Based on EKF Identification Method. J. Mar. Sci. Eng. 2022, 10, 294. [Google Scholar] [CrossRef]
- Guan, W.; Zhou, H.T.; Su, Z.J.; Zhang, X.K.; Zhao, C. Ship Steering Control Based on Quantum Neural Network. Complexity 2019, 2019, 3821048. [Google Scholar] [CrossRef]
- Zhang, X.-K.; Han, X.; Guan, W.; Zhang, G.-Q. Improvement of integrator backstepping control for ships with concise robust control and nonlinear decoration. Ocean. Eng. 2019, 189, 106349. [Google Scholar] [CrossRef]
- Perera, L.P.; Oliveira, P.; Guedes Soares, C. System Identification of Nonlinear Vessel Steering. J. Offshore Mech. Arct. Eng. 2015, 137, 031302. [Google Scholar] [CrossRef] [Green Version]
- Nomoto, K.; Taguchi, T.; Honda, K.; Hirano, S. On the steering qualities of ships. Int. Shipbuild. Prog. 1957, 4, 354–370. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, X.; Chen, X.; Sang, L.; Zhang, D. A novel approach for assistance with anti-collision decision making based on the International Regulations for Preventing Collisions at Sea. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2012, 226, 250–259. [Google Scholar] [CrossRef]
- Vagale, A.; Oucheikh, R.; Bye, R.T.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles I: A review. J. Mar. Sci. Technol. 2021, 26, 1292–1306. [Google Scholar] [CrossRef]
- Dearden, R. Bayesian Q-learning. In Proceedings of the Fifteenth National/tenth Conference on Artificial Intelligence/innovative Applications of Artificial Intelligence, Madison, WI, USA, 26–30 July 1998. [Google Scholar]
- Rumelhart, D.; Hinton, G.E.; Williams, R.J. Learning Representations by Back Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Hasselt, H.V.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
- Fan, Y.; Sun, Z.; Wang, G. A Novel Reinforcement Learning Collision Avoidance Algorithm for USVs Based on Maneuvering Characteristics and COLREGs. Sensors 2022, 22, 2099. [Google Scholar] [CrossRef] [PubMed]
- Duguleana, M.; Mogan, G. Neural networks based reinforcement learning for mobile robots obstacle avoidance. Expert Syst. Appl. 2016, 62, 104–115. [Google Scholar] [CrossRef]









| Experimental Parameters | Symbol | Value |
|---|---|---|
| Discounted rate | 0.95 | |
| Lambda | 0.99 | |
| Clipping hyperparameter | 0.20 | |
| Target reward weight | 10.0 | |
| Reward coefficient | 1.00 | |
| Yaw angle reward weight | 0.30 | |
| COLREGs reward weight | 1.20 | |
| Safe distance | 0.50 | |
| Radar radius | 4.50 |
| Gazebo Environment | Initial Position | End Position |
|---|---|---|
| Env 1(Train) | (1.0, −7.0) | (2.0, 7.0) |
| Env 2(Train) | (6.0, −3.0) | (−4.5, 3.0) |
| Env 3(Verification) | (5.0, 2.0) | (−4.0, 1.0) |
| Env 4(Verification) | (5.0, −1.0) | (−5.0, 1.0) |
| Env 5(Verification) | (1.0, 5.0) | (1.0, −5.0) |
| Env 6(Verification) | (1.0, 4.0) | (2.0, −5.0) |
| Env 7(Verification) | (3.0, 2.0) | (−1.0, −4.0) |
| Env 8(Verification) | (−3.0, 1.0) | (4.0, −1.0) |
| Env 9(Verification) | (0.0, 7.0) | (1.0, −6.0) |
| Env 10(Verification) | (9.0, −4.0) | (−9.0, 3.0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, W.; Cui, Z.; Zhang, X. Intelligent Smart Marine Autonomous Surface Ship Decision System Based on Improved PPO Algorithm. Sensors 2022, 22, 5732. https://doi.org/10.3390/s22155732
Guan W, Cui Z, Zhang X. Intelligent Smart Marine Autonomous Surface Ship Decision System Based on Improved PPO Algorithm. Sensors. 2022; 22(15):5732. https://doi.org/10.3390/s22155732
Chicago/Turabian StyleGuan, Wei, Zhewen Cui, and Xianku Zhang. 2022. "Intelligent Smart Marine Autonomous Surface Ship Decision System Based on Improved PPO Algorithm" Sensors 22, no. 15: 5732. https://doi.org/10.3390/s22155732
APA StyleGuan, W., Cui, Z., & Zhang, X. (2022). Intelligent Smart Marine Autonomous Surface Ship Decision System Based on Improved PPO Algorithm. Sensors, 22(15), 5732. https://doi.org/10.3390/s22155732








