The Experimental Registration of the Evanescent Acoustic Wave in YX LiNbO3 Plate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Methods
2.1.1. Boundary Transfer Matrix Method
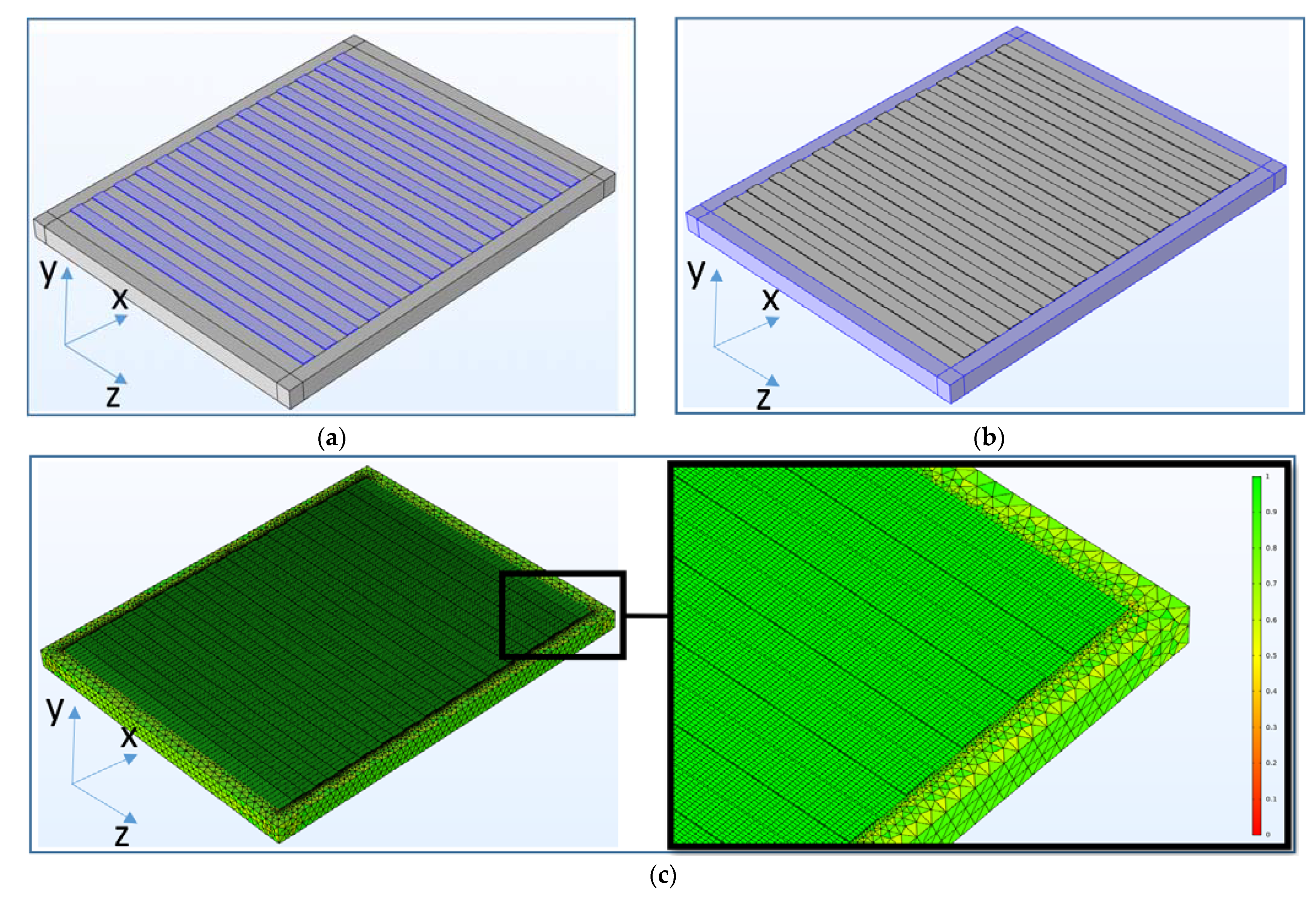
2.1.2. FEM Simulation
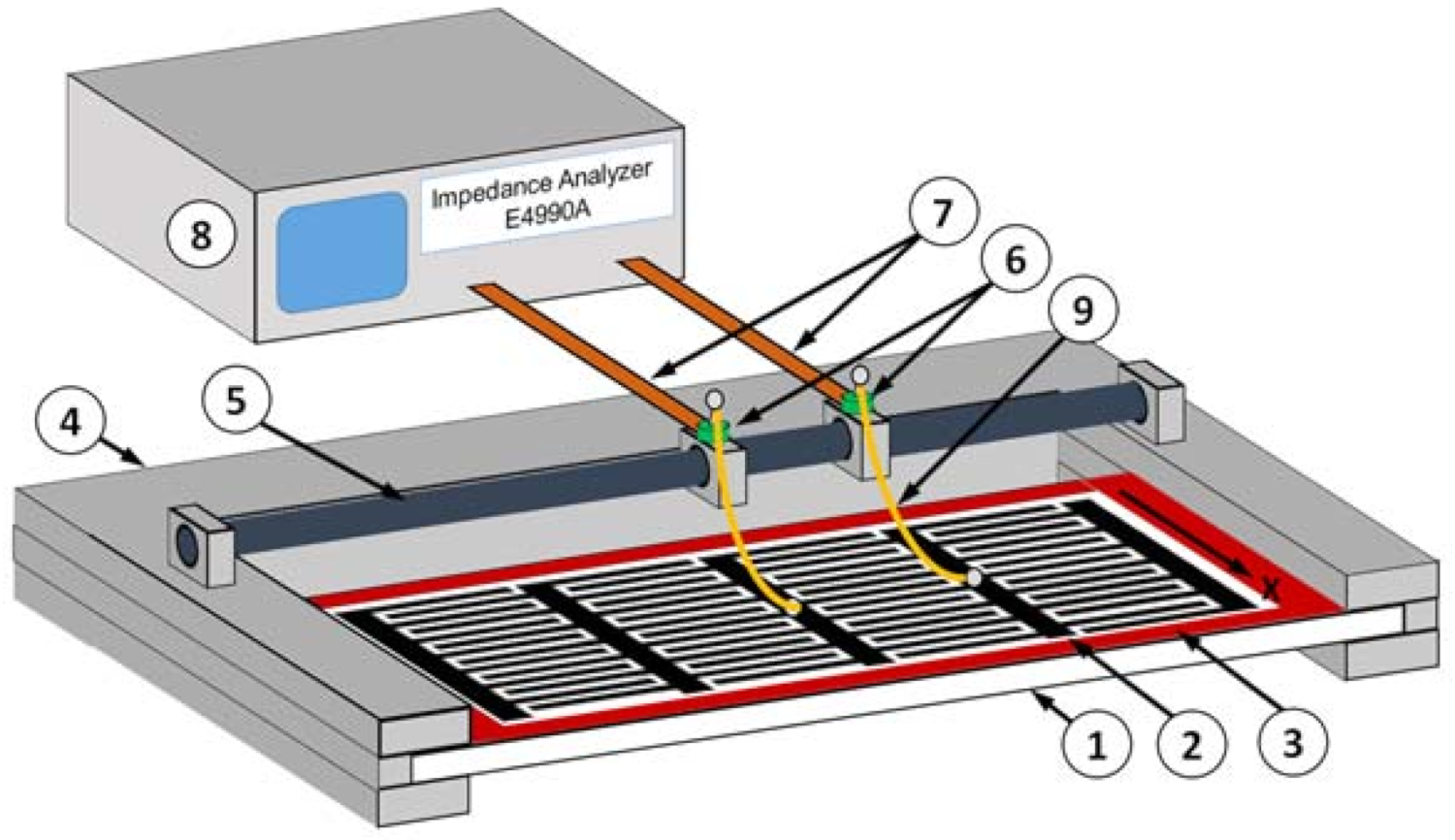
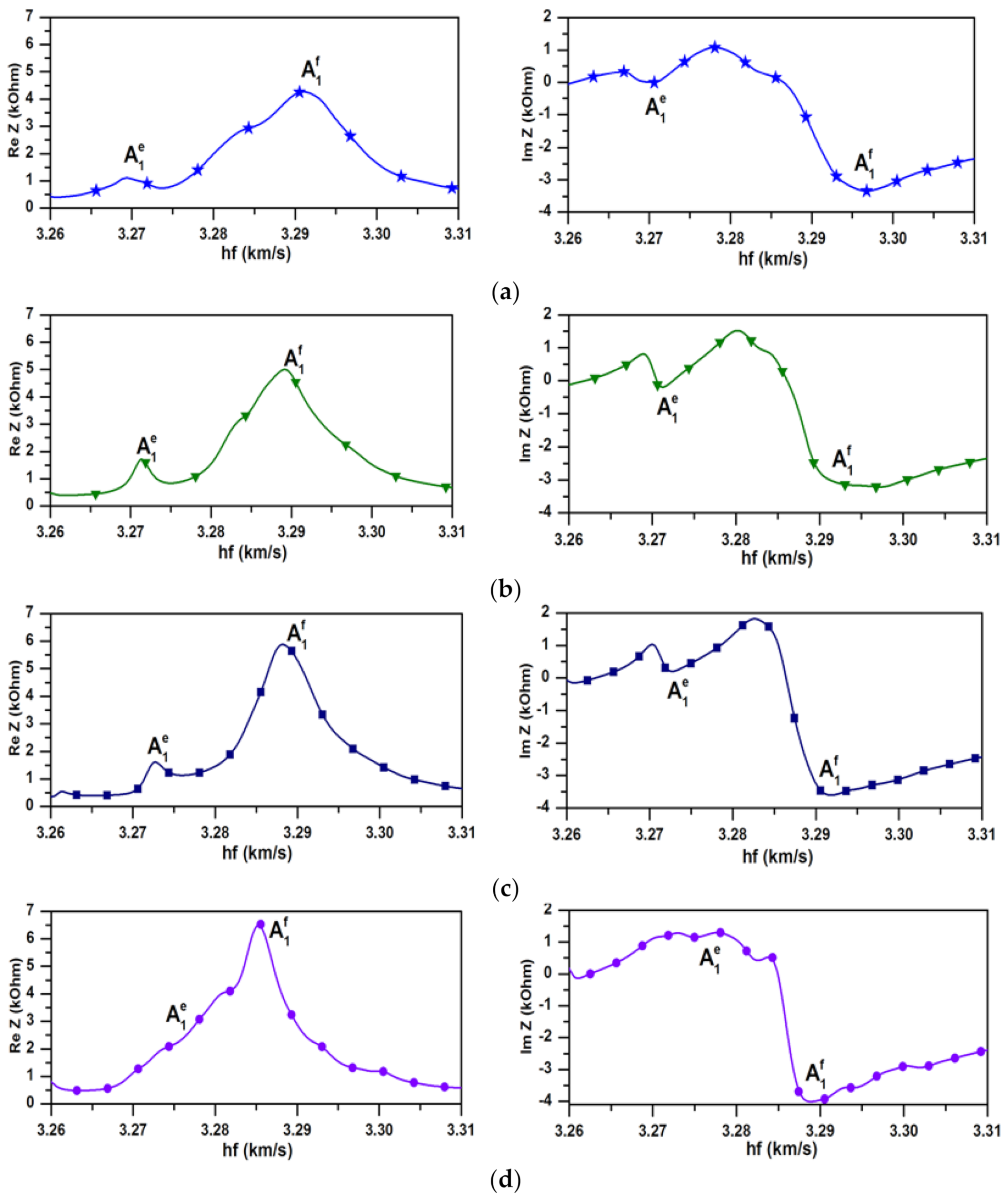
2.2. Experimental Study
3. Results and Discussion
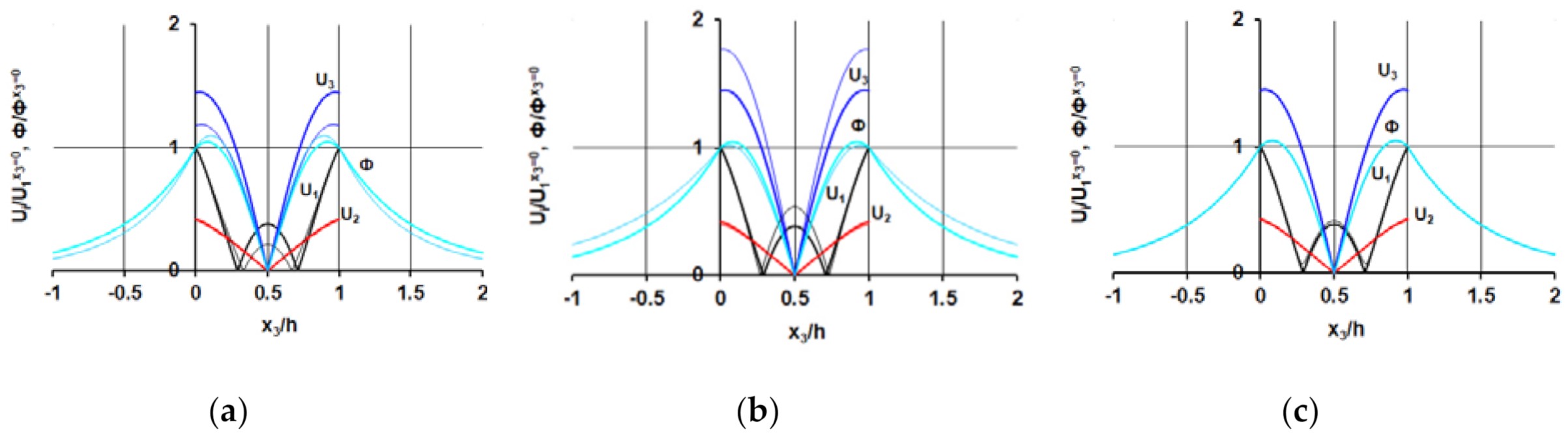
3.1. Theoretical Results
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Auld, B.A. Acoustic Fields and Waves in Solids; John Wiley & Sons: New York, NY, USA, 1973; Volume 2, p. 83. [Google Scholar]
- Lyon, R.H. Response of an elastic plate to localized driving forces. J. Acoust. Soc. Am. 1955, 27, 259–265. [Google Scholar] [CrossRef]
- Pagneux, V.; Maurel, A. Determination of Lamb mode eigenvalues. J. Acoust. Soc. Am. 2001, 110, 1307–1314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mindlin, R.D.; Yang, J. An Introduction to the Mathematical Theory of Vibrations of Elastic Plates; World Scientific Publishing: New York, NY, USA, 2006; p. 190. [Google Scholar]
- Chen, H.; Wang, ·.J.; Du, ·.J.; Yang, ·.J. Propagation of shear-horizontal waves in piezoelectric plates of cubic crystals. Arch. Appl. Mech. 2016, 86, 517–528. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Yu, J. The Computation of Complex Dispersion and Properties of Evanescent Lamb Wave in Functionally Graded Piezoelectric-Piezomagnetic Plates. Materials 2018, 11, 1186. [Google Scholar] [CrossRef] [Green Version]
- Romero-García, V.; Sánchez-Pérez, J.V.; Castiñeira-Ibáñez, S.; Garcia-Raffi, L.M. Evidences of evanescent Bloch waves in phononic crystals. Appl. Phys. Lett. 2010, 96, 124102. [Google Scholar] [CrossRef] [Green Version]
- Quintanilla, F.H.; Lowe, M.J.S.; Craster, R.V. Full 3D dispersion curve solutions for guided waves in generally anisotropic media. J. Sound Vib. 2016, 363, 545–559. [Google Scholar] [CrossRef]
- Simonetti, F.; Lowe, M.J.S. On the meaning of Lamb mode evanescent branches. J. Acoust. Soc. Am. 2005, 118, 186–192. [Google Scholar] [CrossRef]
- Philippe, F.D.; Clorennec, D.; Ces, M.; Anankine, R.; Prada, C. Analysis of backward waves and quasi-resonance of shells with the invariants of the time reversal operator. Proc. Meet. Acoust. ICA 2013, 19, 055022. [Google Scholar]
- Fay, R.D.; Fortier, O.V. Transmission of sound through steel plates immersed in water. J. Acoust. Soc. Am. 1951, 23, 339–346. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Chimenti, D.E.; Nayfeh, A.H. On the topology of the complex wave spectrum in a fluid-coupled elastic layer. J. Acoust. Soc. Am. 1989, 85, 1074–1080. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Yu, J.; ·Ming, P. Guided evanescent waves in spherically curved plates composed of fiber reinforced composites. Acta Mech. 2019, 230, 1219–1231. [Google Scholar] [CrossRef]
- Kaduchak, G.; Hughes, D.H.; Marston, P.L. Enhancement of the backscattering of high frequency tone bursts by thin spherical shells associated with a backwards wave: Observations and ray approximation. J. Acoust. Soc. Am. 1994, 96, 3704–3714. [Google Scholar] [CrossRef]
- Nedospasov, I.A.; Mozhaev, V.G.; Kuznetsova, I.E. Unusual energy properties of leaky backward Lamb waves in a submerged plate. Ultrasonics 2017, 77, 95–99. [Google Scholar] [CrossRef]
- Song, X.; Chen, T.; Zhu, J.; Ding, W.; Liang, Q.; Wang, X. Broadband and broad-angle asymmetric acoustic transmission by unbalanced excitation of surface evanescent waves based on single-layer metasurface. Phys. Lett. A 2020, 384, 126419. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Zhang, S.-Y.; Wang, Y.-S.; Laude, V. Hybridization of resonant modes and Bloch waves in acoustoelastic phononic crystals. Phys. Rev. 2020, B102, 144303. [Google Scholar] [CrossRef]
- Miranda, E.J.P., Jr.; Nobrega, E.D.; Rodrigues, S.F.; Aranas, C., Jr.; Dos Santos, J.M.C. Wave attenuation in elastic metamaterial thick plates: Analytical, numerical and experimental investigations. Int. J. Sol. Struct. 2020, 204–205, 138–152. [Google Scholar] [CrossRef]
- Wang, T.-T.; Wang, Y.-F.; Wang, Y.-S.; Laude, V. Evanescent-wave tuning of a locally resonant sonic crystal. Appl. Phys. Lett. 2018, 113, 231901. [Google Scholar] [CrossRef] [Green Version]
- Tavaf, V.; Banerjee, S. Generalized analytical dispersion equations for guided Rayleigh-Lamb (RL) waves and shear horizontal (SH) waves in corrugated waveguides. Int. J. Sol. Struct. 2020, 202, 75–86. [Google Scholar] [CrossRef]
- Long, Y.; Ren, J.; Chen, H. Intrinsic spin of elastic waves. Proc. Natl. Acad. Sci. USA 2018, 115, 9951–9955. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Zhao, R.; Long, Y.; Yang, S.; Wang, Y.; Chen, H.; Ren, J.; Zhang, X. Observation of acoustic spin. Nat. Sci. Rev. 2019, 6, 707–712. [Google Scholar] [CrossRef] [Green Version]
- Bliokh, K.Y.; Nori, F. Transverse spin and surface waves in acoustic metamaterials. Phys. Rev. 2019, B99, 020301. [Google Scholar] [CrossRef] [Green Version]
- Torvik, P.J. Reflection of wave trains in semi-infinite plates. J. Acoust. Soc. Am. 1967, 41, 346–353. [Google Scholar] [CrossRef]
- Cho, Y.; Rose, J. A boundary element solution for a mode conversion study on the edge reflection of Lamb waves. J. Acoust. Soc. Am. 1996, 99, 2097–2109. [Google Scholar] [CrossRef]
- Gregory, R.D.; Gladwell, I. The reflection of a symmetric Rayleigh-Lamb wave at the fixed or free edge of a plate. J. Elast. 1983, 13, 185–206. [Google Scholar] [CrossRef]
- Clezio, E.L.; Predoi, M.; Castaings, M.; Hosten, B.; Rousseau, M. Numerical predictions and experiments on the free-plate edge mode. Ultrasonics 2003, 41, 25–40. [Google Scholar] [CrossRef]
- Santhanam, S.; Demirli, R. Reflection of Lamb waves obliquely incident on the free edge of a plate. Ultrasonics 2013, 53, 271–282. [Google Scholar] [CrossRef]
- Ratassepp, M.; Klauson, A.; Chati, F. Application of orthogonality-relation for the separation of Lamb modes at a plate edge: Numerical and experimental predictions. Ultrasonics 2015, 57, 90–95. [Google Scholar] [CrossRef]
- Yan, X.; Yuan, F.G. A semi-analytical approach for SH guided wave mode conversion from evanescent into propagating. Ultrasonics 2018, 84, 430–437. [Google Scholar] [CrossRef]
- Diligent, O.; Lowe, M.J.S.; Clezio, E.L.; Castaings, M.; Hosten, B. Prediction and measurement of evanescent Lamb modes at the free end of a plate when the fundamental antisymmetric mode A0 is incident. J. Acoust. Soc. Am. 2003, 113, 3032–3042. [Google Scholar] [CrossRef]
- Cès, M.; Clorennec, D.; Royer, D.; Prada, C. Edge resonance and zero group velocity Lamb modes in a free elastic plate. J. Acoust. Soc. Am. 2011, 130, 689–694. [Google Scholar] [CrossRef] [PubMed]
- An, Y.K.; Sohn, H. Visualization of non-propagating Lamb wave modes for fatigue crack evaluation. J Appl. Phys. 2015, 117, 114904. [Google Scholar] [CrossRef] [Green Version]
- Cawley, P.; Alleyne, D. The use of Lamb waves for the long range inspection of large structures. Ultrasonics 1996, 34, 287–290. [Google Scholar] [CrossRef]
- Kee, S.-H.; Lee, J.-W.; Candelaria, M.D. Evaluation of delamination in concrete by IE testing using multi-channel elastic data. Sensors 2020, 20, 201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.; Kee, S.-H.; Kang, J.-W.; Choi, B.-J.; Lee, J.-W. Interpretation of impact-echo testing data from a fire-damaged reinforced concrete slab using a discrete layered concrete damage model. Sensors 2020, 20, 5838. [Google Scholar] [CrossRef] [PubMed]
- Fujii, A.; Wakatsuki, N.; Mizutani, K. A planar acoustic transducer for near field acoustic communication using evanescent wave. Jpn. J. App. Phys. 2014, 53, 07KB07. [Google Scholar] [CrossRef]
- Cheng, H.; Shao, G.; Ebadi, S.; Ren, X.; Harris, K.; Liu, J.; Xu, C.; An, L.; Gong, X. Evanescent-mode-resonator-based and antenna-integrated wireless passive pressure sensors for harsh-environment applications. Sens. Actuators A 2014, 220, 22–33. [Google Scholar] [CrossRef] [Green Version]
- Kazys, R.J.; Vilpisauskas, A. Air-coupled reception of a slow ultrasonic A0 mode wave propagating in thin plastic film. Sensors 2020, 20, 516. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aubert, V.; Wunenburger, R.; Valier-Brasier, T.; Rabaud, D.; Kleman, J.-P.; Poulan, C. A simple acoustofluidic chip for microscale manipulation using evanescent Scholte waves. Lab Chip 2016, 16, 2532–2539. [Google Scholar] [CrossRef]
- Zaitsev, B.; Kuznetsova, I.; Nedospasov, I.; Smirnov, A.; Semyonov, A. New approach to detection of guided waves with negative group velocity: Modeling and experiment. J. Sound Vib. 2019, 442, 155–166. [Google Scholar] [CrossRef]
- Kuznetsova, I.; Nedospasov, I.; Smirnov, A.; Qian, Z.; Wang, B.; Dai, X. Excitation and detection of evanescent acoustic waves in piezoelectric plates: Theoretical and 2D FEM modeling. Ultrasonics 2019, 99, 105961. [Google Scholar] [CrossRef]
- Rotter, M.; Ruile, V.; Wixforth, A.; Kotthaus, J.P. Voltage controlled SAW velocity in GaAs/LiNbO3-hybrids. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 120–125. [Google Scholar] [CrossRef]
- Pedros, J.; Calle, F.; Cuerdo, R.; Grajal, J.; Bougrioua, Z. Voltage tunable surface acoustic wave phase shifter on AlGaN/GaN//. Appl. Phys. Lett. 2010, 96, 123505. [Google Scholar]
- Zaitsev, B.D.; Joshi, S.G.; Kuznetsova, I.E.; Borodina, I.A. Influence of conducting layer and conducting electrode on acoustic waves propagating in potassium niobateplates. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 624–626. [Google Scholar] [CrossRef]
- Kuznetsova, I.E.; Nedospasov, I.A.; Kolesov, V.V.; Qian, Z.; Wang, B.; Zhu, F. Influence of electrical boundary conditions on profiles of acoustic field and electric potential of shear-horizontal acoustic waves in potassium niobate plates. Ultrasonics 2018, 86, 6–13. [Google Scholar] [CrossRef]
- Zhu, F.; Wang, B.; Qian, Z.; Kuznetsova, I.; Ma, T. Influence of surface conductivity on dispersion curves, mode shapes, stress and potential for Lamb waves propagating in piezoelectric plate. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 855–862. [Google Scholar] [CrossRef]
- Jakubik, W.; Wrotniak, J.; Powrozhnik, P. Theoretical analysis of a surface acoustic wave gas sensor mechanism using electrical conductive bi-layer nanostructures. Sens. Actuators B 2018, 262, 947–952. [Google Scholar] [CrossRef]
- Drichko, I.L.; Diakonov, A.M.; Lebedeva, E.V.; Smirnov, I.Y.; Mironov, O.A.; Kummer, M.; von Kaenel, H. Acoustoelectric effects in very high-mobility p-SiGe/Ge/SiGeheterostructure. J. Appl. Phys. 2009, 106, 094305. [Google Scholar] [CrossRef] [Green Version]
- Adler, E.L. SAW and pseudo-SAW properties using matrix-methods. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1994, 41, 876–882. [Google Scholar] [CrossRef]
- Royer, D.; Dieulesaint, E. Elastic Waves in Solids; John Wiley & Sons: New York, NY, USA, 1980; Volume 1, p. 216. [Google Scholar]
- Kuznetsova, I.E.; Zaitsev, B.D.; Teplykh, A.A.; Joshi, S.G.; Kuznetsova, A.S. The power flow angle of acoustic waves in thin piezoelectric plates. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 1984–1991. [Google Scholar] [CrossRef] [Green Version]
- Available online: http://www.bostonpiezooptics.com/lithium-niobate (accessed on 16 December 2020).
- Bliokh, K.Y.; Bekshaev, A.Y.; Nori, F. Extraordinary momentum and spin in evanescent waves. Nat. Commun. 2014, 5, 3300. [Google Scholar] [CrossRef]





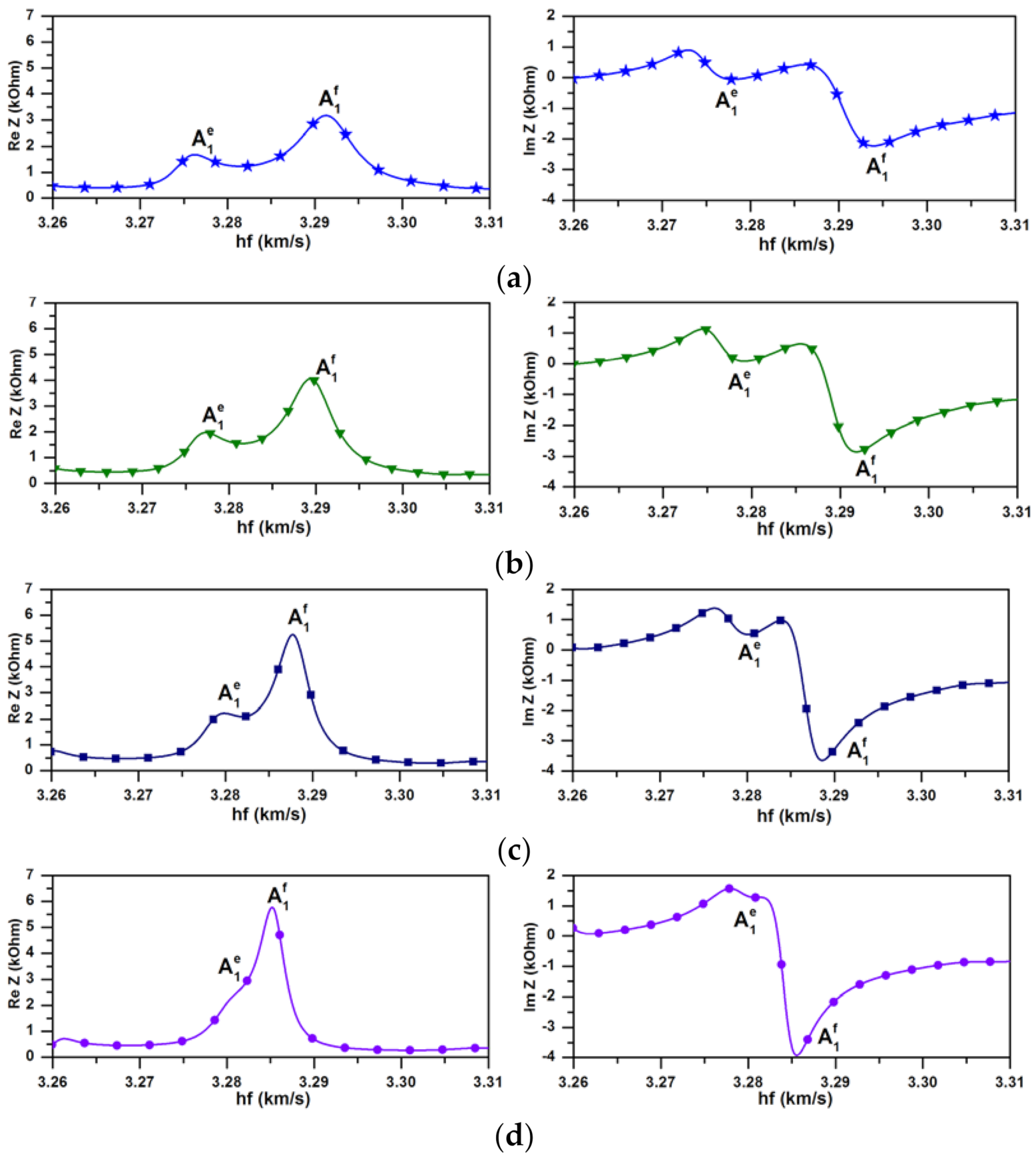
| λ, mm | Theory | Experiment | ||
|---|---|---|---|---|
| hf(A1f), km/s | hf(A1e), km/s | hf(A1f), km/s | hf(A1e), km/s | |
| 1.40 | 3.295 | 3.275 | 3.293 | 3.267 |
| 1.42 | 3.290 | 3.277 | 3.290 | 3.272 |
| 1.44 | 3.288 | 3.279 | 3.288 | 3.274 |
| 1.46 | 3.285 | 3.283 | 3.285 | 3.277 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnov, A.; Zaitsev, B.; Teplykh, A.; Nedospasov, I.; Golovanov, E.; Qian, Z.-h.; Wang, B.; Kuznetsova, I. The Experimental Registration of the Evanescent Acoustic Wave in YX LiNbO3 Plate. Sensors 2021, 21, 2238. https://doi.org/10.3390/s21062238
Smirnov A, Zaitsev B, Teplykh A, Nedospasov I, Golovanov E, Qian Z-h, Wang B, Kuznetsova I. The Experimental Registration of the Evanescent Acoustic Wave in YX LiNbO3 Plate. Sensors. 2021; 21(6):2238. https://doi.org/10.3390/s21062238
Chicago/Turabian StyleSmirnov, Andrey, Boris Zaitsev, Andrey Teplykh, Ilya Nedospasov, Egor Golovanov, Zheng-hua Qian, Bin Wang, and Iren Kuznetsova. 2021. "The Experimental Registration of the Evanescent Acoustic Wave in YX LiNbO3 Plate" Sensors 21, no. 6: 2238. https://doi.org/10.3390/s21062238








