Comparison of DOFS Attachment Methods for Time-Dependent Strain Sensing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
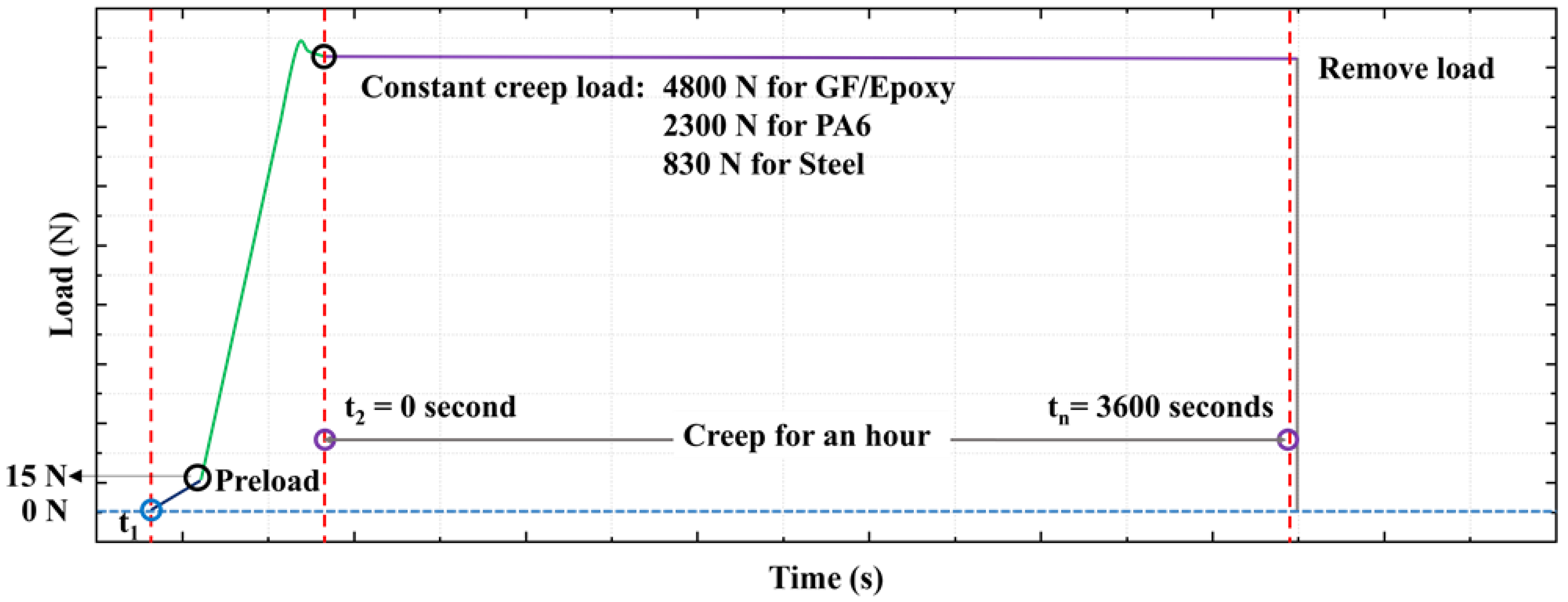
2.2. Creep Testing
2.3. Strain Measurements
3. Results
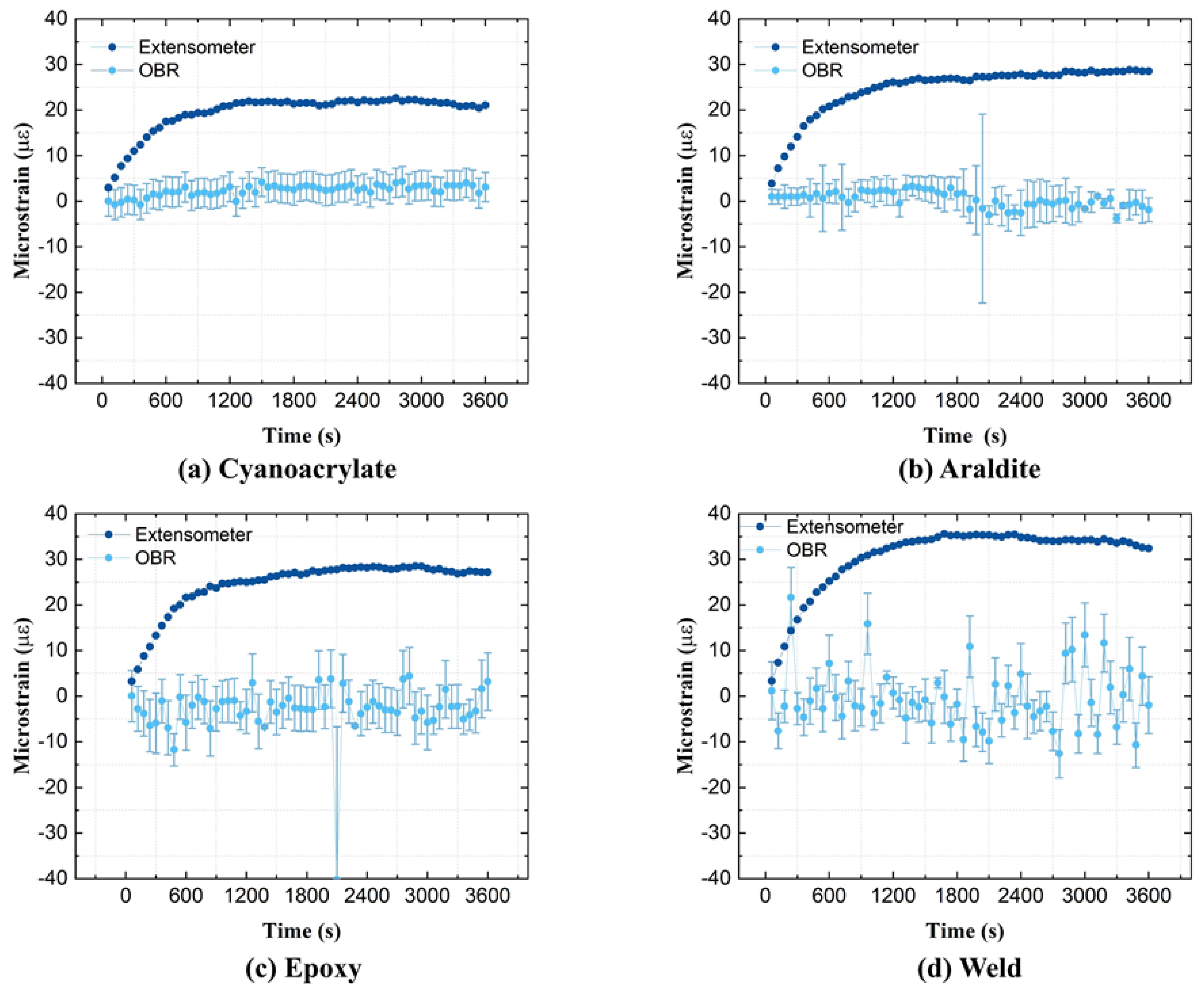
3.1. GF/Epoxy Composite
3.2. Thermoplastic PA6
3.3. Steel
4. Discussion
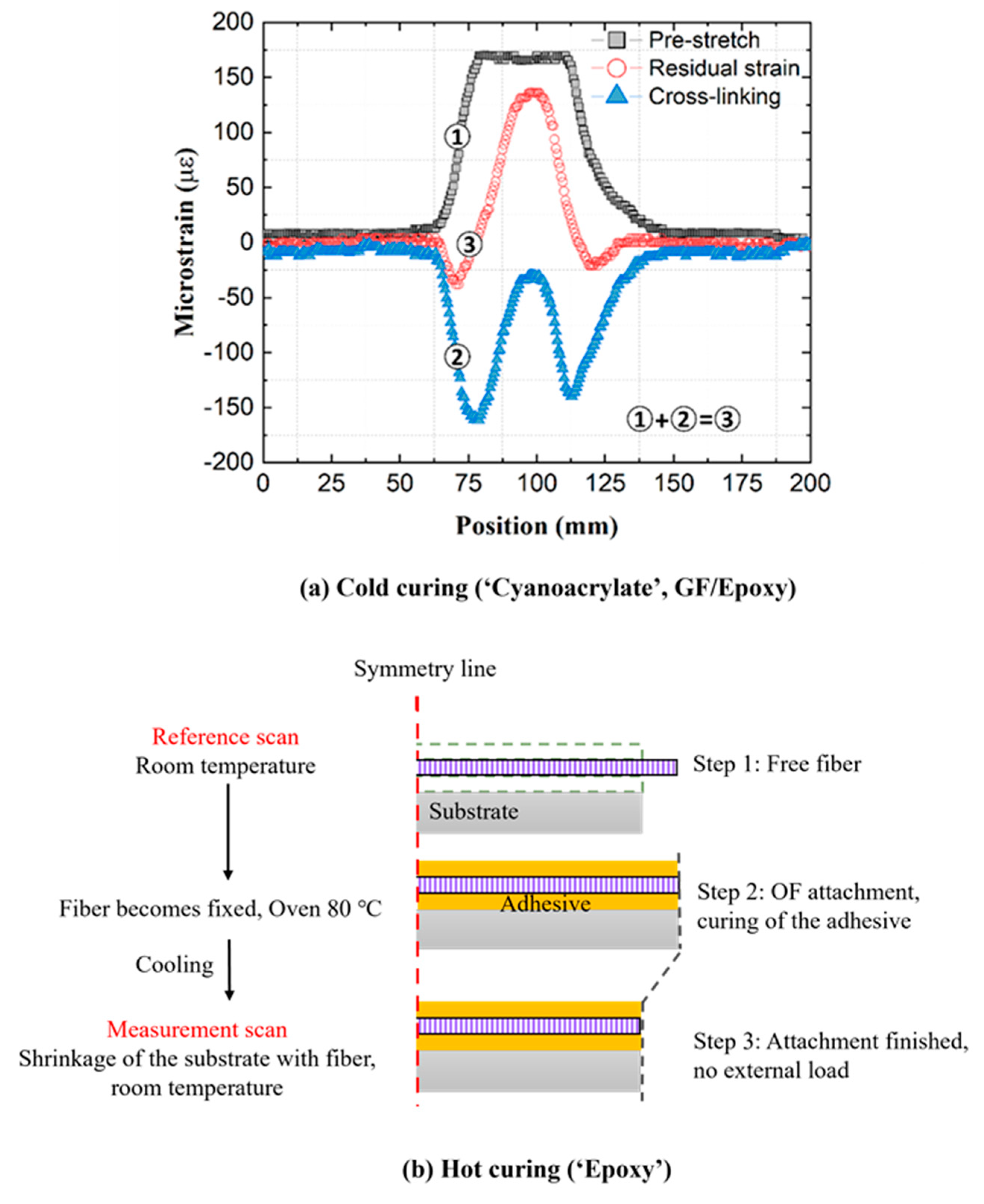
4.1. The OF Attachment Process
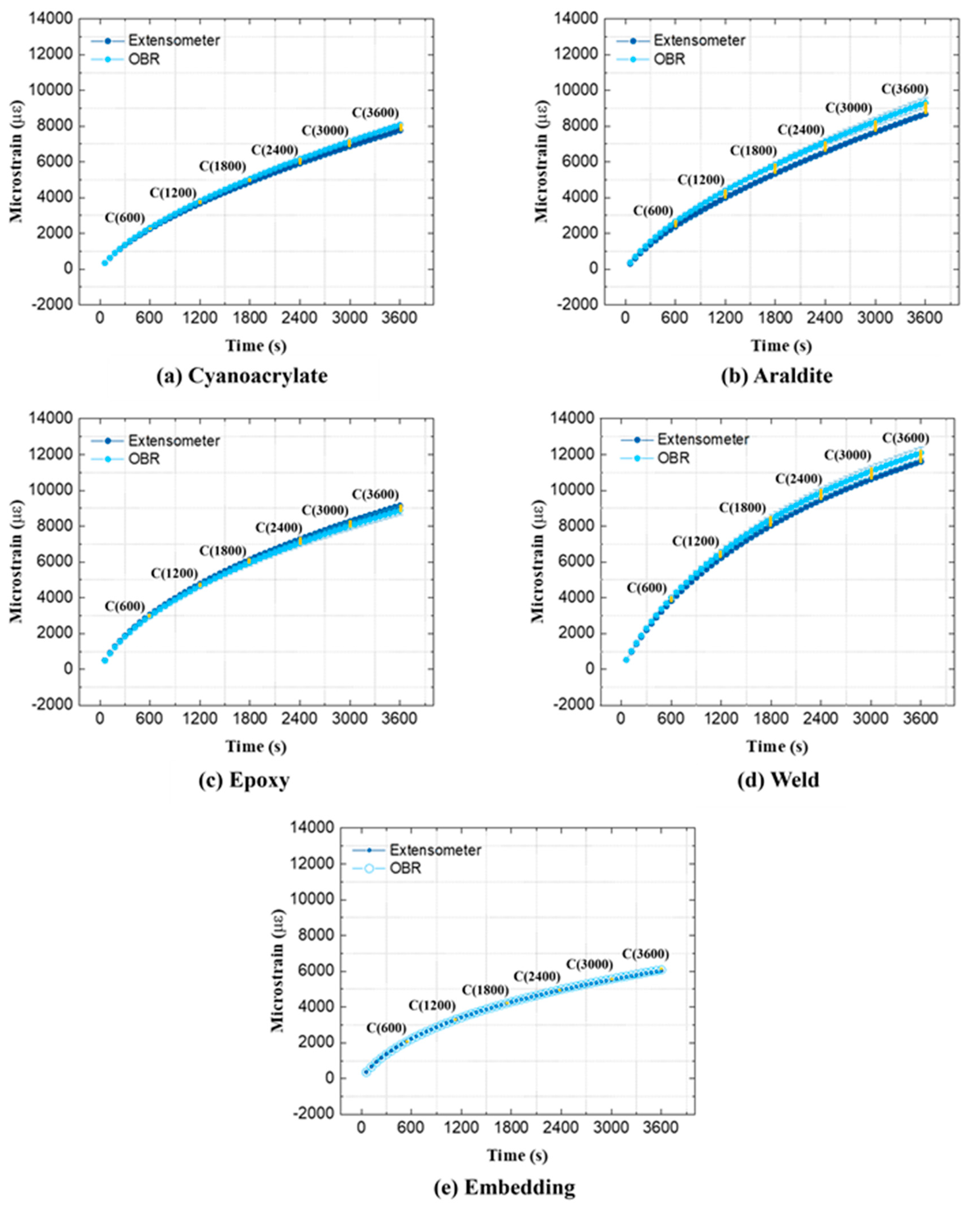
4.1.1. Residual Strains
4.1.2. Correlation between Residual Strains and Creep Strains
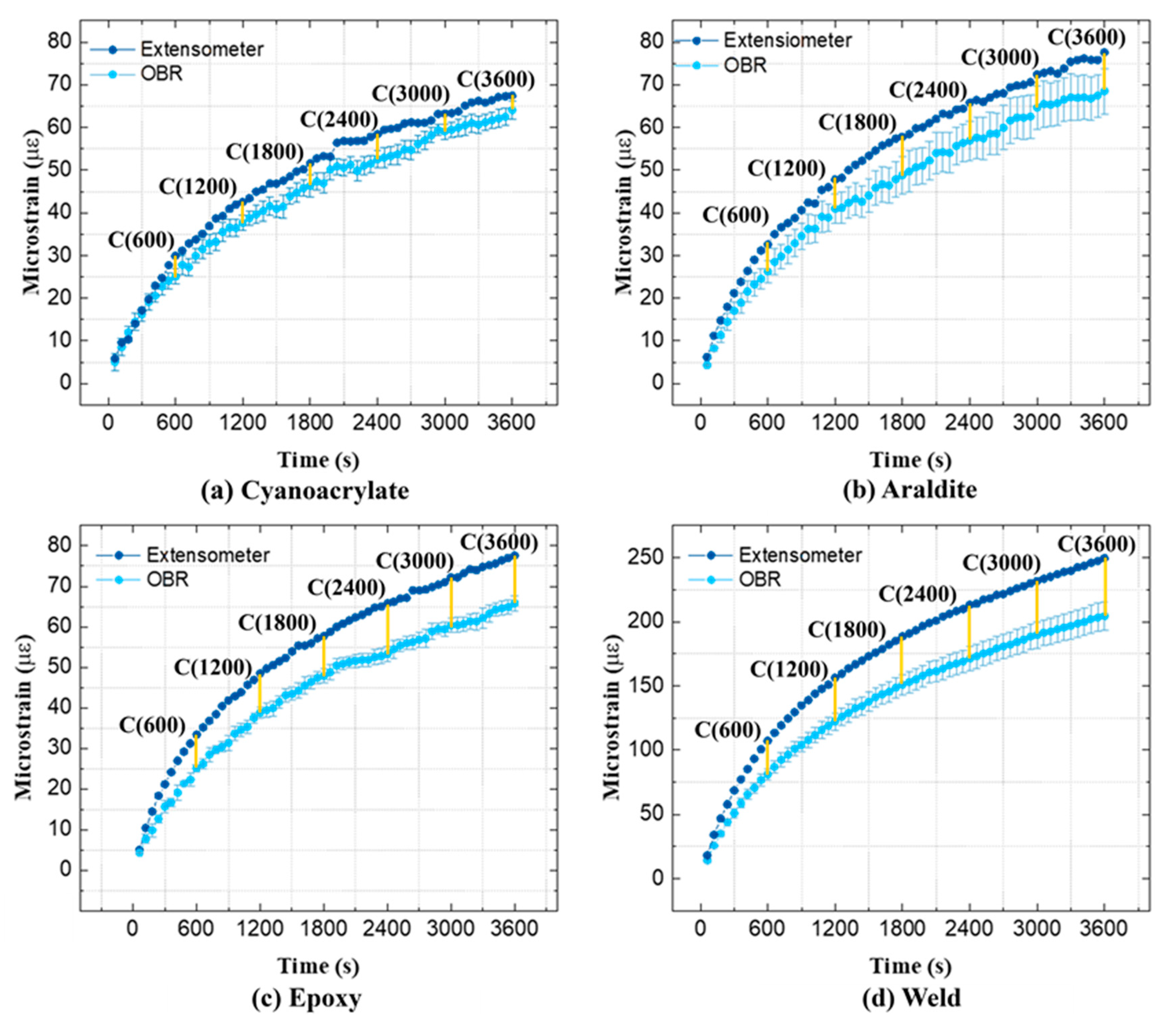
4.1.3. Variability of Creep Strains
4.2. The Accuracy of OBR Strains
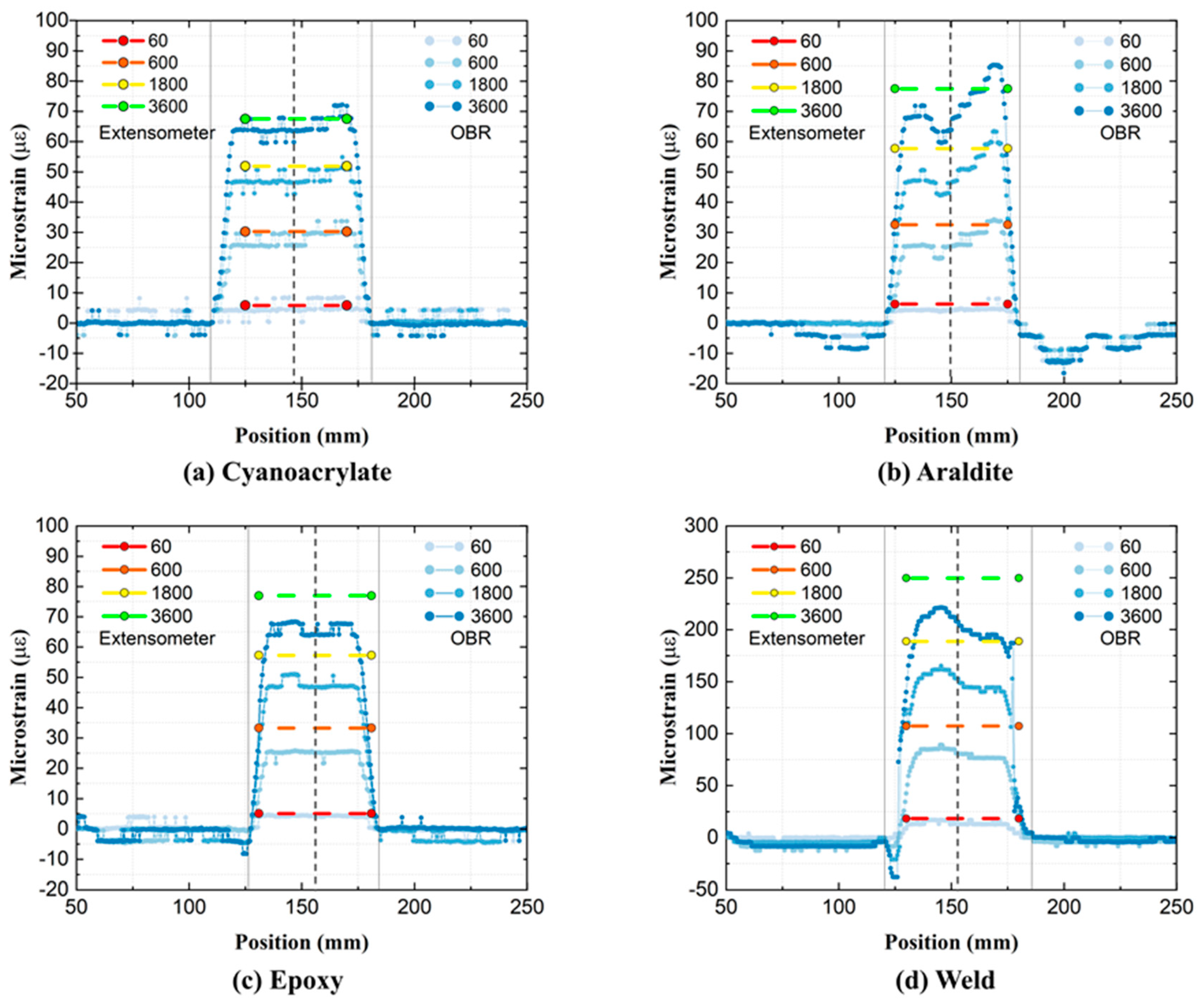
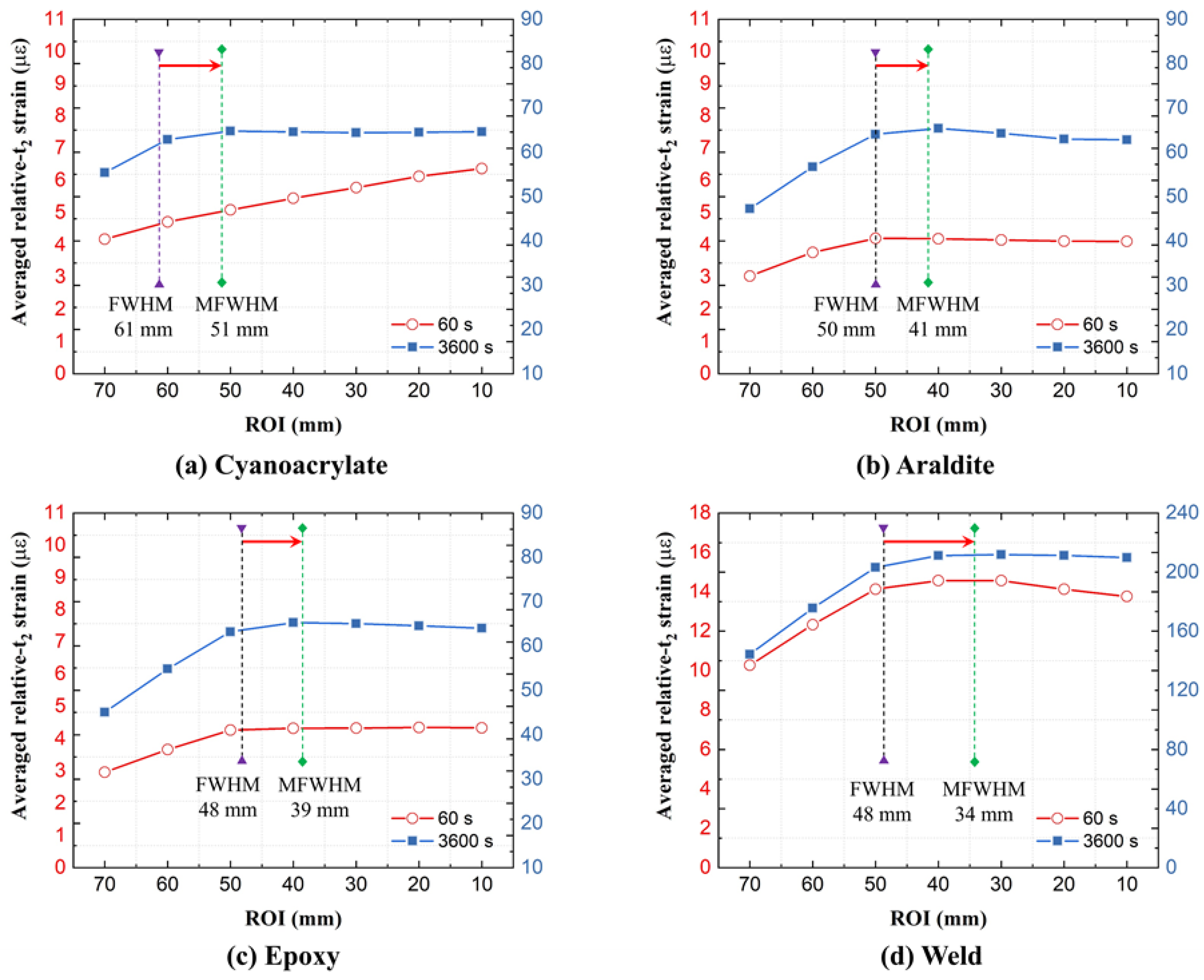
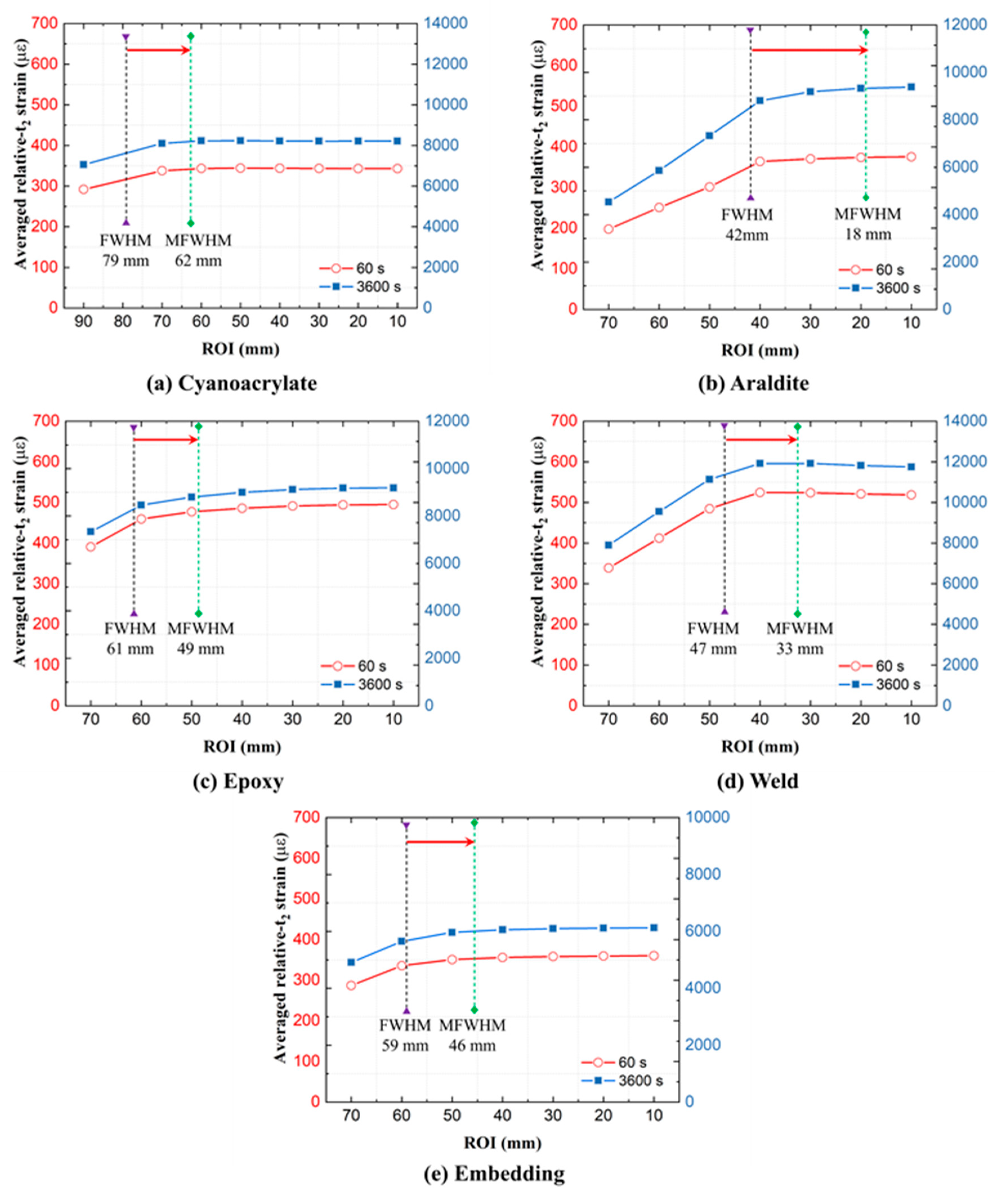
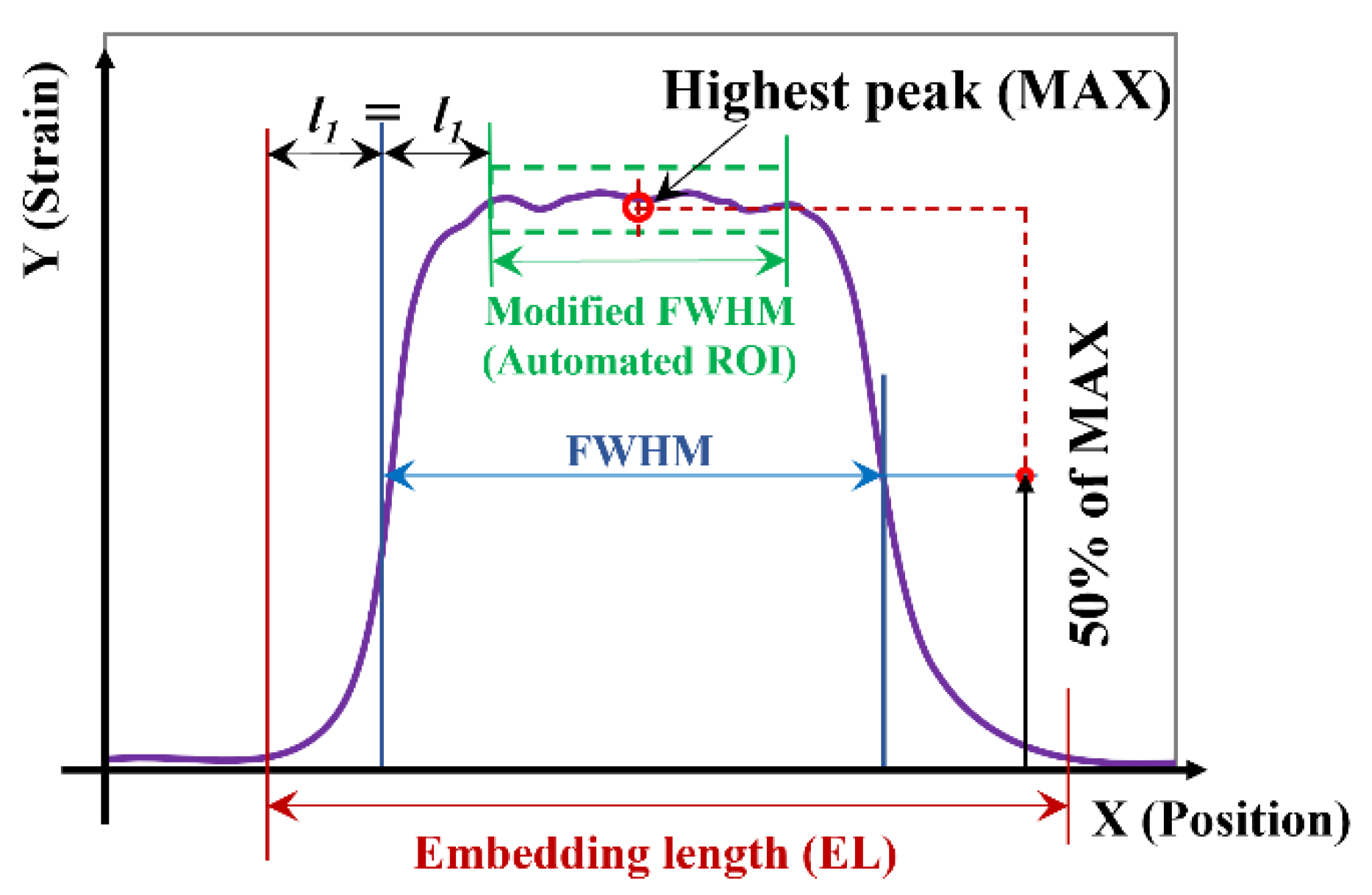
4.2.1. The Choice of ROI (and Disturbed End Regions)
4.2.2. The Difference between OBR and Contact Extensometer Strains
5. Conclusions
- As experimentally demonstrated, optical fiber sensors can be used to measure residual strains created by their own attachment process. The mechanisms of residual strain creation were briefly discussed. Correlations between residual strain and creep strains were observed for ‘Epoxy’ and ’Embedding’ attachment methods.
- Creep strains up to 3% were measured from OFs fixed with five different attachment methods on three types of substrate specimens.
- Unreinforced PA6 and GF/Epoxy substrates gave a satisfactory agreement between the optical fiber and contact extensometer strains. The relative difference between OF strains and contact extensometer strains either remained constant or converged towards more similar values over time.
- Negligible creep strains of steel specimens were accurately measured only by OFs, as the contact extensometer displayed artificial warmup drift.
- Problem areas for using DOFS over short attachment lengths are identified as follows.
- Unreliable strain data occurs in the ingress and egress regions of the fiber.
- Strain fluctuations along the OF length are caused by nonuniformities created in the fiber attachment process.
- Optical fiber attachment methods were compared from the aspects of residual strains and creep strain development. The main takeaways from the experiments are summarized in Table 5. The best performing attachments were ‘Cyanoacrylate’ and ‘Embedding’. Concluding from these qualitative observations, an optimal optical fiber attachment method:
- Is machine-controlled, e.g., utilizes an attachment process, such as 3-D printing, to achieve a uniform residual strain profile and a high strain transfer coefficient;
- Uses a low-viscosity adhesive, such as cyanoacrylate, for the same reasons as previous;
- Aims to minimize residual strains, e.g., by using room temperature curing or annealing.
- Practical and easily automated approaches can be devised for defining the disturbed ingress/egress region lengths for strain measurement. For example, the modified FWHM approach gives fairly accurate estimations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Distributed Strain Sensing System

| Laser | Tunable Laser Source (TLS) |
| Wavelength Range | 1525–1610 nm |
| Internal laser module maximum rated output power | 10.0 mW |
| Standard mode | 30 m/70 m |
| Extended mode | 2000 m |
| Scan time (30 m mode) | 3 s |
| Sensitivity | −130 dB |
| Dynamic range | 80 dB |
| Spatial resolution (30 m mode) | 20 μm |
| Strain resolution | ±1.0 µϵ |
| Temperature resolution | ±0.1 °C |
Appendix B. Uncertainties of Contact Extensometer Strains


References
- Betz, D.C.; Staudigel, L.; Trutzel, M.N.; Kehlenbach, M. Structural monitoring using fiber-optic Bragg grating sensors. Struct. Health Monit. 2003, 2, 145–152. [Google Scholar] [CrossRef]
- Rodriguez, G.; Casas, J.R.; Villalba, S. SHM by DOFS in civil engineering: A review. Struct. Monit. Maint. 2015, 2, 357–382. [Google Scholar] [CrossRef] [Green Version]
- Hoult, N.A.; Ekim, O.; Regier, R. Damage/Deterioration Detection for Steel Structures Using Distributed Fiber Optic Strain Sensors. J. Eng. Mech. 2014, 140, 04014097. [Google Scholar] [CrossRef]
- Bin Lin, Y.; Chang, K.C.; Chern, J.C.; Wang, L. Packaging methods of fiber-Bragg grating sensors in civil structure applications. IEEE Sens. J. 2005, 5, 419–424. [Google Scholar] [CrossRef]
- Yang, J.; Yuan, L. Package and installation of embeddable fiber optic sensors. Opt. Lasers Eng. 2009, 47, 1085–1090. [Google Scholar] [CrossRef]
- Meng, L.; Wang, L.; Hou, Y.; Yan, G. A Research on Low Modulus Distributed Fiber Optical Sensor for Pavement Material Strain Monitoring. Sensors 2017, 17, 2386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, A.; Qiao, X.G.; Jia, Z.A.; Li, M.; Zhao, D.Z. Study of simultaneous measurement of temperature and pressure using double fiber Bragg gratings with polymer package. Opt. Eng. 2005, 44, 034402. [Google Scholar] [CrossRef]
- Jockwer, R.; Grönquist, P.; Frangi, A. Long-term deformation behaviour of timber columns: Monitoring of a tall timber building in Switzerland. Eng. Struct. 2021, 234, 111855. [Google Scholar] [CrossRef]
- Montesano, J.; Selezneva, M.; Poon, C.; Fawaz, Z.; Behdinan, K. Application of fiber optic sensors for elevated temperature testing of polymer matrix composite materials. Sci. Eng. Compos. Mater. 2011, 18, 109–116. [Google Scholar] [CrossRef]
- Li, W.; Cheng, C.; Lo, Y. Investigation of strain transmission of surface-bonded FBGs used as strain sensors. Sens. Actuators A Phys. 2009, 149, 201–207. [Google Scholar] [CrossRef]
- Saeter, E.; Lasn, K.; Nony, F.; Echtermeyer, A.T. Embedded optical fibres for monitoring pressurization and impact of filament wound cylinders. Compos. Struct. 2019, 210, 608–617. [Google Scholar] [CrossRef]
- Wosniok, A.; Skoczowsky, D.; Schukar, M.; Pötzsch, S.; Pötschke, S.; Krüger, S. Fiber optic sensors for high-temperature measurements on composite tanks in fire. J. Civ. Struct. Health Monit. 2019, 9, 361–368. [Google Scholar] [CrossRef] [Green Version]
- Tsukada, T.; Minakuchi, S.; Takeda, N. Assessing residual stress redistribution during annealing in thick thermoplastic composites using optical fiber sensors. J. Thermoplast. Compos. Mater. 2018, 33, 53–68. [Google Scholar] [CrossRef]
- Arhant, M.; Meek, N.; Penumadu, D.; Davies, P.; Garg, N. Residual Strains using Integrated Continuous Fiber Optic Sensing in Thermoplastic Composites and Structural Health Monitoring. Exp. Mech. 2017, 58, 167–176. [Google Scholar] [CrossRef]
- Wang, S.; Lasn, K.; Elverum, C.W.; Wan, D.; Echtermeyer, A. Novel in-situ residual strain measurements in additive manufacturing specimens by using the Optical Backscatter Reflectometry. Addit. Manuf. 2020, 32, 101040. [Google Scholar] [CrossRef]
- Biswas, P.; Bandyopadhyay, S.; Kesavan, K.; Parivallal, S.; Sundaram, B.A.; Ravisankar, K.; Dasgupta, K. Investigation on packages of fiber Bragg grating for use as embeddable strain sensor in concrete structure. Sens. Actuators A Phys. 2010, 157, 77–83. [Google Scholar] [CrossRef]
- Zhang, J.; de Souza, M.; Creighton, C.; Varley, R. New approaches to bonding thermoplastic and thermoset polymer composites. Compos. Part A Appl. Sci. Manuf. 2020, 133, 105870. [Google Scholar] [CrossRef]
- ASTM E8. Standard Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, UAS, 2016. [Google Scholar]
- ASTM D638. Standard Test Method for Tensile Properties of Plastics; ASTM International: West Conshohocken, PA, UAS, 2010. [Google Scholar]
- Luna Technologies Inc. User Guide: Optical Backscatter Reflectometer Model OBR 4600; Luna Technologies Inc.: Roanoke, VA, USA, 2006; Available online: https://lunainc.com/sites/default/files/assets/files/resource-library/OBR-4600-UG6_SW3.10.1.pdf (accessed on 1 October 2018).
- Epsilon Technologies Corp, User Guide. Available online: https://www.epsilontech.com/understanding-extensometer-warmup-drift/ (accessed on 1 July 2021).








| Substrate | Attachment Method | Adhesives | Application Case |
|---|---|---|---|
| Concrete, steel, and timber | Surface mounting | Cyanoacrylate, epoxy, quartz glue, polyester | Strain, cracking, and vibration [2,3,4] |
| Pre-embedded bar | Epoxy, silicone, rubber | Strain [5,6,7] | |
| Specialized optical cables | Epoxy | Creep strains and temperature [8] | |
| Thermosets and thermoset composites | Surface mounting | Cyanoacrylate | Stiffness degradation and strain [9] |
| Embedding | Epoxy resin | Impact damage [10,11] | |
| Thermoplastics and thermoplastic composites | Surface mounting | Cyanoacrylate | Strain [12] |
| Embedding (Hand-layup) | Inside the composite | Residual strains [13] | |
| Embedding (Hot-pressing) | Partially fixed with epoxy | Relaxation [14] | |
| In situ embedding (3-D printing) | Inside the polymer | Residual strains and defects [15] |
| Dimensions | PA6 | GF/Epoxy | Steel |
|---|---|---|---|
| GL—Gauge length | 50 | 50 | 25 |
| GW—Width | 13 | 13 | 6 |
| T—Thickness | 6.4 | 7 | 3 |
| R—Radius of fillet | 76 | 76 | 6 |
| L—Overall length | 165 | 165 | 100 |
| A—Length of reduced parallel section | 57 | 57 | 32 |
| B—Distance between grips | 115 | 115 | 40 |
| W—Width of grip section | 19 | 19 | 10 |
| OF L—Attached optical fiber length | 50 | 50 | 25 |
| EXT L—Extensometer gauge length | 50 | 50 | 25 |
| Attachment Denotation | Shorthand Name | Method | Details 1 |
|---|---|---|---|
| a | ‘Cyanoacrylate’ | Cyanoacrylate adhesive | Standard adhesive for strain gauges. |
| b | ‘Araldite’ | Araldite Rapid adhesive | Two component rapid curing epoxy. |
| c | ‘Epoxy’ | Epoxy film adhesive | Adhesive film (Gurit SA 80) is placed over the OF, and cured for 12 h at 80 °C under vacuum. |
| d | ‘Weld’ | OF is manually fused/glued on the substrate by a filament of thermoplastic material | A PA6 filament (1.75 mm, natural, Ultrafuse) is melted and extruded with a Leister Triac hot-air tool. |
| e | ‘Embedding’ | The OF is 3-D printed under a cuboid volume (64 mm × 10 mm × 0.4 mm) embedding it directly on the surface of the PA6 specimen. | PA6 (1.75 mm filament, natural, Ultrafuse). |
| Specimen, Attachment Method | Actual OF Attachment Length | Disturbed Ingress Region l | Disturbed Egress Region l | ||
|---|---|---|---|---|---|
| OBR GL = 10 | OBR GL = 20 | OBR GL = 10 | OBR GL = 20 | ||
| GF/Epoxy, Cyanoacrylate | 70 | 9.0 | 17.5 | 8.0 | 19.0 |
| GF/Epoxy, Araldite | 51 | 9.5 | 16.5 | 9.0 | 16.5 |
| GF/Epoxy, Epoxy | 53 | 8.0 | 17.5 | 11.5 | 22.0 |
| GF/Epoxy, Weld | 55 | 14.5 | 16.5 | 9.0 | 19.0 |
| PA6, Cyanoacrylate | 77 | 22.0 | 29.5 | 18.5 | 30.5 |
| PA6, Araldite | 54 | 15.0 | 23.5 | 28.0 | 30.5 |
| PA6, Epoxy | 58 | 11.0 | 25.0 | 10.0 | 24.0 |
| PA6, Weld | 59 | 16.0 | 16.5 | 14.0 | 16.5 |
| PA6, Embedding | 64 | 24.0 | 31.5 | 13.0 | 25.0 |
| Attachment Method | Substrate | Residual Strain (Figure 10) | Creep Strain Variability (Figure 13) | Creep Strain Accuracy (Figure 17) | Attachment Process |
|---|---|---|---|---|---|
| ‘Cyanoacrylate’ | GF/Epoxy | Low/Nonuniform | Low | High | Manual |
| PA6 | Low/Nonuniform | Low | Medium | Manual | |
| Steel | Low/Nonuniform | - | - | Manual | |
| ‘Araldite’ | GF/Epoxy | Low/Nonuniform | High | Medium | Manual |
| PA6 | Low/Nonuniform | High | Low | Manual | |
| Steel | Low/Nonuniform | - | - | Manual | |
| ‘Epoxy’ | GF/Epoxy | Medium/Uniform | Low | Low | Manual |
| PA6 | High/Uniform | High | Medium | Manual | |
| Steel | Medium/Uniform | - | - | Manual | |
| ‘Weld’ | GF/Epoxy | Medium/Nonuniform | Low | Low | Manual |
| PA6 | High/Nonuniform | High | Medium | Manual | |
| Steel | Medium/Nonuniform | - | - | Manual | |
| ‘Embedding’ | GF/Epoxy | - | - | - | - |
| PA6 | High/Uniform | Low | High | Automated | |
| Steel | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Sæter, E.; Lasn, K. Comparison of DOFS Attachment Methods for Time-Dependent Strain Sensing. Sensors 2021, 21, 6879. https://doi.org/10.3390/s21206879
Wang S, Sæter E, Lasn K. Comparison of DOFS Attachment Methods for Time-Dependent Strain Sensing. Sensors. 2021; 21(20):6879. https://doi.org/10.3390/s21206879
Chicago/Turabian StyleWang, Shaoquan, Erik Sæter, and Kaspar Lasn. 2021. "Comparison of DOFS Attachment Methods for Time-Dependent Strain Sensing" Sensors 21, no. 20: 6879. https://doi.org/10.3390/s21206879





