Methods of Precise Distance Measurements for Laser Rangefinders with Digital Acquisition of Signals
Abstract
:1. Introduction
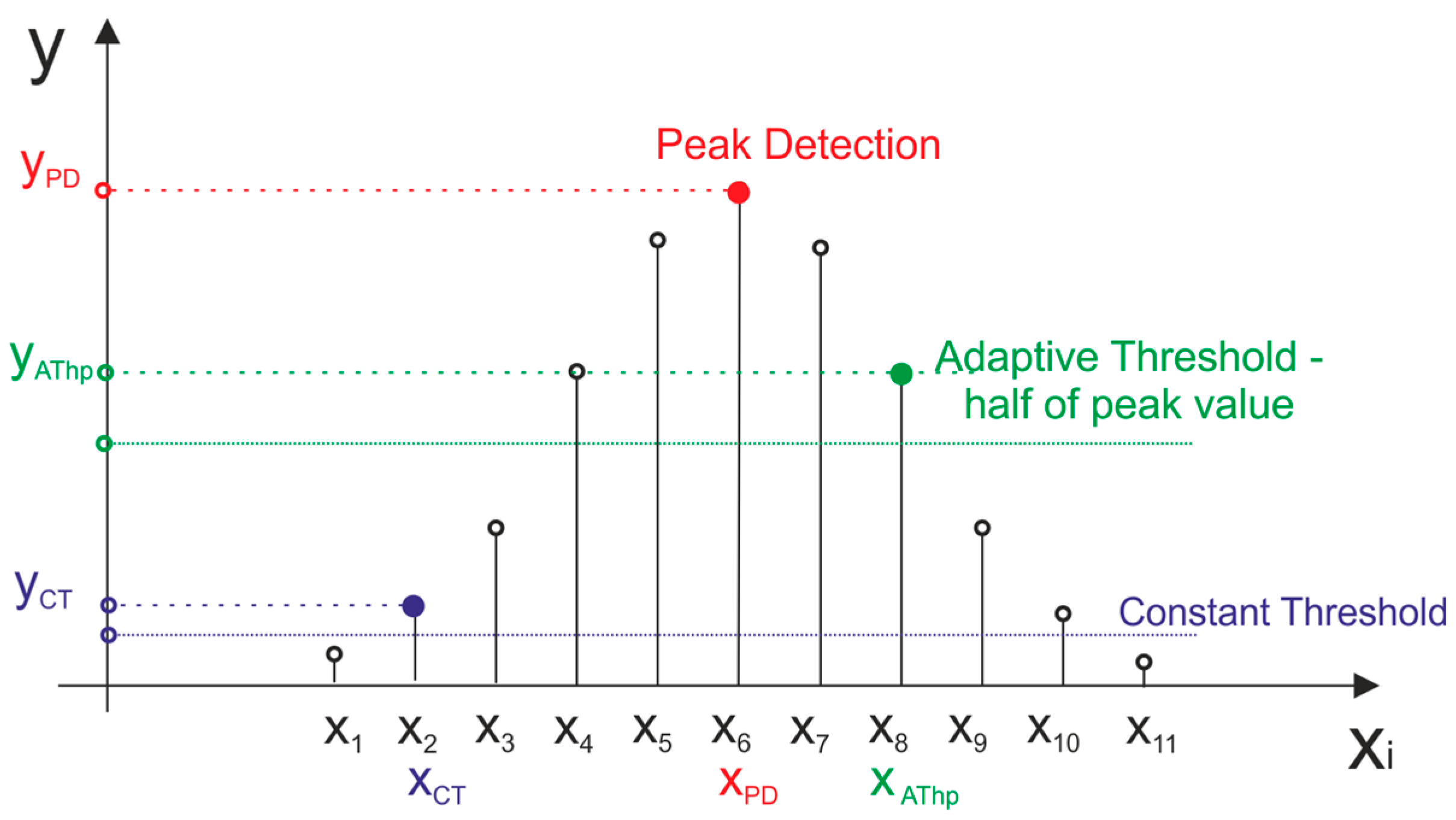
2. Methods of Generation of the START and STOP Signals for Digital Counters in Laser ToF Measurements
- (a)
- Peak Detection,
- (b)
- Constant Threshold Detection,
- (c)
- Adaptive Threshold Detection.
3. Improving Precision of Measurements with Least Square Approximation of Pulse Samples with a Second Degree Polynomial
- (1)
- detection of presence of the echo pulse signal using the chosen detection method; i.e., using constant threshold discrimination,
- (2)
- constitution of the set of N samples of echo pulse, which values are greater than the chosen threshold,
- (3)
- calculation of parabola coefficients using solution of formula (9),
- (4)
- calculation of distance using formula (12).
Analysis of Uncertainty of Presented Method
4. Simulations
4.1. Description of Simulation Assumptions
4.2. Examination of the Influence of Changes in Signal to Noise Ratio (SNR) and Pulse’s Full Width at Half Maximum (FWHM) on the Total Measurement Error of SDPA Method
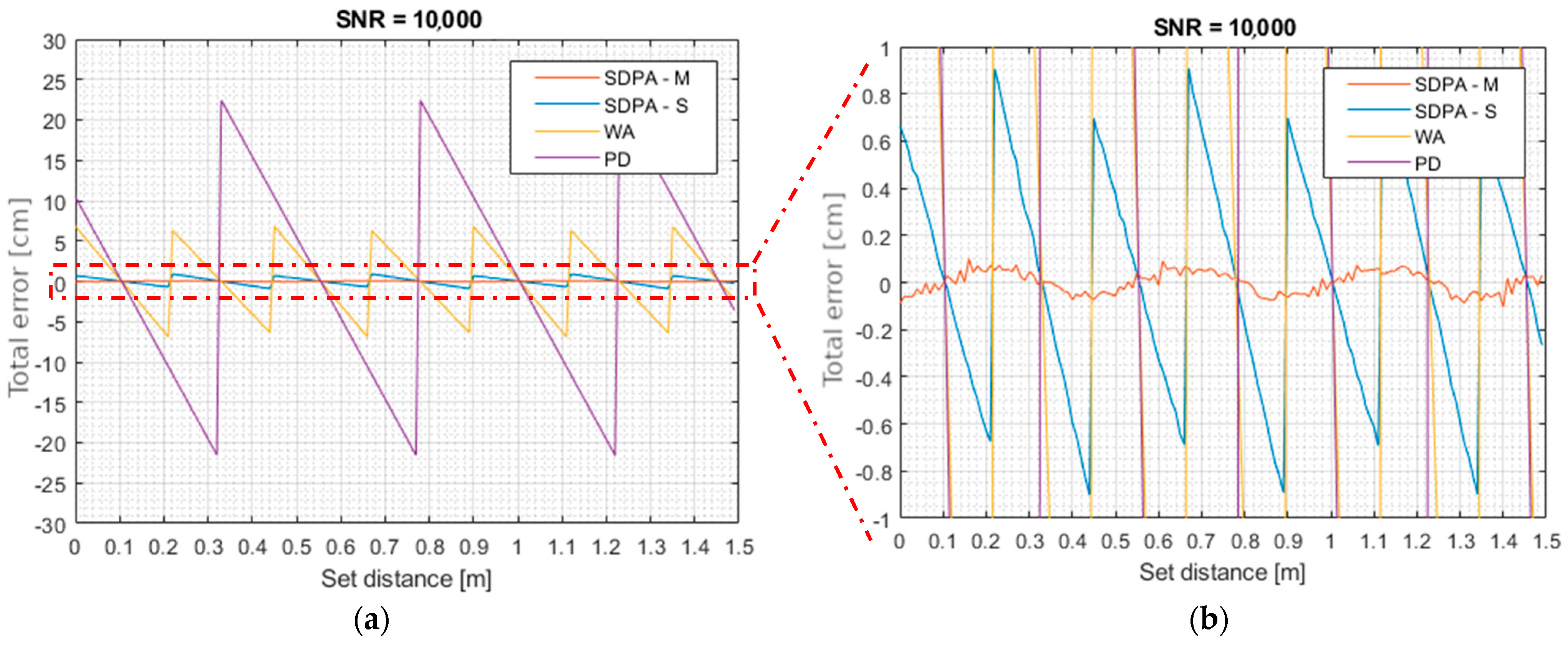
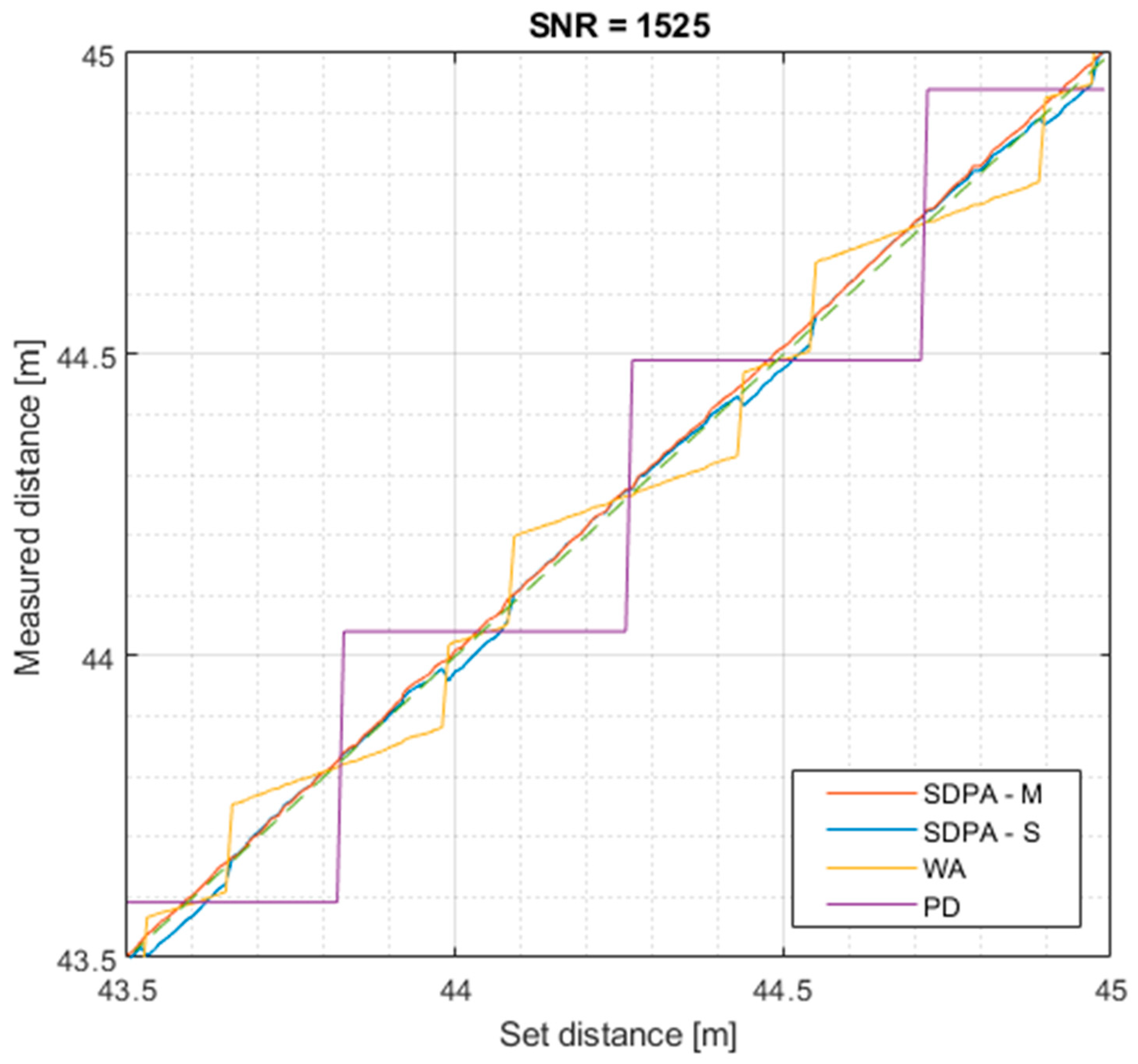
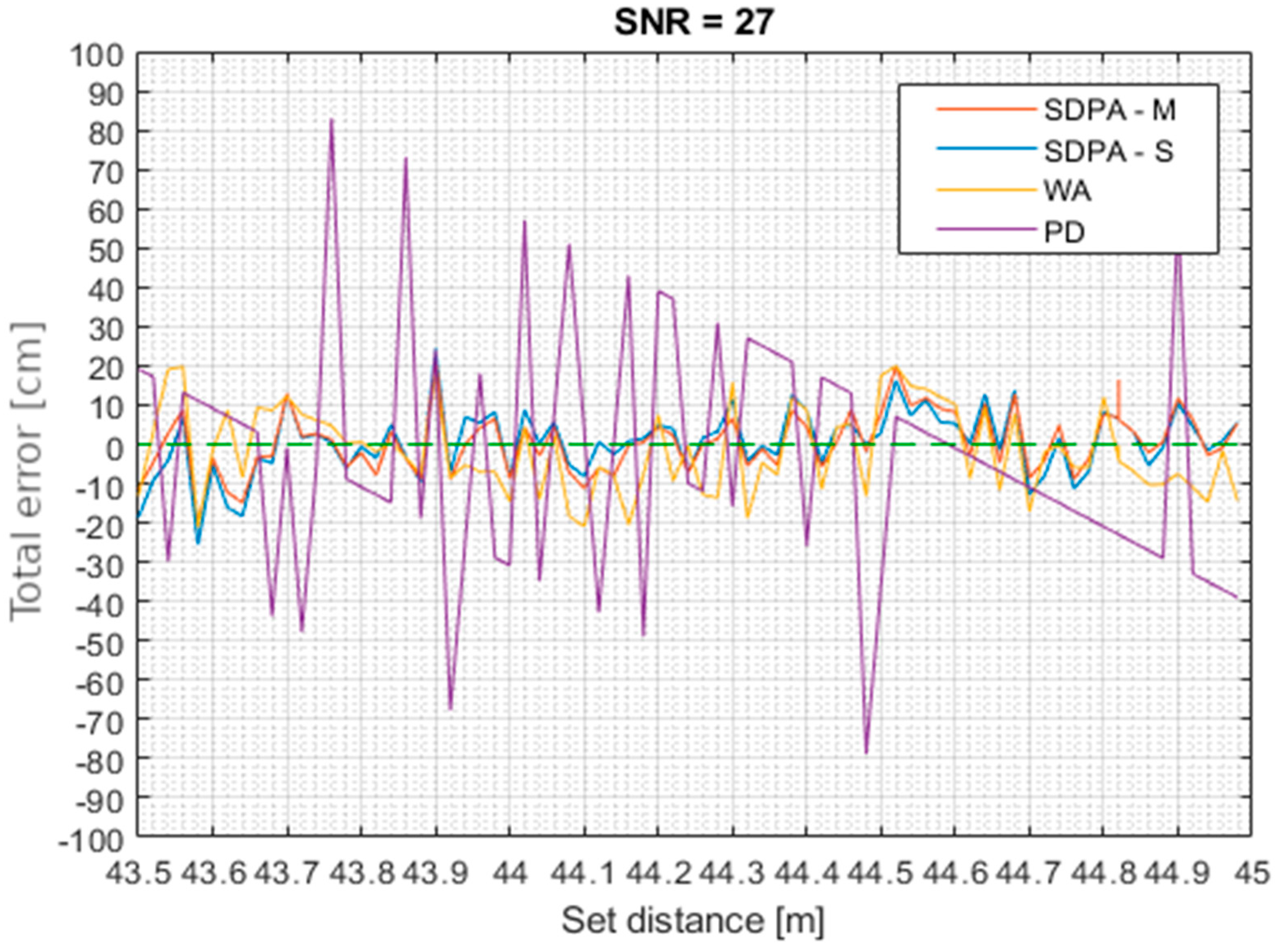
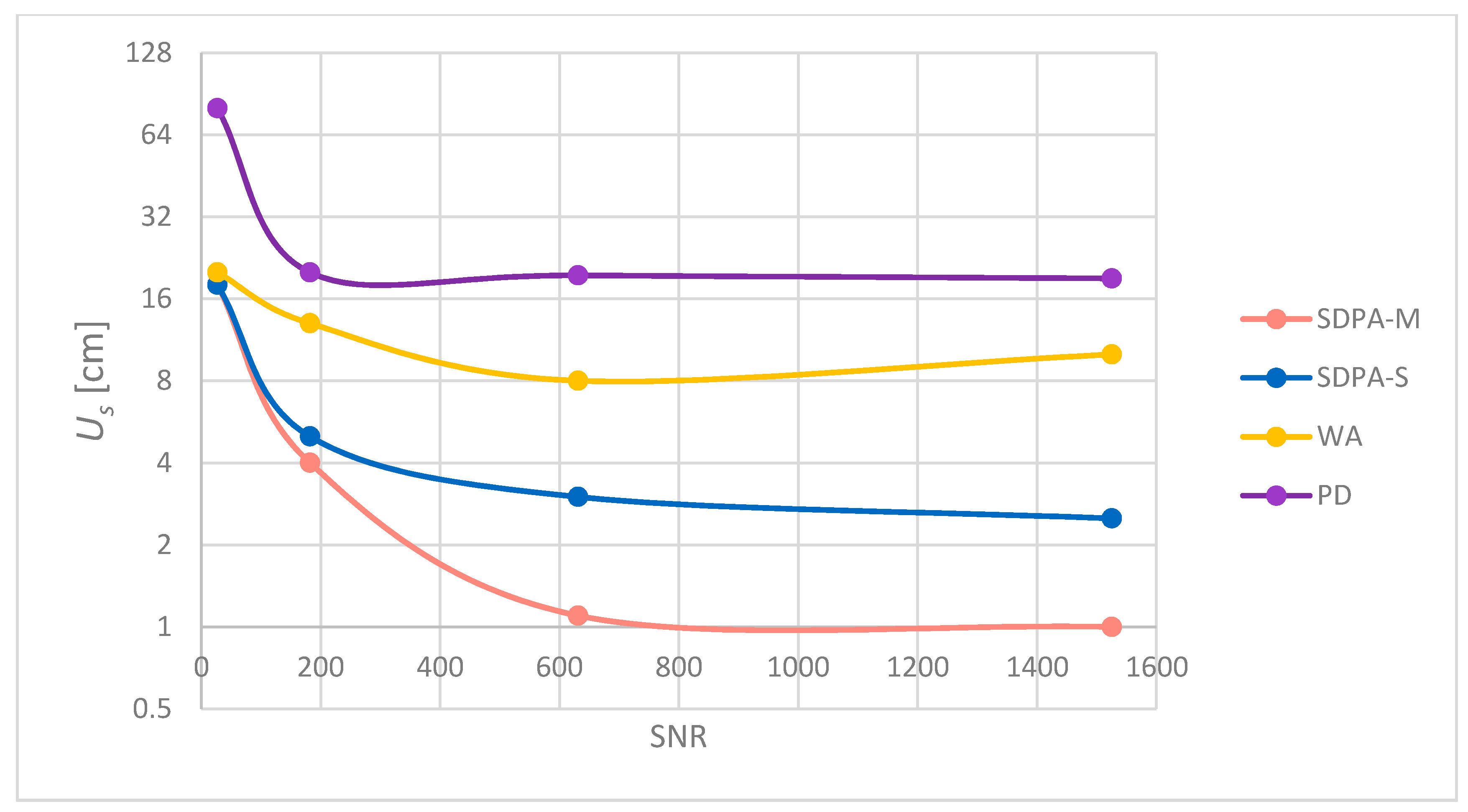
4.3. Examination of the Influence of Changes in Distance on the Total Measurement Error—Comparison of Results Given by Different Distance Calculation Algorithms
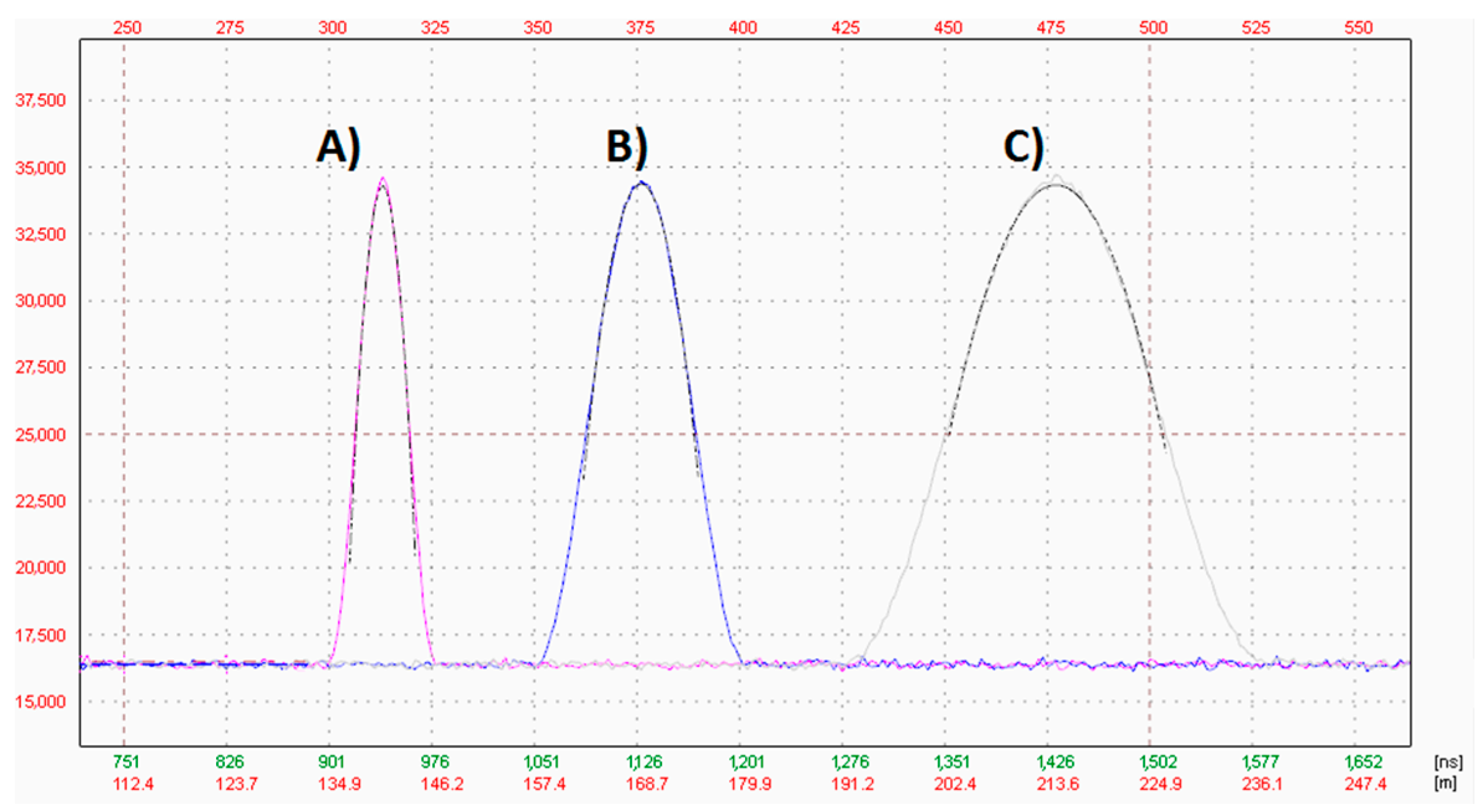
5. System Tests and Experimental Results
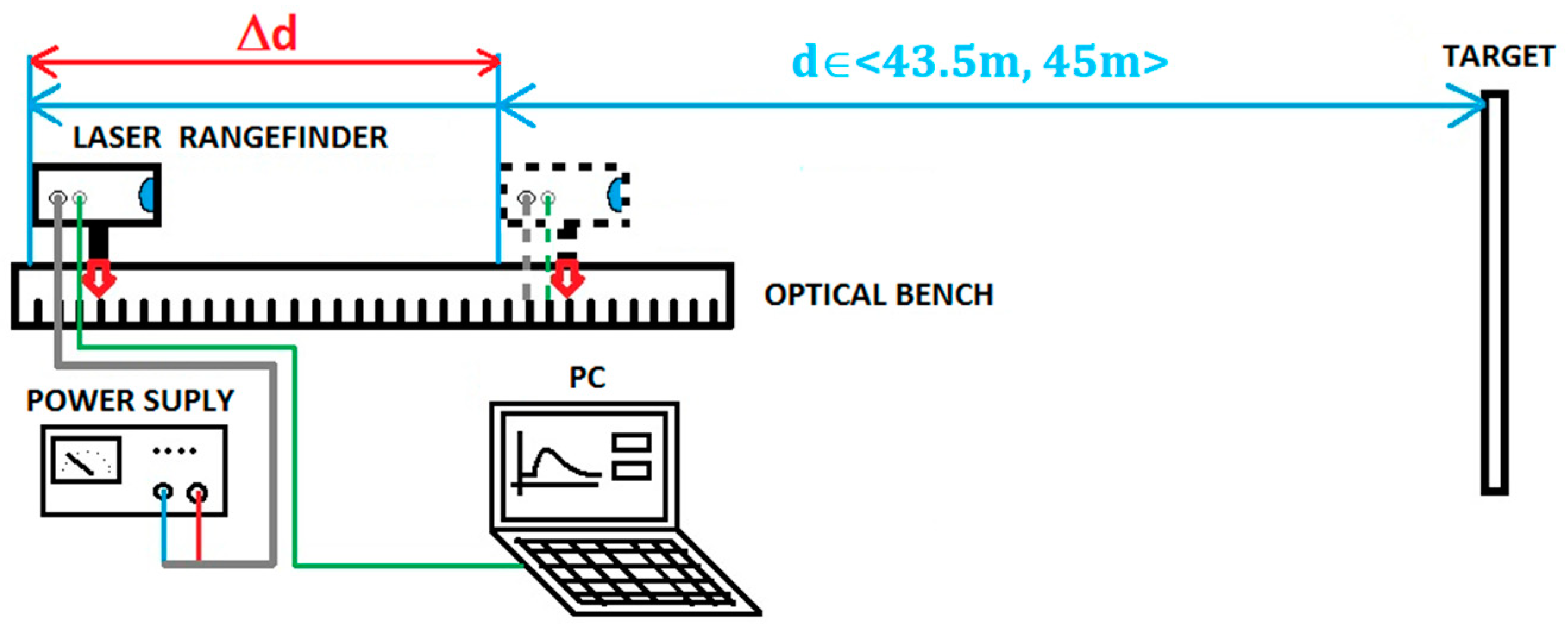
5.1. Description of the Test Stand
- -
- a laser rangefinder module with a sighting scope (Figure 9),
- -
- an optical bench with a millimeter scale,
- -
- targets with precisely defined reflectance,
- -
- a computer with an application for system control, data processing and displaying of the results,
- -
- a power supply.
5.2. Methodology of Experiments
5.3. Results
- -
- peak detection (PD): finding the time of occurrence of the sample with the maximum value,
- -
- weighted average (WA): calculation of the “center of gravity” of selected signal samples,
- -
- approximation with a second-degree polynomial, simple set of samples (SDPA-S): finding the position of the apex of parabola approximated on the set of echo signal samples selected using the simple threshold discrimination method,
- -
- approximation with a second-degree polynomial, modified set of samples (SDPA-M): finding the average position of the apex of parabola approximated on multiple sets of signal samples selected by the modified sample qualification method.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muzal, M.; Mierczyk, Z.; Zygmunt, M.; Wojtanowski, J.; Piotrowski, W. Measurement of vehicles speed with full waveform lidar. In Laser Technology 2016: Progress and Applications of Lasers; International Society for Optics and Photonics: Jastarnia, Poland, 2016; Volume 10159, p. 1015914. [Google Scholar] [CrossRef]
- Muzal, M.; Wojtanowski, J.; Mierczyk, Z.; Zygmunt, M.; Drozd, T.; Knysak, P.; Piotrowski, W.; Traczyk, M. Laserowy miernik prędkości pojazdów. Elektronika 2016, 57, 38–40. (In Polish) [Google Scholar] [CrossRef]
- Villa, F.A.; Tisa, S.; Bronzi, D.; Zappa, F. Indirect time-of-flight 3D ranging based on SPADs. In Quantum Sensing and Nanophotonic Devices IX; International Society for Optics and Photonics: San Francisco, CA, USA, 2012; Volume 8268, p. 82681C. [Google Scholar] [CrossRef]
- Li, L. Time-of-Flight Camera—An Introduction; Technical White Paper SLOA190B; Texas Instruments: Dallas, TX, USA, 2014. [Google Scholar]
- Rüeger, J.M. Electronic Distance Measurement; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Kilpelä, A. Pulsed Time-of-Flight Laser Range Finder Techniques for Fast, High Precision Measurement Applications; Oulu Press, University of Oulu: Oulu, Finland, 2004. [Google Scholar] [CrossRef]
- Berkovic, G.; Shafir, E. Optical methods for distance and displacement measurements. Adv. Opt. Photonics 2012, 4, 441–471. [Google Scholar] [CrossRef]
- IEC 60825–1 “Safety of Laser Products—Part 1: Equipment Classification and Requirements”. Available online: https://webstore.iec.ch/publication/3587 (accessed on 23 September 2021).
- Brun, R. Gallium arsenide eyesafe laser rangefinder. In Proceedings of the Laser Safety, Eyesafe Laser Systems, and Laser Eye Protection, SPIE Proceedings, Los Angeles, CA, USA, 16–17 January 1990; Volume 1207. [Google Scholar] [CrossRef]
- Shi, H.; Yu, L.; Chunyang, W.; Yu, Y.; Liu, X.; Li, L. Study on multi-pulse long range laser ranging system. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 4838–4843. [Google Scholar] [CrossRef]
- Palojärvi, P. Integrated Electronic and Optoelectronic Circuits and Devices for Pulsed Time-of-Flight Laser Rangefinding; Oulu Press, University of Oulu: Oulu, Finland, 2003; Available online: http://jultika.oulu.fi/files/isbn9514269667.pdf (accessed on 3 August 2021).
- Kilpelä, A.; Ylitalo, J.; Määttä, K.; Kostamovaara, J. Timing discriminator for pulsed time-of-flight laser rangefinding measurements. Rev. Sci. Instrum. 1998, 69, 1978–1984. [Google Scholar] [CrossRef] [Green Version]
- Zheng, R.; Wu, G. Constant fraction discriminator in pulsed time-of-flight laser rangefinding. Front. Optoelectron. 2012, 5, 182–186. [Google Scholar] [CrossRef]
- Jutzi, B.; Neulist, J.; Stilla, U. High-resolution waveform acquisition and analysis of lasers pulses. Int. Arch. Photogramm. Remote Sens. 2005, 36, W3. Available online: https://publikationen.bibliothek.kit.edu/1000073818/4347356 (accessed on 3 August 2021).
- Huising, E.J.; Gomes Pereira, L.M. Errors and accuracy estimates of laser data acquired by various laser scanning systems for topographic applications. ISPRS J. Photogramm. Remote Sens. 1998, 53, 245–261. [Google Scholar] [CrossRef]
- SteinVal, O.K. Effects of Target Shape and Reflection on Laser Radar Cross Sections. Appl. Opt. 2000, 39, 4381–4391. [Google Scholar] [CrossRef] [PubMed]







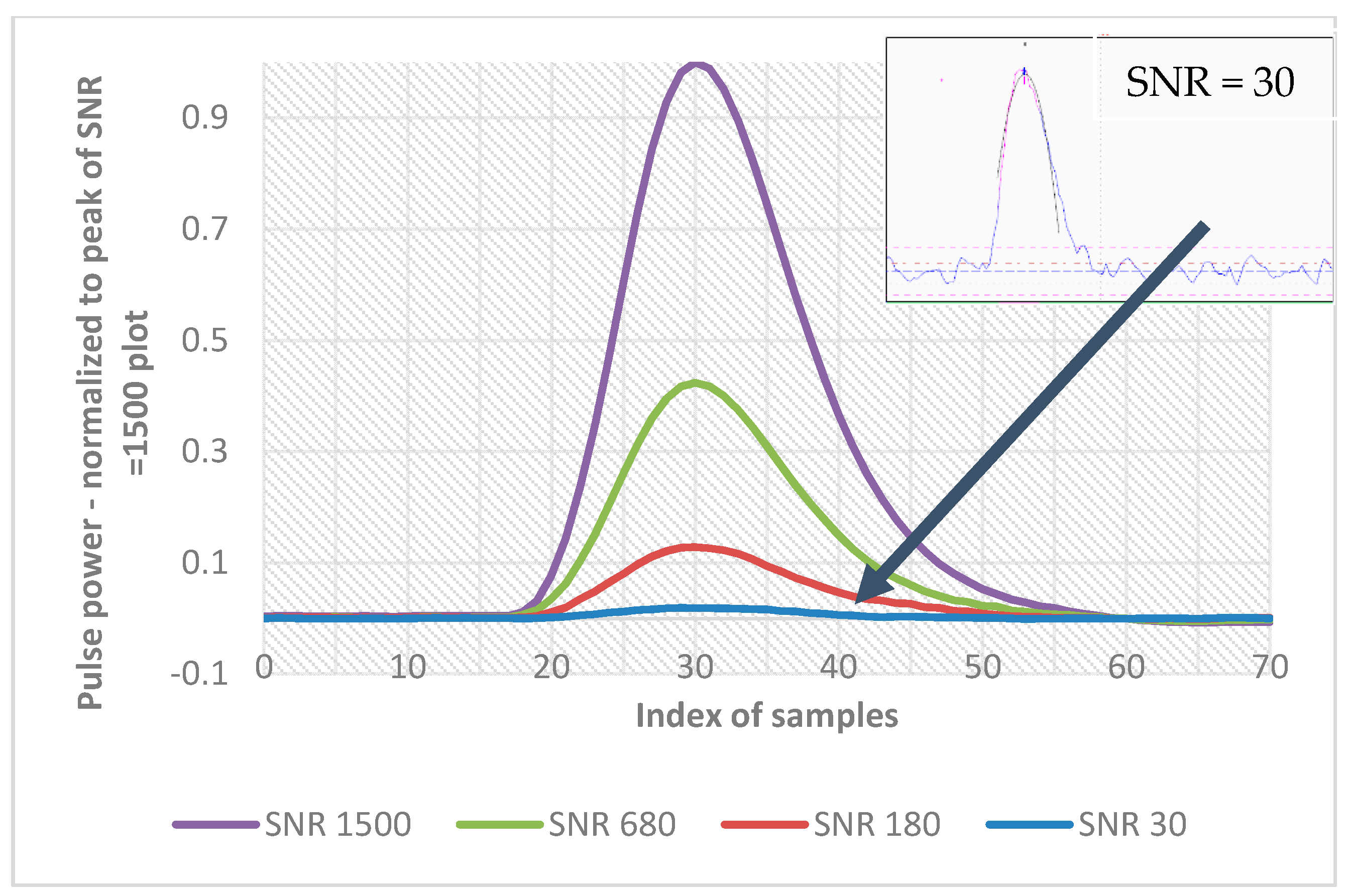



| Trial Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Sampling frequency fpr (MHZ) | 333 | ||||
| FWHM τ [ns] | 39 | 78 | 156 | 39 | 156 |
| SNR | 181 | 631 | |||
| Trial Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Standard deviation of the trial, data analysis, σs (cm) | 1.05 | 1.17 | 1.70 | 0.27 | 0.46 |
| Calculated standard deviation, us (cm) | 1.01 | 1.15 | 1.65 | 0.25 | 0.46 |
| Expanded uncertainty Us = 3·us | 3.03 | 3.45 | 4.95 | 0.75 | 1.38 |
| SNR | 10,000 | |||
|---|---|---|---|---|
| Method | SDPA-M | SDPA-S | WA | PD |
| Total uncertainty Us (cm) | 0.1 | 0.8 | 6 | 19.5 |
| Trial Number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Target reflectance | 98% | 47% | 10% | 1% |
| Range of distance change | 1.5 m | |||
| Distance change step | 1 cm | 2 cm | ||
| SNR | 1525 | 631 | 182 | 27 |
| Calculation Method | Estimated Uncertainty Us (cm) | |||
|---|---|---|---|---|
| SNR = 27 | SNR = 182 | SNR = 631 | SNR = 1525 | |
| SDPA-M | 18 | 4 | 1.1 | 1 |
| SDPA-S | 18 | 5 | 3 | 2.5 |
| WA | 20 | 13 | 8 | 10 |
| PD | 80 | 20 | 19.5 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muzal, M.; Zygmunt, M.; Knysak, P.; Drozd, T.; Jakubaszek, M. Methods of Precise Distance Measurements for Laser Rangefinders with Digital Acquisition of Signals. Sensors 2021, 21, 6426. https://doi.org/10.3390/s21196426
Muzal M, Zygmunt M, Knysak P, Drozd T, Jakubaszek M. Methods of Precise Distance Measurements for Laser Rangefinders with Digital Acquisition of Signals. Sensors. 2021; 21(19):6426. https://doi.org/10.3390/s21196426
Chicago/Turabian StyleMuzal, Michał, Marek Zygmunt, Piotr Knysak, Tadeusz Drozd, and Marcin Jakubaszek. 2021. "Methods of Precise Distance Measurements for Laser Rangefinders with Digital Acquisition of Signals" Sensors 21, no. 19: 6426. https://doi.org/10.3390/s21196426






