Combination of Sensor Data and Health Monitoring for Early Detection of Subclinical Ketosis in Dairy Cows
Abstract
:1. Introduction
2. Materials and Methods
2.1. Animal Data and Sampling Procedures
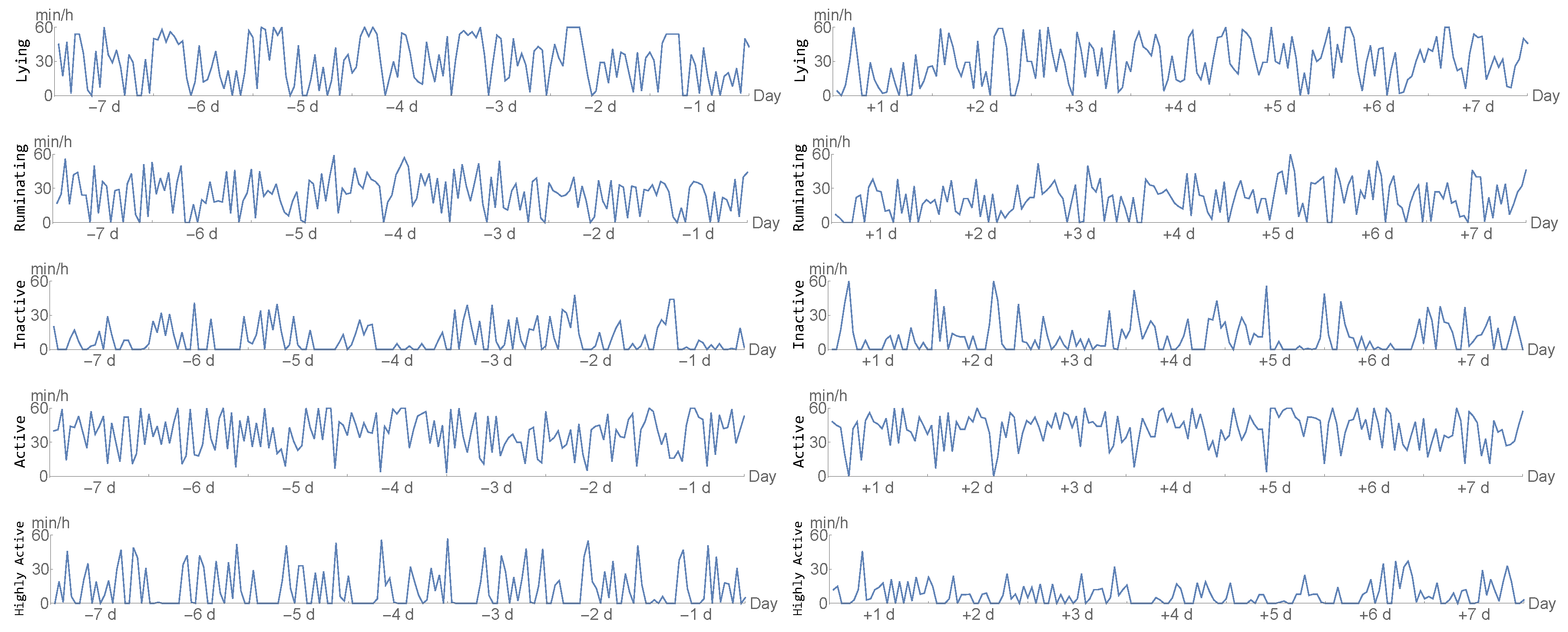
2.2. Accelerometer
- lying/not lying,
- ruminating/not ruminating,
- inactive/active/highly active.
2.3. Health Data
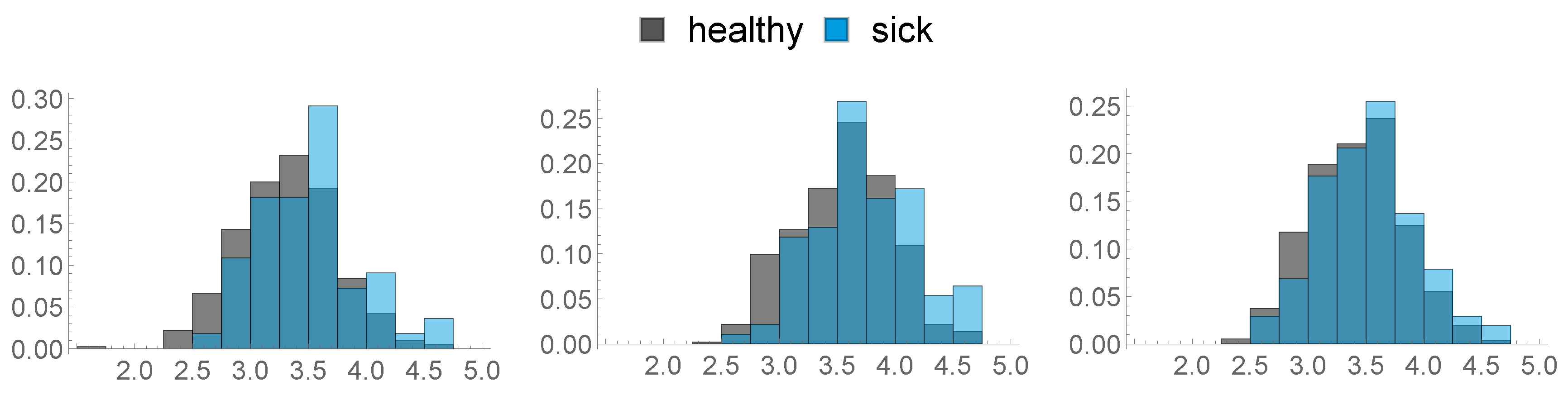
- Body Condition Score (BCS): A total of three measurements were made, 8 weeks before calving ( w), 3 weeks before calving ( w) and on the day of calving (D0).
- 1.
- w
- 2.
- w
- 3.
- D0
In Figure 3, the distribution of these three features is visualised: - Back Fat Thickness (BFT): As described above, three measurements were made:
- 4.
- w
- 5.
- w
- 6.
- D0
In Figure 4, the distribution of the BFT is visualised:- 7.
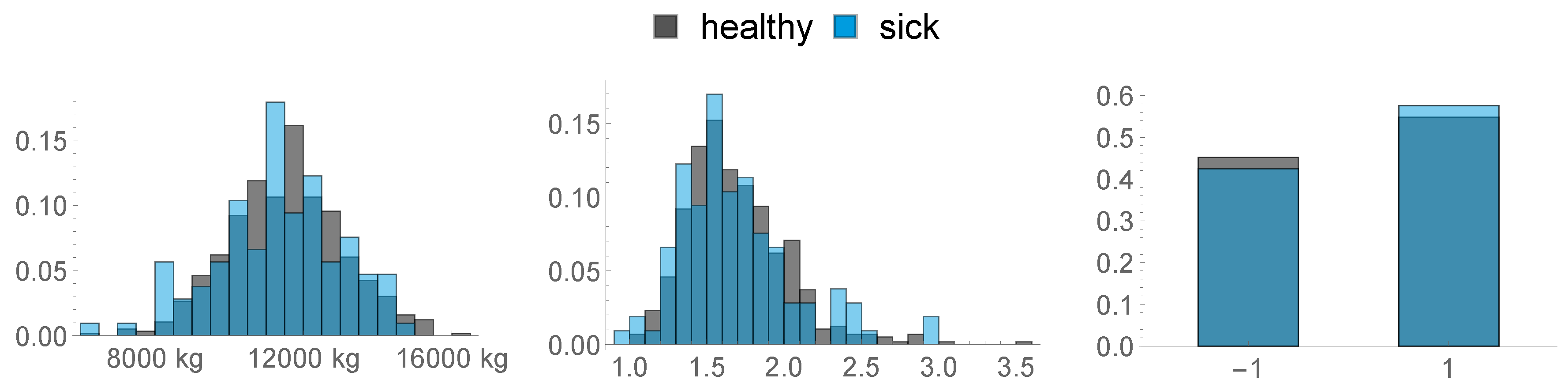
- Non-Esterified Fatty Acids (NEFA): We used the maximal NEFA Value of all measurements as described in Section 2.1. This feature is vizualised in Figure 5.
- 8.
- 305 day Milk-Yield Equivalent: A measure that standardizes the milk yield of the previous lactation. Its impact on different diseases can be found in [21].
- 9.
- This feature consists of the maximum observed fat/protein ratio during the previous lactation.
- 10.
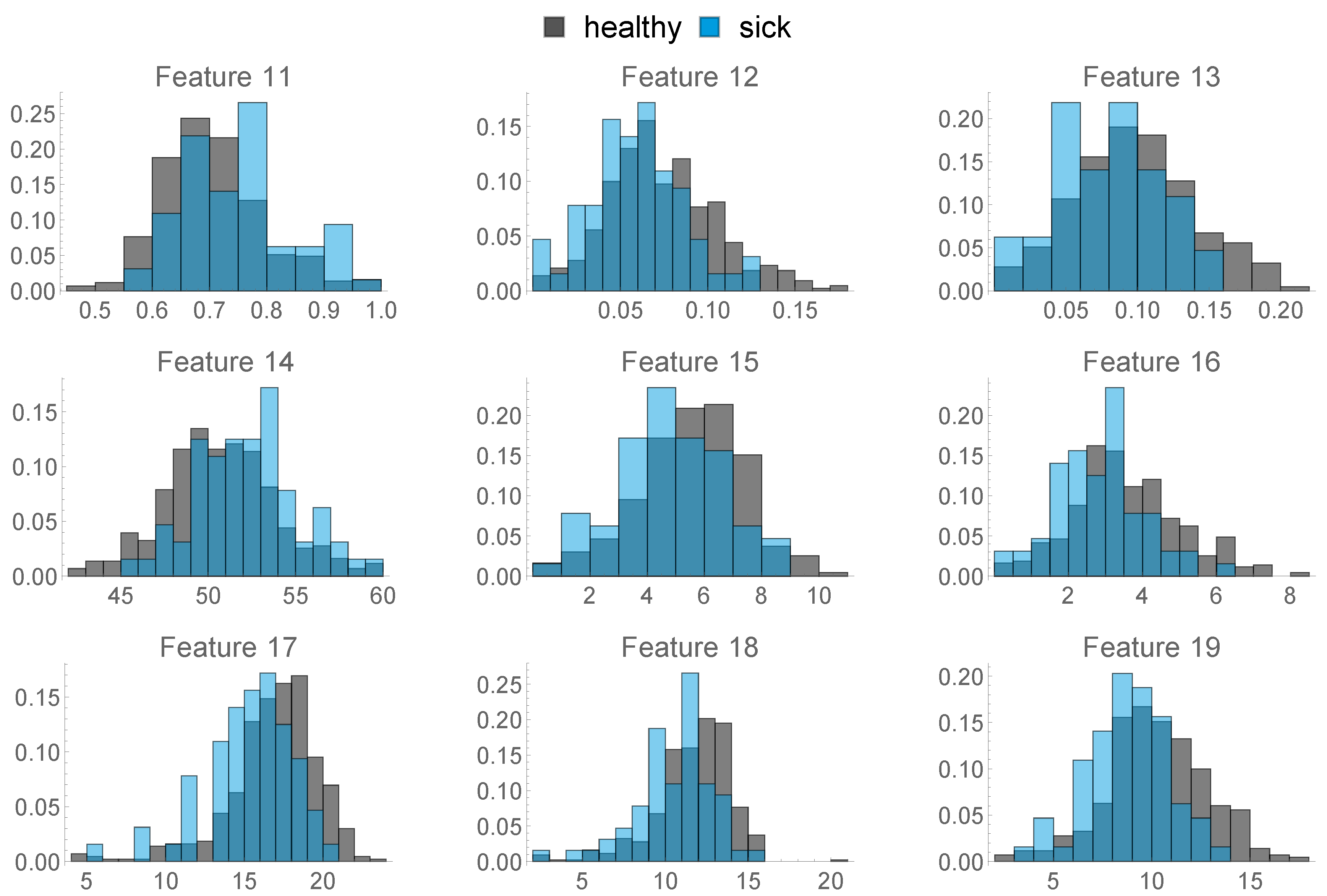
- Parity: We distinguished between primi- and multiparous cows and transformed these categories as follows: primiparous →−1, multiparous → 1.Feature 8, 9 and 10 are depicted in Figure 6.
- The following features are based on the locations the animals spent their time in the last two weeks before calving. We distinguished between three functional areas, namely cubicles (FA 1), feed alley (FA 2), and passageways (FA 3). These 9 features are depicted in Figure 7.
- 11.
- Ratio of Hours spent only in FA 1
- 12.
- Ratio of Hours where the animal spent more time in FA 3 than in FA 1
- 13.
- Ratio of Hours where the animal spent more time in FA 2 than in FA 1
- 14.
- Mean time spent per hour in FA 1
- 15.
- Mean time spent per hour in in FA 2
- 16.
- Mean time spent per hour in in FA 3
- 17.
- Standard Deviation of Time spent per hour in FA 1
- 18.
- Standard Deviation of Time spent per hour in FA 2
- 19.
- Standard Deviation of Time spent per hour in FA 3
- 20.
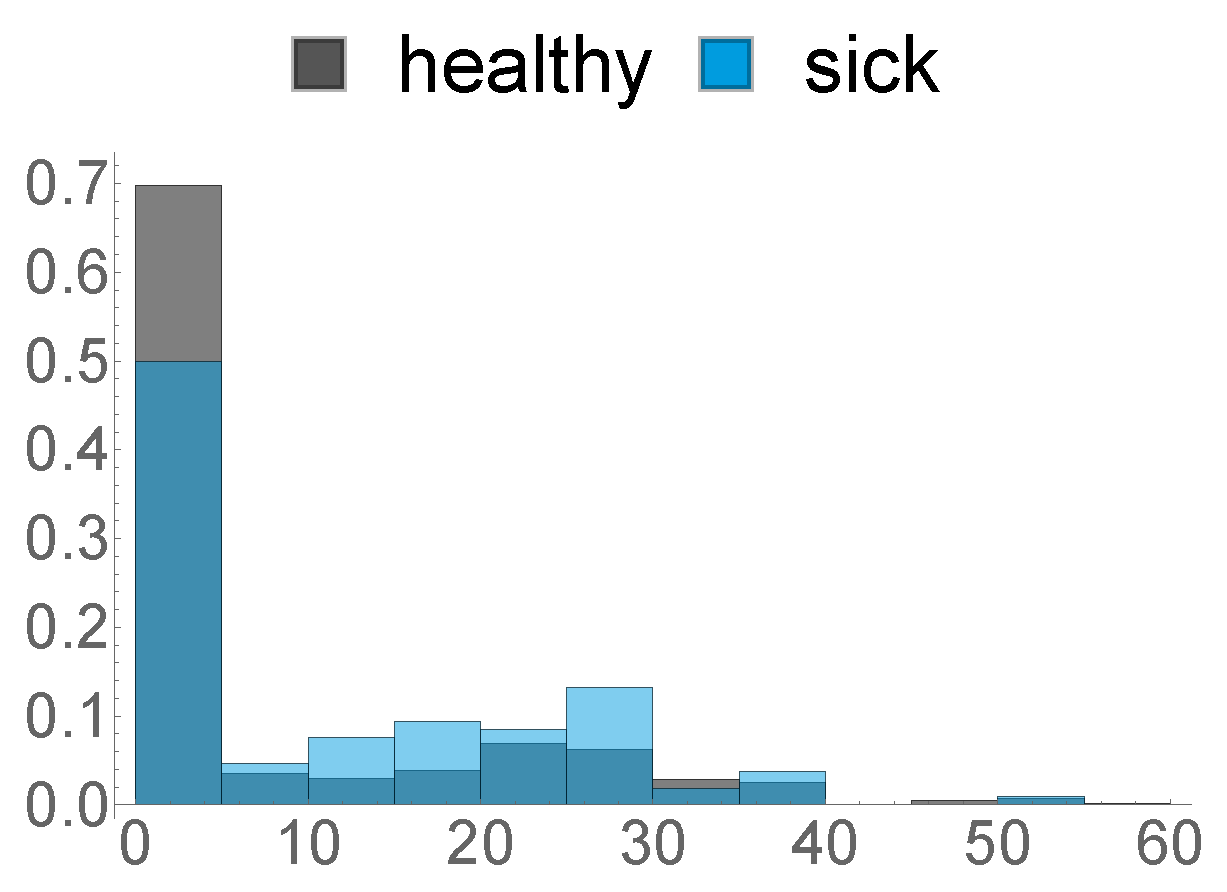
- This feature describes the amount of hours in the last week before calving, where the animal was exposed to a temperature–humidity index (THI) of 72 or higher, where a THI ≥ 72 is defined by the Austrian Chamber of Agriculture as “moderate heat-stress”, based on [22,23]. We can see the distribution of this feature in Figure 8 below.
2.4. Mathematical Section
2.5. Machine Learning in Animal Disease Detection
2.6. Proposed Algorithm
- For every data stream of the sensor data, we learn an optimal parameter such that the leave-one-out inner cross validation balanced error is minimised using an NCC with distance function with . In case of ties, the highest value of is chosen.
- Using these 5 (possibly different) parameters, we assume an animal to be sick or healthy, if the five trained NCCs from Step 1 decided at least 4 out of 5 times for a certain class label.
- The remaining examples are classified as follows:
- (a)
- The features are sorted according to the results from using Relief on the whole training set. For using this algorithm, we need a complete data-set where we only include examples in which all features are available.
- (b)
- Afterwards, we employ an inner 10-fold cross validation to find the optimal amount of features to take, starting with the ones ranked highest and consecutively add the following according to our ordering. The optimum is calculated with respect to balanced accuracy. In this step, we also only include training examples that are complete.
- (c)
- The features are finally processed using a Naive Bayes algorithm to classify the yet undecided examples.
3. Results
3.1. Statistical Comparison
3.2. Classification Results
- Sensor data before calving, location features included
- Sensor data before calving, location features not included
- Sensor data after calving, location features included
- Sensor data after calving, location features not included

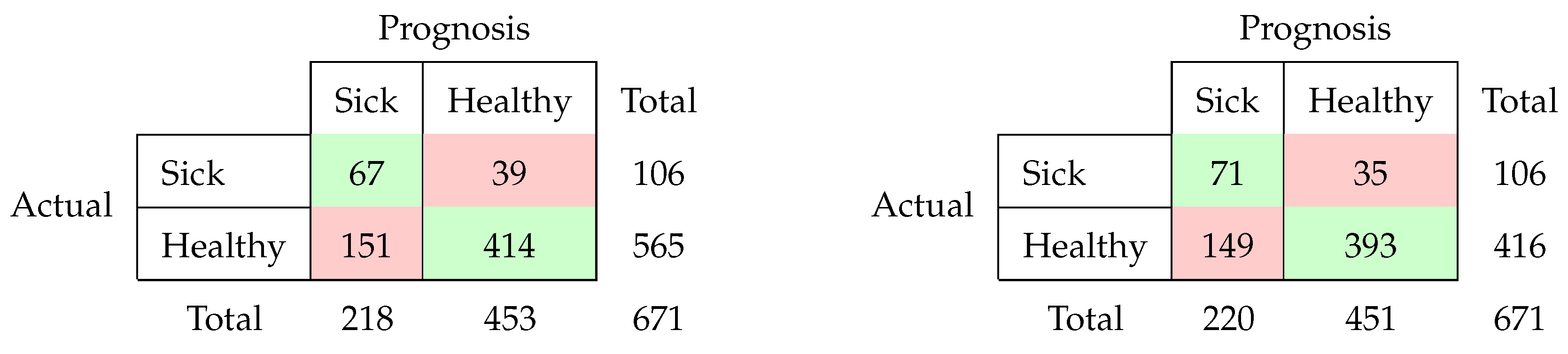
3.3. Parameters and Relevant Features Learned
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Andersson, L. Subclinical Ketosis in Dairy Cows. Veter-Clin. N. Am. 1988, 4, 233–251. [Google Scholar] [CrossRef]
- Duffield, T.; Sandals, D.; Leslie, K.; Lissemore, K.; McBride, B.; Lumsden, J.; Dick, P.; Bagg, R. Efficacy of Monensin for the Prevention of Subclinical Ketosis in Lactating Dairy Cows. J. Dairy Sci. 1998, 81, 2866–2873. [Google Scholar] [CrossRef]
- Duffield, T.F.; Lissemore, K.; McBride, B.; Leslie, K. Impact of hyperketonemia in early lactation dairy cows on health and production. J. Dairy Sci. 2009, 92, 571–580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geishauser, T.; Leslie, K.; Kelton, D.; Duffield, T. Evaluation of Five Cowside Tests for Use with Milk to Detect Subclinical Ketosis in Dairy Cows. J. Dairy Sci. 1998, 81, 438–443. [Google Scholar] [CrossRef]
- Bach, K.; Heuwieser, W.; McArt, J. Technical note: Comparison of 4 electronic handheld meters for diagnosing hyperketonemia in dairy cows. J. Dairy Sci. 2016, 99, 9136–9142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iwersen, M.; Klein-Jöbstl, D.; Pichler, M.; Roland, L.; Fidlschuster, B.; Schwendenwein, I.; Drillich, M. Comparison of 2 electronic cowside tests to detect subclinical ketosis in dairy cows and the influence of the temperature and type of blood sample on the test results. J. Dairy Sci. 2013, 96, 7719–7730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chapinal, N.; Leblanc, S.J.; Carson, M.; Leslie, K.; Godden, S.; Capel, M.; Santos, J.; Overton, M.; Duffield, T. Herd-level association of serum metabolites in the transition period with disease, milk production, and early lactation reproductive performance. J. Dairy Sci. 2012, 95, 5676–5682. [Google Scholar] [CrossRef]
- Suthar, V.; Canelas-Raposo, J.; Deniz, A.; Heuwieser, W. Prevalence of subclinical ketosis and relationships with postpartum diseases in European dairy cows. J. Dairy Sci. 2013, 96, 2925–2938. [Google Scholar] [CrossRef] [Green Version]
- Liang, D.; Arnold, L.; Stowe, C.; Harmon, R.; Bewley, J. Estimating US dairy clinical disease costs with a stochastic simulation model. J. Dairy Sci. 2017, 100, 1472–1486. [Google Scholar] [CrossRef] [Green Version]
- Vanholder, T.; Papen, J.; Bemers, R.; Vertenten, G.; Berge, A. Risk factors for subclinical and clinical ketosis and association with production parameters in dairy cows in the Netherlands. J. Dairy Sci. 2015, 98, 880–888. [Google Scholar] [CrossRef] [Green Version]
- Itle, A.; Huzzey, J.; Weary, D.M.; Von Keyserlingk, M.A.G. Clinical ketosis and standing behavior in transition cows. J. Dairy Sci. 2015, 98, 128–134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stangaferro, M.; Wijma, R.; Caixeta, L.; Al Abri, M.A.; Giordano, J. Use of rumination and activity monitoring for the identification of dairy cows with health disorders: Part III. Metritis. J. Dairy Sci. 2016, 99, 7422–7433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rutten, C.; Velthuis, A.; Steeneveld, W.; Hogeveen, H. Invited review: Sensors to support health management on dairy farms. J. Dairy Sci. 2013, 96, 1928–1952. [Google Scholar] [CrossRef] [PubMed]
- Wathes, C.M.; Kristensen, H.H.; Aerts, J.M.; Berckmans, D. Is precision livestock farming an engineer’s daydream or nightmare, an animal’s friend or foe, and a farmer’s panacea or pitfall? Comput. Electron. Agric. 2008, 64, 2–10. [Google Scholar] [CrossRef]
- Edmonson, A.; Lean, I.; Weaver, L.; Farver, T.; Webster, G. A Body Condition Scoring Chart for Holstein Dairy Cows. J. Dairy Sci. 1989, 72, 68–78. [Google Scholar] [CrossRef]
- Schröder, U.; Staufenbiel, R. Invited Review: Methods to Determine Body Fat Reserves in the Dairy Cow with Special Regard to Ultrasonographic Measurement of Backfat Thickness. J. Dairy Sci. 2006, 89, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Borchers, M.; Chang, Y.; Tsai, I.; Wadsworth, B.; Bewley, J. A validation of technologies monitoring dairy cow feeding, ruminating, and lying behaviors. J. Dairy Sci. 2016, 99, 7458–7466. [Google Scholar] [CrossRef]
- Reiter, S.; Sattlecker, G.; Lidauer, L.; Kickinger, F.; Öhlschuster, M.; Auer, W.; Schweinzer, V.; Klein-Jöbstl, D.; Drillich, M.; Iwersen, M. Evaluation of an ear-tag-based accelerometer for monitoring rumination in dairy cows. J. Dairy Sci. 2018, 101, 3398–3411. [Google Scholar] [CrossRef] [Green Version]
- Schweinzer, V.; Gusterer, E.; Kanz, P.; Krieger, S.; Süss, D.; Lidauer, L.; Berger, A.; Kickinger, F.; Öhlschuster, M.; Auer, W.; et al. Evaluation of an ear-attached accelerometer for detecting estrus events in indoor housed dairy cows. Theriogenology 2019, 130, 19–25. [Google Scholar] [CrossRef]
- Sturm, V.; Efrosinin, D.; Gusterer, E.; Iwersen, M.; Drillich, M.; Öhlschuster, M. Time Series Classification for Detecting Subclinical Ketosis in Dairy Cows. In Proceedings of the 2019 International Conference on Biotechnology and Bioengineering (9th ICBB 2019), Poznan, Poland, 25–28 September 2019. submitted. [Google Scholar]
- Grohn, Y.; Eicker, S.; Hertl, J. The Association between Previous 305-day Milk Yield and Disease in New York State Dairy Cows. J. Dairy Sci. 1995, 78, 1693–1702. [Google Scholar] [CrossRef]
- Thom, E.C. The Discomfort Index. Weatherwise 1959, 12, 57–61. [Google Scholar] [CrossRef]
- Zimbelman, R.B.; Rhoads, R.P.; Rhoads, M.L.; Duff, G.C.; Baumgard, L.H.; Collier, R.J. A re-evaluation of the impact of temperature humidity index (THI) and black globe humidity index (BGHI) on milk production in high producing dairy cows. In Proceedings of the Southwest Nutrition Conference, Tempe, AZ, USA, 26–27 February 2009; pp. 158–169. [Google Scholar]
- Bagnall, A.; Lines, J.; Bostrom, A.; Large, J.; Keogh, E. The great time series classification bake off: a review and experimental evaluation of recent algorithmic advances. Data Min. Knowl. Discov. 2016, 31, 606–660. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucas, B.; Shifaz, A.; Pelletier, C.; O’Neill, L.; Zaidi, N.; Goethals, B.; Petitjean, F.; Webb, G.I. Proximity Forest: an effective and scalable distance-based classifier for time series. Data Min. Knowl. Discov. 2019, 33, 607–635. [Google Scholar] [CrossRef] [Green Version]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef] [Green Version]
- Kruskal, J.B. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 1964, 29, 1–27. [Google Scholar] [CrossRef]
- Clarkson, K.L. Nearest-neighbor searching and metric space dimensions. In Nearest-Neighbor Methods for Learning and Vision: Theory and Practice; MIT Press: Cambridge, MA, USA, 2006; pp. 15–59. [Google Scholar]
- Wagner, N.; Antoine, V.; Mialon, M.-M.; Lardy, R.; Silberberg, M.; Koko, J.; Veissier, I. Machine learning to detect behavioural anomalies in dairy cows under subacute ruminal acidosis. Comput. Electron. Agric. 2020, 170, 105233. [Google Scholar] [CrossRef]
- Cowton, J.; Kyriazakis, I.; Ploetz, T.; Bacardit, J. A Combined Deep Learning GRU-Autoencoder for the Early Detection of Respiratory Disease in Pigs Using Multiple Environmental Sensors. Sensors 2018, 18, 2521. [Google Scholar] [CrossRef] [Green Version]
- Haladjian, J.; Haug, J.; Nüske, S.; Bruegge, B. A Wearable Sensor System for Lameness Detection in Dairy Cattle. Multimodal Technol. Interact. 2018, 2, 27. [Google Scholar] [CrossRef] [Green Version]
- Manning, C.D.; Raghavan, P.; Schutze, H. Introduction to Information Retrieval; Cambridge University Press (CUP): Cambridge, UK, 2008; pp. 292–297. [Google Scholar]
- Maron, M.E. Automatic Indexing: An Experimental Inquiry. J. ACM 1961, 8, 404–417. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. A practical approach to feature selection. In Machine Learning Proceedings 1992; Morgan Kaufmann: San Francisco, CA, USA, 1992; pp. 249–256. [Google Scholar]
- Cao, Y.; Zhang, J.; Yang, W.; Xia, C.; Zhang, H.-Y.; Wang, Y.-H.; Xu, C. Predictive value of plasma parameters in the risk of postpartum ketosis in dairy cows. J. Veter. Res. 2017, 61, 91–95. [Google Scholar] [CrossRef] [Green Version]
- Gantner, V.; Kuterovac, K.; Potočnik, K. 11. Effect of Heat Stress on Metabolic Disorders Prevalence Risk and Milk Production in Holstein Cows in Croatia. Ann. Anim. Sci. 2016, 16, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Mellado, M.; Davila, A.; Gaytan, L.; Macías-Cruz, U.; Avendaño-Reyes, L.; García, E. Risk factors for clinical ketosis and association with milk production and reproduction variables in dairy cows in a hot environment. Trop. Anim. Health Prod. 2018, 50, 1611–1616. [Google Scholar] [CrossRef] [PubMed]




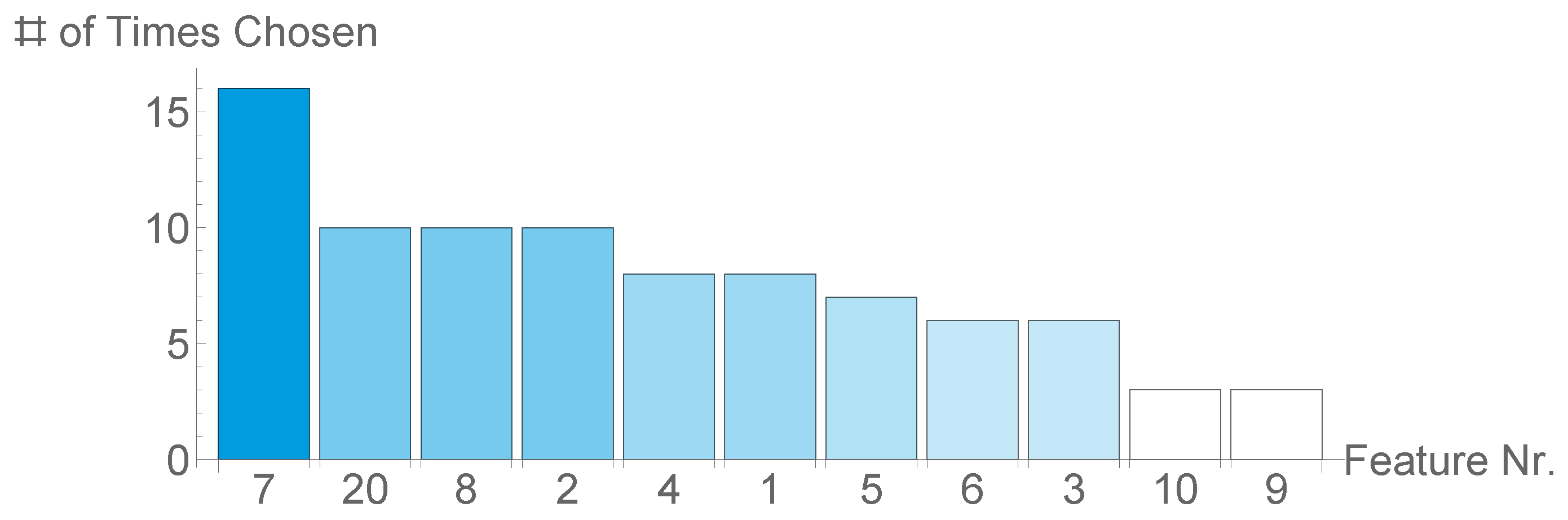
| Health Status | Examples | Frequency |
|---|---|---|
| Healthy | 565 | 84.20% |
| Sick | 106 | 15.80% |
| BCS -8 w | BCS -3 w | BCS Day0 | BFT -8 w | BFT -3 w | |
| healthy | 3.19 ± 0.432 | 3.426 ± 0.428 | 3.298 ± 0.41 | 13.425 ± 5.002 | 15.393 ± 5.261 |
| sick | 3.377 ± 0.446 | 3.613 ± 0.445 | 3.395 ± 0.424 | 15.527 ± 5.83 | 17.581 ± 5.261 |
| p-value | 0.00753024 | 0.000629145 * | 0.0493177 | 0.0148332 | 0.000184263 * |
| BFT Day0 | NEFA | 305-D Milk | Max f/p Ratio | Parity | |
| healthy | 15.248 ± 4.846 | 0.296 ± 0.222 | 11538.3 ± 1528.18 | 1.686 ± 0.327 | 0.096 ± 0.996 |
| sick | 16.892 ± 5.577 | 0.384 ± 0.256 | 11317.7 ± 1713.15 | 1.676 ± 0.372 | 0.151 ± 0.993 |
| p-value | 0.00630105 | 0.00015792 * | 0.33808 | 0.449638 | 0.600132 |
| Location1 | Location2 | Location3 | Time Area 1 | Time Area 2 | |
| healthy | 0.703 ± 0.09 | 0.074 ± 0.032 | 0.098 ± 0.042 | 50.658 ± 3.188 | 5.564 ± 1.853 |
| sick | 0.748 ± 0.093 | 0.059 ± 0.026 | 0.08 ± 0.037 | 52.285 ± 2.96 | 4.705 ± 1.857 |
| p-value | 0.00020492 * | 0.000434685 * | 0.00242925 * | 0.0000765469 * | 0.000498528 * |
| Time Area 3 | SD Area 1 | SD Area 2 | SD Area 3 | Hours THI Greater 72 | |
| healthy | 3.563 ± 1.478 | 16.821 ± 2.937 | 11.711 ± 2.309 | 10.233 ± 2.577 | 6.981 ± 11.911 |
| sick | 2.825 ± 1.155 | 15.336 ± 2.811 | 10.538 ± 2.374 | 8.799 ± 2.039 | 10.858 ± 12.576 |
| p-value | 0.000151992 * | 0.0000174387 * | 0.0000541604 * | 0.0000066027 * | 0.0000583004 * |
| Feature | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11–19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % Missing | 31.45 | 11.03 | 1.19 | 31.45 | 11.03 | 1.19 | 1.79 | 0.15 | 0.00 | 0.15 | 26.23 | 0.00 |
| Experiment | Acc | Sens | Spec | J | F-Score | Prec | MCC | NPV | Lift | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.6051 | 0.6698 | 0.5929 | 0.2627 | 0.1504 | 0.3489 | 0.2359 | 0.1927 | 0.9054 | 1.6454 |
| 2 | 0.6140 | 0.6604 | 0.6053 | 0.2657 | 0.1548 | 0.3509 | 0.2389 | 0.1954 | 0.9048 | 1.6732 |
| 3 | 0.7168 | 0.6321 | 0.7327 | 0.3648 | 0.2553 | 0.4136 | 0.3073 | 0.2841 | 0.9139 | 2.3651 |
| 4 | 0.7258 | 0.6698 | 0.7363 | 0.4061 | 0.2826 | 0.4356 | 0.3227 | 0.3155 | 0.9224 | 2.5399 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sturm, V.; Efrosinin, D.; Öhlschuster, M.; Gusterer, E.; Drillich, M.; Iwersen, M. Combination of Sensor Data and Health Monitoring for Early Detection of Subclinical Ketosis in Dairy Cows. Sensors 2020, 20, 1484. https://doi.org/10.3390/s20051484
Sturm V, Efrosinin D, Öhlschuster M, Gusterer E, Drillich M, Iwersen M. Combination of Sensor Data and Health Monitoring for Early Detection of Subclinical Ketosis in Dairy Cows. Sensors. 2020; 20(5):1484. https://doi.org/10.3390/s20051484
Chicago/Turabian StyleSturm, Valentin, Dmitry Efrosinin, Manfred Öhlschuster, Erika Gusterer, Marc Drillich, and Michael Iwersen. 2020. "Combination of Sensor Data and Health Monitoring for Early Detection of Subclinical Ketosis in Dairy Cows" Sensors 20, no. 5: 1484. https://doi.org/10.3390/s20051484





