Nonlinear Vibration Study Based on Uncertainty Analysis in MEMS Resonant Accelerometer
Abstract
:1. Introduction
2. Working Principle and Theoretical Analysis
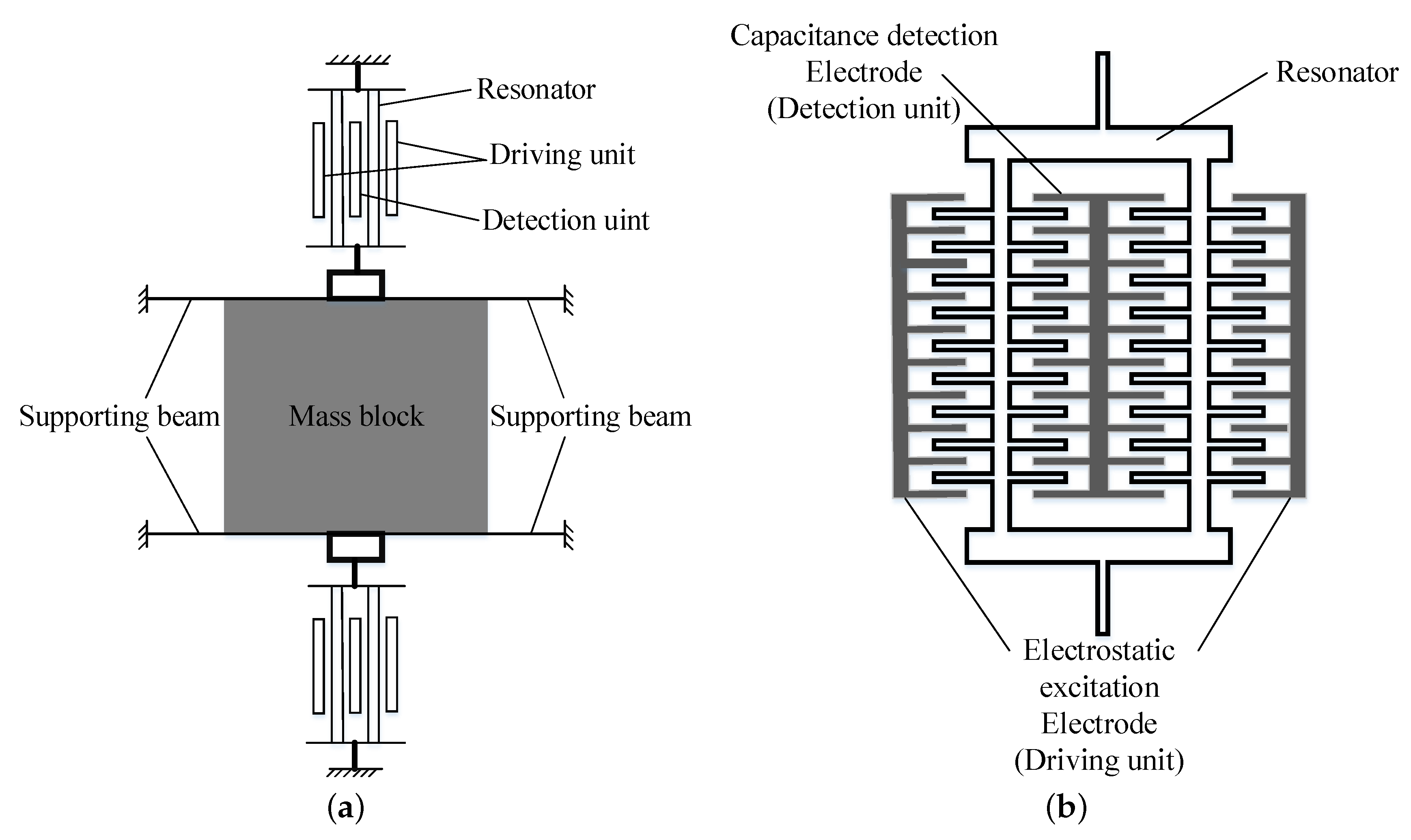
2.1. Working Principle
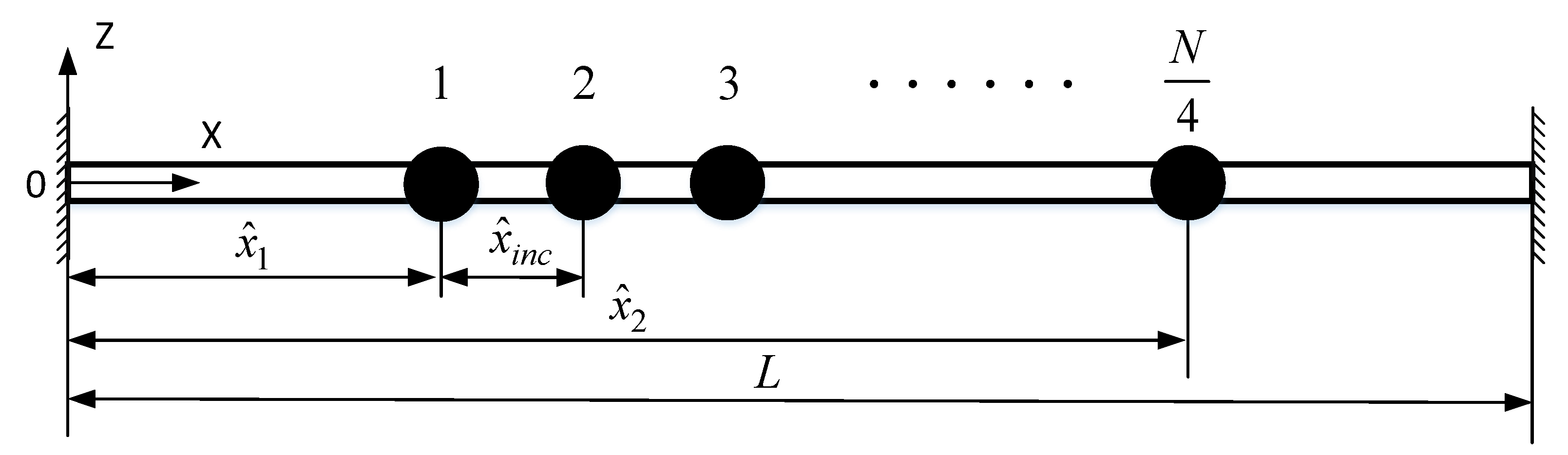
2.2. Nonlinear Vibration Model of Resonator with Comb Fingers
2.3. Natural Frequency-Tracking Error Caused by Nonlinear Vibration
3. Uncertainty Analysis Method
3.1. Uncertainty Analysis Method
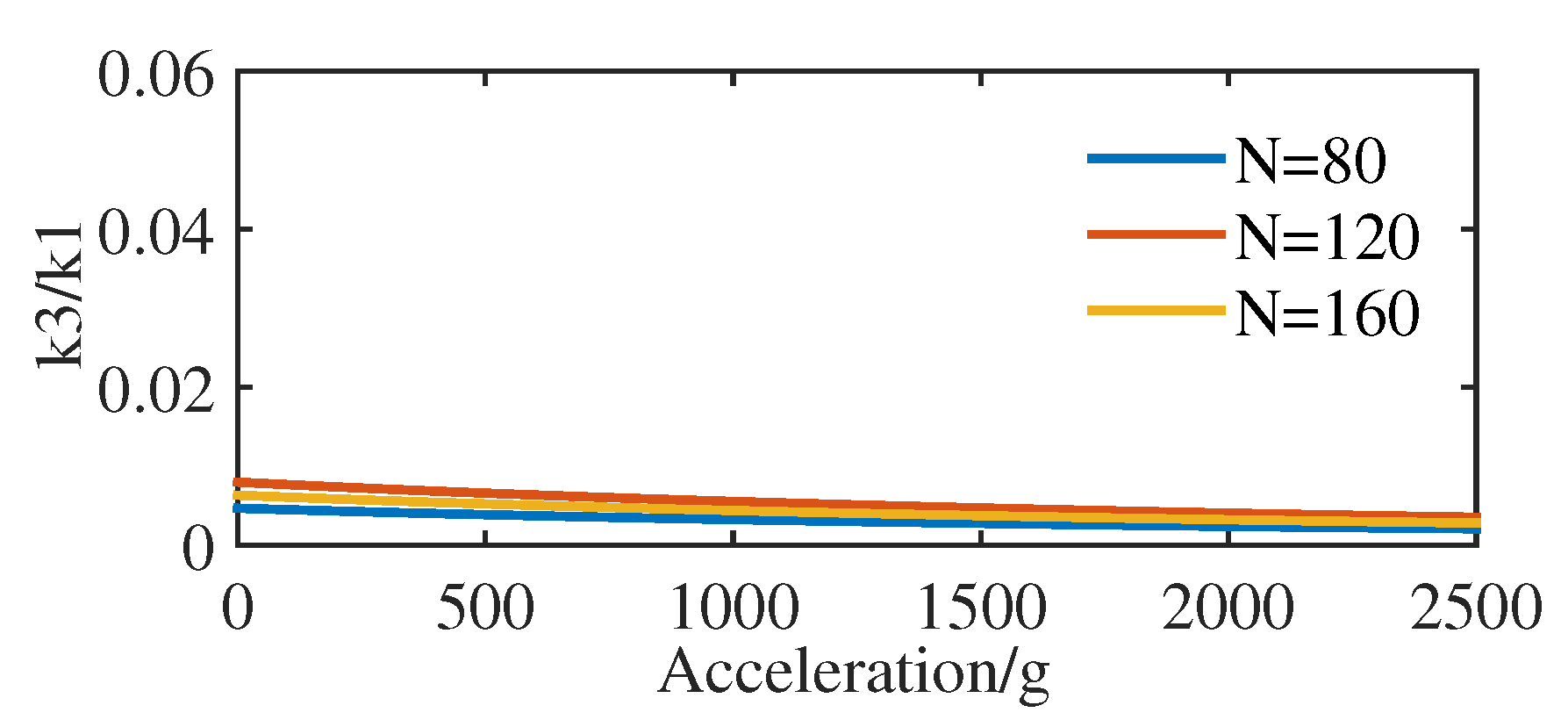
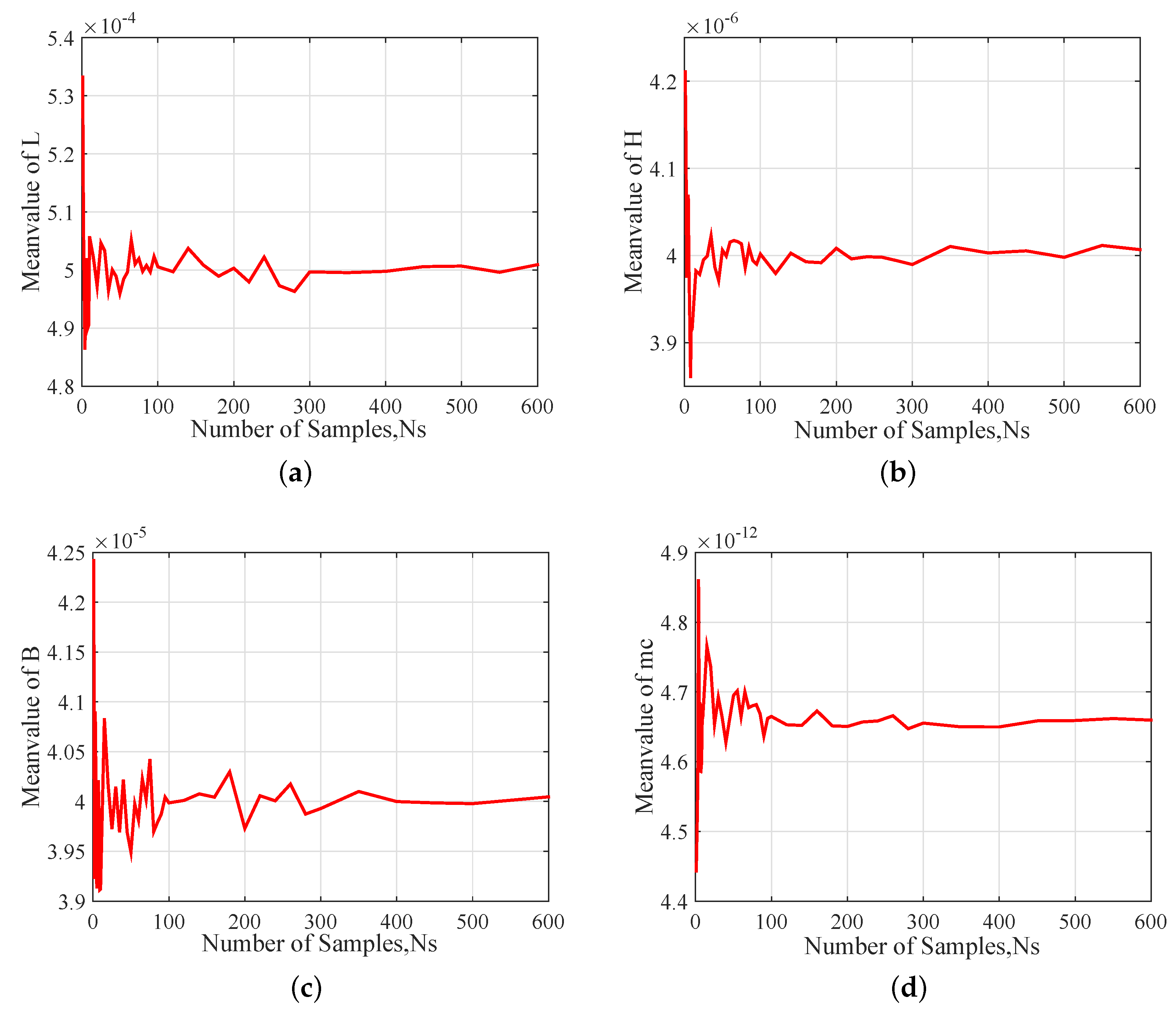
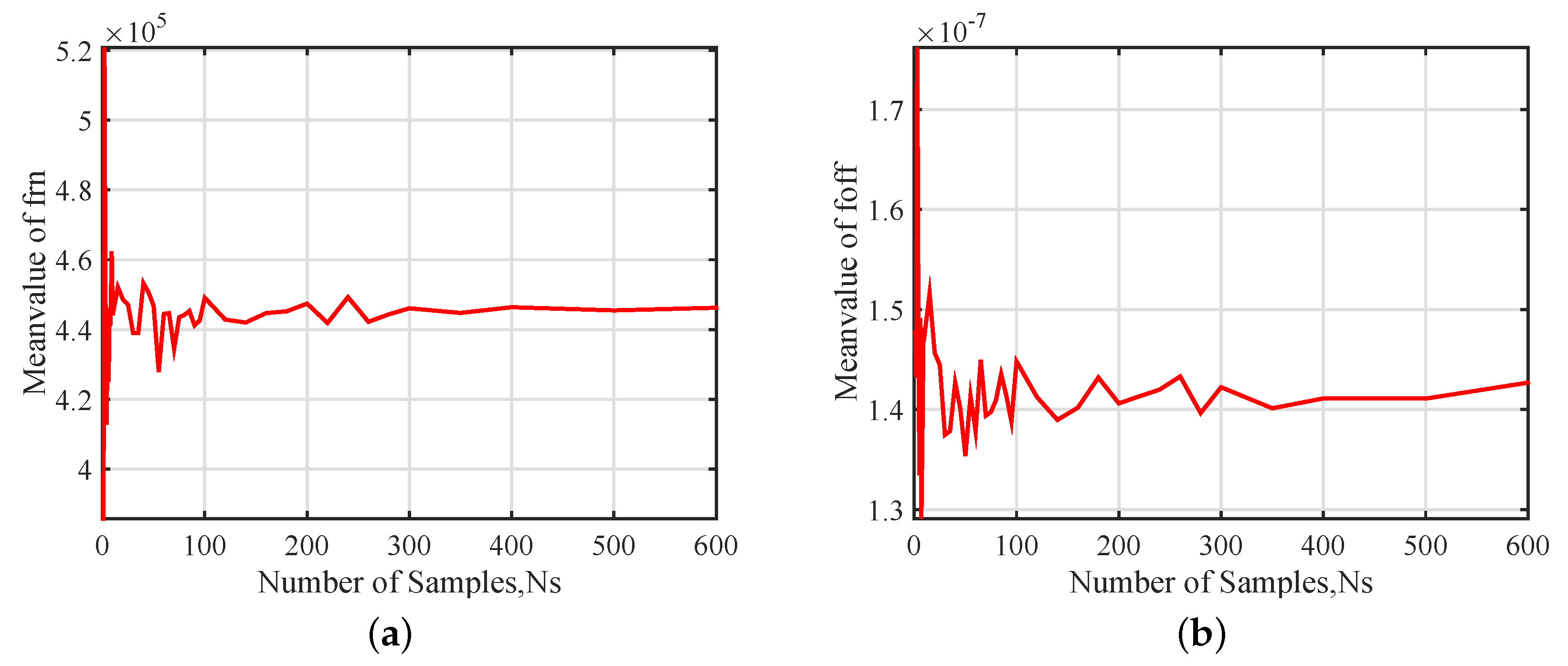
3.2. Results and Siscussions
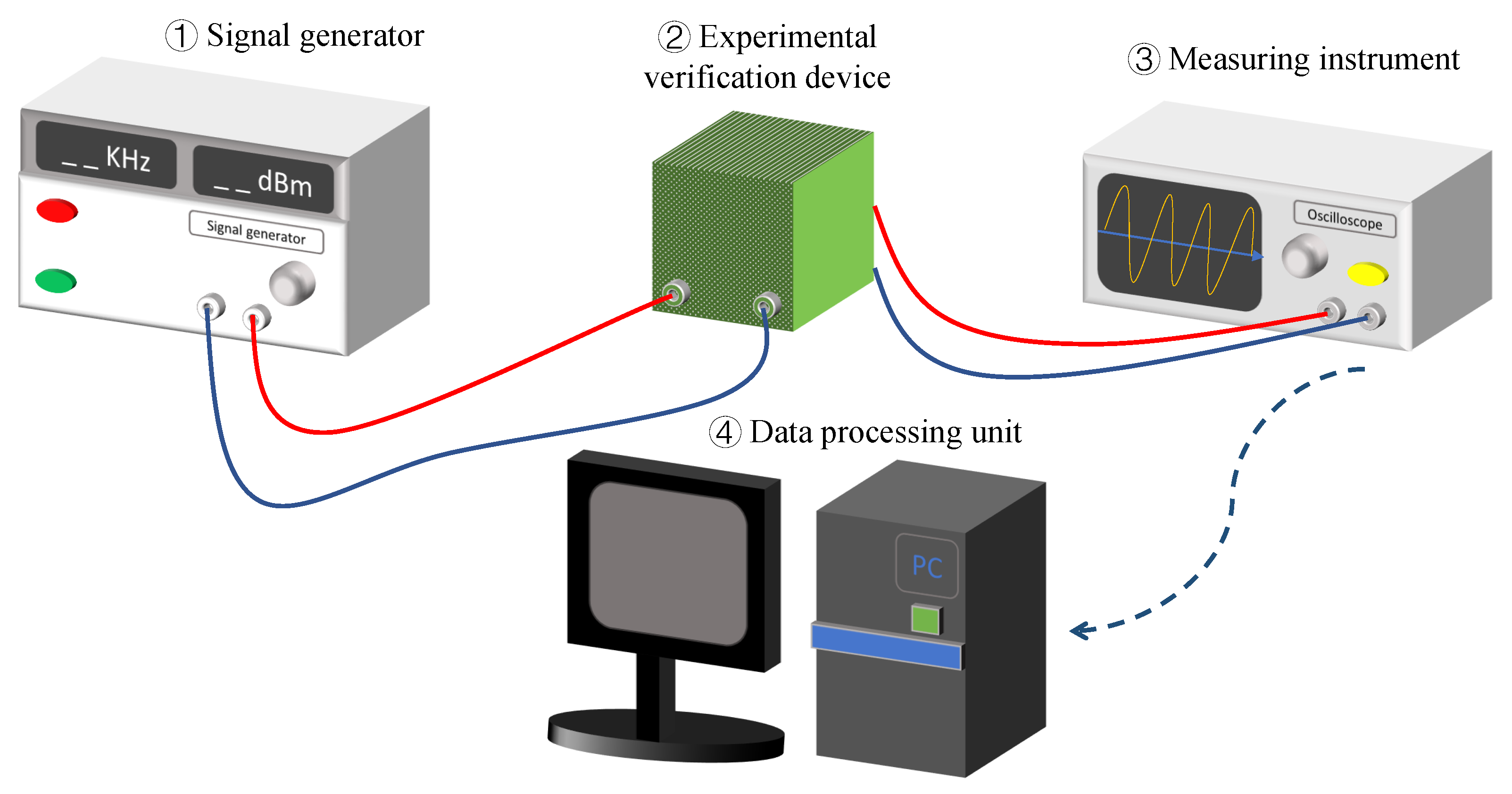
4. Experimental Verification
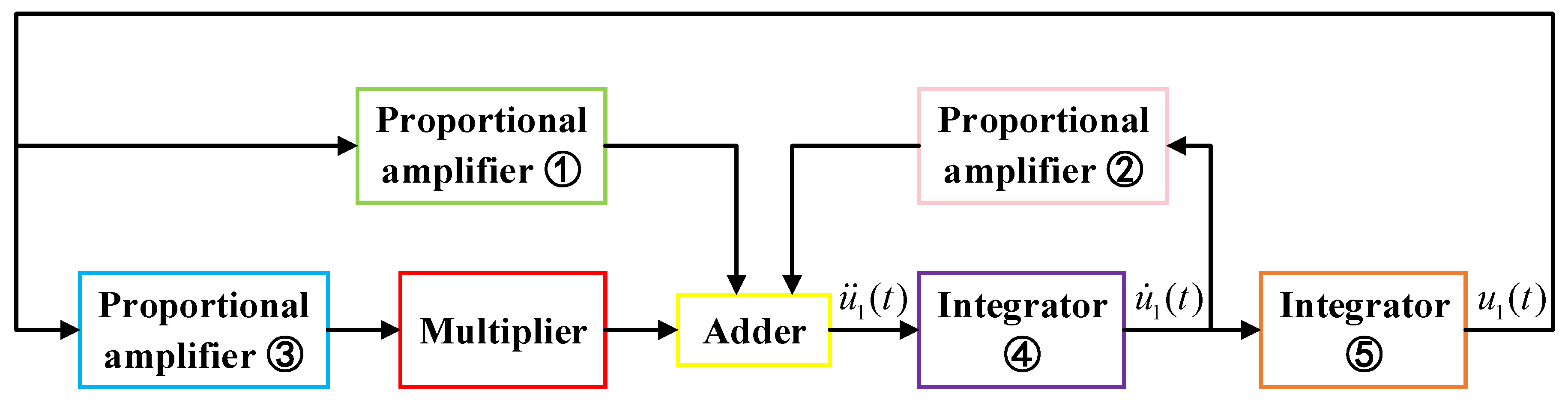
4.1. The Equivalent Circuit Model
4.2. Experimental Results
5. Conclusions
- The nonlinear vibration model of resonator with comb fingers has been established. The nonlinear stiffness coefficient and the linear stiffness coefficient have been calculated and analyzed with the Galérkin principle. The linear natural frequency , the nonlinear frequency offset and the scaling factor are obtained by multi-scale method.
- According to theoretical analysis, it is found that the pairs of comb fingers have little effect on the nonlinear vibration of the resonator. After further analyzing the relationship between the natural frequency-tracking error and the geometric parameters of the resonant beam, we can find that the frequency-tracking error increases with the increase of the length L of the resonant beam, and decreases with the increase of the width B and thickness H of the resonant beam. The nonlinear effect can be reduced by reducing the length L and increasing the width B and thickness H of the resonant beam.
- Based on the nonlinear vibration model of the resonator and considering uncertainty distributions of structure size due to fabricating errors, a sample-based stochastic model is established to further investigate the effect of input parameters (L, B, H, ) on the output parameters (, , ). The results show that the length L and thickness H of the resonant beam have a greater influence than the width B and the single concentrated mass of the comb finger on the nonlinear vibration of the resonator, which are consistent with the results of theoretical analysis.
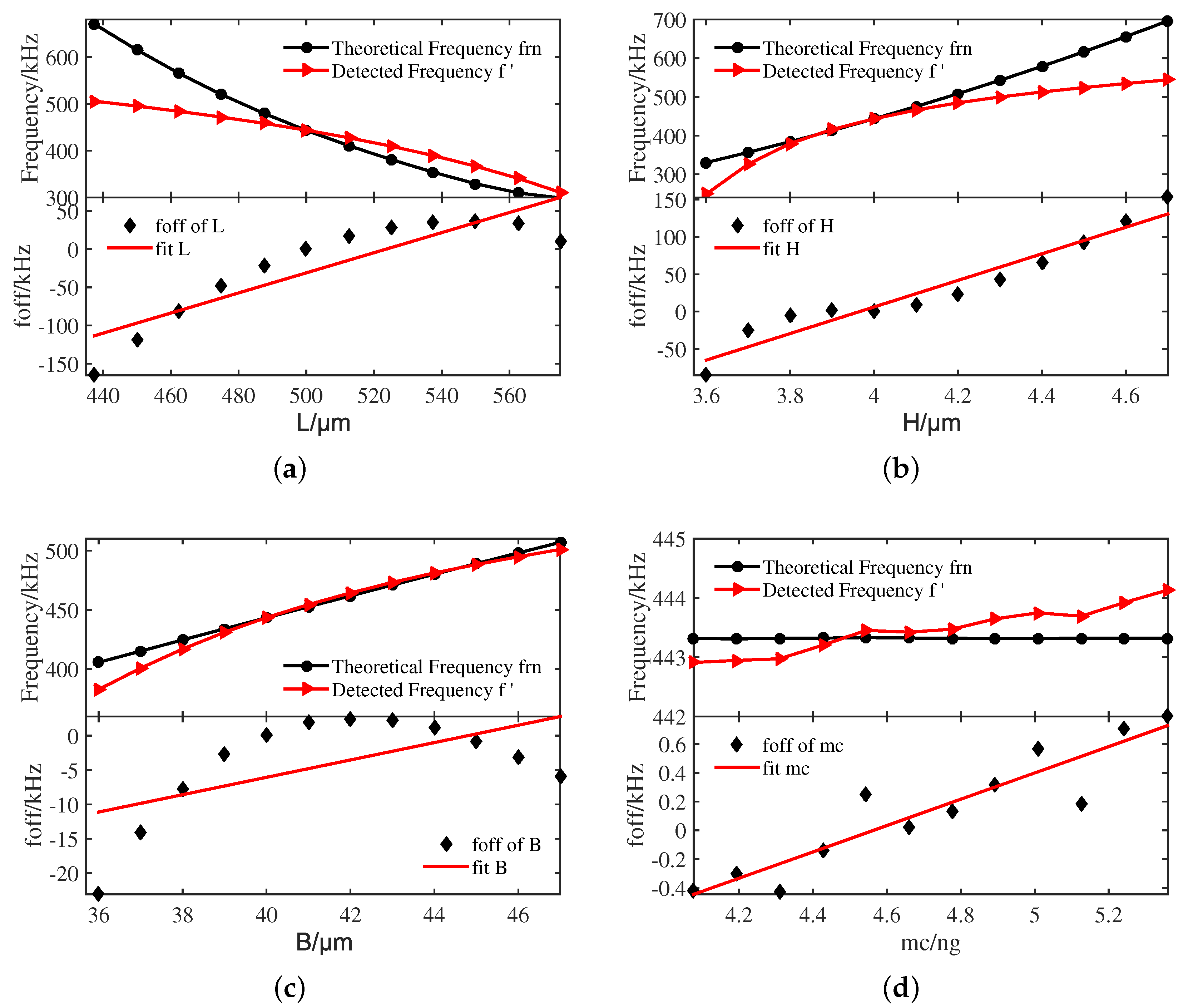
- In the experimental verification, the detected frequency of the circuit output and the theoretical frequency change significantly with the increase of the length L and the thickness H, followed by B and . Meanwhile, the length L and the thickness H are the main factors affecting the nonlinear frequency offset , which is consistent with the results of the uncertainty analysis method. According to the above conclusions, to reduce the nonlinear characteristics of the sensor, four geometric parameters can be properly adjusted to increase the stiffness and obtain better structural performance.
Author Contributions
Funding
Conflicts of Interest
References
- Meldrum, M. Application of vibrating beam technology to digital acceleration measurement. Sens. Actuators Phys. 1990, 21, 377–380. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Zega, V.; Su, Y.; Corigliano, A. Nonlinear dynamics under varying temperature conditions of the resonating beams of a differential resonant accelerometer. J. Micromech. Microeng. 2018, 28, 075004. [Google Scholar] [CrossRef]
- Defoort, M.; Taheri-Tehrani, P.; Horsley, D.A. Exploiting nonlinear amplitude-frequency dependence for temperature compensation in silicon micromechanical resonators. Appl. Phys. Lett. 2016, 109, 153502. [Google Scholar] [CrossRef]
- Shin, D.D.; Chen, Y.; Flader, I.B.; Kenny, T.W. Temperature compensation of resonant accelerometer via nonlinear operation. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, Ireland, 21–25 January 2018; pp. 1012–1015. [Google Scholar]
- Gusso, A. Nonlinear damping in doubly clamped beam resonators due to the attachment loss induced by the geometric nonlinearity. J. Sound Vib. 2016, 372, 255–265. [Google Scholar] [CrossRef]
- Zou, X.; Seshia, A.A. Non-linear frequency noise modulation in a resonant mems accelerometer. IEEE Sens. J. 2017, 17, 4122–4127. [Google Scholar] [CrossRef]
- Juillard, J.; Mostafa, A.; Ferreira, P.M. Nonlinear operation of resonant sensors based on weakly coupled resonators: Theory and modeling. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1950–1961. [Google Scholar] [CrossRef]
- Lv, R.; Fu, Q.; Chen, W.; Yin, L.; Zhang, Y. A digital interface asic for triple-axis mems vibratory gyroscopes. Sensors 2020, 20, 5460. [Google Scholar] [CrossRef]
- Agarwal, M.; Park, K.K.; Candler, R.N.; Kim, B.; Hopcroft, M.A.; Chandorkar, S.A.; Jha, C.M.; Melamud, R.; Kenny, T.W.; Murmann, B. Nonlinear characterization of electrostatic mems resonators. In Proceedings of the 2006 IEEE International Frequency Control Symposium and Exposition, Miami, FL, USA, 4–7 June 2006; pp. 209–212. [Google Scholar]
- Mahmoodi, S.; Daqaq, M.F.; Jalili, N. On the nonlinear-flexural response of piezoelectrically driven microcantilever sensors. Sens. Actuators Phys. 2009, 153, 171–179. [Google Scholar] [CrossRef]
- Hashemi Kachapi, S.H.; Mohammadi Daniali, H.; Dardel, M.; Fathi, A. Nonlinear vibration and stability analysis of double-walled piezoelectric nanoresonator with nonlinear van der waals and electrostatic excitation. JVC J. Vib. Control 2019, 26, 680–700. [Google Scholar] [CrossRef]
- Behbahani, A.H.; M’Closkey, R.T. Frequency analysis of a uniform ring perturbed by point masses and springs. J. Sound Vib. 2017, 397, 204–221. [Google Scholar] [CrossRef] [Green Version]
- Behbahani, A.H.; M’Closkey, R.T. Multimodal tuning of an axisymmetric resonator. J. Dyn. Syst. Meas. Control 2019, 141, 091010. [Google Scholar] [CrossRef] [Green Version]
- Behbahani, A.H.; Kim, D.; Stupar, P.; DeNatale, J.; M’Closkey, R.T. Tailored etch profiles for wafer-level frequency tuning of axisymmetric resonators. J. Microelectromech. Syst. 2017, 26, 333–343. [Google Scholar] [CrossRef] [Green Version]
- Allaei, D.; Soedel, W.; Yang, T.Y. Natural frequencies and modes of rings that deviate from perfect axisymmetry. J. Sound Vib. 1986, 111, 9–27. [Google Scholar] [CrossRef]
- Rourke, A.K.; McWilliam, S.; Fox, C.H.J. Multi-mode trimming of imperfect rings. J. Sound Vib. 2001, 248, 695–724. [Google Scholar] [CrossRef]
- Bisegna, P.; Caruso, G. Frequency split and vibration localization in imperfect rings. J. Sound Vib. 2007, 306, 691–711. [Google Scholar] [CrossRef]
- Campbell, J.; Rao, B. An uncertainty analysis methodology applied to sheetpile cofferdam design. Hydraul. Eng. 1987, 41, 36–41. [Google Scholar]
- Padmanabhan, S.; Pitchumani, R. Stochastic modeling of nonisothermal flow during resin transfer molding. Int. J. Heat Mass Transf. 1999, 42, 3057–3070. [Google Scholar] [CrossRef]
- Diwekar, U.; Rubin, E. Stochastic modeling of chemical processes. Comput. Chem. Eng. 1991, 15, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Mawardi, A.; Pitchumani, R. Numerical simulations of an optical fiber drawing process under uncertainty. J. Light. Technol. 2008, 26, 580–587. [Google Scholar] [CrossRef]
- Hibino, Y.; Hanawa, F.; Horiguchi, M. Drawing-induced residual stress effects on optical characteristics in pure-silica-core single-mode fibers. J. Appl. Phys. 1989, 65, 30–34. [Google Scholar] [CrossRef]
- Myers, M.R. A model for unsteady analysis of preform drawing. AIChE J. 1989, 35, 592–602. [Google Scholar] [CrossRef]
- Apostolakis, G. The concept of probability in safety assessments of technological systems. Science 1990, 250, 1359–1364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mawardi, A.; Pitchumani, R. Cure cycle design for thermosetting-matrix composites fabrication under uncertainty. Ann. Oper. Res. 2004, 132, 19–45. [Google Scholar] [CrossRef]
- Mawardi, A.; Pitchumani, R. Effects of parameter uncertainty on the performance variability of proton exchange membrane (pem) fuel cells. J. Power Sources 2006, 160, 232–245. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, Y.; Pai, P.F. Uncertainty analysis of solid-liquid-vapor phase change of a metal particle subject to nanosecond laser heating. J. Manuf. Sci. Eng. 2013, 135, 021009. [Google Scholar] [CrossRef]
- Shi, H.; Fan, S.; Li, W. Design and optimization of detf resonator based on uncertainty analysis in a micro-accelerometer. Microsyst. Technol. 2018, 24, 2025–2034. [Google Scholar] [CrossRef]
- Afrin, N.; Zhang, Y. Uncertainty analysis of thermal damage to living biological tissues by laser irradiation based on a generalized duel-phase lag model. Numer. Heat Transf. Part Appl. 2017, 71, 693–706. [Google Scholar] [CrossRef]
- Meng, T.; Fan, S.; Wang, C.; Shi, H. Influence analysis of fluctuation parameters on flow stability based on uncertainty method. Rev. Sci. Instrum. 2018, 89, 055005. [Google Scholar] [CrossRef]
- Shi, H.; Fan, S.; Zhang, Y.; Sun, J. Nonlinear dynamics study based on uncertainty analysis in electro-thermal excited mems resonant sensor. Sens. Actuators Phys. 2015, 232, 103–114. [Google Scholar] [CrossRef]
- Noll, M.U.; Lentz, L.; Wagner, U.V. On the discretization of a bistable cantilever beam with application to energy harvesting. Facta Univ. Ser. Mech. Eng. 2019, 17, 125–139. [Google Scholar] [CrossRef]
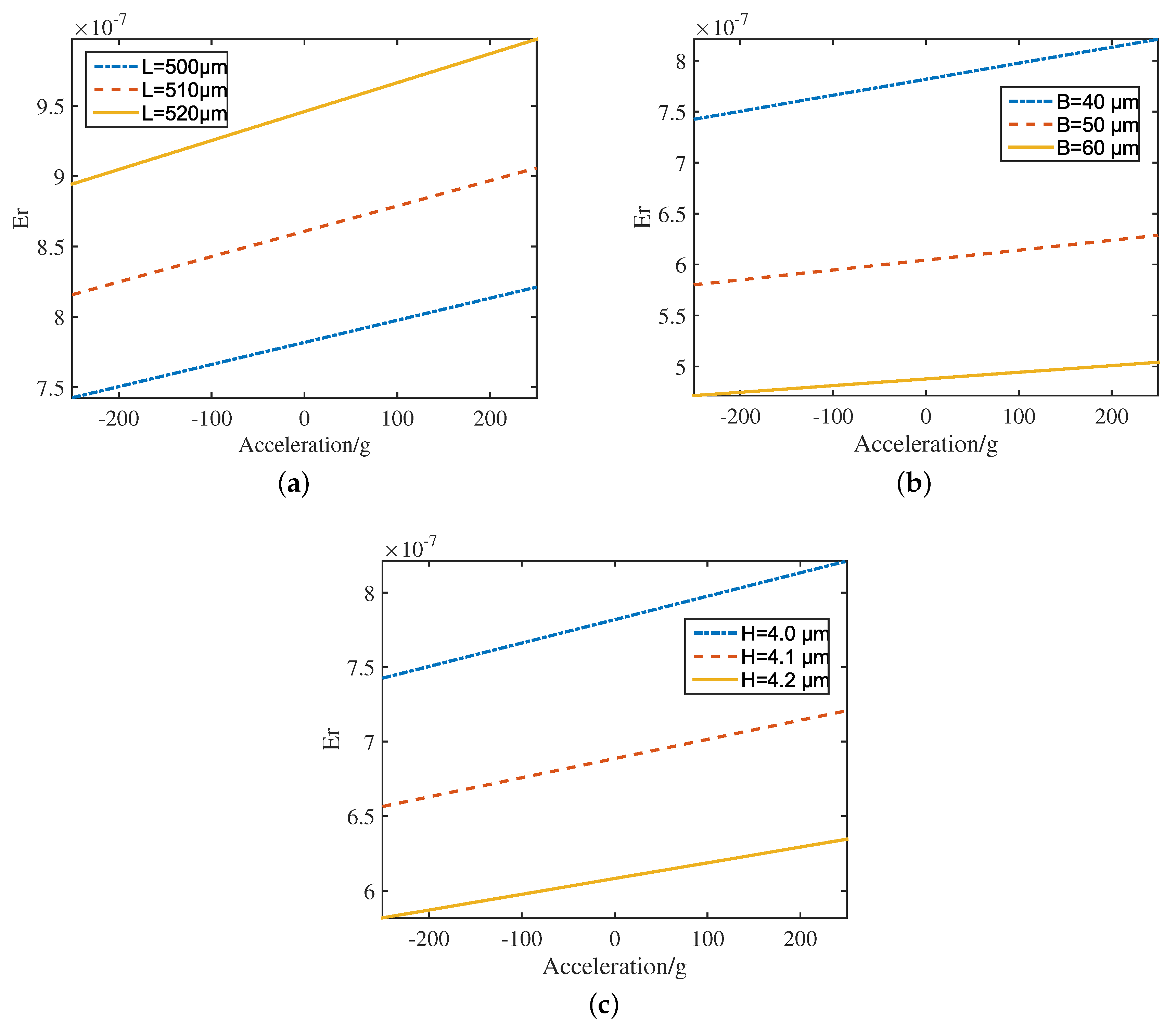




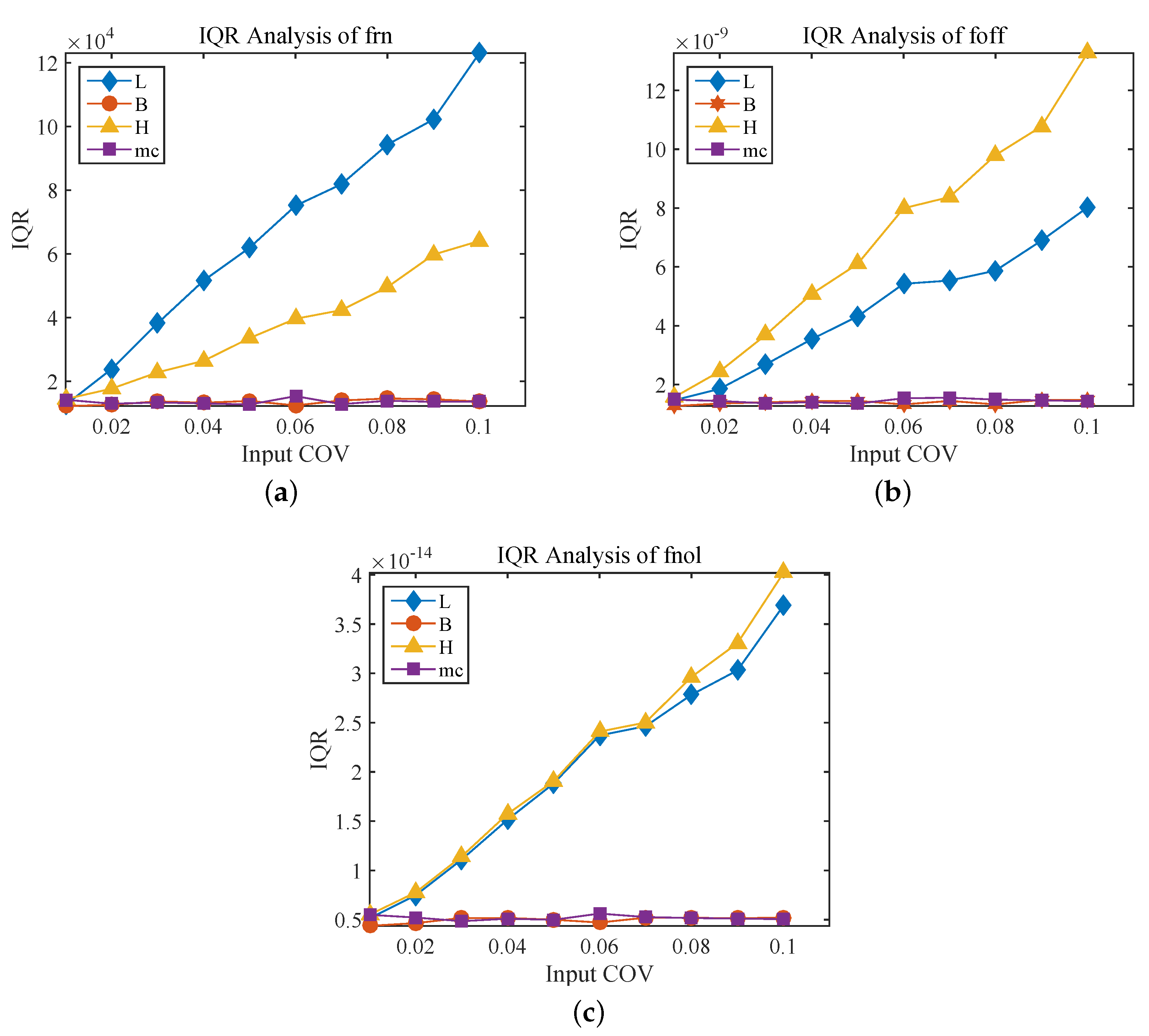

| Parameter | Expression | Dimensions |
|---|---|---|
| Length of the resonant beam | L | m |
| Width of the resonant beam | B | m |
| Thickness of the resonant beam | H | m |
| Pairs of the comb fingers | N | 80 |
| Single concentrated mass of comb finger | kg | |
| Material density | ||
| Young’s modulus of the material | E | |
| Poisson’s ratio | 0.278 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Song, L.; Liang, S.; Xiao, Y.; Yang, F. Nonlinear Vibration Study Based on Uncertainty Analysis in MEMS Resonant Accelerometer. Sensors 2020, 20, 7207. https://doi.org/10.3390/s20247207
Li Y, Song L, Liang S, Xiao Y, Yang F. Nonlinear Vibration Study Based on Uncertainty Analysis in MEMS Resonant Accelerometer. Sensors. 2020; 20(24):7207. https://doi.org/10.3390/s20247207
Chicago/Turabian StyleLi, Yan, Linke Song, Shuai Liang, Yifeng Xiao, and Fuling Yang. 2020. "Nonlinear Vibration Study Based on Uncertainty Analysis in MEMS Resonant Accelerometer" Sensors 20, no. 24: 7207. https://doi.org/10.3390/s20247207






