High-Sensitivity Cuboid Interferometric Fiber-Optic Hydrophone Based on Planar Rectangular Film Sensing
Abstract
:1. Introduction
2. Theory
2.1. General Principle
2.2. Theory Model
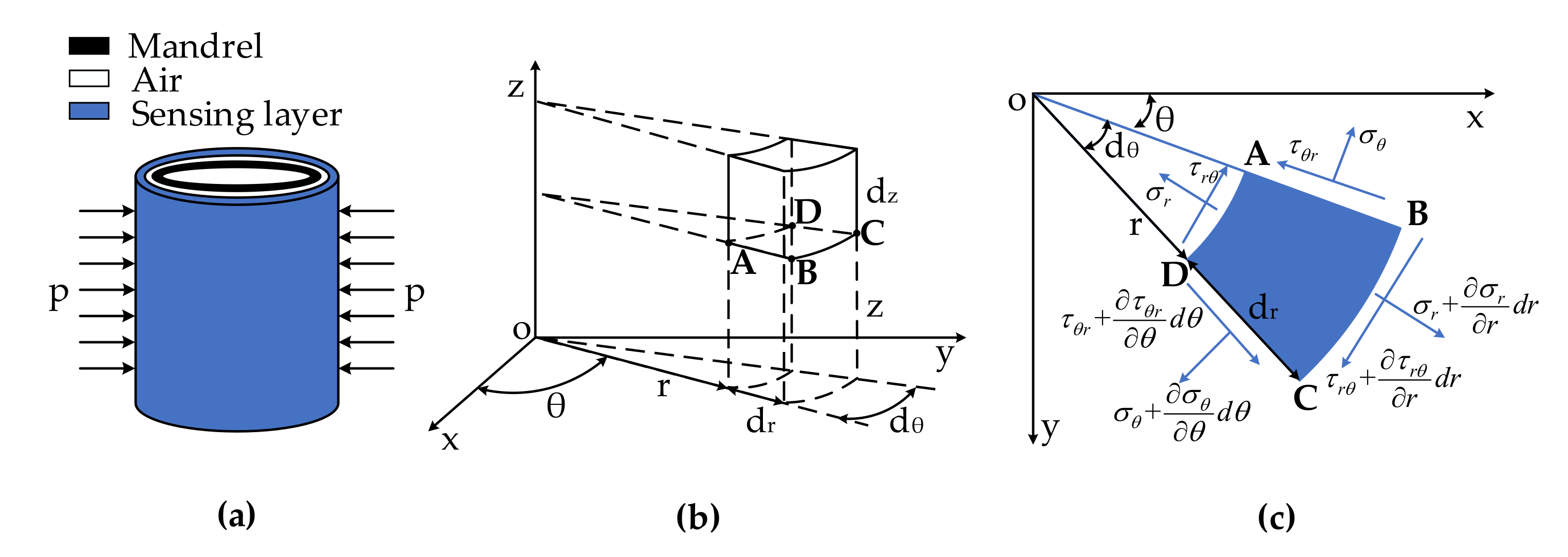
2.2.1. Mandrel Type
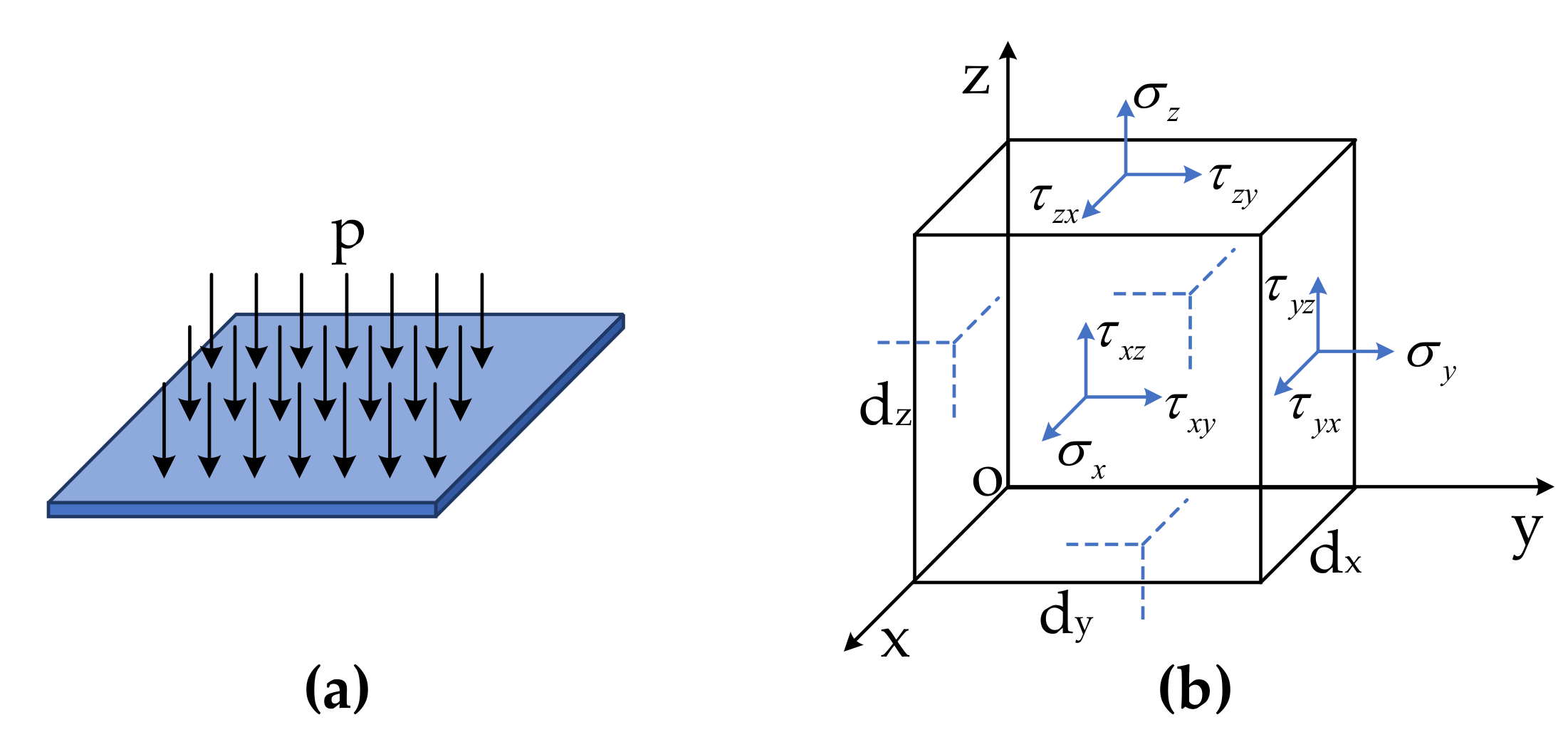
2.2.2. Cuboid Type
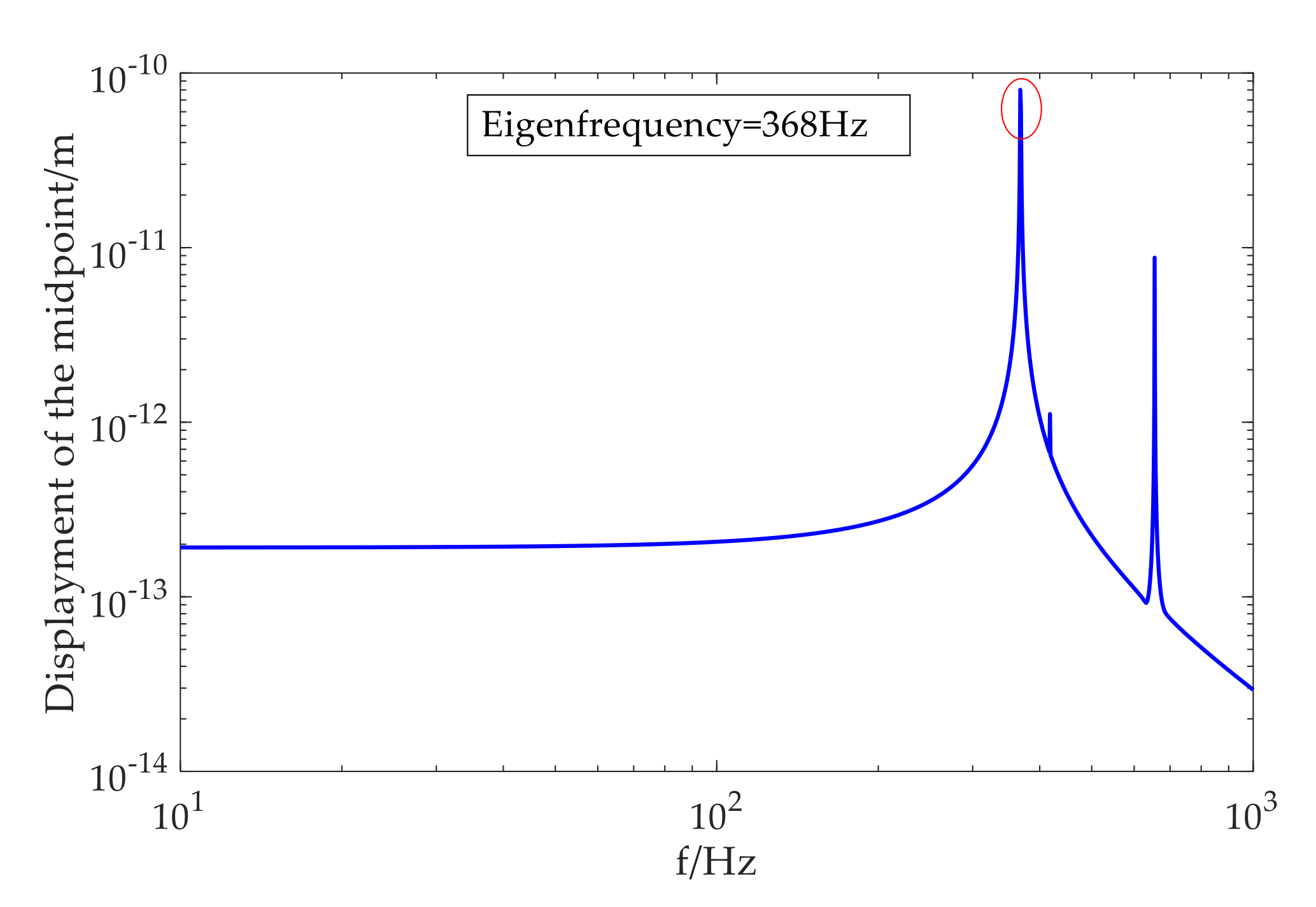
2.3. Theoretical-Calculation Result
3. Experiments
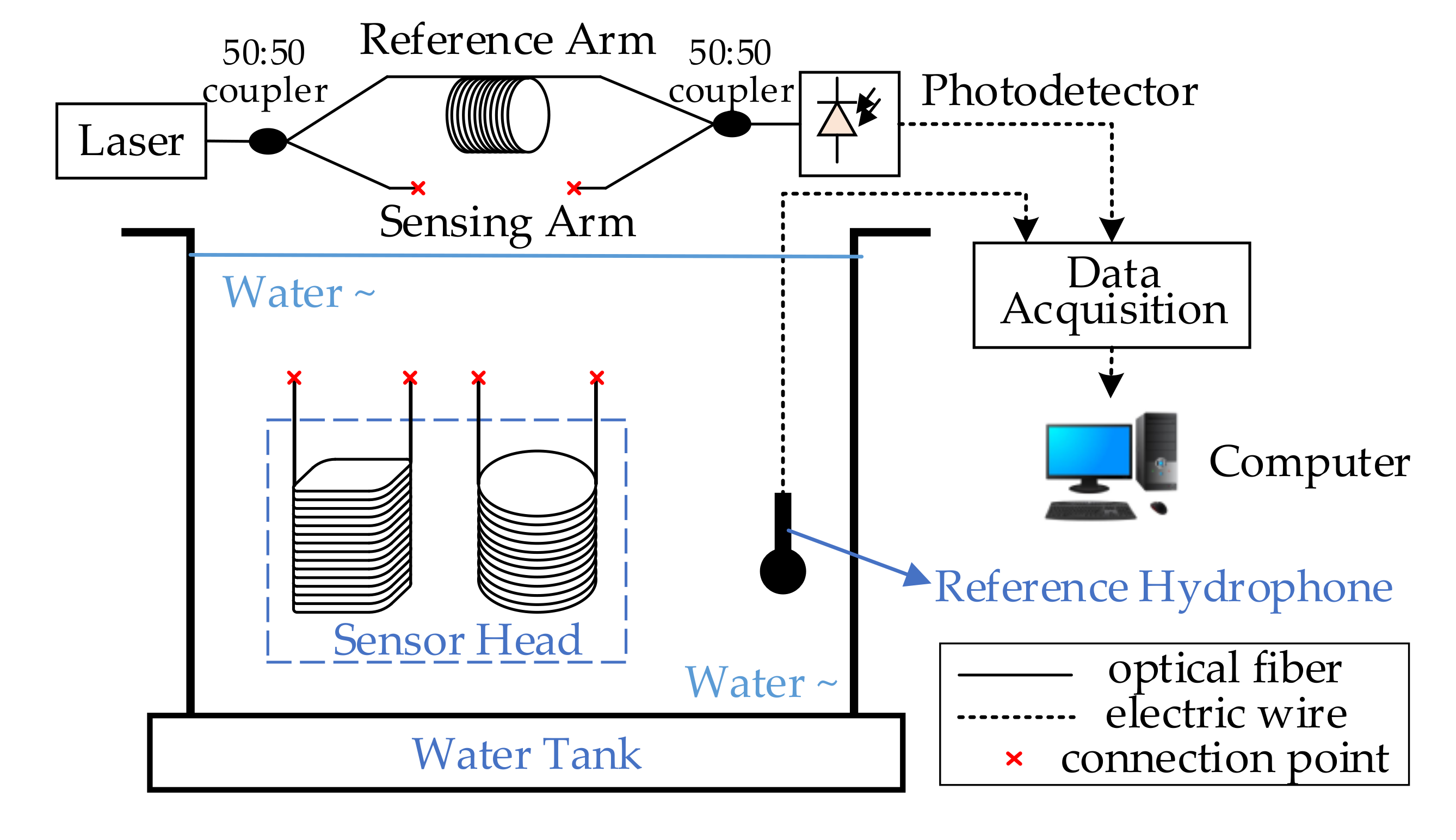
3.1. Experiment Methods
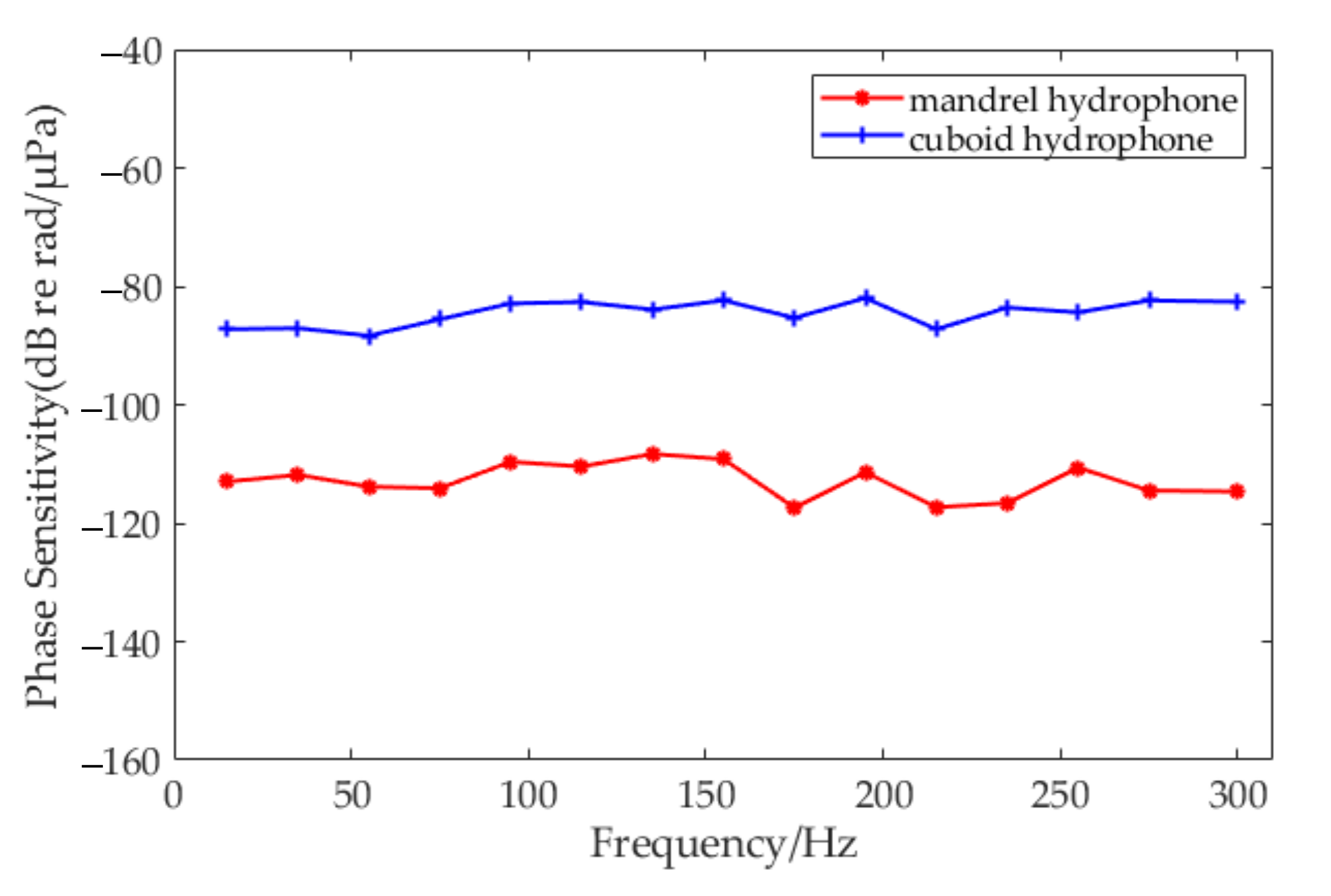
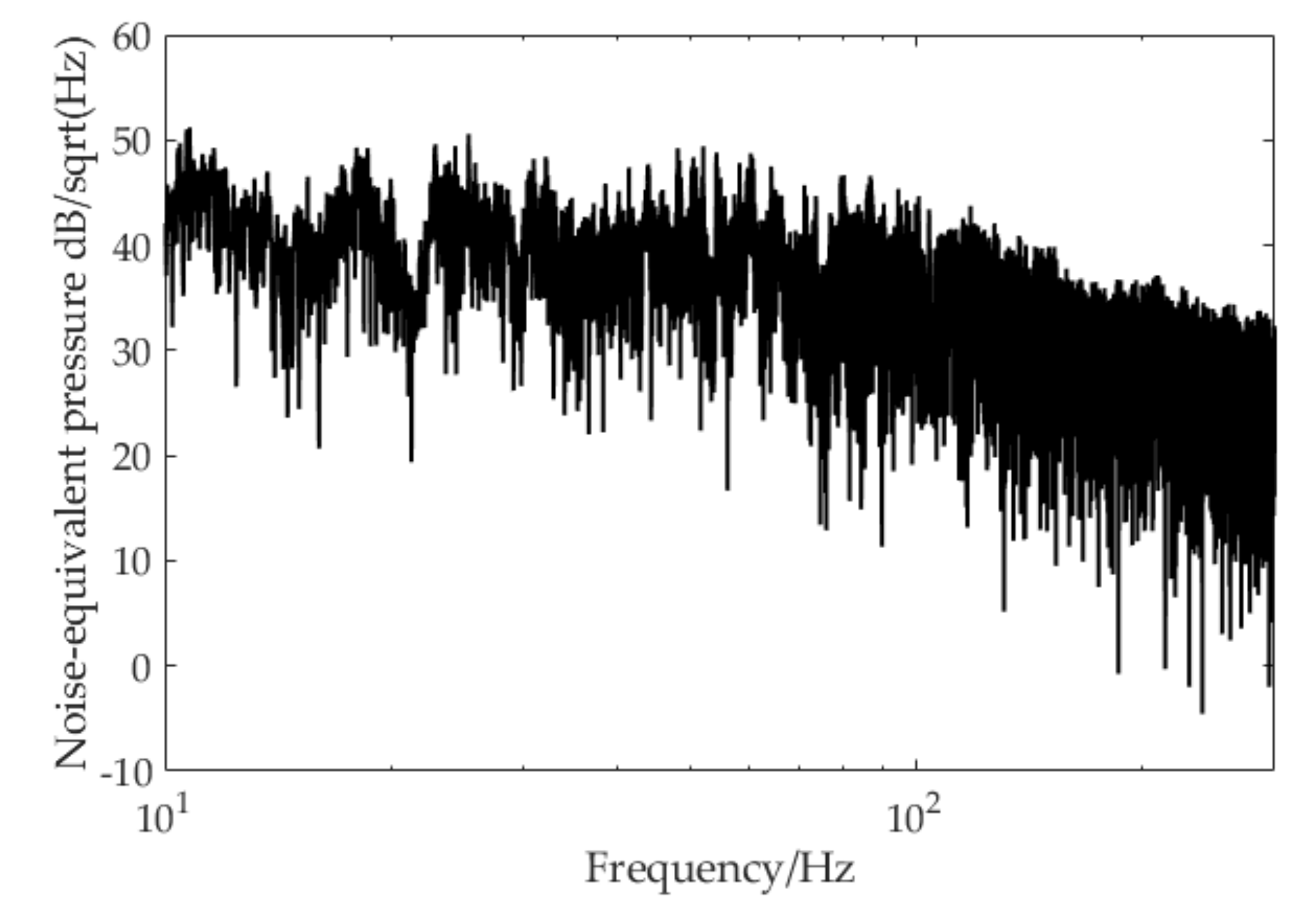
3.2. Experiment Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bucaro, J.A.; Dardy, H.D.; Carome, E.F. Fiber-optic hydrophone. J. Acoust. Soc. Am. 1977, 62, 1302–1304. [Google Scholar] [CrossRef]
- Yang, W.Z.; Jin, L.; Liang, Y.Z.; Ma, J.; Guan, B.O. Corrugated-Diaphragm Based Fiber Laser Hydrophone with Sub-100 μPa/Hz1/2 Resolution. Sensors 2017, 17, 6. [Google Scholar]
- Murray, M.J.; Davis, A.; Redding, B. Fiber-Wrapped Mandrel Microphone for Low-Noise Acoustic Measurements. J. Light. Technol. 2018, 36, 3205–3210. [Google Scholar] [CrossRef]
- Campopiano, S.; Cutolo, A.; Cusano, A.; Giordano, M.; Parente, G.; Lanza, G.; Laudati, A. Underwater Acoustic Sensors Based on Fiber Bragg Gratings. Sensors 2009, 9, 4446–4454. [Google Scholar] [CrossRef] [Green Version]
- Jin, M.; Ge, H.; Li, D.; Ni, C. Three-component homovibrational vector hydrophone based on fiber Bragg grating F-P interferometry. Appl. Opt. 2018, 57, 9195–9202. [Google Scholar] [CrossRef]
- Gong, Z.; Chen, K.; Yang, Y.; Zhou, X.; Yu, Q. Photoacoustic spectroscopy based multi-gas detection using high-sensitivity fiber-optic low-frequency acoustic sensor. Sens. Actuators B Chem. 2018, 260, 357–363. [Google Scholar] [CrossRef]
- Xia, Y.; Liu, J.Y.T.; Cui, X.; Li, J.; Chen, W.; Liu, C. Abnormal infrasound signals before 92 m ≧ 7.0 worldwide earthquakes during 2002–2008. J. Asian Earth Sci. 2011, 41, 434–441. [Google Scholar] [CrossRef]
- Egorov, E.; Shabalina, A.; Zaitsev, D.; Kurkov, S.; Gueorguiev, N. Frequency Response Stabilization and Comparative Studies of MET Hydrophone at Marine Seismic Exploration Systems. Sensors 2020, 20, 1944. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanimola, F.; Hill, D. Distributed fibre optic sensors for pipeline protection. J. Nat. Gas Sci. Eng. 2009, 1, 134–143. [Google Scholar] [CrossRef]
- Luo, Z.; Yang, Y.; Wang, Z.; Yu, M.; Wu, C.; Chang, T.; Wu, P.; Cui, H.-L. Low-frequency fiber optic hydrophone based on weak value amplification. Opt. Express 2020, 28, 25935. [Google Scholar] [CrossRef]
- Xu, S.; Huang, H.; Cai, W.; Zhong, Y.; Li, D.; Chen, X.; Zhang, J. Compact, low-cost, and highly sensitive optical fiber hydrophone based on incident angle sensing. Appl. Opt. 2019, 58, 7774–7780. [Google Scholar] [CrossRef] [PubMed]
- Kirkendall, C.K.; Dandridge, A. Overview of high performance fibre-optic sensing. J. Phys. D Appl. Phys. 2004, 37, R197–R216. [Google Scholar] [CrossRef]
- Jan, C.; Jo, W.; Digonnet, M.; Solgaard, O. Photonic-Crystal-Based Fiber Hydrophone with Sub-100 μPa/√Hz Pressure Resolution. IEEE Photonics Technol. Lett. 2015, 28, 123–126. [Google Scholar] [CrossRef]
- Fan, P.; Yan, W.; Lu, P.; Zhang, W.; Zhang, W.; Fu, X.; Zhang, J. High Sensitivity Fiber-Optic Michelson Interferometric Low-Frequency Acoustic Sensor Based on a Gold Diaphragm. Opt. Express 2020, 28, 25238. [Google Scholar] [CrossRef] [PubMed]
- Lima, S.E.U.; Frazao, O.; Farias, R.G.; Araujo, F.M.; Ferreira, L.A.; Santos, J.L.; Miranda, V. Mandrel-Based Fiber-Optic Sensors for Acoustic Detection of Partial Discharges—A Proof of Concept. IEEE Trans. Power Deliv. 2010, 25, 2526–2534. [Google Scholar] [CrossRef]
- Ames, G.H.; Maguire, J.M. Miniaturized mandrel-based fiber optic hydrophone. J. Acoust. Soc. Am. 2007, 121, 1392–1395. [Google Scholar] [CrossRef]
- Fu, X.; Lu, P.; Zhang, J.; Qu, Z.; Zhang, W.; Li, Y.; Hu, P.; Yan, W.; Ni, W.; Liu, D.; et al. Micromachined extrinsic Fabry-Pérot cavity for low-frequency acoustic wave sensing. Opt. Express 2019, 27, 24300–24310. [Google Scholar] [CrossRef]
- Niu, S.; Hu, Y.; Hu, Z.; Luo, H. Fiber Fabry–Pérot Hydrophone Based on Push–Pull Structure and Differential Detection. IEEE Photon. Technol. Lett. 2011, 23, 1499–1501. [Google Scholar] [CrossRef]
- Rajesh, R.; Sreehari, C.V.; Praveen Kumar, N.; Awasthi, R.L.; Vivek, K.; Vishnu, M.B.; Santhanakrishnan, T.; Moosad, K.P.B.; Mathew, B. Air backed mandrel type fiber optic hydrophone with low noise floor. In Proceedings of the Light and Its Interactions with Matter, Kerala, India, 19–21 March 2014. [Google Scholar]
- Zhang, W.; Li, F.; Liu, Y. Theoretical Analysis of Acoustic Sensitivity of Fiber Optic Hydrophone with Multilayer Fiber Coils. Sens. Lett. 2012, 10, 1448–1451. [Google Scholar] [CrossRef]
- Waagaard, O.; Havsgard, G.; Wang, G. An investigation of the pressure-to-acceleration responsivity ratio of fiber-optic mandrel hydrophones. J. Light. Technol. 2001, 19, 994–1003. [Google Scholar] [CrossRef]
- Pawar, D.; Rao, C.N.; Choubey, R.K.; Kale, S.N. Mach-Zehnder interferometric photonic crystal fiber for low acoustic frequency detections. Appl. Phys. Lett. 2016, 108, 041912. [Google Scholar] [CrossRef]
- Gallego, D.; Rivera, H.L. High-sensitivity ultrasound interferometric single-mode polymer optical fiber sensors for biomedical applications. Opt. Lett. 2009, 34, 1807–1809. [Google Scholar] [CrossRef] [PubMed]
- Yin, K.; Zhang, M.; Ding, T.; Wang, L.; Jing, Z.; Liao, Y. An investigation of a fiber-optic air-backed mandrel hydrophone. Opt. Commun. 2008, 281, 94–101. [Google Scholar] [CrossRef]
- Fan, Q.S. Theoretical Mechanics, 1st ed.; Tsinghua University Press: Beijing, China, 2014; pp. 51–53. [Google Scholar]
- Lifshitz, E.; Kosevich, A.; Pitaevskii, L. Theory of Elasticity; Pergamon: Oxford, UK, 1986; pp. 38–86. [Google Scholar]
- Roselló-Mechó, X.; Delgado-Pinar, M.; Díez, A.; Andrés, M.V. Measurement of Pockels’ coefficients and demonstration of the anisotropy of the elasto-optic effect in optical fibers under axial strain. Opt. Lett. 2016, 41, 2934–2937. [Google Scholar] [CrossRef]
- Timoshenko, S. Theory of Plates and Shells, 2nd ed.; McGraw-Hill Book Co.: Singapore, 1959; pp. 2–20. [Google Scholar]




| Property. | Value |
|---|---|
| Refractive index of fiber | = 1.45 |
| Number of fiber turns | = 400 |
| Pockels’ coefficients of fiber | = 0.116, = 0.255 |
| Poisson’s ratio of fiber | = 0.17 |
| Wavelength | = 1550 nm |
| Sound pressure level | 0 dB re 1V/μPa |
| Acoustic signal frequency range | 10–300 Hz |
| Young’s modulus of equivalent sensing layer | = 4GPa |
| Poisson’s ratio of equivalent sensing layer | = 0.45 |
| Thickness of equivalent sensing layer | = 2.5 mm |
| Inner radius of mandrel type | = 63.5 mm |
| Outer radius of mandrel type | = 66 mm |
| Deformation radius of mandrel type | = 64.5 mm |
| Width of cuboid type sensing layer | = 100 mm |
| Length of cuboid type sensing layer | = 140 mm |
| Cylinder skeleton radius of cuboid type | = 20 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Pei, Y.; Ye, L.; Song, K. High-Sensitivity Cuboid Interferometric Fiber-Optic Hydrophone Based on Planar Rectangular Film Sensing. Sensors 2020, 20, 6422. https://doi.org/10.3390/s20226422
Wang W, Pei Y, Ye L, Song K. High-Sensitivity Cuboid Interferometric Fiber-Optic Hydrophone Based on Planar Rectangular Film Sensing. Sensors. 2020; 20(22):6422. https://doi.org/10.3390/s20226422
Chicago/Turabian StyleWang, Wenrui, Yeye Pei, Lingyun Ye, and Kaichen Song. 2020. "High-Sensitivity Cuboid Interferometric Fiber-Optic Hydrophone Based on Planar Rectangular Film Sensing" Sensors 20, no. 22: 6422. https://doi.org/10.3390/s20226422




