Performance Analysis of Cognitive Relay-Assisted Ambient Backscatter with MRC over Nakagami-m Fading Channels
Abstract
:1. Introduction
- The AmBC and SWIPT improve performance of distance user in cognitive radio network, and this paper studies ability of the relay node to concurrently perform both SWIPT and AmBC operations.
- Since the proposed network benefit by multiple antennas designed at the primary destination, a maximal ratio combining (MRC) mechanism is adopted at non-AmBC destination. For the evaluation of system performance, the impact of AmBC on two destinations is studied in two main metrics, such as outage probability and achievable throughput.
- For both the primary and secondary communications, we derive the closed-form formula of both the throughput and the outage probability. We verify theoretical computation via simulation results and also evaluate the effect of different system parameters on the system performance.
2. System Model
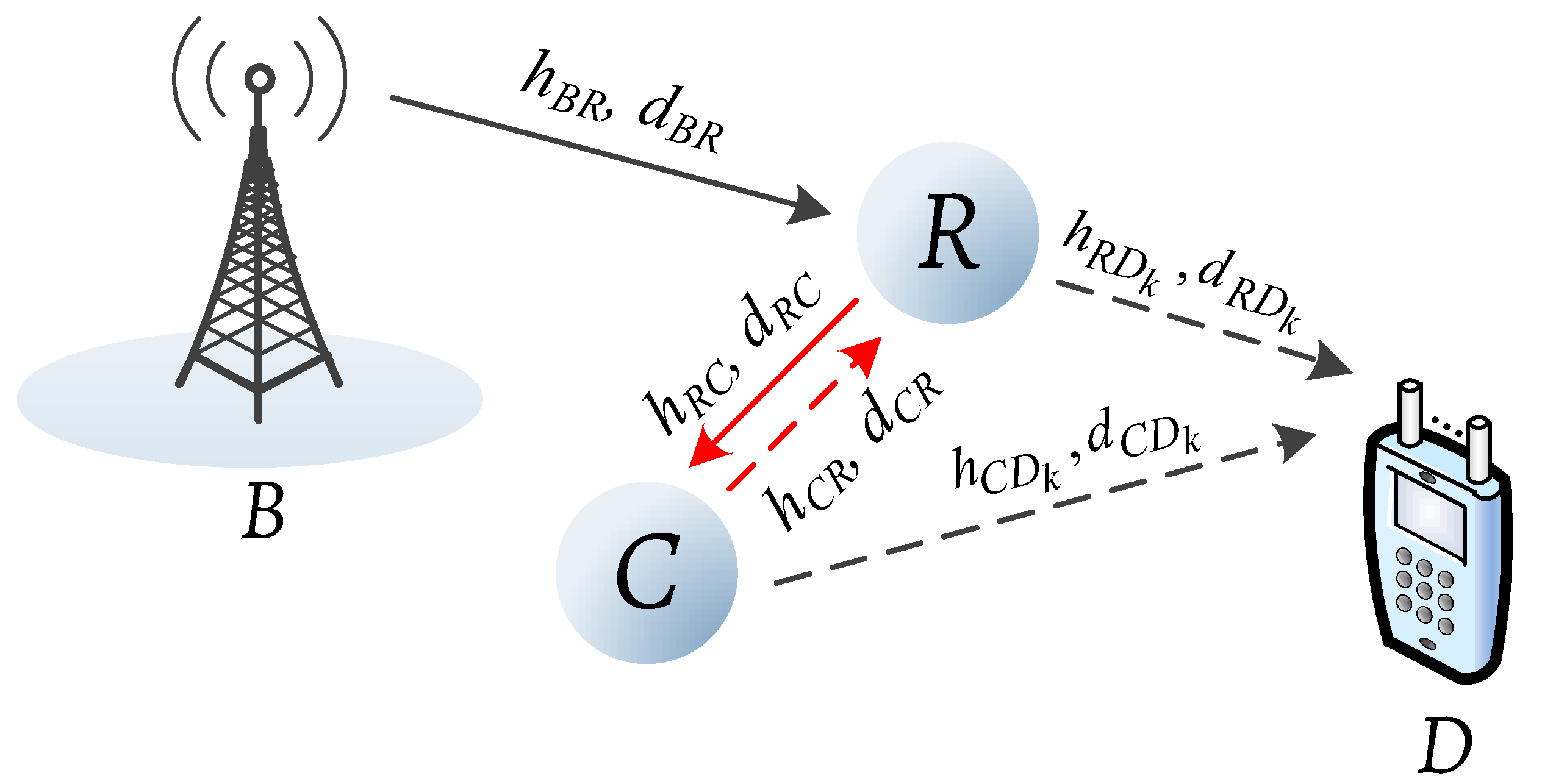
2.1. System Model
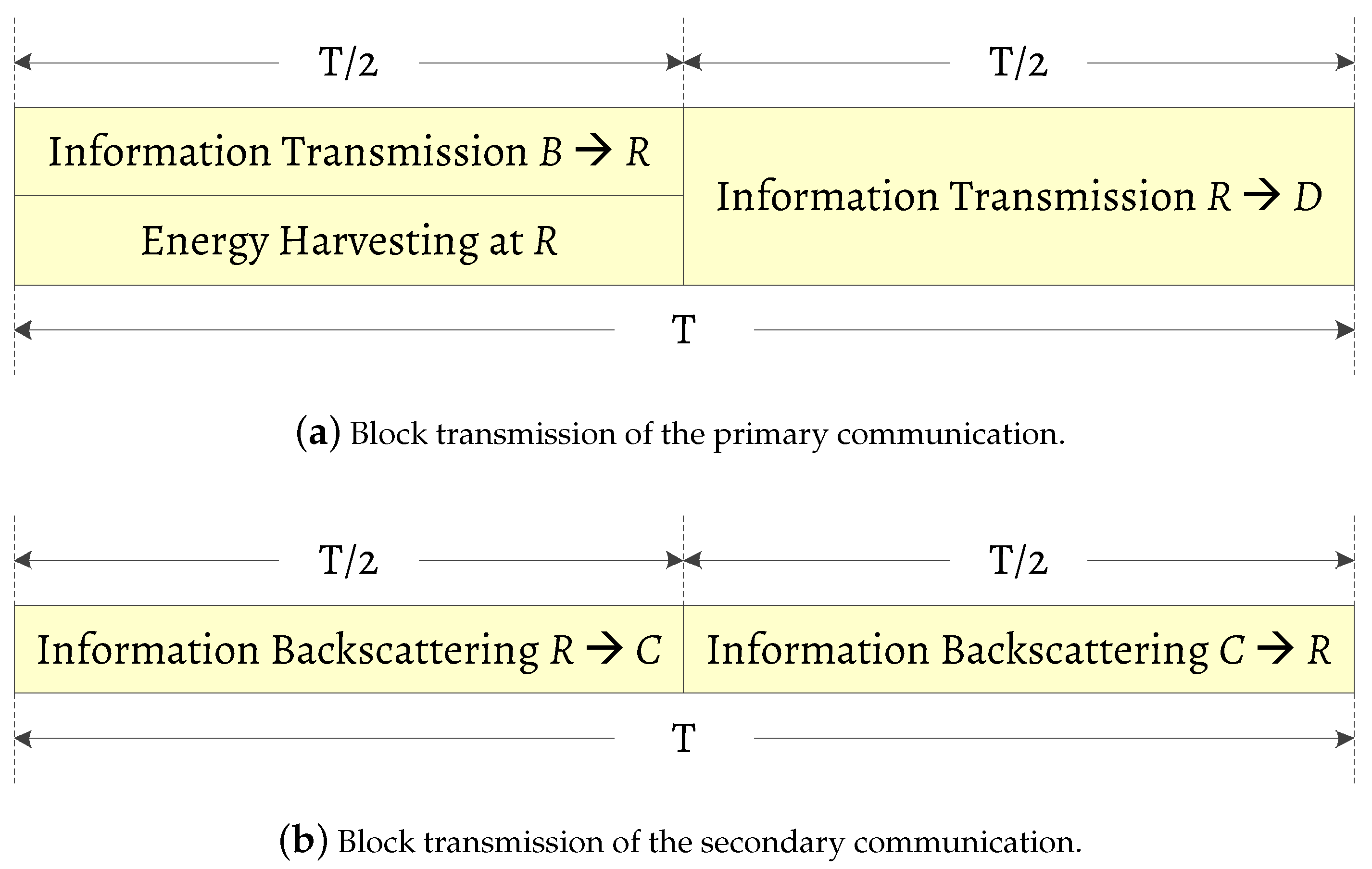
2.2. Energy Harvesting, Information Decoding, and Ambient Backscatter Operations
3. System Performance Analysis
3.1. Preliminary Results
3.2. Outage Probability Analysis
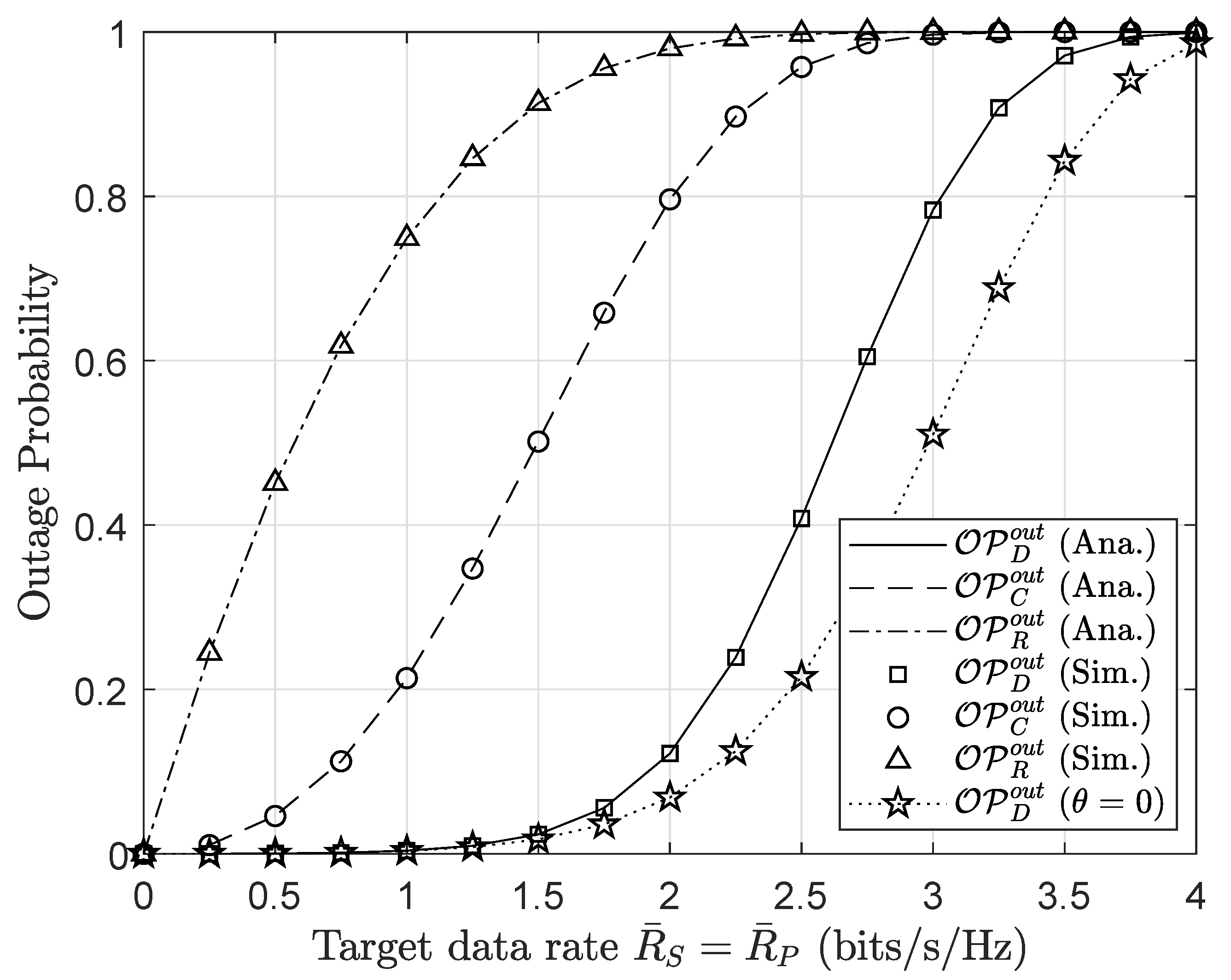
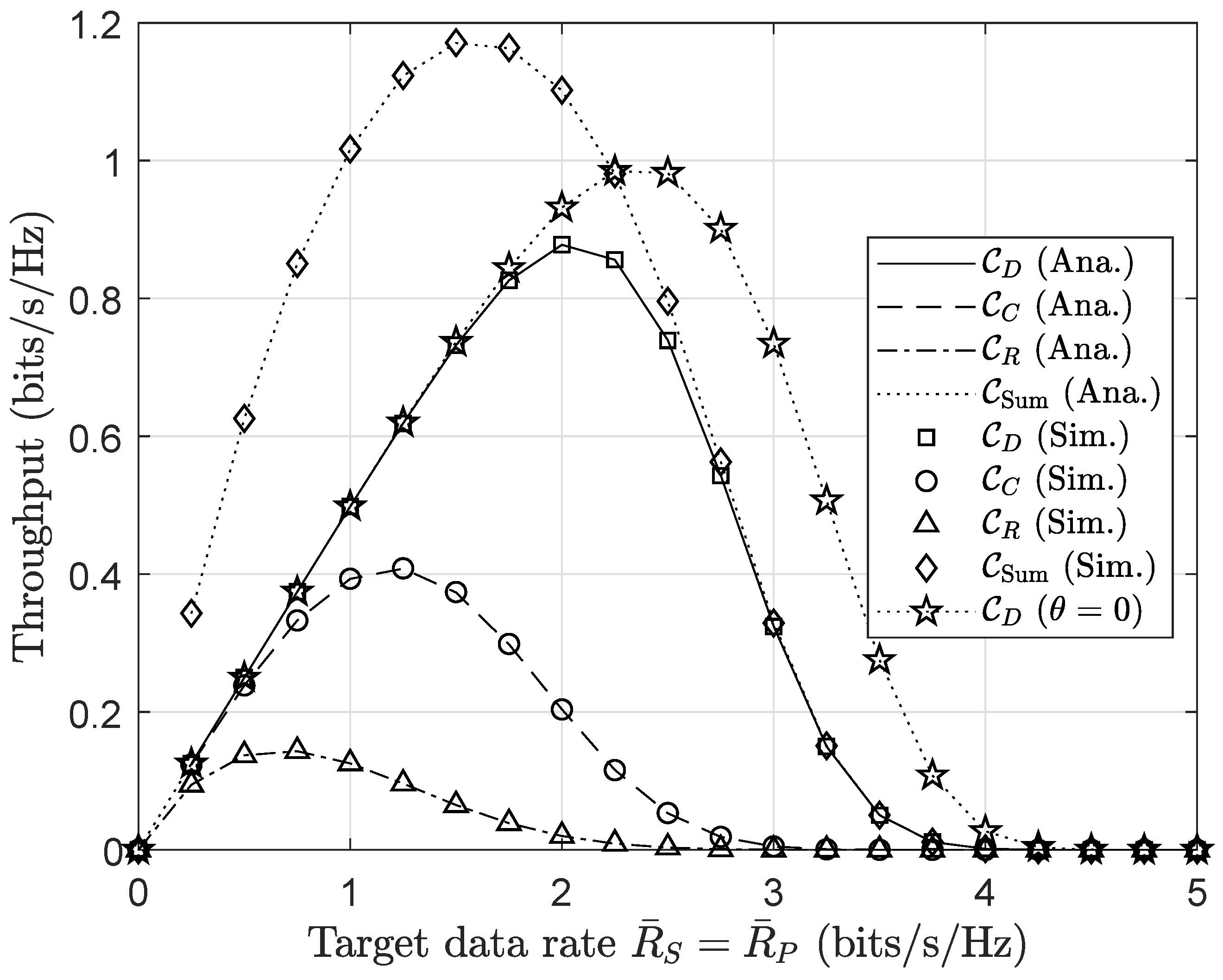
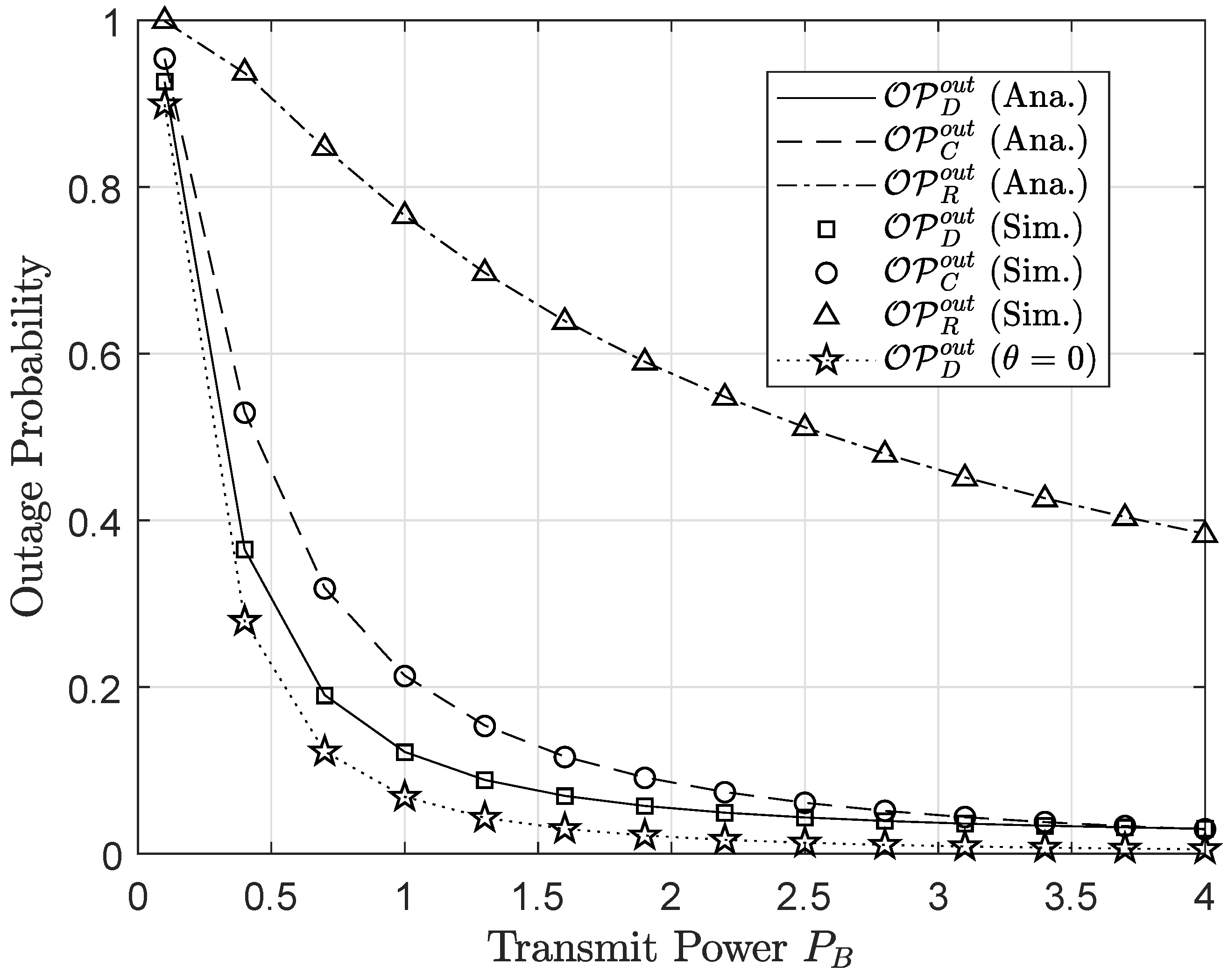
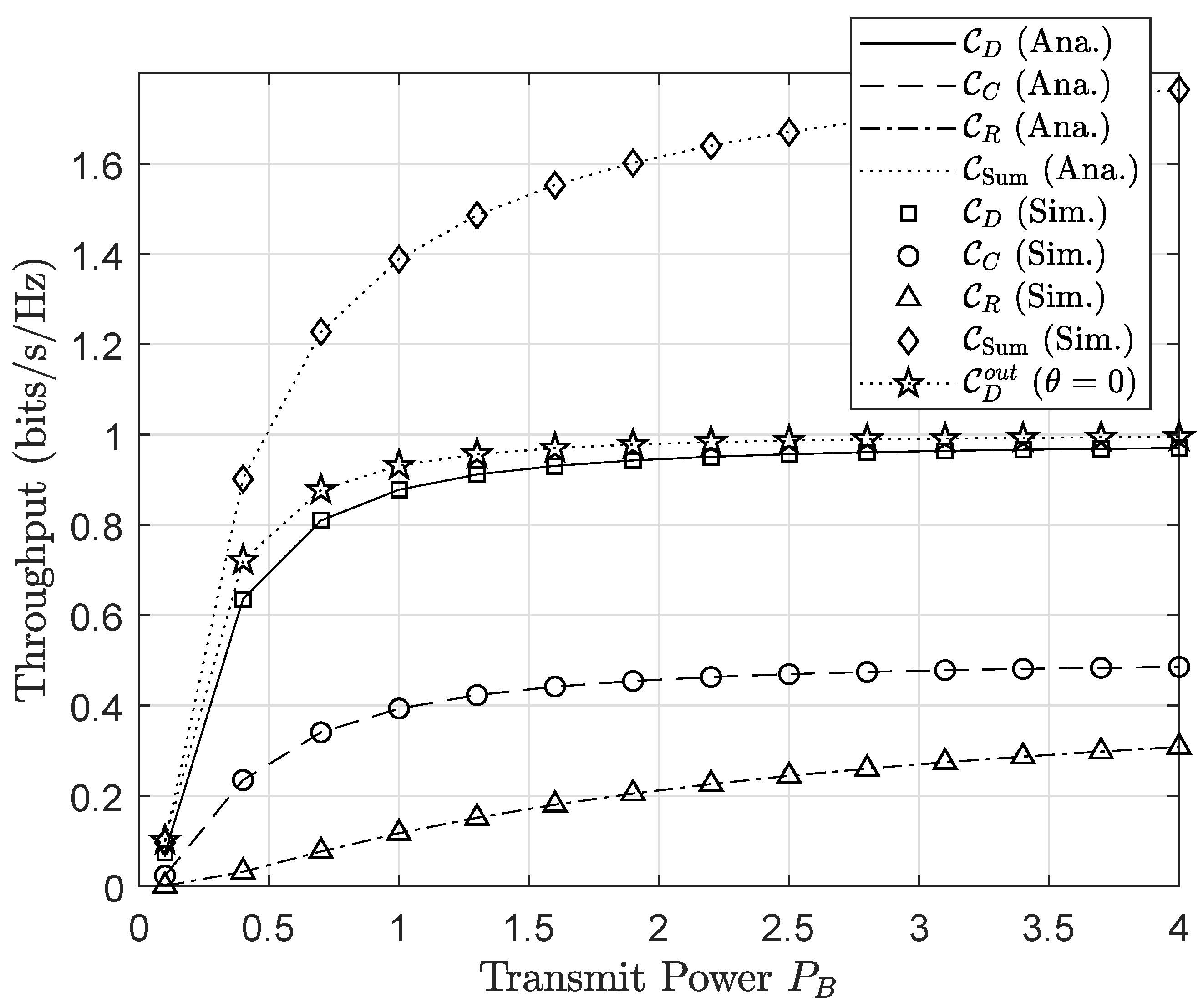
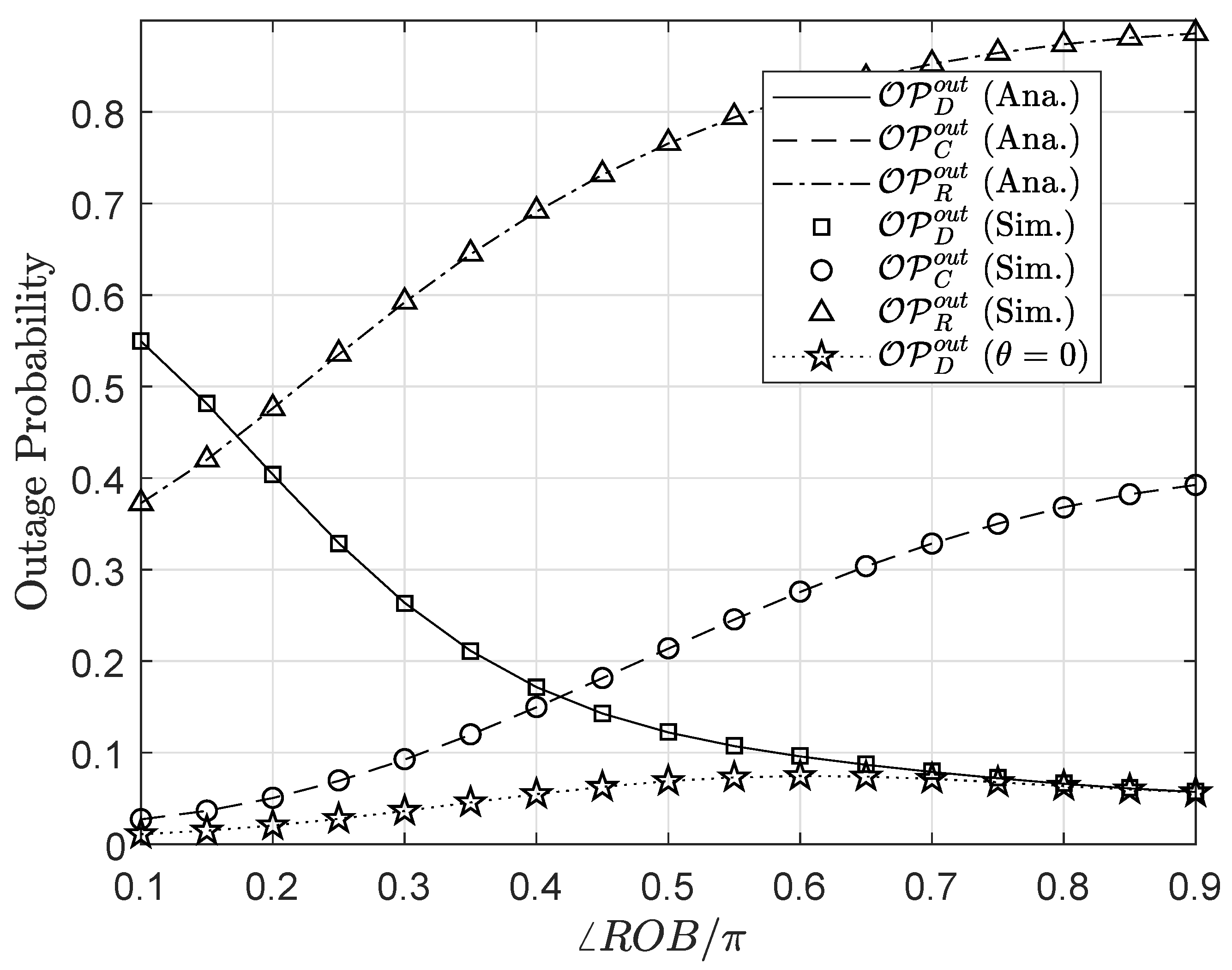
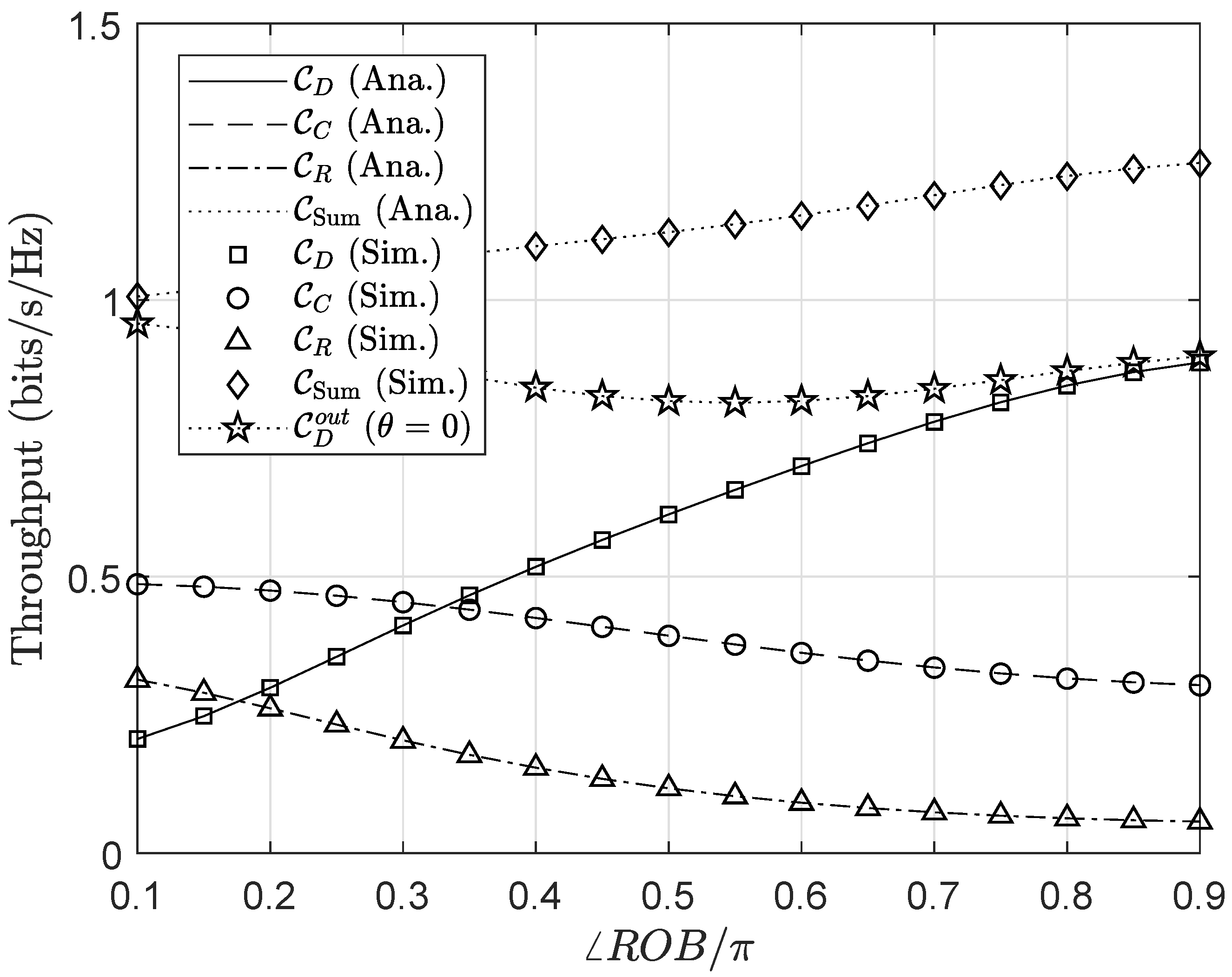
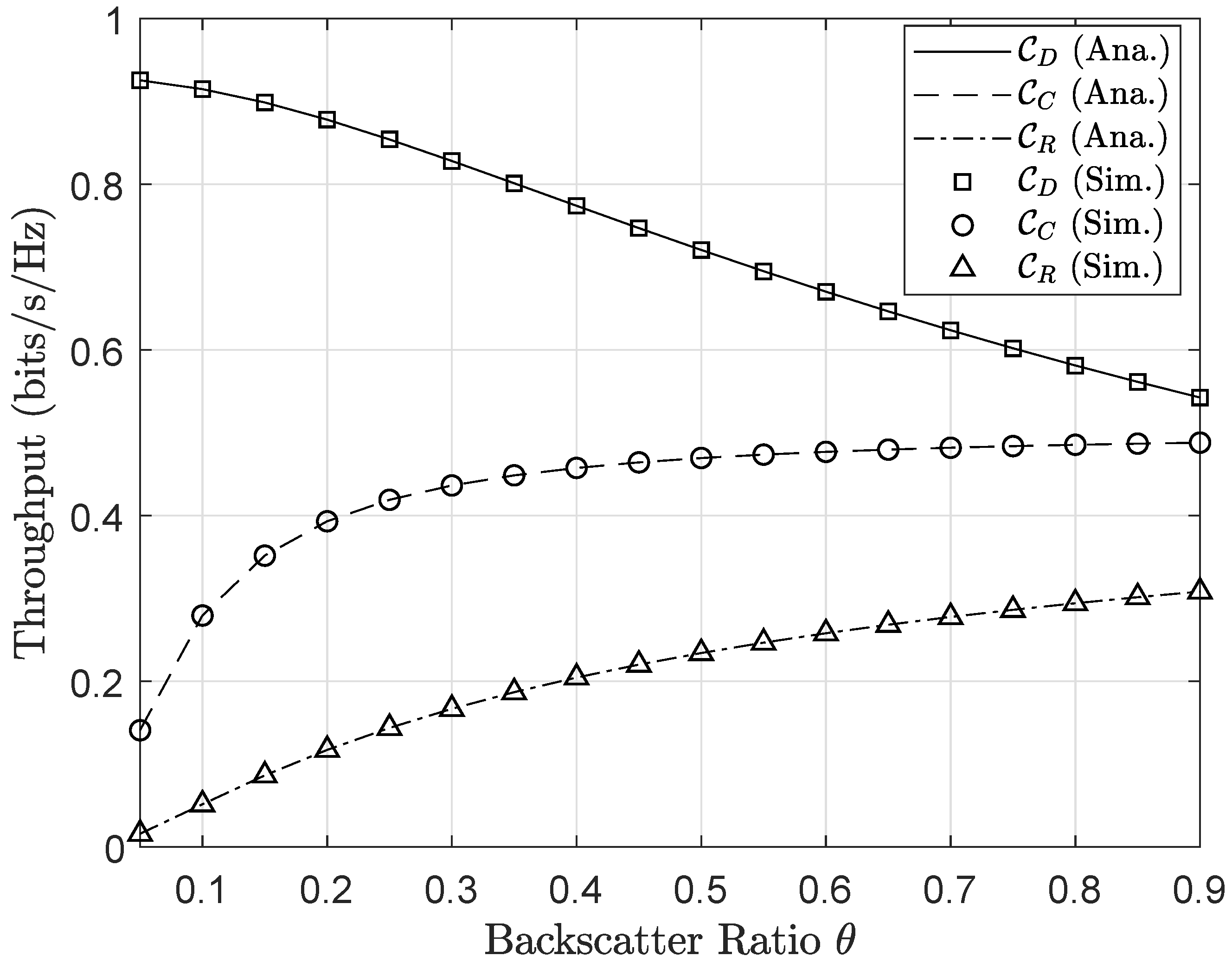
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of (17)
Appendix B. Proof of Proposition 1
Appendix C. Proof of Proposition 3
References
- Liu, V.; Parks, A.; Talla, V.; Gollakota, S.; Wetherall, D.; Smith, J.R. Ambient backscatter: Wireless communication out of thin air. In Proceedings of the ACM SIGCOMM, Hong Kong, China, 12–16 August 2013; Volume 43, pp. 39–50. [Google Scholar]
- Zhang, L.; Liang, Y.-C.; Xiao, M. Spectrum sharing for Internet of Things: A survey. arXiv 2018, arXiv:1810.04408. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Liang, P.P.; Huang, Y.-D.; Pei, Y.; Liang, Y.-C. Label assisted transmission for short packet communications: A machine learning approach. IEEE Trans. Veh. Technol. 2018, 67, 8846–8859. [Google Scholar] [CrossRef]
- Kang, X.; Liang, Y.-C.; Yang, J. Riding on the primary: A new spectrum sharing paradigm for wireless-powered IoT devices. IEEE Trans. Wireless Commun. 2018, 17, 6335–6347. [Google Scholar] [CrossRef]
- Darsena, D.; Gelli, G.; Verde, F. Modeling and performance analysis of wireless networks with ambient backscatter devices. IEEE Trans. Commun. 2017, 65, 1797–1814. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, Q.; Liang, Y.-C. Cooperative ambient backscatter communications for green Internet-of-Things. IEEE Internet Things J. 2018, 5, 1116–1130. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Jiang, H.; Niyato, D.; Kim, D.I.; Han, Z. Wireless-Powered Device-to-Device Communications With Ambient Backscattering: Performance Modeling and Analysis. IEEE Trans. Wirel. Commun. 2018, 17, 1528–1544. [Google Scholar] [CrossRef]
- Lu, X.; Jiang, H.; Niyato, D.; Kim, D.I.; Wang, P. Analysis of Wireless-Powered Device-to-Device Communications with Ambient Backscattering. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–6. [Google Scholar]
- Huynh, N.V.; Hoang, D.T.; Lu, X.; Niyato, D.; Wang, P.; Kim, D.I. Ambient Backscatter Communications: A Contemporary Survey. IEEE Commun. Surv. Tutor. 2018, 20, 2889–2922. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Wang, G.; Fan, R.; Fan, L.; Atapattu, S. Ambient Backscatter Communication Systems: Capacity and Outage Performance Analysis. IEEE Access 2018, 6, 22695–22704. [Google Scholar] [CrossRef]
- Do, D.T. Power Switching Protocol for Two-way Relaying Network under Hardware Impairments. Radioengineering 2015, 24, 765–771. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Do, D.T. A Tractable Approach to Analyze the Energy-Aware Two-way Relaying Networks in Presence of Co-channel Interference. Eurasip J. Wirel. Commun. Netw. 2016, 2016, 271. [Google Scholar]
- Do, D.-T.; Nguyen, M.-S.V. Device-to-device transmission modes in NOMA network with and without Wireless Power Transfer. Comput. Commun. 2019, 139, 67–77. [Google Scholar] [CrossRef]
- Do, D.-T. Optimal Throughput under Time Power Switching based Relaying Protocol in Energy Harvesting Cooperative Network. Wirel. Pers. Commun. 2016, 87, 551–564. [Google Scholar] [CrossRef]
- Varshney, L.R. Transporting Information and Energy Simultaneously. In Proceedings of the IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1612–1616. [Google Scholar]
- Do, D.-T. Time Power Switching based Relaying Protocol in Energy Harvesting Mobile Node: Optimal Throughput Analysis. Mob. Inf. Syst. 2015, 2015, 769286. [Google Scholar] [CrossRef]
- Nguyen, T.-L.; Do, D.-T. Power Allocation Schemes for Wireless Powered NOMA Systems with Imperfect CSI: System model and performance analysis. Int. J. Commun. Syst. 2018, 31, e3789. [Google Scholar] [CrossRef]
- Nguyen, H.-S.; Bui, A.-H.; Do, D.-T.; Voznak, M. Imperfect Channel State Information of AF and DF Energy Harvesting Cooperative Networks. China Commun. 2016, 13, 11–19. [Google Scholar] [CrossRef]
- Nasir, A.; Zhou, X.; Durrani, S.; Kennedy, R. Relaying protocols for wireless energy harvesting and information processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef] [Green Version]
- Do, D.-T. Energy-aware two-way relaying networks under imperfect hardware: Optimal throughput design and analysis. Telecommun. Syst. 2016, 62, 449–459. [Google Scholar] [CrossRef]
- Zhai, C.; Liu, J.; Zheng, L. Relay-Based Spectrum Sharing With Secondary Users Powered by Wireless Energy Harvesting. IEEE Trans. Commun. 2016, 64, 1875–1887. [Google Scholar]
- Kim, S.H.; Kim, D.I. Hybrid Backscatter Communication for Wireless-Powered Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2017, 16, 6557–6570. [Google Scholar] [CrossRef]
- Liu, T.; Qu, X.; Tan, W.; Cheng, Y. An Energy Efficient Cooperative Communication Scheme in Ambient RF Powered Sensor Networks. IEEE Access 2019, 7, 86545–86554. [Google Scholar] [CrossRef]
- Yang, G.; Yuan, D.; Liang, Y.; Zhang, R.; Leung, V.C.M. Optimal Resource Allocation in Full-Duplex Ambient Backscatter Communication Networks for Wireless-Powered IoT. IEEE Internet Things J. 2019, 6, 2612–2625. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Zhu, K.; Wang, R.; Gong, S. Performance analysis of ambient backscatter communications in RF-powered cognitive radio networks. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Le, C.-B.; Do, D.-T. On outage performance of backscatter NOMA relaying systems equipping with multiple antennas. IET Electron. Lett. 2019, 55, 1066–1067. [Google Scholar] [CrossRef]
- Xiao, S.; Guo, H.; Liang, Y. Resource Allocation for Full-Duplex-Enabled Cognitive Backscatter Networks. IEEE Trans. Wirel. Commun. 2019, 18, 3222–3235. [Google Scholar] [CrossRef]
- Kishore, R.; Gurugopinath, S.; Sofotasios, P.C.; Muhaidat, S.; Al-Dhahir, N. Opportunistic Ambient Backscatter Communication in RF-Powered Cognitive Radio Networks. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 413–426. [Google Scholar] [CrossRef] [Green Version]
- Hoang, D.T.; Niyato, D.; Wang, P.; Kim, D.I.; Han, Z. The tradeoff analysis in RF-powered backscatter cognitive radio networks. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Guo, H.; Long, R.; Liang, Y. Cognitive Backscatter Network: A Spectrum Sharing Paradigm for Passive IoT. IEEE Wirel. Commun. Lett. 2019, 8, 1423–1426. [Google Scholar] [CrossRef]
- Shah, S.T.; Choi, K.W.; Lee, T.; Chung, M.Y. Outage Probability and Throughput Analysis of SWIPT Enabled Cognitive Relay Network With Ambient Backscatter. IEEE Internet Things J. 2018, 5, 3198–3208. [Google Scholar] [CrossRef]
- Morales-Jimenez, D.; Paris, J.F.; Lozano, A. Outage Probability Analysis for MRC in η-μ Fading Channels with Co-Channel Interference. IEEE Commun. Lett. 2012, 16, 674–677. [Google Scholar] [CrossRef]
- Wang, G.; Yue, D.; Feng, B. Outage Probability Analysis of MRC with Unequal Power Nakagami-M Co-Channel Interference and AWGN. In Proceedings of the 2006 First International Conference on Communications and Networking in China, Beijing, China, 25–27 October 2006; pp. 1–4. [Google Scholar]
- Aruna, G. Performance analysis of MRC receiver with channel estimation error and co-channel interference in Nakagami-m fading channel. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 5 November 2014; pp. 1–4. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series and Products, 6th ed.; Academic Press: New York, NY, USA, 2000. [Google Scholar]




| AmB | Ambient Backscatter |
| AmBC | Ambient Backscatter Communication |
| AP | Access Point |
| AWGN | Additive White Gaussian Noise |
| BD | Backscatter Device |
| CDF | Cumulative Distribution Function |
| CR | Cognitive Radio |
| CU | Cognitive User |
| DF | Decode-and-Forward |
| EH | Energy Harvesting |
| IoT | Internet-of-Things |
| IT | Information Transmission |
| MRC | Maximal Ratio Combining |
| OFDM | Orthogonal Frequency Division Multiplexing |
| Probability Density Function | |
| PS | Power-Splitting |
| PU | Primary User |
| RF | Radio Frequency |
| RV | Random Variable |
| SINR | Signal-to-Interference-plus-Noise Ratio |
| SNR | Signal-to-Noise Ratio |
| SWIPT | Simultaneous Wireless Information and Power Transfer |
| TPS | Time Power Switching |
| TS | Time Switching |
| WPC | Wireless Powered Communication |
| Parameter | Meaning | Default Value |
|---|---|---|
| Transmit power of node B | 1 W | |
| EH efficiency coefficient | 0.8 | |
| Backscatter ratio | 0.2 | |
| AWGN power | W | |
| K | Number of antennas at node D | 4 |
| Pathloss exponent | 2 | |
| The angle at the vertex O in Figure 3 | 0.5 (rad) | |
| Distance between node B and node D | 4 (m) | |
| Distance between node R and node C | 2 (m) | |
| Shape factor of the channel between R and C | 3 | |
| Shape factor of the channel between B and R | 2 | |
| Shape factor of the channel between R and D | 2 | |
| Shape factor of the channel between C and each antenna of D | 2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do, D.-T.; Nguyen, T.-L.; Lee, B.M. Performance Analysis of Cognitive Relay-Assisted Ambient Backscatter with MRC over Nakagami-m Fading Channels. Sensors 2020, 20, 3447. https://doi.org/10.3390/s20123447
Do D-T, Nguyen T-L, Lee BM. Performance Analysis of Cognitive Relay-Assisted Ambient Backscatter with MRC over Nakagami-m Fading Channels. Sensors. 2020; 20(12):3447. https://doi.org/10.3390/s20123447
Chicago/Turabian StyleDo, Dinh-Thuan, Thanh-Luan Nguyen, and Byung Moo Lee. 2020. "Performance Analysis of Cognitive Relay-Assisted Ambient Backscatter with MRC over Nakagami-m Fading Channels" Sensors 20, no. 12: 3447. https://doi.org/10.3390/s20123447






