Evaluation on Phantoms of the Feasibility of a Smart Bra to Detect Breast Cancer in Young Adults
Abstract
:1. Introduction
- -
- C (xc, yc) (center of the Cole–Cole circle, r: radius of the Cole–Cole circle)
- -
- Rc, Xc, and Fc data, known as characteristic curvature data (characteristic resistance, characteristic reactance and characteristic frequency)
- -
- Ri (modelled resistance of the intracellular zone in ohms)
- -
- Alpha α (the phase angle in degrees at the characteristic frequency)
- -
- Tau τ (the ion relaxation time in µs)where Cm is the capacity of the cell membrane in Farad, as follows:
- -
- Stage/type 1: the breast is almost entirely fat (homogeneous fat) (less than 25% of the mammary gland).
- -
- Stage/type 2: there are scattered fibro-glandular opacities (heterogeneous fat) (approximately 25 to 50% of the gland).
- -
- Stage/type 3: Breast tissue is dense and heterogeneous (heterogeneous density), making it difficult to detect small masses (approximately 51% to 75% of the gland).
- -
- Stage/type 4: the breast tissue is extremely dense (homogeneous density). This can reduce the sensitivity of mammography (>75% of the gland).
- -
- Early diagnosis at any age using non-ionizing technologies,
- -
- Limitation of interval cancers as well as overdiagnosis by daily monitoring and considering physiological “noise”.
2. Materials and Methods
2.1. The Phantoms
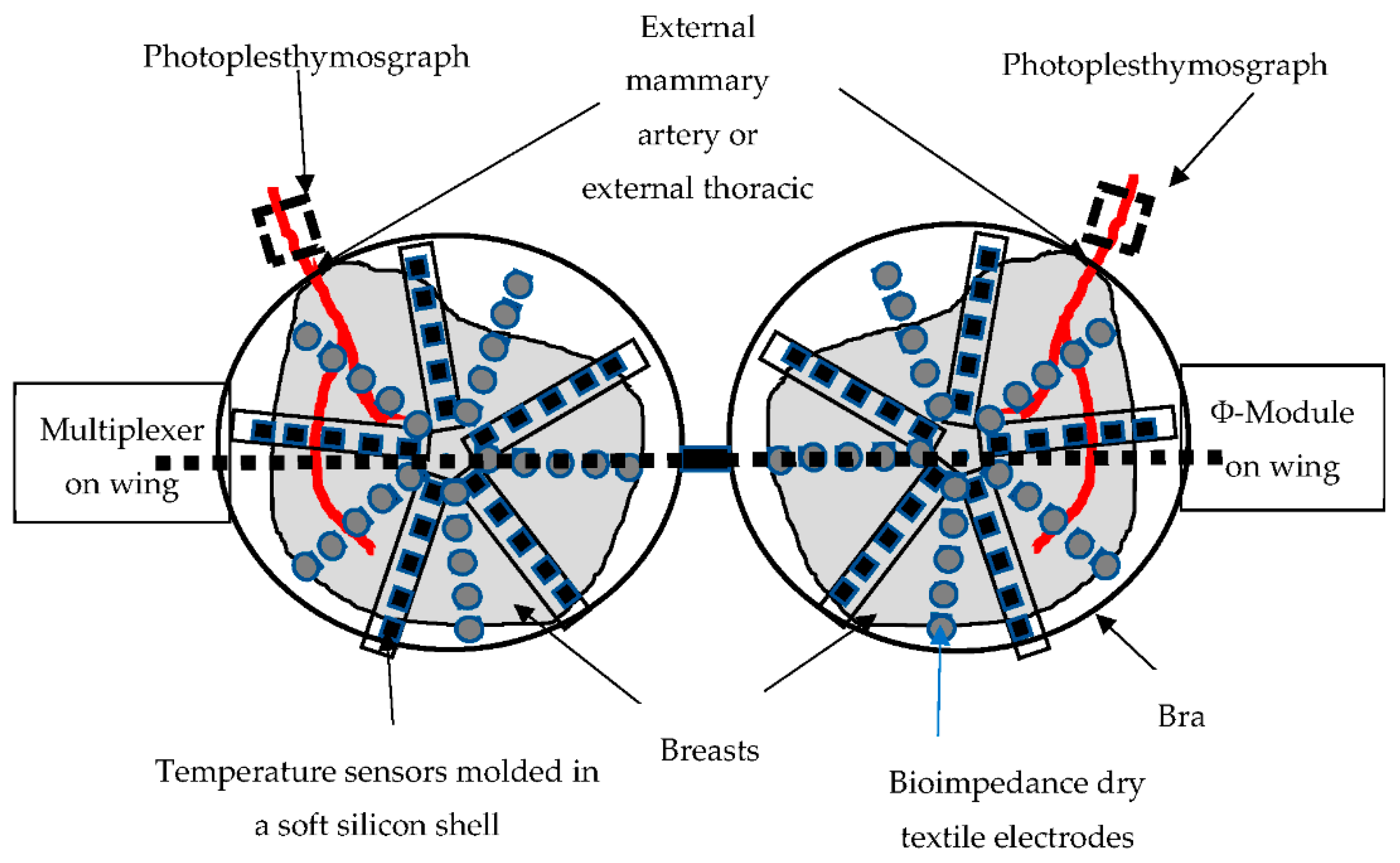
2.2. The Device
2.3. The Algorithms
3. Results
3.1. Repeatability of Measurements
3.2. Raw Data
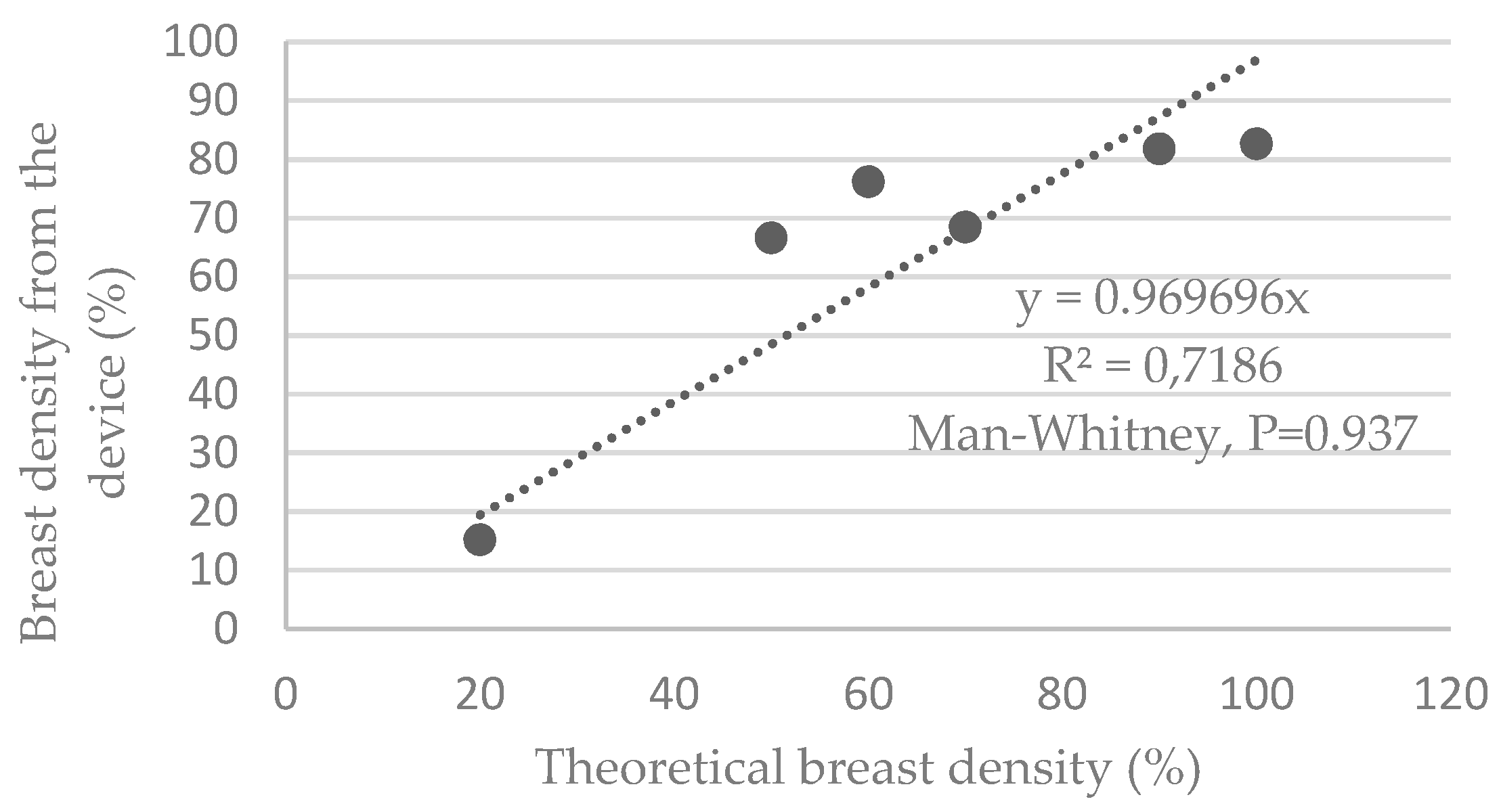
3.3. Estimation of Breast Density Using the Device
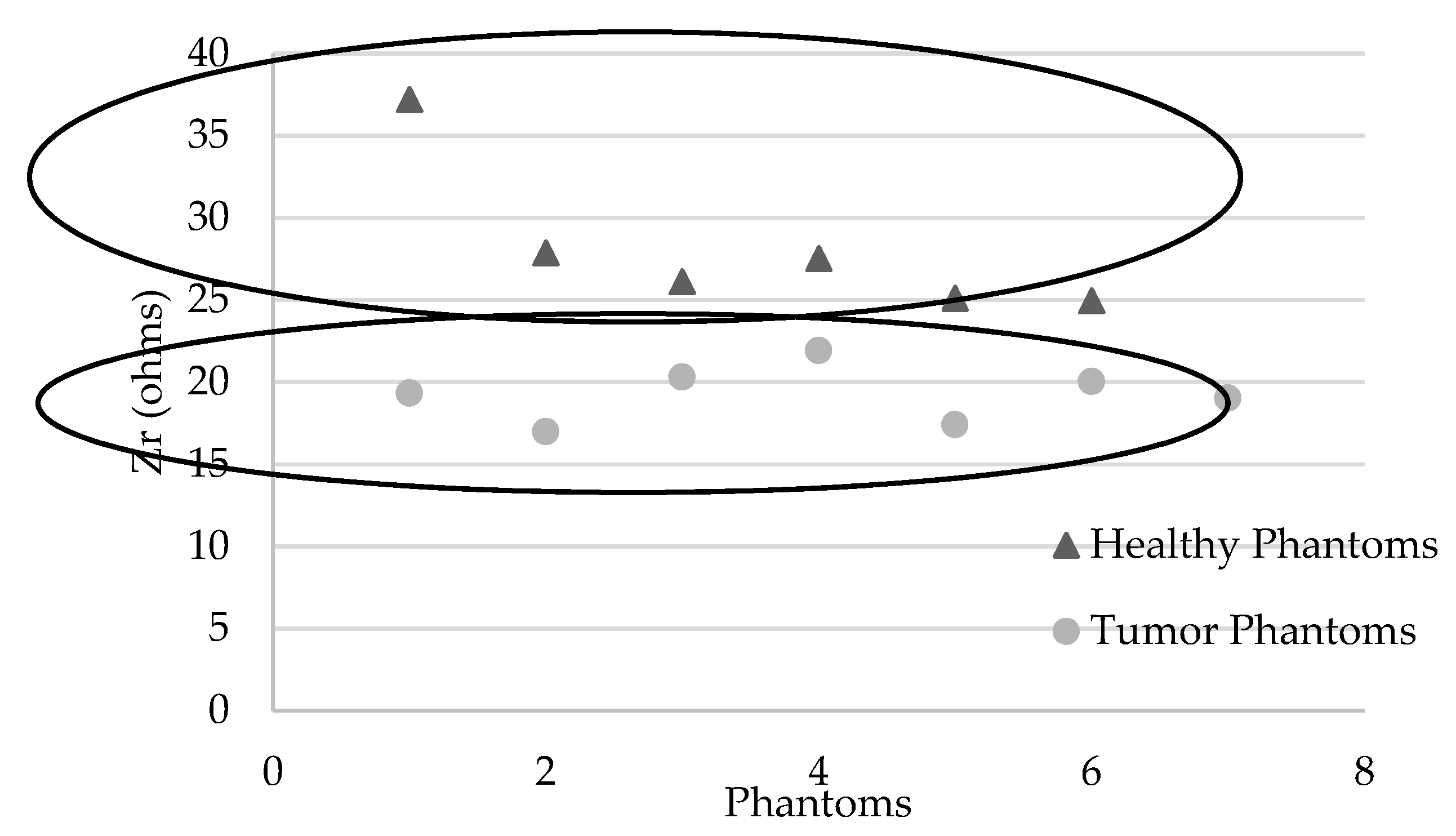
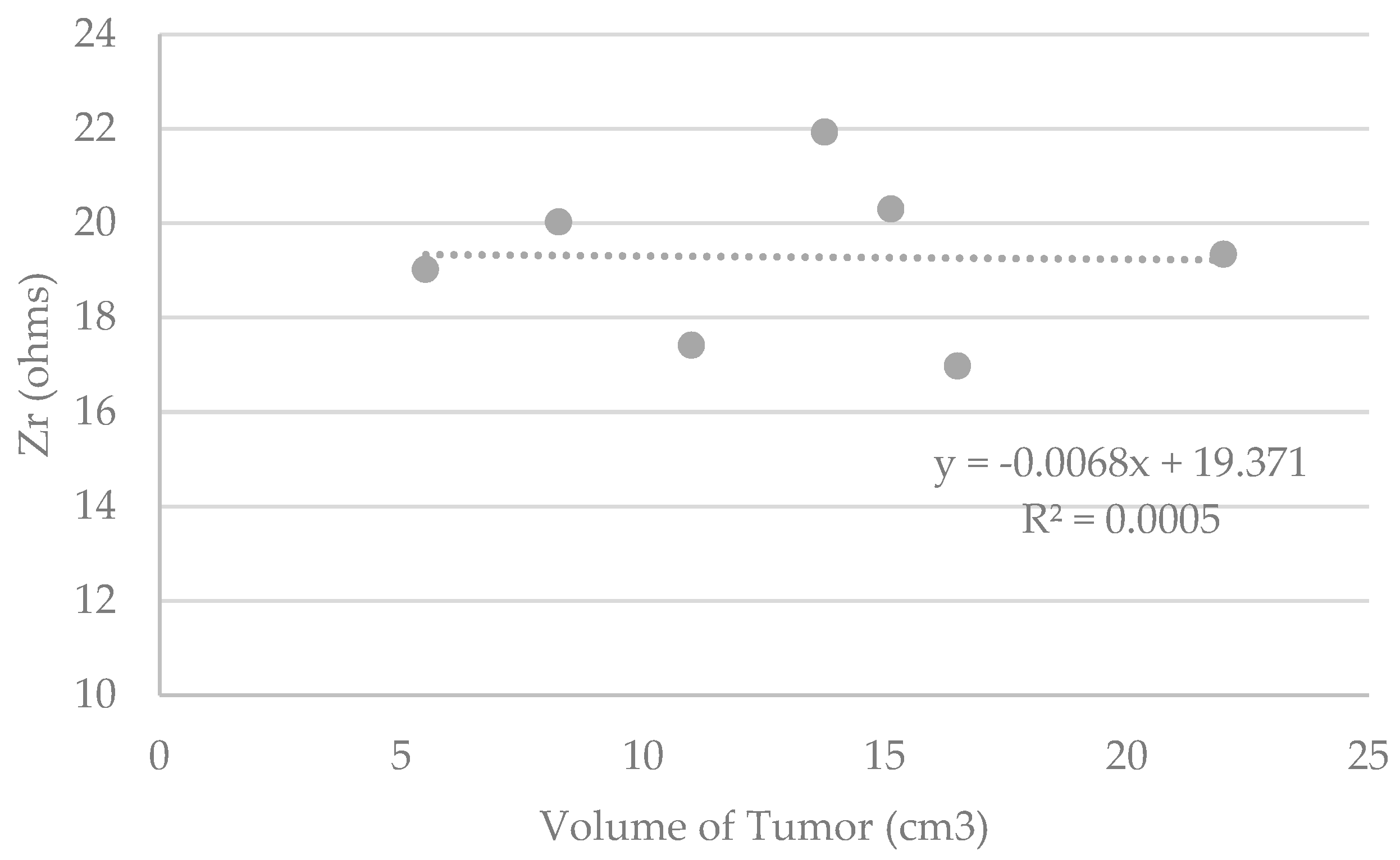
3.4. Detection of the Presence of a Breast Tumor Using the Device
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Conflicts of Interest
References
- InCa. Les Cancers en France; Institut National du Cancer: Paris, France, 2014. [Google Scholar]
- Villet, R.; Séradour, B. 35 ans de Sénologie: Acquis & Limites. In Proceedings of the Conférence de presse en amont des 34èmes journées de la Société française de sénologie et de pathologies mammaires, Paris, France, 18 September 2012. [Google Scholar]
- Ng, E.Y.; Sree, S.V.; Kaw, G. The Use of electrical characteristics for breast cancer detection: A perspective review. Technol. Cancer Res. Treat. 2008, 7, 295–308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, Z. Bioimpedance spectroscopy can precisely discrimate human breast carcinoma from benign tumors. Medecine 2017, 96, e5970. [Google Scholar] [CrossRef] [PubMed]
- Gupta, D.; Lis, C.G.; Dahlk, S.L.; Vashi, P.G.; Grutsch, J.F. Bioelectrical impedance phase angle as a prognostic indicator in breast cancer. BMC Cancer 2008, 8, 249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stojadinovic, A.; Nissan, A.; Gallimidi, Z.; Lenington, S.; Logan, W.; Zuley, M.; Yeshaya, A.; Shriver, C.D. Electrical Impedance Scanning for the early detection of breast cancer in Young Women: Preliminary results of a multicenter prospective clinical trial. J. Clin. Oncol. 2005, 23, 2703–2715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jossinet, J.; Schmitt, M. A review of parameters for the bioelectrical characterization of breast tissue. Ann. N. Y. Acad. Sci. 1999, 873, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Hope, T.; Iles, S.E. Technology review: The use of electrical impedance scanning in the detection of breast cancer. Breast Cancer Res. 2003, 6, 69. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreno, M.V. Etude de la Composition Corporelle par Impédancemétrie sur des Adultes et des Enfants Sains et Pathologiques. Ph.D. Thesis, University of Technology of Compiègne, Compiègne, France, 2007. [Google Scholar]
- Yang, Y.; Ni, W.; Sun, Q.; Wen, H.; Teng, Z. Improved Cole parameter extraction based on the least absolute deviation method. Physiol. Meas. 2013, 34, 1239–1252. [Google Scholar] [CrossRef] [PubMed]
- Estrela da Silva, J.; Marques de Sa, J.P.; Jossinet, J. Classification of breast tissue by electrical impedance spectroscopy. Med. Biol. Eng. Comput. 2000, 38, 26–30. [Google Scholar] [CrossRef] [PubMed]
- Boutet, G. La densité mammaire: Un facteur établi de risque de cancer du sein? J. Radiol. 2008, 8, 1140–1150. [Google Scholar] [CrossRef]
- Vachon, C.M.; Kuni, C.C.; Anderson, K. Association of mammographically defined percent breast density with epidemiologic risk factors for breast cancer (United States). Cancer Causes Control 2000, 11, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Chopier, J.; Gibeault, M.; Salem, C.; Marsault, C.; Nagara, I.T. Comment mesurer la densité mammaire? J. Radiol. 2008, 89, 1151–1155. [Google Scholar] [CrossRef]
- Swann, C.A.; Kopans, D.B.; Mc-Carta, K.A.; White, G.; Haw, D.A. Mammographic density and physical assessment of the breast. Am. J. Roentgenol. 1987, 148, 525–526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- White, E.; Velentgas, P.; Mandelson, M.T. Variation in mammographic breast density by time in menstrual cycle among women aged 40–49 years. J. Natl. Cancer Inst. 1998, 90, 906–910. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Renaud, R.; Gairard, B.; Schaffer, P.; Guldenfels, C.; Haehnel, P.; Dale, G. Europe against cancer: Breast cancer screening program in France. The ADEMAS program in Bas-Rhin. Eur. J. Cancer Prev. 1994, 3, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Roux, E. La Physiologie des Animaux de Laboratoire; INSERM U 885; University of Bordeaux 2: Bordeaux, France, 2017. [Google Scholar]
- Chimarra, M.K.; Hansen, R.; Marvik, R.; Langot, T. Multimodal Phantom of Liver Tissue. PLoS ONE 2013, 8, 1373–1378. [Google Scholar]
- Kao, T.-J.; Saulnier, G.J.; Isaacson, D.; Szabo, T.-L.; Newell, J.-C.; Versatile, A. High-Permittivity Phantom for EIT. IEEE Trans. Biomed. Eng. 2008, 55, 2601–2607. [Google Scholar]
- Onishi, T.; Uebayashi, S. Biological Tissue-Equivalent Phantoms Usable in Broadband Frequency Range. NTT DoCoMo Tech. J. 2006, 7, 61–65. [Google Scholar]
- Boscus, J. Transfert Électro-Osmotique en Milieu Poreux Déformable. Application au gel d’agar-agar. Ph.D. Thesis, University of Montpellier 2, Montpellier, France, 2005. [Google Scholar]
- Jossinet, J. Variability of impedivity in normal and pathological breast tissue. Med. Biol. Eng. Comput. 1996, 34, 346–350. [Google Scholar] [CrossRef]



| Classification | Incidental Studies RR[CI95] | Preliminary Studies RR[CI95] |
|---|---|---|
| Wolfe | ||
| N1 (Adipose Breast) | 1 | 1 |
| P1 (<25% Glandular Density) | 1.8 [1.4–2.2] | 1.3 [1–1.5] |
| P2 (>25% Glandular Density) | 3.1 [2.5–3.7] | 2 [1.3–3] |
| DY (Dysplastic Breast) | 4 [2.5–6.3] | 2.4 [2,3] |
| Density (%) | ||
| <5 | 1 | 1 |
| 5–24 | 1.8 [1.5–2.2] | 1.4 [1.1–1.8] |
| 25–49 | 2.1 [1.7–2.6] | 2.2 [1.8–2.8] |
| 50–74 | 2.9 [2.5–3.4] | 2.9 [2.3–3.8] |
| >75 | 4.6 [3.6–5.9] | 3.7 [2.7–5] |
| BI-RADS | ||
| 1 (<25% Glandular Density) | 1 | 1 |
| 2 (25–50% Glandular Density) | 2.2 [1.6–3] | 1.6 [0.9–2.8] |
| 3 (51–75% Glandular Density) | 3 [2.2–4.1] | 2.3 [1.3–4.3] |
| 4 (>75% Glandular Density) | 4 [2.8–5.7] | 4.5 [1.9–10.6] |
| Type | 50 Years Old | 67 Years Old |
|---|---|---|
| 1 | 14.5% | 28% |
| 2 | 43% | 54% |
| 3 | 38% | 16% |
| 4 | 5.6% | 1.2% |
| Tumor Fabrics | Tissue Surrounding the Tumor | Healthy Breast Tissue | |
|---|---|---|---|
| ⍴ (Ω.cm) | 250–500 | 125 | 1000 |
| Peripheral Tissues of the Tumor, Blue Color | Healthy Mammary Soft Tissues (Fibro-Glandular and Connective Tissue), Clear Color | Adipose Tissue, Yellow Color | |
|---|---|---|---|
| Composition | 4 g/L agarose 1 L demineralized water 10 g/L NaCl | 4 g/L agarose 1 L demineralized water 1 g/L NaCl | 4 g/L agarose 1 L demineralized water 0 g/L NaCl |
| “Breast Density” Phantoms F | % of Healthy Soft Tissue Equivalent to Breast Density (Fibro-Glandular and Connective Tissue) | % of Adipose Tissue |
|---|---|---|
| F1 | 20 | 80 |
| F2 (Breasts equivalent to those of healthy women in their 60s) | 50 | 50 |
| F3 | 60 | 40 |
| F4 | 70 | 30 |
| F5 | 90 | 10 |
| F6 (Theoretical breasts of maximum density, without fat tissue) | 100 | 0 |
| “Tumor” Phantoms F’ | Volume (cm3) of Tumor Phantom Randomly Integrated into a 100% Density Phantom % of Healthy Soft Tissue |
|---|---|
| F1′ | 22.0 |
| F2′ | 16.5 |
| F3′ | 15.1 |
| F4′ | 13.8 |
| F5′ | 11.0 |
| F6′ | 8.3 |
| F7′ | 5.5 |
| “Breast Density” Phantoms | F1 | F2 | F3 | F4 | F5 | F6 | |
|---|---|---|---|---|---|---|---|
| Coefficient of Variation (%) | 0.04 | 1.13 | 0.07 | 2.08 | 0.73 | 0.07 | |
| “Tumor” Phantoms | F1′ | F2′ | F3′ | F4′ | F5′ | F6′ | F7′ |
| Coefficient of Variation (%) | 0.15 | 0.15 | 0.26 | 0.29 | 0.12 | 0.23 | 0.10 |
| “Breast Density” Phantoms | F1 | F2 | F3 | F4 | F5 | F6 | |
|---|---|---|---|---|---|---|---|
| Zr (ohms) | 37.18 | 27.85 | 26.10 | 27.51 | 25.10 | 24.93 | |
| “Tumor” Phantoms | F1′ | F2′ | F3′ | F4′ | F5′ | F6′ | F7′ |
| Zr (ohms) | 19.33 | 16.97 | 20.30 | 21.92 | 17.41 | 20.02 | 19.02 |
| 100% Low-Density Breasts with Tumor in Random Position (from 5 to 22 cm3) | 100% Density Healthy Breasts | Healthy Breasts (Density Varies from 20% to 100%) | |
|---|---|---|---|
| Zr Mean ± SD (Ohms) | 19.3 ± 1.7 | 24.9 ± 2.9 | 28.1 ± 4.6 |
| Difference Mean ± SD (%) | −22.7 ± 6.8** | −30.6 ± 4.2 *** |
| Tumor Risk Score | |
|---|---|
| F6′ | 100% |
| F7′ | 100% |
| F8′ | 100% |
| F1 | 0% |
| F2 | 0% |
| F3 | 0% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, M.-V.; Herrera, E. Evaluation on Phantoms of the Feasibility of a Smart Bra to Detect Breast Cancer in Young Adults. Sensors 2019, 19, 5491. https://doi.org/10.3390/s19245491
Moreno M-V, Herrera E. Evaluation on Phantoms of the Feasibility of a Smart Bra to Detect Breast Cancer in Young Adults. Sensors. 2019; 19(24):5491. https://doi.org/10.3390/s19245491
Chicago/Turabian StyleMoreno, Marie-Valérie, and Edouard Herrera. 2019. "Evaluation on Phantoms of the Feasibility of a Smart Bra to Detect Breast Cancer in Young Adults" Sensors 19, no. 24: 5491. https://doi.org/10.3390/s19245491





