Toward a More Complete, Flexible, and Safer Speed Planning for Autonomous Driving via Convex Optimization
Abstract
:1. Introduction
- We summarize the most common constraints raised in various autonomous driving scenarios as the requirements for speed planner design and metrics to measure the capacity of the existing speed planners roughly for autonomous driving. We clarify which constraints need to be addressed by speed planners to guarantee safety in general.
- In light of these requirements and metrics, we present a more general, flexible and complete speed planning mathematical model including friction circle, dynamics, smoothness, time efficiency, time window, ride comfort, IoD, path and boundary conditions constraints compared to similar methods explained in [3,11]. We addressed the limitations of the method of Lipp et al. [3] by introducing a pseudo jerk objective in longitudinal dimension to improve smoothness, adding time window constraints at certain point of the path to avoid dynamics obstacles, capping a path constraint (most-likely non-smooth) on speed decision variables to deal with task constraints like speed limits, imposing a boundary condition at the end point of the path to guarantee safety for precise stop or merging scenarios. Compared to the approach of Liu et al. [11], our formulation optimizes the time efficiency directly while still staying inside of the friction circle, which ensures our method exploits the full acceleration capacity of the vehicle when necessary.
- We introduce a semi-hard constraint concept to describe unique characters of the comfort box constraints and implement this kind of constraints using slack variables and penalty functions, which emphasizes comfort while guaranteeing fundamental motion safety without sacrificing the mobility of cars. To the best of our knowledge, none of the existing methods handle these constraints like ours. In contrast, Refs. [7,8,9,10,11] regarded comfort box constraints as hard constraints, which dramatically reduces the solution space and in consequence limits the mobility of cars.
- We demonstrate that our problem still preserves convexity with the added constraints, and hence, that the global optimality is guaranteed. This means our problem can be solved using state-of-the-art convex optimization solvers efficiently as well. We also provide some evidence to prove that our solution is able to keep consistent when the boundary conditions encounter some disturbances, which means only the part of results needed to be adjusted will be regulated due to the global optimality. This may benefit the track performance of speed controllers by providing a relative stable reference. It is not the case for these methods that solve the speed planning problem using local optimization techniques like [11]. A small change of boundary conditions or initial guess may result in a totally different solution due to local minimas in their problem.
- We showcase how our formulation can be used in various autonomous driving scenarios by providing several challenging case studies solved in our framework, such as safe stop on a curvy road with different entry speeds, dealing with jaywalking in two different ways and merging from a freeway entrance ramp to expressways with safety guaranteed.
2. Related Work
3. Problem Formulation
3.1. Path Representation
3.2. Vehicle Model and Vehicle Dynamics Constraints
3.3. Friction Circle Constraints
3.4. Time Efficiency Objective
3.5. IoD Objective
3.6. Smoothness Objective
3.7. Path Constraints
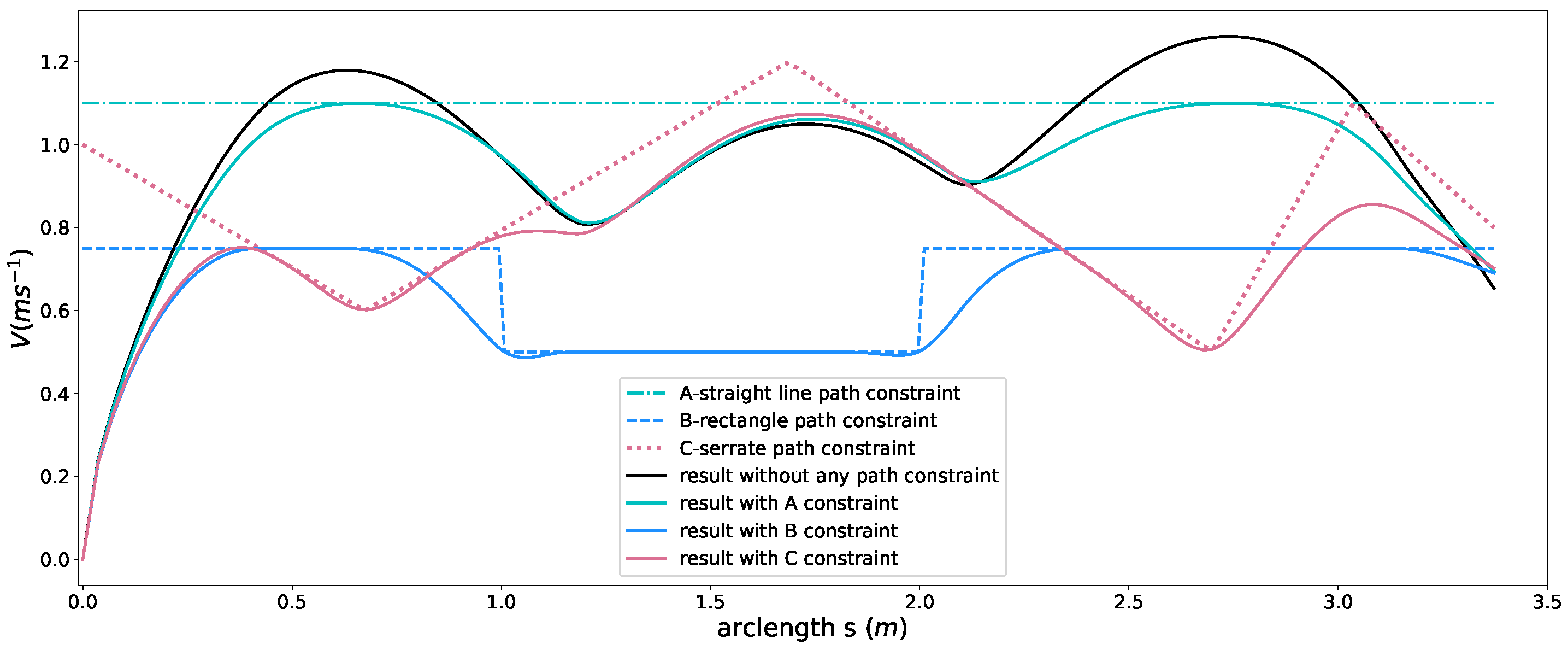
- Speed limits on certain segments of roads happen to be common driving scenarios in urban environments. The speed limits cannot be exceeded by autonomous driving systems, or the driving system will violate the traffic regulations and be fined. The restrictions may happen along the whole path or just segments of the path, which is a little different from an overall speed threshold constraint and the IoD objective.
- A high-level planning system (i.e., behavior planning system, task planning system) may provide the upper boundary or lower boundary of the speed profile to a speed planner to make it behave well or satisfy certain task requirements. A speed planner has to plan a speed profile that stays in the prescribed region or below the envelope.
3.8. Boundary Condition Constraints
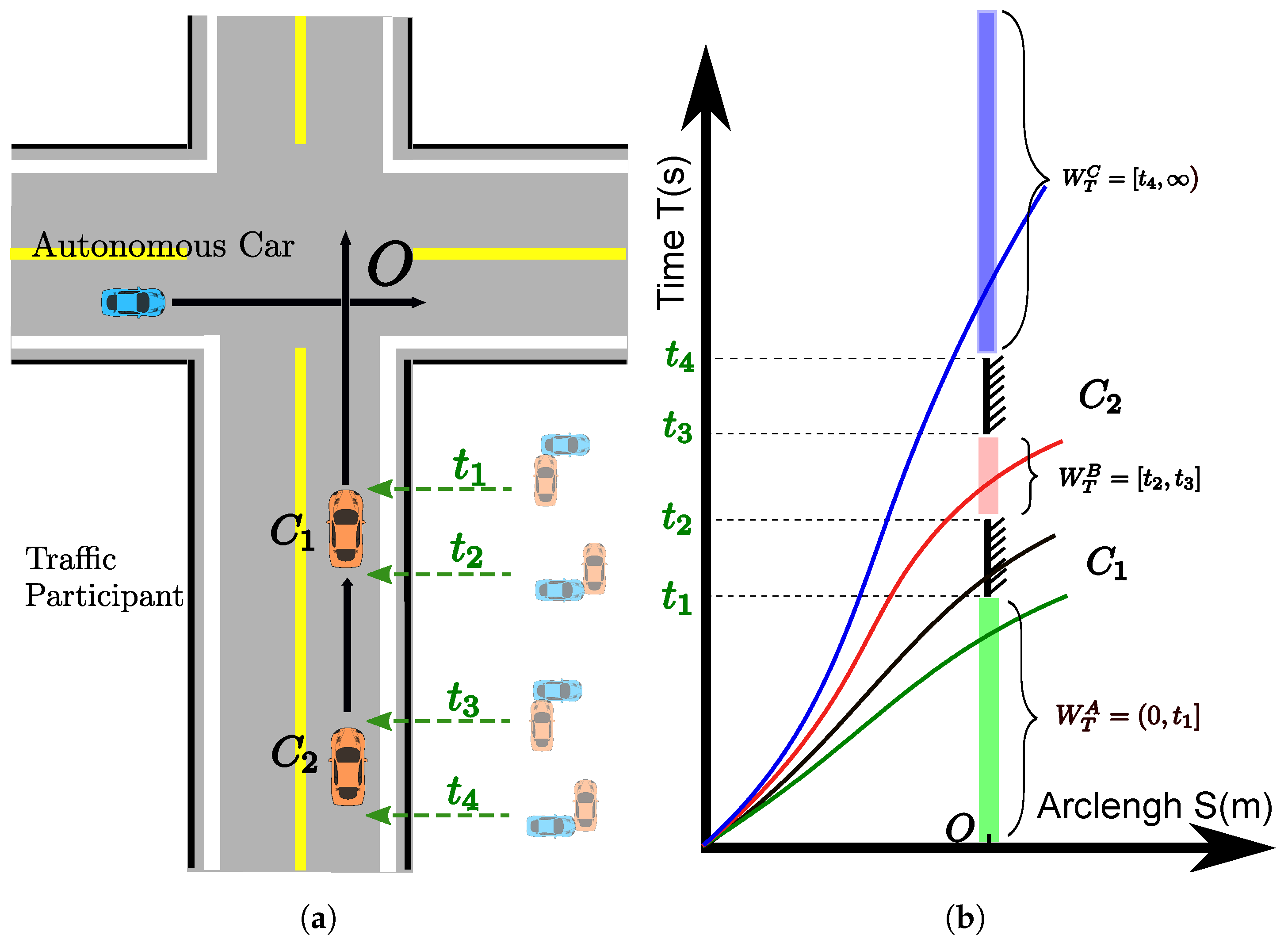
3.9. Time Window Constraints
3.10. Comfort Box Constraints
3.11. Overall Convex Optimization Problem Formulation
- For the objectives, is an integral of a negative power function and is therefore convex. is an integral of a squared power of absolute value and is therefore convex. is an integral of an identity power of absolute value and is therefore convex. So are and . As , , , , are all nonnegative, J as a nonnegative weighted sum of convex functions, is convex.
- For (6), the dynamics equality constraint is affine in , , u and is therefore convex. For equality constraints about decision variables (8), since the derivative is a linear operator, the relation between and is convex. For the inequality path constraint (17), is a sublevel set of convex set in the interval and is thus convex. The equality and inequality constraints about boundary conditions (19) are linear constraints, thus convex. As the is an integral of a negative power function, therefore convex and is a fixed upper boundary, the time window inequality constraint (20) is a convex constraint.
- For the convex set constraint about the friction circle (11), the norm of u is convex, upper bounds are fixed and is fixed, so the control set constraint is the intersection of three convex sets and is therefore convex.
- The comfort box constraints with slack variables and are second-order cone constraints and convex.
4. Implementation
4.1. Discretization of , , and
4.2. Discretization of and
5. Numerical Results
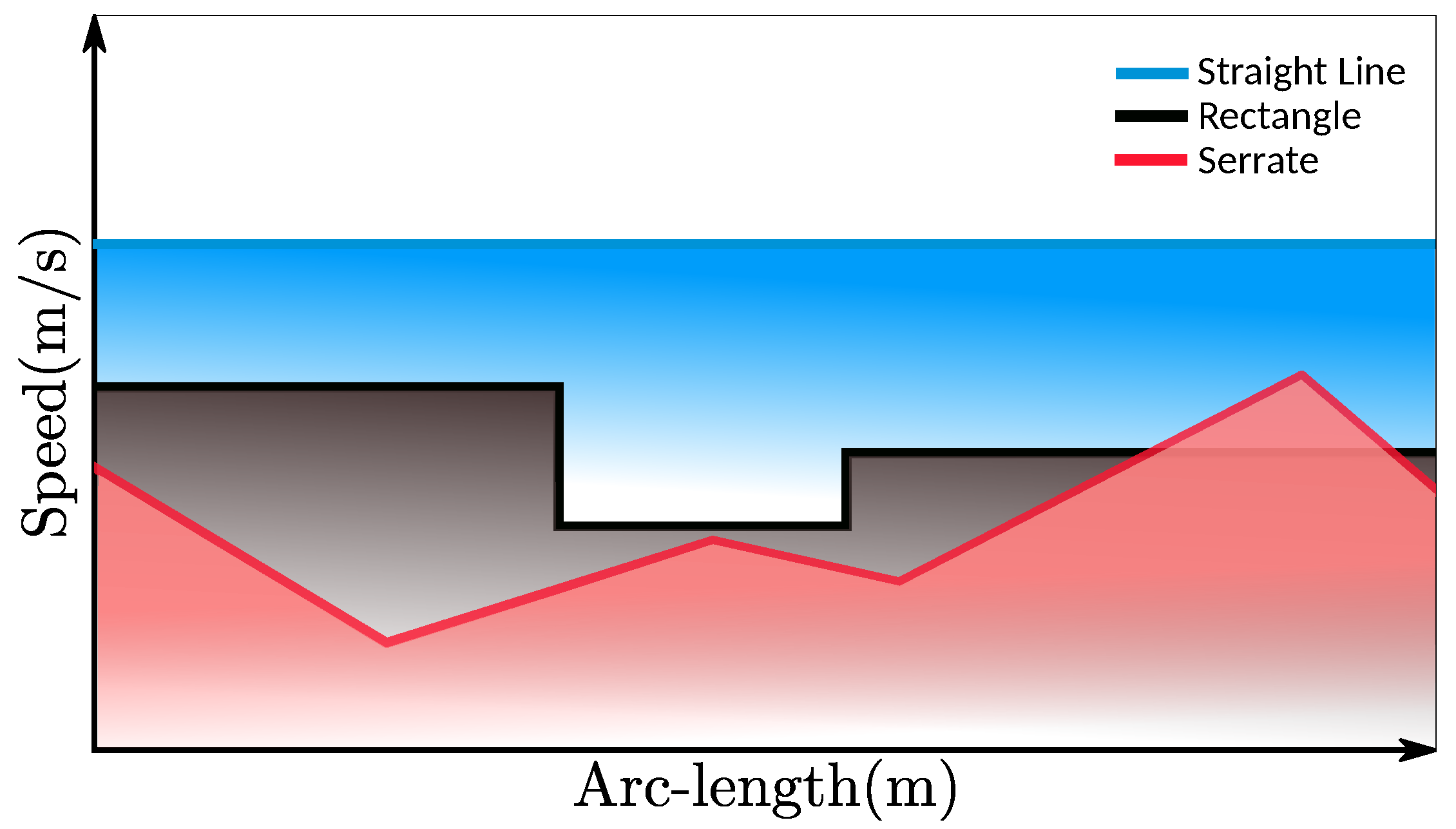
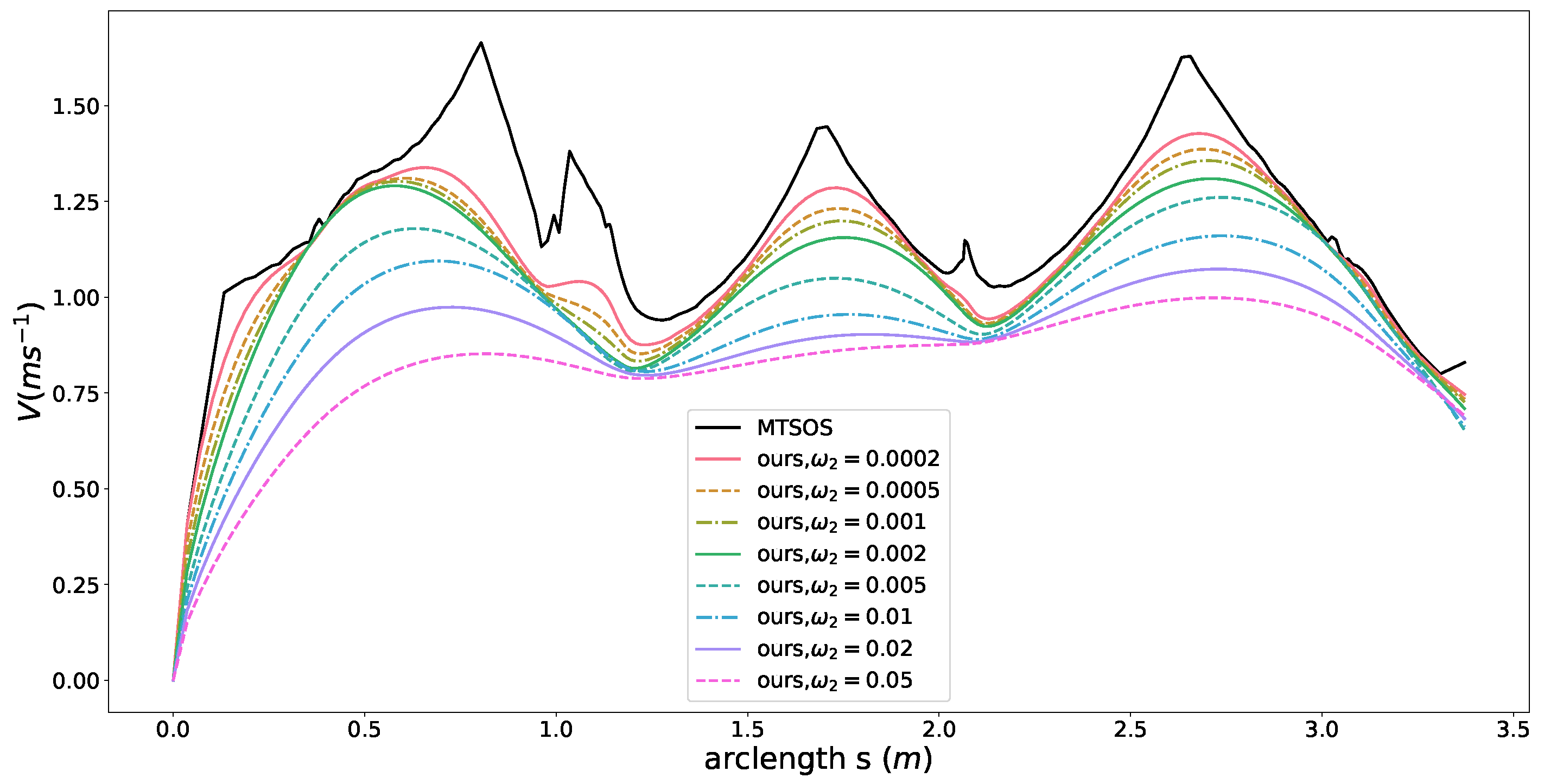
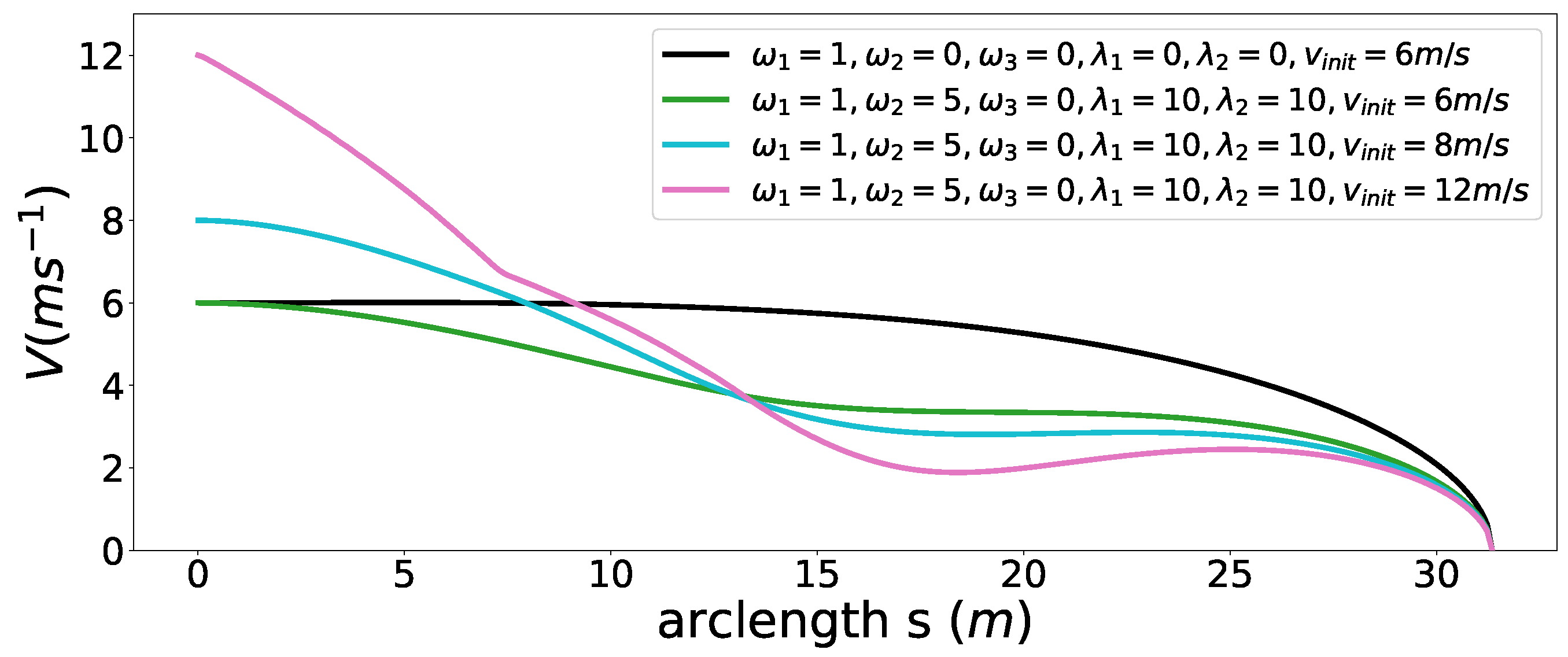
5.1. Smoothness
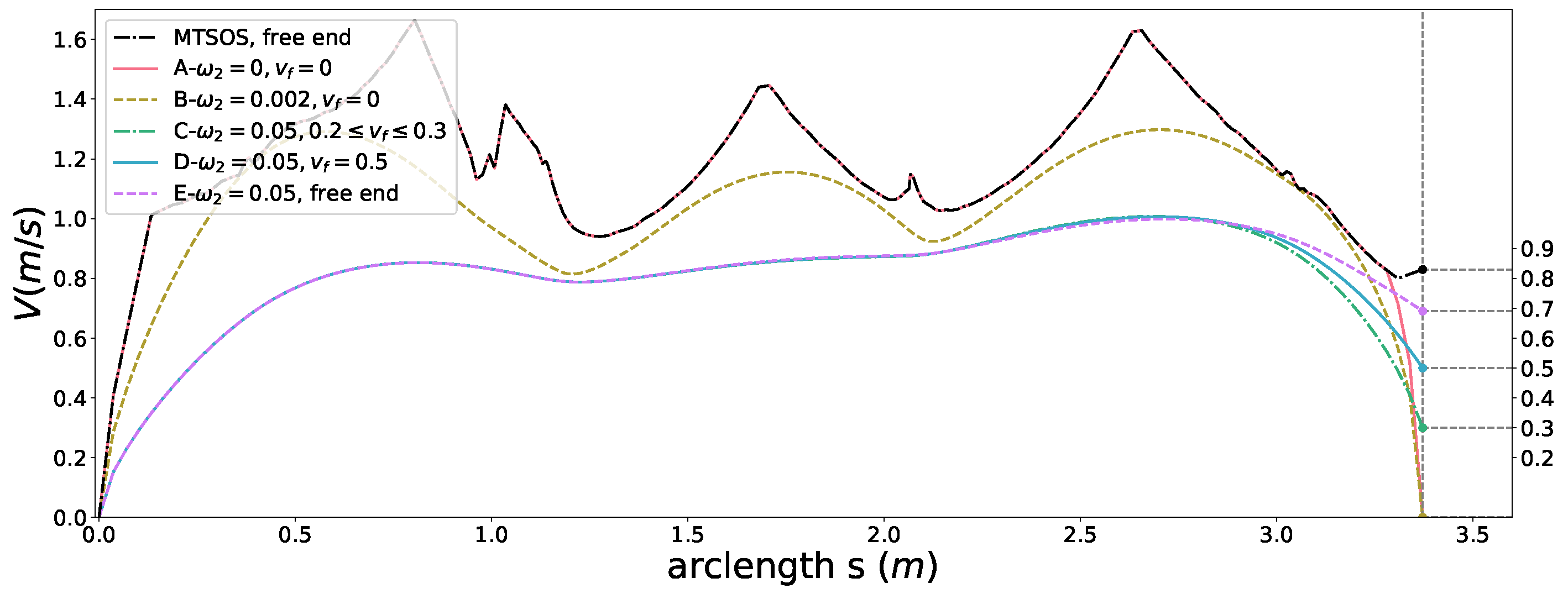
5.2. Boundary Condition Constraint
5.3. Path Constraint
5.4. IoD Task Constraints
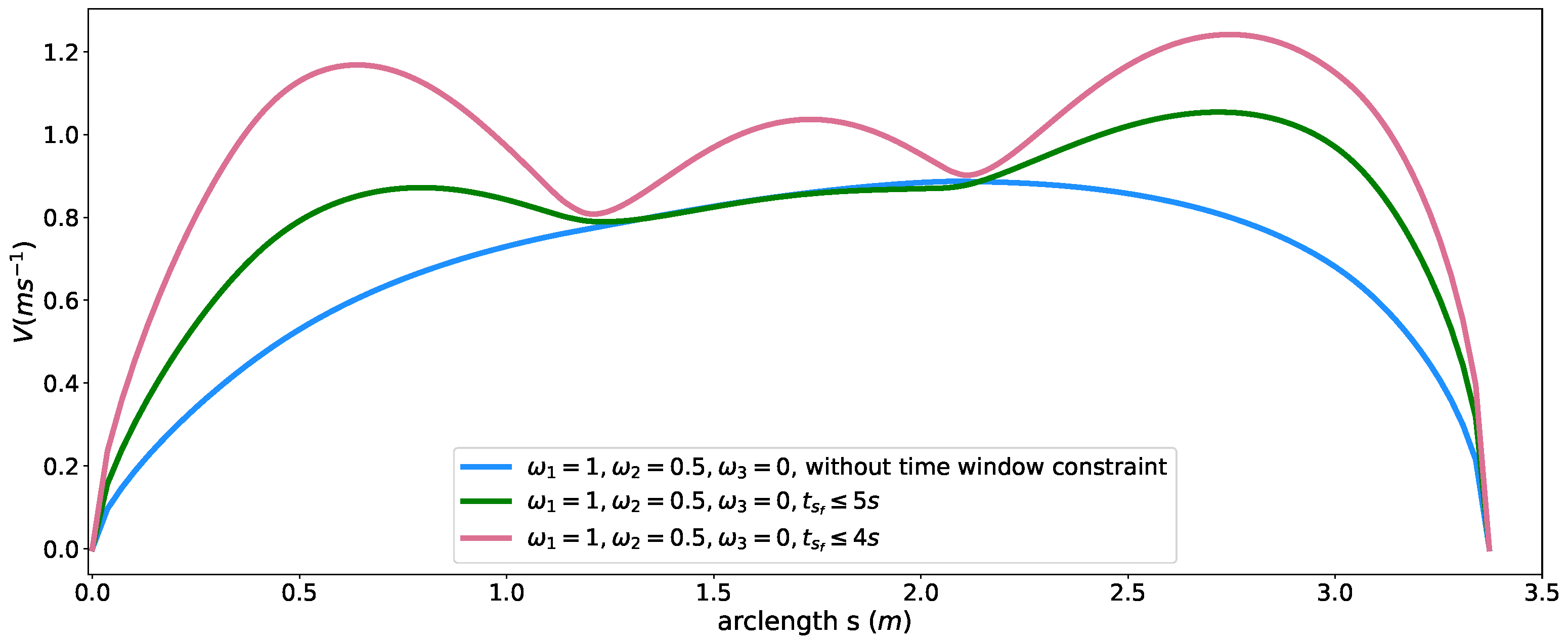
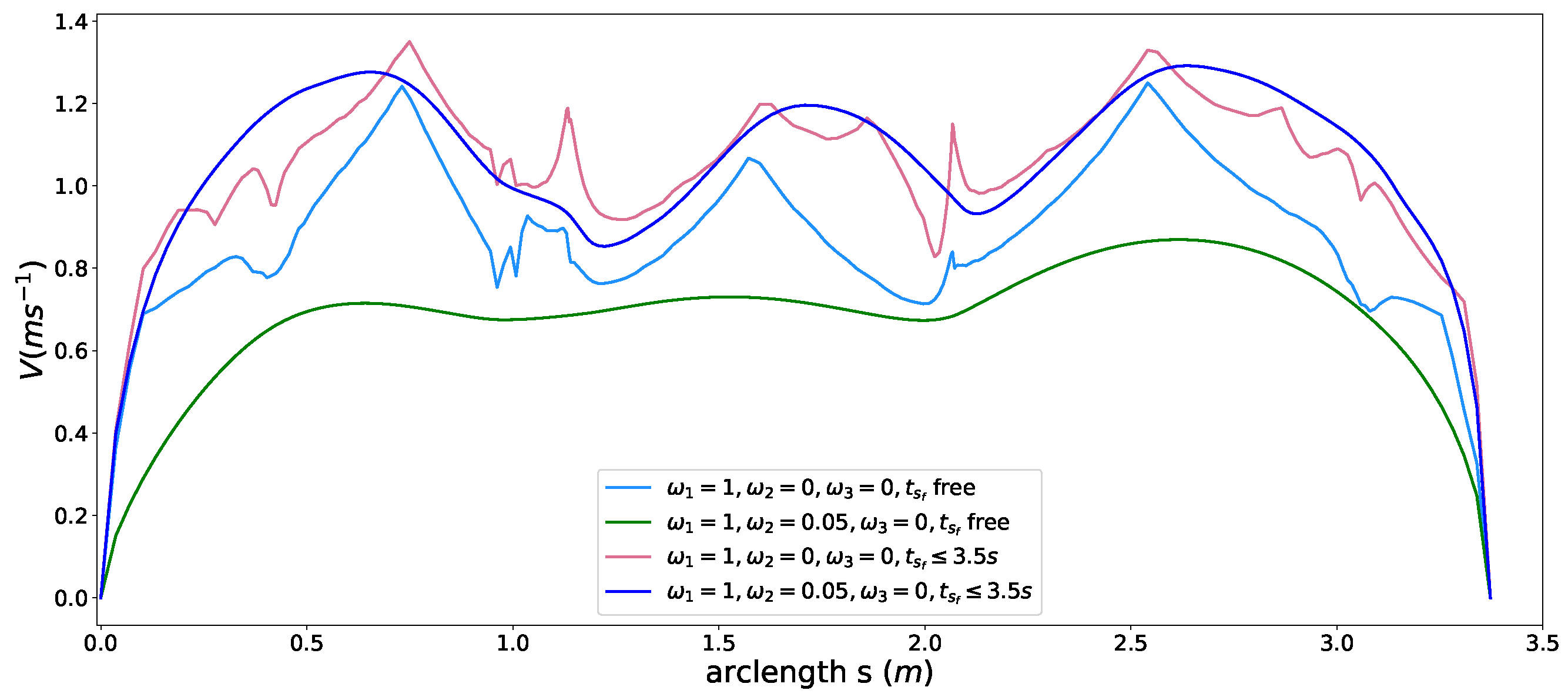
5.5. Time Window Constraint
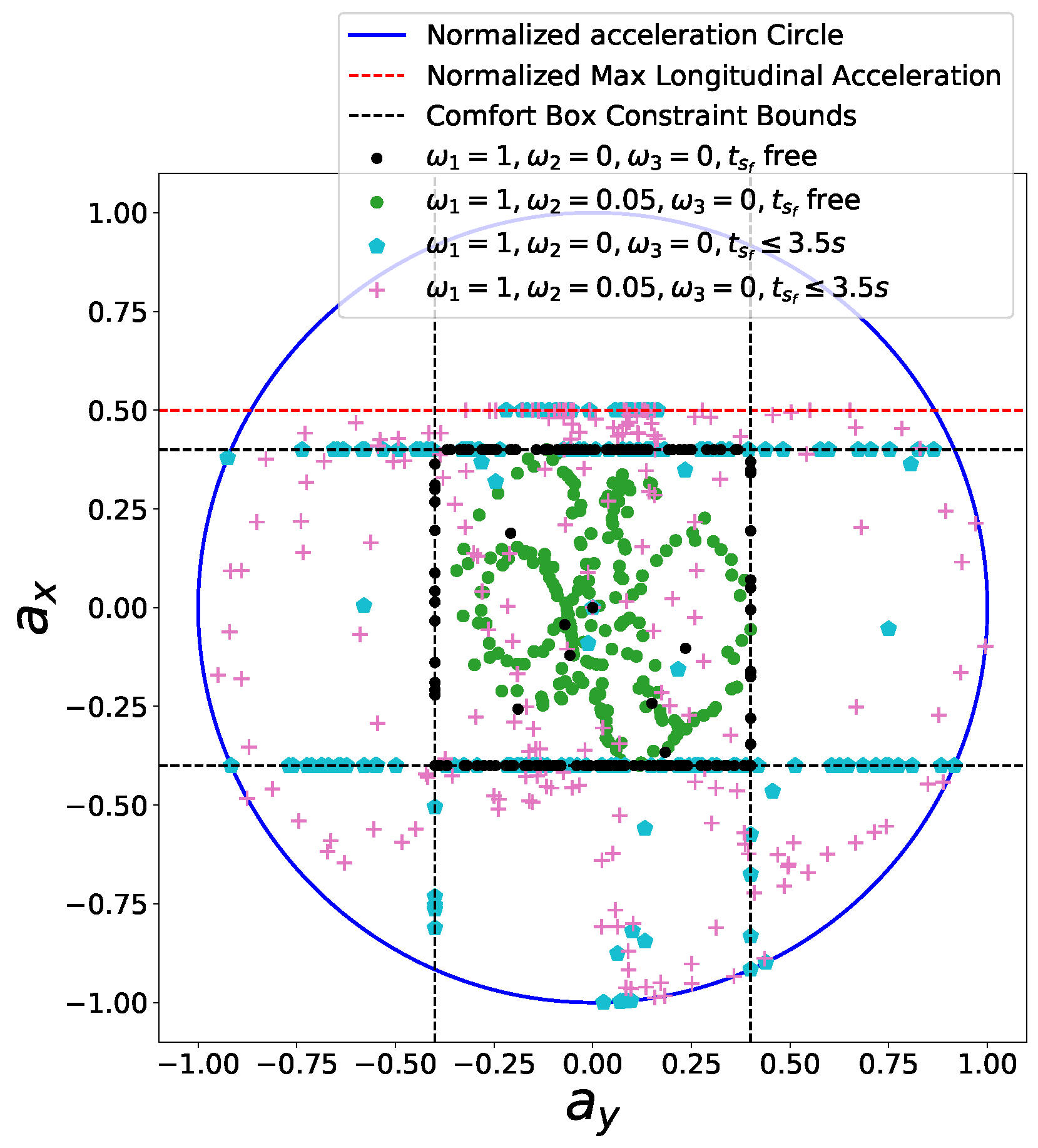
5.6. Semi-Hard Comfort Box Constraint
6. Case Study
6.1. Speed Planning for Safe Stop
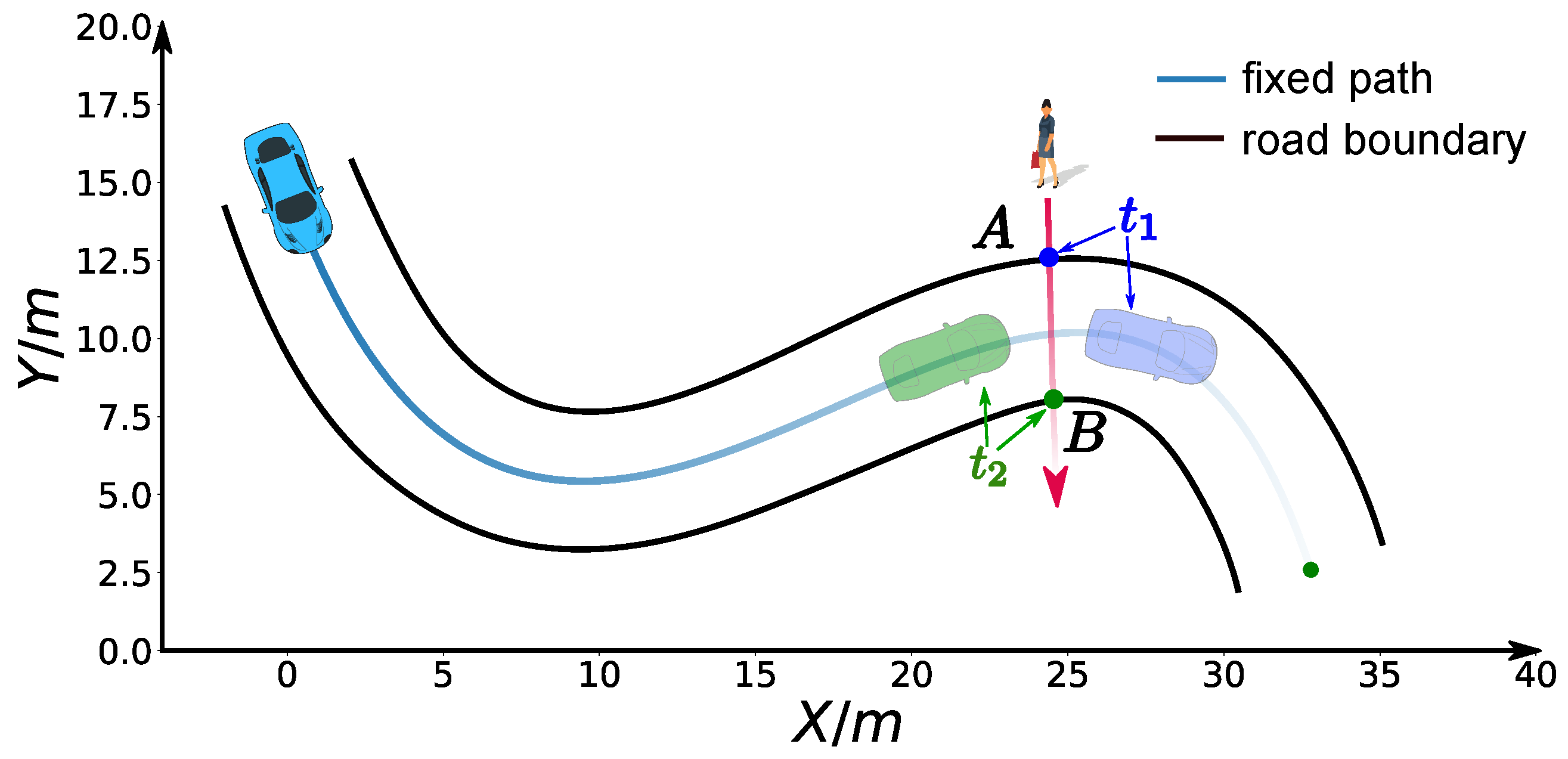
6.2. Speed Planning Dealing with Jaywalking on a Curvy Road
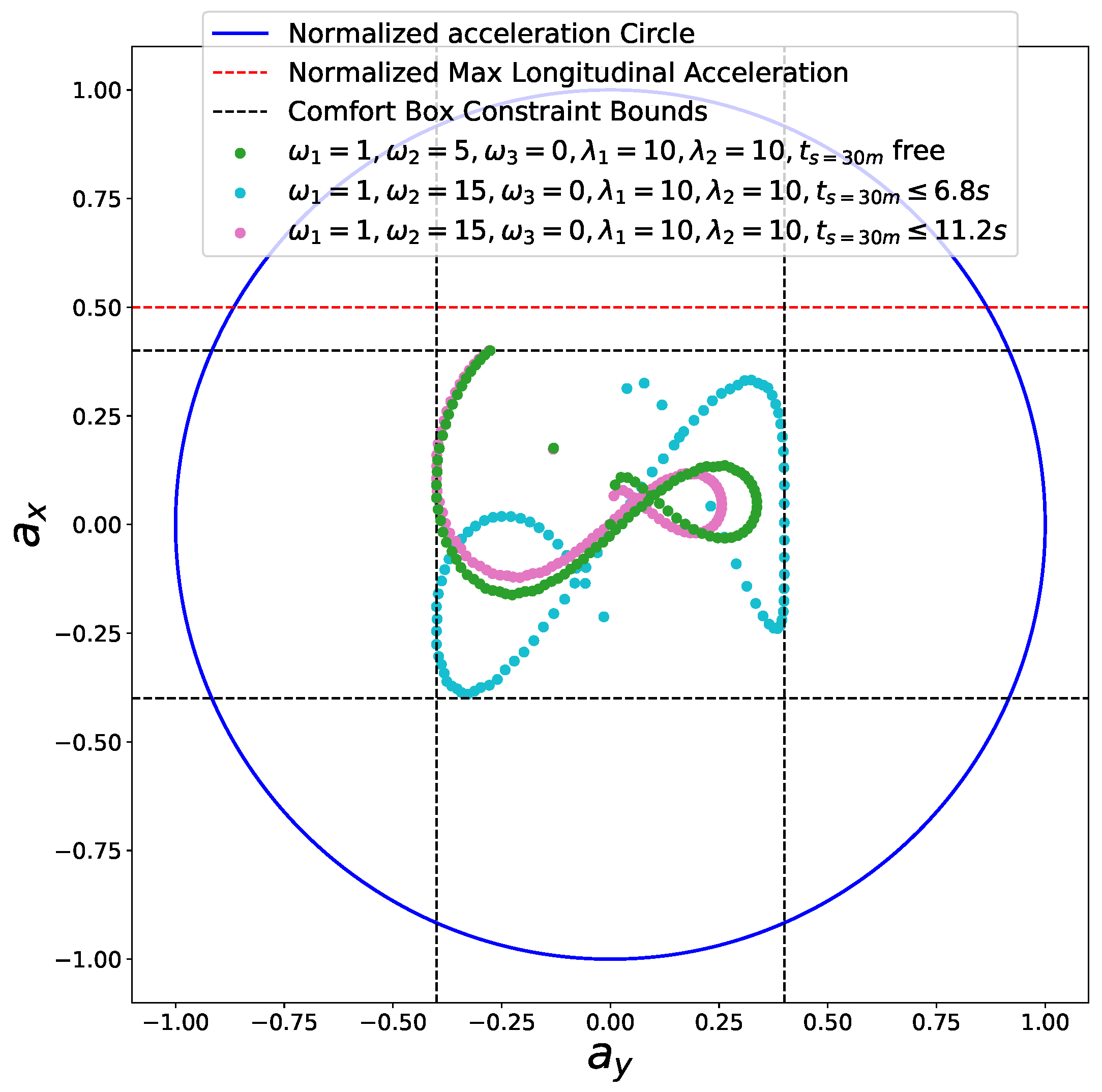
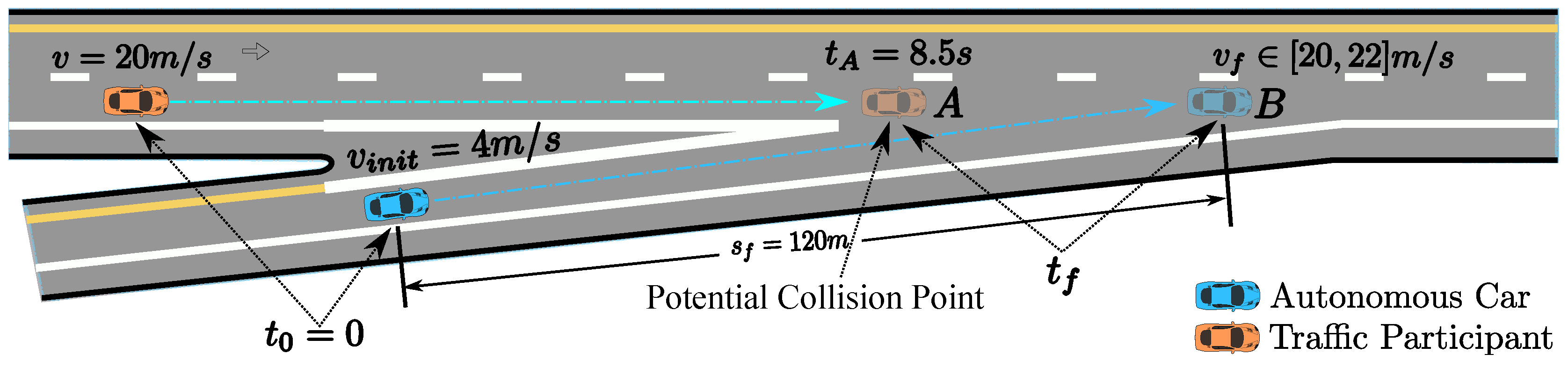
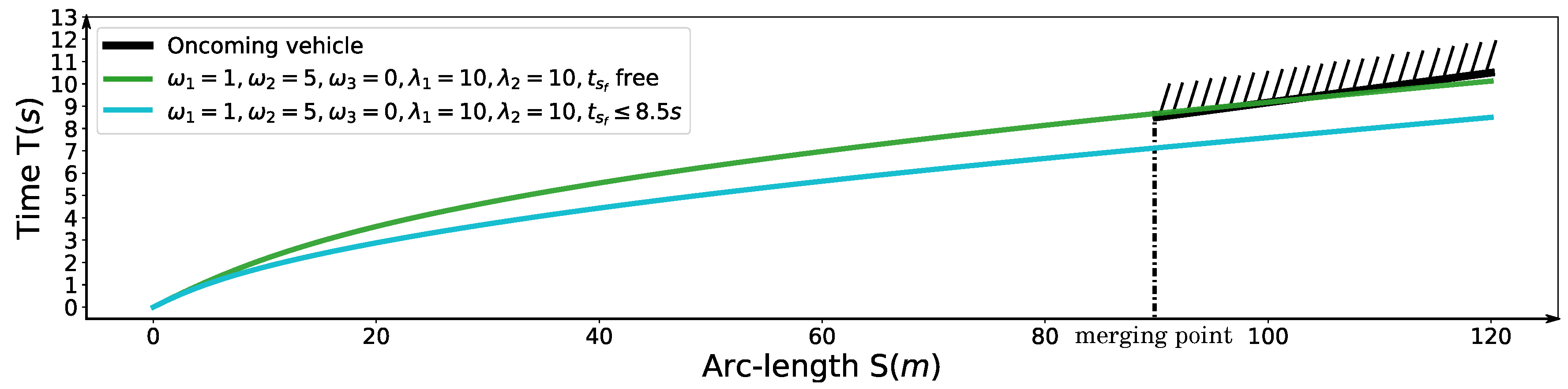
6.3. Speed Planning for Freeway Entrance Ramp Merging
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kritayakirana, K.; Gerdes, J.C. Autonomous vehicle control at the limits of handling. Int. J. Veh. Auton. Syst. 2012, 10, 271–296. [Google Scholar] [CrossRef]
- Verscheure, D.; Demeulenaere, B.; Swevers, J.; De Schutter, J.; Diehl, M. Time-optimal path tracking for robots: A convex optimization approach. IEEE Trans. Autom. Control 2009, 54, 2318–2327. [Google Scholar] [CrossRef]
- Lipp, T.; Boyd, S. Minimum-time speed optimisation over a fixed path. Int. J. Control 2014, 87, 1297–1311. [Google Scholar] [CrossRef]
- Dakibay, A.; Waslander, S.L. Aggressive Vehicle Control Using Polynomial Spiral Curves. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017. [Google Scholar]
- Cabrera, J.A.; Castillo, J.J.; Pérez, J.; Velasco, J.M.; Guerra, A.J.; Hernández, P. A procedure for determining tire-road friction characteristics using a modification of the magic formula based on experimental results. Sensors 2018, 18, 896. [Google Scholar] [CrossRef] [PubMed]
- Yunta, J.; Garcia-Pozuelo, D.; Diaz, V.; Olatunbosun, O. A Strain-Based Method to Detect TiresĹoss of Grip and Estimate Lateral Friction Coefficient from Experimental Data by Fuzzy Logic for Intelligent Tire Development. Sensors 2018, 18, 490. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Sun, Z.; Cao, D.; He, Z.; Zhu, Q. Real-time trajectory planning for autonomous urban driving: Framework, Algorithms, and Verifications. IEEE/ASME Trans. Mechatron. 2016, 21, 740–753. [Google Scholar] [CrossRef]
- Gu, T.; Snider, J.; Dolan, J.M.; Lee, J.W. Focused trajectory planning for autonomous on-road driving. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Gold Coast, Australia, 23–26 June 2013; pp. 547–552. [Google Scholar]
- Gu, T. Improved Trajectory Planning for On-Road Self-Driving Vehicles Via Combined Graph Search, Optimization & Topology Analysis. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2017. [Google Scholar]
- Gu, T.; Atwood, J.; Dong, C.; Dolan, J.M.; Lee, J.W. Tunable and stable real-time trajectory planning for urban autonomous driving. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 250–256. [Google Scholar]
- Liu, C.; Zhan, W.; Tomizuka, M. Speed profile planning in dynamic environments via temporal optimization. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 154–159. [Google Scholar] [CrossRef]
- Wei, J.; Dolan, J.M.; Litkouhi, B. Autonomous vehicle social behavior for highway entrance ramp management. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Gold Coast, Australia, 23–26 June 2013; pp. 201–207. [Google Scholar]
- Xie, Y.; Zhang, H.; Gartner, N.H.; Arsava, T. Collaborative merging strategy for freeway ramp operations in a connected and autonomous vehicles environment. J. Intell. Transp. Syst. 2017, 21, 136–147. [Google Scholar] [CrossRef]
- Serna, C.G.; Ruichek, Y. Dynamic speed adaptation for path tracking based on curvature information and speed limits. Sensors 2017, 17, 1383. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Shao, Z. Simultaneous dynamic optimization: A trajectory planning method for nonholonomic car-like robots. Adv. Eng. Softw. 2015, 87, 30–42. [Google Scholar] [CrossRef]
- Ziegler, J.; Bender, P.; Dang, T.; Stiller, C. Trajectory planning for Bertha—A local, continuous method. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; pp. 450–457. [Google Scholar] [CrossRef]
- Schwarting, W.; Alonso-Mora, J.; Pauli, L.; Karaman, S.; Rus, D. Parallel autonomy in automated vehicles: Safe motion generation with minimal intervention. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May– 3 June 2017; pp. 1928–1935. [Google Scholar]
- Ziegler, J.; Stiller, C. Spatiotemporal state lattices for fast trajectory planning in dynamic on-road driving scenarios. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 1879–1884. [Google Scholar] [CrossRef]
- McNaughton, M.; Urmson, C.; Dolan, J.M.; Lee, J.W. Motion planning for autonomous driving with a conformal spatiotemporal lattice. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 4889–4895. [Google Scholar]
- Zhu, Z.; Schmerling, E.; Pavone, M. A convex optimization approach to smooth trajectories for motion planning with car-like robots. In Proceedings of the IEEE 54th Annual Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 835–842. [Google Scholar]
- Kuwata, Y.; Karaman, S.; Teo, J.; Frazzoli, E.; How, J.; Fiore, G. Real-Time Motion Planning with Applications to Autonomous Urban Driving. IEEE Trans. Control Syst. Technol. 2009, 17, 1105–1118. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Waslander, S.L.; Gong, J.; Xiong, G.; Yang, T.; Liu, K. Hybrid Trajectory Planning for Autonomous Driving in Highly Constrained Environments. IEEE Access 2018. [Google Scholar] [CrossRef]
- Pan, J.; Zhang, L.; Manocha, D.; Hill, U. Collision-free and curvature-continuous path smoothing in cluttered environments. Robot. Sci. Syst. VII 2012, 17, 233. [Google Scholar]
- Elbanhawi, M.; Simic, M.; Jazar, R. Randomized bidirectional B-spline parameterization motion planning. IEEE Trans. Intell. Transp. Syst. 2016, 17, 406–419. [Google Scholar] [CrossRef]
- Yang, K.; Sukkarieh, S. An analytical continuous-curvature path-smoothing algorithm. IEEE Trans. Robot. 2010, 26, 561–568. [Google Scholar] [CrossRef]
- Han, L.; Yashiro, H.; Nejad, H.T.N.; Do, Q.H.; Mita, S. Bezier curve based path planning for autonomous vehicle in urban environment. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), San Diego, CA, USA, 21–24 June 2010; pp. 1036–1042. [Google Scholar]
- Funke, J.; Gerdes, J.C. Simple clothoid paths for autonomous vehicle lane changes at the limits of handling. In Proceedings of the ASME 2013 Dynamic Systems and Control Conference, Palo Alto, CA, USA, 21–23 October 2013; p. V003T47A003. [Google Scholar]
- Knowles, D. Real Time Continuous Curvature Path Planner for an Autonomous Vehicle in an Urban Environment; Technical Report; California Institute of Technology: Pasadena, CA, USA, 2006; Volume 1. [Google Scholar]
- Lee, J.W.; Litkouhi, B. A unified framework of the automated lane centering/changing control for motion smoothness adaptation. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems (ITSC), Anchorage, AK, USA, 16–19 September 2012; pp. 282–287. [Google Scholar]
- Kelly, A.; Nagy, B. Reactive nonholonomic trajectory generation via parametric optimal control. Int. J. Robot. Res. 2003, 22, 583–601. [Google Scholar] [CrossRef]
- Matthew, M. Parallel Algorithms for Real-Time Motion Planning. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2011. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer: New York, NY, USA, 2006; p. 111. [Google Scholar]
- Polack, P.; Altché, F.; d’Andréa Novel, B.; de La Fortelle, A. The kinematic bicycle model: A consistent model for planning feasible trajectories for autonomous vehicles? In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 812–818. [Google Scholar]
- Constantinescu, D.; Croft, E.A. Smooth and time-optimal trajectory planning for industrial manipulators along specified paths. J. Robot. Syst. 2000, 17, 233–249. [Google Scholar] [CrossRef] [Green Version]
- Macfarlane, S.; Croft, E.A. Jerk-bounded manipulator trajectory planning: Design for real-time applications. IEEE Trans. Robot. Autom. 2003, 19, 42–52. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Melendez-Calderon, A.; Burdet, E. A Robust and Sensitive Metric for Quantifying Movement Smoothness. IEEE Trans. Biomed. Eng. 2012, 59, 2126–2136. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, S.; Melendezcalderon, A.; Robybrami, A.; Burdet, E. On the analysis of movement smoothness. J. Neuroeng. Rehabil. 2015, 12, 112. [Google Scholar] [CrossRef] [PubMed]
- Chachuat, B. Nonlinear and Dynamic Optimization: From Theory to Practice; Technical Report; Automatic Control Laboratory EPFL: Lausanne, Switzerland, 2007. [Google Scholar]
- Schwesinger, U.; Siegwart, R.; Furgale, P. Fast collision detection through bounding volume hierarchies in workspace-time space for sampling-based motion planners. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 63–68. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Richards, A. Fast model predictive control with soft constraints. Eur. J. Control 2015, 25, 51–59. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970; pp. 5–101. [Google Scholar]
- Udell, M.; Mohan, K.; Zeng, D.; Hong, J.; Diamond, S.; Boyd, S. Convex Optimization in Julia. In Proceedings of the 1st First Workshop for High Performance Technical Computing in Dynamic Languages (HPTCDL ’14), New Orleans, LA, USA, 16–21 November 2014; IEEE Press: Piscataway, NJ, USA, 2014; pp. 18–28. [Google Scholar] [Green Version]
- Optimization, G. Gurobi Optimizer Reference Manual; Gurobi Optimization Inc.: Houston, TX, USA, 2016. [Google Scholar]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Milliken, W.F.; Milliken, D.L. Race Car Vehicle Dynamics; Society of Automotive Engineers: Warrendale, PA, USA, 1995. [Google Scholar]
- Rice, R.S. Measuring Car-Driver Interaction with the g-g Diagram; Technical Report; SAE International: Warrendale, PA, USA, 1973. [Google Scholar]
- Consolini, L.; Locatelli, M.; Minari, A.; Piazzi, A. An optimal complexity algorithm for minimum-time velocity planning. Syst. Control Lett. 2017, 103, 50–57. [Google Scholar] [CrossRef]









| Category | Constraint Name | Description | Property |
|---|---|---|---|
| Soft Constraints | Smoothness (S) | continuity of speed, acceleration and jerk over the path | performance |
| Time Efficiency (TE) | time used by travelling along the path | performance | |
| IoD | integral of speed deviations | performance | |
| Hard Constraints | Friction Circle (FC) | total force should be within the friction circle | safety |
| Path Constraints (PC) | speed limits on path segments | safety | |
| Time Window (TW) | time window to reach a certain point on path | safety | |
| Boundary Condition (BC) | speed at the end of the path | safety & performance | |
| Semi-hard Constraints | Comfort Box (CB) | comfort acceleration and deceleration bounds | performance |
| Method | S | TE | IoD | FC | PC | TW | BC | CB | Optimality | Safety | Mobility | Flexibility |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Li et al. [7] | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✓ | ✓ | ✗ | low | low | low |
| Gu et al. [8,9,10] | ✓ | ✗ | ✗ | ✗ | ✓ | ✗ | ✓ | ✓ | ✗ | medium | medium | medium |
| Dakibay et al. [4] | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | medium | high | low |
| Liu et al. [11] | ✓ |  | ✓ | ✗ | ✗ | ✓ |  | ✓ | local | medium | medium | medium |
| Lipp et al. [3] | ✗ | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | global | low | high | low |
| Ours | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | global | high | high | high |
| Parameter | Description | Values | Unit |
|---|---|---|---|
| m | Mass of the car | 0.1453 | kg |
| Friction coefficient | 0.70 | 1 | |
| g | Acceleration of gravity | 9.83 | m/s |
| Longitudinal acceleration threshold for comfort | 0.4 g | m/s | |
| Lateral acceleration threshold for comfort | 0.4 g | m/s | |
| Max. longitudinal acceleration of the car. | 0.5 g | m/s | |
| Max. speed of the car. | 1.8 | m/s |
| Profile Figure 11 | Coefficients | Time Window (s) | Travel Time at (s) |
|---|---|---|---|
| blue | free | 6.626 | |
| green | 4.999 | ||
| red | 4.000 |
| Parameter | Description | Values | Unit |
|---|---|---|---|
| w | Car width | 2.45 | m |
| l | Car length | 4.9 | m |
| Car wheelbase | 2.8448 | m | |
| Car track | 1.5748 | m | |
| m | Mass of the car. | 1500.0 | kg |
| Friction coefficient | 0.7 | 1 | |
| g | Acceleration of gravity | 9.83 | m/s |
| Longitudinal acceleration threshold for comfort | 0.4 g | m/s | |
| Lateral acceleration threshold for comfort | 0.4 g | m/s | |
| Max. longitudinal acceleration of the car | 0.5 g | m/s | |
| Max. speed of the car | 30 | m/s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Chen, H.; Waslander, S.L.; Yang, T.; Zhang, S.; Xiong, G.; Liu, K. Toward a More Complete, Flexible, and Safer Speed Planning for Autonomous Driving via Convex Optimization. Sensors 2018, 18, 2185. https://doi.org/10.3390/s18072185
Zhang Y, Chen H, Waslander SL, Yang T, Zhang S, Xiong G, Liu K. Toward a More Complete, Flexible, and Safer Speed Planning for Autonomous Driving via Convex Optimization. Sensors. 2018; 18(7):2185. https://doi.org/10.3390/s18072185
Chicago/Turabian StyleZhang, Yu, Huiyan Chen, Steven L. Waslander, Tian Yang, Sheng Zhang, Guangming Xiong, and Kai Liu. 2018. "Toward a More Complete, Flexible, and Safer Speed Planning for Autonomous Driving via Convex Optimization" Sensors 18, no. 7: 2185. https://doi.org/10.3390/s18072185





