Delay-Aware Energy-Efficient Routing towards a Path-Fixed Mobile Sink in Industrial Wireless Sensor Networks
Abstract
:1. Introduction
- To the best of our knowledge, DERM is the first work concerned about both the delivery delay and energy efficiency for data collection in WSNs with a path-fixed and strictly uncontrollable mobile sink. We design a location-based greedy forwarding algorithm for energy-optimal routing towards dynamic destination regions, and demonstrate that the right-hand rule can also be used for void handling in this new context after being slightly modified.
- An effective location calibration method is presented, which can be combined with the rough estimation based on the mobility pattern to determine the sink location. In this manner, the routing performance can be guaranteed with very low control overhead.
- We propose an approach named track routing to deal with the sink location errors caused by delayed calibration or unpredicted faults. It can guarantee reliable and on-time delivery in an energy-efficient manner, by adopting a “greedily advance, discreetly step back” strategy.
- We verify the effectiveness of our proposed method by extensive experiments and comprehensive performance comparisons. Additionally, we present a delay-constrained rendezvous-based routing, providing a supplementary baseline.
2. Related Work
2.1. Data Collection with Mobile Sinks
2.2. Geographic Routing
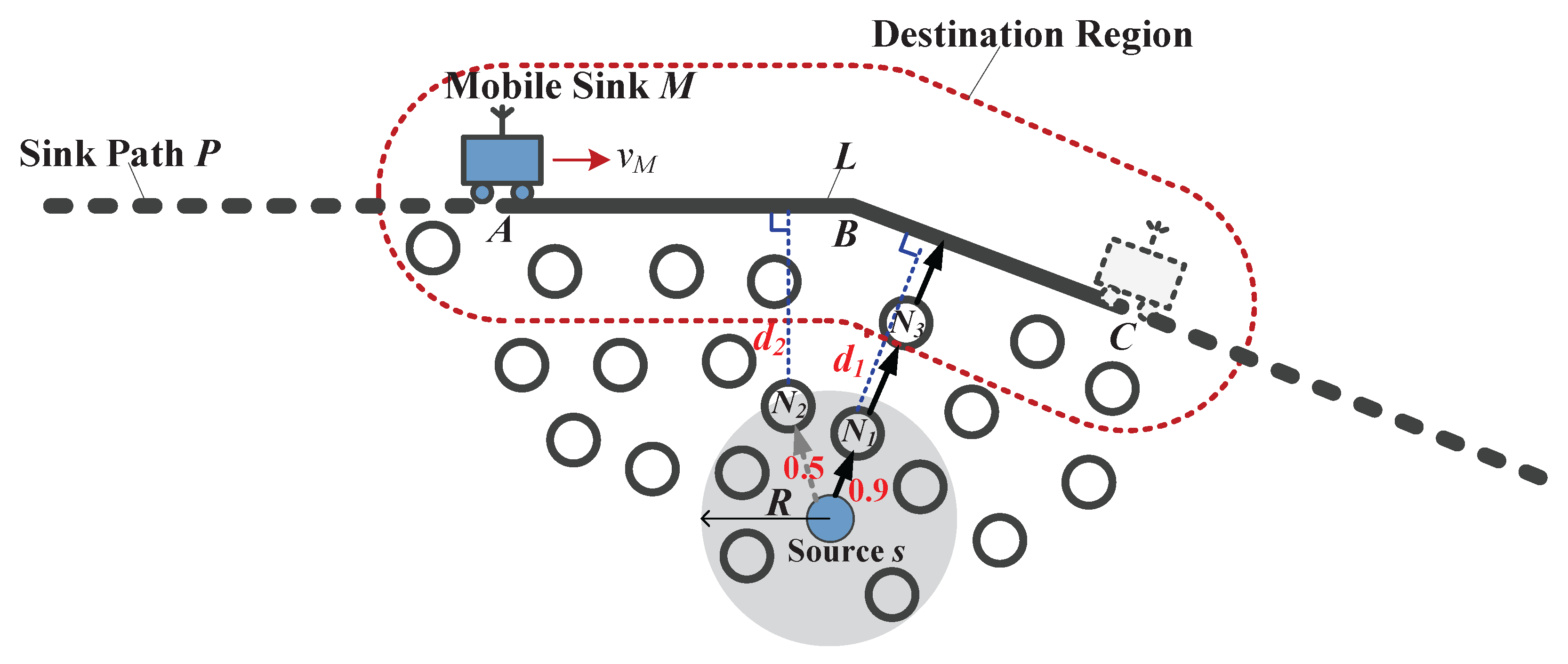
3. Network Model and Problem Description
3.1. Network Model
- Location awareness: All nodes know their physical locations and exchange them with their neighboring nodes in the initial phase. The locations can be obtained by GPS modules outdoors. In indoor environments, many existing methods (e.g., range-based and fingerprint-based techniques) can also achieve satisfactory localization accuracy [44].
- Unreliable links: The wireless communication is unreliable due to channel fading, interference, etc. The MAC (Media Access Control) layer measures the link quality by calculating the Packet Reception Ratio (PRR) [45]. To ensure the reliability of one-hop packet delivery, the ARQ (Automatic Repeat reQuest) mechanism is adopted, by which a packet encountering transmission failures will be retransmitted until being acknowledged. For instance, in CC2530, the receiver can acknowledge a packet with the software ACK [46].
- Data transmission time: The wireless signal travels much faster than the mobile sink. Therefore, compared to the delay constraint and the travel time of the sink, the time for multi-hop transmissions and data uploading from RNs to the sink is negligible [14]. Furthermore, when the RN finds that its cached data cannot be delivered within the communication time with the sink, it will transfer the excess data to a delegation node that can be visited before the deadline (see Section 4.2).
3.2. Problem Description
4. Main Design of DERM
4.1. Design Overview
4.2. Geographic Routing for EO-DRA
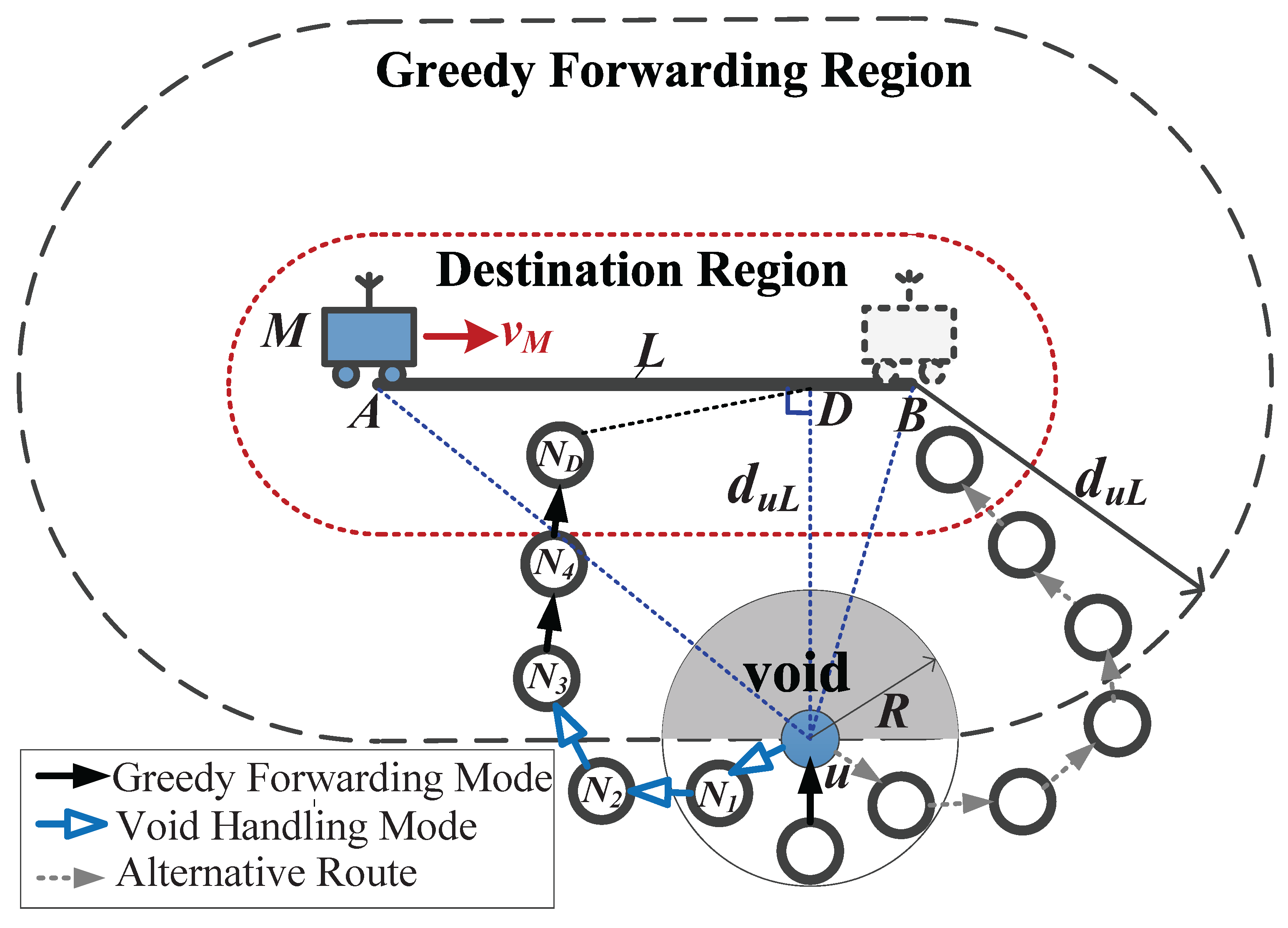
4.2.1. Greedy Forwarding for EO-DRA
4.2.2. Void Handling for EO-DRA
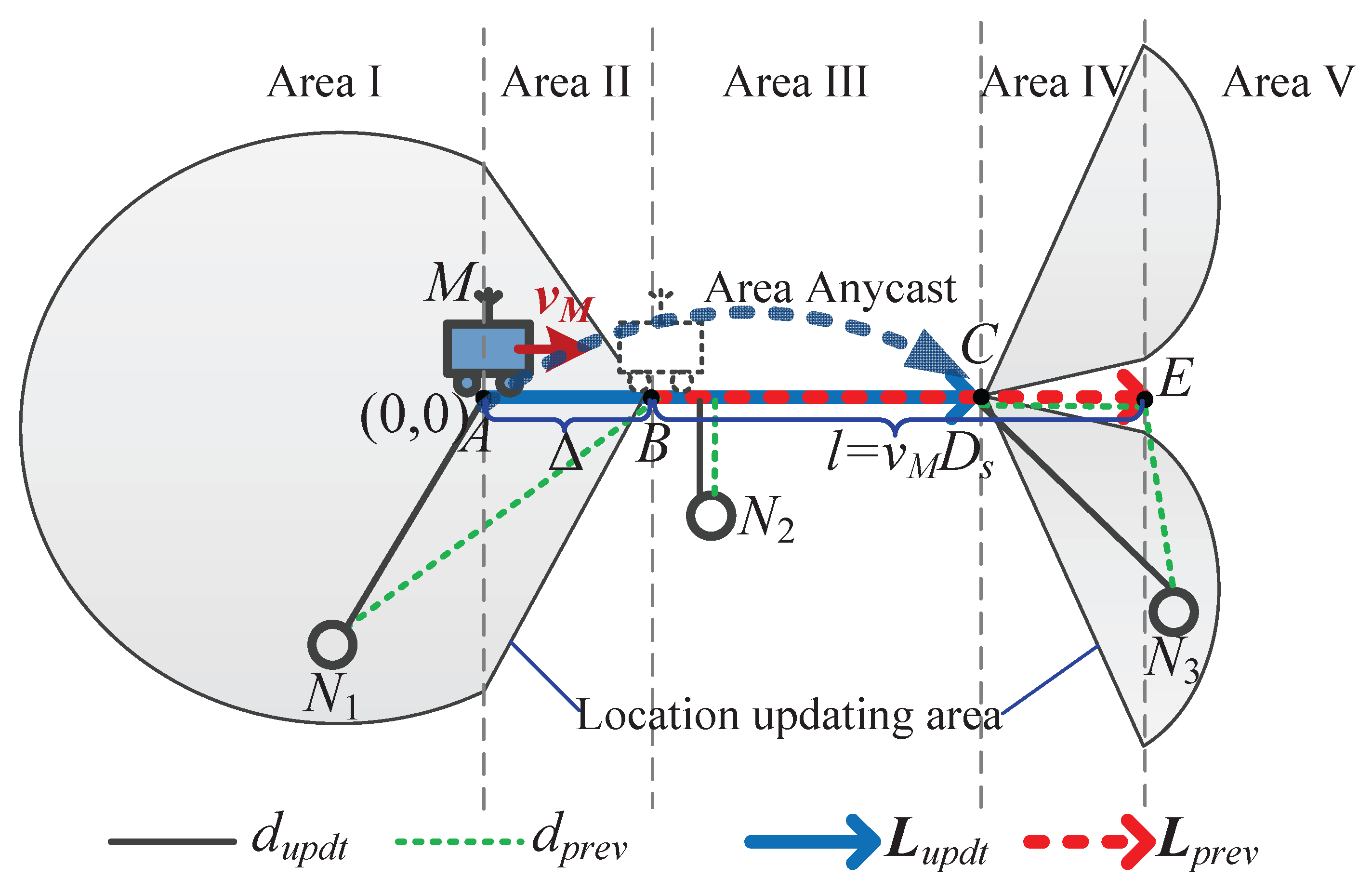
4.3. Sink Location Calibration
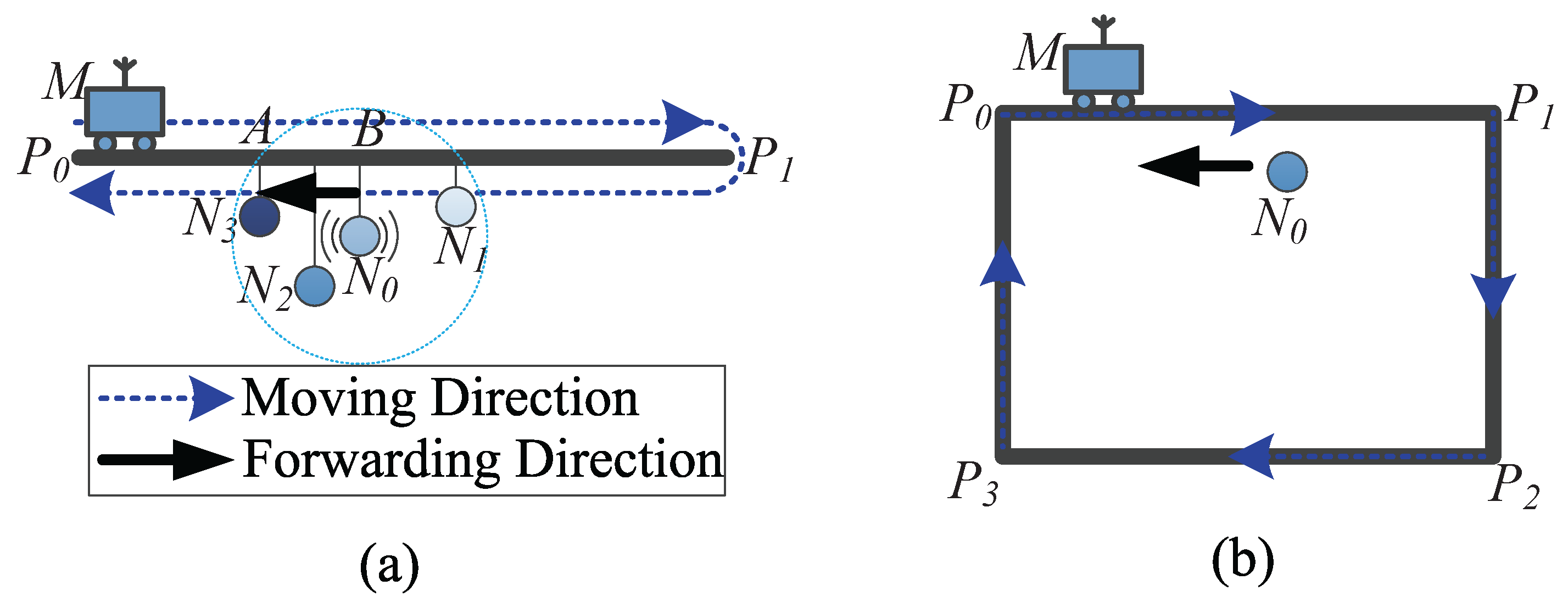
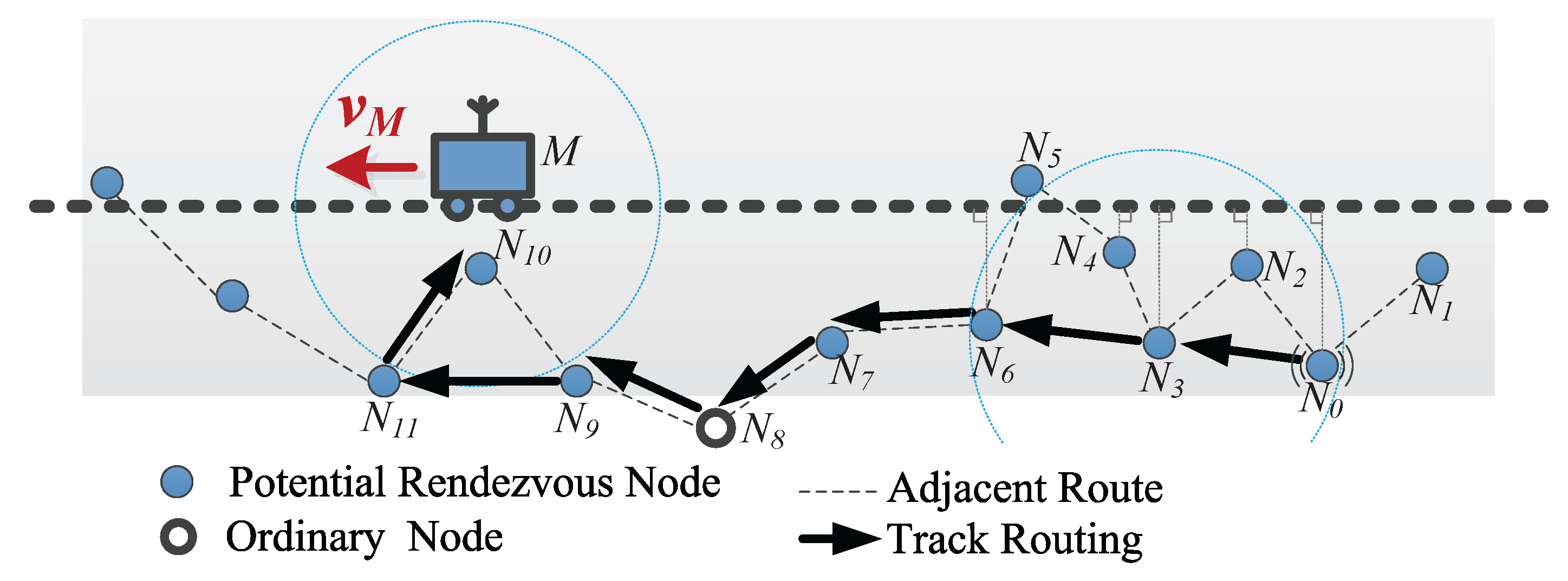
4.4. Track Routing
| Algorithm 1 Sink location calibration algorithm at sensor node i. | |
| Input: , ; , , and their corresponding time; the sink mobility pattern; | |
| Output: newly calibrated sink location; | |
| 1: | while Location check timer expires do |
| 2: | if i is the sink then |
| 3: | if then |
| 4: | Broadcast to its neighbors; |
| 5: | Send an ; |
| 6: | ; |
| 7: | end if |
| 8: | else |
| 9: | if and then |
| 10: | Broadcast to its neighbors; |
| 11: | ; |
| 12: | end if |
| 13: | end if |
| 14: | end while |
| 15: | while Receiving a new do |
| 16: | if i is inside the target area then |
| 17: | Broadcast to its neighbors; |
| 18: | else |
| 19: | Forward the greedily; |
| 20: | end if |
| 21: | end while |
| 22: | while Receiving a new do |
| 23: | ; |
| 24: | if then |
| 25: | Forward to its neighbors; |
| 26: | ; |
| 27: | end if |
| 28: | end while |
4.4.1. Determining the Forwarding Direction
| Algorithm 2 Track routing algorithm at sensor node i. | |
| Input: the neighbor node set ; the sink path, the timestamp ; , ; | |
| Output: the next-hop forwarder; | |
| 1: | while receiving or buffering a packet in the track routing mode do |
| 2: | if node i is the tracking node then |
| 3: | if ==- then |
| 4: | Find the node j with the maximum in ; |
| 5: | if then |
| 6: | Forward the packet to j; |
| 7: | ; |
| 8: | else |
| 9: | Forward the packet to the adjacent node k with the maximum ; |
| 10: | ; |
| 11: | end if |
| 12: | else |
| 13: | Determine based on Equation (15); |
| 14: | Find the node j satisfying Equation (17); |
| 15: | if then |
| 16: | Forward the packet to j; |
| 17: | else |
| 18: | Forward the packet to the adjacent node in ; |
| 19: | end if |
| 20: | end if |
| 21: | else |
| 22: | if then |
| 23: | Deliver the packet to M; |
| 24: | else if then |
| 25: | Forward the packet to the adjacent node in ; |
| 26: | else if then |
| 27: | Reverse and forward the packet to the adjacent node in new ; |
| 28: | ; |
| 29: | else |
| 30: | Find the node j satisfying Equation (17); |
| 31: | if then |
| 32: | Forward the packet to j; |
| 33: | else |
| 34: | Forward the packet to the adjacent node in ; |
| 35: | end if |
| 36: | end if |
| 37: | end if |
| 38: | end while |
4.4.2. Selecting the Forwarder
5. Implementation and Performance Evaluation
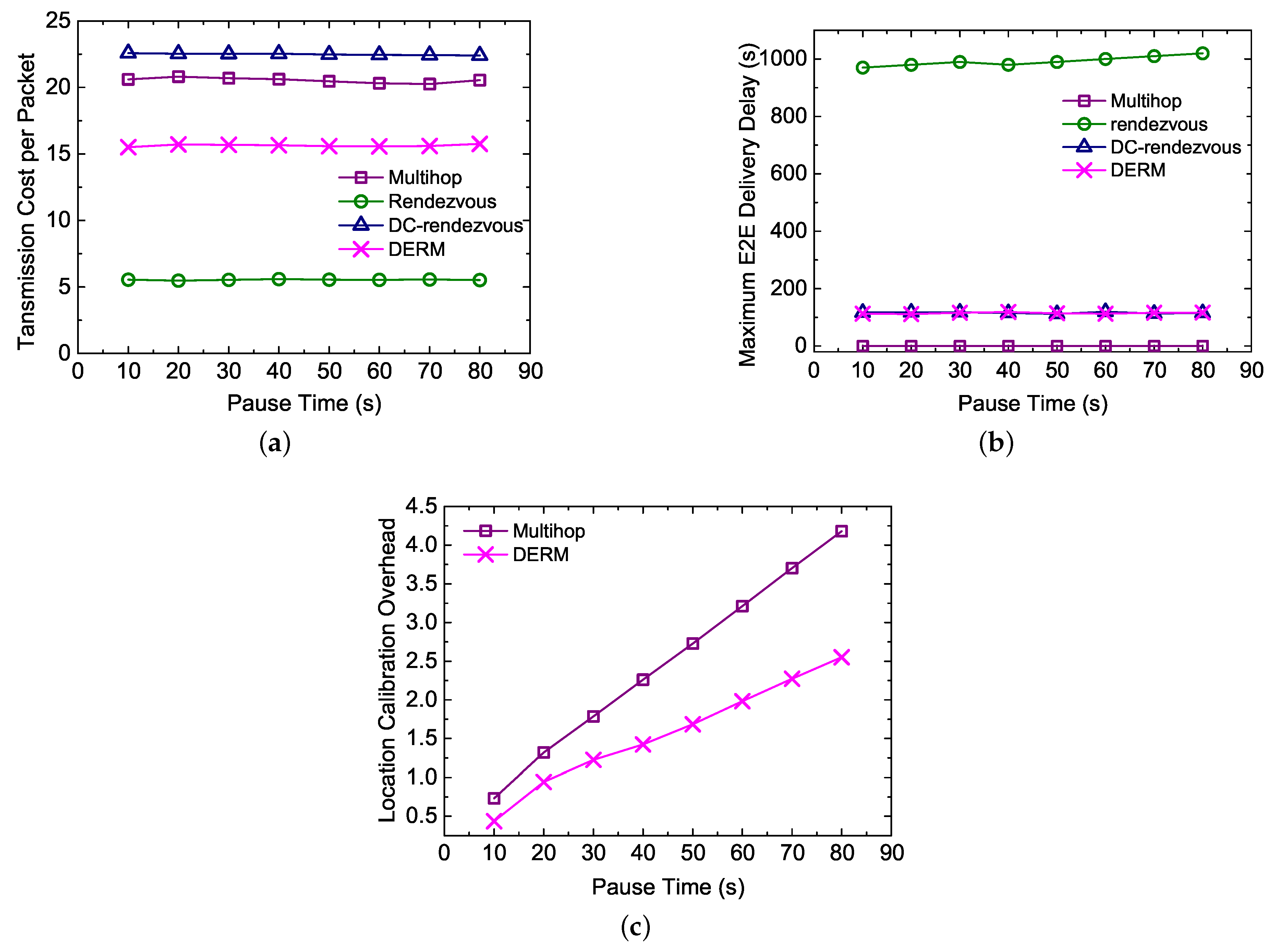
- Immediate Multi-hop Routing (Multihop): All nodes send data packets immediately to the mobile sink using geographic routing. The location of the sink is estimated and calibrated as in DERM, and the track routing mechanism is exploited to dealing with the location deviations.
- Rendezvous-based Routing (Rendezvous): Each data packet is transmitted to an RN via the shortest path using geo-routing and then collected when the sink arrives.
- Delay-Constrained Rendezvous-based Routing (DC-rendezvous): Each packet is first sent to the closest RN as in the traditional rendezvous-based routing. However, if the sink has not arrived within the delay constraint, the packet will be delivered to it via the track routing.
5.1. Simulation Setup
5.2. Evaluation Metrics
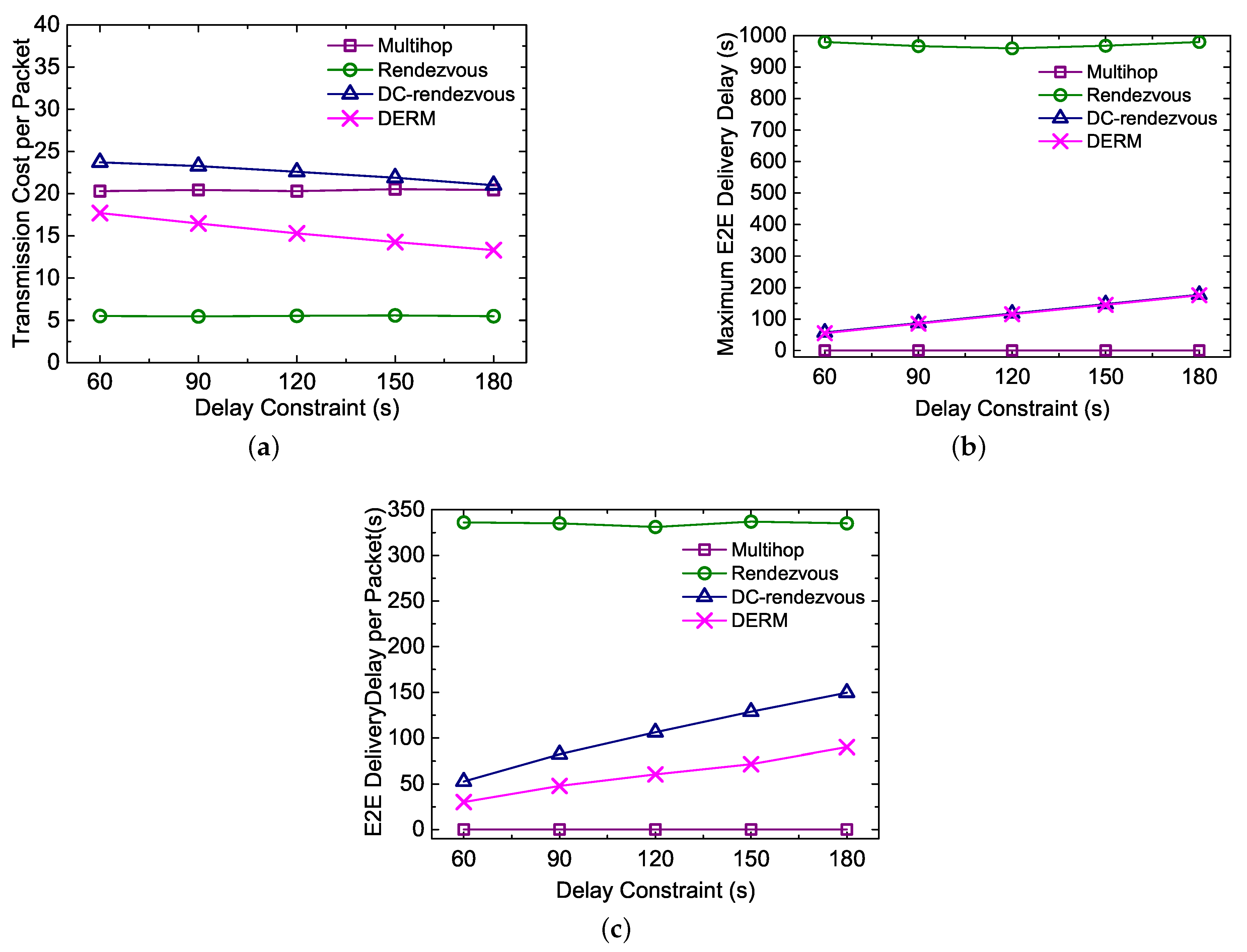
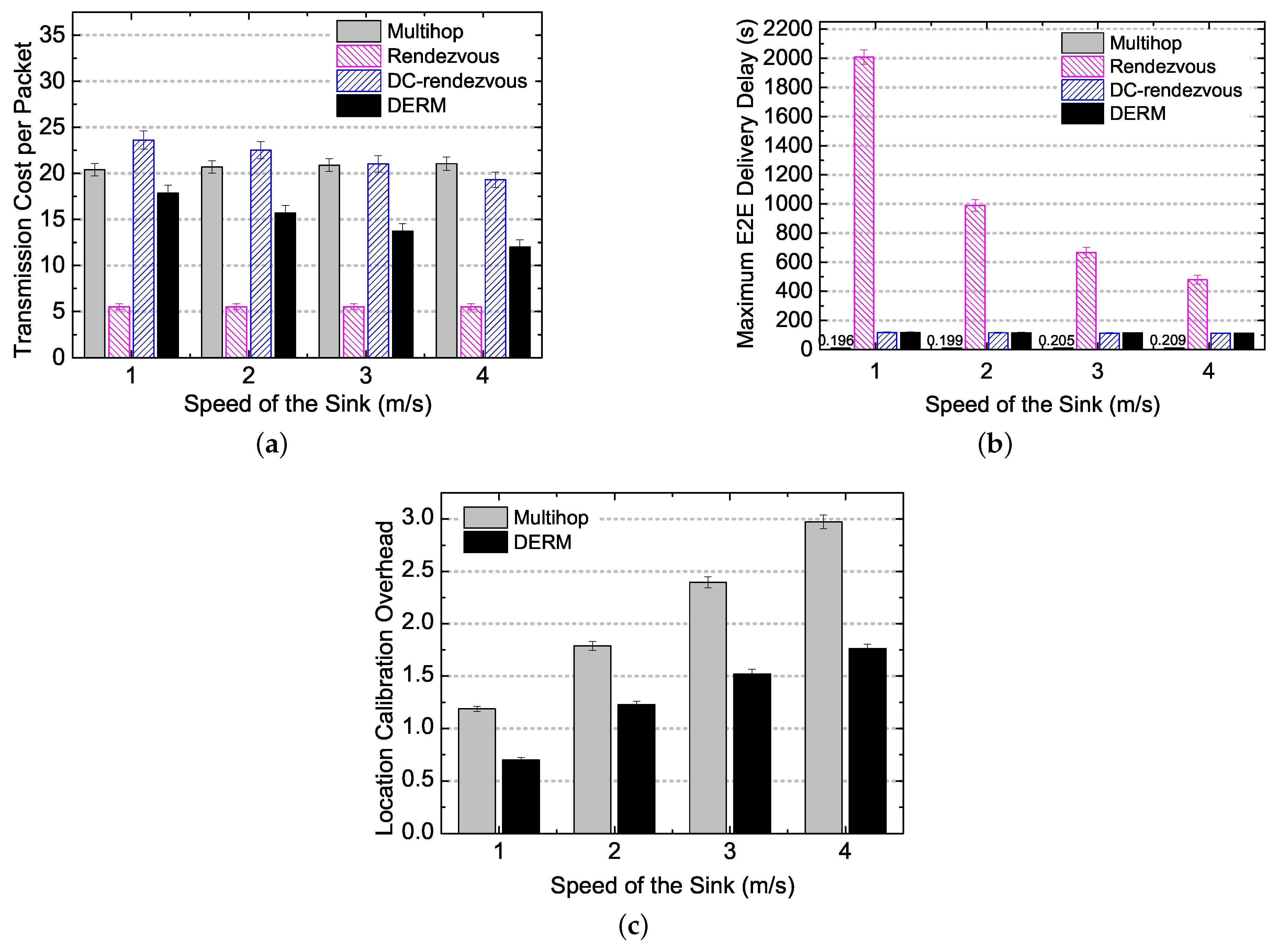
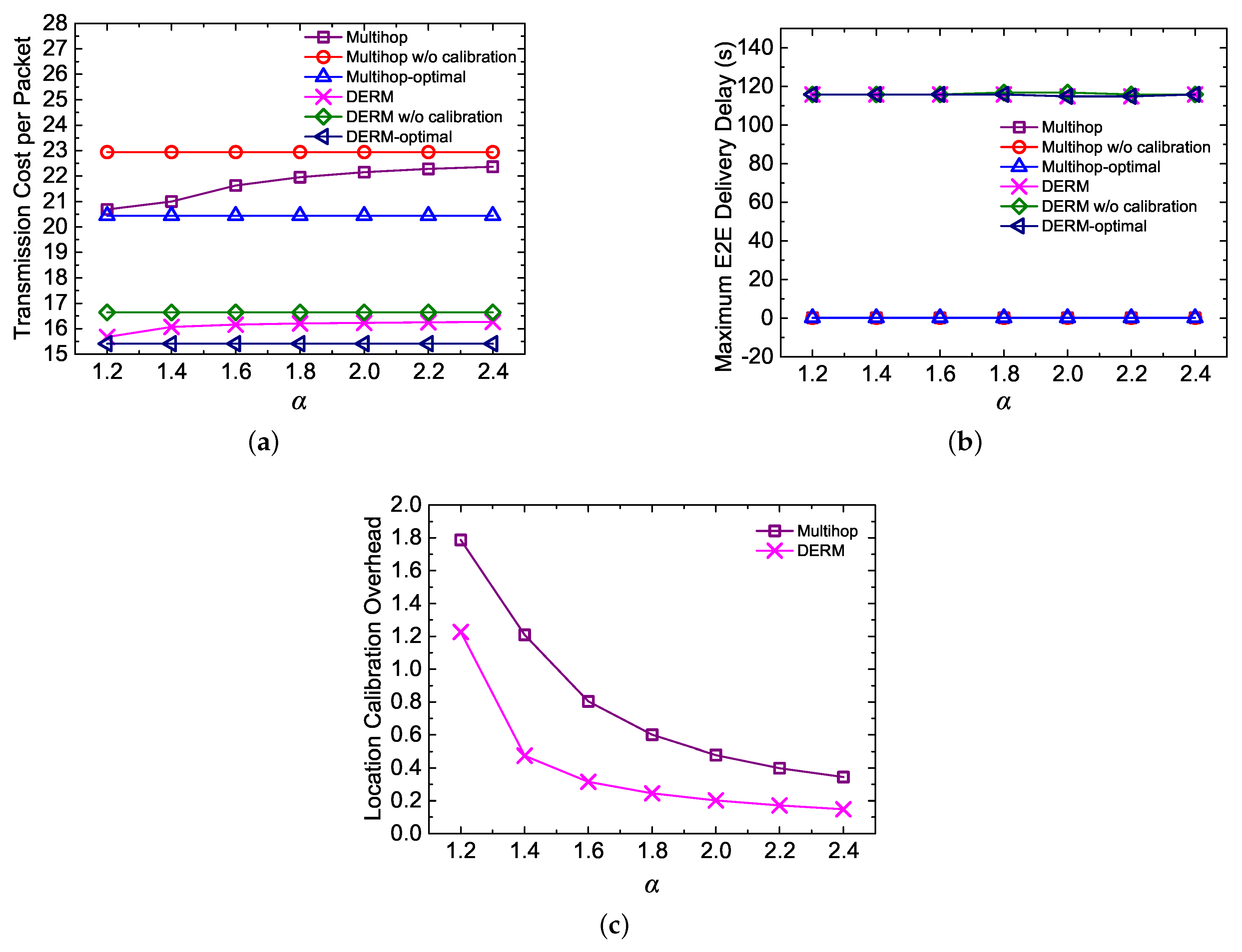
- Transmission Cost per Packet: measured as the average number of transmissions for an end-to-end (E2E) packet delivery.
- E2E Delivery Delay per Packet: the average elapsed time from a data packet being sent out by the source node to finally being collected by the mobile sink.
- Maximum E2E Delivery Delay: the maximum of end-to-end delivery delays of all packets generated at different sensor nodes.
- Location Calibration Overhead: measured as the average number of sink location updates per node during one cycle of sink movement.
- Packet Delivery Success Ratio: the ratio of the number of packets successfully received by the sink to the total number of packets sent from source nodes.
- On-time Delivery Ratio: the ratio of the number of packets delivered to the sink within the delay constraint to the total number of packets sent by source nodes.
5.3. Performance Evaluation in Ideal Movement Scenarios
5.3.1. Performance Overview in Ideal Movement Scenarios
5.3.2. Impact of the Delay Constraint
5.4. Performance Evaluation in Realistic Movement Scenarios
5.4.1. Performance Overview in Realistic Movement Scenarios
5.4.2. Impact of
5.4.3. Impact of the Pause Time
5.4.4. Effectiveness of DERM for Reliable Packet Delivery
5.5. Performance Summary
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gungor, V.C.; Hancke, G.P. Industrial wireless sensor networks: challenges, design principles, and technical approaches. IEEE Trans. Ind. Electron. 2009, 56, 4258–4265. [Google Scholar] [CrossRef]
- Shu, L.; Mukherjee, M.; Hu, L.; Bergmann, N.; Zhu, C. Geographic routing in duty-cycled industrial wireless sensor networks with radio irregularity. IEEE Access 2016, 4, 9043–9052. [Google Scholar] [CrossRef]
- Xia, C.; Jin, X.; Kong, L.; Zeng, P. Scheduling for Emergency Tasks in Industrial Wireless Sensor Networks. Sensors 2017, 17, 1674. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, M.; Shu, L.; Hu, L.; Hancke, G.P.; Zhu, C. Sleep scheduling in industrial wireless sensor networks for toxic gas monitoring. IEEE Wirel. Commun. 2017, 24, 106–112. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, J.; Lv, Z.; Wei, W.; Song, H. A real-time monitoring system of industry carbon monoxide based on wireless sensor networks. Sensors 2015, 15, 29535–29546. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Yan, J.; Lu, N.; Wang, Y.; Yang, X. Ubiquitous monitoring for industrial cyber-physical systems over relay-assisted wireless sensor networks. IEEE Trans. Emerg. Top. Comput. 2015, 3, 352–362. [Google Scholar] [CrossRef]
- Ma, J.; Yang, D.; Zhang, H.; Gidlund, M. A reliable handoff mechanism for mobile industrial wireless sensor networks. Sensors 2017, 17, 1797. [Google Scholar] [CrossRef] [PubMed]
- Di Francesco, M.; Das, S.K.; Anastasi, G. Data collection in wireless sensor networks with mobile elements: A survey. ACM Trans. Sens. Netw. 2011, 8, 1–31. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, B.; Li, C.; Mouftah, H. Routing protocols for wireless sensor networks with mobile sinks: A survey. IEEE Commun. Mag. 2014, 52, 150–157. [Google Scholar] [CrossRef]
- Jain, S.; Shah, R.C.; Brunette, W.; Borriello, G.; Roy, S. Exploiting mobility for energy efficient data collection in wireless sensor networks. Mob. Netw. Appl. 2006, 11, 327–339. [Google Scholar] [CrossRef]
- Li, Z.; Li, M.; Wang, J.; Cao, Z. Ubiquitous data collection for mobile users in wireless sensor networks. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM), Shanghai, China, 10–15 April 2011; pp. 2246–2254. [Google Scholar]
- Kusy, B.; Lee, H.; Wicke, M.; Milosavljevic, N.; Guibas, L. Predictive QoS routing to mobile sinks in wireless sensor networks. In Proceedings of the ACM/IEEE International Conference on Information Processing in Sensor Networks (IPSN), San Francisco, CA, USA, 13–16 April 2009; pp. 109–120. [Google Scholar]
- Lee, H.; Wicke, M.; Kusy, B.; Gnawali, O.; Guibas, L. Data stashing: Energy-efficient information delivery to mobile sinks through trajectory prediction. In Proceedings of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks (IPSN), Stockholm, Sweden, 12–16 April 2010; pp. 291–302. [Google Scholar]
- Cheng, L.; Niu, J.; Francesco, M.D.; Das, S.K.; Luo, C.; Gu, Y. Seamless streaming data delivery in cluster-based wireless sensor networks with mobile elements. IEEE Syst. J. 2016, 10, 805–816. [Google Scholar] [CrossRef]
- Zhou, Z.; Du, C.; Shu, L.; Hancke, G.; Niu, J.; Ning, H. An energy-balanced heuristic for mobile sink scheduling in hybrid WSNs. IEEE Trans. Ind. Inform. 2016, 12, 28–40. [Google Scholar] [CrossRef]
- Salarian, H.; Chin, K.W.; Naghdy, F. An energy-efficient mobile-sink path selection strategy for wireless sensor networks. IEEE Trans. Veh. Technol. 2014, 63, 2407–2419. [Google Scholar] [CrossRef]
- Somasundara, A.A.; Ramamoorthy, A.; Srivastava, M.B. Mobile element scheduling with dynamic deadlines. IEEE Trans. Mob. Comput. 2007, 6, 395–410. [Google Scholar] [CrossRef]
- Luo, J.; Hubaux, J.P. Joint mobility and routing for lifetime elongation in wireless sensor networks. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM), Miami, FL, USA, 13–17 March 2005; pp. 1735–1746. [Google Scholar]
- Wang, Z.M.; Basagni, S.; Melachrinoudis, E.; Petrioli, C. Exploiting sink mobility for maximizing sensor networks lifetime. In Proceedings of the IEEE 38th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 3–6 January 2005; p. 287a. [Google Scholar]
- Gandham, S.R.; Dawande, M.; Prakash, R.; Venkatesan, S. Energy efficient schemes for wireless sensor networks with multiple mobile base stations. In Proceedings of the IEEE Global telecommunications conference (GLOBECOM), San Francisco, CA, USA, 1–5 December 2003; pp. 377–381. [Google Scholar]
- Xing, G.; Wang, T.; Jia, W.; Li, M. Rendezvous design algorithms for wireless sensor networks with a mobile base station. In Proceedings of the 9th ACM international symposium on Mobile ad hoc networking and computing (MobiHoc), Hong Kong, China, 26–30 May 2008; pp. 231–240. [Google Scholar]
- Xing, G.; Wang, T.; Xie, Z.; Jia, W. Rendezvous Planning in Wireless Sensor Networks with Mobile Elements. IEEE Trans. Mob. Comput. 2008, 7, 1430–1443. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, Y. Bounded relay hop mobile data gathering in wireless sensor networks. IEEE Trans. Comput. 2012, 61, 265–277. [Google Scholar] [CrossRef]
- Xu, J.; Wang, C.P.; Dai, H.; Zhang, D.Q.; Yu, J.J. Designing constrained trajectory based on Maximizing Energy Reduction in large-scale wireless sensor networks. Int. J. Distrib. Sens. Netw. 2015, 11, 801831. [Google Scholar] [CrossRef]
- Kumar, N.; Dash, D.; Kumar, P. Optimal Sub-Path Selection for Maximum Data Gathering Using Mobile Sink in WSN. In Proceedings of the 7th International ACM Conference on Computer and Communication Technology, Allahabad, India, 24–26 November 2017; pp. 66–71. [Google Scholar]
- Sha, C.; Qiu, J.M.; Li, S.Y.; Qiang, M.Y.; Wang, R.C. A type of low-latency data gathering method with multi-sink for sensor networks. Sensors 2016, 16, 923. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, A.; Sabharwal, A.; Aazhang, B. Communication power optimization in a sensor network with a path-constrained mobile observer. ACM Trans. Sens. Netw. 2006, 2, 297–324. [Google Scholar] [CrossRef]
- Song, L.; Hatzinakos, D. Architecture of wireless sensor networks with mobile sinks: Sparsely deployed sensors. IEEE Trans. Veh. Technol. 2007, 56, 1826–1836. [Google Scholar] [CrossRef]
- Ren, X.; Liang, W.; Xu, W. Use of a mobile sink for maximizing data collection in energy harvesting sensor networks. In Proceedings of the IEEE International Conference on Parallel Processing (ICPP), Lyon, France, 1–4 October 2013; pp. 439–448. [Google Scholar]
- Mehrabi, A.; Kim, K. Maximizing data collection throughput on a path in energy harvesting sensor networks using a mobile sink. IEEE Trans. Mob. Comput. 2016, 15, 690–704. [Google Scholar] [CrossRef]
- Luo, J.; Panchard, J.; Piórkowski, M.; Grossglauser, M.; Hubaux, J.P. Mobiroute: Routing towards a mobile sink for improving lifetime in sensor networks. In Proceedings of the International Conference on Distributed Computing in Sensor Systems (DCOSS), San Francisco, CA, USA, 18–20 June 2006; pp. 480–497. [Google Scholar]
- Somasundara, A.A.; Kansal, A.; Jea, D.D.; Estrin, D.; Srivastava, M.B. Controllably mobile infrastructure for low energy embedded networks. IEEE Trans. Mob. Comput. 2006, 5, 958–973. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, H.; Das, S.K. Efficient data collection in wireless sensor networks with path-constrained mobile sinks. IEEE Trans. Mob. Comput. 2011, 10, 592–608. [Google Scholar] [CrossRef]
- Yun, Y.S.; Xia, Y. Maximizing the lifetime of wireless sensor networks with mobile sink in delay-tolerant applications. IEEE Trans. Mob. Comput. 2010, 9, 1308–1318. [Google Scholar]
- Gu, Y.; Ji, Y.; Li, J.; Zhao, B. ESWC: Efficient scheduling for the mobile sink in wireless sensor networks with delay constraint. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1310–1320. [Google Scholar] [CrossRef]
- Xu, X.; Huangfu, X.; Wang, W.; Lu, Q. Wireless charging routing algorithm in WSN with a path-fixed sink. Chin. J. Sci. Instrum. 2016, 37, 570–578. [Google Scholar]
- Mauve, M.; Widmer, J.; Hartenstein, H. A survey on position-based routing in mobile ad hoc networks. IEEE Netw. 2001, 15, 30–39. [Google Scholar] [CrossRef]
- He, T.; Stankovic, J.A.; Abdelzaher, T.F.; Lu, C. A spatiotemporal communication protocol for wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2005, 16, 995–1006. [Google Scholar] [CrossRef]
- Lu, C.; Blum, B.M.; Abdelzaher, T.F.; Stankovic, J.A.; He, T. RAP: A real-time communication architecture for large-scale wireless sensor networks. In Proceedings of the IEEE Real-Time and Embedded Technology and Applications Symposium, San Jose, CA, USA, 27 September 2002; pp. 55–66. [Google Scholar]
- Cheng, L.; Niu, J.; Cao, J.; Das, S.K.; Gu, Y. QoS Aware Geographic Opportunistic Routing in Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1864–1875. [Google Scholar] [CrossRef]
- Chen, D.; Varshney, P.K. A survey of void handling techniques for geographic routing in wireless networks. IEEE Commun. Surv. Tutor. 2007, 9, 50–67. [Google Scholar] [CrossRef]
- Bose, P.; Morin, P.; Stojmenović, I.; Urrutia, J. Routing with guaranteed delivery in ad hoc wireless networks. Wirel. Netw. 2001, 7, 609–616. [Google Scholar] [CrossRef]
- Karp, B.; Kung, H.T. GPSR: Greedy perimeter stateless routing for wireless networks. In Proceedings of the ACM 6th annual international conference on Mobile computing and networking (MobiCom), Boston, MA, USA, 6–11 August 2000; pp. 243–254. [Google Scholar]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent advances in indoor localization: A survey on theoretical approaches and applications. IEEE Commun. Surv. Tutor. 2016, 19, 1327–1346. [Google Scholar] [CrossRef]
- Kim, K.H.; Shin, K.G. On accurate measurement of link quality in multi-hop wireless mesh networks. In Proceedings of the ACM 12th annual international conference on Mobile computing and networking (MobiCom), Los Angeles, CA, USA, 23–29 September 2006; pp. 38–49. [Google Scholar]
- CC2530 Datasheet. Available online: http://www.ti.com/product/CC2530 (accessed on 28 February 2018).
- Miklós, M.; Kusy, B.; Simon, G.; Lédeczi, Á. The flooding time synchronization protocol. In Proceedings of the ACM International Conference on Embedded Networked Sensor Systems (SenSys), Baltimore, MD, USA, 3–5 November 2004; pp. 39–49. [Google Scholar]
- Ferrari, F.; Zimmerling, M.; Thiele, L.; Saukh, O. Efficient network flooding and time synchronization with Glossy. In Proceedings of the IEEE International Conference on Information Processing in Sensor Networks (IPSN), Chicago, IL, USA, 12–14 April 2011; pp. 73–84. [Google Scholar]
- Niu, J.; Cheng, L.; Gu, Y.; Jun, J.; Zhang, Q. Minimum-delay and energy-efficient flooding tree in asynchronous low-duty-cycle wireless sensor networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 1261–1266. [Google Scholar]
- The Network Simulator: Ns-2. Available online: http://www.isi.edu/nsnam/ns/ (accessed on 28 February 2018).
- Cheng, L.; Cao, J.; Chen, C.; Ma, J.; Das, S.K. Exploiting geographic opportunistic routing for soft QoS provisioning in wireless sensor networks. In Proceedings of the IEEE 7th International Conference on Mobile Adhoc and Sensor Systems (MASS), San Francisco, CA, USA, 8–12 November 2010; pp. 292–301. [Google Scholar]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Chou, W.; Niu, J.; Guizani, M. Delay-Aware Energy-Efficient Routing towards a Path-Fixed Mobile Sink in Industrial Wireless Sensor Networks. Sensors 2018, 18, 899. https://doi.org/10.3390/s18030899
Wu S, Chou W, Niu J, Guizani M. Delay-Aware Energy-Efficient Routing towards a Path-Fixed Mobile Sink in Industrial Wireless Sensor Networks. Sensors. 2018; 18(3):899. https://doi.org/10.3390/s18030899
Chicago/Turabian StyleWu, Shaobo, Wusheng Chou, Jianwei Niu, and Mohsen Guizani. 2018. "Delay-Aware Energy-Efficient Routing towards a Path-Fixed Mobile Sink in Industrial Wireless Sensor Networks" Sensors 18, no. 3: 899. https://doi.org/10.3390/s18030899




