A Revised Hilbert–Huang Transform and Its Application to Fault Diagnosis in a Rotor System
Abstract
1. Introduction
2. A Review of the Hilbert–Huang Transform
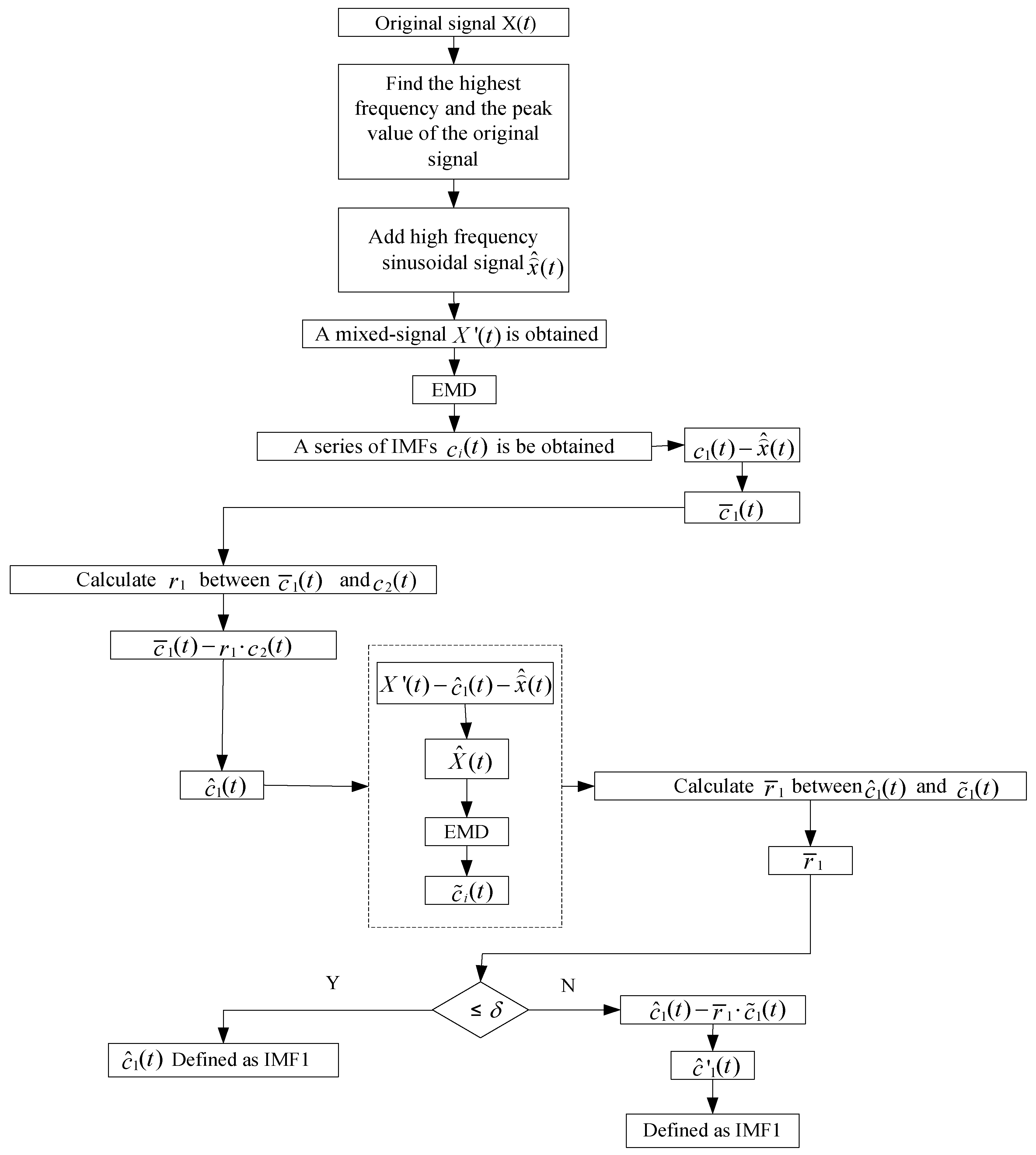
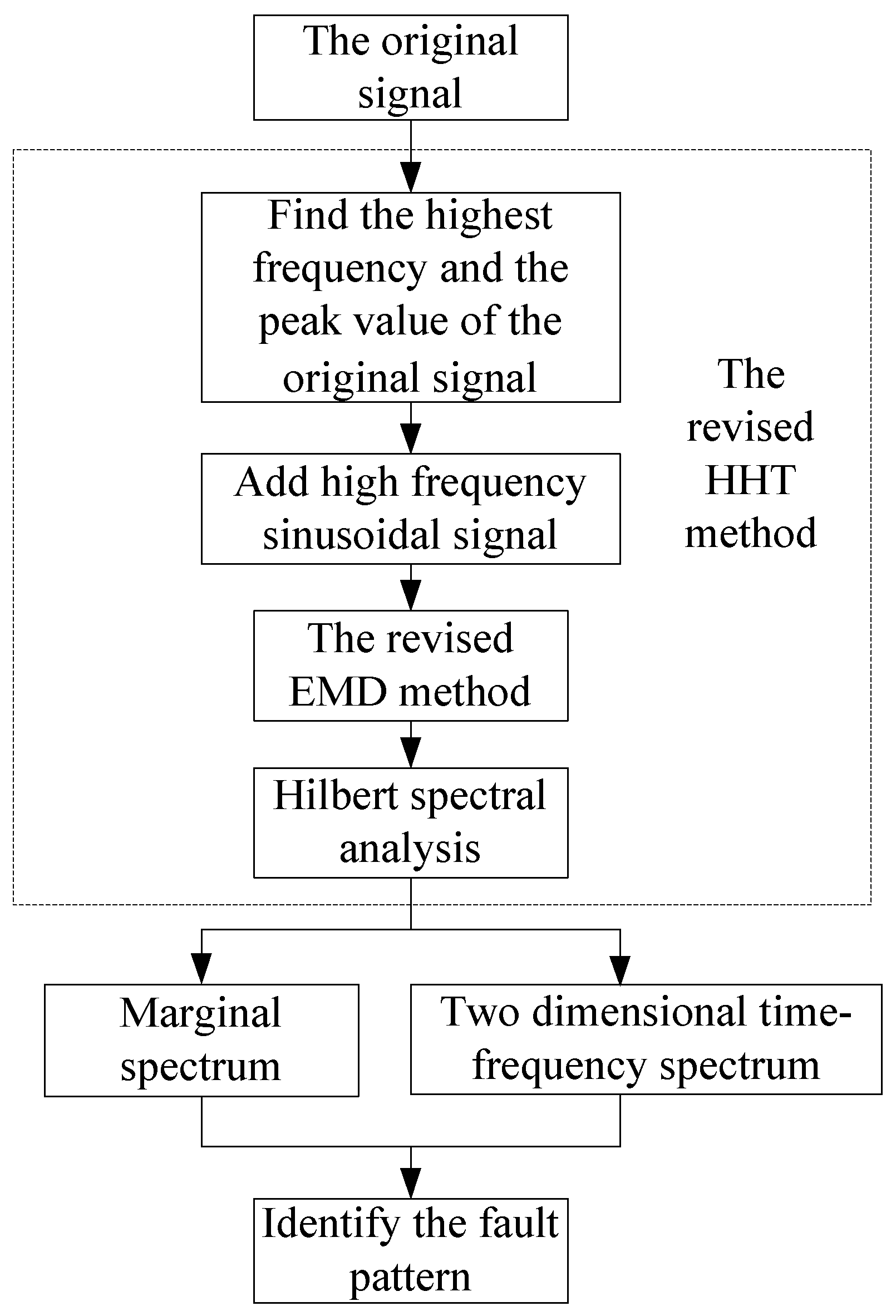
3. A Revised Hilbert–Huang Transform (HHT)
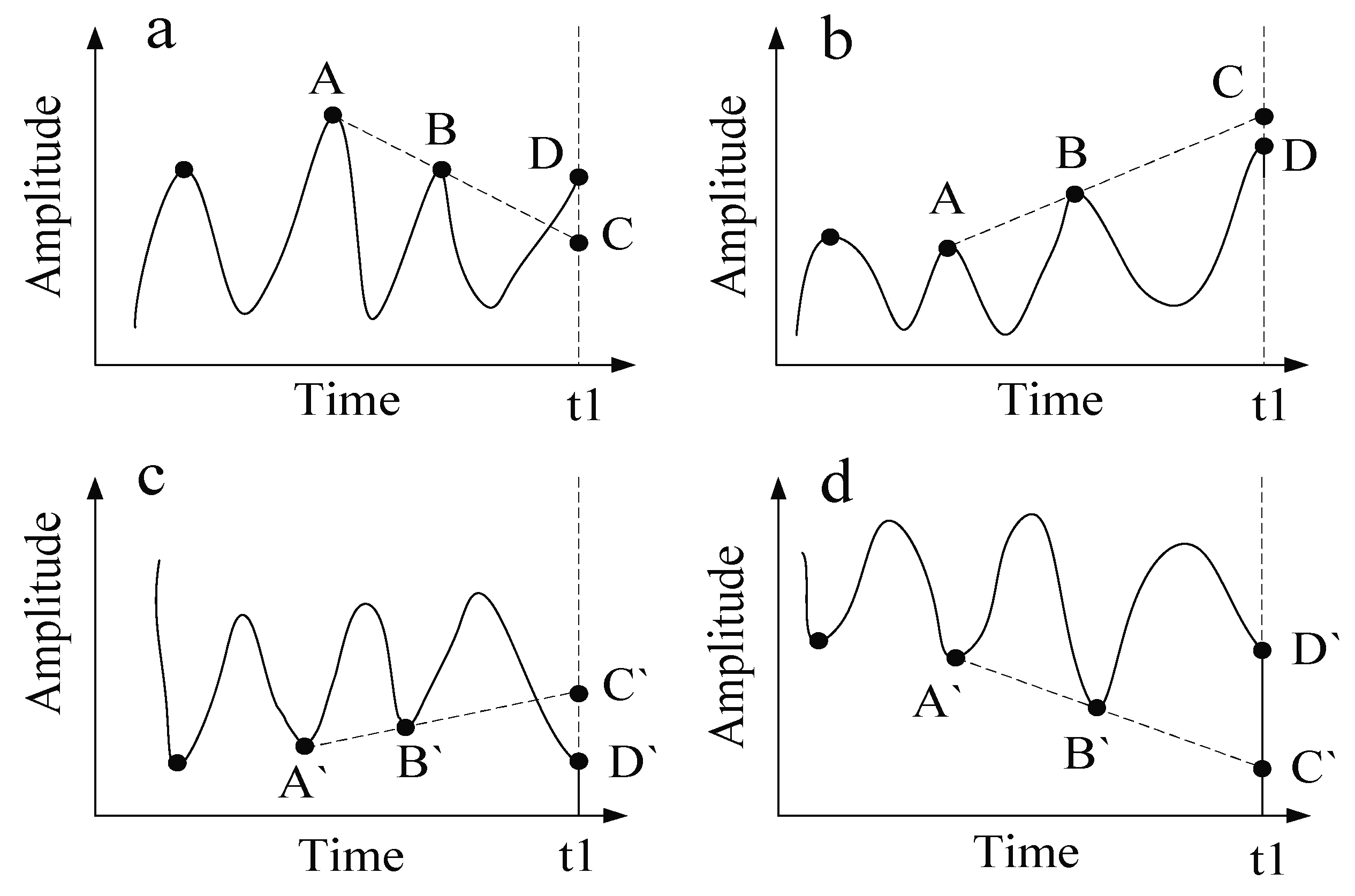
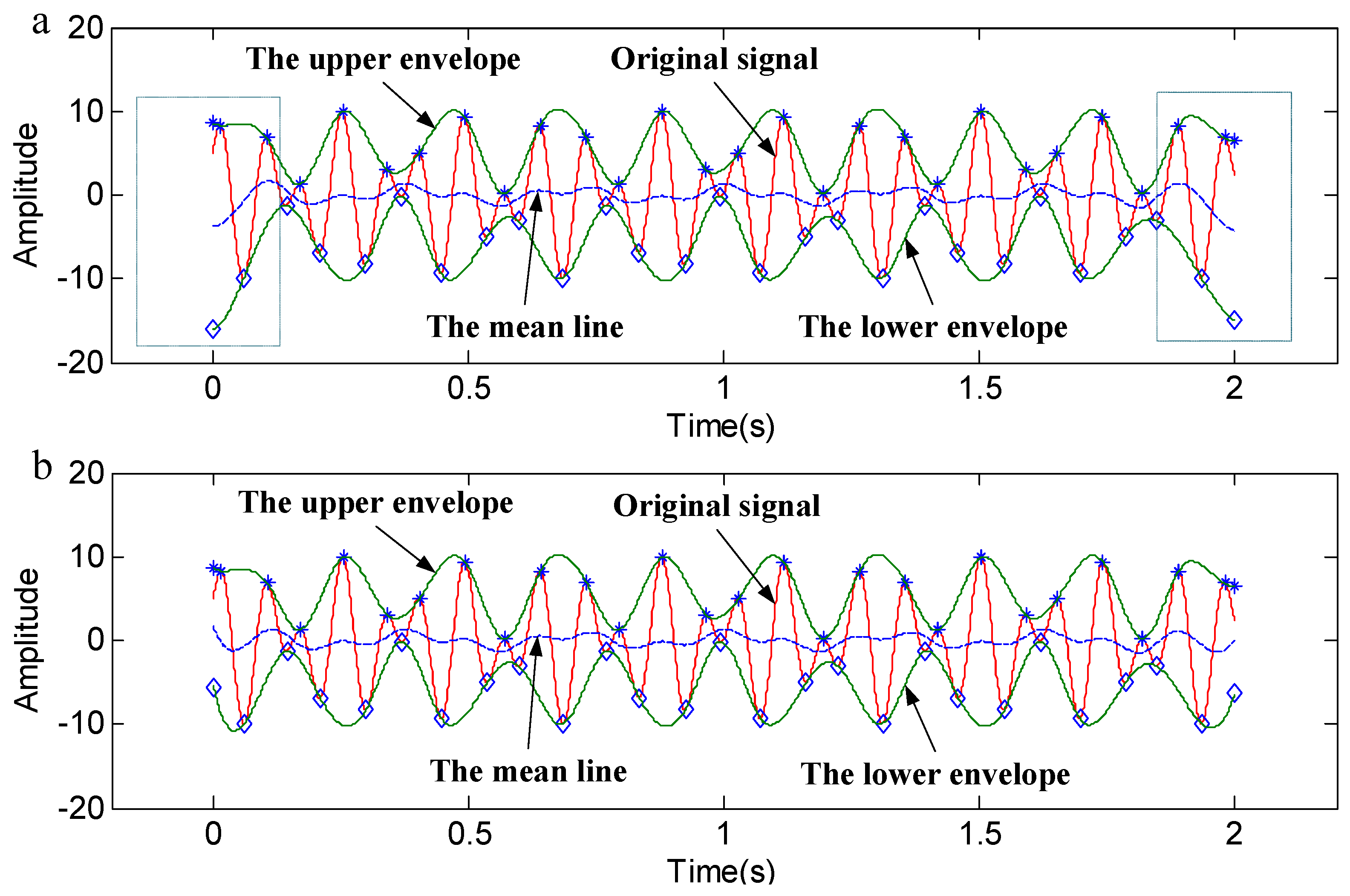
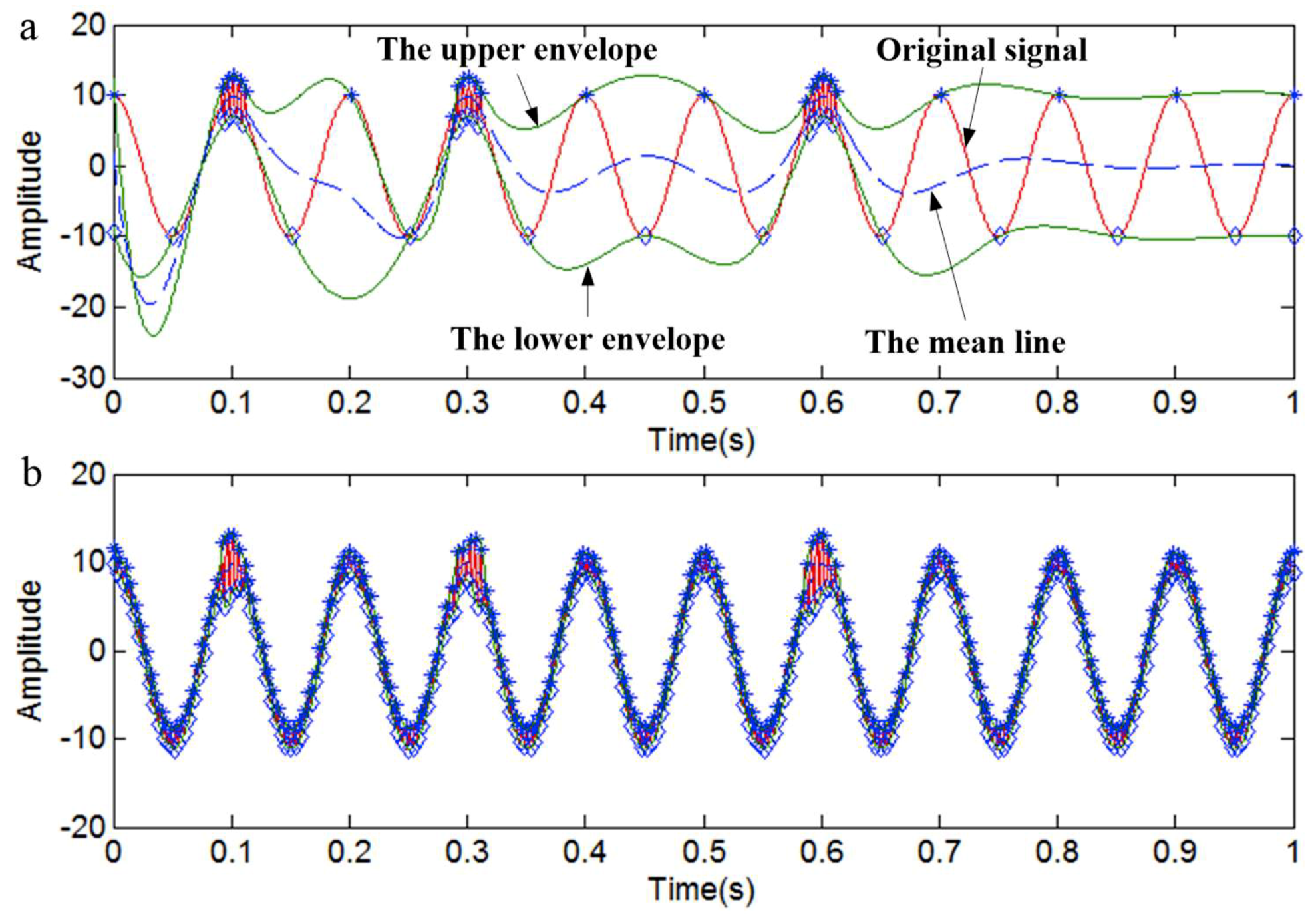
3.1. The Suppression of End Effects by Local Linear Extrapolation
- (1)
- The determination of the right maximum point:
- (1)
- The local maximum value points A and B are determined;
- (2)
- A straight line AB is determined by point A and B. Point C is the intersection point of line AB and the time axis that corresponds to the right endpoint D, as shown in Figure 1a.
- (3)
- If the value of point C is less than the value of the right endpoint D, the right endpoint D is identified as the maximum value; if the value of point C is greater than the value of the right endpoint D, as shown in Figure 1b, the maximum value point is identified in the following situations: if the value of point C is greater than twice the average value of point B + A, the maximum value point is identified as half of the value of adding C to D. Otherwise, the maximum value point is identified as the intersection point C.
- (2)
- The determination of the right minimum point:
- (1)
- The local maximum value points A` and B` are determined;
- (2)
- A straight line A`B` is determined by point A` and B`. Point C` is the intersection point of line A`B` and the time axis that corresponds to the right endpoint D`, as shown in Figure 1c.
- (3)
- If the value of point C` is greater than the value of the right endpoint D`, the right endpoint D` is identified as the minimum value; if the value of point C` is less than the value of the right endpoint D`, as shown in Figure 1d, the minimum value point is identified in the following situations: if the value of point C` is less than twice the average value of point B` + A`, the minimum value point is identified as half of the value of adding C` to D`. Otherwise, the minimum value point is identified as the intersection point C`.
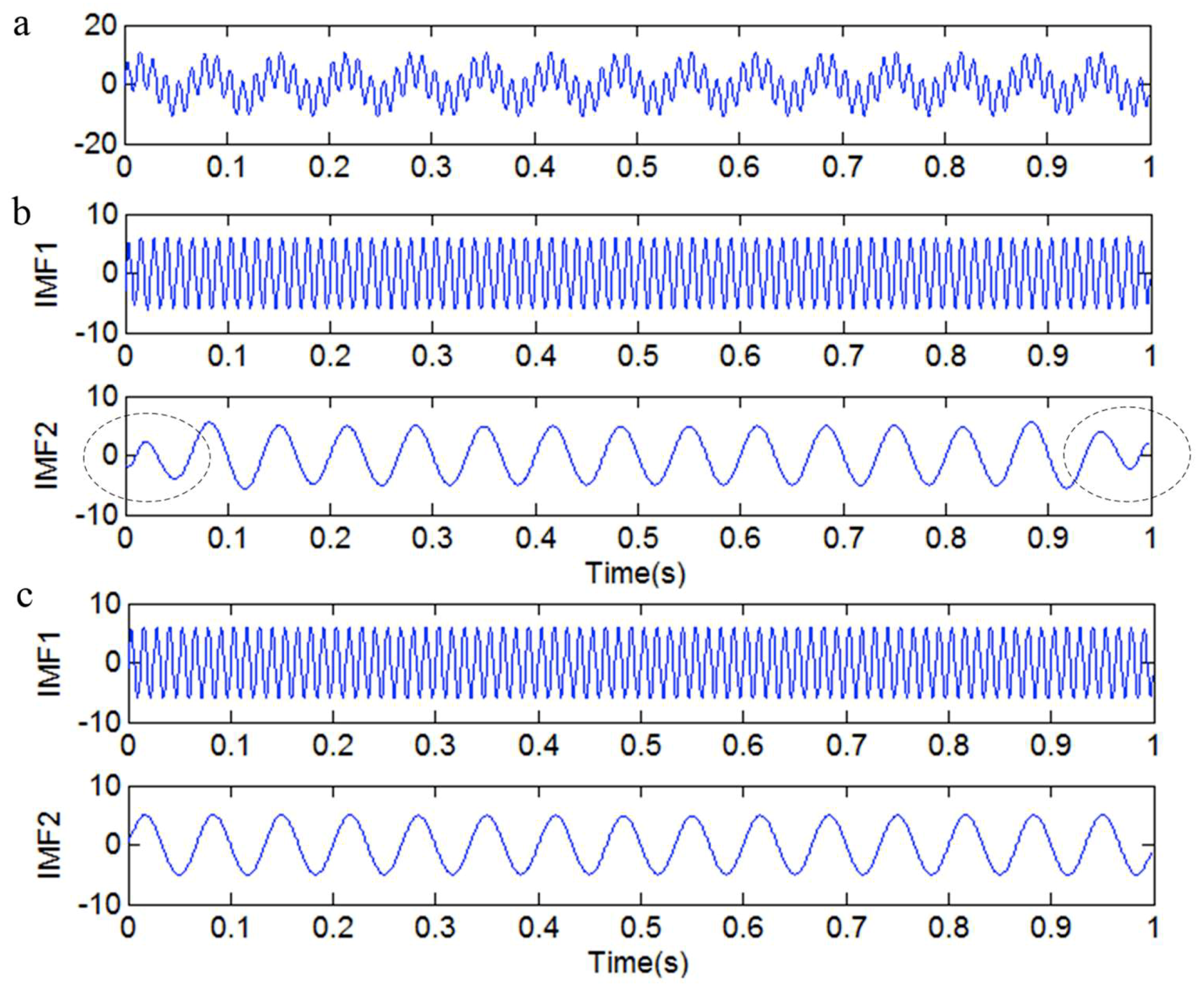
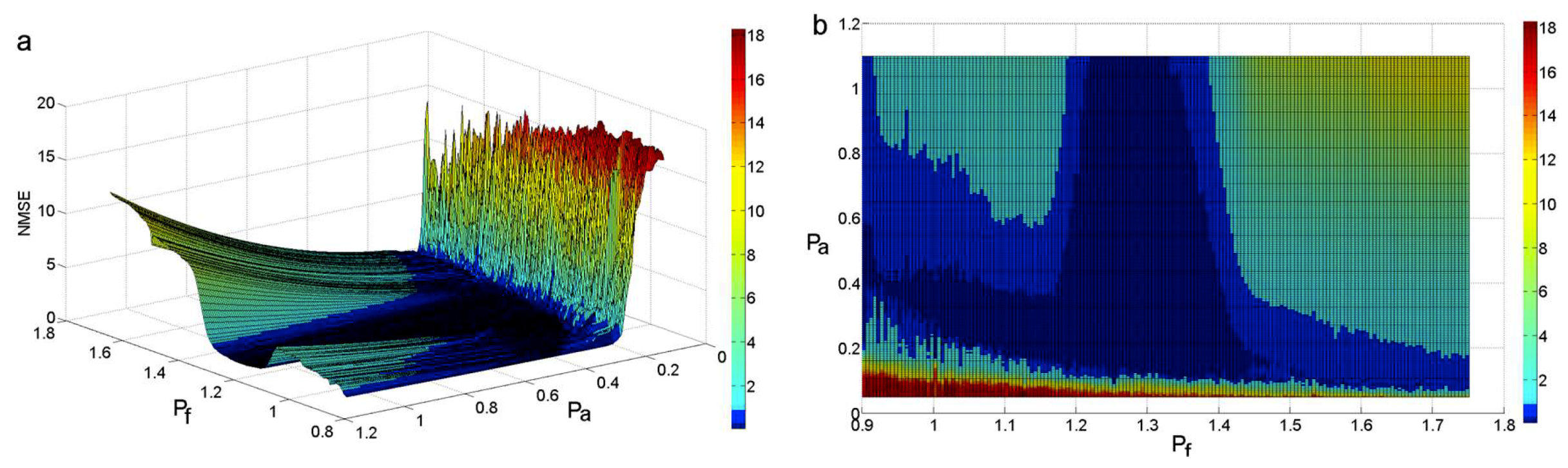
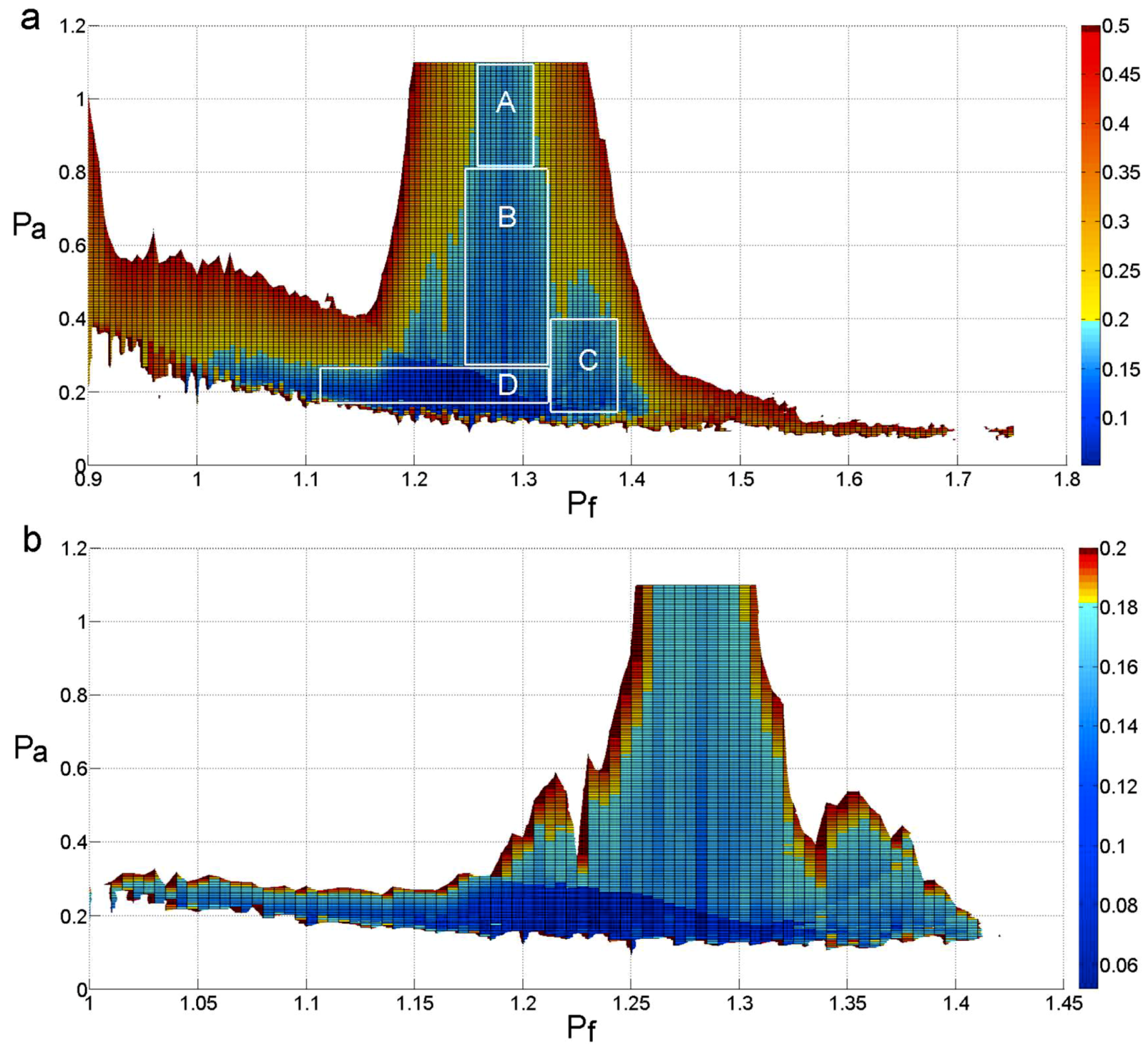
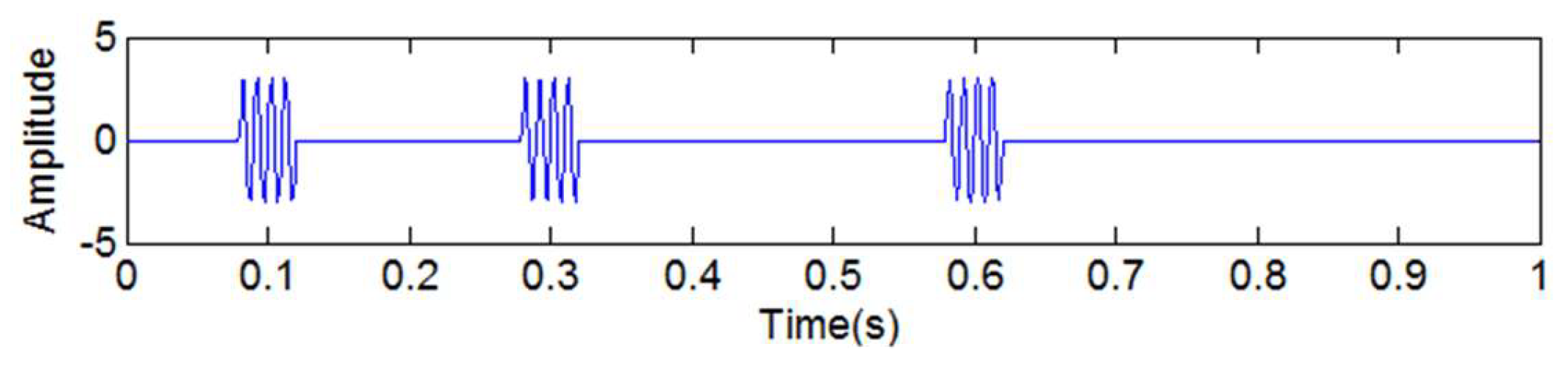
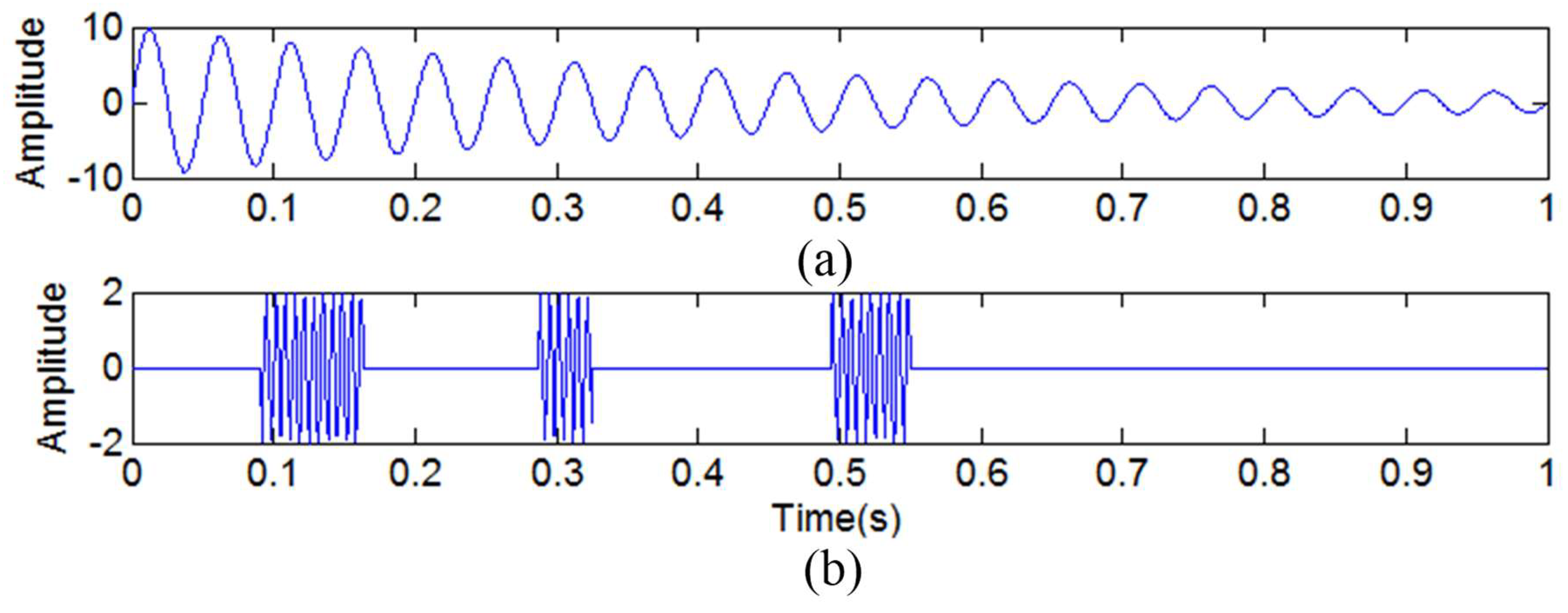
3.2. The Suppression of Mode Mixing by Adding a High-Frequency Sinusoidal Signal and Embedding a Decorrelation Operator
- (1)
- If , then and are uncorrelated;
- (2)
- If , then and are orthogonal;
- (3)
- Obviously, if and are uncorrelated () and , , then and are orthogonal.
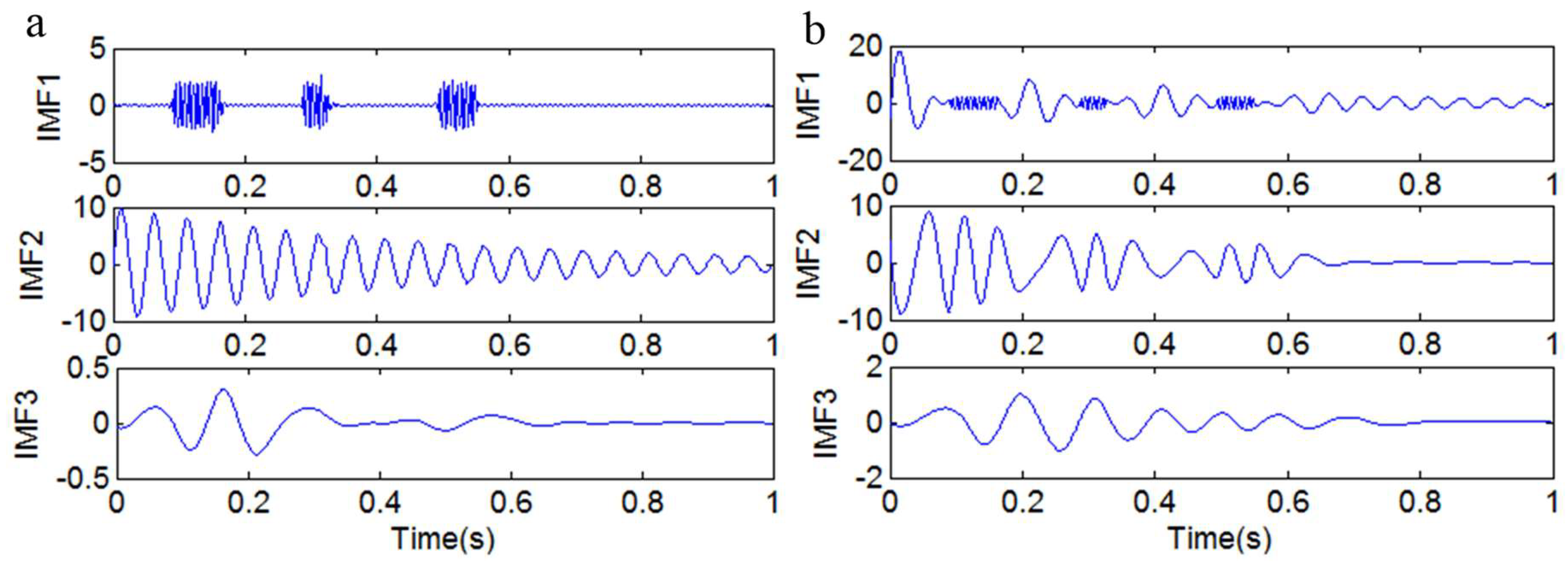
3.3. The Selection of IMF Components
- (1)
- The threshold is determined. Calculate the correlation coefficient between each IMF and the original signal.
- (2)
- The IMF will be eliminated if the correlation coefficient between the IMF and the original signal is less than the threshold; otherwise, the IMF will be reserved.
- (3)
- Rearrange the reserved IMFs according to the frequency from high to low.
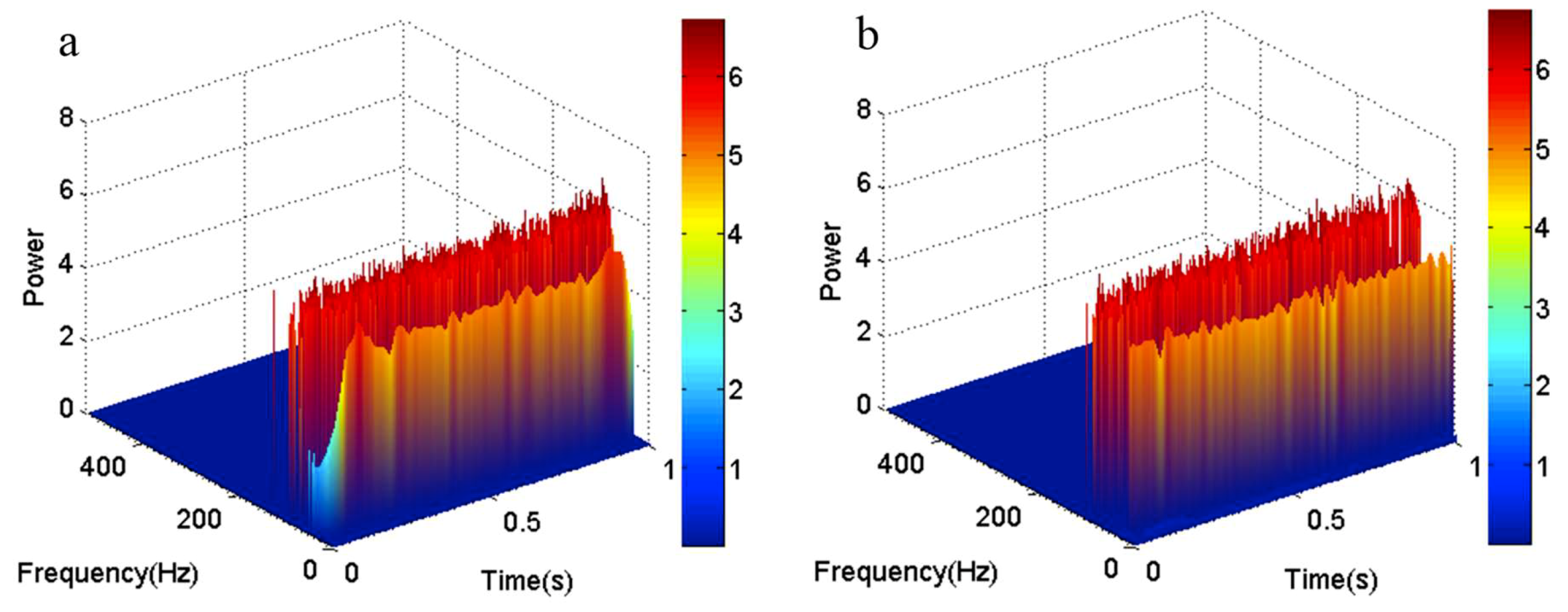
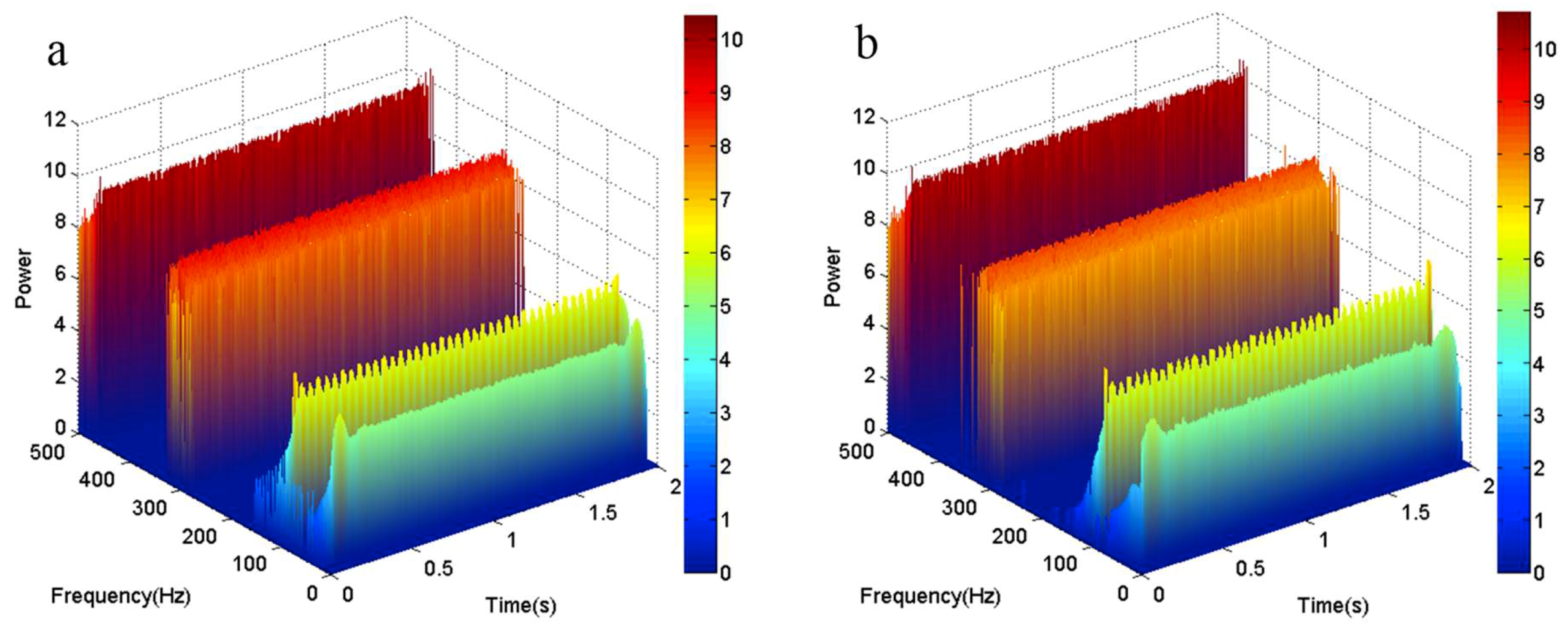
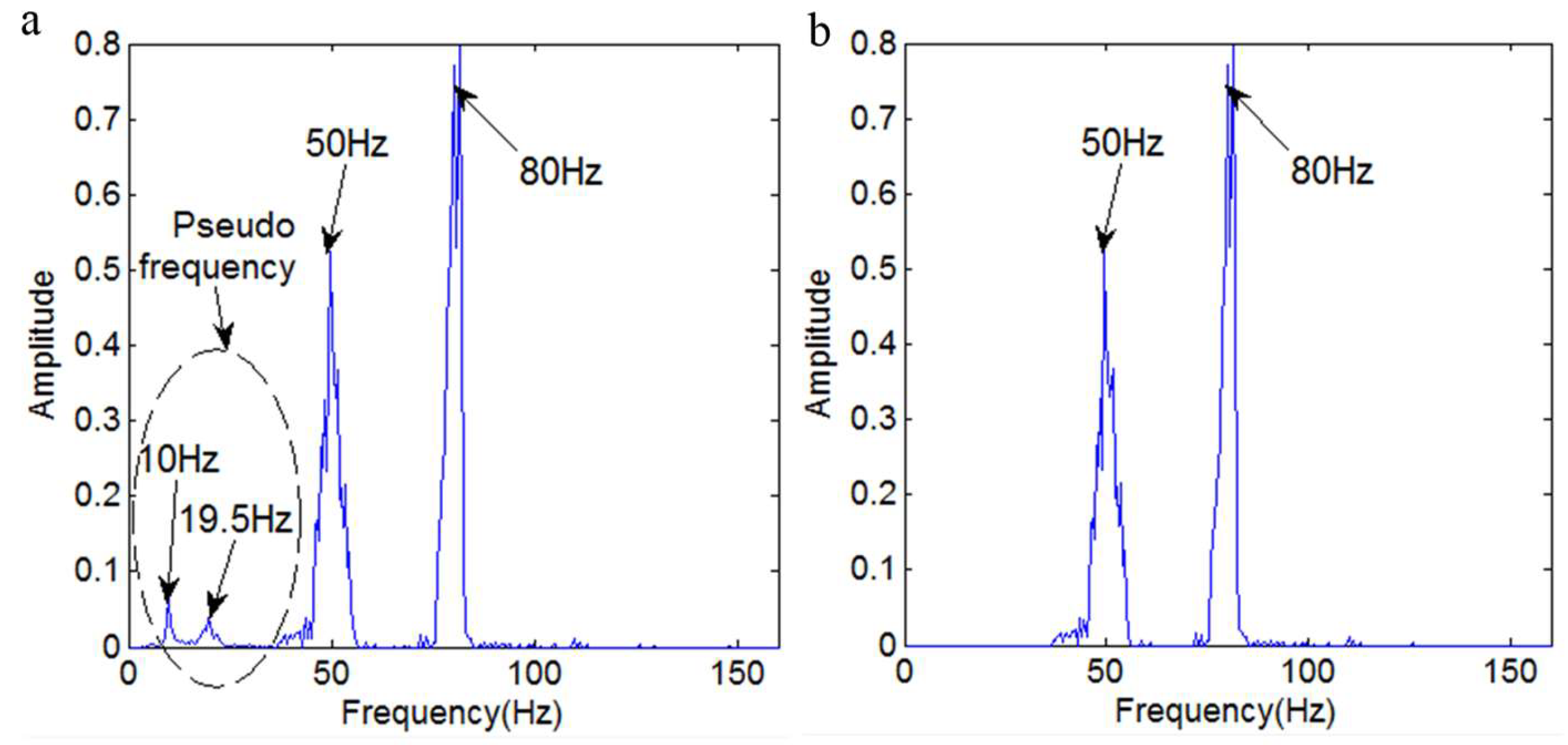
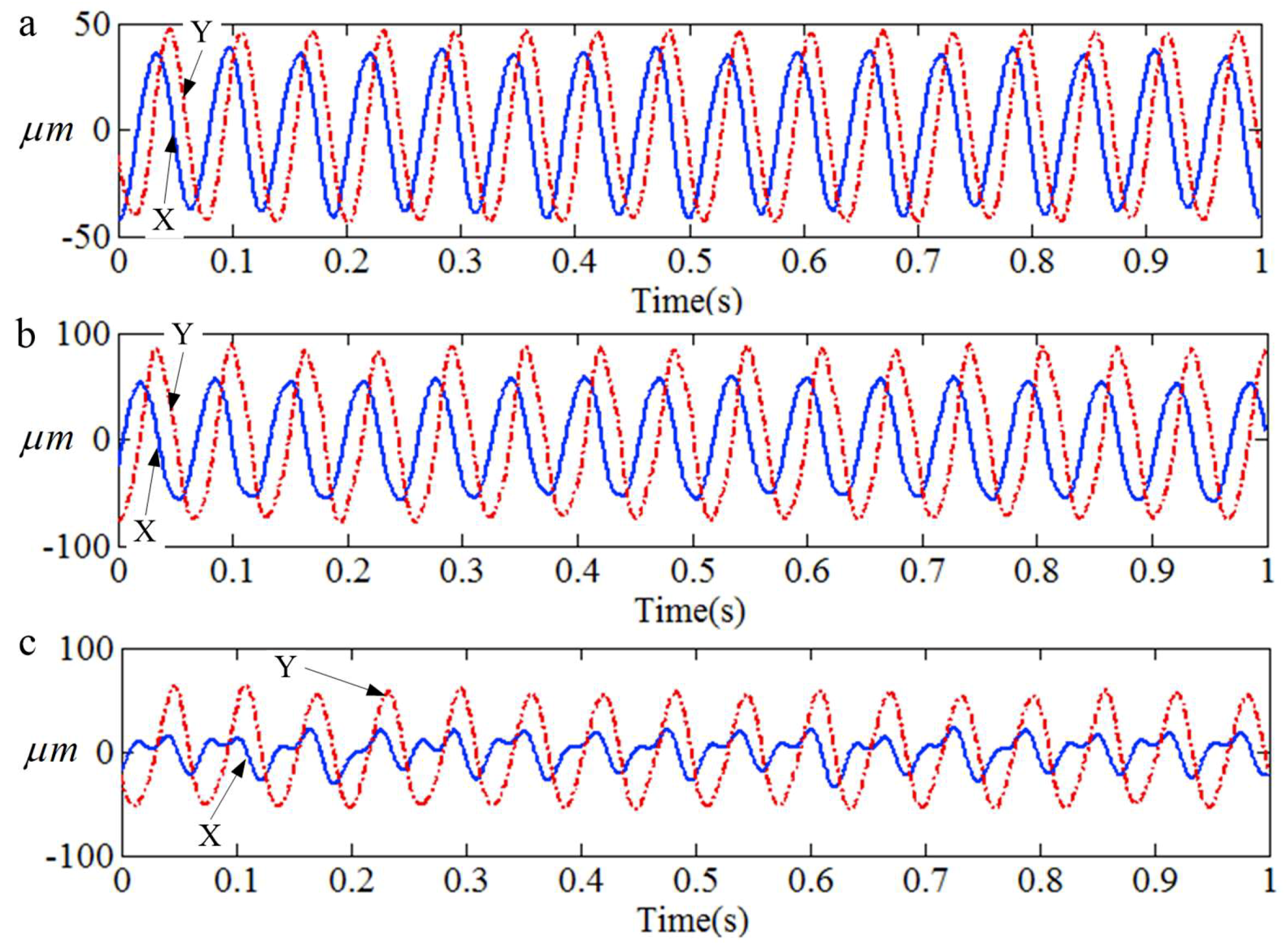
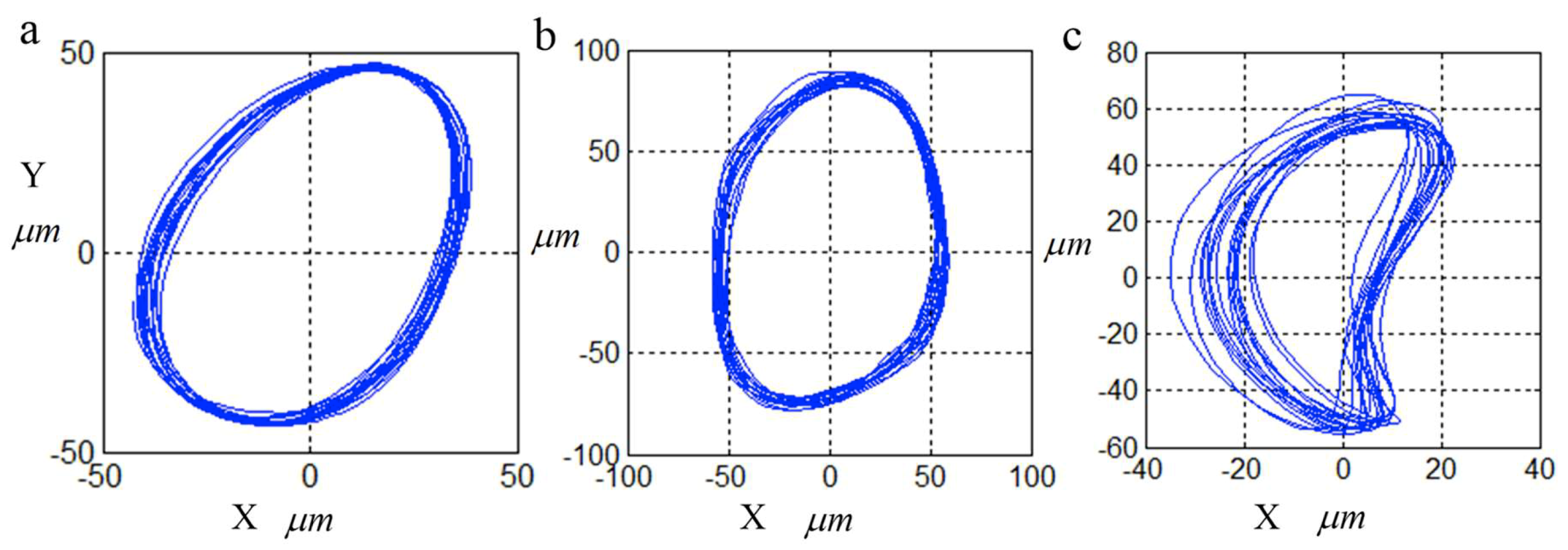
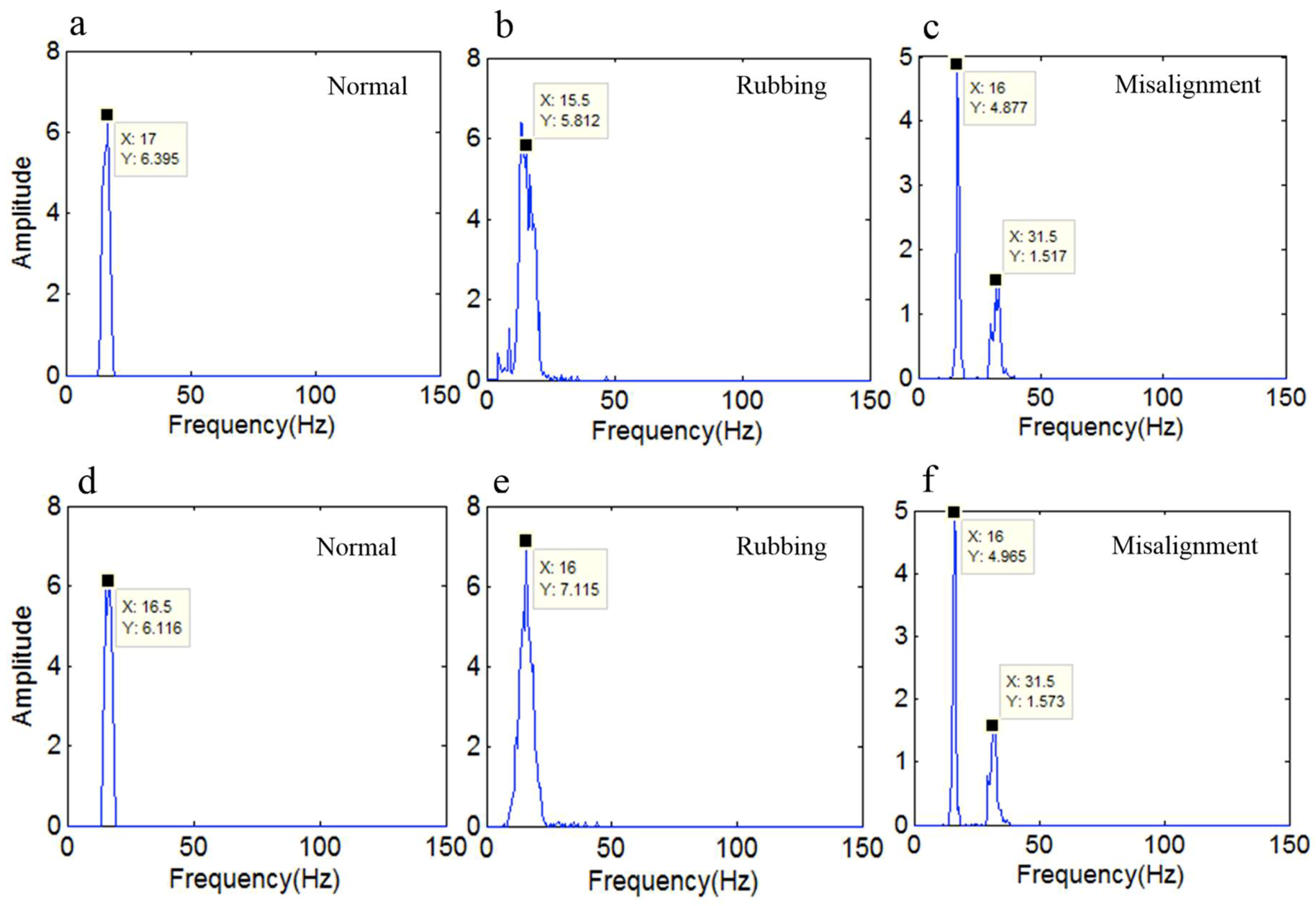
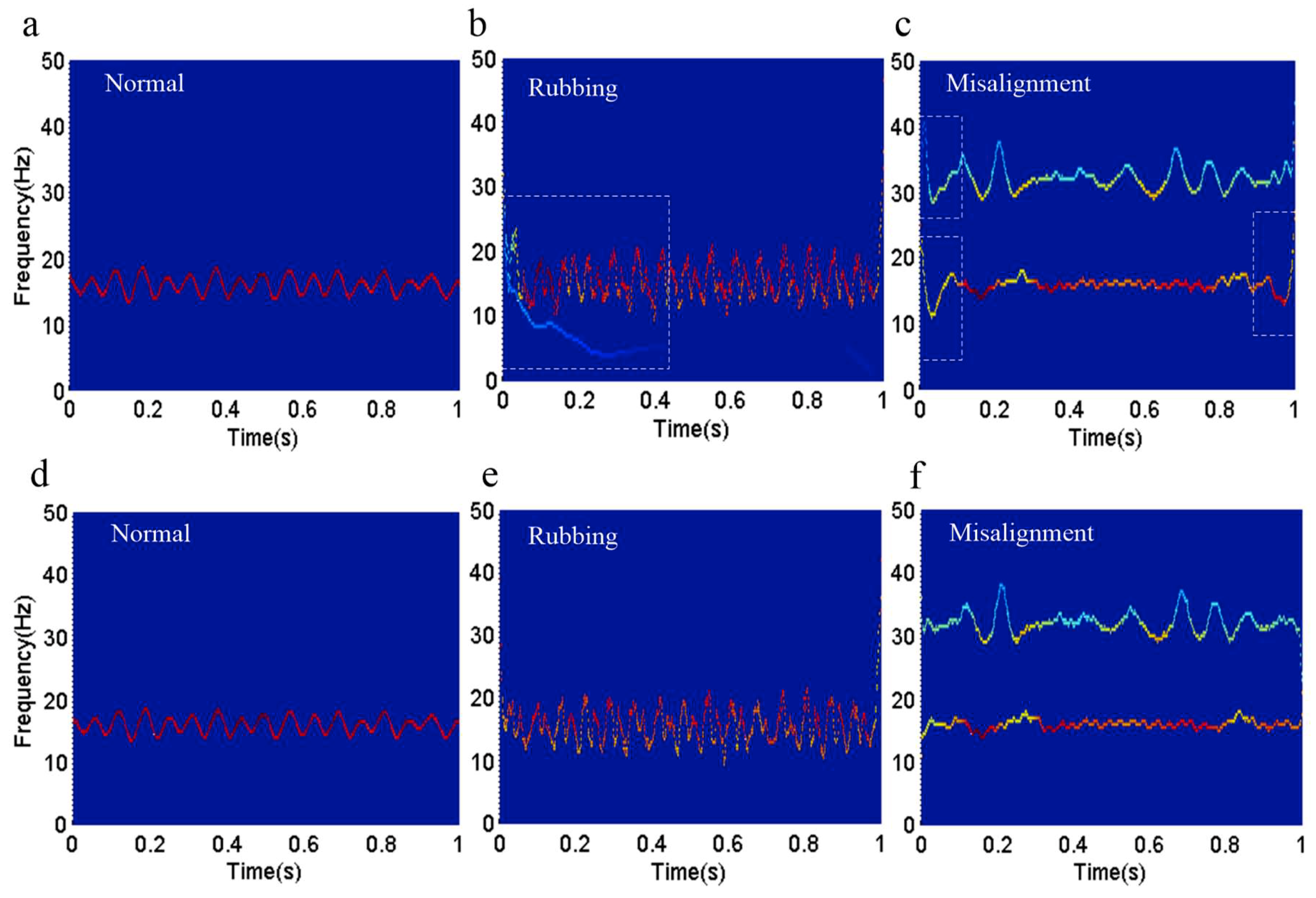
4. Fault Diagnosis in a Rotor System by the Revised HHT Method
5. Conclusions
- (1)
- In order to eliminate end effects and mode mixing, a revised HHT is proposed. The local linear extrapolation method is introduced to suppress end effects. The combination of adding a high-frequency sinusoidal signal to, and embedding a decorrelation operator in, the process of EMD is introduced to eliminate mode mixing.
- (2)
- With respect to eliminating end effects, the local linear extrapolation method can determine the extremum of an endpoint according to the development trend of both ends without extending or predicting the data. The structure of the original data will not be changed with this method, so more original information can be retained.
- (3)
- With respect to eliminating mode mixing, the method of combining a high-frequency sinusoidal signal and a decorrelation operator has excellent performance in decomposing a multicomponent signal that is mixed with high-frequency discontinuous signals and low-frequency ratio signals. What is more, this method requires less computation time, which is very important with respect to real-time signal processing.
- (4)
- In order to verify the effectiveness of the revised HHT, the original HHT and revised HHT are applied to identify the running status of a rotor system, respectively. In the experiment, the vibration displacement signals of a rotor system under normal, rubbing, and misalignment conditions were measured by eddy current sensors. Then, the signals were analyzed by the original and revised HHT methods. The experimental results illustrate that both of the HHT methods can identify the three different running states according to the time-frequency spectrum. By comparing the two methods, we can come to the conclusion that the revised HHT is more reliable than the original with respect to eliminating end effects and mode mixing.
- (5)
- It is worth noting that, although the revised HHT method provides us with good performance in eliminating end effects and mode mixing, it still depends on experience to decide the frequency and amplitude of the added high-frequency sinusoidal signal. More theoretical analysis is necessary if we want to improve the accuracy of the revised HHT. On the positive side, this article provides a new way to improve the performance of HHT.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, F.; Yang, L.J.; Zhou, H.M.; Yang, L.H. Optimal averages for nonlinear signal decompositions-Another alternative for empirical mode decomposition. Signal Process. 2016, 12, 17–29. [Google Scholar] [CrossRef]
- Weng, J.W.; Zhong, J.G. Application of Gabor Transform to 3-D Shape Analysis. Acta Photonica Sin. 2003, 32, 993–996. (In Chinese) [Google Scholar]
- Postnikoy, E.B.; Lebedeva, E.A.; Lavrova, A.I. Computational implementation of the inverse continuous wavelet transform without a requirement of the admissibility condition. Appl. Math. Comput. 2016, 282, 128–136. [Google Scholar]
- Pachori, R.B.; Nishad, A. Cross-terms reduction in the Wigner-Ville distribution using tunable-Q wavelet transform. Signal Process. 2016, 120, 288–304. [Google Scholar] [CrossRef]
- Yao, J.B.; Tang, B.P.; Zhao, J. Improved discrete Fourier transform algorithm for harmonic analysis of rotor system. Measurement 2016, 83, 57–71. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Schlurmann, T. Spectral analysis of nonlinear water waves based on the Hilbert-Huang transformation. J. Offshore Mech. Arct. Eng. Trans. 2002, 124, 22–27. [Google Scholar] [CrossRef]
- Hwang, P.A.; Huang, N.E.; Wang, D.W. A note on analyzing nonlinear and non-stationary ocean wave data. Appl. Ocean Res. 2003, 25, 187–193. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.; Qu, W.D.; Long, S.R.; Shen, S.P. Applications of Hilbert-Huang transform to non-stationary financial time series analysis. Appl. Stoch. Models Bus. Ind. 2003, 19, 245–268. [Google Scholar] [CrossRef]
- Xun, J.; Yan, S.Z. A revised Hilbert-Huang transformation based on the neural networks and its application in vibration signal analysis of a deployable structure. Mech. Syst. Signal Proc. 2008, 22, 1705–1723. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, B.P.; Xiao, X. Time-frequency interpretation of multi-frequency signal from rotating machinery using an improved Hilbert-Huang transform. Measurement 2016, 82, 221–239. [Google Scholar] [CrossRef]
- Wu, J.D.; Liao, S.Y. A self-adaptive data analysis for fault diagnosis of an automotive air-conditioner blower. Expert Syst. Appl. 2011, 38, 545–552. [Google Scholar] [CrossRef]
- Yu, X.; Ding, E.J.; Chen, C.X.; Liu, X.M.; Li, L. A Novel Characteristic Frequency Bands Extraction Method for Automatic Bearing Fault Diagnosis Based on Hilbert Huang Transform. Sensors 2015, 15, 27869–27893. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Wang, K.H.; Zhou, Q.; Fang, J.M.; Zhou, Z.L. Feature extraction for gas metal arc welding based on EMD and time-frequency entropy. Int. J. Adv. Manuf. Technol. 2017, 92, 1439–1448. [Google Scholar] [CrossRef]
- Liu, C.F.; Zhu, L.D.; Ni, C.B. The chatter identification in end milling based on combining EMD and WPD. Int. J. Adv. Manuf. Technol. 2017, 91, 3339–3348. [Google Scholar] [CrossRef]
- Wan, S.K.; Li, X.H.; Chen, W.; Hong, J. Investigation on milling chatter identification at early stage with variance ratio and Hilbert-Huang transform. Int. J. Adv. Manuf. Technol. 2018, 95, 3563–3573. [Google Scholar] [CrossRef]
- Liu, X.M.; Yang, Y.M.; Yang, F.; Shi, Q.Y. Time-frequency analysis of DC bias vibration of transformer core on the basis of Hilbert-Huang transform. Ing. Investig. 2016, 36, 90–97. [Google Scholar] [CrossRef]
- Wang, X.C.; Hu, J.P.; Zhang, D.B.; Qin, H. Efficient EMD and Hilbert spectra computation for 3D geometry processing and analysis via space-filling curve. Vis. Comput. 2015, 31, 1135–1145. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Gonçalves, P. On empirical mode decomposition and its algorithms. In IEEEEURASIP Workshop Nonlinear Signal Image Process (NSIP); École normale supérieure de Lyon: Grado, Italy, 2003; pp. 444–447. [Google Scholar]
- Costa, A.H.; Hengstler, S. Adaptive time-frequency analysis based on autoregressive modeling. Signal Process. 2011, 91, 740–749. [Google Scholar] [CrossRef]
- Qi, K.Y.; He, Z.J.; Zi, Y.Y. Cosine window-based boundary processing method for EMD and its application in rubbing fault diagnosis. Mech. Syst. Signal Proc. 2007, 21, 2750–2760. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Su, N.F.; Li, Z.Y.; Guo, Z.P.; Chen, Q.Y.; Zhang, Y. Assessment of arterial distension based on continuous wave Doppler ultrasound with an improved Hilbert-Huang processing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 203–213. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.P. Improvement of the mirror extending in empirical mode decomposition method and the technology for eliminating frequency mixing. High Technol. Lett. 2002, 8, 40–47. [Google Scholar]
- Liu, H.T.; Zhang, M.; Cheng, J.X. Dealing with the end issue of EMD based on polynomial fitting algorithm. Comput. Eng. Appl. 2004, 16, 84–85. (In Chinese) [Google Scholar]
- Zhu, J.L.; Qiu, X.H. Dealing with the End Issue of EMD Based on Orthogonal Polynomial Fitting Algorithm. Comput. Eng. Appl. 2006, 23, 72–74. [Google Scholar]
- Cheng, J.S.; Yu, D.J.; Yang, Y. Application of support vector regression machines to the processing of end effects of Hilbert-Huang transform. Mech. Syst. Signal Proc. 2007, 21, 1197–1211. [Google Scholar] [CrossRef]
- Yang, X.Z.; Cheng, G.G.; Liu, H.K. Improved Empirical Mode Decomposition Algorithm of Processing Complex Signal for IoT Application. Int. J. Distrib. Sens. Netw. 2015, 3, 1–8. [Google Scholar] [CrossRef]
- Huang, N.E. Wu. Z.H. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46, 1–23. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.; Long, S.R.; Shen, S.S.P.; Qu, W.D.; Gloersen, P.; Fan, K.L. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2003, 459, 2317–2345. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Deering, R.; Kaiser, J.E. The use of a masking signal to improve empirical mode decomposition, International Conference on Acoustics, Speech, and Signal Processing (ICASSP). In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 23 March 2005; pp. 485–488. [Google Scholar]
- Yeh, C.H.; Shi, W.B. Identifying Phase-Amplitude Coupling in Cyclic Alternating Pattern using Masking Signals. Sci. Rep. 2018, 8, 2649. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.P.; Dong, S.J.; Ma, J.H. Study on the method for eliminating mode mixing of empirical mode decomposition based on independent component analysis. Chin. J. Sci. Instrum. 2012, 33, 1477–1482. [Google Scholar]
- Tang, B.P.; Dong, S.J.; Song, T. Method for eliminating mode mixing of empirical mode decomposition based on the revised blind source separation. Signal Process. 2012, 92, 248–258. [Google Scholar] [CrossRef]
- Xiao, Y.; Yin, F.L. Decorrelation EMD: A new method of eliminating mode mixing. J. Vib. Shock 2015, 34, 25–29. [Google Scholar]
- Hu, A.J.; Sun, J.J.; Xiang, L. Mode Mixing in Empirical Mode Decomposition. J. Vib. Meas. Diagn. 2011, 31, 429–434. [Google Scholar]
- Yang, X.Z. Research on fault diagnosis method based on empirical mode decomposition. Wuhan Univ. Sci. Technol. 2012, 29–42. [Google Scholar]
- Peng, Z.K.; Tse, P.W.; Chu, F.L. A comparison study of improved Hilbert-Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing. Mech. Syst. Signal Proc. 2005, 19, 974–988. [Google Scholar] [CrossRef]
- Xu, G.L.; Wang, X.T.; Xu, X.G.; Qin, X.J.; Zhu, T. The conditions and criteria of multi-component decompose into single component by EMD. Prog. Nat. Sci. 2006, 16, 1356–1360. [Google Scholar]




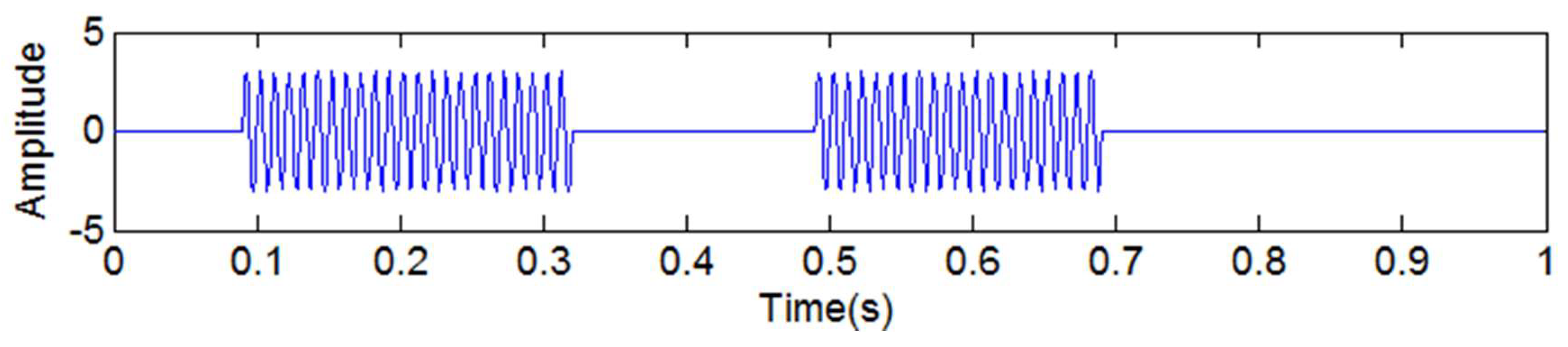
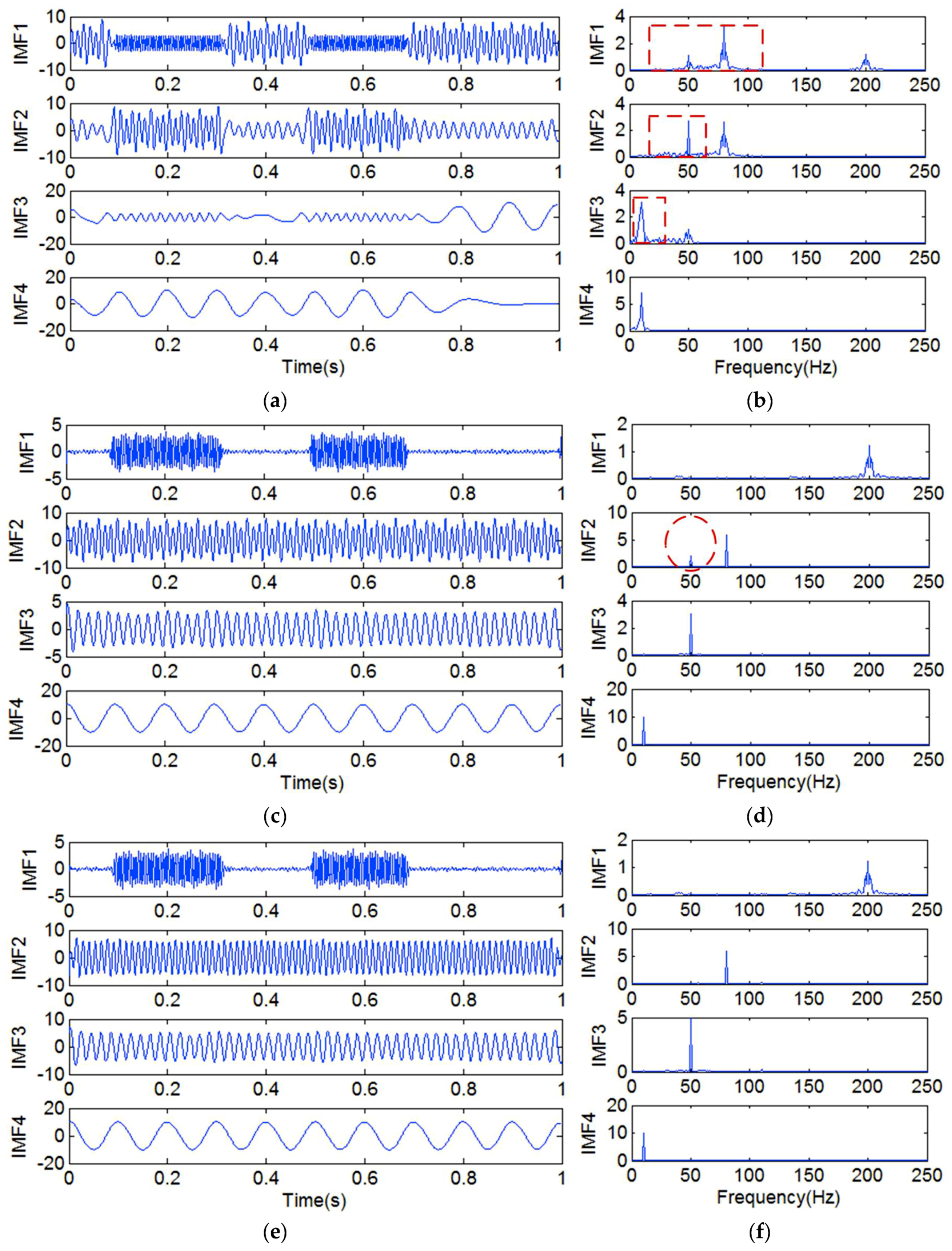
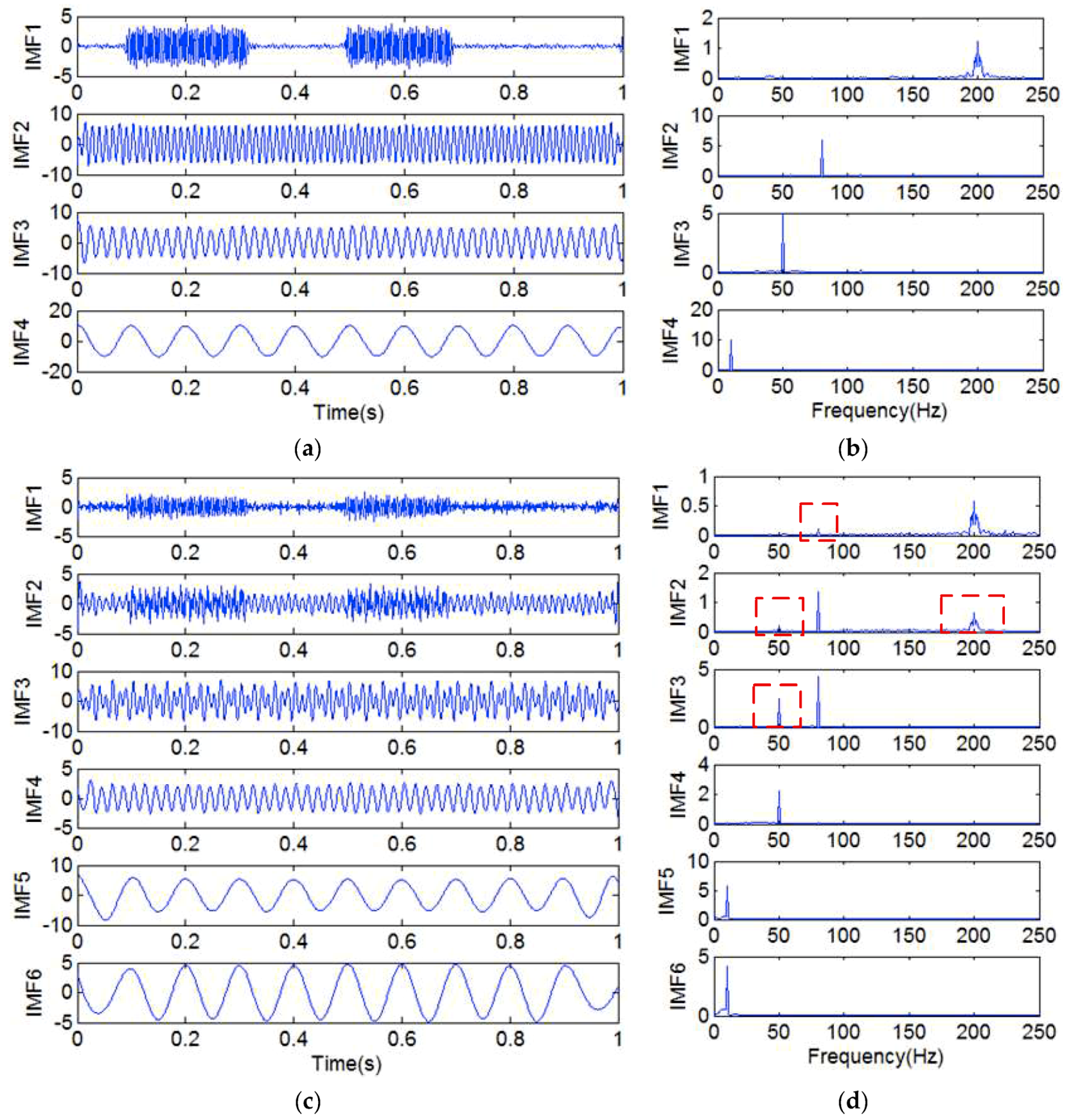

| RMSE | |
|---|---|
| The proposed method | 0.3057 |
| Yang’s method [28] | 0.6548 |
| Item | Time (s) | |||||
|---|---|---|---|---|---|---|
| Label | A | B | C | D | E | Average |
| The revised EMD | 0.53 | 0.57 | 0.53 | 0.58 | 0.55 | 0.55 |
| EEMD | 118.65 | 118.23 | 118.03 | 117.40 | 118.01 | 118.06 |
| IMFs | IMF1 | IMF2 | IMF3 | IMF4 | r4 |
|---|---|---|---|---|---|
| Correlation coefficient | 0.765 | 0.638 | 0.049 | 0.035 | 0.024 |
| Item | Time (s) | |||||
|---|---|---|---|---|---|---|
| Label | A | B | C | D | E | Average |
| The proposed method | 0.93 | 0.98 | 0.95 | 0.95 | 0.95 | 0.95 |
| The original method | 1.28 | 1.29 | 1.28 | 1.30 | 1.30 | 1.29 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Ji, Y. A Revised Hilbert–Huang Transform and Its Application to Fault Diagnosis in a Rotor System. Sensors 2018, 18, 4329. https://doi.org/10.3390/s18124329
Wang H, Ji Y. A Revised Hilbert–Huang Transform and Its Application to Fault Diagnosis in a Rotor System. Sensors. 2018; 18(12):4329. https://doi.org/10.3390/s18124329
Chicago/Turabian StyleWang, Hongjun, and Yongjian Ji. 2018. "A Revised Hilbert–Huang Transform and Its Application to Fault Diagnosis in a Rotor System" Sensors 18, no. 12: 4329. https://doi.org/10.3390/s18124329
APA StyleWang, H., & Ji, Y. (2018). A Revised Hilbert–Huang Transform and Its Application to Fault Diagnosis in a Rotor System. Sensors, 18(12), 4329. https://doi.org/10.3390/s18124329




