An Improved Evidential-IOWA Sensor Data Fusion Approach in Fault Diagnosis
Abstract
1. Introduction
2. Preliminaries
2.1. Dempster–Shafer Evidence Theory
2.2. Jousselme Distance
2.3. Belief Entropy
2.4. IOWA Operator
2.5. Maximum Entropy Method
3. The Evidential IOWA-Based Fault Diagnosis Method
3.1. The Evidential-IOWA Parameter
3.1.1. Definition of in IOWA
3.1.2. Definition of Based on the Distance of Evidence
3.1.3. Definition of Based on the Belief Entropy
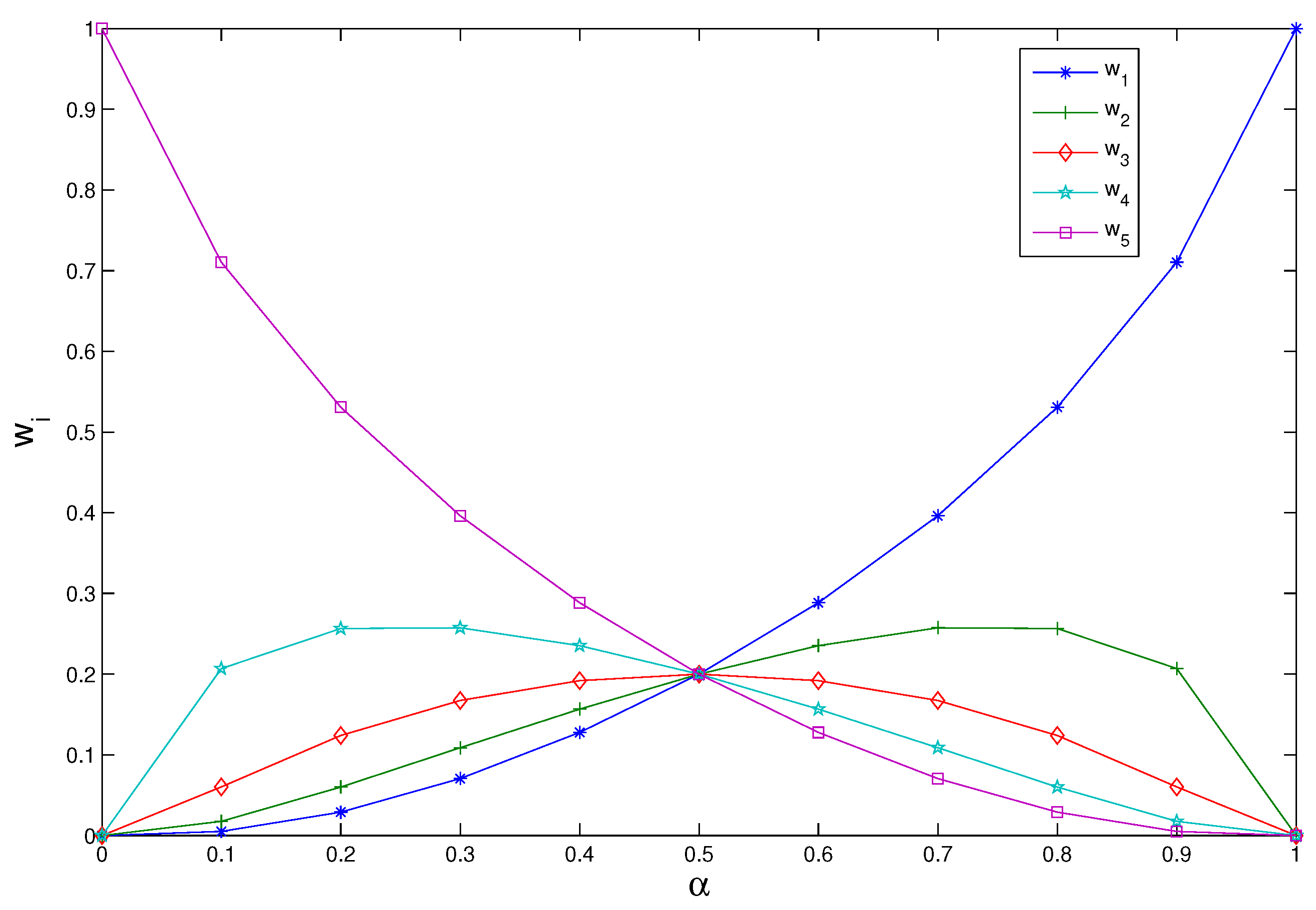
3.1.4. The Weight Vector of IOWA
- Step 1
- Step 2
- Step 3
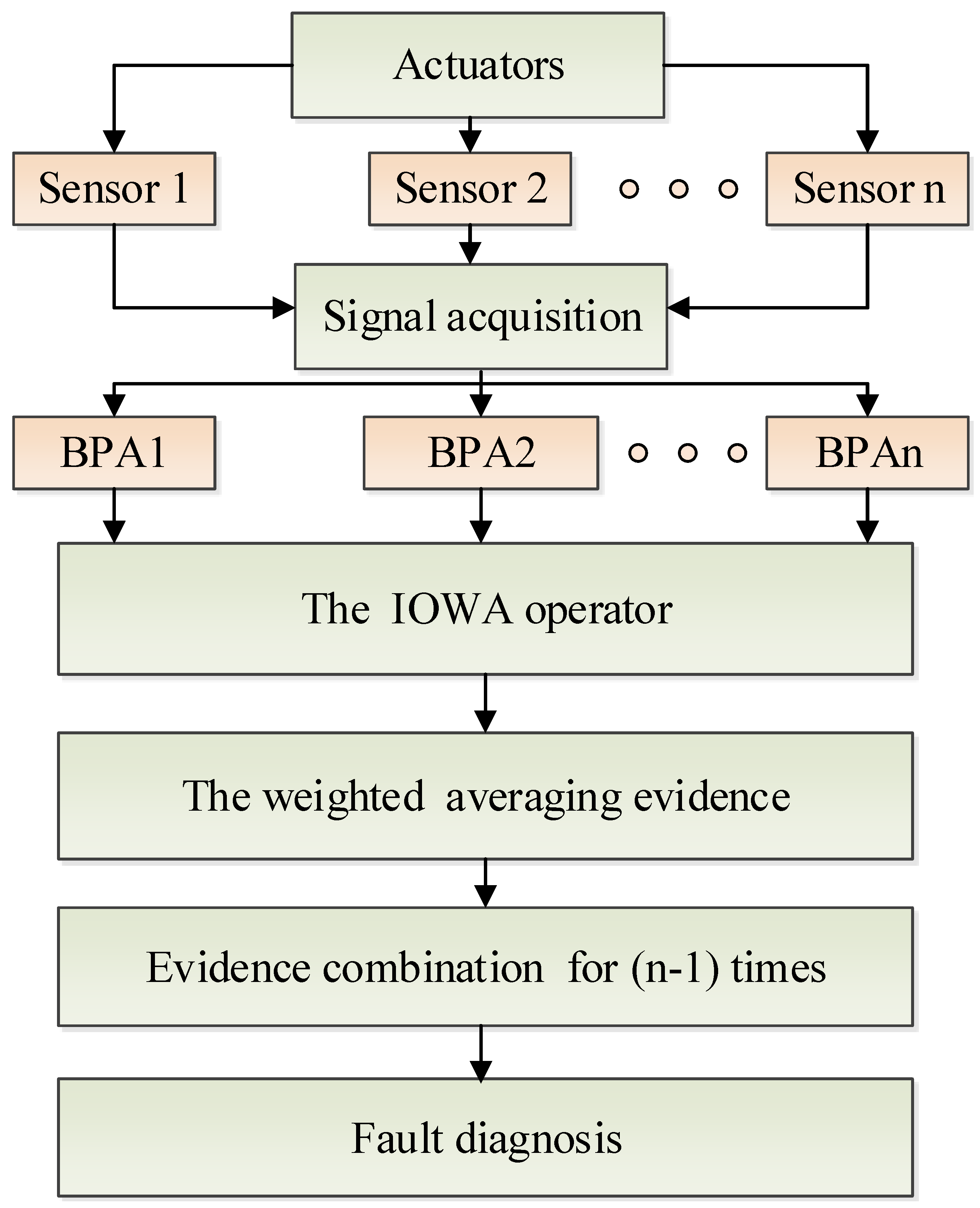
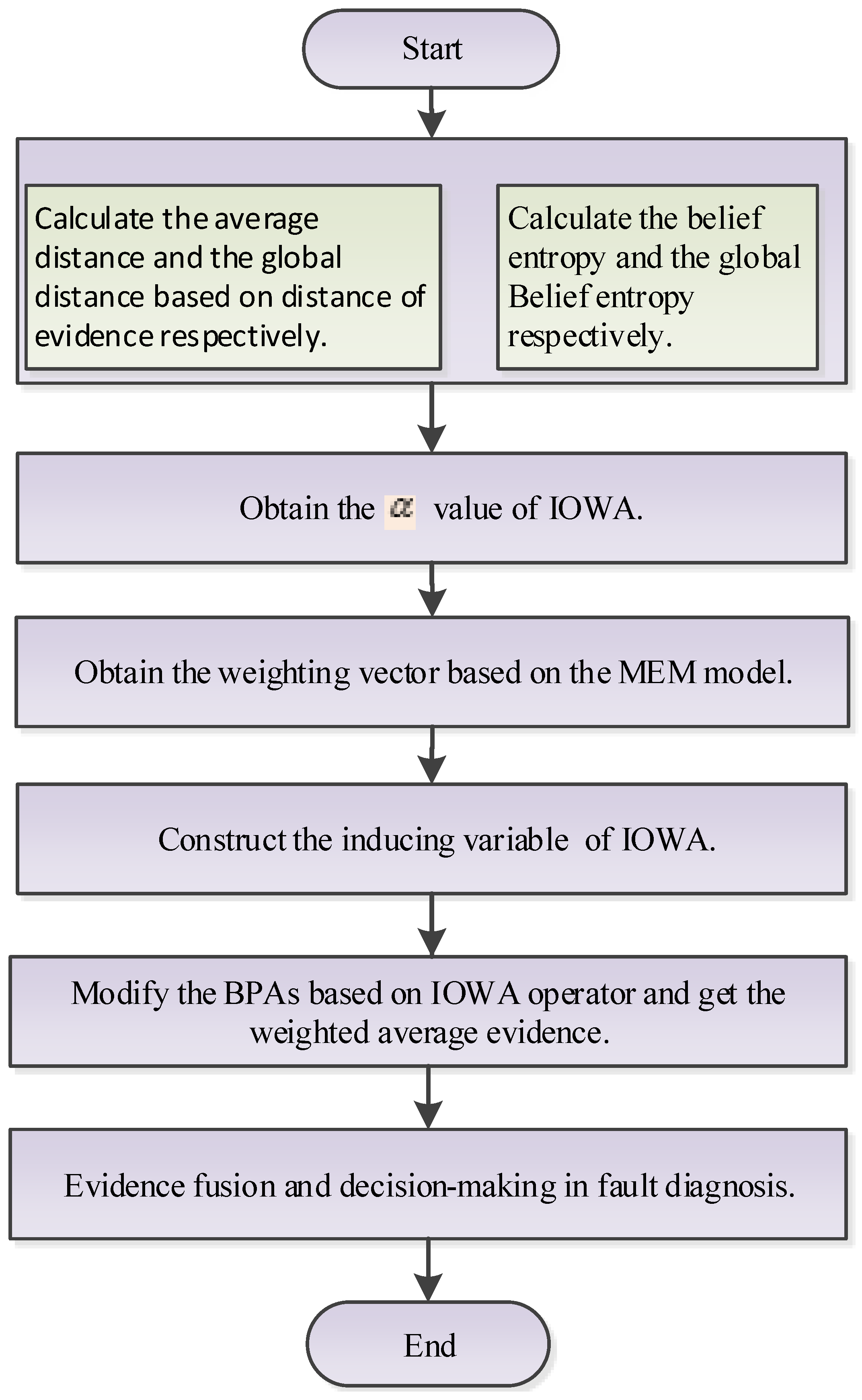
3.2. Multi-Evidential Fusion Model
- Step 1
- Construct the inducing variable :where is the average distance of evidence obtained by Equation (13).
- Step 2
- Obtain the OWA pairs , where is the argument variable, namely, it is the BPAs of the evidence .
- Step 3
- According to Equation (8), the weighted average evidence can be calculated.
- Step 4
- Combine the new evidence with Dempster’s combination rule by () times.
4. Application
4.1. Experiment with Artificial Data
4.2. A Case Study
4.3. Discussion
- FD without fault to be sure that the proposed solution doesn’t give false alarm,
- FD with a misalignment fault to highlight that we detect this fault well,
- FD with pedestal fault.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Patecornell, M. Organizational aspects of engineering system safety: The case of offshore platforms. Science 1990, 250, 1210–1217. [Google Scholar] [CrossRef] [PubMed]
- Oosterom, M.; Babuska, R.; Verbruggen, H.B. Soft computing applications in aircraft sensor management and flight control law reconfiguration. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2002, 32, 125–139. [Google Scholar] [CrossRef]
- Picazo-Rodenas, M.J.; Royo, R.; Antonino-Daviu, J.; Roger-Folch, J. Use of the infrared data for heating curve computation in induction motors: Application to fault diagnosis. Eng. Fail. Anal. 2013, 35, 178–192. [Google Scholar] [CrossRef]
- Zhang, B.; Tan, A.C.C.; Lin, J.H. Gearbox fault diagnosis of high-speed railway train. Eng. Fail. Anal. 2016, 66, 407–420. [Google Scholar] [CrossRef]
- Du, Y.; Lu, X.; Su, X.; Hu, Y.; Deng, Y. New failure mode and effects analysis: An evidential downscaling method. Qual. Reliab. Eng. Int. 2016, 32, 737–746. [Google Scholar] [CrossRef]
- Chen, C.; Brown, D.; Sconyers, C.; Zhang, B.; Vachtsevanos, G.; Orchard, M.E. An integrated architecture for fault diagnosis and failure prognosis of complex engineering systems. Expert Syst. Appl. 2012, 39, 9031–9040. [Google Scholar] [CrossRef]
- Ferreira de Loza, A.; Cieslak, J.; Henry, D.; Zolghadri, A.; Fridman, L.M. Output tracking of systems subjected to perturbations and a class of actuator faults based on HOSM observation and identification. Automatica 2015, 59, 200–205. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Zhuang, M.; Shou, Y.; Tang, Y. Sensor Data Fusion with Z-Numbers and Its Application in Fault Diagnosis. Sensors 2016, 16, 1509. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Deng, Y.; Mahadevan, S.; Bao, Q. An improved method for risk evaluation in failure modes and effects analysis of aircraft engine rotor blades. Eng. Fail. Anal. 2012, 26, 164–174. [Google Scholar] [CrossRef]
- Oukhellou, L.; Debiolles, A.; Denoeux, T.; Aknin, P. Fault diagnosis in railway track circuits using Dempster–Shafer classifier fusion. Eng. Appl. Artif. Intell. 2010, 23, 117–128. [Google Scholar] [CrossRef]
- Sun, S.; Lin, H.; Ma, J.; Li, X. Multi-sensor distributed fusion estimation with applications in networked systems: A review paper. Inf. Fusion 2017, 38, 122–134. [Google Scholar] [CrossRef]
- Pang, C.; Sun, S. Fusion Predictors for Multisensor Stochastic Uncertain Systems With Missing Measurements and Unknown Measurement Disturbances. IEEE Sens. J. 2015, 15, 4346–4354. [Google Scholar] [CrossRef]
- De Loza, A.F.; Cieslak, J.; Henry, D.; Davila, J.; Zolghadri, A. Sensor fault diagnosis using a non-homogeneous high-order sliding mode observer with application to a transport aircraft. IET Control Theory Appl. 2015, 9, 598–607. [Google Scholar] [CrossRef]
- Berdjag, D.; Cieslak, J.; Zolghadri, A. Fault diagnosis and monitoring of oscillatory failure case in aircraft inertial system. Control Eng. Pract. 2012, 20, 1410–1425. [Google Scholar] [CrossRef]
- Berdjag, D.; Zolghadri, A.; Cieslak, J.; Goupil, P. Fault detection and isolation for redundant aircraft sensors. Proceedings of 2010 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 6–8 October 2010; pp. 137–142. [Google Scholar]
- Cieslak, J.; Henry, D.; Zolghadri, A.; Goupil, P. Development of an active fault-tolerant flight control strategy. J. Guid. Control Dyn. 2008, 31, 135–147. [Google Scholar] [CrossRef]
- Efimov, D.; Cieslak, J.; Zolghadri, A.; Henry, D. Actuator fault detection in aircraft systems: Oscillatory failure case study. Annu. Rev. Control 2013, 37, 180–190. [Google Scholar] [CrossRef]
- Li, C.; Mahadevan, S.; Ling, Y.; Choze, S.; Wang, L. Dynamic Bayesian Network for Aircraft Wing Health Monitoring Digital Twin. AIAA J. 2017, 55, 930–941. [Google Scholar] [CrossRef]
- He, Y.; Hu, L.F.; Guan, X.; Deng, Y.; Han, D. New method for measuring the degree of conflict among general basic probability assignments. Sci. Chin.-Inf. Sci. 2012, 55, 312–321. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, D.; Xu, S.; He, Z. A Weighted Belief Entropy–Based Uncertainty Measure for Multi-Sensor Data Fusion. Sensors 2017, 17, 928. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yang, F.B.; Ji, L.; Yuan, H.; Dong, A. A categorization method of infrared polarization and intensity image fusion algorithm based on the transfer ability of difference features. Infrared Phys. Technol. 2016, 79, 91–100. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, F.; Peng, Z.; Chen, L.; Ji, L. Multi-sensor image enhanced fusion algorithm based on NSST and top-hat transformation. Optik Int. J. Light Electron Opt. 2015, 126, 4184–4190. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Li, D.W.; Yang, F.; Wang, X.X. Crop region extraction of remote sensing images based on fuzzy ARTMAP and adaptive boost. J. Intell. Fuzzy Syst. 2015, 29, 2787–2794. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multi-valued Mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Deng, Y. Generalized evidence theory. Appl. Intell. 2015, 43, 530–543. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S. A Bio-Inspired Approach to Traffic Network Equilibrium Assignment Problem. IEEE Trans. Cybern. 2017, PP, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Huang, H.; Liang, L. Fuzzy-robust design optimization with multi-quality characteristics. Eng. Optim. 2010, 42, 87–99. [Google Scholar] [CrossRef]
- Sun, S.; Tian, T.; Lin, H. State estimators for systems with random parameter matrices, stochastic nonlinearities, fading measurements and correlated noises. Inf. Sci. 2017, 397, 118–136. [Google Scholar] [CrossRef]
- Miao, B.; Dou, C.; Jin, X. Main Trend Extraction Based on Irregular Sampling Estimation and Its Application in Storage Volume of Internet Data Center. Comput. Intell. Neurosci. 2016, 2016, 9328062. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.B.; Du, J.J.; Bao, J. Target Tracking of a Linear Time Invariant System Under Irregular Sampling. Int. J. Adv. Rob. Syst. 2012, 9, 219. [Google Scholar]
- Yuan, K.; Xiao, F.; Fei, L.; Kang, B.; Deng, Y. Modeling Sensor Reliability in Fault Diagnosis Based on Evidence Theory. Sensors 2016, 16, 113. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Mercier, G. Credal classification rule for uncertain data based on belief functions. Pattern Recognit. 2014, 47, 2532–2541. [Google Scholar] [CrossRef]
- Han, D.; Liu, W.; Dezert, J.; Yang, Y. A novel approach to pre-extracting support vectors based on the theory of belief functions. Knowl.-Based Syst. 2016, 110, 210–223. [Google Scholar] [CrossRef]
- Liu, Z.G.; Pan, Q.; Dezert, J.; Martin, A. Adaptive imputation of missing values for incomplete pattern classification. Pattern Recognit. 2016, 52, 85–95. [Google Scholar] [CrossRef]
- Zhou, K.; Martin, A.; Pan, Q.; Liu, Z. ECMdd: Evidential c-medoids clustering with multiple prototypes. Pattern Recognit. 2016, 60, 239–257. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Antucheviciene, J. A New Method of Assessment Based on Fuzzy Ranking and Aggregated Weights (AFRAW) for MCDM Problems under Type-2 Fuzzy Environment. Econ. Comput. Econ. Cybern Stud. Res. 2016, 50, 39–68. [Google Scholar]
- Chin, K.S.; Fu, C.; Wang, Y. A method of determining attribute weights in evidential reasoning approach based on incompatibility among attributes. Computer. Ind. Eng. 2015, 87, 150–162. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Y. An interval difference based evidential reasoning approach with unknown attribute weights and utilities of assessment grades. Computer. Ind. Eng. 2015, 81, 109–117. [Google Scholar] [CrossRef]
- Fu, C.; Yang, J.B.; Yang, S.L. A group evidential reasoning approach based on expert reliability. Eur. J. Oper. Res. 2015, 246, 886–893. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S.; Deng, X. Reliability analysis with linguistic data: An evidential network approach. Reliab. Eng. Syst. Saf. 2017, 162, 111–121. [Google Scholar] [CrossRef]
- Su, X.; Mahadevan, S.; Xu, P.; Deng, Y. Dependence Assessment in Human Reliability Analysis Using Evidence Theory and AHP. Risk Anal. 2015, 35, 1296–1316. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Tang, Y.; Jiang, W. A modified model of failure mode and effects analysis based on generalized evidence theory. Math. Probl. Eng. 2016, 2016, 4512383. [Google Scholar] [CrossRef]
- Yager, R.R.; Filev, D.P. Including probabilistic uncertainty in fuzzy logic controller modeling using Dempster–Shafer theory. IEEE Trans. Syst. Man Cybern. 1995, 25, 1221–1230. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, D.; Jiang, W. A New Fuzzy-Evidential Controller for Stabilization of the Planar Inverted Pendulum System. PLoS ONE 2016, 11, e0160416. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Martin, A.; Pan, Q.; Liu, Z.G. Median evidential c-means algorithm and its application to community detection. Knowl.-Based Syst. 2015, 74, 69–88. [Google Scholar] [CrossRef]
- Ma, J.; Liu, W.; Miller, P.; Zhou, H. An Evidential Fusion Approach for Gender Profiling. Inf. Sci. 2015, 333, 10–20. [Google Scholar] [CrossRef]
- Xu, P.; Su, X.; Mahadevan, S.; Li, C.; Deng, Y. A non–parametric method to determine basic probability assignment for classification problems. Appl. Intell. 2014, 41, 681–693. [Google Scholar] [CrossRef]
- Smets, P. Data fusion in the transferable belief model. Inf. Fusion 2000, 1, 21–33. [Google Scholar]
- Lefevre, E.; Colot, O.; Vannoorenberghe, P. Belief functions combination and conflict management. Inf. Fusion 2002, 3, 149–162. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, D.; He, Z.; Xu, S. An improved belief entropy–based uncertainty management approach for sensor data fusion. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef]
- Yager, R.R. On the Dempster–Shafer framework and new combination rules. Inf. Sci. 1987, 41, 93–137. [Google Scholar] [CrossRef]
- Murphy, C.K. Combining belief functions when evidence conflicts. Decis. Support Syst. 2000, 29, 1–9. [Google Scholar] [CrossRef]
- Deng, Y.; Shi, W.; Zhu, Z.; Liu, Q. Combining belief functions based on distance of evidence. Decis. Support Syst. 2004, 38, 489–493. [Google Scholar]
- Chin, K.S.; Fu, C. Weighted cautious conjunctive rule for belief functions combination. Inf. Sci. 2015, 325, 70–86. [Google Scholar] [CrossRef]
- Jiang, W.; Zhuang, M.; Qin, X.; Tang, Y. Conflicting evidence combination based on uncertainty measure and distance of evidence. SpringerPlus 2016, 5, 1217. [Google Scholar] [CrossRef] [PubMed]
- Jousselme, A.L.; Grenier, D.; Bosse, E. A new distance between two bodies of evidence. Inf. Fusion 2001, 2, 91–101. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Deng, Y. Deng entropy. Chaos Solitons Fractals 2016, 91, 549–553. [Google Scholar] [CrossRef]
- Yager, R.R.; Filev, D.P. Induced ordered weighted averaging operators. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1999, 29, 141–150. [Google Scholar] [CrossRef] [PubMed]
- O’Hagan, M. Aggregating template or rule antecedents in real-time expert systems with fuzzy set logic. Sign. Syst. Comput. 1988, 29, 681–689. [Google Scholar]
- Zeng, S.; Merigo, J.M.; Su, W. The uncertain probabilistic owa distance operator and its application in group decision making. Appl. Math. Modell. 2013, 37, 6266–6275. [Google Scholar] [CrossRef]
- Cho, S.B. Fuzzy aggregation of modular neural networks with ordered weighted averaging operators. Int. J. Approx. Reason. 1995, 13, 359–375. [Google Scholar]
- Peng, Y.; Zhang, Y.; Tang, Y.; Li, S. An incident information management framework based on data integration, data mining, and multi-criteria decision making. Decis. Support Syst. 2011, 51, 316–327. [Google Scholar] [CrossRef]
- Fan, X.; Zuo, M.J. Fault diagnosis of machines based on D-S evidence theory. Part 1: D–S evidence theory and its improvement. Pattern Recognit. Lett. 2006, 27, 366–376. [Google Scholar] [CrossRef]
- Henry, D.; Cieslak, J.; Zolghadri, A.; Efimov, D. H ∞/H - LPV solutions for fault detection of aircraft actuator faults: Bridging the gap between theory and practice. Int. J. Robust Nonlinear Control 2015, 25, 649–672. [Google Scholar] [CrossRef]
- Cieslak, J.; Efimov, D.; Zolghadri, A.; Henry, D.; Goupil, P. Design of a non-homogeneous differentiator for actuator oscillatory failure case reconstruction in noisy environment. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2015, 229, 266–275. [Google Scholar] [CrossRef]
| 0.41 | 0.29 | 0.30 | 0.00 | |
| 0.00 | 0.90 | 0.10 | 0.00 | |
| 0.58 | 0.07 | 0.00 | 0.35 | |
| 0.55 | 0.10 | 0.00 | 0.35 | |
| 0.6 | 0.10 | 0.00 | 0.30 |
| BPAs | Methods | Faults | ||||
|---|---|---|---|---|---|---|
| Dempster’s method [25] | 0 | 0.8969 | 0.1031 | 0 | B | |
| Murphy’s method [54] | 0.0964 | 0.8119 | 0.0917 | 0 | B | |
| Deng et al.’s method [55] | 0.0964 | 0.8119 | 0.0917 | 0 | B | |
| The proposed method | 0.0964 | 0.8119 | 0.0917 | 0 | B | |
| Dempster’s method [25] | 0 | 0.6350 | 0.3650 | 0 | B | |
| Murphy’s method [54] | 0.4939 | 0.4180 | 0.0792 | 0.0090 | A | |
| Deng et al.’s method [55] | 0.4974 | 0.4054 | 0.0888 | 0.0084 | A | |
| The proposed method | 0.6960 | 0.1744 | 0.1253 | 0.0056 | A | |
| Dempster’s method [25] | 0 | 0.3321 | 0.6679 | 0 | C | |
| Murphy’s method [54] | 0.8362 | 0.1147 | 0.0410 | 0.0081 | A | |
| Deng et al.’s method [55] | 0.9089 | 0.0444 | 0.0379 | 0.0089 | A | |
| The proposed method | 0.9683 | 0.0020 | 0.0133 | 0.0163 | A | |
| Dempster’s method [25] | 0 | 0.1422 | 0.8578 | 0 | C | |
| Murphy’s method [54] | 0.9620 | 0.0210 | 0.0138 | 0.0032 | A | |
| Deng et al.’s method [55] | 0.9820 | 0.0039 | 0.0107 | 0.0034 | A | |
| The proposed method | 0.9914 | 0.0001 | 0.0025 | 0.0061 | A |
| Sensor Report | ||||
|---|---|---|---|---|
| 0.60 | 0.10 | 0.10 | 0.20 | |
| 0.05 | 0.80 | 0.05 | 0.10 | |
| 0.70 | 0.10 | 0.10 | 0.10 |
| Evidence Distance-Based Parameter | ||||
|---|---|---|---|---|
| Calculation Result | 0.1916 | 0.3477 | 0.2033 | 0.3712 |
| Belief Entropy-Based Parameter | ||||
|---|---|---|---|---|
| Calculation Result | 2.2909 | 1.3819 | 1.7960 | 0.5884 |
| Fault Types | ||||
|---|---|---|---|---|
| Only Dempster’s Rule of Combination | 0.4519 | 0.5048 | 0.0336 | 0.0096 |
| Fan et al’s Method [66] | 0.8119 | 0.1096 | 0.0526 | 0.0259 |
| The Proposed Method | 0.9123 | 0.0810 | 0.0027 | 0.0039 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Zhou, D.; Zhuang, M.; Fang, X.; Xie, C. An Improved Evidential-IOWA Sensor Data Fusion Approach in Fault Diagnosis. Sensors 2017, 17, 2143. https://doi.org/10.3390/s17092143
Tang Y, Zhou D, Zhuang M, Fang X, Xie C. An Improved Evidential-IOWA Sensor Data Fusion Approach in Fault Diagnosis. Sensors. 2017; 17(9):2143. https://doi.org/10.3390/s17092143
Chicago/Turabian StyleTang, Yongchuan, Deyun Zhou, Miaoyan Zhuang, Xueyi Fang, and Chunhe Xie. 2017. "An Improved Evidential-IOWA Sensor Data Fusion Approach in Fault Diagnosis" Sensors 17, no. 9: 2143. https://doi.org/10.3390/s17092143
APA StyleTang, Y., Zhou, D., Zhuang, M., Fang, X., & Xie, C. (2017). An Improved Evidential-IOWA Sensor Data Fusion Approach in Fault Diagnosis. Sensors, 17(9), 2143. https://doi.org/10.3390/s17092143





