Design and Validation of a 150 MHz HFFQCM Sensor for Bio-Sensing Applications
Abstract
:1. Introduction
2. Materials and Methods
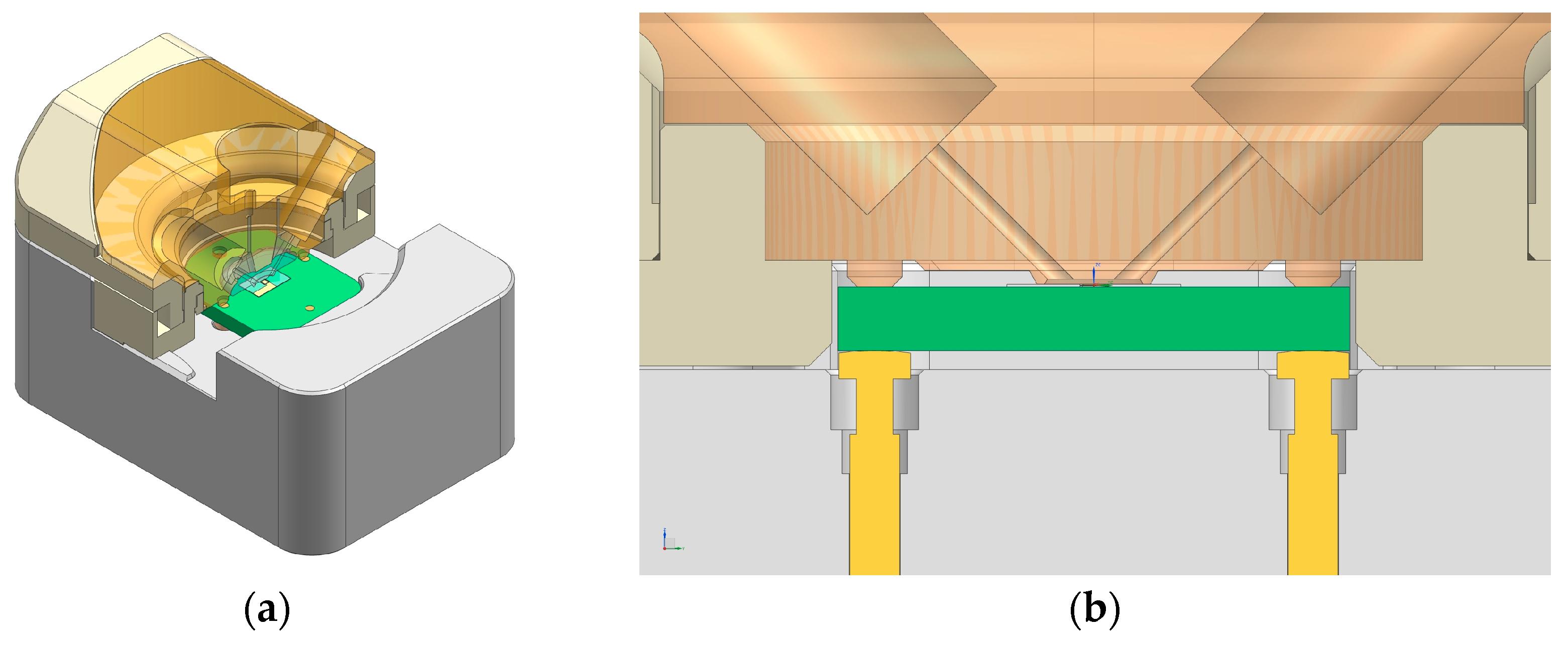
2.1. Sensor Numerical Model
2.2. Chemicals
2.3. Instruments and Devices
2.4. Electrical Characterization of the Sensor
2.5. Flow Cell
2.6. Sensor Cleaning/Preparation
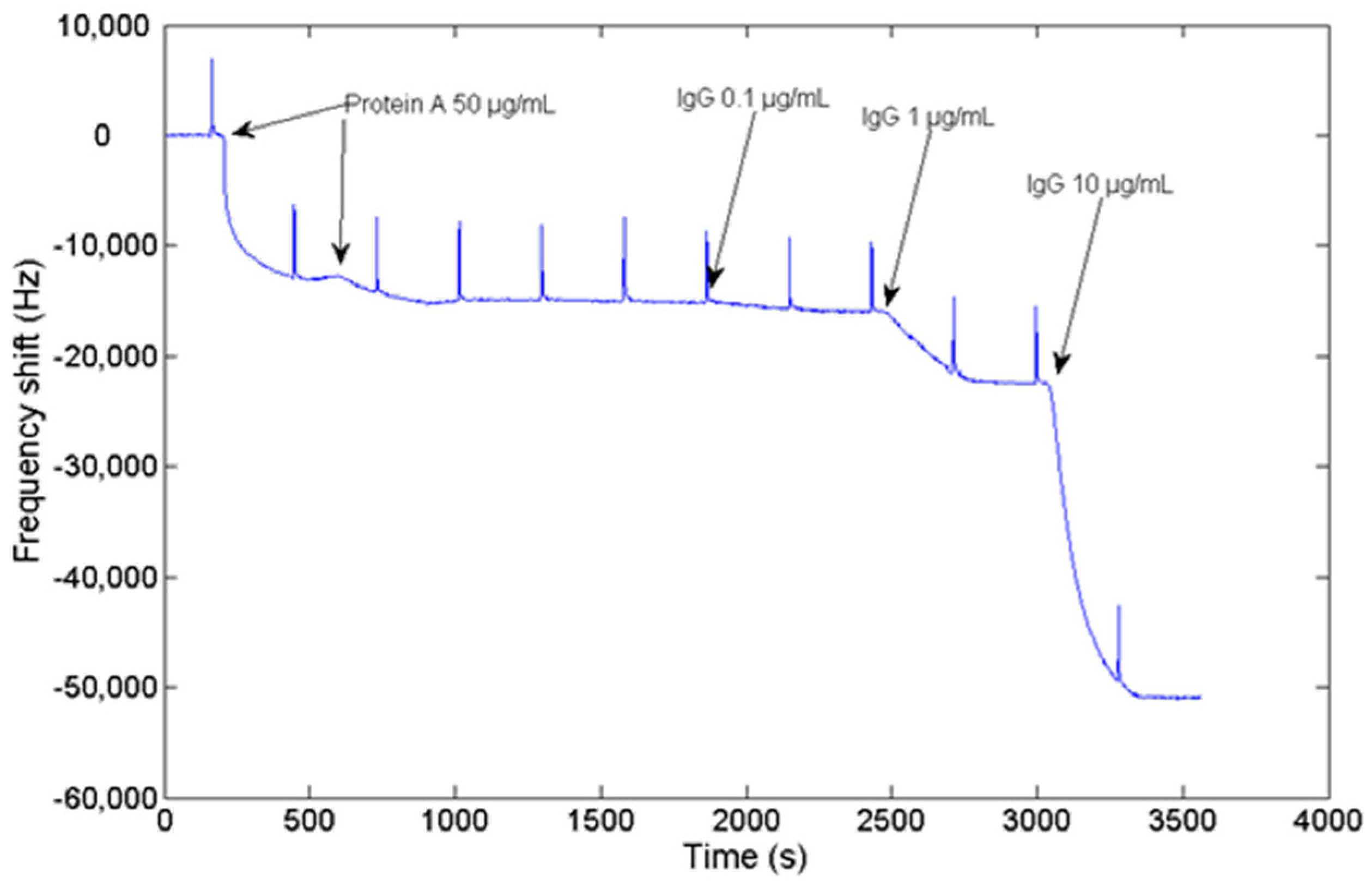
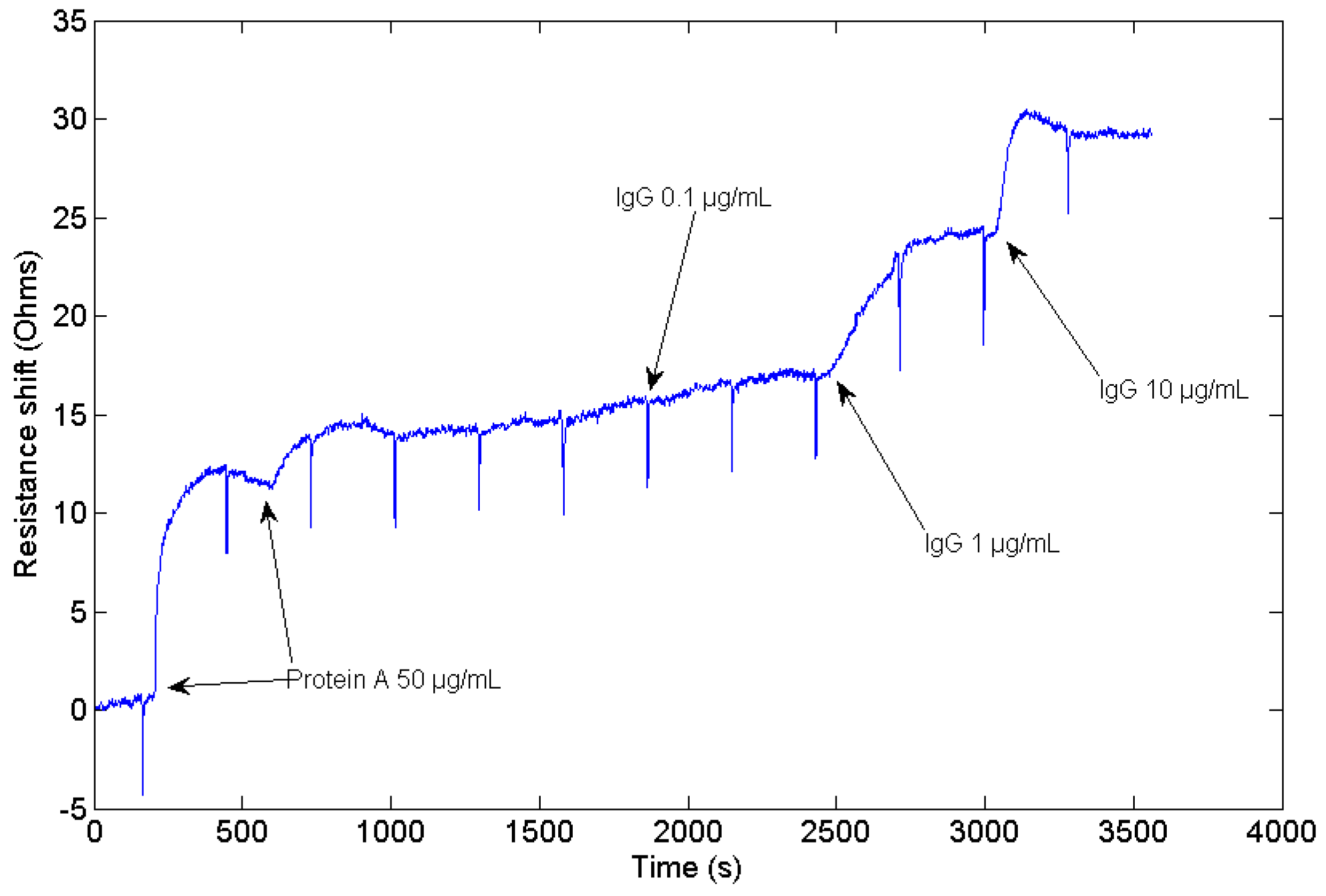
2.7. Protein A Adsorption over Gold Sensor Surface and IgG Binding to the Protein A
3. Results and Discussion
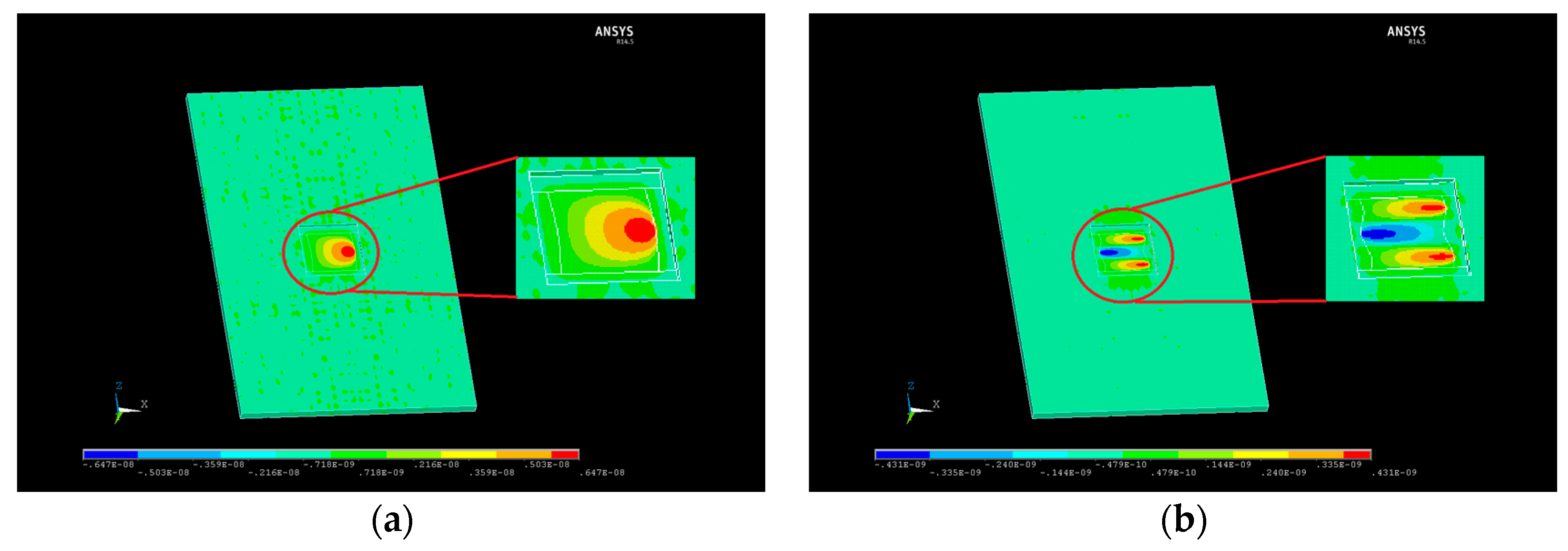
3.1. Simulation
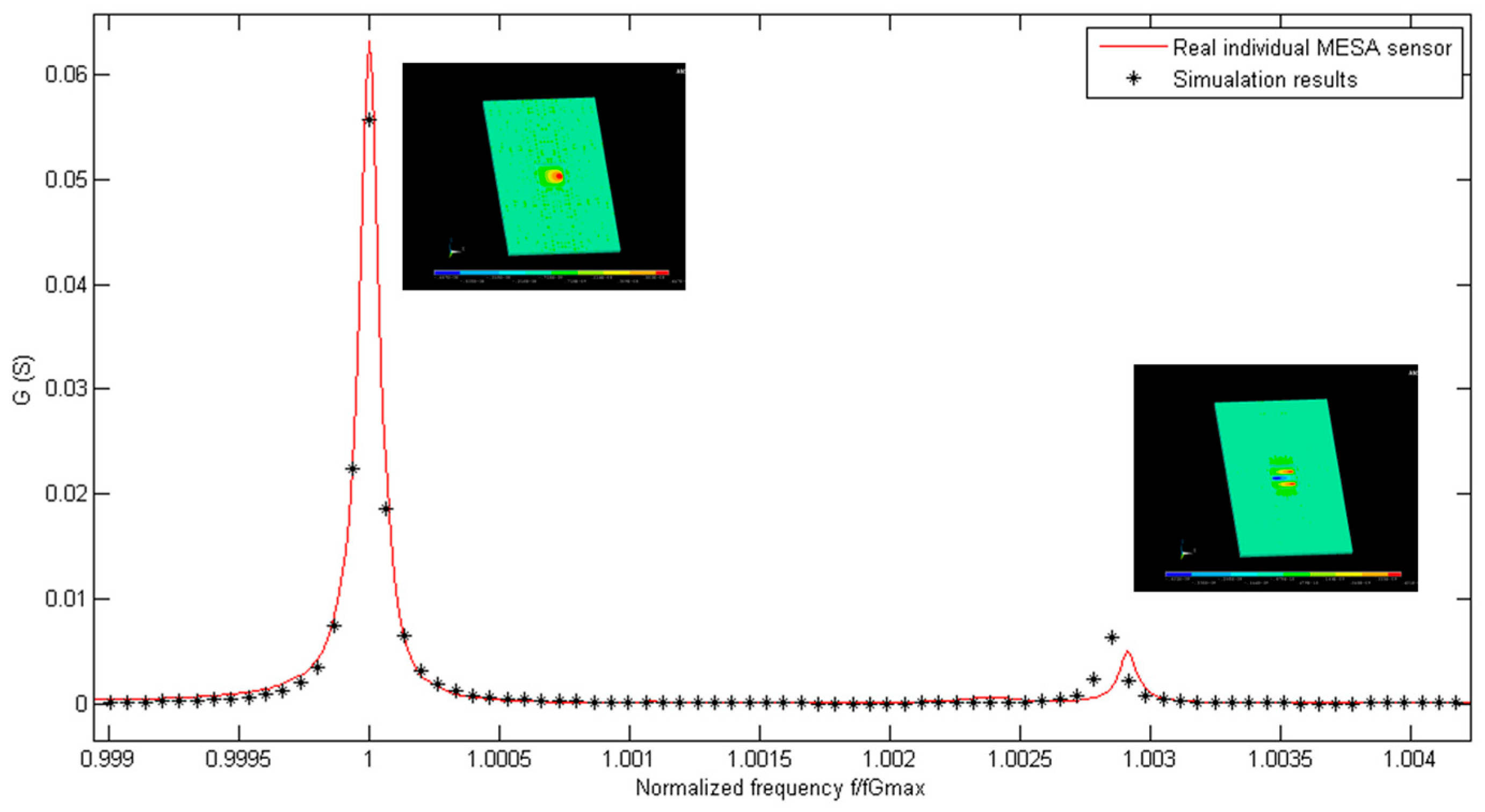
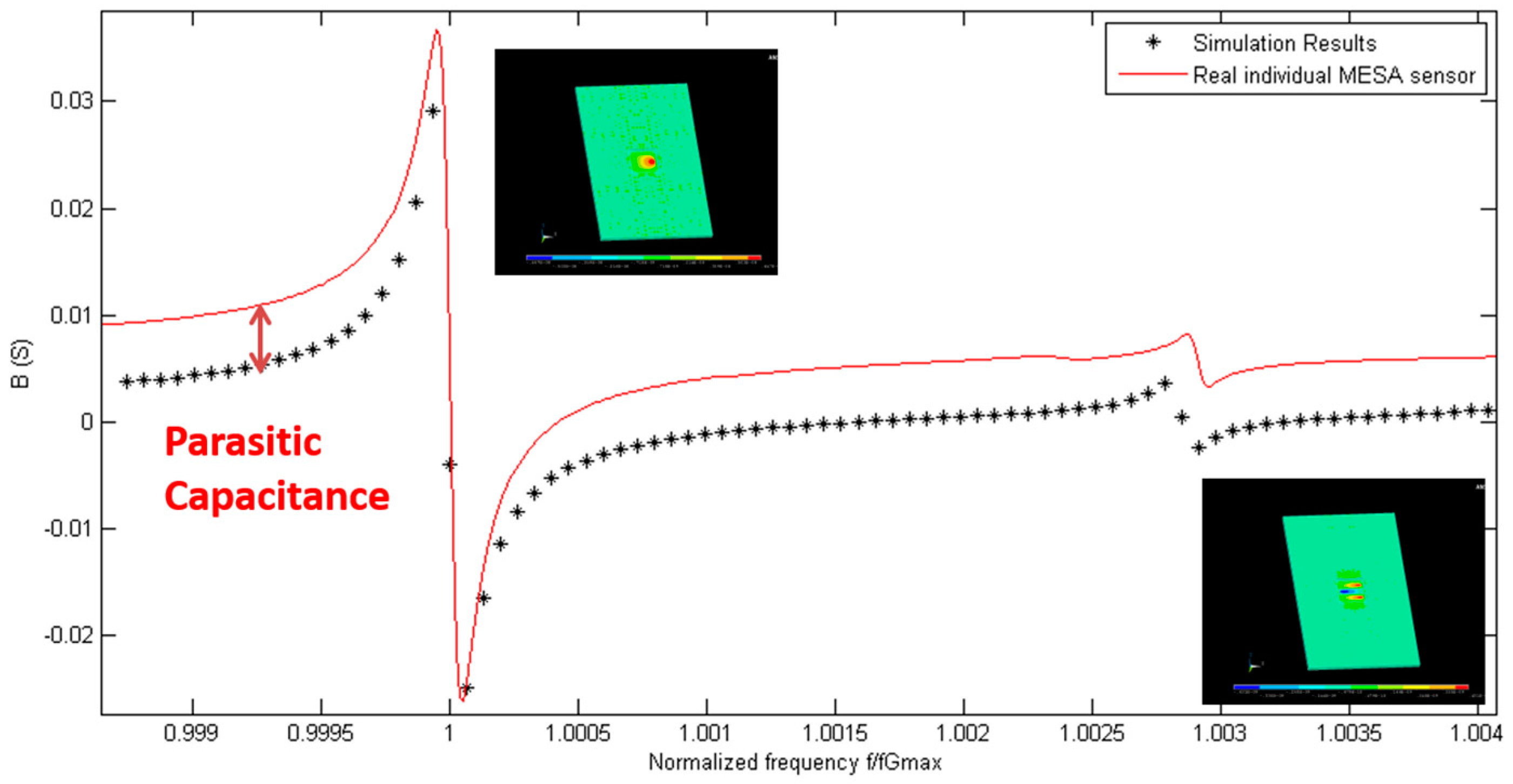
3.2. Sensor Characterization
3.3. Sensor Validation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Dielectric Matrix | |
| Elastic Matrix | |
| Piezoelectric Matrix |
| ρ gold | 19,300 | kg/m3 |
| ρ quartz | 2650 | kg/m3 |
References
- Soper, S.A.; Brown, K.; Ellington, A.; Frazier, B.; Garcia-Manero, G.; Gau, V.; Gutman, S.I.; Hayes, D.F.; Korte, B.; Landers, J.L. Point-of-care biosensor systems for cancer diagnostics/prognostics. Biosens. Bioelectron. 2006, 21, 1932–1942. [Google Scholar] [CrossRef] [PubMed]
- Gubala, V.; Harris, L.F.; Ricco, A.J.; Tan, M.X.; Williams, D.E. Point of care diagnostics: Status and future. Anal. Chem. 2011, 84, 487–515. [Google Scholar] [CrossRef] [PubMed]
- Sauerbrey, G. Use of vibrating quartz for thin film weighing and microweighing. Z. Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Arnau, A. Piezoelectric Transducers and Applications, 2nd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Steinem, C.; Janshoff, A. Piezoelectric Sensors; Springer Science & Business Media: Berlin, Germany, 2007; Volume 5. [Google Scholar]
- Tsortos, A.; Papadakis, G.; Gizeli, E. Shear acoustic wave biosensor for detecting DNA intrinsic viscosity and conformation: A study with qcm-d. Biosens. Bioelectron. 2008, 24, 836–841. [Google Scholar] [CrossRef] [PubMed]
- Tuantranont, A.; Wisitsora-At, A.; Sritongkham, P.; Jaruwongrungsee, K. A review of monolithic multichannel quartz crystal microbalance: A review. Anal. Chim. Acta 2011, 687, 114–128. [Google Scholar] [CrossRef] [PubMed]
- Tao, W.; Lin, P.; Ai, Y.; Wang, H.; Ke, S.; Zeng, X. Multichannel quartz crystal microbalance array: Fabrication, evaluation, application in biomarker detection. Anal. Biochem. 2016, 494, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Rabe, J.; Seidemann, V.; Buettgenbach, S. Monolithic fabrication of wireless miniaturized quartz crystal microbalance (qcm-r) arrays and their application for biochemical sensors. Sens. Mater. 2003, 15, 381–391. [Google Scholar]
- Vig, J.R.; Filler, R.L.; Kim, Y. Microresonator sensor arrays. In Proceedings of the 1995 IEEE International Frequency Control Symposium (49th Annual Symposium), San Francisco, CA, USA, 31 May–2 June 1995; pp. 852–869. [Google Scholar]
- Abe, T.; Esashi, M. One-chip multichannel quartz crystal microbalance (qcm) fabricated by deep rie. Sens. Actuators A Phys. 2000, 82, 139–143. [Google Scholar] [CrossRef]
- Jaruwongrungsee, K.; Waiwijit, U.; Wisitsoraat, A.; Sangworasil, M.; Pintavirooj, C.; Tuantranont, A. Real-time multianalyte biosensors based on interference-free multichannel monolithic quartz crystal microbalance. Biosens. Bioelectron. 2015, 67, 576–581. [Google Scholar] [CrossRef] [PubMed]
- Hung, V.N.; Abe, T.; Minh, P.N.; Esashi, M. Miniaturized, highly sensitive single-chip multichannel quartz-crystal microbalance. Appl. Phys. Lett. 2002, 81, 5069–5071. [Google Scholar] [CrossRef]
- Kao, P.; Doerner, S.; Schneider, T.; Allara, D.; Hauptmann, P.; Tadigadapa, S. A micromachined quartz resonator array for biosensing applications. J. Microelectromech. Syst. 2009, 18, 522–530. [Google Scholar]
- Liang, J.; Huang, J.; Zhang, T.; Zhang, J.; Li, X.; Ueda, T. An experimental study on fabricating an inverted mesa-type quartz crystal resonator using a cheap wet etching process. Sensors 2013, 13, 12140–12148. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, B.; Lucklum, R.; Hauptmann, P.; Rabe, J.; Büttgenbach, S. Electrical characterisation of high-frequency thickness-shear-mode resonators by impedance analysis. Sens. Actuators B Chem. 2001, 76, 47–57. [Google Scholar] [CrossRef]
- Lubczyk, D.; Siering, C.; Lörgen, J.; Shifrina, Z.B.; Müllen, K.; Waldvogel, S.R. Simple and sensitive online detection of triacetone triperoxide explosive. Sens. Actuators B Chem. 2010, 143, 561–566. [Google Scholar] [CrossRef]
- Brutschy, M.; Schneider, M.W.; Mastalerz, M.; Waldvogel, S.R. Porous organic cage compounds as highly potent affinity materials for sensing by quartz crystal microbalances. Adv. Mater. 2012, 24, 6049–6052. [Google Scholar] [CrossRef] [PubMed]
- Brutschy, M.; Schneider, M.W.; Mastalerz, M.; Waldvogel, S.R. Direct gravimetric sensing of gbl by a molecular recognition process in organic cage compounds. Chem. Commun. 2013, 49, 8398–8400. [Google Scholar] [CrossRef] [PubMed]
- Uttenthaler, E.; Schräml, M.; Mandel, J.; Drost, S. Ultrasensitive quartz crystal microbalance sensors for detection of m13-phages in liquids. Biosens. Bioelectron. 2001, 16, 735–743. [Google Scholar] [CrossRef]
- March, C.; García, J.V.; Sánchez, Á.; Arnau, A.; Jiménez, Y.; García, P.; Manclús, J.J.; Montoya, Á. High-frequency phase shift measurement greatly enhances the sensitivity of qcm immunosensors. Biosens. Bioelectron. 2015, 65, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Bottom, V.E. Introduction to Quartz Crystal Unit Design; Van Nostrand Reinhold: Chichester, UK, 1982. [Google Scholar]
- Sagmeister, B.P.; Graz, I.M.; Schwödiauer, R.; Gruber, H.; Bauer, S. User-friendly, miniature biosensor flow cell for fragile high fundamental frequency quartz crystal resonators. Biosens. Bioelectron. 2009, 24, 2643–2648. [Google Scholar] [CrossRef] [PubMed]
- Abe, T.; Hung, V.N.; Esashi, M. Inverted mesa-type quartz crystal resonators fabricated by deep-reactive ion etching. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1234. [Google Scholar] [CrossRef] [PubMed]
- Rabe, J.; Buttgenbach, S.; Zimmermann, B.; Hauptmann, P. Design, manufacturing, and characterization of high-frequency thickness-shear mode resonators. In Proceedings of the 2000 IEEE/EIA International Frequency Control Symposium and Exhibition, Kansas City, MO, USA, 9 June 2000; pp. 106–112. [Google Scholar]
- Rocha-Gaso, M.-I.; March-Iborra, C.; Montoya-Baides, Á.; Arnau-Vives, A. Surface generated acoustic wave biosensors for the detection of pathogens: A review. Sensors 2009, 9, 5740–5769. [Google Scholar] [CrossRef] [PubMed]
- García, J.; Rocha, M.; March, C.; García, P.; Francis, L.; Montoya, A.; Arnau, A.; Jimenez, Y. Love mode surface acoustic wave and high fundamental frequency quartz crystal microbalance immunosensors for the detection of carbaryl pesticide. Proc. Eng. 2014, 87, 759–762. [Google Scholar] [CrossRef]
- Shockley, W.; Curran, D.R.; Koneval, D.J. Energy trapping and related studies of multiple electrode filter crystals. In Proceedings of the 17th Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 27–29 May 1963; pp. 88–126. [Google Scholar]
- Shockley, W.; Curran, D.; Koneval, D. Trapped-energy modes in quartz filter crystals. J. Acoust. Soc. Am. 1967, 41, 981–993. [Google Scholar] [CrossRef]
- Shen, F.; Lu, P.; O’Shea, S.; Lee, K. Frequency coupling and energy trapping in mesa-shaped multichannel quartz crystal microbalances. Sens. Actuators A Phys. 2004, 111, 180–187. [Google Scholar] [CrossRef]
- Beaver, W. Analysis of elastically coupled piezoelectric resonators. J. Acoust. Soc. Am. 1968, 43, 972–981. [Google Scholar] [CrossRef]
- Sheahan, D. An improved resonance equation for at-cut quartz crystals. Proc. IEEE 1970, 58, 260–261. [Google Scholar] [CrossRef]
- Wessels, A.; Klöckner, B.; Siering, C.; Waldvogel, S.R. Practical strategies for stable operation of hff-qcm in continuous air flow. Sensors 2013, 13, 12012–12029. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Lee, H.; Lu, P.; Lim, S. Finite element analysis of interference for the laterally coupled quartz crystal microbalances. Sens. Actuators A Phys. 2005, 119, 90–99. [Google Scholar] [CrossRef]
- Cady, W.G. Piezoelectricity: An Introduction to the Theory and Application of Electromechanical Phenomena in Crystals; McGraw-Hill: New York, NY, USA, 1946. [Google Scholar]
- Pao, S.; Chaos, M.; Lam, C.; Chang, P. An efficient numerical method in calculating the electrical impedance different modes of at-cut quartz crystal resonator. In Proceedings of the 2004 IEEE International Frequency Control Symposium and Exposition, Montreal, QC, Canada, 23–27 August 2004; pp. 396–400. [Google Scholar]
- Mindlin, R.D.; Lee, P. Thickness-shear and flexural vibrations of partially plated, crystal plates. Int. J. Solids Struct. 1966, 2, 125–139. [Google Scholar] [CrossRef]
- Lin, Z.; Yip, C.M.; Joseph, I.S.; Ward, M.D. Operation of an ultrasensitive 30-mhz quartz crystal microbalance in liquids. Anal. Chem. 1993, 65, 1546–1551. [Google Scholar] [CrossRef]
- Ballato, A.; Gualtieri, J.G. Advances in high-q piezoelectric resonator materials and devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1994, 41, 834–844. [Google Scholar] [CrossRef] [PubMed]
- Montagut, Y.; García, J.; Jiménez, Y.; March, C.; Montoya, A.; Arnau, A. Frequency-shift vs. phase-shift characterization of in-liquid quartz crystal microbalance applications. Rev. Sci. Instrum. 2011, 82, 064702. [Google Scholar] [CrossRef] [PubMed]
- Dixon, M.C. Quartz crystal microbalance with dissipation monitoring: Enabling real-time characterization of biological materials and their interactions. J. Biomol. Tech. JBT 2008, 19, 151. [Google Scholar] [PubMed]
- Li, J.; Wu, Z.-Y.; Xiao, L.-T.; Zeng, G.-M.; Huang, G.-H.; Shen, G.-L.; Yu, R.-Q. A novel piezoelectric biosensor for the detection of phytohormone β-indole acetic acid. Anal. Sci. 2002, 18, 403–407. [Google Scholar] [CrossRef] [PubMed]
- Kengne-Momo, R.; Jeyachandran, Y.; Assaf, A.; Esnault, C.; Daniel, P.; Pilard, J.F.; Durand, M.; Lagarde, F.; Dongo, E.; Thouand, G. A simple method of surface functionalisation for immuno-specific immobilisation of proteins. Anal. Bioanal. Chem. 2010, 398, 1249–1255. [Google Scholar] [CrossRef] [PubMed]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, R.; García, P.; García, M.; García, J.V.; Jiménez, Y.; Arnau, A. Design and Validation of a 150 MHz HFFQCM Sensor for Bio-Sensing Applications. Sensors 2017, 17, 2057. https://doi.org/10.3390/s17092057
Fernández R, García P, García M, García JV, Jiménez Y, Arnau A. Design and Validation of a 150 MHz HFFQCM Sensor for Bio-Sensing Applications. Sensors. 2017; 17(9):2057. https://doi.org/10.3390/s17092057
Chicago/Turabian StyleFernández, Román, Pablo García, María García, José V. García, Yolanda Jiménez, and Antonio Arnau. 2017. "Design and Validation of a 150 MHz HFFQCM Sensor for Bio-Sensing Applications" Sensors 17, no. 9: 2057. https://doi.org/10.3390/s17092057
APA StyleFernández, R., García, P., García, M., García, J. V., Jiménez, Y., & Arnau, A. (2017). Design and Validation of a 150 MHz HFFQCM Sensor for Bio-Sensing Applications. Sensors, 17(9), 2057. https://doi.org/10.3390/s17092057





