1. Introduction
Nowadays, one of the most active research areas in the wireless communication field is the design of communication techniques for fifth generation (5G) cellular systems. Although the final technical components of the 5G system are still under discussion, important progress has already been made towards the definition of the set of scenarios and requirements to be addressed by these systems. In particular, the European project Mobile Enablers for the Twenty-Twenty Information Society (METIS) played a key role in this direction by stating that, among other goals, the 5G system shall boost the user data rate of 4G cellular systems by a factor ranging from 10 to 100 [
1].
A promising technology to meet this specific 5G requirement is the use of advanced multiple-input multiple-output (MIMO) techniques with large antenna arrays, where the number of antenna elements is much higher than the number of users to be served, also known as massive MIMO [
2]. Massive MIMO techniques imply the use of, at least, an order of magnitude more antenna elements than in current systems [
3], and their application can be twofold: either it can be used to compensate the propagation losses of backhaul and access links through beamforming, or it can be used to boost capacity with multi-stream transmission. In fact, although it has been historically associated with beamforming, current trends point towards the application of MIMO spatial multiplexing techniques in conjunction with beamforming to best exploit the richness of the channel [
4].
Unfortunately, one of the showstoppers for the successful incorporation of massive MIMO into cellular networks is the large physical size of the antenna arrays at currently used cellular frequencies. For this reason, massive MIMO is being considered in conjunction with millimeter-Wave (mmW) frequencies [
3,
5], where antenna arrays of reasonable physical sizes are feasible [
6]. From a signal processing perspective, transmission with massive arrays increases the processing complexity derived from the computation of the required precoders when digital schemes are applied to hundreds of antennas. Multi-antenna digital precoding is carried out at baseband and, thus, it requires an architecture with as many radio-frequency (RF) chains as antenna ports to do the digital to analog data conversion and subsequent upmixing to RF. However, the use of one RF chain per antenna is not only a very costly option for massive MIMO systems, but it also leads to a extremely high power consumption [
3,
7]. Motivated by this, there is now a growing interest in alternative transmission schemes based on analog beamforming (ABF) and hybrid beamforming (HBF) architectures, where all or part of the processing is based on radio-frequency beamforming. Many ABF and HBF approaches have been proposed in the last years, both for single-user (SU) [
8,
9] and multi-user (MU) transmissions [
10,
11], all of them using a substantially reduced number of RF chains with respect to the number of antennas. The potential of these schemes is well-known; however, to the best of the authors’ knowledge, there is not yet a clear view on the performance of the different beamforming alternatives in a complete system with multiple transmission and reception points and a realistic channel model. In this direction, some preliminary tests were carried out for a single-link case in [
12] and for a multi-link case in [
13].
System level simulations usually rely on a set of ideal assumptions that may have a non negligible impact on the accuracy of the assessments based on these simulations [
13]. One such assumption is the perfect knowledge of the channel state at the transmitter, the receiver or both entities. In practice, channel measurements present errors and, additionally, channel state changes within the time elapsed from the channel measurement until the transmission/reception phase. Therefore, perfect channel knowledge is not realistic. Another common assumption is the use of ideal hardware components in all the devices involved in the communication. However, the presence of non-ideal devices in real implementations brings in several error sources that may affect the performance of the algorithms under study. In particular, real phase shifter implementations introduce phase errors whose magnitude was studied in [
14,
15], and non-ideal combiners introduce power losses that were characterized, for instance, in [
16]. The effect of hardware-constrained base stations in massive MIMO systems was extensively analyzed in [
17], where a scaling law of the increase of some particular imperfections with the number of antennas was provided. In addition, hardware constraints impose practical limitations that should be desirably considered in the algorithms design. This was highlighted in [
18,
19], which propose constant envelope precoders suitable for the use of power-efficient RF power amplifiers as a constraint to avoid the problems of such non-ideal amplifiers with their inherent non-linear behaviour. Overall, it is of paramount importance to consider the effect of hardware impairments and other practical limitations when analyzing the system performance achieved by massive MIMO cellular systems.
Motivated by the lack of concluding results on the mmW multi-cell performance of ABF, this paper provides a thorough assessment of ABF schemes for MU single-stream transmission under realistic channel conditions in the lower edge of the mmW frequency band. In particular, a carrier frequency of 28 GHz is considered, which, although it does not strictly belong to the mmW band (defined from 30 and 300 GHz), it has been widely adopted by industry as a mmW frequency, as any other frequency above 10 GHz [
20]. To this end, exhaustive system simulations have been conducted, assuming a multi-cell deployment in which the channel is accurately emulated and there is a coexistence of users with very different channel conditions. The main objective is to complement existing theoretical studies by assessing under which conditions ABF schemes can approach the performance of fully-digital precoders. In addition, the performance of the analog schemes with inter-beam interference in the system (i.e., when multiple users are simultaneously scheduled) is also investigated.
Simulation results with ideal assumptions on aspects such as the timely availability of channel state information (CSI), ideal phase-shifters and combiners for ABF and lack of per-antenna power constraints (PAPC) will be contrasted with results including more realistic assumptions on these aspects. More specifically, the following realistic assumptions were selected and analyzed:
outdated CSI at the transmitters;
PAPC in the precoding design;
Inaccuracy errors caused by real phase shifters;
Losses introduced by real combiners.
The rest of the paper is organized as follows.
Section 2 details the system model and multi-antenna schemes assessed in this work, namely fully-digital and analog schemes.
Section 3 describes the simulation assumptions and includes the performance evaluation with ideal assumptions.
Section 4 and
Section 5 are devoted to the performance evaluation including practical limitations and hardware impairments, respectively. Finally,
Section 6 draws the main findings of the paper.
2. System Model and Evaluated Precoding Schemes
This paper studies an MU mmW downlink system with
Base Stations (BSs) and
K User Equipment devices (UEs). Each BS is equipped with
antennas and
RF chains. For the sake of simplicity in the simulations, a single narrow receive beam is assumed at each UE (which would require an antenna array in practice), in order to simulate a beamforming gain at the receiver as in [
21]. Furthermore, the pointing direction of the directive beam is selected by the user to maximize the signal to noise ratio (SNR) at the receiver.
The downlink transmission resources are partitioned in the time-frequency plane. In the time domain, the resource space is divided into subframes of a certain time duration. In the frequency domain, resources are grouped in frequency blocks (FB). The minimum time-frequency resource is known as resource block (RB), and it is composed of one frequency block during one subframe period. This terminology is the same as the one used by the the 3rd Generation Partnership Project (3GPP) and the METIS project [
1] to carry out performance evaluations.
In order to exploit the BS multi-antenna architecture to either multiplex different data streams or to provide beamforming gains to the different users, some form of precoding or beamforming must be applied at the transmitter side. The schemes considered in this work are next detailed.
2.1. Fully Digital Precoding Schemes
In fully digital implementations, where
, precoding is commonly done in the digital baseband, thus allowing a very flexible design of the precoding matrix or vector. Many fully-digital precoding designs for MU-MIMO systems can be found in the literature [
22]. Although the optimum precoders, in terms of achieving capacity, require non-linear implementation, in this work, we will focus on linear precoding, which is known to provide a good tradeoff between performance and complexity. In particular, we selected the well-known Maximum Ratio Transmission (MRT) linear precoder, which is designed to maximize the SNR at the intended user and, thus, it only requires the knowledge of the channel vector between UE
k and its serving BS in FB
b, denoted by
. The MRT precoder in FB
b for UE
k,
, is computed as:
where the superscript
stands for conjugate-transpose operation. The main reason for the selection of this digital precoder is that, when the number of antennas is very high, its performance is very close to the performance of other precoding schemes that require higher computational complexity, such as zero-forcing (ZF) or regularized ZF [
23].
We focus on digital MU transmission, that is, a set of as many users as BS antennas can be served simultaneously at each subframe by multiplexing them in the spatial domain. Furthermore, we will investigate the effect of multiplexing different sets of users in different FBs of each subframe. To this end, two variants of digital precoding have been implemented and simulated, denoted by digital precoding non frequency selective (DP NFS) and digital precoding frequency selective (DP FS). In DP NFS, all FBs are allocated to a single set of UEs per subframe, while, in DP FS, the allocation is optimized per RB, thereby allowing different sets of UEs to be scheduled per subframe in different FBs.
2.2. Analog Beamforming Schemes
As mentioned above, in mmW systems, the high number of antennas required to achieve a high quality link makes fully-digital implementations hardly feasible in practice, due to the high cost and power consumption of having as many RF chains as antennas. For that reason, less complex precoding schemes either in the analog (i.e., radio-frequency) domain or combining the processing in both digital baseband and analog domain are receiving increasing attention [
11].
In RF beamforming, phase shifts are applied to each antenna element of the array in order to steer the beam towards a certain direction.
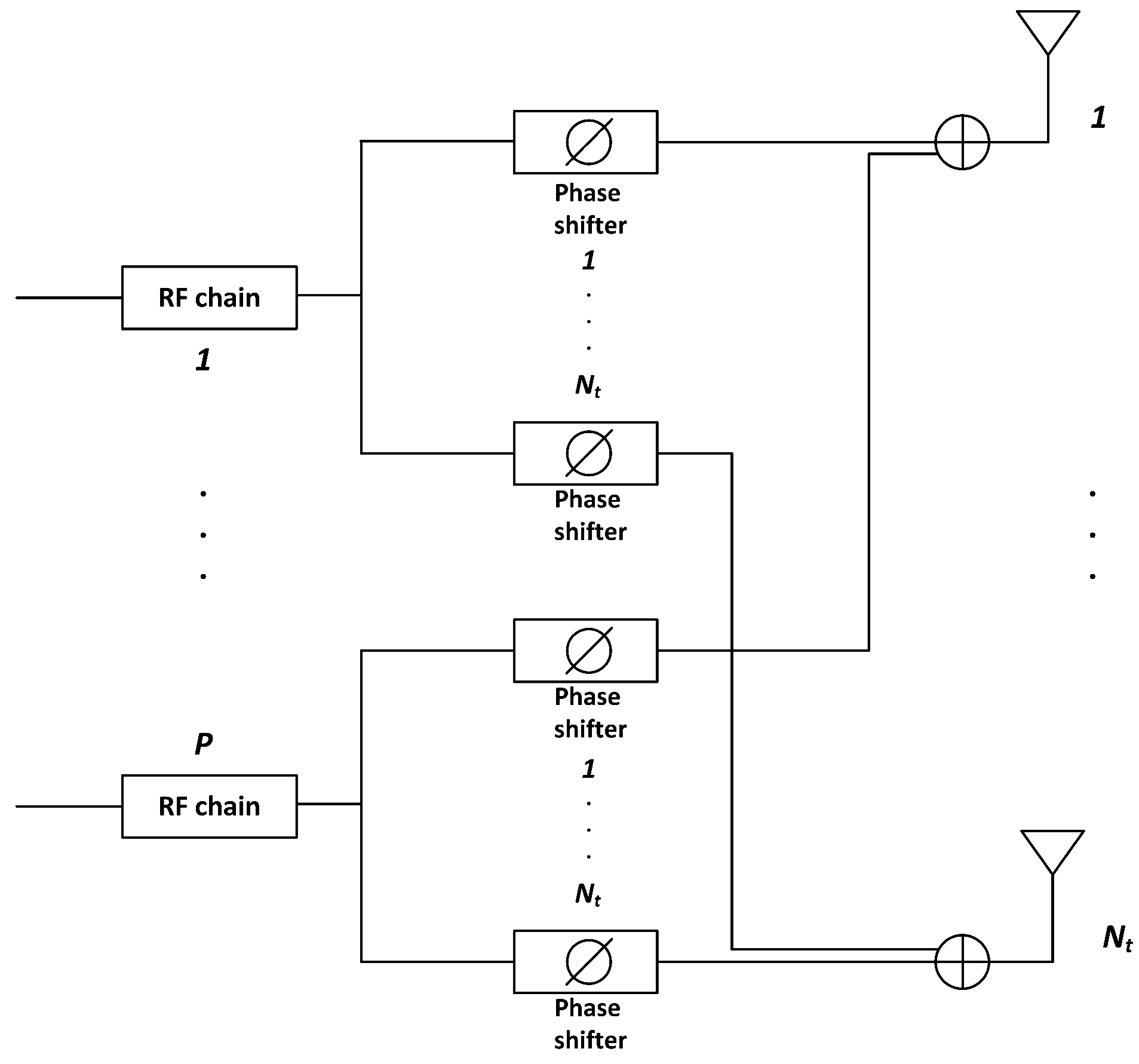
Figure 1 shows an example of analog beamforming (ABF) architecture, with
RF chains and a set of
phase shifters applied to each RF chain. The outputs of the
i-th phase shifters of every RF chain are combined to feed the
i-th antenna element in the array. Using this architecture,
P data streams can be simultaneously transmitted with full array gain and up to
P different users can be spatially multiplexed. In this work, we consider a simple and practical method for mmW beamforming. Motivated by the fact that the channel at high frequencies is characterized by limited scattering, in particular for the UEs in line of sight (LoS) condition, we assume that (a) beamformers are designed only in the RF domain, and (b) the digital stage is optimized to schedule up to
P UEs in each subframe, each UE being served by a specific RF beamformer. More sophisticated schemes could be used [
10,
11], for instance, by optimizing the digital precoding weights to be used in the baseband domain. However, these schemes are expected to provide relevant gain only when most of the UEs have a highly frequency selective channel, as in scenarios where there are mostly UEs in non line of sight (NLoS) conditions. Therefore, in our analysis, we will intentionally compare a simple ABF scheme against fully DP. Future work will include a more thorough evaluation on how much of the performance gap between these two schemes can be filled by more advanced (but at the same time more complex) hybrid beamformers.
The RF beamforming vector for the
k-th UE, denoted by
, is selected from a codebook based on the discrete Fourier transform (DFT) matrix, which provides a grid of beams such as in [
10], useful also for channel limited feedback setups. Elements of the codebook are of this form:
where
is the index of the codebook elements and
C the number of vectors in the codebook. We assume
, that is to say, maximum diversity order. The specific beamforming vector for UE
k is chosen to maximize the sum rate over the whole allocated band
as:
where
is the transmit power, and
N and
I are the noise and long term interference power at the receiver, respectively. Although many other codebook designs could be used, DFT-based precoding is chosen in this work to achieve a good tradeoff between complexity and performance.
Note that the whole bandwidth is available at each RF chain and multiple UEs are multiplexed in the spatial domain. Equal power sharing among users is considered, meaning, for example, that, when P users are simultaneously multiplexed by a BS, the available power per RF chain must be scaled by to fulfill a per-BS power restriction.
4. Performance with Practical Limitations
4.1. Performance with Outdated Channel State Information
A very usual ideal assumption for simulation is the perfect knowledge of the instantaneous (per-subframe) channel at every BS, which allows the BS precoder to be adapted to the actual channel. However, practical systems must often deal with the problem of having imperfect CSI. In frequency division duplex (FDD) systems, the downlink channel is estimated at the UE and fed back to the BS. These estimation and feedback stages can, in practice, impair the CSI with quantization noise, due to the usually limited resources on the feedback channel. In addition, the presence of noise in the channel during the transmission of training sequences for CSI estimation contributes to an imperfect channel estimation. The latter effect is also present in the channel estimation stage of time division duplex (TDD) systems. Another important practical limitation in both FDD and TDD systems is the unavoidable delay between the instant the channel is estimated and the instant the channel is used in designing the precoder for data transmission, which, in turn, can further degrade the system performance.
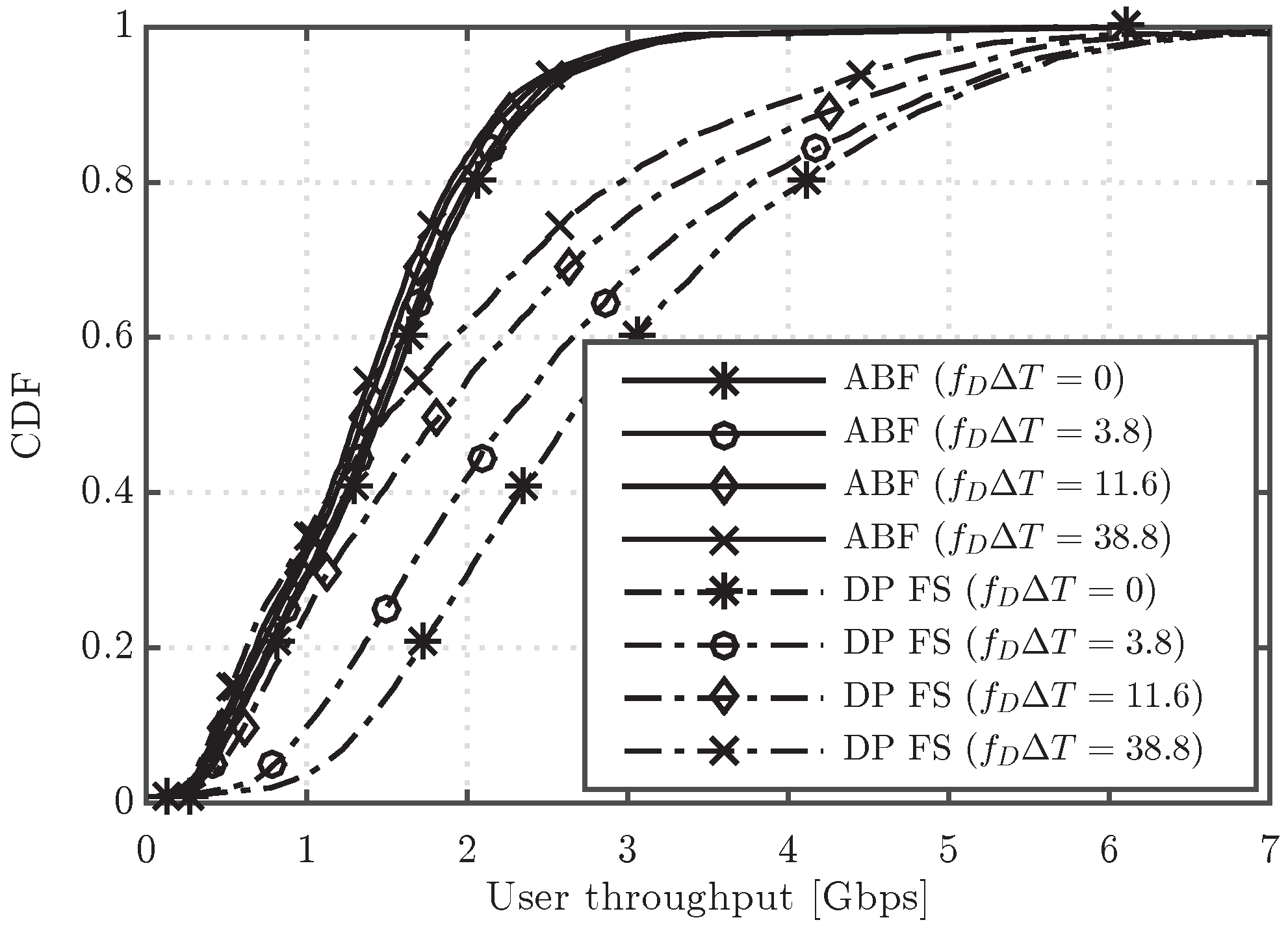
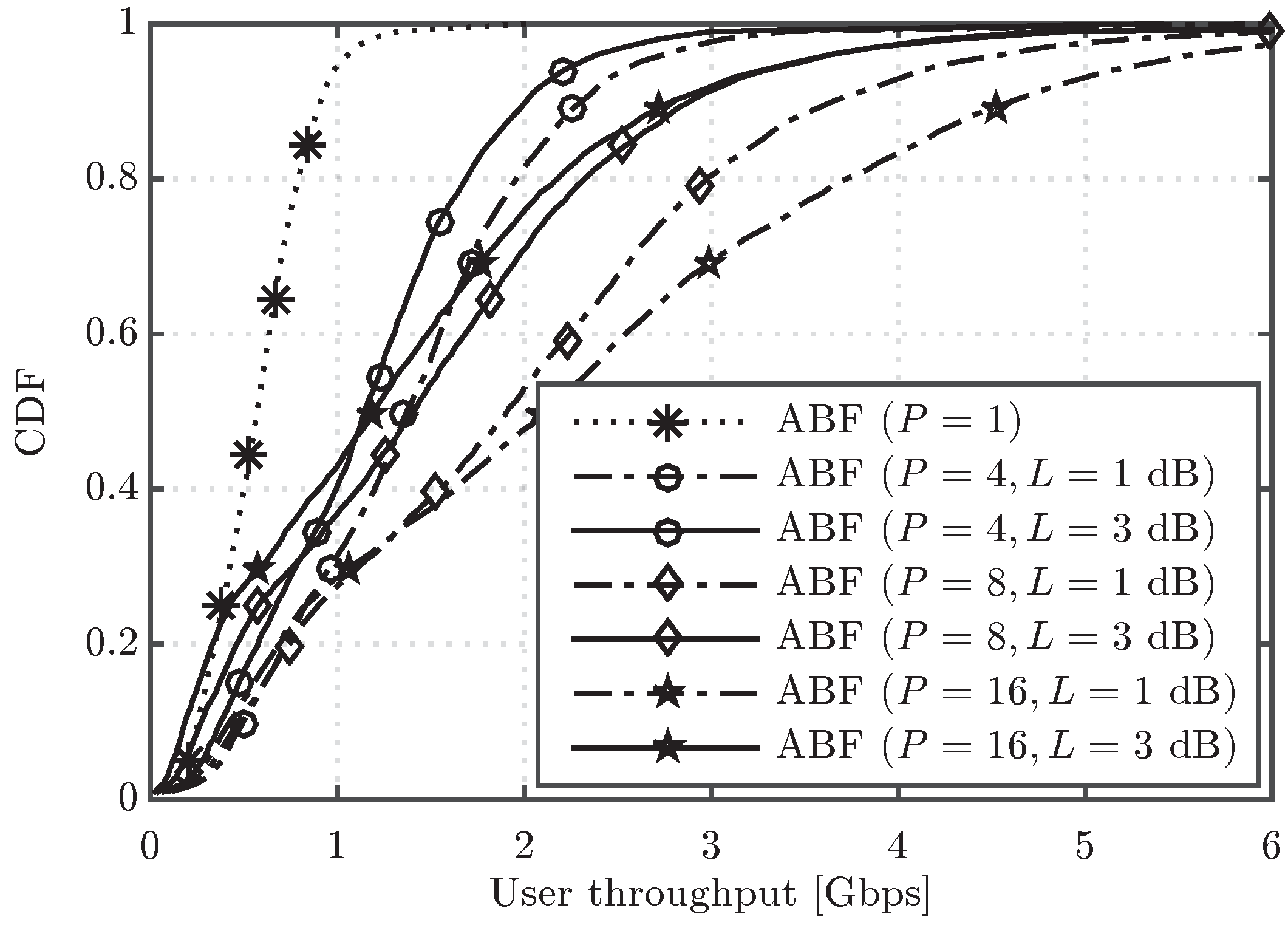
In this work, we will focus on the effect of outdated CSI over the performance of ABF with , DP NFS and DP FS. To this end, it is here assumed that each BS receives an update of the channel coefficients only every certain period T, higher than the subframe duration ms. It is worth noting that we consider T values that cause changes only in the small scale fading components of the channel, i.e., the large scale fading components like path loss, shadowing and path angles of arrival/departure remain constant during T. For a better illustration of the small scale channel variation during the period T, the results will be presented as a function of the product , where is the maximum Doppler shift at carrier frequency f with user speed equal to v, and is the CSI delay with respect to the subframe duration.
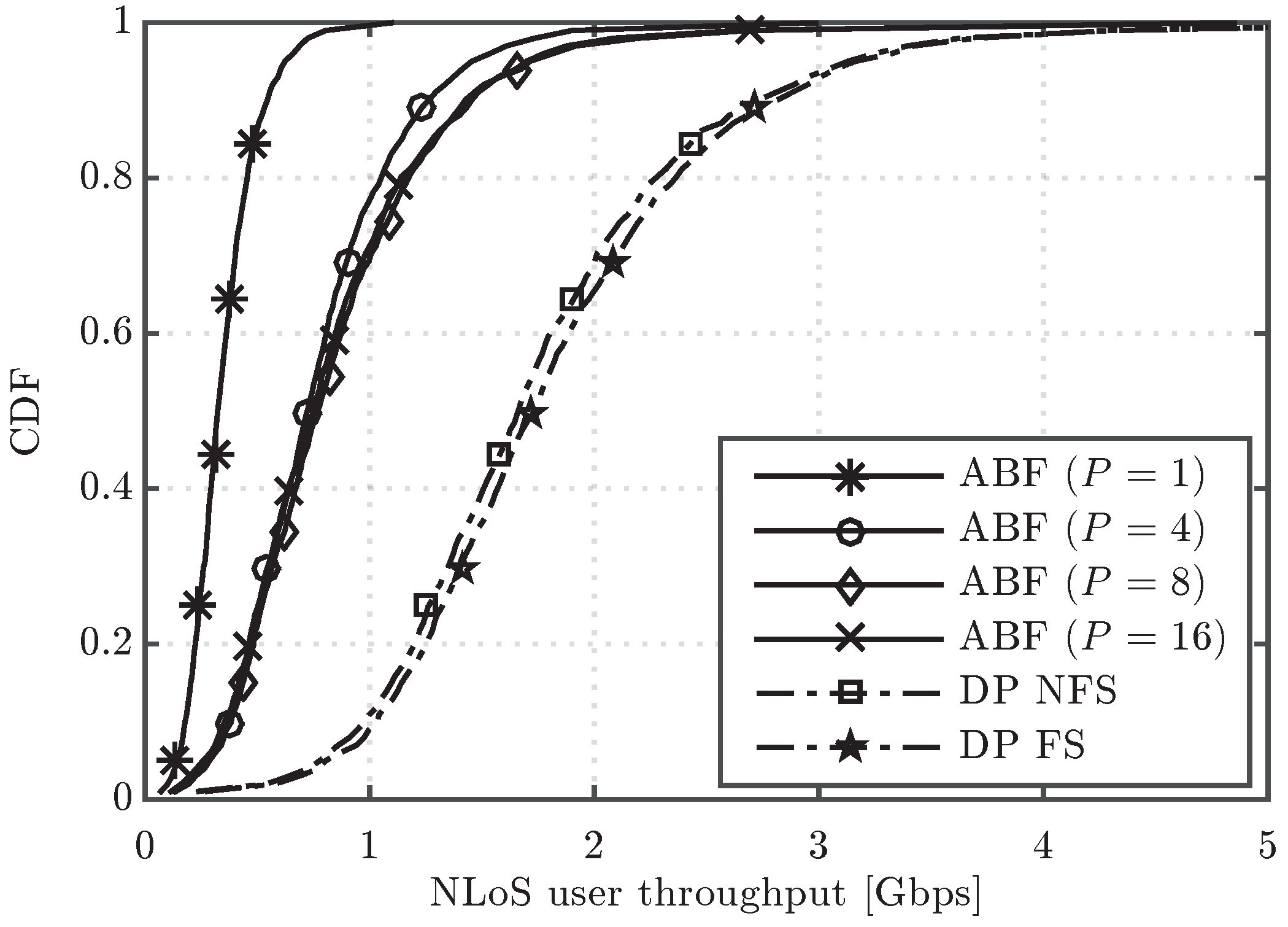
Figure 6 shows the CDF of user throughput for the ABF and DP FS schemes, considering different values of the channel update period, in particular
and 500 ms, which lead to
and
, respectively. Note that
corresponds to the ideal case, where the channel is supposed to be updated every subframe. It can be first observed that the ABF scheme is more robust to outdated CSI, as it presents a nearly negligible performance degradation with
. Such degradation of ABF is also much lower than for the DP FS approach, which results in a reduced performance gap between ABF and DP as
T increases. The lower robustness to outdated CSI of DP is well justified by the fact that this scheme has a strong dependence on the small scale channel fading, whereas the ABF mainly relies on the large scale components, since it typically tends to point the beamformer towards the angle of departure of the strongest path. In fact, while in a practical mmW system it is expected that the channel is tracked every few milliseconds or few tens of milliseconds, the higher values of
T considered here, e.g.,
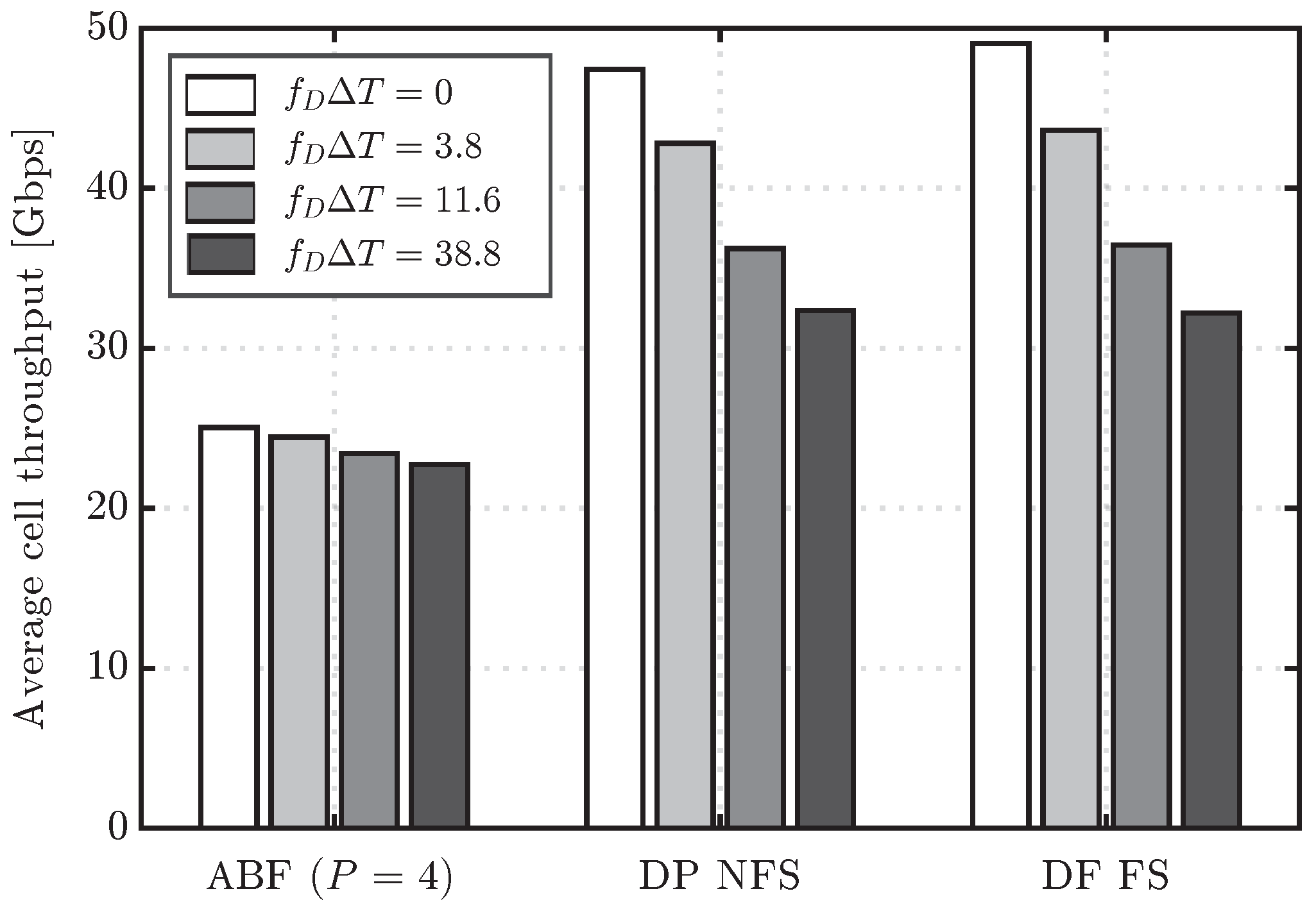
ms, are useful to understand the robustness of the different schemes when there is basically no knowledge of the small scale fading, and, thus, beamformers are designed mainly based on the large scale fading components of the channel. In such a scenario, ABF, by simply selecting the beam that points toward the direction that maximizes the signal to interference plus noise ratio (SINR) at the receiver, turns out to be much more robust than DP. For completeness, the average cell throughput for different values of the channel update period including also the DP NFS scheme is depicted in
Figure 7. The latter results also confirm the robustness of ABF to the effect of outdated CSI, which presents a maximum penalty in cell throughput of 9.8% for
. On the other hand, the cell throughput values of DP FS and DP NFS are reduced up to 32% and 34%, respectively. Regarding the comparison between DP NFS and DF FS, both show very similar performance, meaning that the additional complexity of DP FS to adapt the precoder per RB does not pay off with an outdated CSI.
4.2. Performance with PAPC
In practical multi-antenna systems, each element of the antenna array may be powered by its own amplifier and, thus, is limited by the linearity of that amplifier. For that reason, precoding schemes should apply a more restrictive assumption than the sum power constraint, that is, a per-antenna power constraint. In order to study the effect of limiting the maximum available power per antenna in the DP NFS and DP FS schemes, we consider, in this section, a second digital precoding alternative that takes into account this practical limitation: the Equal-Gain Transmission (EGT) scheme with per-antenna power constraints [
19]. EGT ensures the allocation of the same amount of power per element of the antenna array. Moreover, its implementation is simple and has shown a bounded performance degradation in comparison to the MRT precoder when the number of antenna elements in the array is sufficiently high [
26]. If the channel vector between UE
k and its serving BS in FB
b is expressed as:
then, the corresponding EGT precoding vector for UE
k in FB
b,
, is
As before, equal power allocation among users is considered. Note that PAPC is implicitly satisfied by the ABF scheme considered in this work, and, thus, the selection of EGT for DP allows a fair comparison from a power allocation perspective.
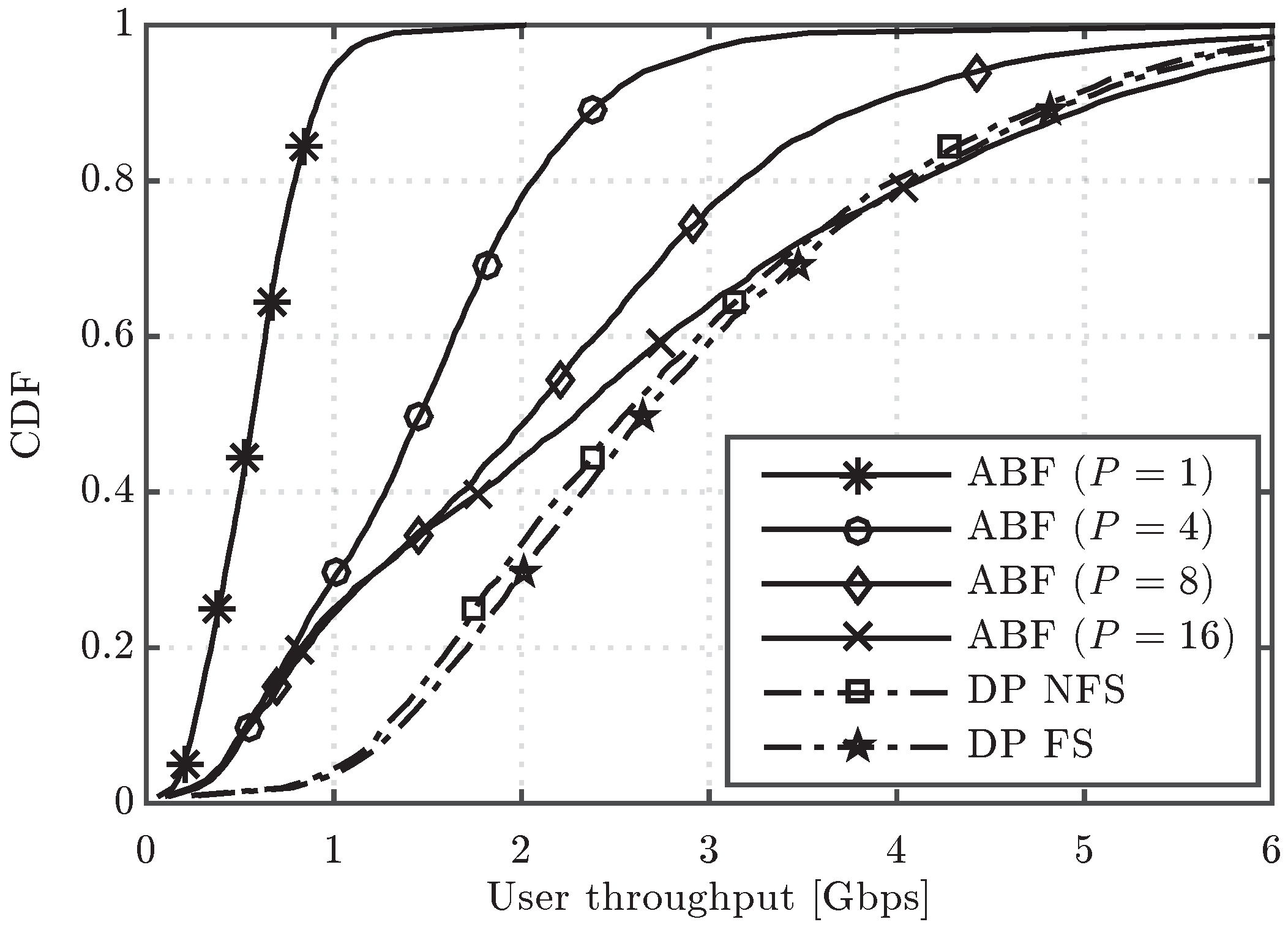
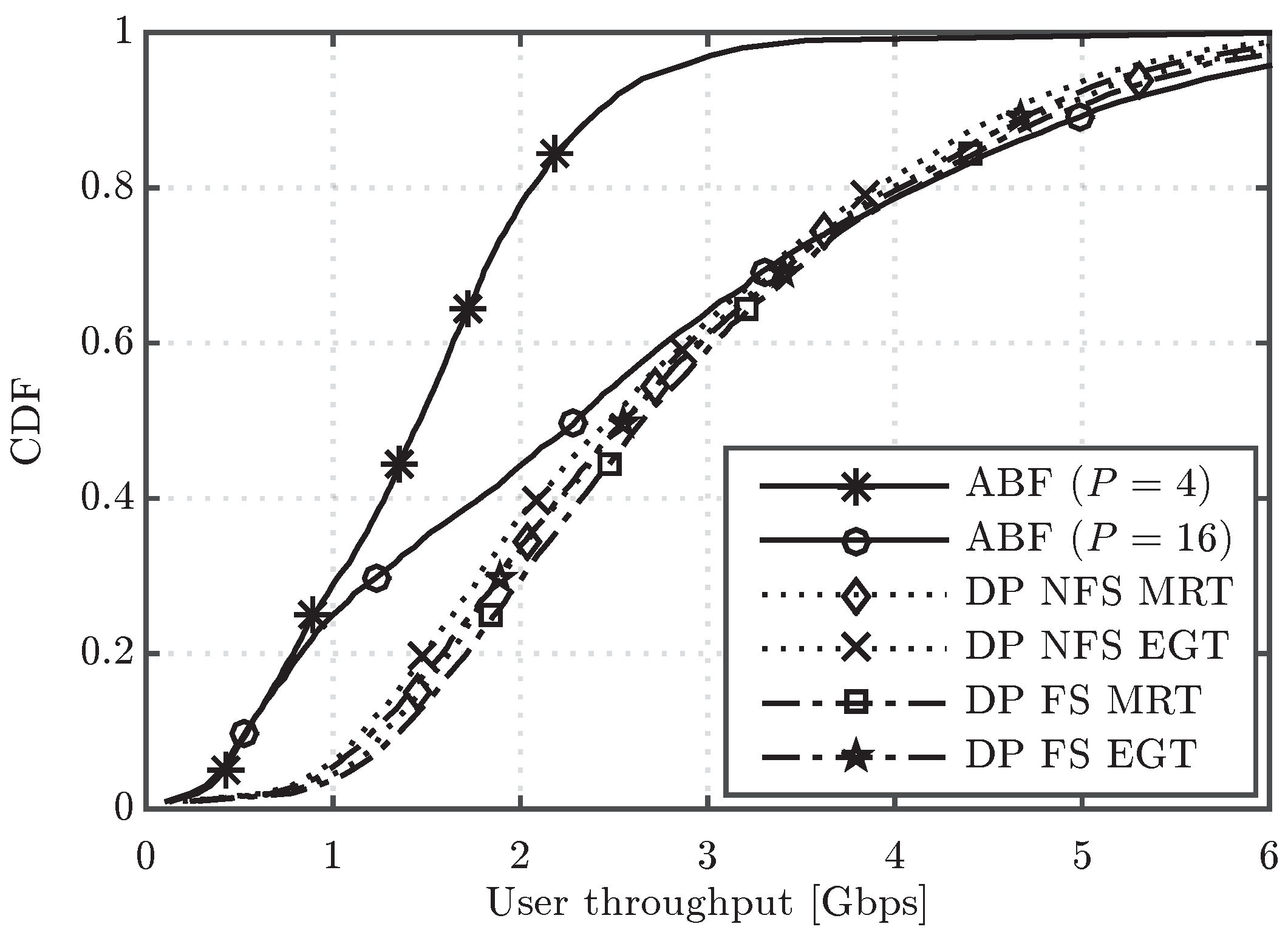
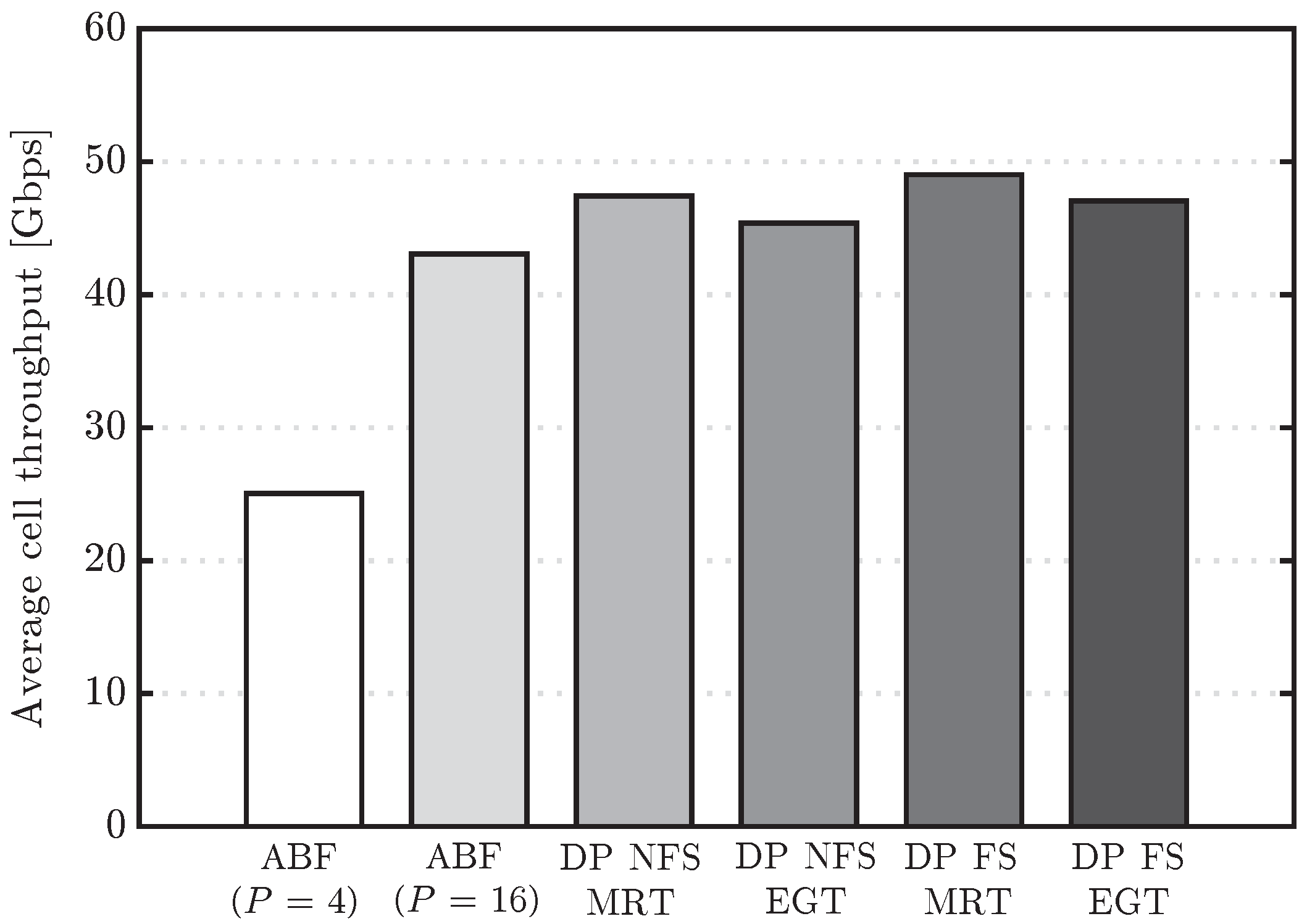
Figure 8 shows the CDF of user throughput for the two digital precoding alternatives, MRT and EGT with PAPC, both of them configured according to the two scheduling variants under study (DP NFS and DP FS). The performance results of ABF with
and
RF chains with ideal assumptions are also included in the figure for the sake of comparison. In general, the EGT precoder worsens the throughput performance of both DP variants, although not very significantly. A meaningful result is that MRT DP NFS achieves very similar performance to EGT DP FS. Therefore, the performance loss due to the PAPC constraint can be, in this case, compensated by a more elaborated scheduler (per FB instead of per subframe). Moreover, the power per antenna element limitation brings the performance of digital precoders a bit closer to the one of ABF with
RF chains, i.e., with the same multiplexing capacity, although there is still a substantial performance gap for NLoS UEs (lower part of the CDF curve). Finally, the average cell throughput values for the ABF, MRT and EGT evaluated schemes are included in
Figure 9. From this figure, we can confirm that the EGT-PAPC precoder causes approximately a 4% performance loss over both DP variants, a percentage much lower than the one caused by outdated CSI over DP.
6. Conclusions
This paper has presented a thorough performance evaluation of digital precoding and analog beamforming schemes in a massive MIMO multi-cell deployment operating in the mmW frequency band. In the first part, a comparison among analog and digital precoding schemes has been carried out under ideal assumptions, namely, perfect and timely CSI at the transmitters, ideal phase-shifters and combiners in the analog scheme and lack of PAPC in digital precoding. MU schemes have been compared against ABF without spatial multiplexing of users, considered here as the baseline scheme. It was observed that by scheduling multiple users at a time, the throughput is substantially increased. Simulation results have further shown that analog beamforming schemes can reach the performance of fully digital precoders when working under LoS conditions and with a sufficient number of parallel RF chains. On the other hand, analog schemes have been shown to be more sensitive to interference and, thus, more degraded in NLoS conditions, in which increasing the number of RF chains can not provide any advantage.
After the initial performance comparison, the effect of several realistic impairments has been included in the simulation setup. To this aim, the effect of having only outdated CSI for precoding at the BS has been firstly analyzed by considering a more realistic period to update the channel in all the evaluated schemes. In addition, PAPC have been set in the two considered digital precoding variants to also see the effect of this realistic constraint. Lastly, the errors introduced by both the phase shifters and combiners in the analog architecture have been modeled.
From the results with outdated channel information, it can be concluded that digital precoding schemes are more sensitive to imperfections on the CSI knowledge at the BS, presenting large losses (up to 34%) when the CSI update period is increased. On the other hand, analog beamforming schemes have shown to be robust against the channel information inaccuracy, presenting a negligible reduction of performance when the channel reporting period is increased.
The results with PAPC have exhibited a performance reduction in digital precoding schemes based on MRT of about 4%, which leads to a small reduction of the performance gap between digital and analog implementations. In practice, the performance loss due to the PAPC could be compensated, for instance, by means of a more elaborated scheduler with a more frequent update of precoders.
Regarding the effect of phase-shifter errors, simulation results have shown that this impairment has little impact on the ABF performance, even when the magnitude of the introduced phase error is significantly higher than current state-of-the-art values known from manufacturing. Nevertheless, LoS UEs suffer a stronger degradation due to this impairment when compared to the NLoS UEs, due to their narrower received beams. Conversely, combiner losses have indeed a great impact on the system performance, mainly when the number of RF chains in the analog scheme is high. In fact, the magnitude of the power loss introduced by the combiner determines in the end the optimum number of RF chains to be selected for analog beamforming. Overall, it is more suitable to employ a low number of RF chains when the losses introduced by the combiner are large.
Future work includes studying the performance of mmW beamforming methods with different planar array solutions and also the evaluation of more advanced hybrid precoding designs with an optimized baseband processing stage. In addition, analyzing the performance in the presence of more realistic user mobility would be of future interest.