Studies of Scattering, Reflectivity, and Transmitivity in WBAN Channel: Feasibility of Using UWB
Abstract
:1. Introduction
2. Mathematical Model
2.1. Wave Propagation through Biological Media
2.2. Scattering, Reflection, and Anti-Reflection
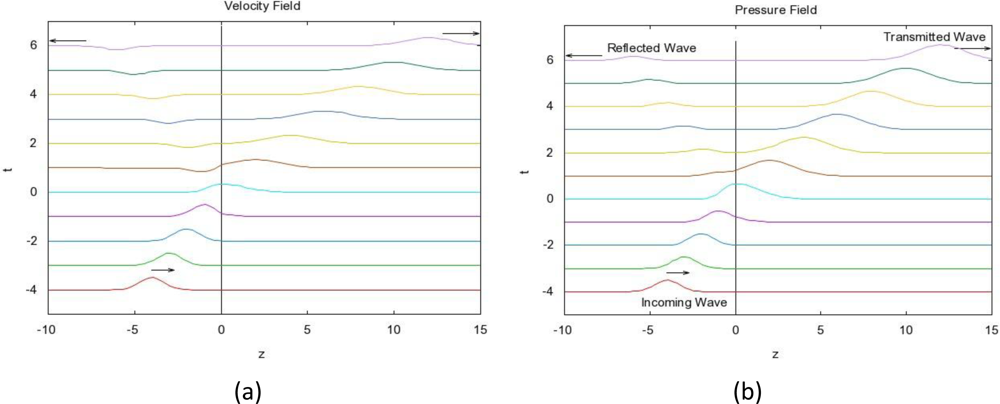
2.2.1. Scattering by a Single Interface
2.2.2. Single-Layer Case: Scattering
2.2.3. Single-Layer Case: Reflection and Transmission Coefficients
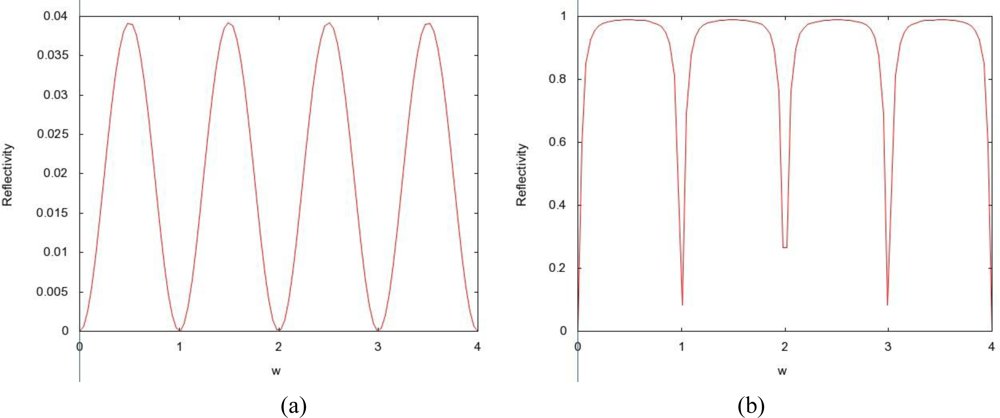
2.3. Filtering Property of the Layer
2.3.1. Reflection
2.3.2. Anti-Reflection
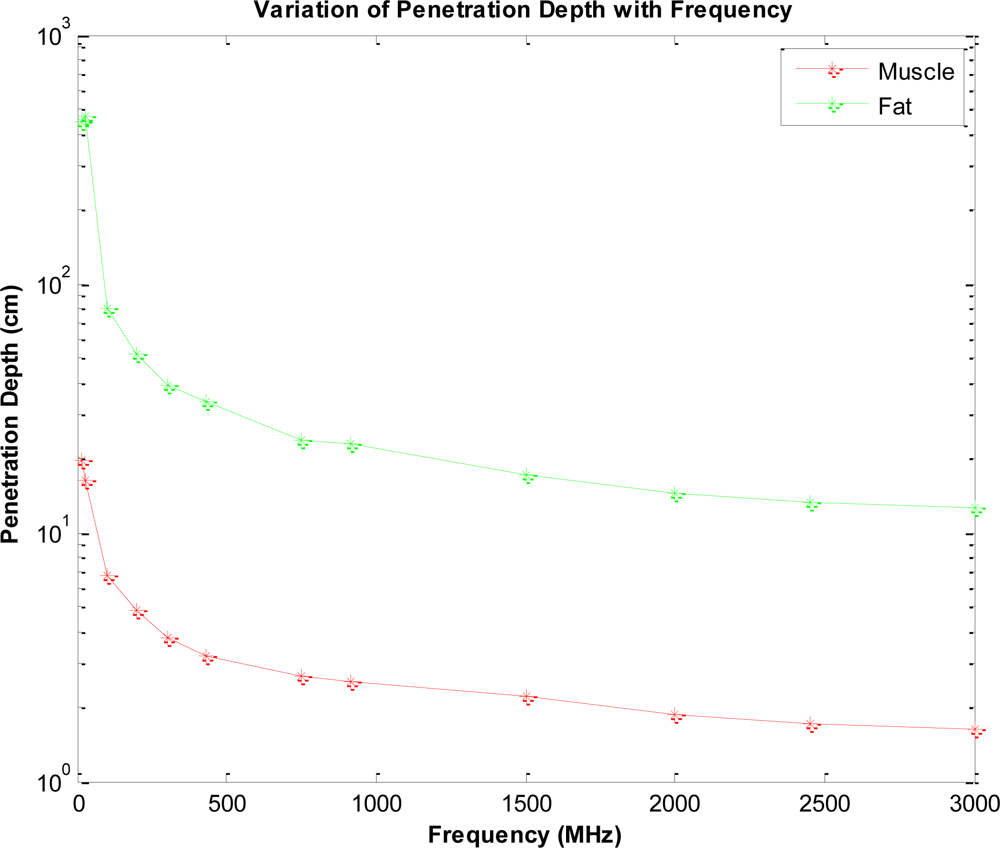
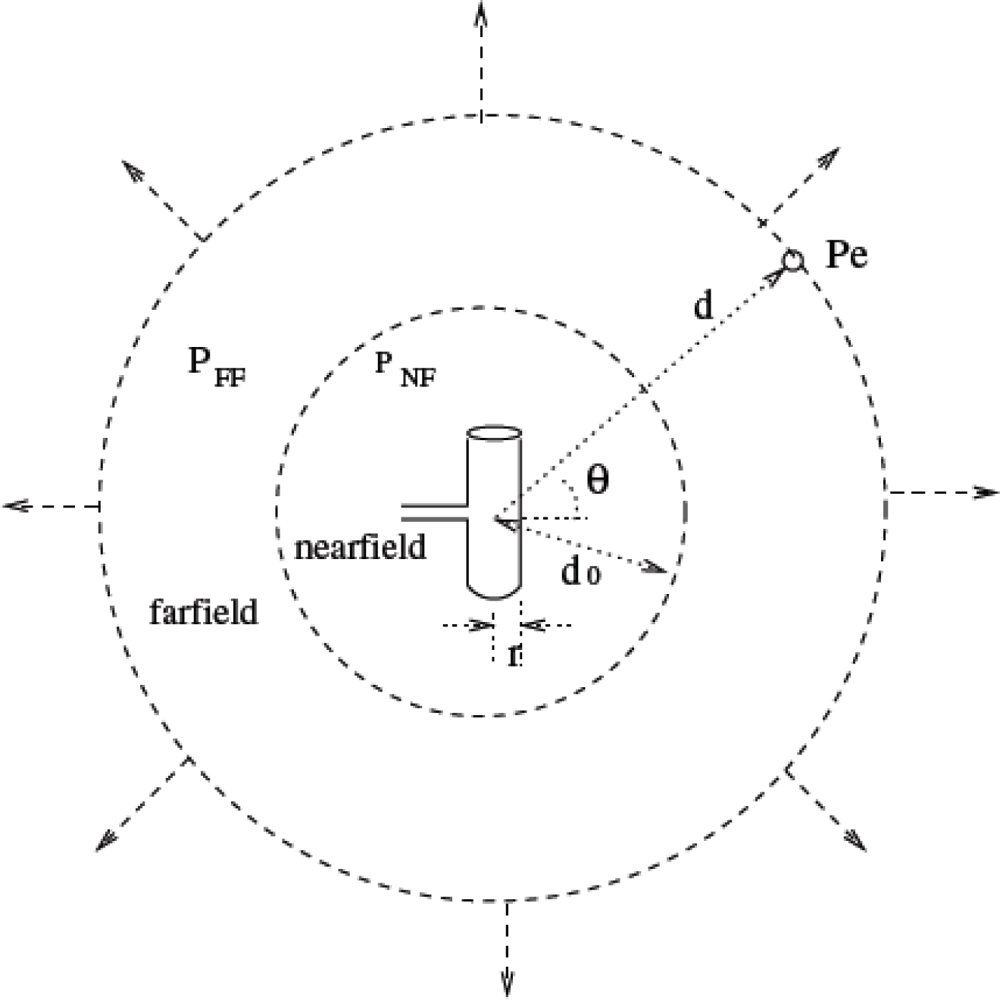
2.4. Path Loss in the Human Body (Near Field Far Field Consideration)
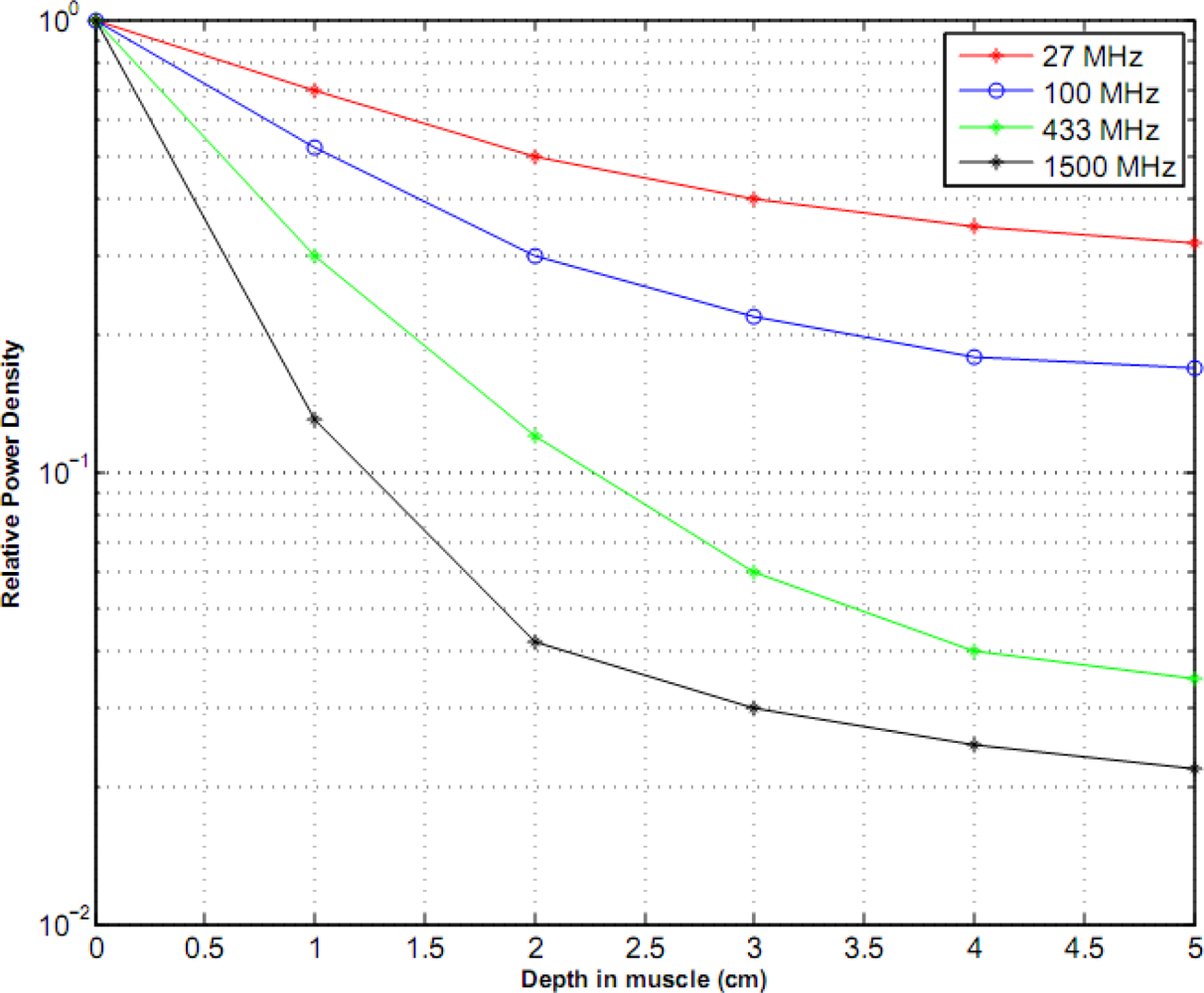
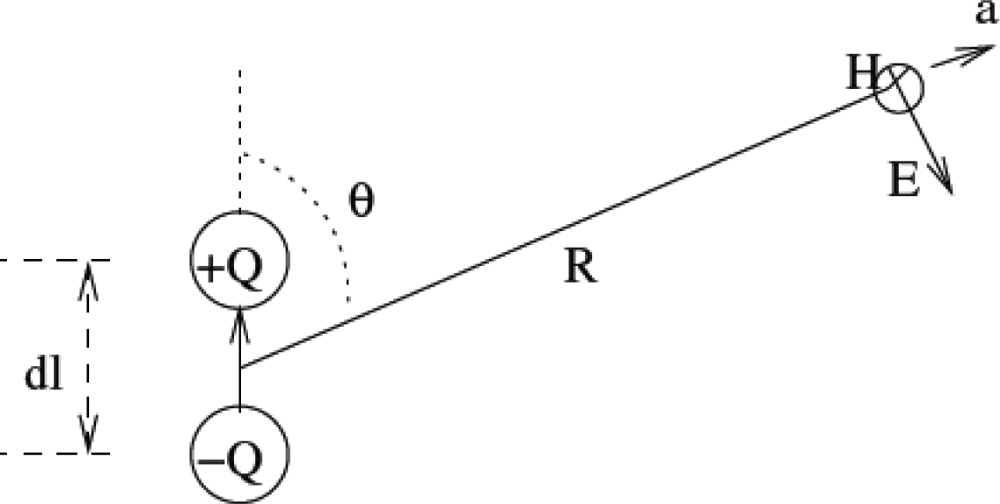
2.4.1. Power Absorbed in the Near Field
2.4.2. Power Absorbed in the Far Field
Power received
- PR in the Near Field: There is no general formula for the estimation of field strength in the near field zone [30]. Only measurements can provide a simple means of field evaluation. However, reasonable calculations can be made for antennas like dipole or monopole. When the receiving antenna is in the near field region of the transmitting antenna, the power density does not necessarily depend on the distance from the antenna, but varies rapidly with distance, and may exhibit oscillatory behavior. The magnitude of on-axis (main beam) power density varies according to the location in the near field and its maximum value is approximated by [32] Pe = 16 δP / πL2, where L is the largest dimension of the antenna, P is PT − PNF, and δ is the aperture efficiency (typically 0.5–0.75) [32]. It can be approximated as δ = Ae/A (Ae is the effective aperture and A is the physical area of the antenna). The power received by the receiving antenna in the near field can be approximated by:
- PR in the Far Field: On the other hand when the receiving antenna is in the far field region of the transmitting antenna, the power density is dependent on the distance d and is given by:
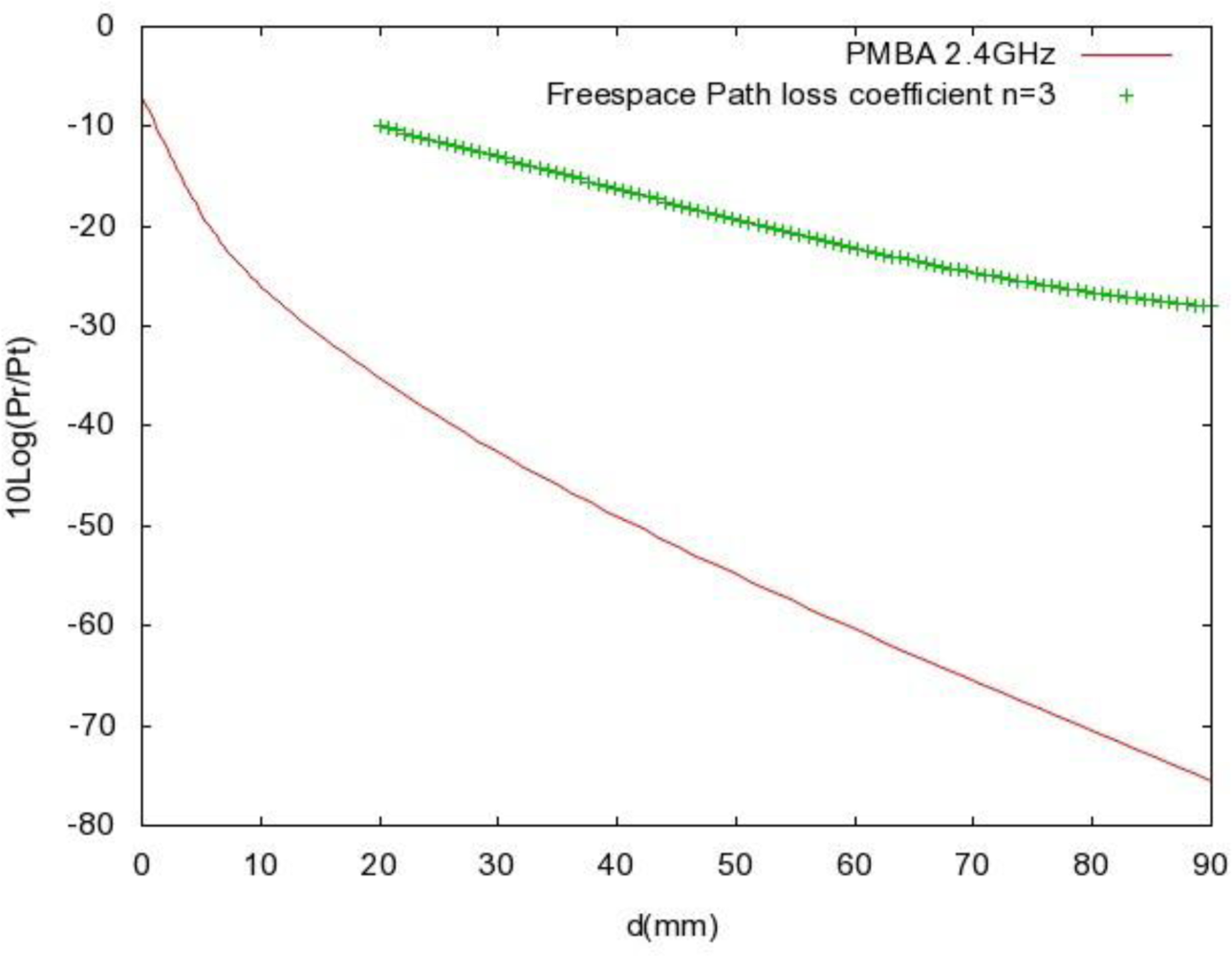
3. Numerical Results
4. Conclusions
Acknowledgments
References
- Jung, S.; Lauterbach, C; Strasser, M.; Weber, W. Enabling technologies for disappearing electronics in smart textiles. Proceedings of IEEE ISSCC03, San Francisco, CA, USA, February 9–13, 2003; 1, pp. 386–387.
- Stoica, L.; Rabbachin, A.; Repo, H.O.; Tiuraniemi, T.S.; Oppermann, I. An ultrawideband system architecture for tag based wireless sensor networks. IEEE Trans. Veh. Technol 2005, 54, 1632–1645. [Google Scholar]
- Zasowski, T.; Althaus, F.; Wittneben, A. Temporal cognitive UWB medium access in the presence of multiple strong signal interferers. Proceedings of the 14th IST Mobile and Wireless Communications Summit, Dresden, Germany, June 19–23, 2005.
- Somayazulu, V.S.; Foerster, J.R.; Roy, S. Design challenges for very high data rate UWB systems. Proceedings of the 36th Asilomar Conference on Signals, Systems and Computer, Hillsboro, OR, USA, November 2002; 1, pp. 717–721.
- Porcino, D.; Hirt, W. Ultra-wideband radio technology: potential and challenges ahead. IEEE Commun. Mag 2003, 41, 66–74. [Google Scholar]
- Win, M.Z.; Scholtz, R.A. Impulse radio: how it works. IEEE Commun. Lett 1998, 2, 36–38. [Google Scholar]
- Barras, D.; Ellinger, F.; Jäckel, H. A comparison between ultrawideband and narrowband transceivers. Proceedings of Conference on TR-Labs/IEEE Wireless, Piscataway, NJ, USA, July 2002; pp. 211–213.
- FCC. Tissue Dielectric Properties Calculator; Tech. Rep. AL/OE-TR-1996-0037;. Brooks Air Force Base: San Antonio, TX, USA, June 1996. Available online: http://www.fcc.gov/fcc-bin/dielec.sh (accessed on 7 February2010).
- Fouque, J.P.; Garnier, J.; Papanicolaou, G.; Sølna, K. Wave Propagation and Time Reversal in Randomly Layered Media; Springer: New York, NY, USA, 2000. [Google Scholar]
- Kabir, M.H.; Sultana, M.N.; Kwak, K.S. WBAN in-body channel: dielectric perspective. Int. J. Digital Content Technol. Appl. (JDCTA) 2009, 3, 173–177. [Google Scholar]
- Bashshur, R.L.; Mandil, S.H.; Gary, W.; Shannon, G.W. State-of-the-Art Telemedicine/Telehealth: An International Perspective; Mary Ann Liebert: Larchmont, NY, USA, March 2002. [Google Scholar]
- Coronel, P.; Schott, W.; Schwieger, K.; Zimmermann, E.; Zasowski, T.; Maass, H.; Oppermann, I; Ran, M.; Chevillat, P. Wireless Body Area and Sensor Networks; Wireless World Research Forum (WWRF) Briefings; WWRF: Aachen, Germany, December 2004; pp. 19–21. [Google Scholar]
- Cramer, R.J.; Scholtz, R.A.; Win, M.Z. An Evaluation of the Ultra-wideband propagation channel. IEEE Trans. Antennas Propag 2002, 50, 561–570. [Google Scholar]
- Gezici, S.; Sahinoglu, Z. Theoretical limits for estimation of vital signal parameters using impulse radio UWB. Proceedings of IEEE International Conference on Communications (ICC 2007), Ankara, Turkey, August 2007; pp. 5751–5756.
- Ghassemzadeh, S.S.; Tarokh, V. The Ultra-Wideband Indoor Path Loss Model; Technical Report P802.15 02/277r1SG3a; AT&T Labs: Florham Park, NJ, USA, 2002; (IEEE P802.15 SG3a contribution). [Google Scholar]
- Kannan, B. Characterization of UWB Channels: large-scale parameters for indoor and outdoor office environment. Proceedings of IEEE P802.15 Working Group for Wireless Personal Area Networks (WPANs), San Antonio, TX, USA, November 15–19, 2004.
- Proakis, J.G. Digital Communications, 4th ed; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Alamouti, S. A simple transmit diversity technique for wireless communications. IEEE J. Sel. Areas Commun, Oct 1998, 16, 1451–1458. [Google Scholar]
- Lee, T.H. The Design of CMOS Radio-Frequency Integrated Circuits; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Fort, A.; Desset, C.; Ryckaert, J.; De Doncker, P.; Van Biesen, L.; Wambacq, P. Characterization of the ultra wideband body area propagation channel. Proceedings of International Conference ICU, Zurich, Switzerland, September 5–8, 2005; pp. 22–27.
- Time-Domain Corporation, n.d., P210 Integratable Module Data Sheet, 320-0095 Rev B; Time-Domain Corporation: Huntsville, AL, USA, 2010.
- Molisch, A. Statistical properties of the RMS delay-spread of mobile radio channels with independent Rayleigh-fading paths. IEEE Trans. Veh. Technol 1996, 45, 201–214. [Google Scholar]
- Schuster, U.G.; Bölcskei, H.; Durisi, G. Ultra-wideband channel modeling on the basis of information-theoretic criteria. Proceedings of International Symposium on Information Theory (ISIT), Adelaide, Australia, September 4–9, 2005; 27, pp. 97–101.
- Federal Commissions Commission (FCC). Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission Systems; First Report and Order, ET Docket 98-153, FCC 02-48; FCC: Washington, DC, USA, 2002. [Google Scholar]
- Gupta, S.K.S.; Lalwani, S.; Prakash, Y.; Elsharawy, E.; Schwiebert, L. Towards a propagation model for wireless biomedical applications. Proceedings of IEEE International Conference on Communications (ICC’03), Anchorage, AK, USA, May 11–15, 2003; 3, pp. 1993–1997.
- Wegmueller, M.S.; Kuhn, A.; Froehlich, J.; Oberle, M.; Felber, N.; Kuster, N.; Fichter, W. An Attempt to Model the Human Body as a Communication Channel. IEEE Trans. Bio-med. Eng 2007, 54, 1851–1857. [Google Scholar]
- Plonsey, R.; Heppner, D.B. Considerations of quasi-stationarity in electrophysiological systems. Bull Math. Biophys 1967, 29, 657–664. [Google Scholar]
- Cheng, D.K. Field and Wave Electromagnetics, 2nd ed; Addison-Wesley Publications: Reading, MA, USA, 1989. [Google Scholar]
- A Practical Guide to the Determination of Human Exposure to Radiofrequency Fields: Recommendations of the National Council on Radiation Protection A (NCRP Report No. 119); NCRP Publications: Bethesda, ML, USA; December 1993.
- Office of Engineering Technology. Understanding The FCC Regulations for Low-Power, Non-Licensed Transmitters; OET Bulletin NO. 63; OET: Washington, DC, USA; October 1993.
- Kuster, N.; Balzano, Q. Energy absorption mechanism by biological bodies in the near field of dipole antennas above 300 MHz. IEEE Trans. Veh. Technol 1992, 41, 17–23. [Google Scholar]
- RF/Microwave Hazard Recognition and Measurement. Available online: http://www.oshaslc.gov/SLTC/radiofrequencyradiation/rfpresentation/microwavemeasure/non2.html (accessed on 10 February 2010).
- Dissanayake, T.; Esselle, K.P.; Yuce, M.R. UWB Antenna Impedance Matching in Biomedical Implants. Proceedings of the 3rd European Conference on Antennas and Propagation, Berlin, Germany, March 23–27, 2009; 7, pp. 230–233.
- Dissanayake, T.; Esselle, K.P.; Yuce, M.R. Dielectric loaded impedance matching for wideband implanted anteenas. IEEE Trans. Microwave Theory Techn 2009, 57, 2480–2487. [Google Scholar]
- Forbes, R.M.; Cooper, A.R.; Mitchell, H.H. The composition of the adult human body as determined by chemical analysis. J. Biol. Chem 1953, 203, 359–366. [Google Scholar]
Appendix A
Appendix B
Right- and Left-Going Waves
Appendix C
Homogenization:




© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kabir, M.H.; Ashrafuzzaman, K.; Chowdhury, M.S.; Kwak, K.S. Studies of Scattering, Reflectivity, and Transmitivity in WBAN Channel: Feasibility of Using UWB. Sensors 2010, 10, 5503-5529. https://doi.org/10.3390/s100605503
Kabir MH, Ashrafuzzaman K, Chowdhury MS, Kwak KS. Studies of Scattering, Reflectivity, and Transmitivity in WBAN Channel: Feasibility of Using UWB. Sensors. 2010; 10(6):5503-5529. https://doi.org/10.3390/s100605503
Chicago/Turabian StyleKabir, Md. Humaun, Kazi Ashrafuzzaman, M. Sanaullah Chowdhury, and Kyung Sup Kwak. 2010. "Studies of Scattering, Reflectivity, and Transmitivity in WBAN Channel: Feasibility of Using UWB" Sensors 10, no. 6: 5503-5529. https://doi.org/10.3390/s100605503



