Design and Analysis of Impedance Pumps Utilizing Electromagnetic Actuation
Abstract
:1. Introduction
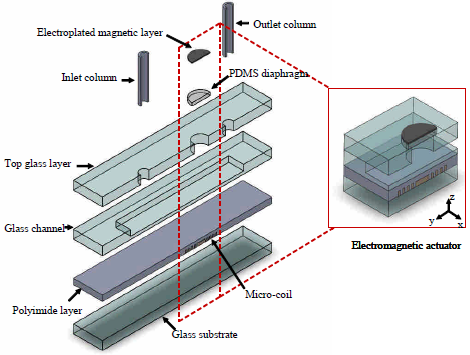
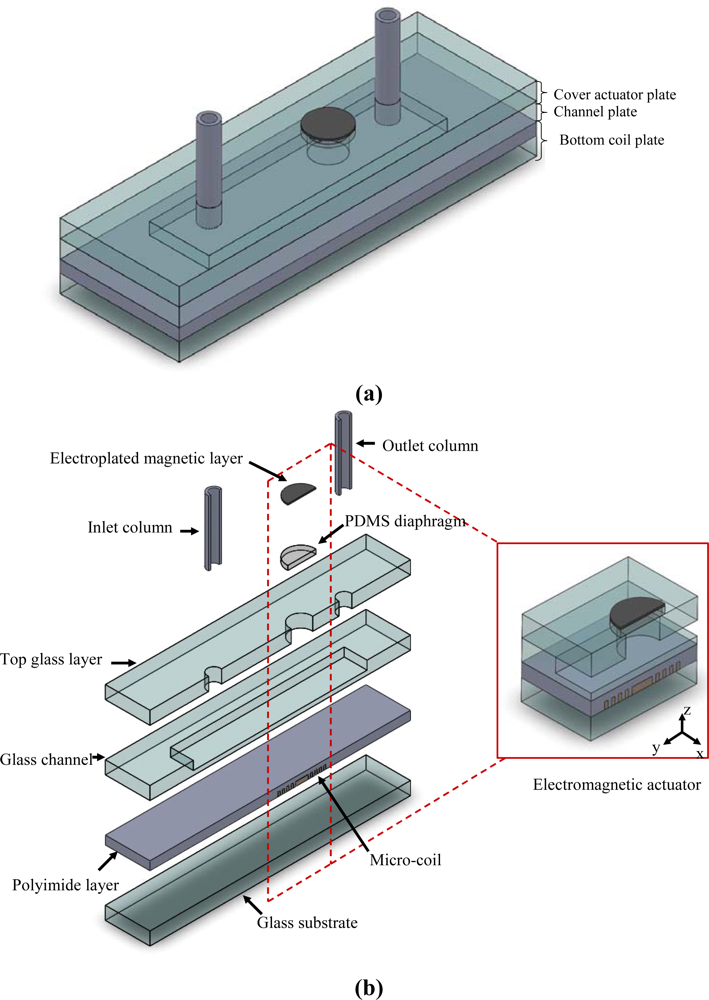
2. Designs
3. Analysis
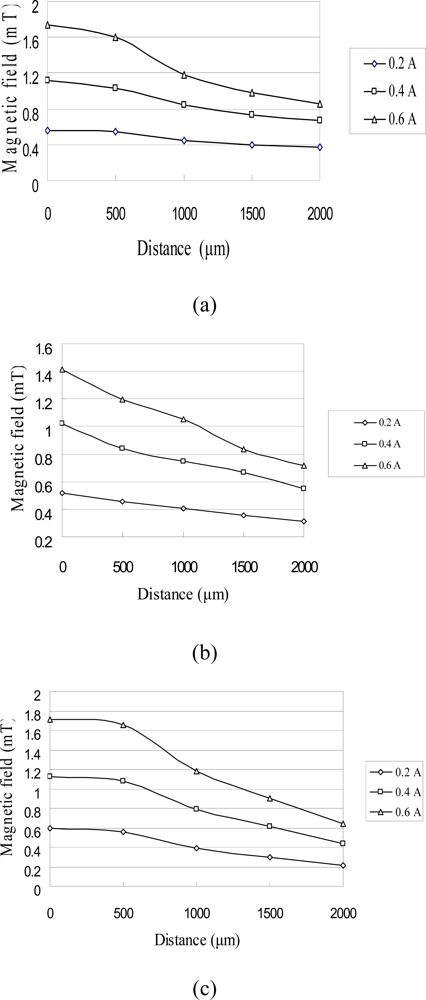
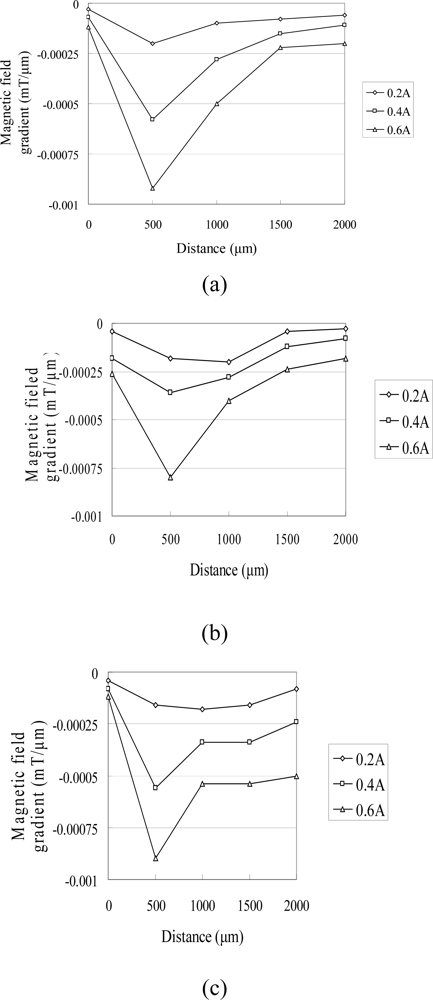
3.1. Magnetic Analysis
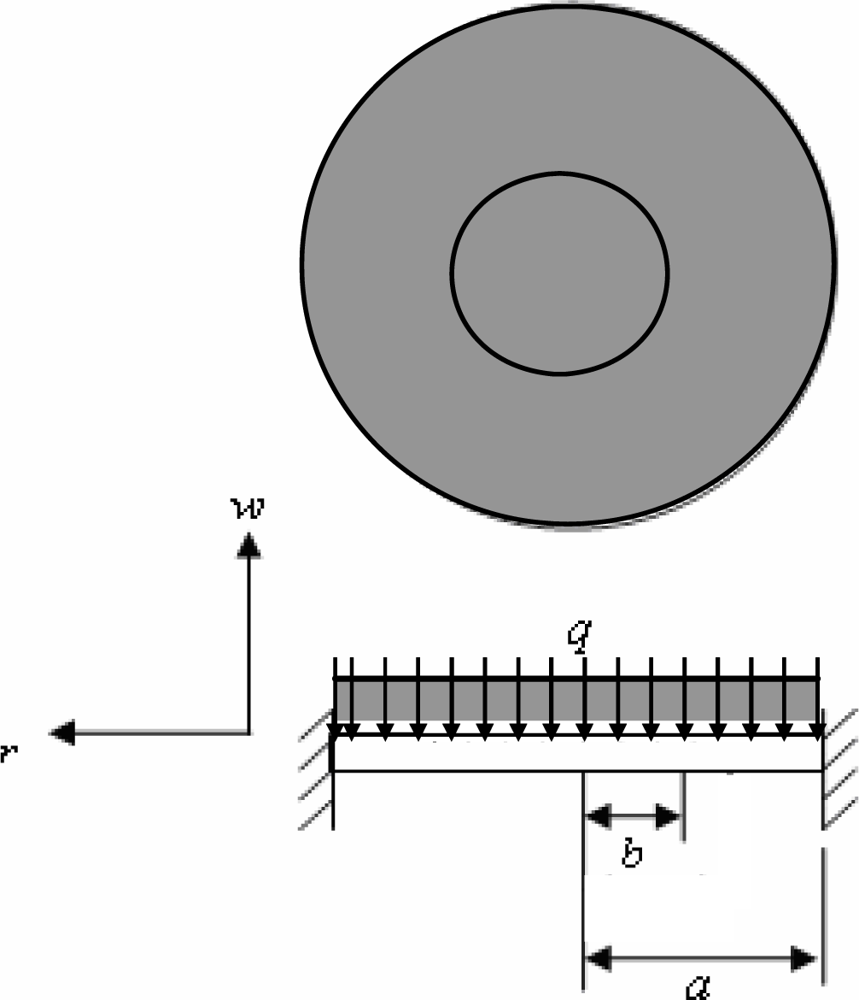
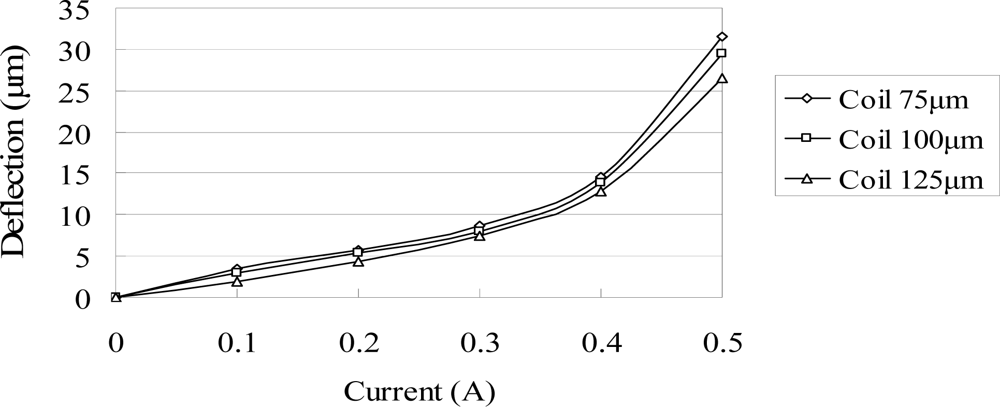
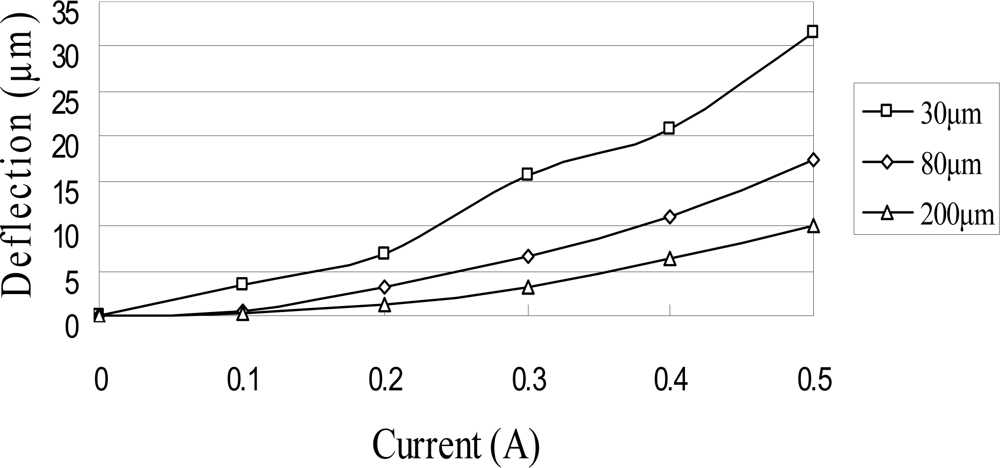
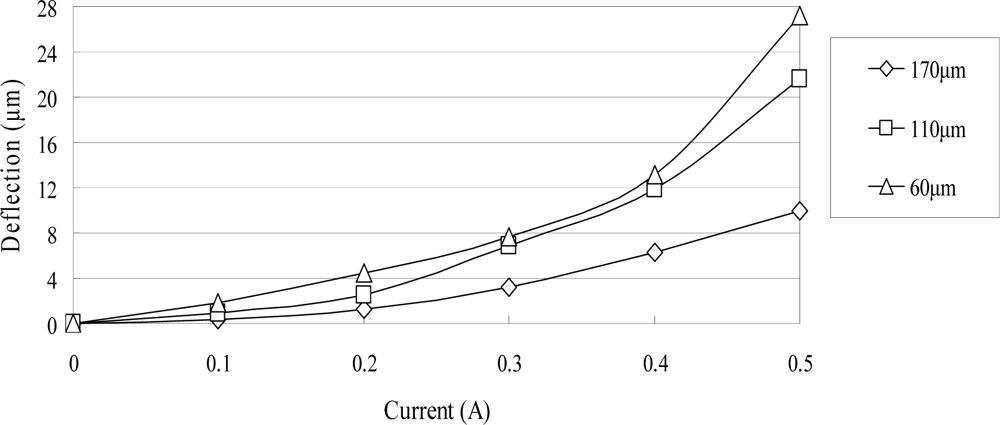
3.2. Actuator Displacement Analysis
3.3. Pumping Analysis
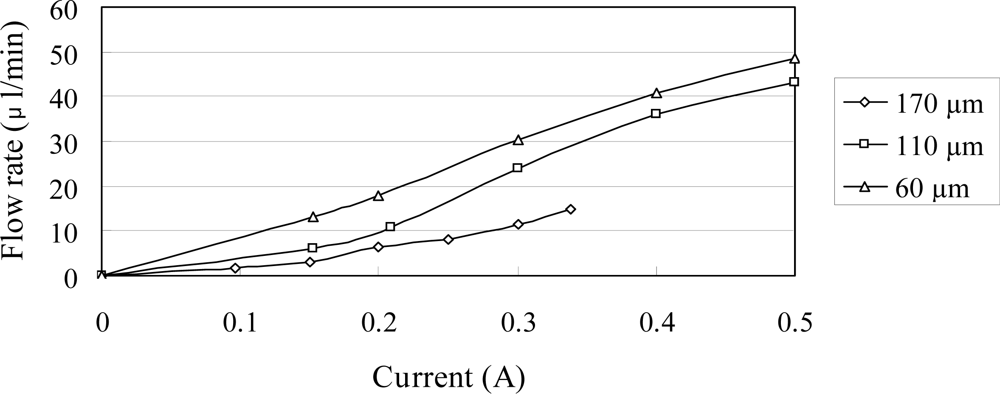
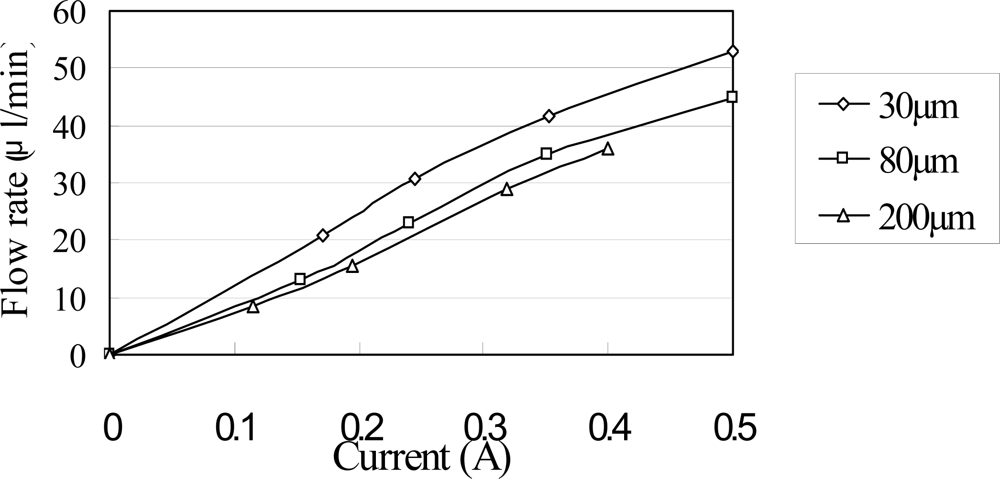
4. Results and Discussion
5. Conclusions
Acknowledgments
References and Notes
- Zhu, H.; Miao, J.; Chen, B.; Wang, Z.; Zhu, W. Membrane microcantilever arrays fabrication with PZT thin films for nanorange movement. Microsyst. Technol 2005, 11, 1121–1126. [Google Scholar]
- Xu, H.; Ono, T.; Zhang, D.Y.; Esashi, M. Fabrication and characterizations of a monolithic PZT microstage. Microsyst. Technol 2006, 12, 883–890. [Google Scholar]
- Ma, H.K.; How, B.R.; Wu, H.Y.; Lin, M.Y.; Gao, J.J.; Kou, M.C. Development and application of a diaphragm micro-pump with piezoelectric device. Microsyst. Technol 2008, 14, 1001–1007. [Google Scholar]
- Liu, C.; Tsao, T.; Tai, Y.C.; Ho, C.M. Surface micromachined magnetic actuators. Proceedings of IEEE MEMS, Oiso, Japan, January 25–28, 1994.
- Lagorce, L.K.; Brand, O.; Allen, M.G. Magnetic microactuators based on polymer magnets. IEEE J. MEMS 1999, 8, 2–9. [Google Scholar]
- Hickerson, A.I.; Rinderkecht, D.; Gharib, M. Experimental study of the behavior of a valveless impedance pump. Exp. Fluid 2005, 38, 534–540. [Google Scholar]
- Hickerson, A.I.; Gharib, M. On the resonance of a pliant tube as a mechanism for valveless pumping. J. Fluid Mech 2006, 555, 141–148. [Google Scholar]
- Yeo, C.Y.; Shim, W.K.; Wouterson, E.; Li, T.; Ma, J. Piezoelectric materials for impedance driven micro-channel flow. Funct. Mater. Lett 2008, 1, 225–228. [Google Scholar]
- Chang, H.T.; Lee, C.Y.; Wen, C.Y.; Hong, B.S. Theoretical analysis and optimization of electromagnetic actuation in a valveless microimpedance pump. Microelectr. J 2007, 38, 791–799. [Google Scholar]
- Lee, C.Y.; Chang, H.T.; Wen, C.Y. A MEMS-based valveless impedance pump utilizing electromagnetic actuation. J. Micromech. Microeng 2008. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chen, Z.H.; Chang, H.T.; Wen, C.Y.; Cheng, C.H. Design and fabrication of novel micro electromagnetic actuator. Microsyst. Technol 2009, 15, 1171–1177. [Google Scholar]
- Chang, H.T.; Wen, C.Y.; Lee, C.Y. Design, analysis and optimization of an electromagnetic actuator for a micro impedance pump. J. Micromech. Microeng 2009. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chen, Z.H. Valveless impedance micropump with integrated magnetic diaphragm. Biomed. Microdevices 2010, 12, 197–205. [Google Scholar]
- Borzi, A.; Propst, G. Numerical investigation of the Liebau phenomenon. Z. Angew. Math. Phys 2003, 54, 1050–1072. [Google Scholar]
- Feustel, A.; Krusemark, O.; Muller, J. Numerical simulation and optimization of planar electromagnetic actuators. Sensor. Actuat. A 1998, 70, 276–282. [Google Scholar]
- Choi, K.M.; Rogers, J.A. A photocurable poly (dimethysiloxane) chemistry designed for soft lithographic molding and printing in the nanometer regime. J. Am. Chem 2003, 125, 4060–4061. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plate and Shells, 2nd ed.; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Wu, J.K.; Lu, L.J. Liquid-solid coupled system of micropumps. Acta Mech. Solid. Sinica 2006, 19, 40–49. [Google Scholar]
- Liakopoulos, T.M.; Zhang, W.J.; Ahn, C.H. Electroplated thick CoNiMnP permanent magnet arrays for micromachined magnetic device applications. Proceedings of IEEE MEMS, Piscataway, NJ, USA, February 11–15, 1996.

© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, Y.-H.; Tsai, Y.-W.; Tsai, C.-H.; Lee, C.-Y.; Fu, L.-M. Design and Analysis of Impedance Pumps Utilizing Electromagnetic Actuation. Sensors 2010, 10, 4040-4052. https://doi.org/10.3390/s100404040
Wang Y-H, Tsai Y-W, Tsai C-H, Lee C-Y, Fu L-M. Design and Analysis of Impedance Pumps Utilizing Electromagnetic Actuation. Sensors. 2010; 10(4):4040-4052. https://doi.org/10.3390/s100404040
Chicago/Turabian StyleWang, Yu-Hisang, Yao-Wen Tsai, Chien-Hsiung Tsai, Chia-Yen Lee, and Lung-Ming Fu. 2010. "Design and Analysis of Impedance Pumps Utilizing Electromagnetic Actuation" Sensors 10, no. 4: 4040-4052. https://doi.org/10.3390/s100404040