4.1. Motivation
In ExCo, at each round r, each sensor j constructs the MAC
of its sensed value
and sends
to a random subset
of sensors. Within the round r, each sensor j has certain possibility of receiving MACs from the other sensors. If this happens, it temporarily keeps them in the local memory. At the end of round r, each sensor j constructs and stores the MAC,
, where ‖ denotes the bit-string concatenation, if it receives MACs from the sensors q1, . . ., qϕ. Afterwards, except for
, all the MACs generated and received in the round r are deleted. From the sink point of view, to authenticate the
, it involves the verification of MAC,
, and the MACs in
, where
is the set of sensors that send the authentication tags to sj. Note that the sensors in
are called the co-authenticators of sj at round r. For example, if
contains q1, . . ., qϕ, then, in addition to the verification of
, the MACs,
are required to be verified as well.
First, although it is claimed in [4] that ExCo is stronger than CoMAC in terms of sensor compromises, their resilience against sensor compromises is actually the same in practice. Particularly, according to [
4], it is claimed that the adversary needs to compromise all the sensors in
, where
is the set of sensors that receive the authentication tags from
sj and
is the set of sensors that send the authentication tags to the sensors in
, before the round
r, to successfully subvert the security ExCo provides. Nevertheless, if
r̄ is the target round, the adversary is aware of
r̄ at the round
r̄ + 1, and the adversary only compromises the sensors in
, then the adversary can still provide to the sink a counterfeit sensed data without being detected. It can proceed as follows. At first, we assume that, for each round
r, each compromised sensor keeps the data received in rounds
r − 1 and
r in its local memory. As soon as the compromised sensor
sj and compromised sensors in
are aware of
r̄,
sj instantly replaces the original sensor reading
with the value
the adversary wants to report to the sink. In addition, the compromised sensors in
pretend that they also receive
. Hence, before the end of round
r̄ + 1,
sj can collaborate with the sensors in
to generate their own MACs that are consistent with each other and are consistent with
. With these generated MACs, the
to be reported to the sink will not be recognized to be counterfeit. Moreover, this is not an attack in an ideal case. Instead, this is a practical attack, because, in practice, the length of each round will not be too short and the adversary can be aware of the target round right after something desired happens. Hence, ExCo is not as strong as [
4] claims and has the same security strength as CoMAC.
Second, Exco is vulnerable to PDoS attacks. In particular, after the adversary compromises a few sensors, these compromised sensors can be used to intentionally inject a large amount of useless traffic claimed to be the MACs in ExCo to waste the precious energy of sensors so that the network lifetime will be significantly reduced. Although a simple defense that limits the number of message forwarding at each sensor seems to be helpful in alleviating PDoS attacks, it is indeed useless because the network traffic on each sensor cannot be estimated in advance. As a consequence, if some limits are applied on the number of message forwarding at each sensor, some packets such as transmitted MACs in ExCo will be dropped somewhere on its way to the destination Under the circumstance, the verification will fail and some sensor readings will be regarded as falsified ones because some of the co-authenticators cannot provide the MACs.
Third, ExCo is also vulnerable to FEDoS attacks. In fact, this is a common attack if only a simply designed collaboration scheme is used. Specifically, after a sensor is compromised and is inquired by the sink to ask for the MAC used for authenticating the sensed data of the other sensors, it can always reply a random string to the sink. This implies that some data sensed by genuine sensors will be thought of as fake. This is because the MACs involved in a large number of sensors are necessary for authentication, leading to be easily vulnerable to FEDoS attacks. Simply taking the majority of the verification results of MACs from different co-authenticators seems to be helpful in alleviating FEDoS attacks, but it also reduces the resilience against sensor compromises. As a matter of fact, without the proper design, there always exists a dilemma of enhancing the resilience against sensor compromises or enhancing the resilience against FEDoS attacks. In addition, it has been demonstrated [
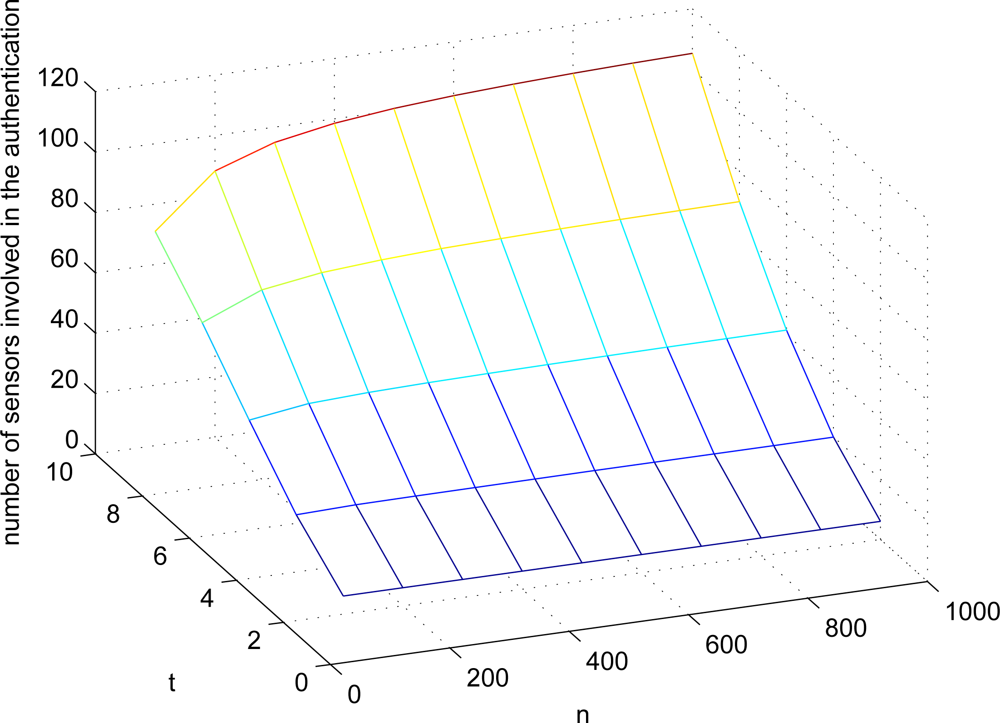
4] that the expected number
ν(
n, t) of sensors involved in the authentication of the sensed data of one sensor in ExCo is
where
is the number of co-authenticators.
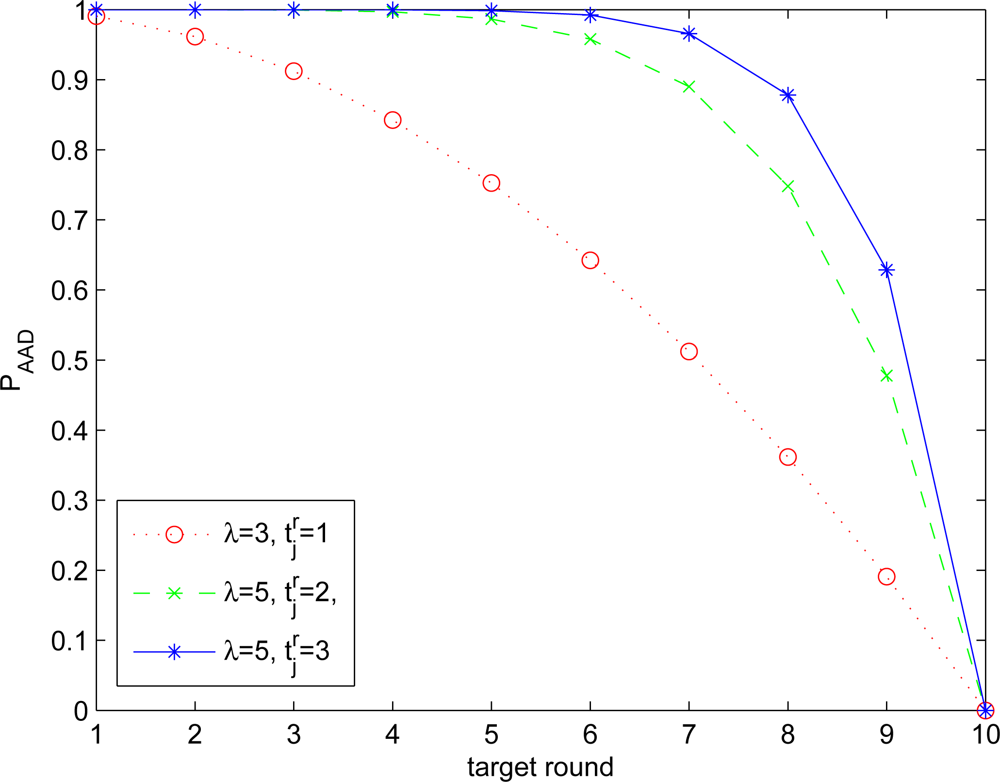
Figure 3 shows different settings of
ν(
n, t). Here, we further define a metric
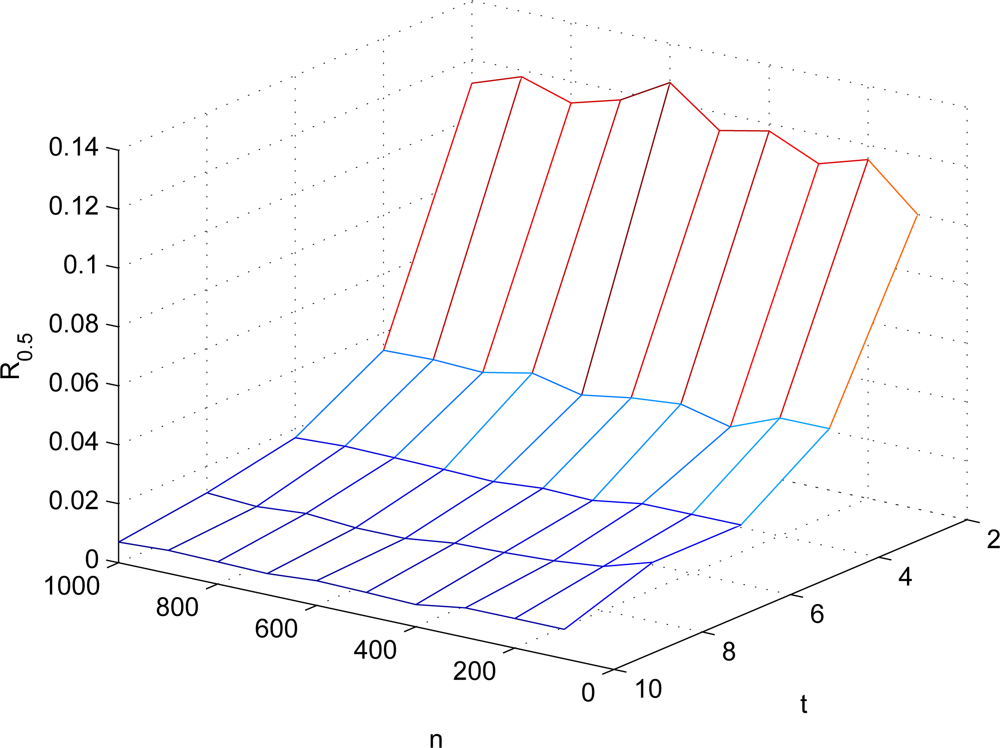
Rr, called
FEDoS ratio of
r, which denotes the ratio of the number of sensors required to be compromised to the total number of sensors in the network. Note that the parameter
r means that
r × 100% of the verifications of sensor readings are affected. FEDoS ratio is used to evaluate and quantify the resilience against FEDoS attacks. According to the
ν(
n, t)’s derived as above,
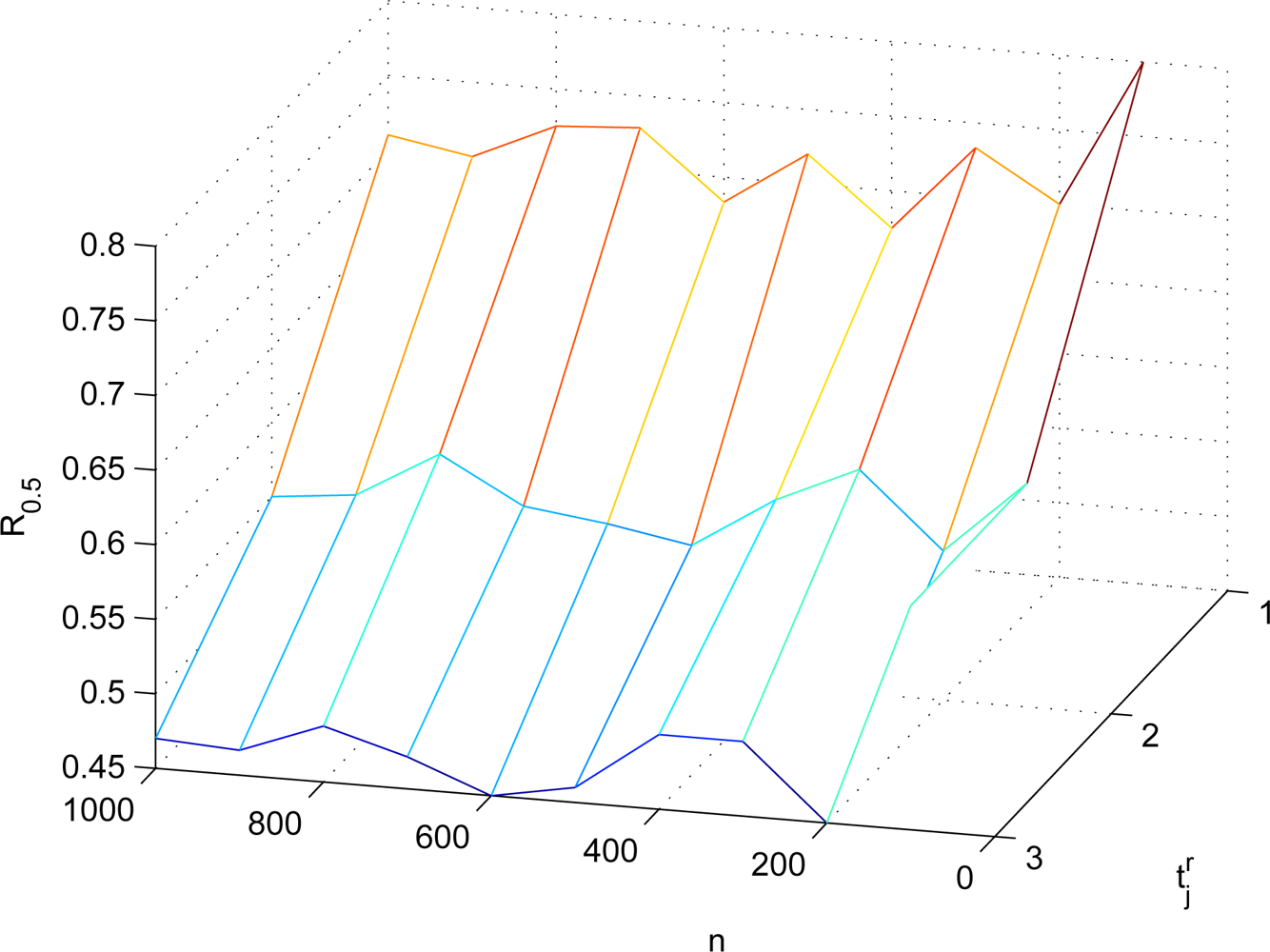
R0.5’s in different settings are shown in
Figure 4. It can be observed that when the number of co-authenticators used in ExCo is 2 and approximately 10% of sensors are compromised, over 50% of sensor readings will be regarded as bogus by the sink because of the bogus authentication tags provided by the compromised sensors. When
t = 4, less than 2% of sensor compromises would result in above 50% of contaminated sensor readings, which will be a disaster in terms of the network security.
4.3. Proposed Method: AAD
Our proposed AAD scheme consists of five phases: pre-deployment phase, post-deployment phase, sensing phase, receiving/forwarding phase, and verification phase. The pre-deployment phase is executed by the network owner to store necessary materials into the sensors. As its name shows, the post-deployment phase is performed by the sink right after the sensor deployment in order to store the materials required for the authentic data acquisition in the sensors. Sensing phase is executed by each sensor so as to sense data, and distribute the sensed data and the necessary MACs. Once receiving the packet, each sensor executes forwarding phase to forward the received message to the destination sensor. Verification phase is performed by the sink to collect the sensed data and verify their authenticity. The notations used in the following discussion are listed in
Table 1. The details of these five phases are described as follows.
Pre-Deployment Phase. For each sensor sj, the sink randomly selects a unique key Kj and a prime number pj. Note that the prime numbers to be stored in different sensors should be chosen to be distinct. Afterwards, Kj and pj are stored in the sensor sj. The sensors are then deployed over the sensing region.
Post-Deployment Phase. Let λ be a user-selected parameter, which leverages the security and the energy consumption. The post-deployment phase is used to equip each sensor with a proper Bloom filter for the query of its λ-hop proximity relationship. Here, we say that the sensor sj has λ-hop proximity relationship with the sensor si (or, sj is the λ-hop neighbor of si) if the hop distance between sj and si is within λ. The post-deployment phase is automatically accomplished when sensors are deterministically deployed by the sink. This is because when deploying the sensor sj, the sink can also store the Bloom filter j containing the λ-hop proximity information of sj in sj, given that the position of each sensor is pre-determined by the network owner.
On the other hand, the post-deployment phase will be accomplished within a period of time right after the sensor deployment if sensors are randomly deployed. More specifically, after the sensor deployment, each sensor acquires its geographic position using well-known positioning techniques [
16–
19], and then reports the acquired position to the sink. Such a reporting should be accompanied by the message authentication code (MAC) with the unique key
Kj so that the authenticity of the reported position can be guaranteed. Note that, the falsified position information could be injected by the adversary. Nevertheless, the falsified position information will be found by the sink because the sink will move to the position, trying to collect the sensed data. Thus, if falsified positions are injected by the adversary, they will be easily detected. After receiving each sensor’s position information, the sink first checks its authenticity by examining whether it has the correct MAC. In particular, when the received message is 〈
ℓj, ħ〉, if
ħ is equal to
hKj(
ℓj), then
ℓj is regarded as the position of
sj. With the geographic position of each sensor, the sink can construct the
network graph, wherein the vertices denote the sensors and the edge between two vertices exists if the corresponding sensors can communicate with each other directly, according to the communication range predefined on each sensor. With the constructed network graph, the sink can be aware of the λ-hop proximity relationship of each sensor. Now, before the sensors start to sense data, the mobile sink starts its first itinerary over the network. For the contact of each sensor
sj, the sink stores a Bloom filter,
j, containing the λ-hop proximity information of
sj, in
sj.
j can be constructed by the sink according to the topology of the network graph. Specifically, for each
si that has λ-hop proximity relationship with
sj, the sink embeds
sj‖
si into
j. Note that although the number of λ-hop neighbors of
sj could be different for each
sj, the size of Bloom filter used is chosen to be the same.
Sensing Phase. The description of sensing phase is shown in
Figure 5. The sensing phase is executed by each sensor at each round. The sensor
sj constructs the corresponding MAC,
, after it has the sensed data
at round
r. If the sensed data and corresponding MAC are simply stored in its local memory, once the sensor is compromised by the adversary, all the security materials will be exposed to the adversary, and
and
can be arbitrarily generated so that the security breach will occur. Thus, in the sensing phase, the sensed data and its corresponding MACs of a sensor will be distributed over some sensors randomly chosen from its λ-hop neighbors. Specifically, a subset
of
t sensors is first randomly sampled from {
s1, . . .,
sn} (line 3 in
Figure 5).
SELECT −
DISTINCT (
t,
n,
j,
) is a function randomly generating
t sensor IDs from {
s1, . . .,
sn} \ {
sj}. It can be implemented by using the hash function whose output is of length ⌈log
n⌉ bits. Then, a subset
of
is constructed by choosing the sensors in
whose hop distance to
sj is within the pre-determined threshold λ. Here, each sensor
sj uses the Bloom filter
j constructed in post-deployment phase to check the hop distances to the randomly selected sensors in
. To construct
, what each sensor
sj needs to do is to check whether the
sj itself has λ-hop proximity relationship with the generated sensors in
. For example, for
, the sensor issues
sj‖
si to query
j. We can know that
if the query result is positive and
otherwise (line 4 in
Figure 5). Afterwards, the MAC,
, is transmitted to the sensors in
. Note that
may vary as
j and
r vary. In general,
is not a constant. Nonetheless, for ease of the explanation,
is described as if it is a constant. In the following, the term “authentication tag of
sj” is used to denote
and the term “co-authenticator of
sj at round
r” is used to denote the sensors in
. Then,
sj, according to
, derives
and
to guarantee the data privacy and authenticity, respectively. Lastly,
sj sends
to the sensors in
whose second and third fields are always fixed to be 1 (lines 5 and 6 in
Figure 5).
Receiving/Forwarding Phase. The algorithm of this phase is described in
Figure 6. This phase is executed by each sensor when a message is received. According to the role it acts, each sensor executes different tasks (lines 1∼7 in
Figure 6); the receiving task will be executed if the received message is destined to itself, and the forwarding task (lines 8∼13 in
Figure 6) is performed otherwise. Assume that
sj is the forwarding sensor and receives Ω = 〈
si, P, C, E, Z, si′〉 (line 9 in
Figure 6). At first,
sj checks if it has λ-hop proximity relationship to the destination sensor
si′ (lines 9∼13 in
Figure 6).
sj proceeds the procedures if
sj has λ-hop proximity relationship to the destination sensor
si′ and drops the received Ω otherwise.
sj then adds the existence evidence of itself on the forwarding path on Ω so that the sink can check whether the received authentication tag passes through exactly those sensors it should pass. To achieve this goal,
sj applies the keyed hash function with its secret key
on
Z to have
. Moreover, to enable the sink to accomplish the verification, the information about the forwarding path should be included in Ω; it is the usage of
P and
C in Ω.
C means that
sj is on the (
C + 1)-th sensor of the forwarding path and
P can be used to extract all the sensor IDs on the forwarding path (The details will be stated in the description of the verification phase later). More specifically, after receiving Ω,
sj increases
C by one and multiplies
P with
, where
pj is the prime number stored in
sj in pre-deployment phase. Afterwards, the packet
will be forwarded to the next sensor on the forwarding path. Note that the selection of the next sensor depends on the routing protocol the underlying network uses and is not the focus of this paper. Nevertheless, due to the fact that each sensor knows its position, geographic routing [
20] is a reasonable choice.
On the other hand, assume that
sj is the destination sensor and receives Ω = 〈
si, P, C, E, Z, sj〉 (line 4 in
Figure 6). Under this situation,
sj simply extracts 〈
si, P, E, Z〉 from Ω and then stores it into an ordered set
(line 5 in
Figure 6). At the end of the round
r, the key
will be evolved to the key
of the next round
r + 1 using the publicly-known hash function
h (line 7 in
Figure 6).
Verification Phase. The algorithm describing the verification phase is shown in
Figure 7. Assume that the sink would like to obtain the data
sensed by sensor
sj at the round
r̄. What the sink should do is to perform the verification phase. Since the initial key of
sj is given by the sink, the key
will be known by the sink. Thus, the co-authenticators of
sj at
r̄ will also be known by the sink. This prevents the traces from being deleted by the adversary. The strategy of the sink is to move to the positions near those co-authenticators to collect
, acquiring the proper authentication tags. More specifically, assume that the co-authenticators of
sj are
. For each
, the sink acquires
and extracts 〈
sj, P, E, Z〉 (lines 3∼4 in
Figure 7). Here, 〈
sj, P, E, Z〉’s extracted from different co-authenticators will not be the same in essence. We, however, omit the necessary subscript and superscript of
P, E, and
Z without the ambiguity for convenience. From the acquired 〈
sj,
P,
E,
Z〉, with the proper key, the sink can decrypt to obtain the
(line 6 in
Figure 7), which is claimed by
sqi to be the data sensed by
sj at round
r̄. Based on the decrypted
, the sink would try to verify if the authentication tag can be regenerated to match the authentication tag extracted from
. Here, to reproduce the authentication tag, the sink needs to obtain the sensor IDs on the forwarding path of Ω in the correct order. Then, since the sink knows the keys of all the sensors on the forwarding path, if we can know that
sj →
sm1 →
sm2 → ⋯ →
smϕ is the correct order of sensors on the forwarding path connecting
sj and
sqi, the sink can construct
, where
sm1, . . .,
smϕ are the sensors on the route from
sj to
sqi, and see if it is equal to the authentication tag extracted from 〈
sj, P, E, Z〉. To know
sm1, . . .,
smϕ (line 5 in
Figure 7), the sink simply performs prime number factorization of
P, obtaining
, where
ϕ is the length of the path connecting the sensor
sj and its co-authenticator being examined by the sink. Here, we should note that
ϕ varies when different co-authenticators are considered. Nonetheless, for ease of explanation, we also omit the necessary subscript and superscript. Then, the sink knows that
smi =
sxi for all 1 ≤
i ≤
ϕ. Note that after the factorization of
P, if
P cannot be represented as the form of
, then the authentication material provided by the co-authenticator being examined will be ignored. The authentication material 〈
sj, P, E, Z〉 extracted from
sqi is dropped by the sink if the regenerated authentication tag does not match the authentication tag in 〈
sj, P, E, Z〉 (line 7 in
Figure 7). The decrypted data
is stored if
is equal to the authentication tag extracted from
. After the sink accomplishes the above procedures, if no authentication tag can be successfully verified, then all the data claimed to be the data sensed by
sj at round
r̄ are dropped. Assume that the sink accomplishes the above procedures and at least one authentication tag of co-authenticators can be successfully verified. If and only if
extracted from the authentication materials sent from co-authenticators are all the same,
are regarded as genuine (lines 9
∼12 in
Figure 7).
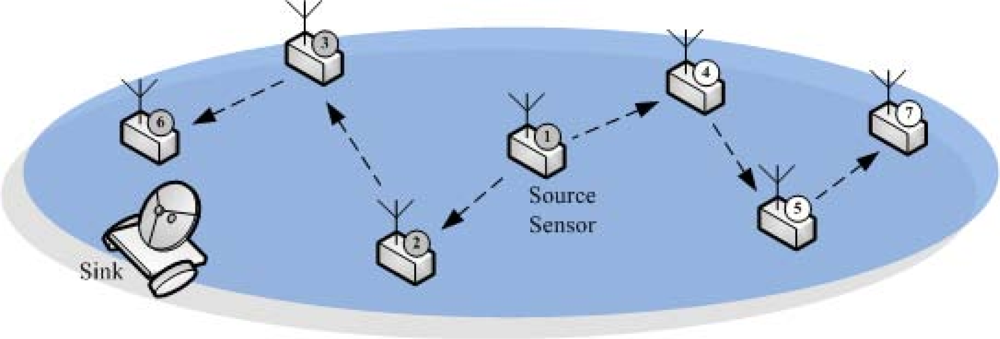
Example. Assume that λ = 3 and a specific round
r is considered. For the sensor
s1, we have the assumption that
,
,
, and
. In addition, we assume that after the execution of
SELECT −
DISTINCT and the checking procedure on
j,
. Suppose that the shortest path connecting
s1 and
s6 is
s1 →
s2 →
s3 →
s6, and the shortest path connecting
s1 and
s7 is
s1 →
s4 →
s5 →
s7. The network topology in this example is shown in
Figure 8. Then, since
s1 has to transmit
E7(5) and
to
s6 and
s7,
s1 will send
and
to
s2 and
s3, respectively. Since the sensors on these two paths work similarly, we only discuss the path
s1 →
s2 →
s3 →
s6. When
s2 receives 〈
s1, 1, 1, 10, 8,
s6〉, it first check its λ-hop proximity relationship to
s1. Here, since we assume that
λ = 3, the check can be passed. Thus, assuming that
p2 = 3,
s2 forwards 〈
s1, 9, 2, 10,
,
s6〉 to
s3. Similarly, if we assume that
p3 = 7, after receiving 〈
s1, 9, 2, 10,
,
s6〉,
s3 sends 〈
s1, 3087, 3, 10,
,
s6〉 to
s6. When
s6 receives 〈
s1, 3087, 3, 10,
,
s6〉, it stores 〈
s1, 3087, 10,
,
s6〉 in its local memory.
Now consider that the sink wants to obtain
. In our method, the sink has to perform two verifications on s6 and s7. Basically, because the verification performed on s6 is the same as the one performed on s7, we only describe the one performed on s6. From s6, the sink can obtain 〈s1, 3087, 10,
〉. After performing the prime number factorization of the value 3087, the sink can know that 3087 = 32 × 73, which means that the second hop sensor and the third hop sensor on the path connecting s1 and s6 are s2 and s3, respectively. The sink also extracts
from
. Then, the sink checks if
is equal to the value obtained by sequentially applying three keyed hash functions
,
, and
on
.
will be temporarily stored if the above check is passed and dropped otherwise. Finally, when all the co-authenticators are visited, the sink checks the consistency of
’s obtained from different co-authenticators. Note that for the notational simplicity, we do not put additional subscript on
to distinguish different
’s obtained from different co-authenticators.
is deemed to be genuine if they are consistent and bogus otherwise.