Relaxation Time and the Problem of the Pleistocene
Abstract
:1. Introduction
2. Numerical Simulations
| Model | Jm | θ | Probability of Death | Area Change | Relaxation Time (tr, in years) |
|---|---|---|---|---|---|
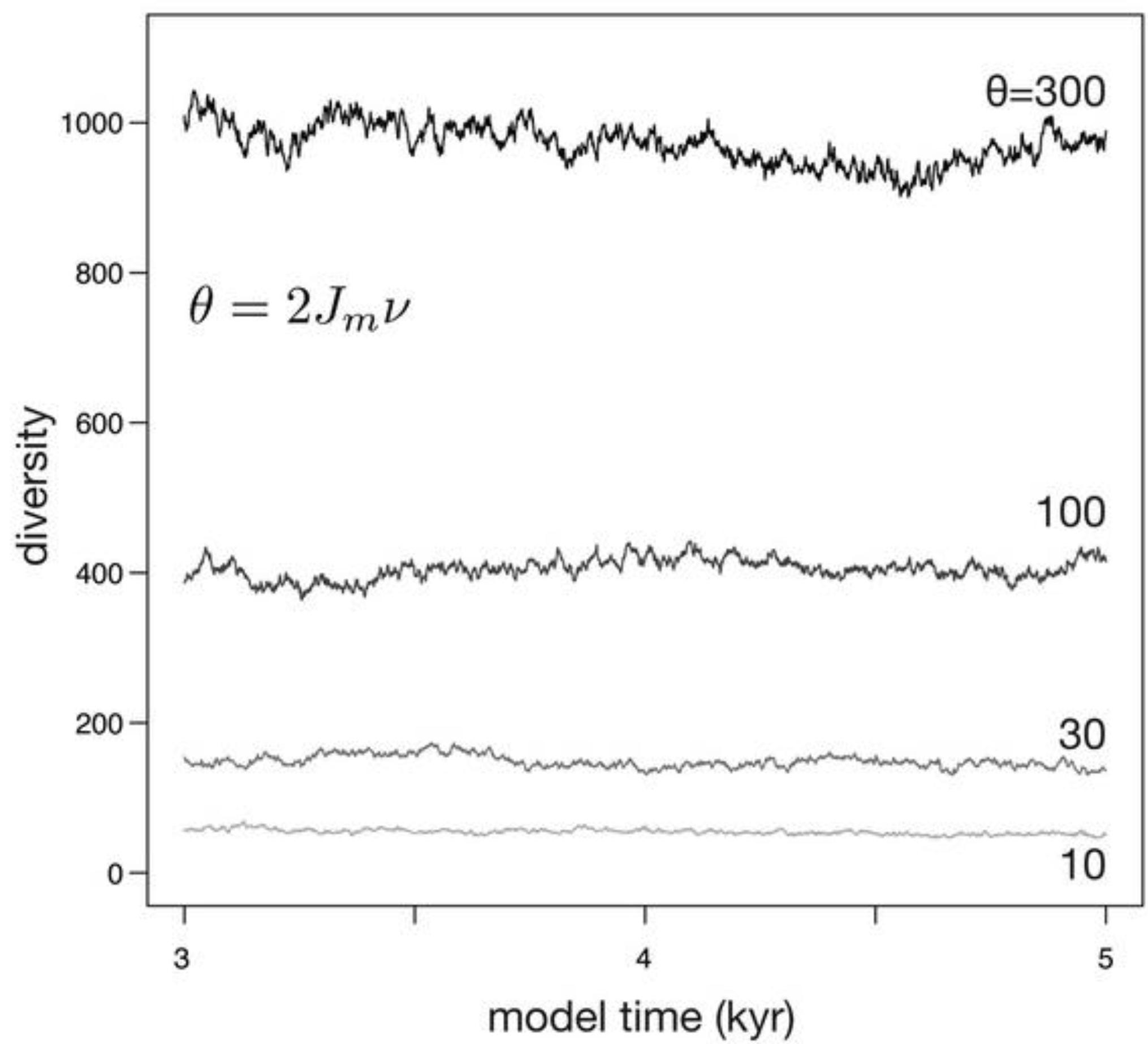
| Constant area (Figure 4) | 100000 | 10, 30, 100, 300 | 0.1 | 0 | not applicable |
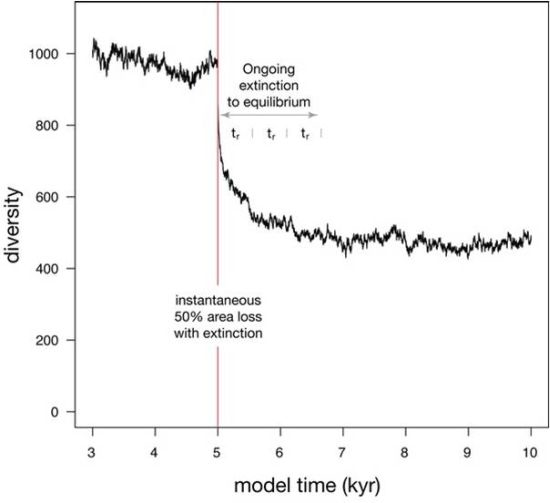
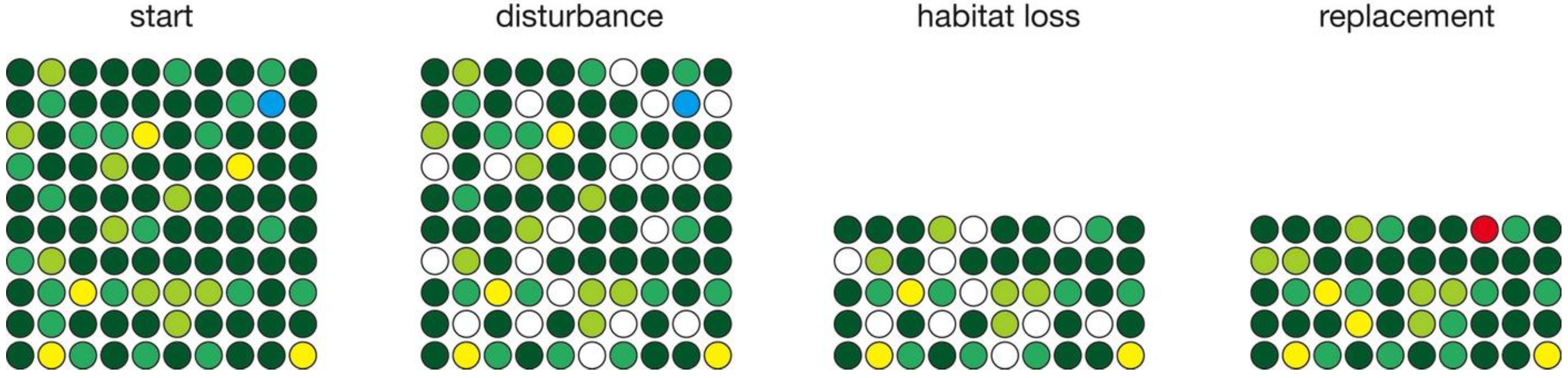
| Habitat loss (Figure 5) | 100000 | 300 | 0.1 | −50% | 553 |
| Effect of lifespan (Figure 6) | 100000 | 300 | 0.333, 0.1, 0.333, 0.01 | −50% | 318, 1100, 972, 1465 |
| Effect of lifespan, small θ | 100000 | 30 | 0.333, 0.1, 0.333, 0.01 | −50% | 623, 553, 2335, 1212 |
| Effect of Jm (Figure 7) | 1000, 10000, 100000, 1000000 | 30 | 0.1 | −50% | *, 934, 553, 4636 |
| Habitat gain (Figure 8) | 100000 | 300 | 0.1 | +50% | 573 |
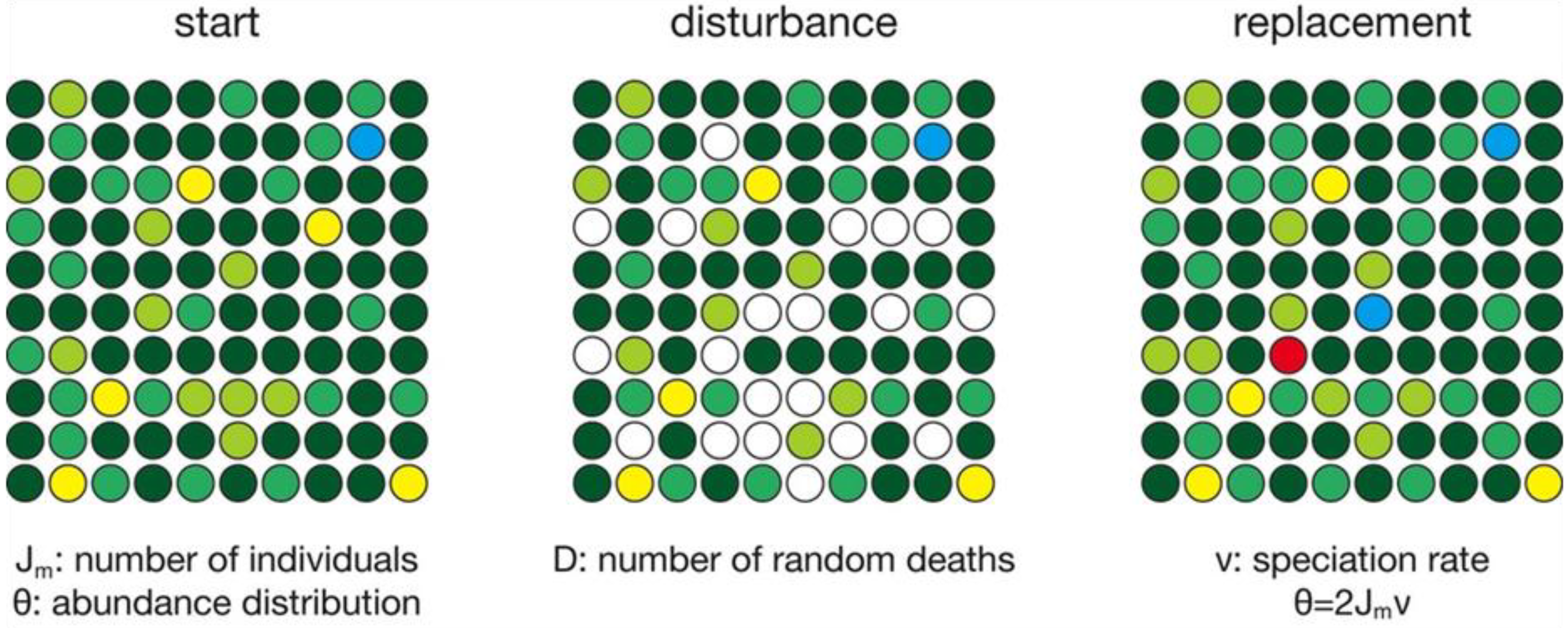

3. Results
3.1. Constant Habitat Area
3.2. Habitat Loss

3.2.1. Effect of Lifespan
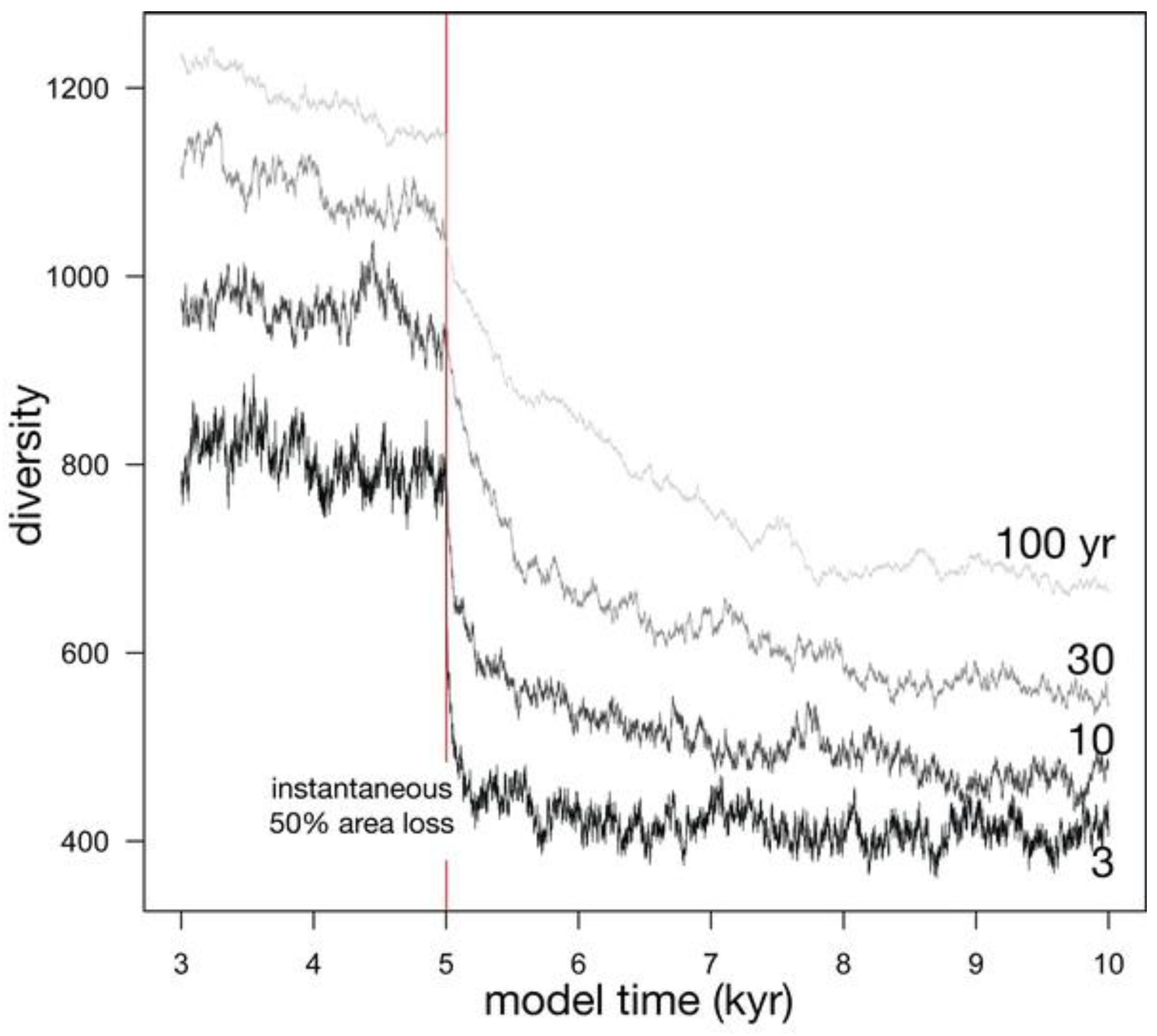
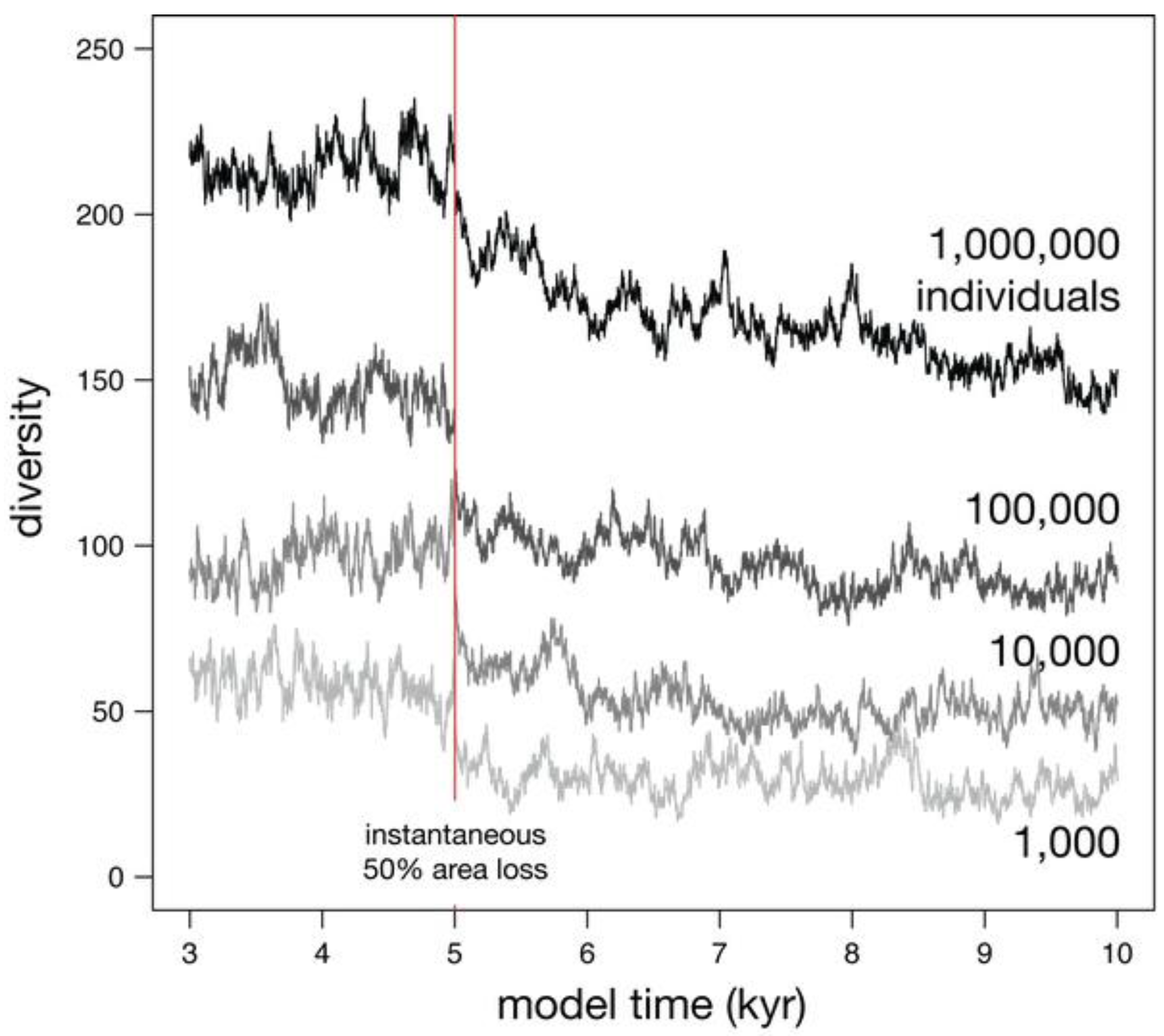
3.2.2. Effect of Metacommunity Size
3.3. Habitat Gain

3.4. Summary
4. Pleistocene Simulation
4.1. Introduction
4.2. Model
4.3. Results
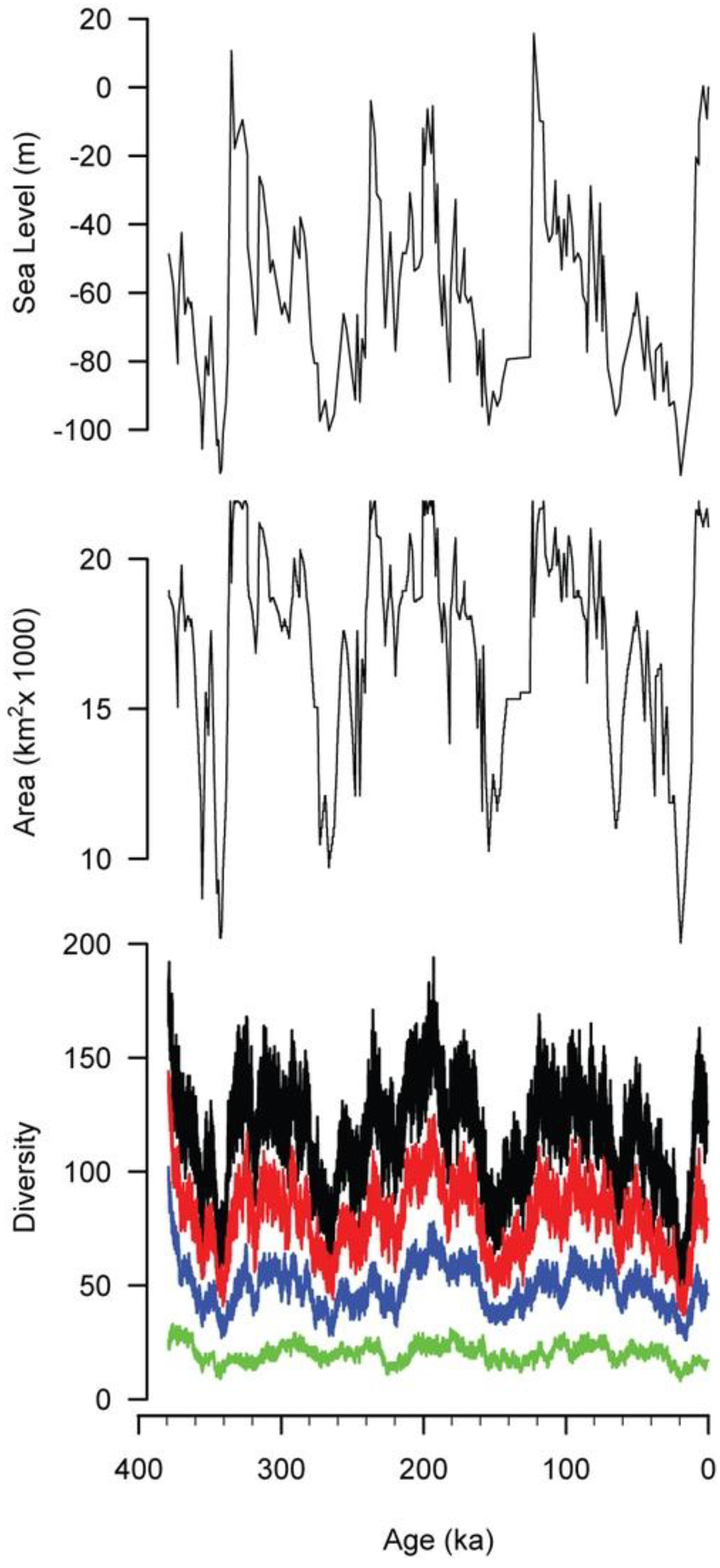
5. Discussion
5.1. Departures between Diversity, Habitat Area, and Sea Level
5.2. Complicating Factors and Their Implications
5.3. Other Explanations for the Lack of Pleistocene Extinction
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Harrison, C.G.A.; Brass, G.W.; Saltzman, E.S.; Sloan, J.L., II; Southam, J.; Whitman, J.M. Sea level variations, global sedimentation rates, and the hypsographic curve. Earth Planet. Sc. Lett. 1981, 54, 1–16. [Google Scholar] [CrossRef]
- Harrison, C.G.A.; Brass, G.W.; Saltzman, E.S.; Sloan, J.L., II. Continental hypsography. Tectonics 1983, 2, 357–377. [Google Scholar] [CrossRef]
- Wyatt, A.R. Relationship between continental area and elevation. Nature 1984, 311, 370–372. [Google Scholar] [CrossRef]
- Wyatt, A.R. Shallow water areas in space and time. J. Geol. Soc. London 1987, 144, 115–120. [Google Scholar] [CrossRef]
- Algeo, T.J.; Wilkinson, B.H. Modern and ancient continental hyposometries. J. Geol. Soc. London 1991, 148, 643–653. [Google Scholar] [CrossRef]
- Holland, S.M. Sea level change and the area of shallow-marine habitat: implications for marine biodiversity. Paleobiology 2012, 38, 205–217. [Google Scholar] [CrossRef]
- Chamberlin, T.C. Diastrophism as the ultimate basis of correlation. J. Geol. 1909, 17, 689–693. [Google Scholar]
- Moore, R.C. Evolution of late Paleozoic invertebrates in response to major oscillations of shallow seas. Bull. Harv. Mus. Comparat. Zool. 1954, 122, 259–286. [Google Scholar]
- Newell, N.D. Revolutions in the history of life. Geol. Soc. Am. 1967, 89, 63–91. [Google Scholar] [CrossRef]
- Flessa, K.W.; Sepkoski, J.J., Jr. On the relationship between Phanerozoic diversity and changes in habitable area. Paleobiology 1978, 4, 359–366. [Google Scholar]
- Bayer, U.; McGhee, G.R. Evolution in marginal epicontinental basins: The role of phylogenetic and ecologic factors (Ammonite replacements in the German Lower and Middle Jurassic). In Sedimentary and Evolutionary Cycles; Bayer, U., Seilacher, A., Eds.; Springer-Verlag: New York, NY, USA, 1985; pp. 164–220. [Google Scholar]
- Jablonski, D. Causes and consequences of mass extinctions: A comparative approach. In Dynamics of Extinction; Elliot, D.K., Ed.; John Wiley & Sons: New York, NY, USA, 1986; pp. 183–229. [Google Scholar]
- Hallam, A. Radiations and extinctions in relation to environmental change in the marine Lower Jurassic of northwest Europe. Paleobiology 1987, 13, 152–168. [Google Scholar]
- Hallam, A. Phanerozoic. Sea-level Changes; Columbia University Press: New York, NY, USA, 1992. [Google Scholar]
- Brett, C.E. Sequence stratigraphy, paleoecology, and evolution: Biotic clues and responses to sea-level fluctuations. Palaios 1998, 13, 241–262. [Google Scholar] [CrossRef]
- Raup, D.M. Species diversity in the Phanerozoic: An interpretation. Paleobiology 1976, 4, 1–15. [Google Scholar]
- Wise, K.P.; Schopf, T.J.M. Was marine faunal diversity in the Pleistocene affected by changes in sea level? Paleobiology 1981, 7, 394–399. [Google Scholar]
- Valentine, J.W.; Jablonski, D. Biotic effects of sea level change: The Pleistocene test. J. Geophys. Res. 1991, 96, 6873–6878. [Google Scholar]
- McGhee, G.R., Jr. Extinction and diversification in the Devonian brachiopoda of New York state: No correlation with sea-level? Hist. Biol. 1991, 5, 215–227. [Google Scholar]
- McGhee, G.R., Jr. Evolutionary biology of the Devonian brachiopoda of New York state: No correlation with rate of change of sea-level? Lethaia 1992, 25, 165–172. [Google Scholar] [CrossRef]
- Crampton, J.S.; Foote, M.; Beu, A.G.; Maxwell, P.A.; Cooper, R.A.; Matcham, I.; Marshall, B.A.; Jones, C.M. The ark was full! Constant to declining cenozoic shallow marine biodiversity on an isolated midlatitude continent. Paleobiology 2006, 32, 509–532. [Google Scholar] [CrossRef]
- Peters, S.E.; Ausich, W.I. A sampling-adjusted macroevolutionary history for Ordovician–Early Silurian crinoids. Paleobiology 2008, 34, 104–116. [Google Scholar] [CrossRef]
- Lisiecki, L.E.; Raymo, M.R. A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records. Paleoceanography 2005. [Google Scholar] [CrossRef]
- Miller, K.G.; Kominz, M.; Browning, J.V.; Wright, J.D.; Mountain, G.S.; Katz, M.E.; Sugarman, P.J.; Cramer, B.S.; Christie-Blick, N.; Pekar, S.F. The Phanerozoic record of global sea-level change. Science 2005, 310, 1293–1298. [Google Scholar] [CrossRef]
- Siddall, M.; Rohling, E.J.; Almogi-Labin, A.; Hemleben, C.; Meischner, D.; Schmelzer, I.; Smeed, D.A. Sea-level fluctuations during the last glacial cycle. Nature 2003, 423, 853–858. [Google Scholar]
- Diamond, J.M. Biogeographic kinetics: estimation of relaxation times for avifaunas of Southwest Pacific Islands. Proc. Natl. Acad. Sci. USA 1972, 69, 3199–3203. [Google Scholar]
- Tilman, D.; May, R.M.; Lehman, C.L.; Nowak, M.A. Habitat destruction and the extinction debt. Nature 1994, 371, 65–66. [Google Scholar]
- Smith, A.B.; Gale, A.S.; Monks, N.E.A. Sea-level change and rock-record bias in the Cretaceous: a problem for extinction and biodiversity studies. Paleobiology 2001, 27, 241–253. [Google Scholar] [CrossRef]
- Hubbell, S.P. The Unified Neutral Theory of Biodiversity and Biogeography; Monographs in Population Biology 32; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- R Core Team, R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012.
- Hankin, R. Introducing untb, an R package for simulating ecological drift under the unified neutral theory of biodiversity. J. Stat. Softw. 2007, 22, 1–15. [Google Scholar]
- Thorson, G. Bottom communities (sublittoral or shallow shelf). Geol. Soc. Am. Mem. 1957, 67, 461–534. [Google Scholar]
- Abele, D.; Brey, T.; Philipp, E. Bivalve models of aging and the determination of molluscan lifespans. Exp. Gerontol. 2009, 44, 307–315. [Google Scholar] [CrossRef]
- Holland, S.M. The stratigraphic distribution of fossils. Paleobiolog 1995, 21, 92–109. [Google Scholar]
- Holland, S.M. The quality of the fossil record—a sequence stratigraphic perspective. In Deep Time: Paleobiology’s Perspective; Erwin, D.H., Wing, S.L., Eds.; The Paleontological Society: Lawrence, KS, USA, 2000; pp. 148–168. [Google Scholar]
- Boecklin, W.J.; Simberloff, D. Area-based extinction models in conservation. In Dynamics of Extinction; Elliot, D.K., Ed.; John Wiley: New York, NY, USA, 1986; pp. 247–272. [Google Scholar]
- Vellend, M.; Verheyen, K.; Jacquemyn, H.; Kolb, A.; van Calster, H.; Peterken, G.; Hermy, M. Extinction debt of forest plants persists for more than a century following habitat fragmentation. Ecology 2006, 87, 542–548. [Google Scholar]
- Halley, J.M.; Iwasa, Y. Neutral theory as a predictor of avifaunal extinctions after habitat loss. Proc. Natl. Acad. Sci. USA 2011, 108, 2316–2321. [Google Scholar] [CrossRef]
- Mouquet, N.; Matthiessen, B.; Miller, T. Gonzalez, Extinction debt in source-sink metacommunities. PloS One 2011, 6, e17567. [Google Scholar] [CrossRef]
- Revelle, R. Sea-Level Change; National Academy Press: Washington, DC, 1990. [Google Scholar]
- ETOPO1 Global Relief Model. Available online: http://www.ngdc.noaa.gov/mgg/global/global.html/ (accessed on 1 April 2013).
- Berger, A. Pleistocene climatic variability at astronomical frequencies. Quatern. Int. 1989, 2, 1–14. [Google Scholar] [CrossRef]
- Rosindell, J.; Hubbell, S.P.; Etienne, R.S. The Unified Neutral Theory of Biodiversity and Biogeography at age ten. Trends Ecol. Evol. 2011, 26, 340–348. [Google Scholar] [CrossRef]
- Goodman, D. The demography of chance extinction. In Viable Populations for Conservation; Soulé, M., Ed.; Cambridge University Press: Cambridge, UK, 1987; pp. 11–34. [Google Scholar]
- McPeek, M.A.; Rodenhouse, N.L.; Holmes, R.T.; Sherry, T.W. A general model of site-dependent population regulation: population-level regulation without individual-level interactions. Oikos 2001, 94, 417–424. [Google Scholar]
- Holt, R.D. Population dynamics in two-patch environments: some anomalous consequences of an optimal habitat distribution. Theor. Popul. Biol. 1985, 28, 181–208. [Google Scholar] [CrossRef]
- Morris, D.W. Habitat-dependent population regulation and community structure. Evol. Ecol. 1988, 2, 253–269. [Google Scholar] [CrossRef]
- Erwin, D.H. The end and the beginning: Recoveries from mass extinctions. Trends Ecol. Evol. 1998, 13, 344–349. [Google Scholar] [CrossRef]
- Erwin, D.H. Lessons from the past: Biotic recoveries from mass extinctions. Proc. Natl. Acad. Sci. USA 2001, 98, 5399–5403. [Google Scholar] [CrossRef]
- Alroy, J.; Aberhan, M.; Bottjer, D.J.; Foote, M.; Fürsich, F.T.; Harries, P.J.; Hendy, A.J.W.; Holland, S.M.; Ivany, L.C.; Kiessling, W.; et al. Phanerozoic trends in the global diversity of marine invertebrates. Science 2008, 321, 97–100. [Google Scholar] [CrossRef]
- Stanley, S.M. Marine mass extinction: A dominant role for temperature. In Extinctions; Nitecki, M.H., Ed.; University of Chicago Press: Chicago, IL, USA, 1984; pp. 69–117. [Google Scholar]
- Schopf, T.J.M.; Fisher, J.B.; Smith, C.A.F., III. Is the marine latitudinal diversity gradient merely another example of the species-area curve? In Marine Organisms: Genetics, Ecology, and Evolution; Battaglia, B., Beardmore, J.A., Eds.; Plenum: New York, NY, USA, 1978; pp. 365–386. [Google Scholar]
- Kowalewski, M.; Gürs, K.; Nebelsick, J.H.; Oschmann, W.; Piller, W.E.; Hoffmeister, A.P. Multivariate hierarchical analyses of miocene mollusk assemblages of europe: Palaeogeographic, palaeoecological, and biostratigraphic implications. Geol. Soc. Am. Bull. 2002, 114, 239–256. [Google Scholar]
- Okuda, T.; Noda, T.; Yamamoto, T.; Ito, N.; Nakaoka, M. Latitudinal gradient of species diversity: Multi-scale variability in rocky intertidal sessile assemblages along the northwestern Pacific coast. Popul. Ecol. 2004, 46, 159–170. [Google Scholar]
- Patzkowsky, M.E.; Holland, S.M. Diversity partitioning of a Late Ordovician marine biotic invasion: Controls on diversity in regional ecosystems. Paleobiology 2007, 33, 295–309. [Google Scholar] [CrossRef]
- McKinney, M.L.; Lockwood, J.L.; Frederick, D.R. Does ecosystem and evolutionary stability include rare species? Palaeogeogr. Palaeocl. 1996, 127, 191–207. [Google Scholar] [CrossRef]
- Holland, S.M.; Miller, A.I.; Meyer, D.L.; Dattilo, B.F. The detection and importance of subtle biofacies within a single lithofacies: The Upper Ordovician Kope Formation of the Cincinnati, Ohio region. Palaios 2001, 16, 205–217. [Google Scholar] [CrossRef]
- Harnik, P.G. Unveiling rare diversity by integrating museum, literature, and field data. Paleobiology 2009, 35, 190–208. [Google Scholar] [CrossRef]
- Roy, K.; Jablonski, D.; Valentine, J.W. Thermally anomalous assemblages revisited: Patterns in the extraprovincial latitudinal range shifts of Pleistocene marine mollusks. Geology 1995, 23, 1071–1074. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Holland, S.M. Relaxation Time and the Problem of the Pleistocene. Diversity 2013, 5, 276-292. https://doi.org/10.3390/d5020276
Holland SM. Relaxation Time and the Problem of the Pleistocene. Diversity. 2013; 5(2):276-292. https://doi.org/10.3390/d5020276
Chicago/Turabian StyleHolland, Steven M. 2013. "Relaxation Time and the Problem of the Pleistocene" Diversity 5, no. 2: 276-292. https://doi.org/10.3390/d5020276
APA StyleHolland, S. M. (2013). Relaxation Time and the Problem of the Pleistocene. Diversity, 5(2), 276-292. https://doi.org/10.3390/d5020276