The Species-Area Relationship in the Late Ordovician: A Test Using Neutral Theory
Abstract
:1. Introduction
2. Overview of Hubbell’s Neutral Theory
2.1. The Parameters θ and m

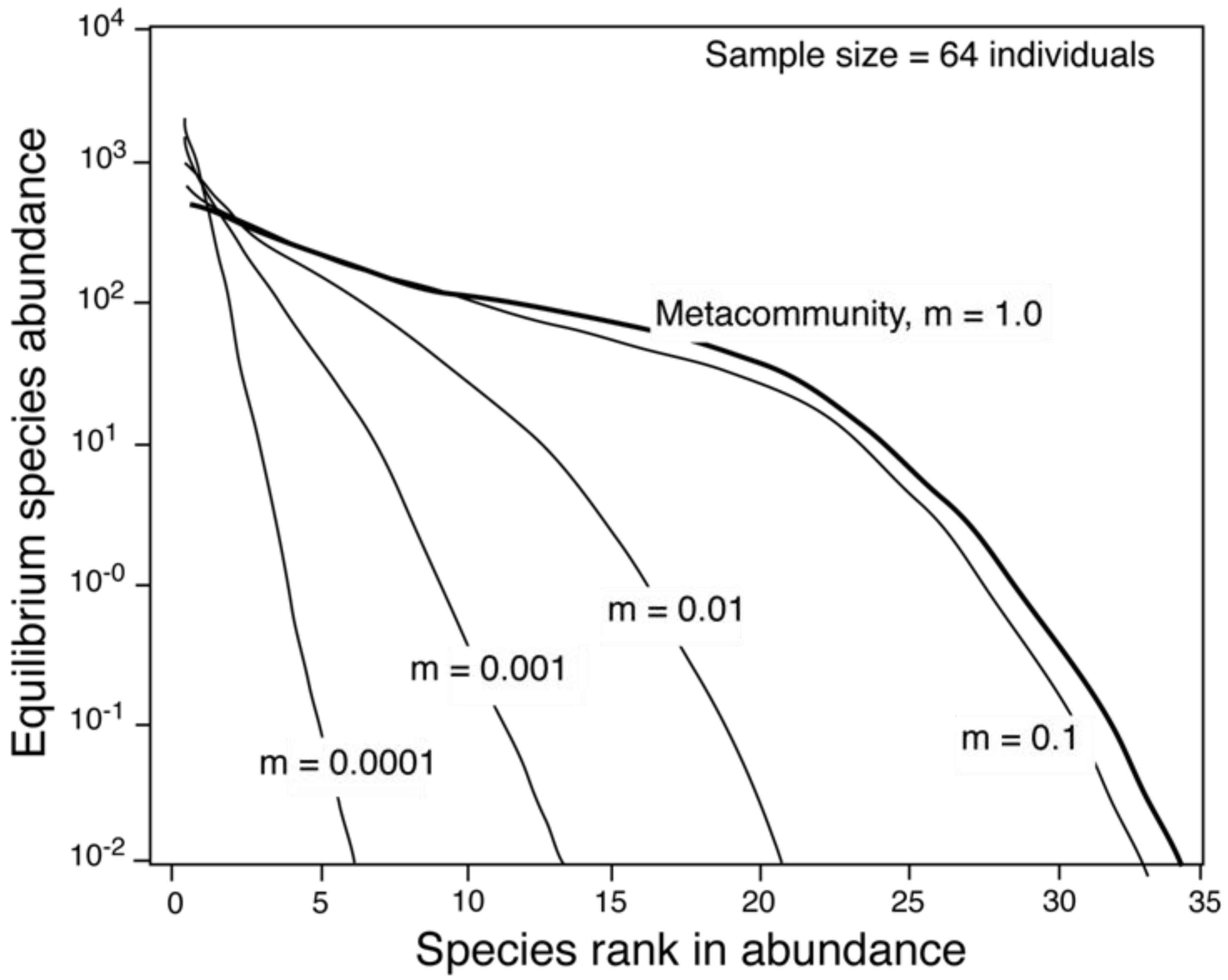
2.2. The Relationship between θ and Area
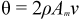
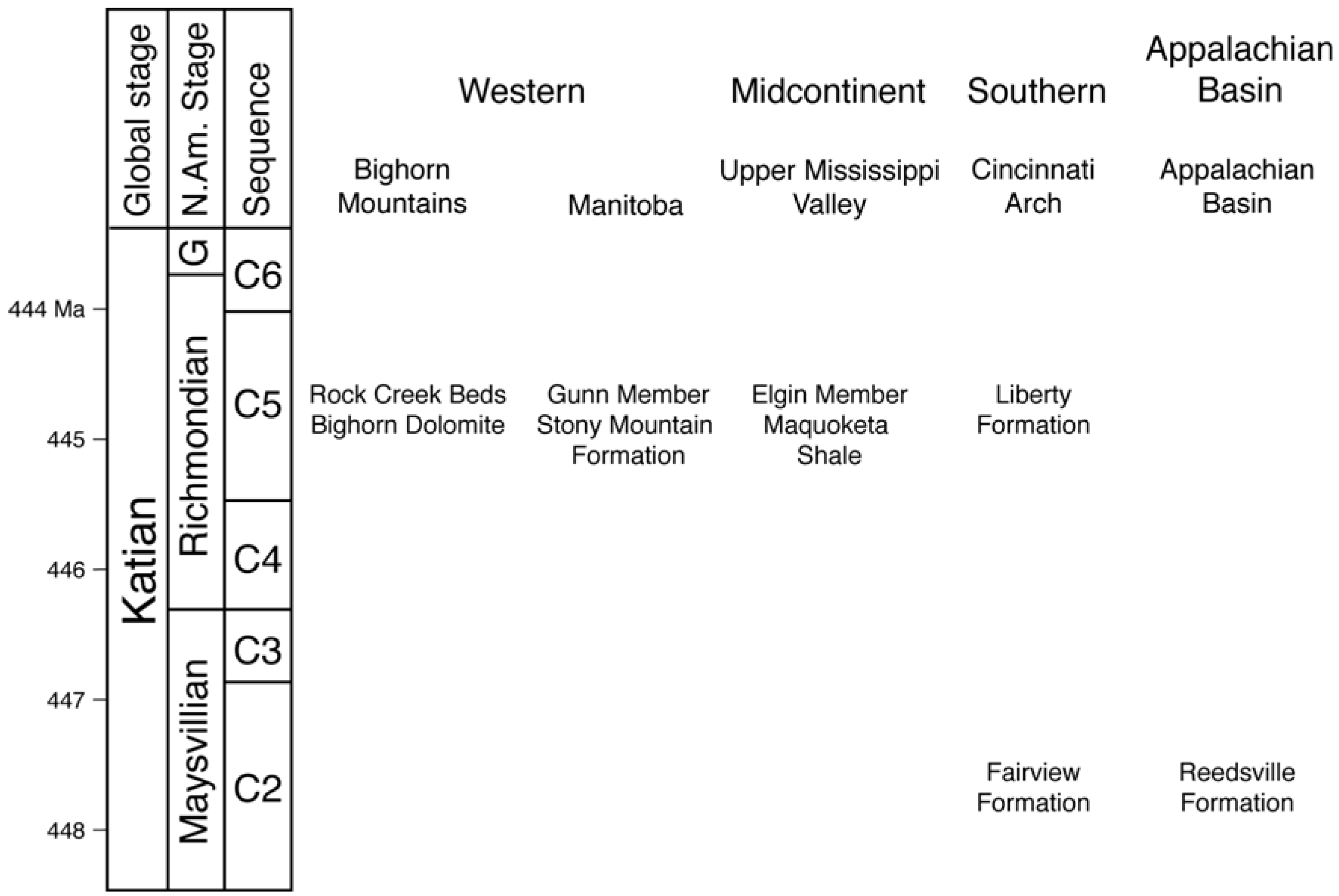
3. The Late Ordovician of Laurentia
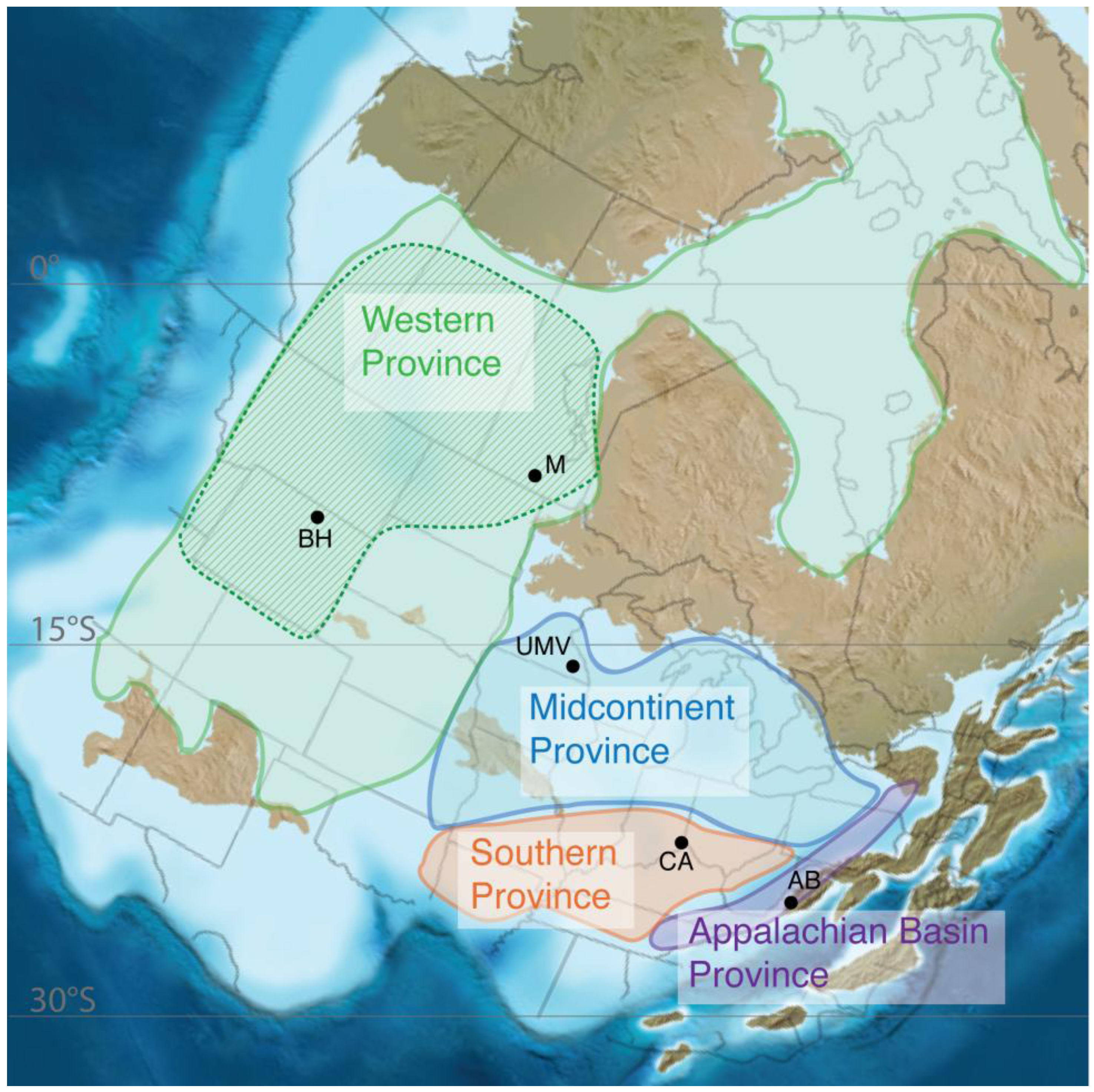
3.1. Geochemical Provinces
3.2. Biogeographic Studies Support These Regions as Provinces
4. Methods
4.1. Data Collection
| Taxa Included | Taxa Excluded |
|---|---|
| detritivore gastropods (ex: Liospira) | carnivorous gastropods (ex: Subulites) |
| detritivore trilobites (ex: Isotelus) | carnivorous trilobites (ex: Ceraurinus) |
| all brachiopods | all nautiloids |
| all corals | all crinoids |
| all bryozoans | all algae |
| all bivalves |
4.2. Data Analysis
4.2.1. Relative Abundance Distributions
4.2.2. Estimation of θ
4.2.3. Estimation of Area
5. Results
5.1. Relative Abundance Distributions

| Data set | Number of samples | Metacommunity species richness | Mean local community species richness |
|---|---|---|---|
| Appalachian Basin | 23 | 20 | 7 |
| C2 Cincinnati Arch | 63 | 31 | 8 |
| C5 Cincinnati Arch | 99 | 43 | 9 |
| Upper Mississippi Valley | 9 | 21 | 7 |
| Manitoba | 12 | 22 | 11 |
| Bighorn Mountains | 39 | 49 | 11 |
5.2. Estimation of θ and Area
| Data set | θ 2007 method [40] | θ 2009 method [41] | Province area (km2) |
|---|---|---|---|
| Appalachian Basin | 5.22 | 5.43 | 1.35 x 105 |
| C2 Cincinnati Arch | 6.32 | not calculated | 4.81 x 105 |
| C5 Cincinnati Arch | 8.49 | not calculated | 4.81 x 105 |
| Upper Mississippi Valley | 8.79 | 8.68 | 9.27 x 105 |
| Manitoba | 5.47 | not calculated | 13.9 x 105 |
| Bighorn Mountains | 11.9 | 10.0 | 13.9 x 105 |
5.3. Likelihood Surfaces

5.4. Correlation between θ and Area

6. Discussion
6.1. The Correlation between θ and Area
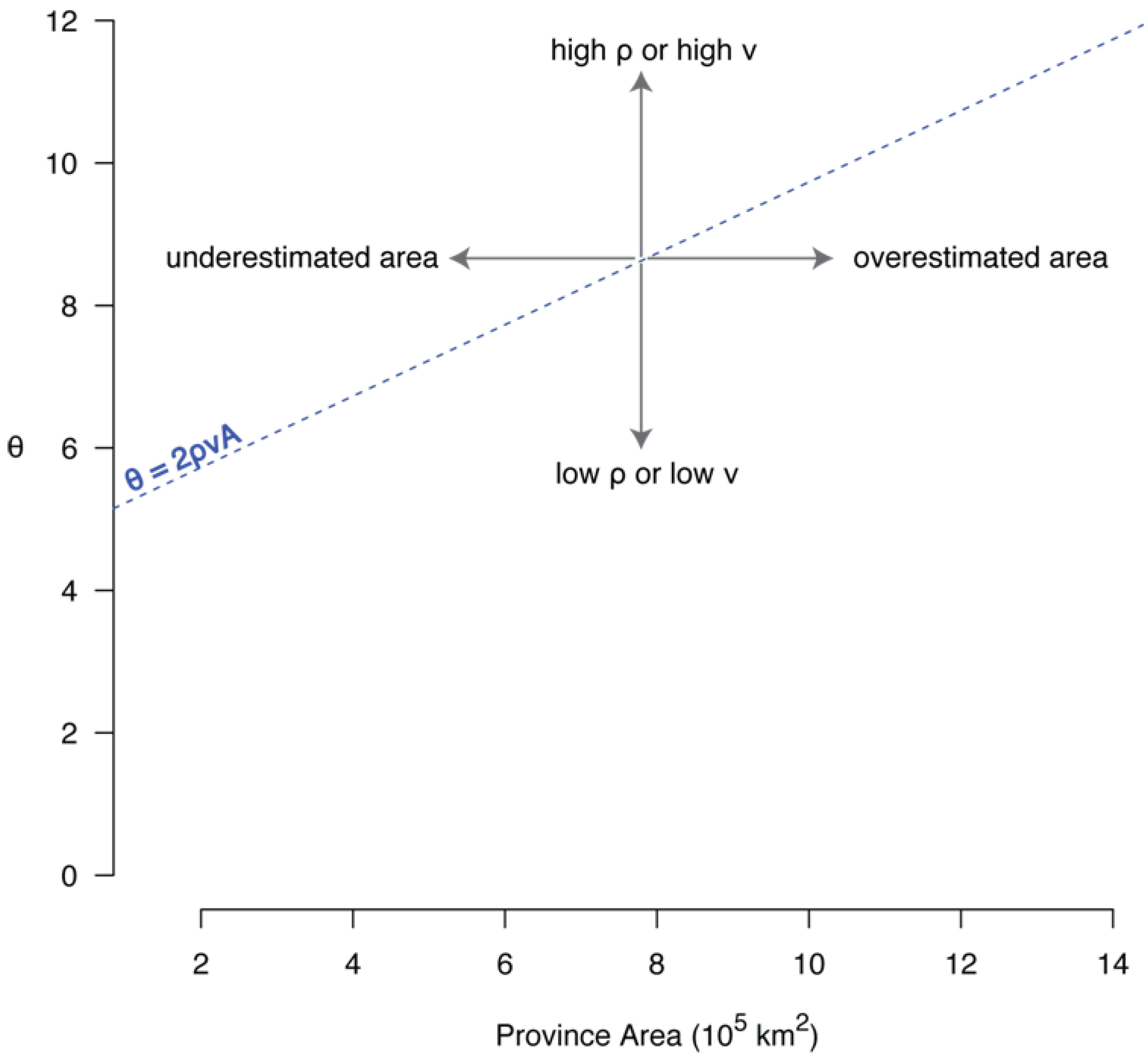
6.2. The Species-Area Relationship and θ
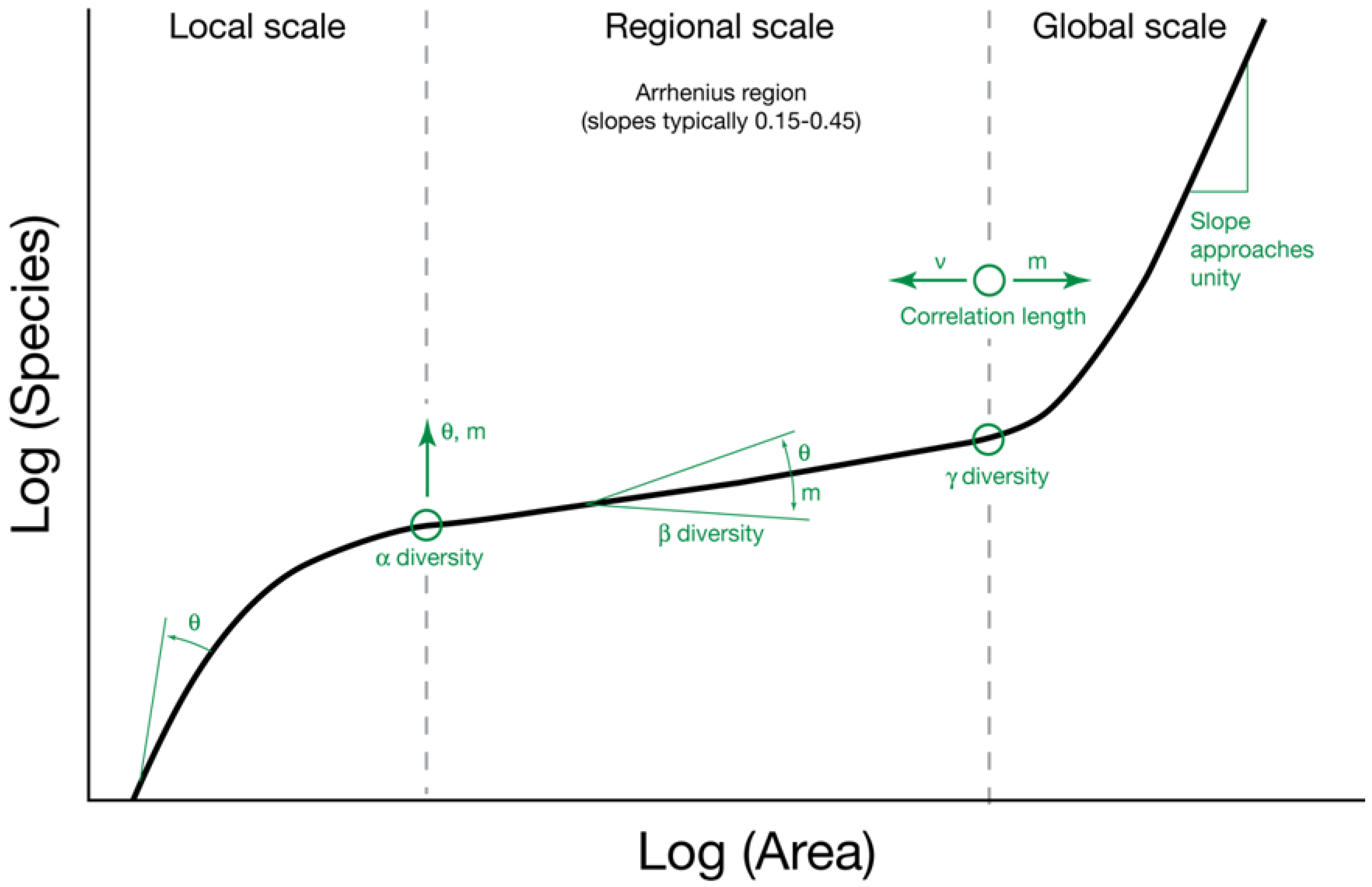
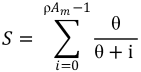
7. Conclusions
Acknowledgments
Conflict of Interest
References
- Hubbell, S.P. The Unified Neutral Theory of Biogeography; Princeton University Press: Princeton, NJ, USA, 2001; p. 375. [Google Scholar]
- Holmden, C.; Creaser, R.A.; Muehlenbachs, K.; Leslie, S.A.; Bergström, S.M. Isotopic evidence for geochemical decoupling between ancient epeiric seas and bordering oceans: implications for secular curves. Geology 1998, 26, 567–570. [Google Scholar]
- Jin, J.; Harper, D.A.T.; Rasmussen, J.A.; Sheehan, P.M. Late Ordovician massive-bedded Thalassinoides ichnofacies along the paleoequator of Laurentia. Palaeogeogr. Palaeocl. 2012, 367–368, 73–88. [Google Scholar]
- Panchuk, K.M.; Holmden, C.E.; Leslie, S.A. Local controls on carbon cycling in the Ordovician midcontinent region of North America, with implications for carbon isotope secular curves. J. Sediment. Res. 2006, 76, 200–211. [Google Scholar] [CrossRef]
- Alonso, D.; Etienne, R.S.; McKane, A.J. The merits of neutral theory. Trends Ecol. Evol. 2006, 21, 451–457. [Google Scholar] [CrossRef]
- Purves, D.W.; Turnbull, L.A. Different but not equal: the implausible assumption at the heart of neutral theory. J. Anim. Ecol. 2010, 79, 1215–1225. [Google Scholar] [CrossRef] [Green Version]
- Rosindell, J.; Hubbell, S.P.; Etienne, R.S. The unified neutral theory of biodiversity and biogeography at age ten. Trends Ecol. Evol. 2010, 26, 340–348. [Google Scholar] [CrossRef]
- Hubbell, S.P. The neutral theory of biodiversity and biogeography and Stephen Jay Gould. Paleobiology 2005, 31, 122–132. [Google Scholar] [CrossRef]
- Olszewski, T.D.; Erwin, D.H. Dynamic response of Permian brachiopod communities to long-term environmental change. Nature 2004, 428, 738–741. [Google Scholar] [CrossRef]
- Tomašových, A.; Kidwell, S.M. Predicting the effects of increasing temporal scale on species composition, diversity, and rank abundance distributions. Paleobiology 2010, 36, 672–695. [Google Scholar] [CrossRef]
- Scotese, C.R.; McKerrow, W.S. Ordovician plate tectonic reconstructions. Geol. S. Can. Paper 1991, 90, 271–282. [Google Scholar]
- Beaumont, C.; Quinlan, G.; Hamilton, J. Orogeny and stratigraphy: Numerical models of the Paleozoic in the eastern interior of North America. Tectonics 1988, 7, 389–416. [Google Scholar] [CrossRef]
- Sweet, W.C.; Bergström, S.M. Provincialism exhibited by Ordovician conodont faunas. SEPM Spec. P. 1974, 21, 189–202. [Google Scholar]
- Barnes, C.R.; Fåhræus, L.E. Provinces, communities, and the proposed nektobenthic habit of Ordovician conodontophorids. Lethaia 1975, 8, 133–149. [Google Scholar] [CrossRef]
- Elias, R.J. Solitary rugose corals of the Stony Mountain Formation, Southern Manitoba, and its equivalents. J. Paleontol. 1983, 57, 924–956. [Google Scholar]
- Antsey, R.L. Bryozoan provinces and patterns of generic evolution and extinction in the Late Ordovician of North America. Lethaia 1986, 19, 33–51. [Google Scholar] [CrossRef]
- Blakey, R. Global Paleogeography. Available online: http://jan.ucc.nau.edu/rcb7/globaltext2.html/ (accessed on 18 April 2012).
- Piepgras, D.J.; Wasserburg, G.J. Neodymium isotopic variations in seawater. Earth Planet. Sc. Lett. 1980, 50, 128–138. [Google Scholar] [CrossRef]
- Patterson, W.P.; Walter, L.M. Depletion of 13C in seawater ΣCO2 on modern carbonate platforms: significance for the carbon isotopic record of carbonates. Geology 1994, 22, 885–888. [Google Scholar] [CrossRef]
- Bergström, S.M. Biogeography, evolutionary relationships, and biostratigraphic significance of Ordovician platform conodonts. Foss. Strata 1983, 15, 35–58. [Google Scholar]
- Riva, J. A revision of some Ordovician graptolites of eastern North America. Palaeontology 1974, 17, 1–40. [Google Scholar]
- Bergström, S.M.; Mitchell, C.E. The graptolite correlation of the North American Upper Ordovician standard. Lethaia 1986, 19, 247–266. [Google Scholar] [CrossRef]
- Berry, W.B.N. Review of late Middle Ordovician graptolites in eastern New York and Pennsylvania. Am. J. Sci. 1970, 269, 304–313. [Google Scholar] [CrossRef]
- Goldman, D.; Bergström, S.M.; Mitchell, C.E. Revision of the Zone 13 graptolite biostratigraphy in the Marathon, Texas, standard succession and its bearing on Upper Ordovician graptolite biostratigraphy. Lethaia 1995, 28, 115–128. [Google Scholar] [CrossRef]
- Mohibullah, M.; Williams, M.; Vandenbroucke, T.R.A.; Sabbe, K.; Zalasiewicz, J.A. Marine ostracod provinciality in the Late Ordovician of palaeocontinental Laurentia and its environmental and geographical expression. PLOS one 2012, 7, e41682. [Google Scholar]
- Bretsky, P.W. Central Appalachian Late Ordovician communities. Geol. Soc. Am. Bull. 1969, 80, 193–212. [Google Scholar] [CrossRef]
- Elias, R.J.; Young, G.A. Coral diversity, ecology, and provincial structure during a time of crisis: the latest Ordovician to earliest Silurian Edgewood Province in Laurentia. Palaios 1998, 13, 98–112. [Google Scholar] [CrossRef]
- Elias, R.J. Latest Ordovician solitary rugose corals of eastern North America. Bull. Am. Paleontol. 1982, 81, 1–85. [Google Scholar]
- Flower, R.H. Ordovician cephalopods of the Cincinnati region, part 1. Bull. Am. Paleontol. 1946, 29, 1–656. [Google Scholar]
- Nelson, S.J. Arctic Ordovician fauna: an equatorial assemblage. J. Alberta Soc. Petr. Geol. 1959, 7, 45–47. [Google Scholar]
- Jin, J.; Zhan, R.B. Late Ordovician Articulate Brachiopods from the Red River and Stony Mountain Formations, Southern Manitoba; NRC Research Press: Ottawa, Canada, 2001; p. 117. [Google Scholar]
- Jin, J.; Caldwell, W.G.E.; Norford, B.S. Late Ordovician brachiopods Rafinesquina lata Whiteaves, 1896 and Kjaerina hartae n. sp. from southern Manitoba and the Hudson Bay lowlands. Can. J. Earth Sci. 1995, 32, 1255–1266. [Google Scholar] [CrossRef]
- Jin, J.; Harper, D.A.T.; Cocks, L.R.M.; McCausland, P.J.A.; Rasmussen, C.M.Ø.; Sheehan, P.M. Precisely locating the Ordovician equator in Laurentia. Geology 2013, 41, 107–110. [Google Scholar] [CrossRef]
- Holland, S.M.; Patzkowsky, M.E. Sequence stratigraphy and long-term paleoceanographic change in the Middle and Upper Ordovician of the eastern United States. Geol. Soc. Am. S. 1996, 306, 117–129. [Google Scholar]
- Holland, S.M.; Patzkowsky, M.E. Ecosystem structure and stability: Middle Upper Ordovician of central Kentucky, USA. Palaios 2004, 19, 316–331. [Google Scholar] [CrossRef]
- Holland, S.M.; Patzkowsky, M.E. Gradient ecology of a biotic invasion: biofacies of the type Cincinnatian Series (Upper Ordovician), Cincinnati, Ohio region, USA. Palaios 2007, 22, 392–407. [Google Scholar] [CrossRef]
- Holland, S.M.; Patzkowsky, M.E. Stratigraphic architecture of a tropical carbonate platform and its effect on the distribution of fossils: Ordovician Bighorn Dolomite, Wyoming, USA. Palaios 2009, 24, 303–317. [Google Scholar] [CrossRef]
- Paleobiology Database Home Page. Available online: http://paleodb.org/ (accessed on 29 September 2012).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2011. ISBN 3-900051-07-0. Available online: http://www.R-project.org/ (accessed on 19 August 2011).
- Etienne, R.S. A neutral sampling formula for multiple samples and an ‘exact’ test of neutrality. Ecol. Lett. 2007, 10, 608–618. [Google Scholar] [CrossRef]
- Etienne, R.S. Maximum likelihood estimation of neutral model parameters for multiple samples with different degrees of dispersal limitation. J. Theor. Biol. 2009, 257, 510–514. [Google Scholar] [CrossRef]
- PARI/GP Home Page. Available online: http://pari.math.u-bordeaux.fr/ (accessed on 3 April 2012).
- ESRI, ArcGIS Desktop: Release 10, Environmental Systems Research Institute: Redlands, CA, USA, 2011.
- Holland, S.M.; Patzkowsky, M.E. Sequence architecture of the Bighorn Dolomite, Wyoming, USA: Transition to the Late Ordovician icehouse. J. Sediment. Res. 2012, 82, 599–615. [Google Scholar] [CrossRef]
- Lobdell, F.K. Arthrostylidae (Bryozoa: Cryptostomata) from the Gunn Member, Stony Mountain Formation (Upper Ordovician), North Dakota and Manitoba. N. Dak. Geol. Survey Misc. Series 1992, 76, 99–115. [Google Scholar]
- Richards, P.W.; Nieschmidt, C.L. The Bighorn Dolomite and Correlative Formations in Southern Montana and Northern Wyoming (Oil and Gas Investigations Map, OM-202) [Map]; U.S. Geological Survey: Reston, Virginia, VA, USA, 1961. [Google Scholar]
- Longman, M.W.; Fertal, T.G.; Glennie, J.S. Origin and geometry of Red River Dolomite reservoirs, western Williston Basin. AAPG Bull. 1983, 67, 744–771. [Google Scholar]
- Sweet, W.C. Harding and Fremont Formations, Colorado. AAPG Bull. 1954, 38, 284–305. [Google Scholar]
- Preston, F.W. The commonness and rarity of species. Ecology 1948, 29, 254–283. [Google Scholar] [CrossRef]
- Rex, M.A. Community structure in the deep-sea benthos. Annu. Rev. Ecol. Syst. 1981, 12, 331–353. [Google Scholar]
- Patzkowsky, M.E.; Holland, S.M. Extinction, invasion, and sequence stratigraphy: patterns of faunal change in the Middle and Upper Ordovician of the eastern United States. Geol. S. Am. S. 1996, 306, 131–142. [Google Scholar]
- Allen, A.P.; Gillooly, J.F.; Savage, V.M.; Brown, J.H. Kinetic effects of temperature on rates of genetic divergence and speciation. Proc. Natl. Acad. Sci. USA 2006, 103, 9130–9135. [Google Scholar]
- Jablonski, D.; Roy, K.; Valentine, J.W. Out of the tropics: evolutionary dynamics of the latitudinal diversity gradient. Science 2006, 314, 102–106. [Google Scholar] [CrossRef]
- Crame, J.A. Evolution of taxonomic diversity gradients in the marine realm: a comparison of Late Jurassic and Recent bivalve faunas. Paleobiology 2002, 28, 184–207. [Google Scholar] [CrossRef]
- Rosenzweig, M.L. Species Diversity in Space and Time; Cambridge University Press: Cambridge, UK, 1995; p. 436. [Google Scholar]
- Palmer, M.W.; White, P.S. Scale dependence and the species-area relationship. Am. Nat. 1994, 144, 717–740. [Google Scholar]
- Shmida, A.; Wilson, M.V. Biological Determinants of species diversity. J. Biogeogr. 1985, 12, 1–20. [Google Scholar] [CrossRef]
- Preston, F.W. Time and space variation of species. Ecology 1960, 41, 611–627. [Google Scholar] [CrossRef]
- Hu, X.-S.; He, F.; Hubbell, S.P. Species diversity in local neutral communities. Am. Nat. 2007, 170, 844–853. [Google Scholar]
- Bush, A.M.; Bambach, R.K. Does alpha diversity increase during the Phanerozoic? Lifting the veils of taphonomic, latitudinal, and environmental biases. J. Geol. 2004, 112, 625–642. [Google Scholar] [CrossRef]
- Sepkoski, J.J., Jr. Alpha, beta, or gamma: where does all the diversity go? Paleobiology 1988, 14, 221–234. [Google Scholar]
- Valentine, J.W.; Foin, T.C.; Peart, D. A provincial model of Phanerozoic marine diversity. Paleobiology 1978, 4, 55–66. [Google Scholar]
- Alroy, J.; Aberhan, M.; Bottjer, D.J.; Foote, M.; Fürsich, F.T.; Harries, P.J.; Hendy, A.J.W.; Holland, S.M.; Ivany, L.C.; Kiessling, W.; et al. Phanerozoic trends in the global diversity of marine invertebrates. Science 2008, 321, 97–100. [Google Scholar]
Appendix 1—Locality descriptions for newly collected data sets
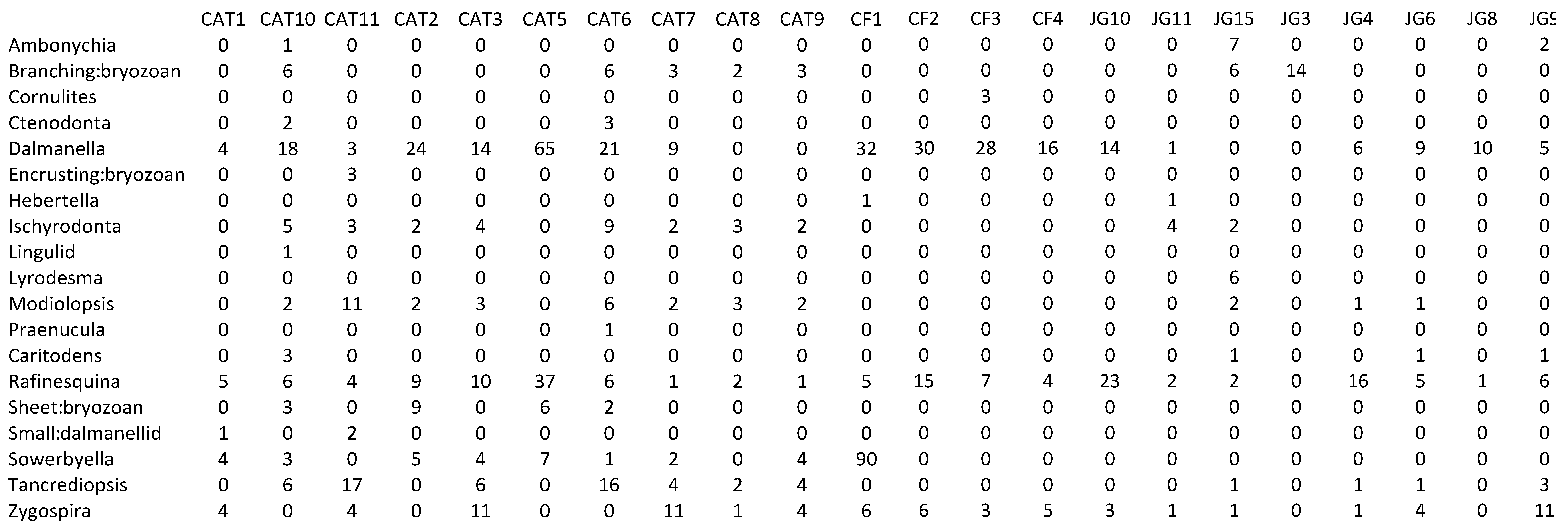
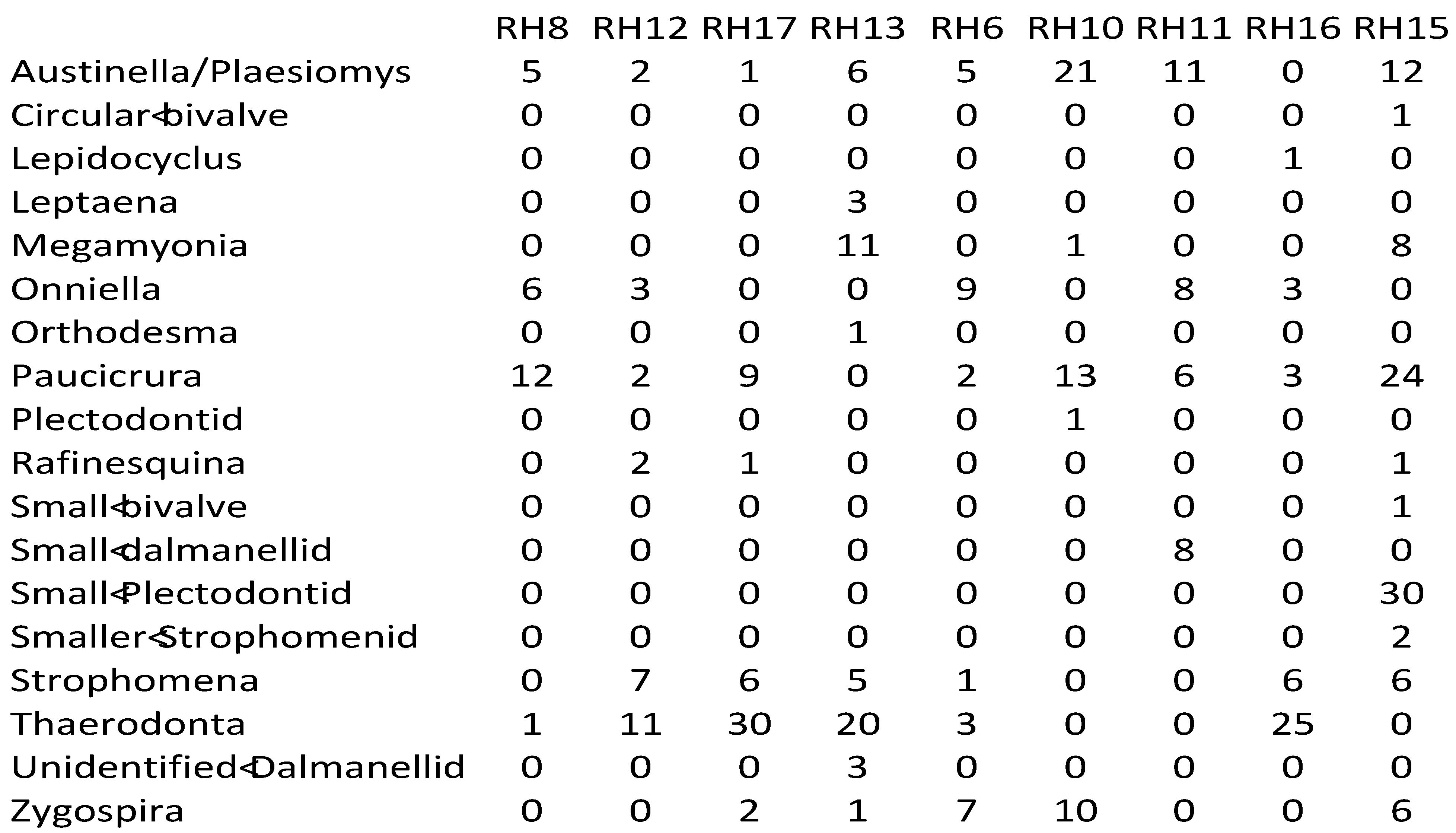
Appendix 2—Newly collected abundance data

© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sclafani, J.A.; Holland, S.M. The Species-Area Relationship in the Late Ordovician: A Test Using Neutral Theory. Diversity 2013, 5, 240-262. https://doi.org/10.3390/d5020240
Sclafani JA, Holland SM. The Species-Area Relationship in the Late Ordovician: A Test Using Neutral Theory. Diversity. 2013; 5(2):240-262. https://doi.org/10.3390/d5020240
Chicago/Turabian StyleSclafani, Judith A., and Steven M. Holland. 2013. "The Species-Area Relationship in the Late Ordovician: A Test Using Neutral Theory" Diversity 5, no. 2: 240-262. https://doi.org/10.3390/d5020240




