Exact and Effective Pair-Wise Potential for Protein-Ligand Interactions Obtained from a Semiempirical Energy Partition
Abstract
:1. Introduction
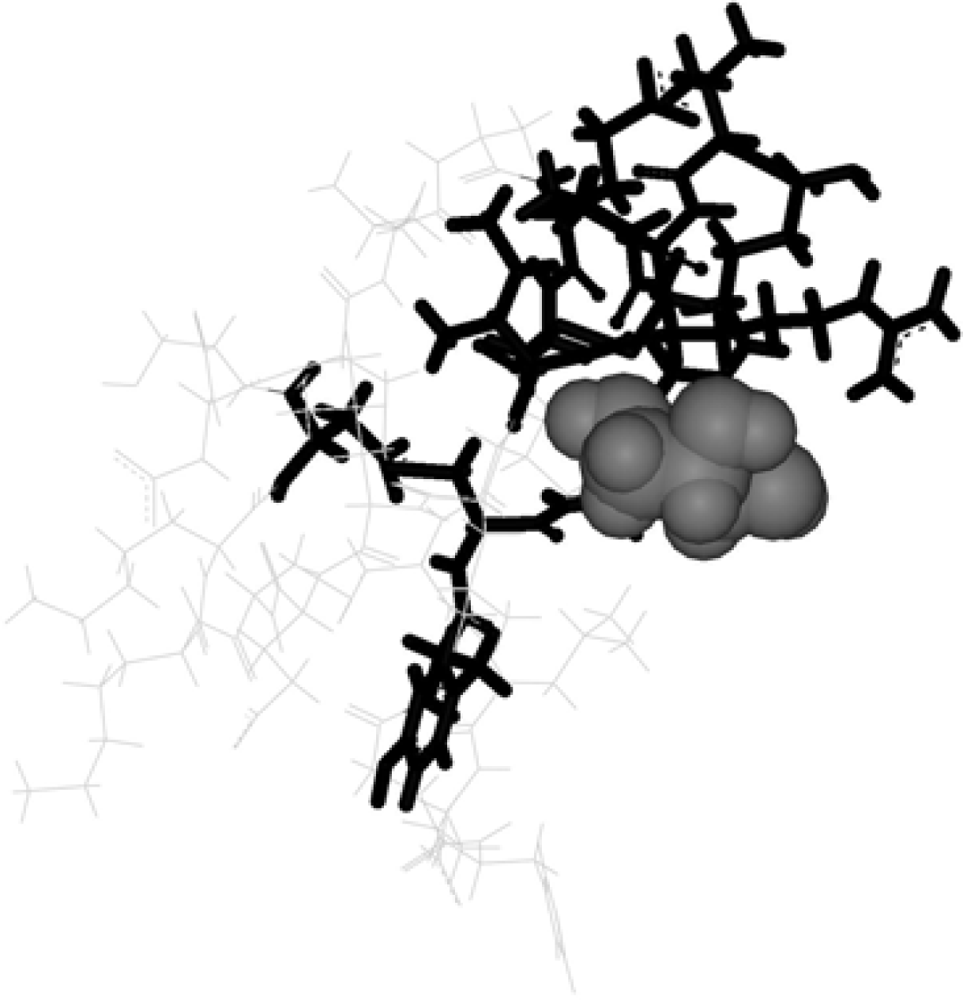
2. Methods
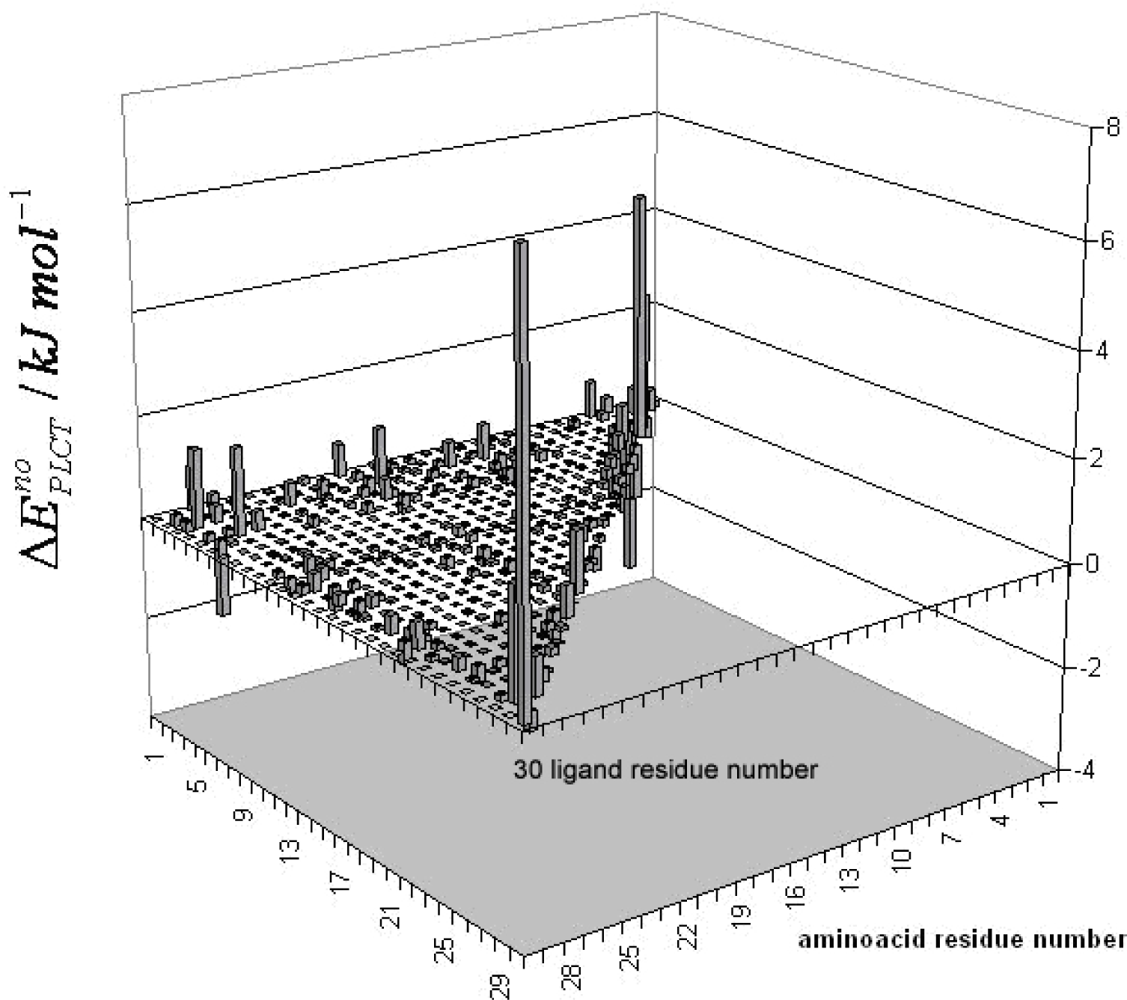
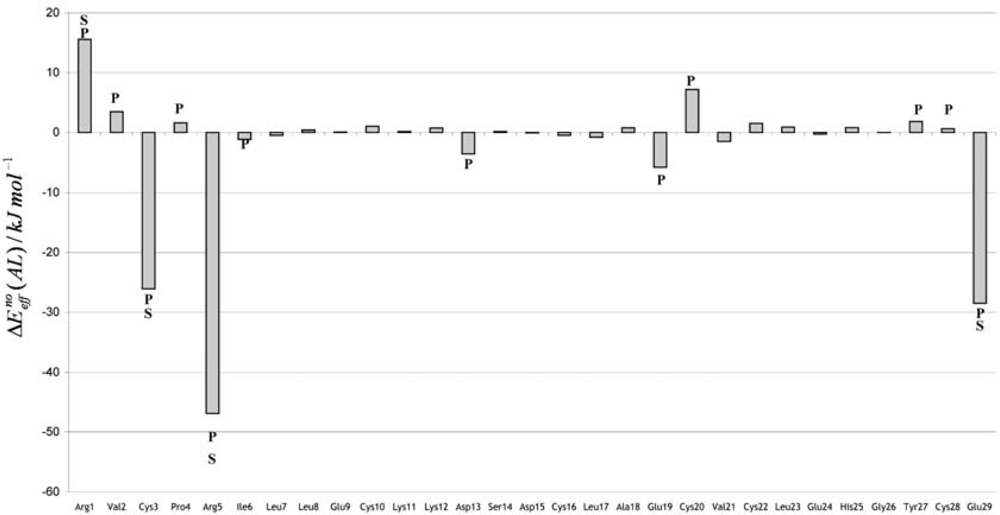
3. Discussion
4. Conclusions
Acknowledgments
Appendix A
Detailed Description of the Physically Meaningful Decomposition
Appendix B
Detailed description and justification of the pair-wise decomposition
References and Notes
- Kuntz, ID. Structure-based strategies for drug design and discovery. Science 1992, 257, 1078–1082. [Google Scholar]
- Netzeva, TI; Aptula, AO; Benfenati, E; Cronin, MTD; Gini, G; Lessigiarska, I; Maran, U; Vracko, M; Schüürmann, G. Description of the Electronic Structure of Organic Chemicals Using Semiempirical and Ab Initio Methods for Development of Toxicological QSARs. J. Chem. Inf. Model 2005, 45, 106–114. [Google Scholar]
- Weiner, PK; Kollman, PA. AMBER: Assisted model building with energy refinement. A general program for modeling molecules and their interactions. J. Comp. Chem 1981, 2, 287–303. [Google Scholar]
- Weiner, SJ; Kollman, PA; Case, DA; Singh, UC; Ghio, C; Alagona, G; Profeta, S; Weiner, PK. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc 1984, 106, 765–784. [Google Scholar]
- Cornell, WD; Cieplak, P; Bayly, CI; Gould, IR; Merz, KM; Ferguson, DM; Spellmeyer, DC; Fox, T; Caldwell, JW; Kollman, PA. A Second Generation Force Field for the Simulation of Proteins. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- Brooks, BR; Bruccoleri, RF; Olafson, BD; States, DJ; Swaminathan, S; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comp. Chem 1983, 4, 187–217. [Google Scholar]
- MacKerell, AD, Jr; Wiorkiwicz-Kuczera, J; Karplus, M. An all-atom empirical energy function for the simulation of nucleic acids. J. Am. Chem Soc 1995, 117, 11946–11975. [Google Scholar]
- Raha, K; Merz, KM, Jr. Large-Scale Validation of a Quantum Mechanics Based Scoring Function: Predicting the Binding Affinity and the Binding Mode of a Diverse Set of Protein-Ligand Complexes. J. Med. Chem 2005, 48, 4558–4575. [Google Scholar]
- Lipkowitz, KB; Boyd, DB. Methods and Applications of Combined Quantum Mechanical and Molecular Mechanical Potentials. Rev. Computat. Chem 1996, 7, 119–185. [Google Scholar]
- Friesner, RA; Guallar, V. Ab Initio Quantum Chemical and Mixed Quantum Mechanics/Molecular Mechanics (QM/MM) Methods for Studying Enzymatic Catalysis. Annu. Rev. Phys. Chem 2005, 56, 389–427. [Google Scholar]
- Melo, A; Ramos, M. A new partitioning scheme for molecular interacting systems within a multiconfigurational or monoconfigurational Hartree-Fock formalism. J. Int. J. Quantum Chem 1999, 72, 157–176. [Google Scholar]
- Dixon, SL; Merz, KM, Jr. Combined quantum mechanical/molecular mechanical methodologies applied to biomolecular systems. J. Chem. Phys 1996, 104, 6643–6649. [Google Scholar]
- Mayer, I; Salvador, P. Overlap populations, bond orders and valences for ‘fuzzy’ atoms. Chem. Phys. Lett 2004, 383, 368–375. [Google Scholar]
- Putz, MV; Lacrămă, AM. Enzymatic control of the bio-inspired nanomaterials at the spectroscopic level. J. Optoel. Adv. Mat 2007, 9, 2529–2534. [Google Scholar]
- Putz, MV; Lacrămă, AM; Ostafe, V. Introducing logistic enzyme kinetics. J. Optoel. Adv. Mat 2007, 9, 2910–2916. [Google Scholar]
- Putz, MV; Lacrămă, AM; Ostafe, V. Full Analytic Progress Curves of the Enzymic Reactions in Vitro. Int. J. Mol. Sci 2006, 7, 469–484. [Google Scholar]
- Carvalho, ARF; Melo, A. Energy partitioning in association processes. Int J Quantum Chem 2005, 104, 240–248. [Google Scholar]
- Carvalho, ARF; Melo, A. Natural inhibitors of proteases – pharmacological target for destabilization/stabilization of the protease/inhibitor complex. Fund. Clin. Pharmacol. 2004, 18. [Google Scholar]
- Wynn, R; Laskowski, M, Jr. Inhibition of human β-factor XIIA by squash family serine proteinase inhibitors. Biochem. Biophys. Res. Commun 1990, 166, 1406–1410. [Google Scholar]
- Mitchell, EP; Garman, EF. Flash freezing of protein crystals: investigation of mosaic spread and diffraction limit with variation of cryoprotectant concentration. J. Appl. Cryst 1994, 27, 1070–1074. [Google Scholar]
- Case, DA; et al. AMBER 8; University of California: San Francisco, 2004. [Google Scholar]
- Mulliken, RS; Mulliken, RS. Electronic Population Analysis on LCAO-MO Molecular Wave Functions. I. J. Chem. Phys 1955, 23, 1833–1840. [Google Scholar]
- Besler, HB; Merz, MK; Kollman, PA. Atomic Charges Derived from Semiempirical Methods. J. Comput. Chem 1990, 11, 431–439. [Google Scholar]
- Thaimattam, R; Tykarska, E; Bierzynski, A; Sheldrick, GM; Jaskolski, M. Atomic resolution structure of squash trypsin inhibitor: unexpected metal coordination. Acta Cryst. D 2002, 58, 1448–1461. [Google Scholar]
- Stewart, JJP. MOPAC 2002.
- Bredow, T; Jug, K. Theory and Range of Modern Semiempirical Molecular Orbital Methods. Theor. Chem. Acc 2005, 113, 1–14. [Google Scholar]
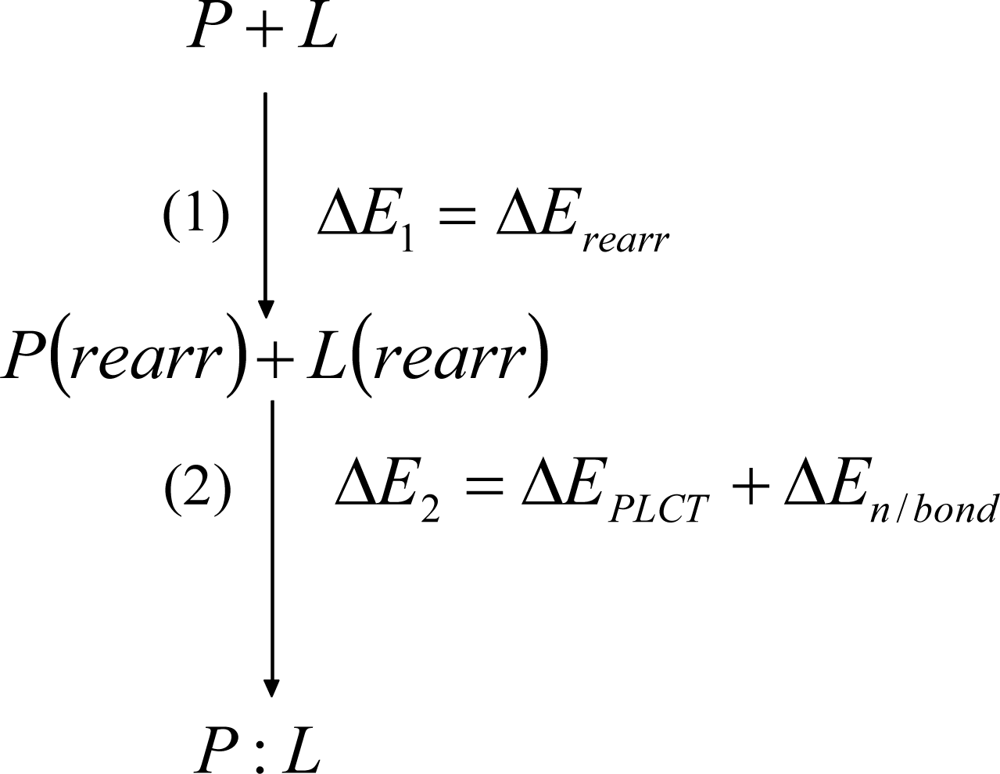



| ΔEno | ||||
|---|---|---|---|---|
| Protein | -
| 35.30
| 33.11
| -
|
| Ligand | -
| 33.14
| 16.89
| -
|
| Total | −147.50 | 68.45 | 50.00 | −29.05 |
| ΔEno | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Q | Ml | MK | |||||||
| 50.00 | 1.86 | 1.277 | 0.300 | 1.347 | 3.13 | 66.59 | −148.77 | - | - |
© 2008 by MDPI This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Carvalho, A.R.F.; Puga, A.T.; Melo, A. Exact and Effective Pair-Wise Potential for Protein-Ligand Interactions Obtained from a Semiempirical Energy Partition. Int. J. Mol. Sci. 2008, 9, 1652-1664. https://doi.org/10.3390/ijms9091652
Carvalho ARF, Puga AT, Melo A. Exact and Effective Pair-Wise Potential for Protein-Ligand Interactions Obtained from a Semiempirical Energy Partition. International Journal of Molecular Sciences. 2008; 9(9):1652-1664. https://doi.org/10.3390/ijms9091652
Chicago/Turabian StyleCarvalho, Alexandre R. F., André T. Puga, and André Melo. 2008. "Exact and Effective Pair-Wise Potential for Protein-Ligand Interactions Obtained from a Semiempirical Energy Partition" International Journal of Molecular Sciences 9, no. 9: 1652-1664. https://doi.org/10.3390/ijms9091652





