PI Polynomial of V-Phenylenic Nanotubes and Nanotori
Abstract
:1. Introduction
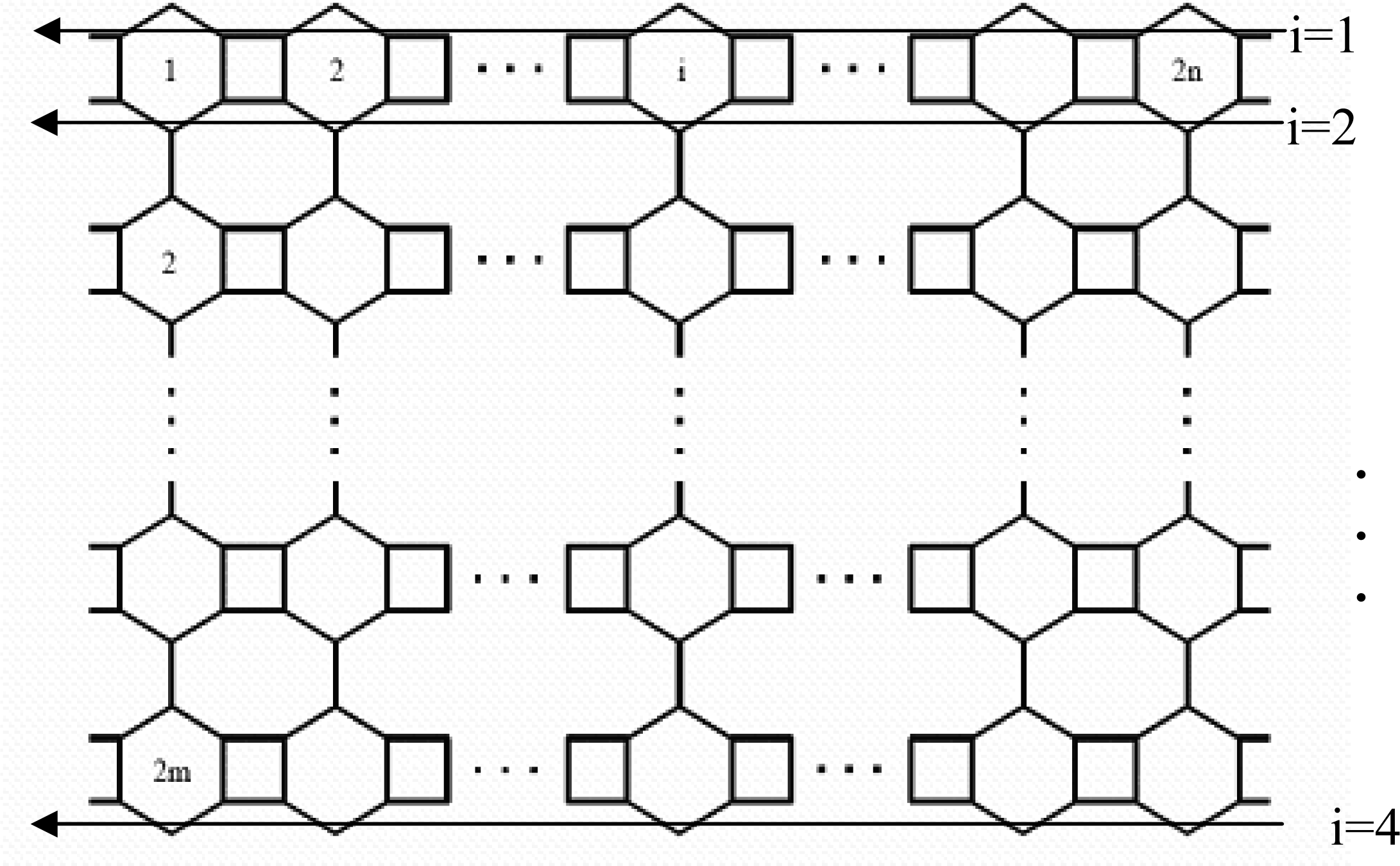
2. Results and Discussion
References and Notes
- Wiener, H. Structural determination of the paraffine boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar]
- Hosoya, H. On some counting polynomials in chemistry. Disc. Appl. Math. 1988, 19, 239–257. [Google Scholar]
- Khadikar, PV. On a novel structural descriptor PI index. Nat. Acad. Sci. Lett. 2000, 23, 113–118. [Google Scholar]
- Khadikar, PV; Karmarkar, S; Agrawal, VK. PI index of polyacenes and its use in developing QSPR. Nat. Acad. Sci. Lett. 2000, 23, 124–128. [Google Scholar]
- Ashrafi, AR; Manoochehrian, B; Yousefi-Azari, H. On the PI polynomial of a graph. Util. Math. 2006, 71, 97–108. [Google Scholar]
- Manoochehrian, B; Yousefi-Azari, H; Ashrafi, AR. PI polynomial of some benzenoid graphs. MATCH Commun. Math. Comput. Chem. 2007, 57, 653–664. [Google Scholar]
- Diudea, MV. Hosoya Polynomial in Tori. MATCH Commun. Math. Comput. Chem. 2002, 45, 109–122. [Google Scholar]
- Konstantinova, EV; Diudea, MV. The Wiener polynomial derivatives and other topological indexes in chemical research. Croat. Chem. Acta. 2000, 73, 383–403. [Google Scholar]
- Gutman, I; Klavzar, S; Petkovsek, ME; Zigert, P. On Hosoya Polynomials of Benzenoid Graphs. MATCH Commun. Math. Comput. Chem. 2001, 43, 49–66. [Google Scholar]
- Shoujun, X; Heping, Z. Hosoya polynomials of armchair open-ended nanotubes. Int. J. Quantum Chem. 2007, 107, 586–596. [Google Scholar]
- Cameron, PJ. Combinatorics: Topics, Techniques, Algorithms; Cambridge University Press: Cambridge, 1994; pp. 1–50. [Google Scholar]
- Trinajstic, N. Chemical graph theory, 2nd ed; CRC Press: Boca Raton, FL, 1992; pp. 20–75. [Google Scholar]
- Diudea, MV. Phenylenic and naphthylenic tori. Fuller. Nanotub. Carbon Nanostruct. 2002, 10, 273–292. [Google Scholar]
- Ashrafi, AR; Loghman, A. Padmakar-Ivan Index of TUC4C8(S) Nanotubes. J. Comput. Theor. Nanosci. 2006, 3, 378–381. [Google Scholar]

Share and Cite
Alamian, V.; Bahrami, A.; Edalatzadeh, B. PI Polynomial of V-Phenylenic Nanotubes and Nanotori. Int. J. Mol. Sci. 2008, 9, 229-234. https://doi.org/10.3390/ijms9030229
Alamian V, Bahrami A, Edalatzadeh B. PI Polynomial of V-Phenylenic Nanotubes and Nanotori. International Journal of Molecular Sciences. 2008; 9(3):229-234. https://doi.org/10.3390/ijms9030229
Chicago/Turabian StyleAlamian, Vahid, Amir Bahrami, and Behrooz Edalatzadeh. 2008. "PI Polynomial of V-Phenylenic Nanotubes and Nanotori" International Journal of Molecular Sciences 9, no. 3: 229-234. https://doi.org/10.3390/ijms9030229



