Schultz Index of Armchair Polyhex Nanotubes
Abstract
:1. Introduction
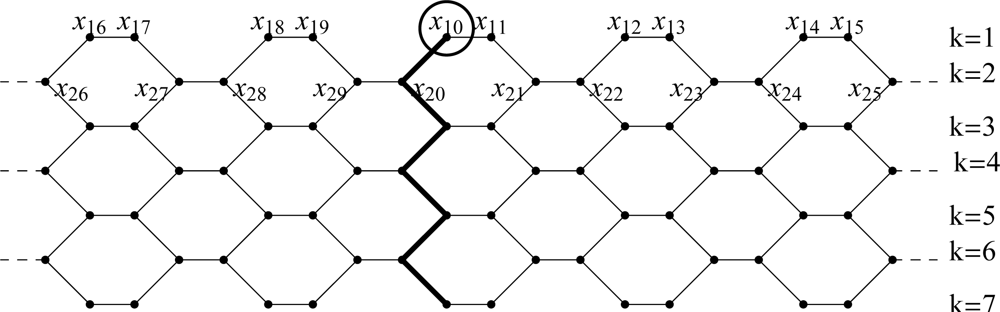
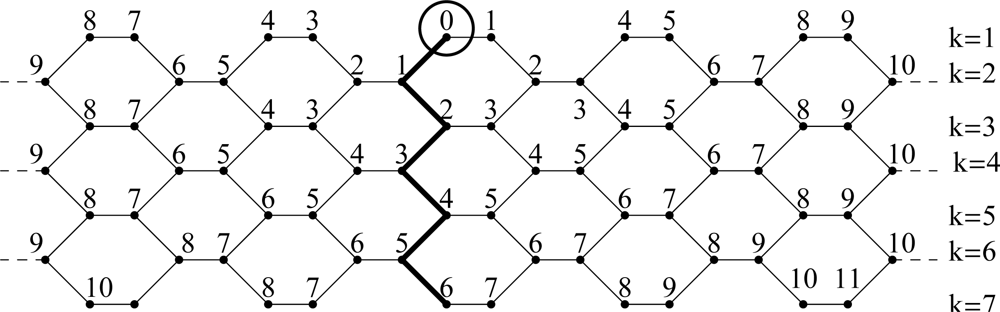
2. Schultz index of armchair polyhex nanotubes
3. Experimental Section
4. Appendix
Acknowledgments
References and Notes
- Wiener, H. Structural Determination of Paraffin Boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar]
- Wiener, H. Correlation of Heats of Isomerization and differences in heats of vaporization of isomers among the paraffin Hydrocarbons. J. Am. Chem. Soc. 1947, 69, 2636–2638. [Google Scholar]
- Wiener, H. Influence of Interatomic Forces on Paraffin Properties. J. Chem. Phys. 1947, 15, 766–766. [Google Scholar]
- Balaban, AT; Devillers, J (Eds.) Topological Indices and Related Descriptors in QSAR and QSPR 1999.
- Diudea, MV. Indices of Reciprocal Properties or Harary Indices. J. Chem. Inf. Comput. Sci. 1997, 37, 292–299. [Google Scholar]
- Gutman, I; Polansky, OE. Mathematical Concepts in Organic Chemistry 1986.
- Gutman, I. Relation Between Hyper-Wiener and Wiener Index. Chem. Phys. Lett. 2002, 364, 352–356. [Google Scholar]
- Gutman, I; Furtula, B. Hyper-Wiener Index vs. Wiener index. Monatshefte für Chemie 2003, 134, 975–981. [Google Scholar]
- Randić, M; Trinajstić, N. In Search for Graph Invariants of Chemical Interest. J. Mol. Struct. (THEOCHEM) 1993, 300, 551–571. [Google Scholar]
- Todeschini, R; Consonni, V. Handbook of Molecular Descriptors 2000.
- Schultz, HP. Topological organic chemistry 1. Graph Theory and Topological Indices of Alkanes. J. Chem. Inf. Comput. Sci. 1989, 29, 227–228. [Google Scholar]
- Mihalić, Z; Nikolić, S; Trinajstić, N. Comparative Study of Molecular Descriptors Derived from the Distance Matrix. J. Chem. Inf. Comput. Sci. 1992, 32, 28–37. [Google Scholar]
- Müller, WR; Szymanski, K; Knop, JV; Trinajstić, N. Mulecular Topological Index. J. Chem. Inf. Comput. Sci 1990, 30, 160–163. [Google Scholar]
- Schultz, HP; Schultz, TP. Topological Organic Chemistry. 6. Graph Theory and Topological Indices of Cycloalkanes. J. Chem. Inf. Comput. Sci. 1993, 33, 240–243. [Google Scholar]
- Schultz, HP; Schultz, TP. Topological Organic Chemistry. 7. Graph Theory and Topological Indices of Cycloalkanes. J. Chem. Inf. Comput. Sci 1993, 33, 863–867. [Google Scholar]
- Gutman, I; Klavžar, S. Comparison of the Schultz Molecular Topological Index with the Wiener Index. J. Chem. Inf. Comput. Sci 1996, 36, 1001–1003. [Google Scholar]
- Gutman, I; Klavžar, S. Bounds for the Schultz Molecular Topological Index of Benzenoid Systems in Terms of the Wiener Index. J. Chem. Inf. Comput. Sci. 1997, 37, 741–744. [Google Scholar]
- Plavšić, D; Nikolić, S; Trinajstić, N; Klein, DJ. Relation between the Wiener Index and the Schultz Index for Several Classes of Chemical Graphs. Croat. Chem. Acta 1993, 66, 345–353. [Google Scholar]
- Diudea, MV; Stefu, M; Parv, B; John, PE. Wiener Index of Armchair Polyhex Nanotubes. Croat. Chem. Acta 2004, 77, 111–115. [Google Scholar]
- Ping Lu, J. Elastic Properties of Carbon Nanotubes and Nanoropes. Phys. Rev. Lett 1997, 79, 1297–1300. [Google Scholar]
- Wong, EW; Sheehan, PE; Lieber, CM. Nanobeam mechanics: Elasticity, strength, and toughness of nanorods and nanotubes. Science 1997, 277, 1971–1975. [Google Scholar]
- Heck, A. Introduction to Maple 2003.
| p | q | S(G) | p | q | S(G) |
|---|---|---|---|---|---|
| 6 | 2 | 6912 | 5 | 2 | 4000 |
| 6 | 3 | 18366 | 5 | 3 | 10650 |
| 6 | 4 | 35424 | 5 | 4 | 20720 |
| 6 | 5 | 58656 | 9 | 5 | 193266 |
| 10 | 2 | 32000 | 9 | 6 | 288432 |
| 10 | 5 | 264160 | 9 | 7 | 404514 |
| 10 | 6 | 393440 | 9 | 8 | 542880 |
| 10 | 7 | 550560 | 15 | 8 | 2425440 |
| 10 | 8 | 736960 | 15 | 7 | 1823310 |
| 10 | 9 | 954400 | 15 | 6 | 1310160 |
| p | q | S(G) | p | q | S(G) |
|---|---|---|---|---|---|
| 4 | 4 | 10816 | 3 | 4 | 4752 |
| 4 | 5 | 18304 | 3 | 5 | 8262 |
| 4 | 6 | 28352 | 3 | 6 | 13104 |
| 4 | 7 | 41344 | 3 | 7 | 19494 |
| 4 | 8 | 57664 | 3 | 8 | 27648 |
| 10 | 21 | 6810400 | 11 | 11 | 1954502 |
| 10 | 22 | 7641600 | 11 | 12 | 2371952 |
| 10 | 23 | 8536800 | 11 | 13 | 2839524 |
| 10 | 24 | 9498400 | 11 | 14 | 3359312 |
| 10 | 25 | 10528800 | 11 | 15 | 3935030 |
© 2008 by MDPI This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Eliasi, M.; Salehi, N. Schultz Index of Armchair Polyhex Nanotubes. Int. J. Mol. Sci. 2008, 9, 2016-2026. https://doi.org/10.3390/ijms9102016
Eliasi M, Salehi N. Schultz Index of Armchair Polyhex Nanotubes. International Journal of Molecular Sciences. 2008; 9(10):2016-2026. https://doi.org/10.3390/ijms9102016
Chicago/Turabian StyleEliasi, Mehdi, and Nafiseh Salehi. 2008. "Schultz Index of Armchair Polyhex Nanotubes" International Journal of Molecular Sciences 9, no. 10: 2016-2026. https://doi.org/10.3390/ijms9102016