Self-assembly and Fractal Feature of Chitosan and Its Conjugate with Metal Ions: Cu (II) / Ag (I)
Abstract
:1. Introduction
2. Results and discussion
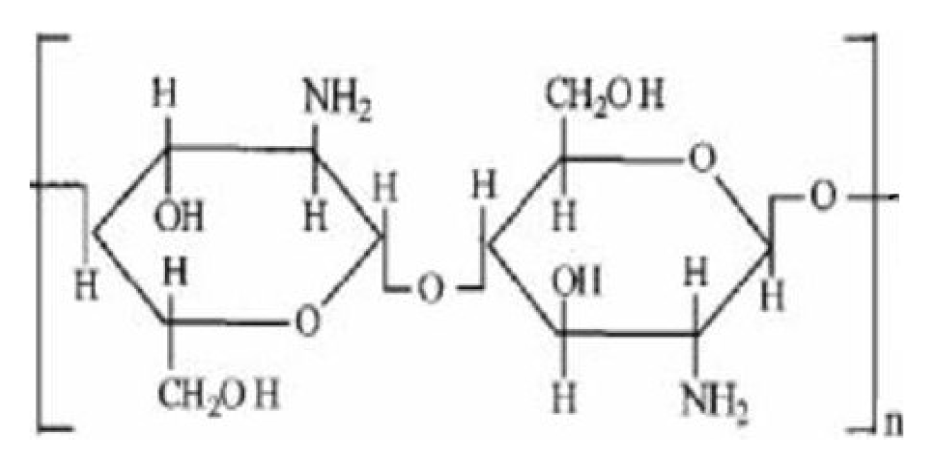
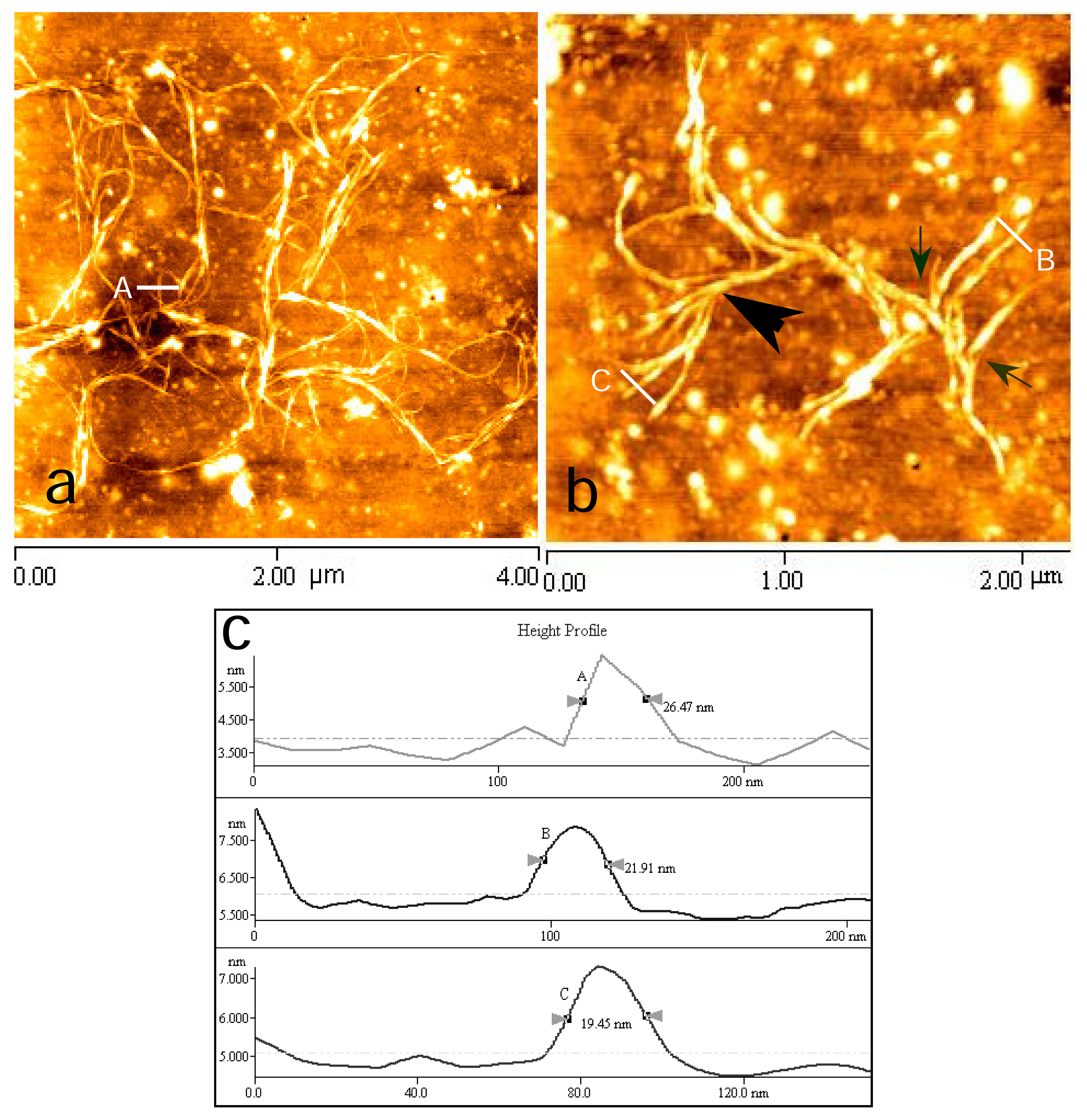
2.1 Chitosan molecule chain
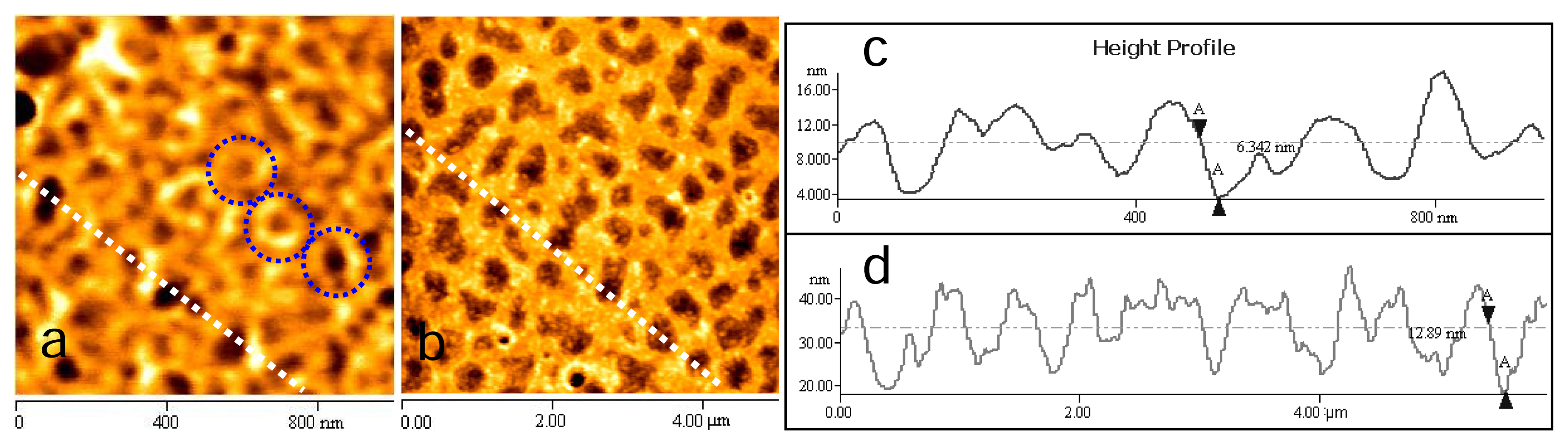
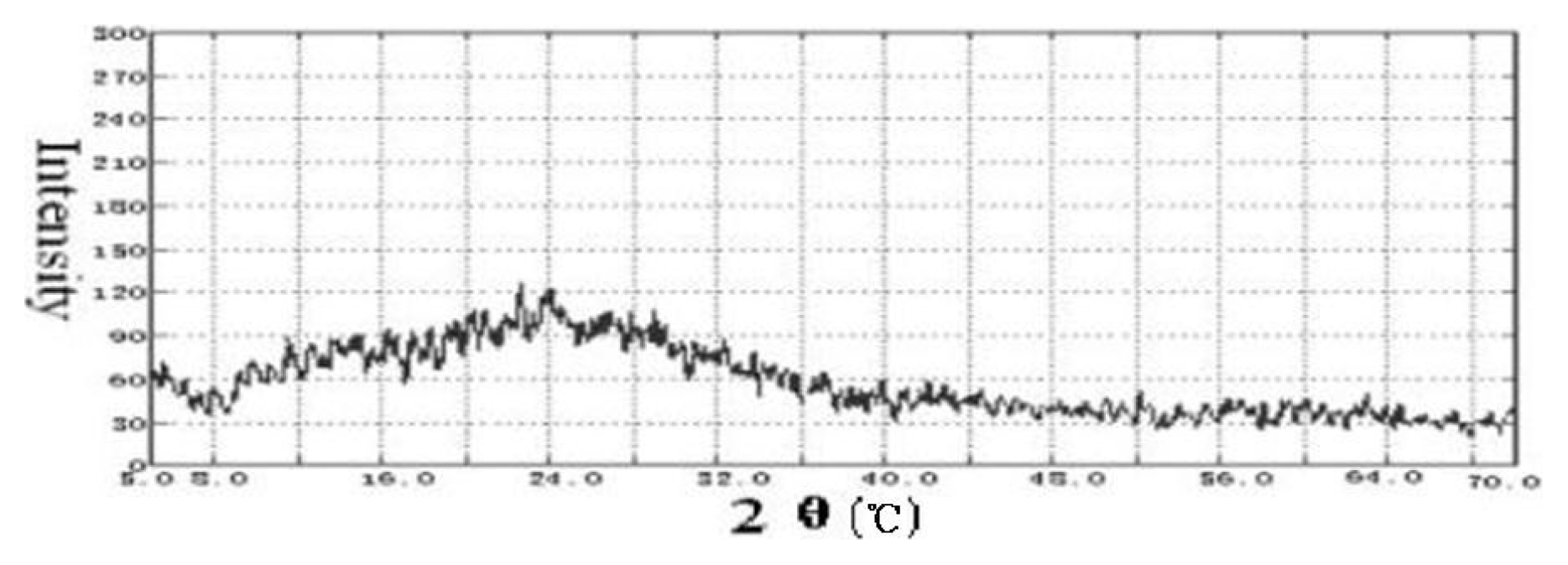
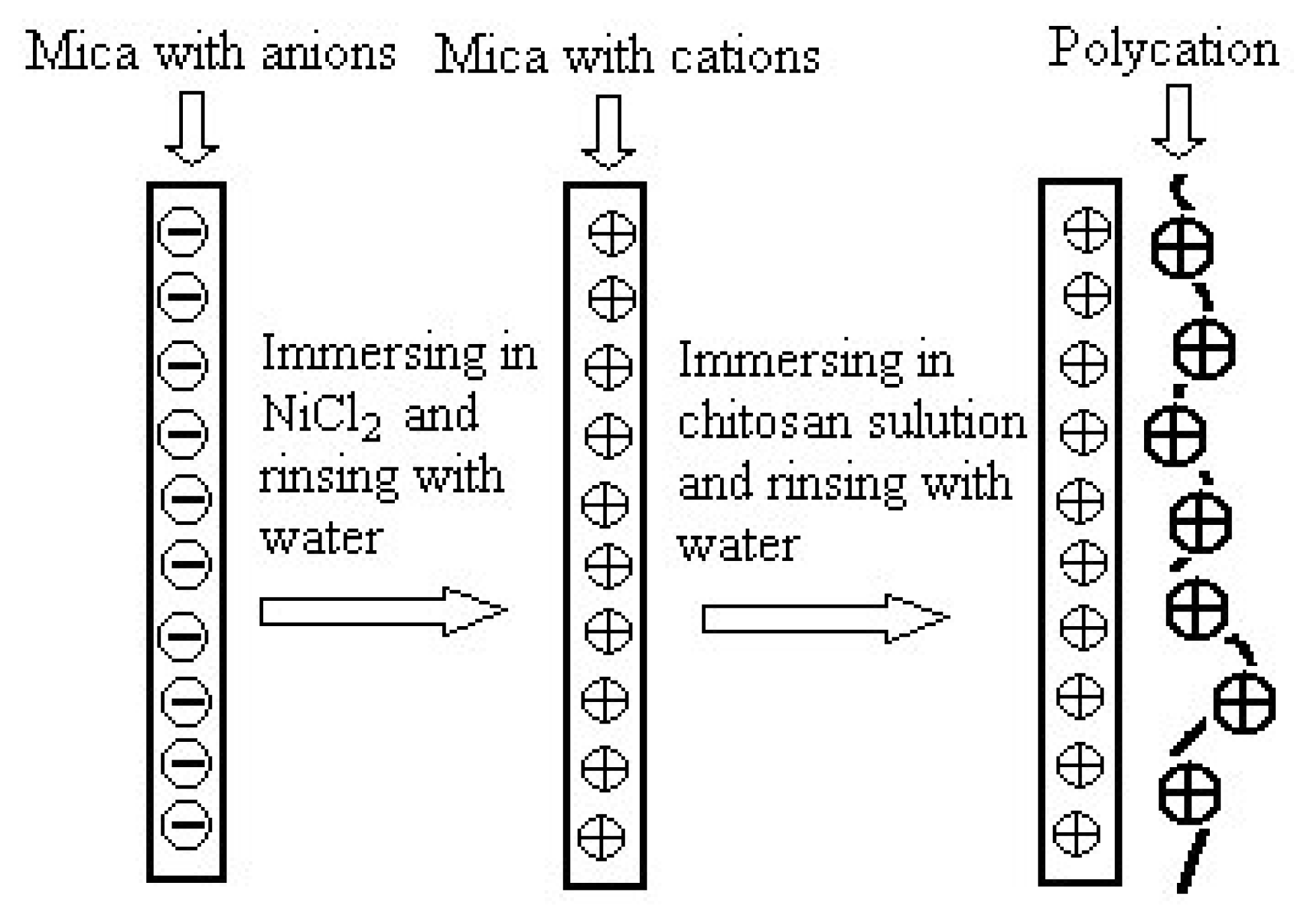
2.2 Chitosan film
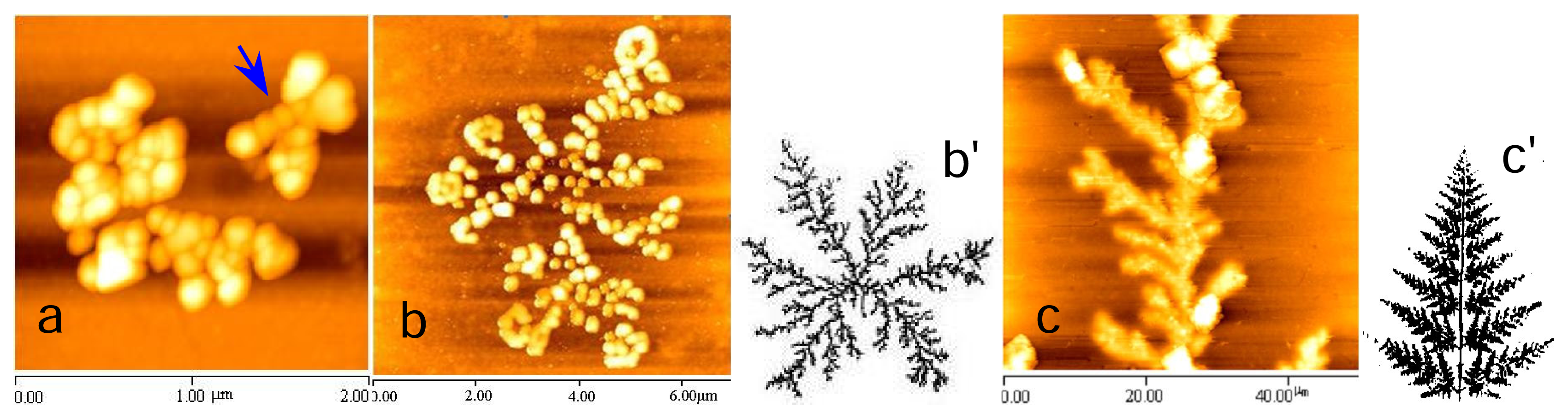
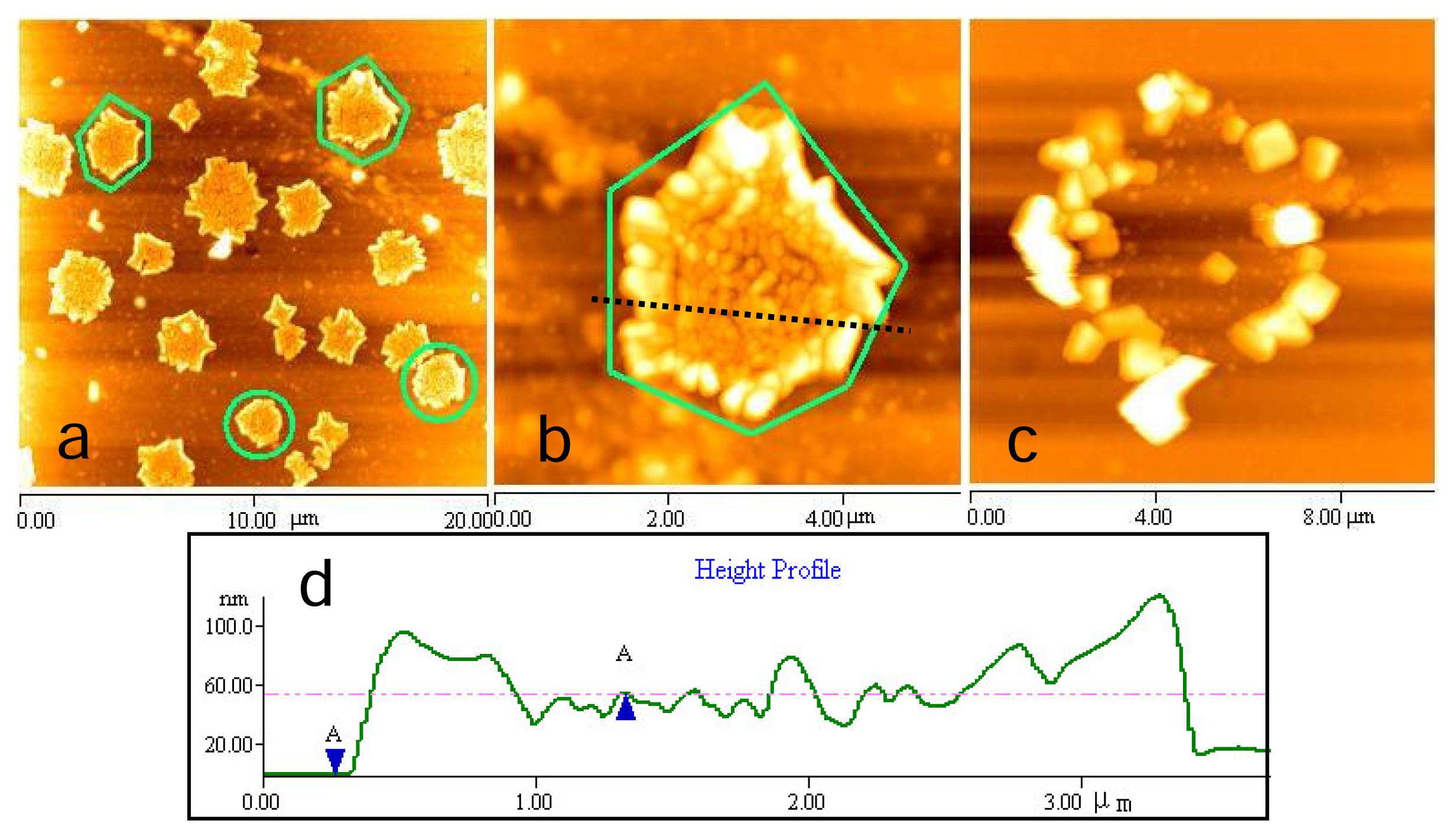
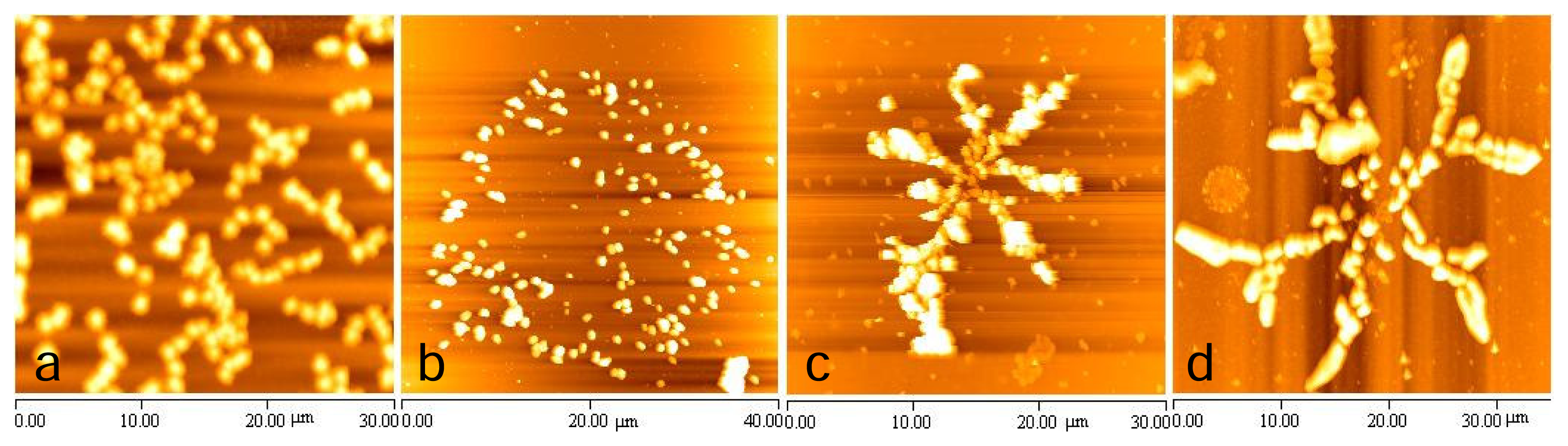
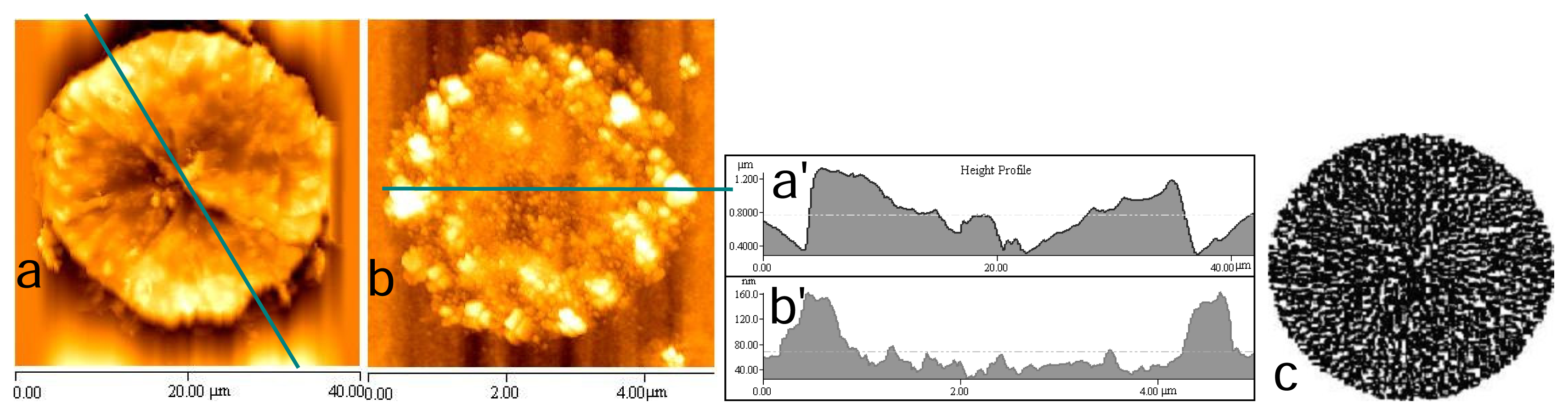
2.3 Fractal structures of chitosan
2.4 Liquid crystal feature of chitosan
2.5 The self-assembly and fractal feature of Cu (II), Ag (I)-chitosan conjugates
3. Conclusion
4. Experimental
Material and Reagent
Sample preparation
Atomic force microscope imaging
Fractal dimensional calculation
Acknowledgements
References
- Nauta, K.; Miller, R.E. Nonequilibrium self-assembly of long chains of polar molecules in superfluid helium. Science 1999, 283, 1895–1897. [Google Scholar]
- Serizawa, T.; Yamaguchi, M.; Akashi, M. Alternating Bioactivity of Polymeric Layer-by-Layer Assemblies: Anticoagulation vs Procoagulation of Human Blood. Biomacromolecules 2002, 3, 724–731. [Google Scholar]
- Yi, H.; Wu, L.Q.; Sumner, J.J.; Gillespie, J.B.; Payne, G.F.; Bentley, W.E. Chitosan Scaffolds for Biomolecular Assembly: Coupling Nucleic Acid Probes for Detecting Hybridization. Biotechnol. Bioeng 2003, 83, 646–652. [Google Scholar]
- Cai, J.Y.; Chen, Y.; Xu, Q.C.; Chen, Y.; Zhao, T.; Wang, X.Y.; Xia, K. Atomic Force Microscope Imaging of the Aggregation of Mouse Immunoglobulin G Molecules. Molecules 2003, 8, 86–91. [Google Scholar]
- Nilsson, K.P.R.; Rydberg, J.; Baltzer, L.; Inganas, O. Twisting macromolecular chains: Self-assembly of a chiral supermolecule from nonchiral polythiophene polyanions and random-coil synthetic peptides. PNAS 2004, 101, 11197–11202. [Google Scholar]
- Li, X.; Wei, X.L.; Husson, S.M. Thermodynamic Studies on the Adsorption of Fibronectin Adhesion-Promoting Peptide on Nanothin Films of Poly(2-vinylpyridine) by SPR. Biomacromolecules 2004, 5, 869–876. [Google Scholar]
- Chen, Y.; Cai, J.Y.; Xu, Q.C.; Chen, Z.W. Atomic force bio-analytics of polymerization and aggregation of phycoerythrin-conjugated immunoglobulin G molecules. Mol. Immunol 2004, 41, 1247–1252. [Google Scholar]
- Yi, H.; Wu, L.Q.; Ghodssi, R.; Rubloff, G.W.; Payne, G.F.; Bentley, W.E. A Robust Technique for Assembly of Nucleic Acid Hybridization Chips Based on Electrochemically Templated Chitosan. Anal. Chem 2004, 76, 365–372. [Google Scholar]
- Feng, Q.; Zeng, G.C.; Yang, P.H.; Wang, C.X.; Cai, J.Y. Self-assembly and characterization of polyelectrolyte complex films of hyaluronic acid/chitosan. Colloids and Surfaces A. Physicochem Eng Aspects 2005, 257–258, 85–88. [Google Scholar]
- Shih, W.M.; Quispe, J.D.; Joyce, G.F. A 1.7-kilobase single-stranded DNA that folds into a nanoscale octahedron. Nature 2004, 427, 618–621. [Google Scholar]
- Dang, J.M.; Sun, D.D.; Shin-Ya, Y.; Sieber, A.N.; Kostuik, J.P.; Leong, K.W. Temperature-responsive hydroxybutyl chitosan for the culture of mesenchymal stem cells and intervertebral disk cells. Biomaterials 2005. [Google Scholar]
- Haque, T.; Chen, H.; Ouyang, W.; Martoni, C.; Lawuyi, B.; Urbanska, A.; Prakash, S. Investigation of a new microcapsule membrane combining alginate; chitosan; polyethylene glycol and poly-L-lysine for cell transplantation applications. Int. J. Artif. Organs 2005, 28, 631–637. [Google Scholar]
- Funakoshi, T.; Majima, T.; Iwasaki, N. Application of tissue engineering techniques for rotator cuff regeneration using a chitosan-based hyaluronan hybrid fiber scaffold. Am. J. Sports Med 2005, 33, 1193–1201. [Google Scholar]
- Zheng, C.H.; Liang, W.Q.; Li, F. Optimization and characterization of chitosan-coated alginate microcapsules containing albumin. Pharmazie 2005, 60, 434–438. [Google Scholar]
- Matsumoto, T.; Kawai, M.; Masuda, T. Rheological properties and fractal structure of concentrated polyion complexes of chitosan and alginate. Biorheology 1993, 30, 435–441. [Google Scholar]
- Zhang, C.; Qineng, P.; Zhang, H.J. Self-assembly and characterization of paclitaxel-loaded N-octyl- O-sulfate chitosan micellar system. Colloid Surface B. Biointerfaces 2004, 39, 69–75. [Google Scholar]
- Liu, Y.J.; Li, Y.L.; Liu, S.C.; Li, J.; Yao, S.Z. Monitoring the self-assembly of chitosan/glutaraldehyde/cysteamine/Au-colloid and the binding of human serum albumin with hesperidin. Biomaterials 2004, 25, 5725–5733. [Google Scholar]
- Montembault, A.; Viton, C.; Domard, A. Rheometric study of the gelation of chitosan in a hydroalcoholic medium. Biomaterials 2005, 26, 1633–1643. [Google Scholar]
- Lee, J.B.; Kim, D.J.; Choi, J.W.; Koo, K.K. Formation of a protein monomolecular layer by a combined technique of LB and SA methods. Colloid Surface B. Biointerfaces 2005, 41, 163–168. [Google Scholar]
- Lvov, Y.; Onda, M.; Ariga, K. Ultrathin films of charged polysaccharides assembled alternately with linear polyions. J. Biomater. Sci. Polym. Ed 1998, 9, 345–355. [Google Scholar]
- Liu, H.; Mao, J.; Yao, K.; Yang, G.; Cui, L.; Cao, Y. A study on a chitosan-gelatin-hyaluronic acid scaffold as artificial skin in vitro and its tissue engineering applications. J. Biomater. Sci. Polym. Ed 2004, 15, 25–40. [Google Scholar]
- Ma, L.; Gao, C.; Mao, Z.; Zhou, J.; Shen, J.; Hu, X.; Han, C. Collagen/chitosan porous scaffolds with improved biostability for skin tissue engineering. Biomaterials 2003, 24, 4833–4841. [Google Scholar]
- Dureja, H.; Tiwary, A.K.; Gupta, S. Simulation of skin permeability in chitosan membranes. Int. J. Pharm 2001, 213, 193–198. [Google Scholar]
- Hirano, S.; Tobetto, K.; Noishiki, Y. SEM ultrastructure studies of N-acyl- and N-benzylidene-chitosan and chitosan membranes. J. Biomed. Mater. Res 1981, 15, 903–911. [Google Scholar]
- Williams, N. Fractal Geometry Gets the Measure of Life’s Scales. Science 1997, 276, 34. [Google Scholar]
- Groebe, G.; Marsch, W.C.; Holzmann, H. The fractals theory and its significance for dermatology. Hautarzt 1990, 41, 388–391. [Google Scholar]
- Losa, G.A.; Nonnenmacher, T.F. Self-similarity and fractal irregularity in pathologic tissues. Mod. Pathol 1996, 9, 174–182. [Google Scholar]
- Maier, T. Chaos theory and complexity in psychiatry. Psychother. Psychosom. Med. Psychol 1998, 48, 314–317. [Google Scholar]
- Tang, S.; Ma, Y.; Sebastine, I.M. The fractal nature of Escherichia coli biological flocs. Colloids and Surfaces B. Biointerfaces 2001, 20, 211–218. [Google Scholar]
- Mandelbrot, B.B.; Kol, B.; Aharony, A. Angular gaps in radial diffusion-limited aggregation: two fractal dimensions and nontransient deviations from linear self-similarity. Phys. Rev. Lett 2002, 88, 055501. [Google Scholar]
- Rout, D.K.; Barman, S.P.; Pulapura, S.K.; Gross, R.A. Cholesteric Mesophases Formed by the Modified Biological Macromolecules 3; 6-O-(Butyl Carbamate)-N-phthaloyl Chitosan. Macromolecules 1994, 27, 2945–2949. [Google Scholar]
- Murray, S.B.; Neville, A.C. The role of pH; temperature and nucleation in the formation of cholesteric liquid crystal spherulites from chitin and chitosan. Int. J. Biol. Macromol 1998, 22, 137–144. [Google Scholar]
- Reiniger, M.; Basnar, B.; Friedbacher, G.; Schleberger, M. Atomic force microscopy of thin organic films on silicon in ultrahigh vacuum and under ambient conditions. Surf. Interface Anal 2002, 33, 85–88. [Google Scholar]
- Nittrnann, J.; Stanley, H.E. Tip splitting without interfacial tension and dendritic growth patterns arising from molecular anisotropy. Nature 1986, 321, 663. [Google Scholar]
- Tokuyama, M.; Kawasaki, K. Fractal dimensions for diffusion-limited aggregation. Phys. Lett. A 1984, 100, 337–340. [Google Scholar]
© 2007 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Hu, Y.; Wu, Y.; Cai, J.; Ma, Y.; Wang, B.; Xia, K.; He, X. Self-assembly and Fractal Feature of Chitosan and Its Conjugate with Metal Ions: Cu (II) / Ag (I). Int. J. Mol. Sci. 2007, 8, 1-12. https://doi.org/10.3390/i8010001
Hu Y, Wu Y, Cai J, Ma Y, Wang B, Xia K, He X. Self-assembly and Fractal Feature of Chitosan and Its Conjugate with Metal Ions: Cu (II) / Ag (I). International Journal of Molecular Sciences. 2007; 8(1):1-12. https://doi.org/10.3390/i8010001
Chicago/Turabian StyleHu, Yi, Yangzhe Wu, Jiye Cai, Yufeng Ma, Bin Wang, Ke Xia, and Xiaoqing He. 2007. "Self-assembly and Fractal Feature of Chitosan and Its Conjugate with Metal Ions: Cu (II) / Ag (I)" International Journal of Molecular Sciences 8, no. 1: 1-12. https://doi.org/10.3390/i8010001



