Large Aberration Correction by Magnetic Fluid Deformable Mirror with Model-Based Wavefront Sensorless Control Algorithm
Abstract
1. Introduction
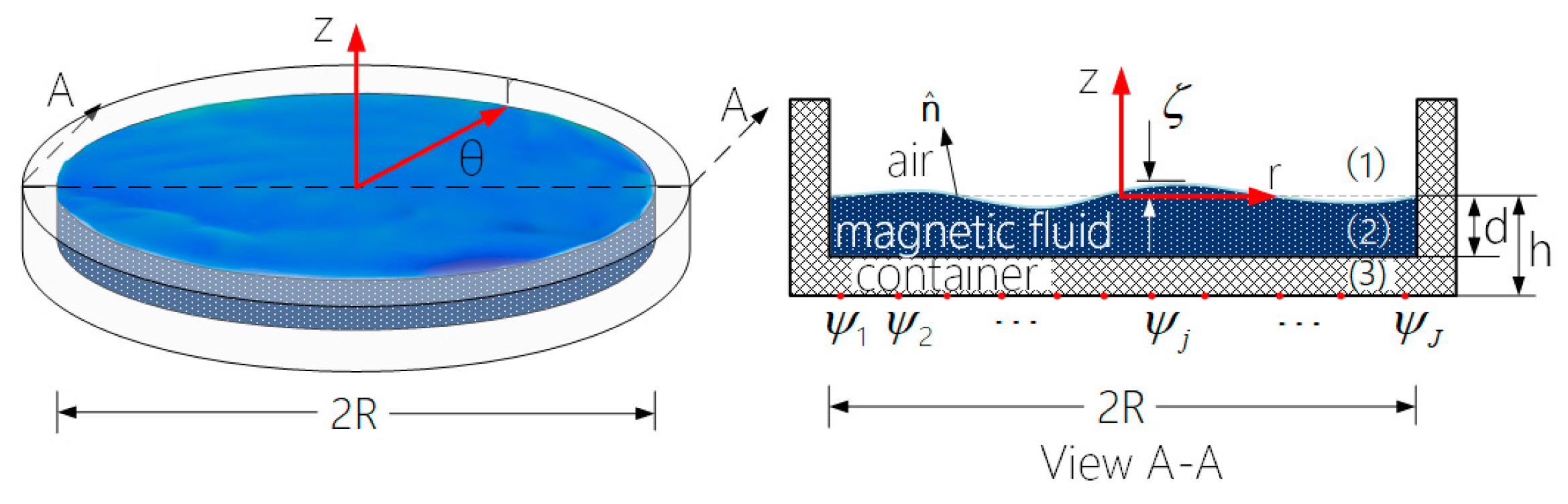
2. Modeling of Magnetic Fluid Deformable Mirror
3. The Model-Based Control Algorithm
3.1. Relationship Between the Second Moment of the Aberration Gradients and the Far-Field Intensity Distribution
3.2. Control Algorithm
3.2.1. Preprocessing
3.2.2. Iterative algorithm
- (1)
- Gather the corresponding far-field intensity with the wavefront from CCD, then calculate by Equation (52).
- (2)
- For each step , denote , where only the element of the row is and the others are zero. Bring the coefficient into the Equation (62) to obtain the optimal voltage for each Zernike mode and apply the voltage vector to the actuators of the MFDM. The wavefront shape introduced by the MFDM is then superimposed to the wavefront . Detect the far-field optical intensity of the modified wavefront aberration from CCD and then calculate according to Equation (52).
- (3)
- Repeating (2), obtain for each Zernike mode, respectively.
- (4)
- Compute according to Equation (54).
- (5)
- Obtain the corresponding Zernike parameters of the wavefront aberration based on Equation (53). Plug the control parameters into Equation (62) to obtain the voltage vector applied to the actuators of MFDM.
- (6)
- Regarding the residual wavefront aberration, repeat the iterative step (1)–(5) until the algorithm satisfies the termination conditions, such as certain number of iterations.
4. Experimental Verification
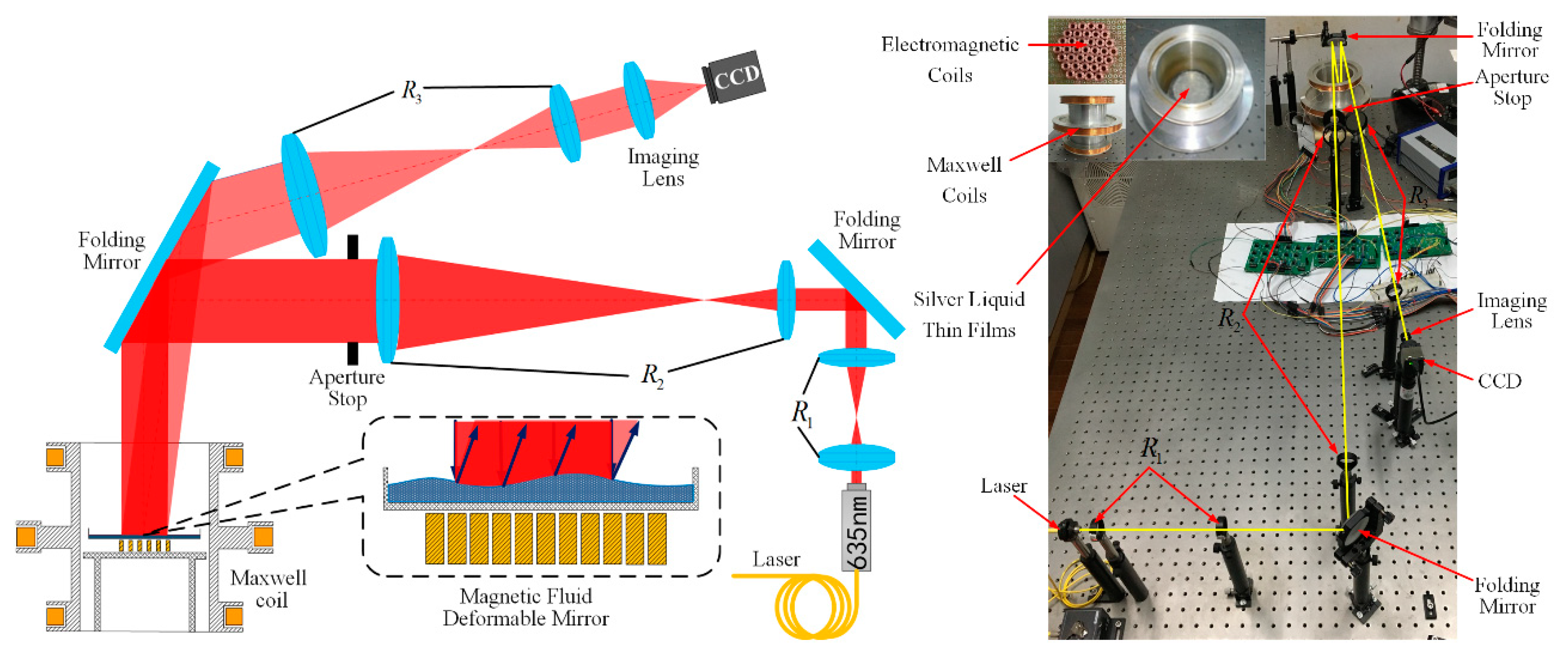
4.1. Experiment Setup
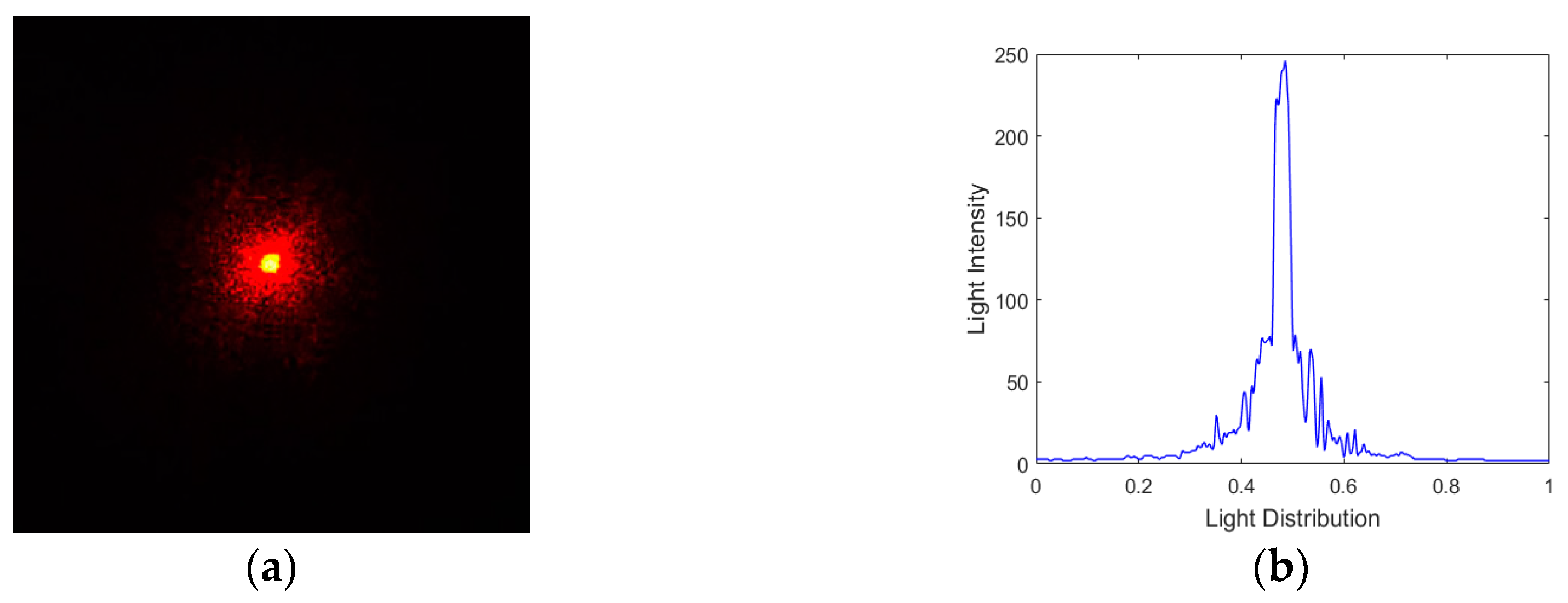
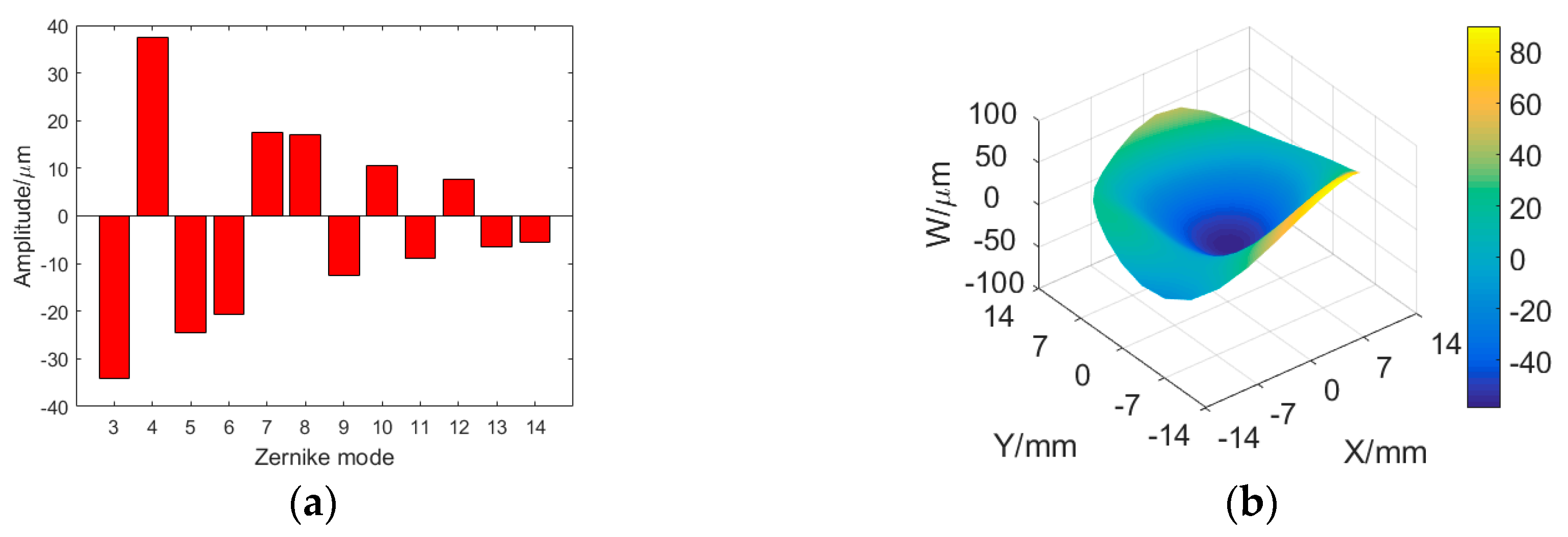
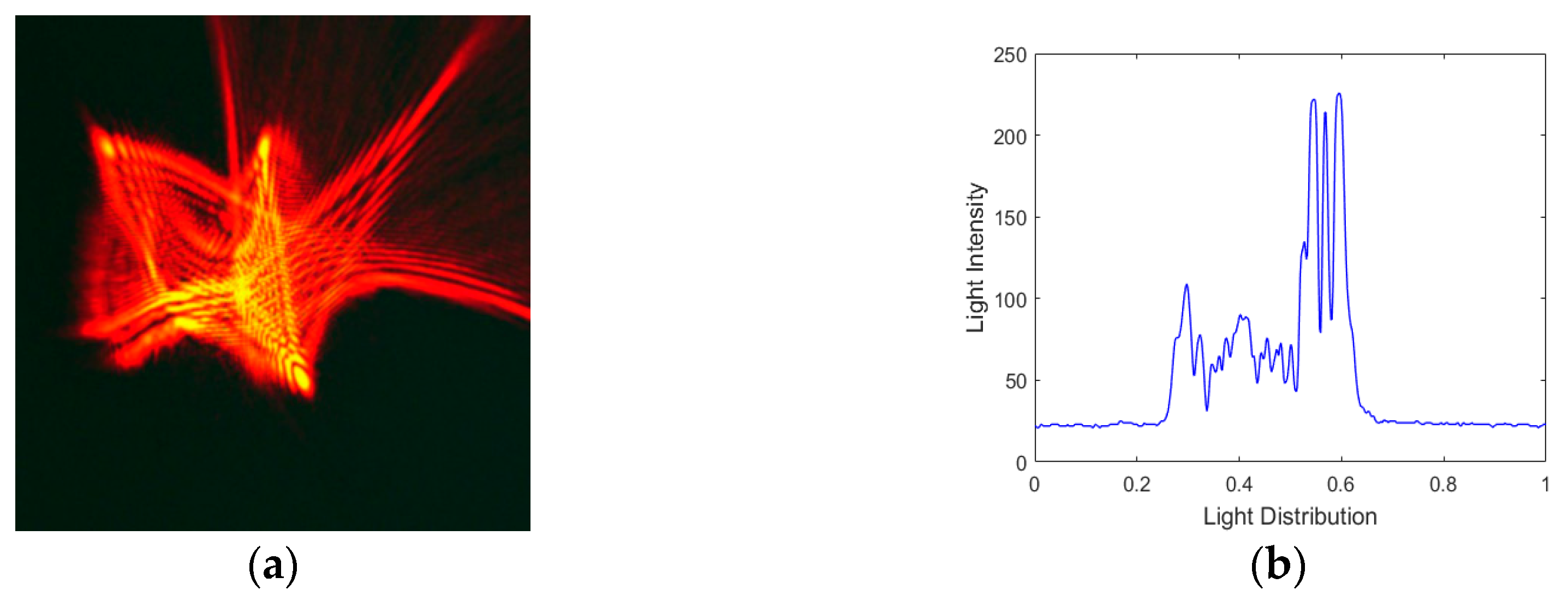
4.2. Experimental Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Brousseau, D.; Borra, E.F.; Thibault, S. Wavefront correction with a 37-actuator ferrofluid deformable mirror. Opt. Express 2007, 15, 18190–18199. [Google Scholar] [CrossRef] [PubMed]
- Fortin, M.; Piché, M.; Brousseau, D.; Thibault, S. Generation of optical Bessel beams with arbitrarily curved trajectories using a magnetic-liquid deformable mirror. Appl. Optics 2018, 57, 6135–6144. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Kong, X.; Zhang, Z.; Wu, J.; Wang, T.; Liu, M. Magnetic fluid deformable mirror with a two-layer layout of actuators. Micromachines 2017, 8, 72. [Google Scholar] [CrossRef]
- Matsumoto, N.; Konno, A.; Ohbayashi, Y.; Inoue, T.; Matsumoto, A.; Uchimura, K.; Kadomatsu, K.; Okazaki, S. Correction of spherical aberration in multi-focal multiphoton microscopy with spatial light modulator. Opt. Express 2017, 25, 7055–7068. [Google Scholar] [CrossRef] [PubMed]
- Starobrat, J.; Wilczynska, P.; Makowski, M. Aberration-corrected holographic projection on a two-dimensionally highly tilted spatial light modulator. Opt. Express 2019, 27, 19270–19281. [Google Scholar] [CrossRef]
- Cartella, A.; Bonora, S.; Först, M.; Cerullo, G.; Cavalleri, A.; Manzoni, C. Pulse shaping in the mid-infrared by a deformable mirror. Opt. Lett. 2014, 39, 1485–1488. [Google Scholar] [CrossRef] [PubMed]
- Turcotte, R.; Liang, Y.; Ji, N. Adaptive optical versus spherical aberration corrections for in vivo brain imaging. Biomed. Opt. Express 2017, 8, 3891–3902. [Google Scholar] [CrossRef] [PubMed]
- Žurauskas, M.; Dobbie, I.M.; Parton, R.M.; Phillips, M.A.; Göhler, A.; Davis, I.; Booth, M.J. IsoSense: frequency enhanced sensorless adaptive optics through structured illumination. Optica 2019, 6, 370–379. [Google Scholar] [CrossRef]
- Wu, J.; Wu, Z.; Kong, X.; Zhang, Z.; Liu, M. Magnetic fluid based deformable mirror for aberration correction of liquid telescope. Optoelectron. Lett. 2017, 13, 90–94. [Google Scholar] [CrossRef]
- Hickson, P. Hydrodynamics of rotating liquid mirrors. I. Synchronous disturbances. Appl. Optics 2006, 45, 8052–8062. [Google Scholar] [CrossRef]
- Yen, Y.; Lu, T.; Lee, Y.; Yu, C.; Tsai, Y.; Tseng, Y.; Chen, H. Highly reflective liquid mirrors: Exploring the effects of localized surface plasmon resonance and the arrangement of nanoparticles on metal liquid-like films. ACS Appl. Mater. Inter. 2014, 6, 4292–4300. [Google Scholar] [CrossRef]
- Ritcey, A.M.; Borra, E. Magnetically deformable liquid mirrors from surface films of silver nanoparticles. ChemPhysChem 2010, 11, 981–986. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Iqbal, A.; Amara, F.B. LMI-based multivariable PID controller design and its application to the control of the surface shape of magnetic fluid deformable mirrors. IEEE T. Contr. Syst. T. 2011, 19, 717–729. [Google Scholar] [CrossRef]
- Iqbal, A.; Wu, Z.; Amara, F.B. Mixed-Sensitivity H∞ Control of Magnetic-Fluid-Deformable Mirrors. IEEE/ASME T. Mech. 2010, 15, 548–556. [Google Scholar] [CrossRef]
- Tyson, R. Principles of Adaptive Optics; CRC press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Geng, C.; Luo, W.; Tan, Y.; Liu, H.; Mu, J.; Li, X. Experimental demonstration of using divergence cost-function in SPGD algorithm for coherent beam combining with tip/tilt control. Opt. Express 2013, 21, 25045–25055. [Google Scholar] [CrossRef]
- Yang, P.; Ao, M.; Liu, Y.; Xu, B.; Jiang, W. Intracavity transverse modes controlled by a genetic algorithm based on Zernike mode coefficients. Opt. Express 2007, 15, 17051–17062. [Google Scholar] [CrossRef]
- Fayyaz, Z.; Mohammadian, N.; Salimi, F.; Fatima, A.; Tabar, M.R.R.; Avanaki, M.R. Simulated annealing optimization in wavefront shaping controlled transmission. Appl. Optics 2018, 57, 6233–6242. [Google Scholar] [CrossRef] [PubMed]
- Facomprez, A.; Beaurepaire, E.; Débarre, D. Accuracy of correction in modal sensorless adaptive optics. Opt. Express 2012, 20, 2598–2612. [Google Scholar] [CrossRef]
- Song, H.; Fraanje, R.; Schitter, G.; Kroese, H.; Vdovin, G.; Verhaegen, M. Model-based aberration correction in a closed-loop wavefront-sensor-less adaptive optics system. Opt. Express 2010, 18, 24070–24084. [Google Scholar] [CrossRef]
- Linhai, H.; Rao, C. Wavefront sensorless adaptive optics: a general model-based approach. Opt. Express 2011, 19, 371–379. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Z.; Wu, J. Performance comparison of wavefront-sensorless adaptive optics systems by using of the focal plane. Int. J. Opt. 2015, 2015. [Google Scholar] [CrossRef][Green Version]
- Rosensweig, R.E. Ferrohydrodynamics; Dover Publications: New York, NY, USA, 2013. [Google Scholar]
- Wu, Z.; Iqbal, A.; Amara, F.B. Modeling and Control of Magnetic Fluid Deformable Mirrors for Adaptive Optics Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]




| Magnetic Fluid | Parameters |
|---|---|
| Saturation magnetization | 22 mT |
| Relative permeability | 2.89 |
| Density | 1190 kg/m3 |
| Viscosity | 3 cP |
| Thickness | 1 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Wang, Y.; Cao, Z.; Mbemba, D.; Iqbal, A.; Wu, Z. Large Aberration Correction by Magnetic Fluid Deformable Mirror with Model-Based Wavefront Sensorless Control Algorithm. Int. J. Mol. Sci. 2019, 20, 3697. https://doi.org/10.3390/ijms20153697
Wei X, Wang Y, Cao Z, Mbemba D, Iqbal A, Wu Z. Large Aberration Correction by Magnetic Fluid Deformable Mirror with Model-Based Wavefront Sensorless Control Algorithm. International Journal of Molecular Sciences. 2019; 20(15):3697. https://doi.org/10.3390/ijms20153697
Chicago/Turabian StyleWei, Xiang, Yuanyuan Wang, Zhan Cao, Dziki Mbemba, Azhar Iqbal, and Zhizheng Wu. 2019. "Large Aberration Correction by Magnetic Fluid Deformable Mirror with Model-Based Wavefront Sensorless Control Algorithm" International Journal of Molecular Sciences 20, no. 15: 3697. https://doi.org/10.3390/ijms20153697
APA StyleWei, X., Wang, Y., Cao, Z., Mbemba, D., Iqbal, A., & Wu, Z. (2019). Large Aberration Correction by Magnetic Fluid Deformable Mirror with Model-Based Wavefront Sensorless Control Algorithm. International Journal of Molecular Sciences, 20(15), 3697. https://doi.org/10.3390/ijms20153697





