Multi-Scale Computational Enzymology: Enhancing Our Understanding of Enzymatic Catalysis
Abstract
:1. Introduction
1.1. Experimental and Computational Enzymology
1.2. Computational Enzymology Methods
2. Computational Enzymatic Studies
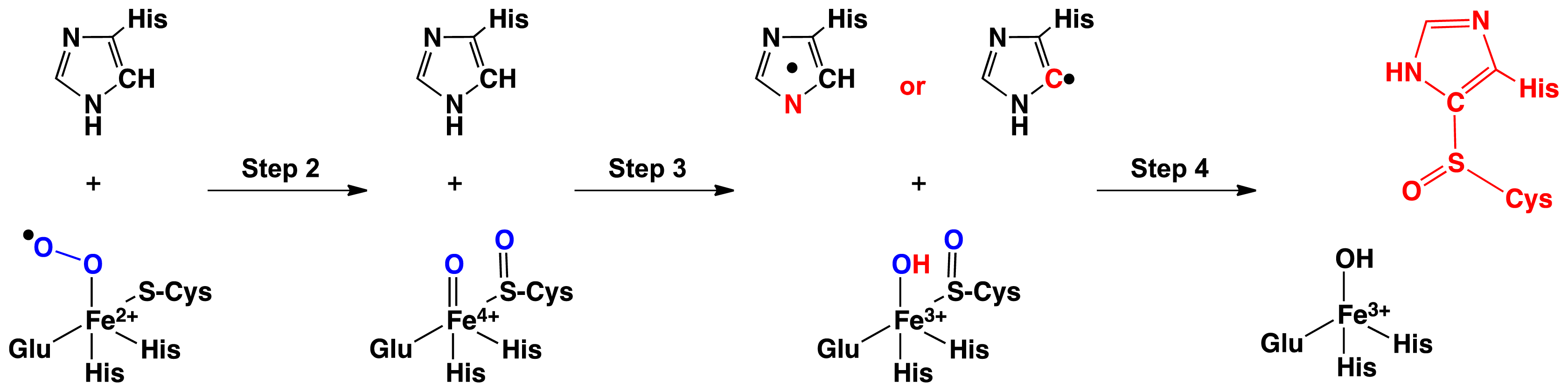
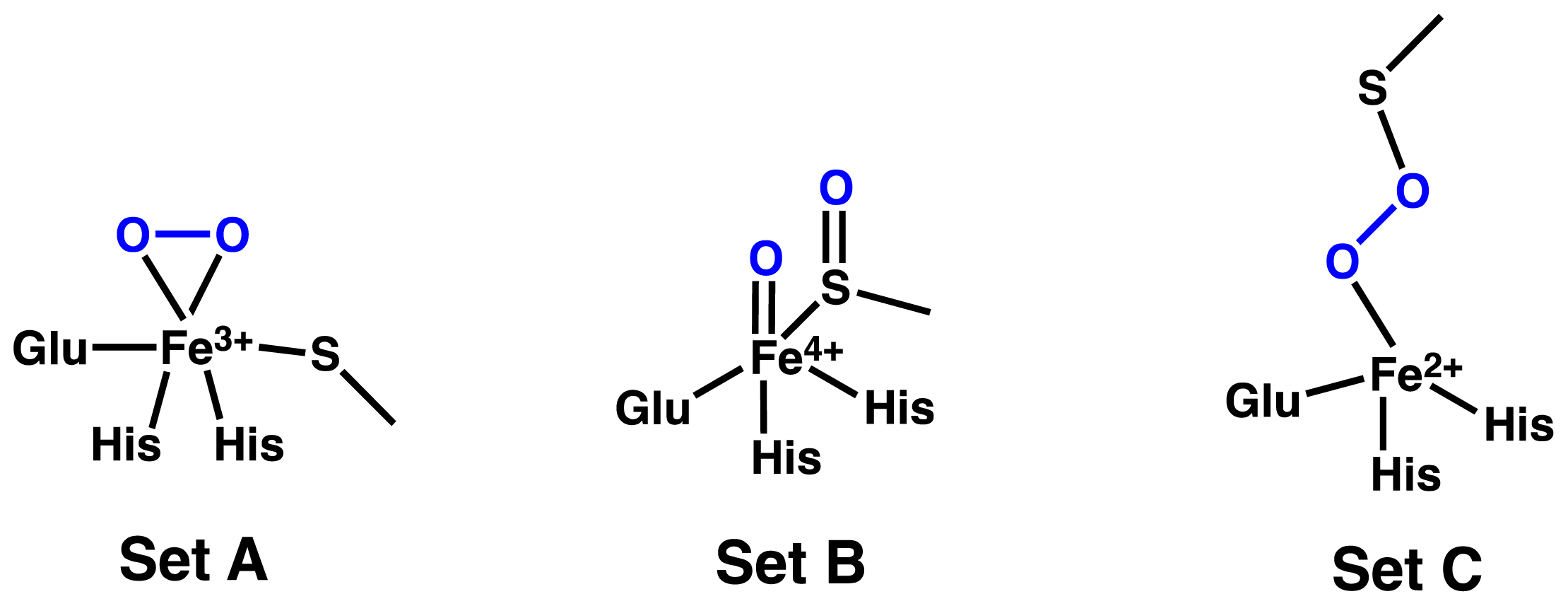
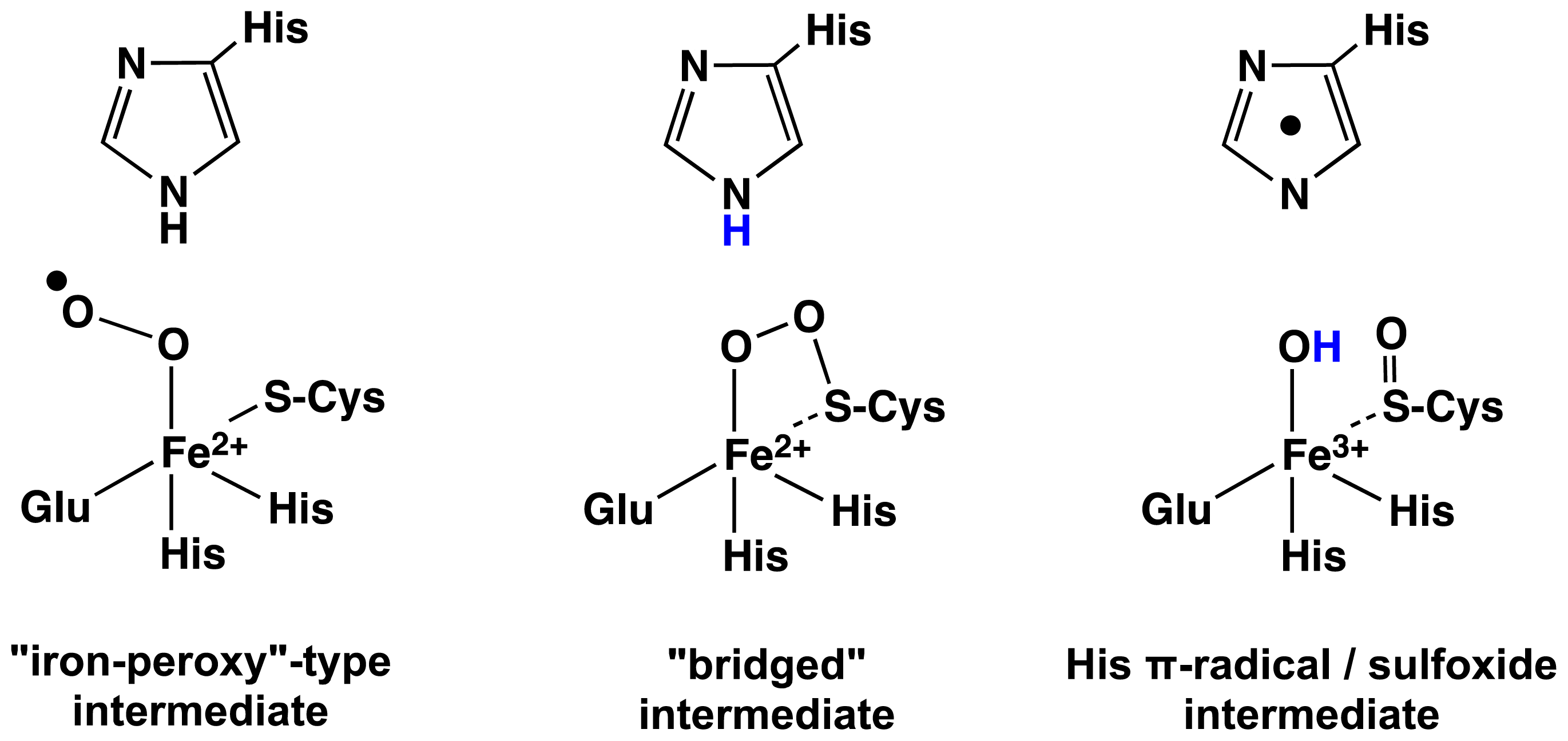
2.1. OvoA and EgtB: Characterizing Potential Mechanistic Oxidants
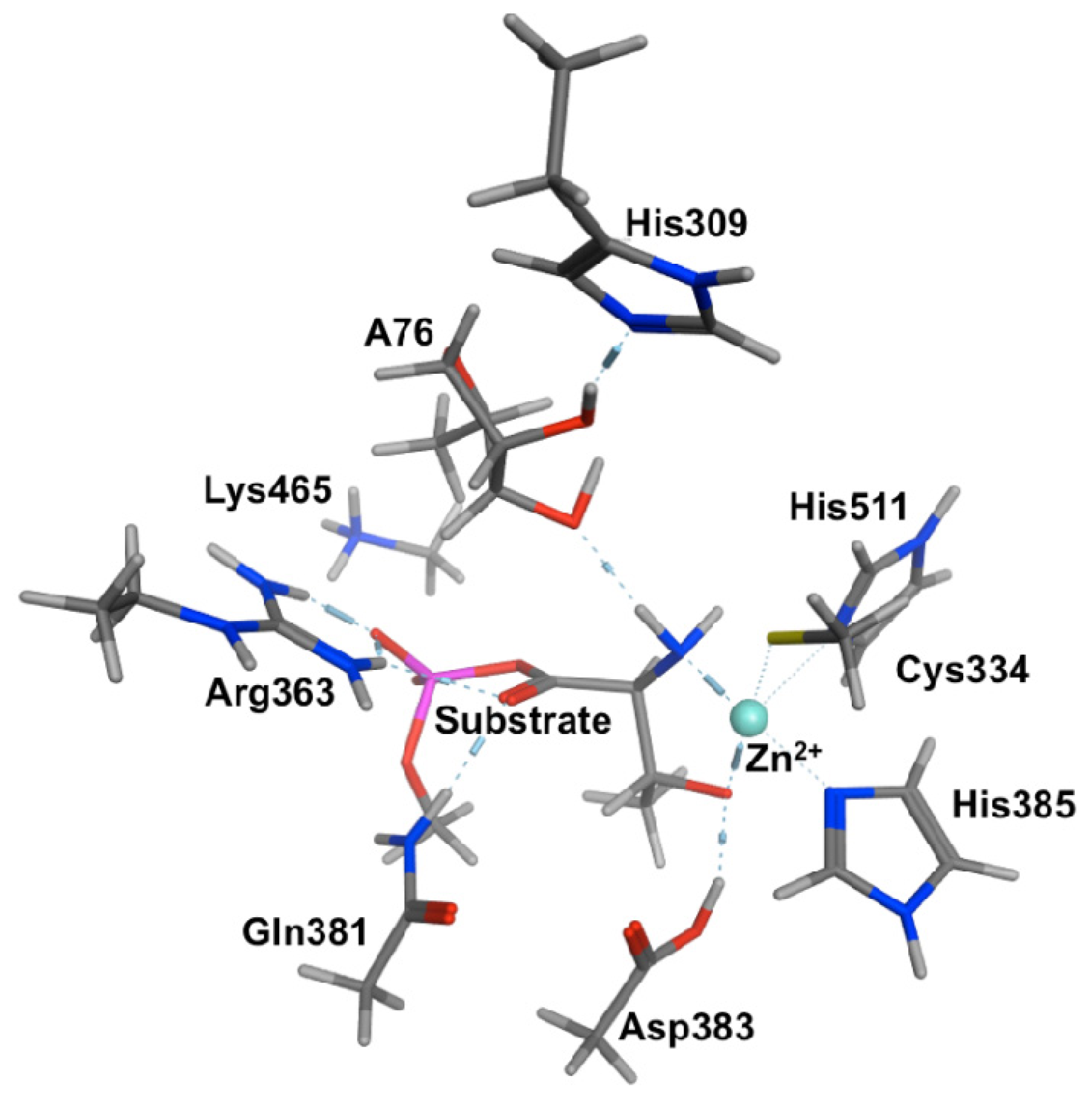
2.2. Threonyl-tRNA Synthetase (ThrRS): Identifying a Mechanistic Base?
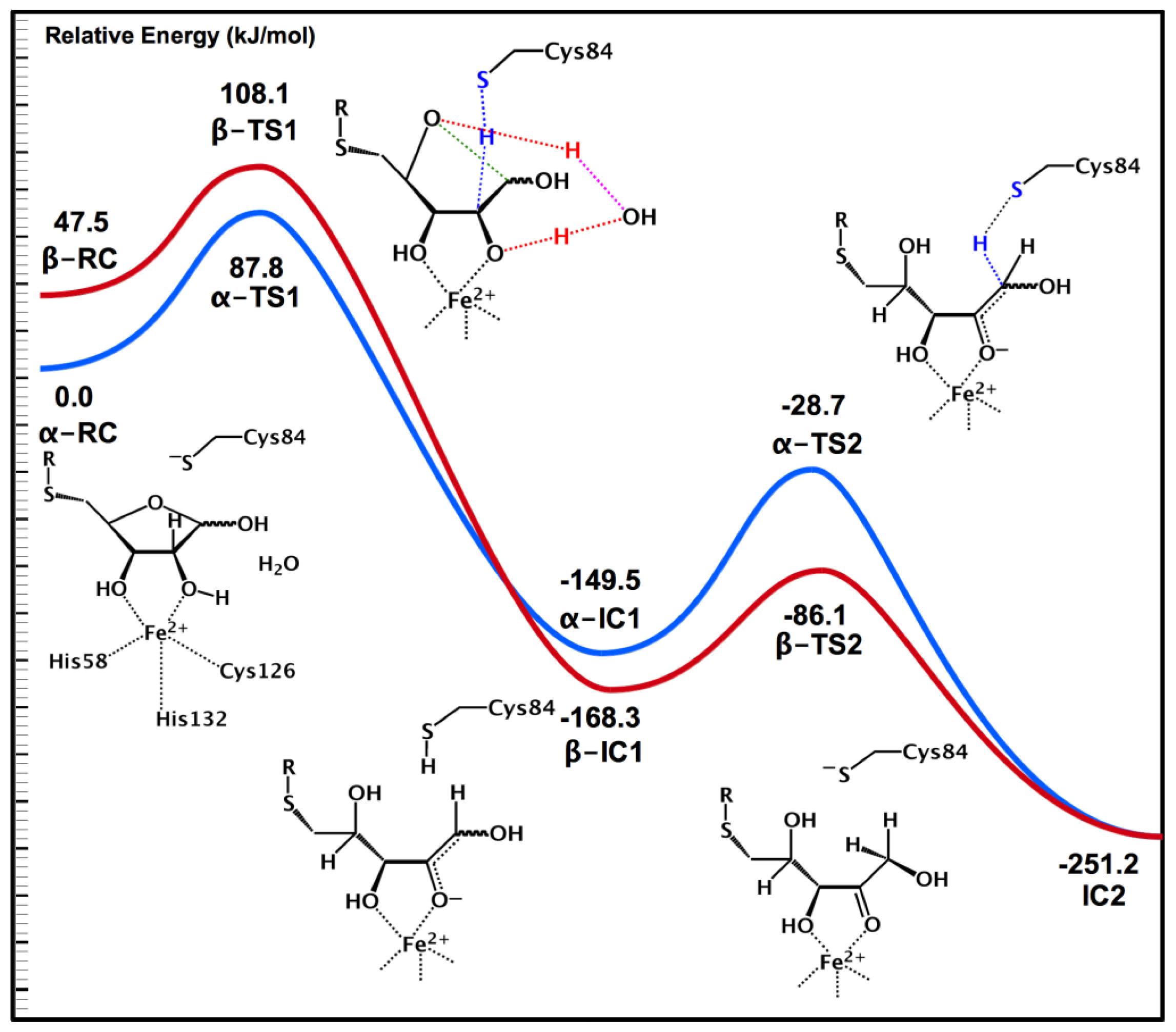
2.3. Substrate Specificity and Initial Mechanisms of S-ribosylhomocysteinase (LuxS)
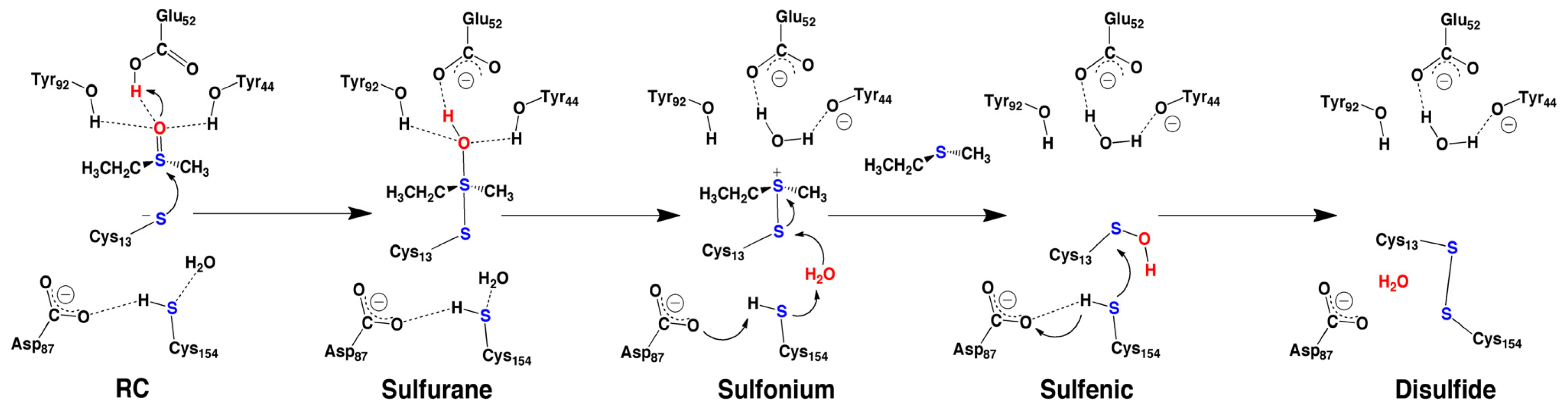
2.4. MsrA and Its Reductive Ability: A Docking, MD and Multi-Model QM/MM Study
3. Conclusions
Acknowledgments
Conflicts of Interest
References
- Stodulski, M.; Gulder, T. Nanoparticles and peptides: A fruitful liaison for biomimetic catalysis. Angew. Chem. Int. Ed 2012, 51, 11202–11204. [Google Scholar]
- Lehn, J.M.; Benyus, J.; Swiegers, G. Bioinspiration and Biomimicry in Chemistry: Reverse-Engineering Nature; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2012. [Google Scholar]
- Frushicheva, M.P.; Cao, J.; Chu, Z.T.; Warshel, A. Exploring challenges in rational enzyme design by simulating the catalysis in artificial kemp eliminase. Proc. Natl. Acad. Sci. USA 2010, 107, 16869–16874. [Google Scholar]
- Llano, J.; Gauld, J.W. Mechanistics of Enzyme Catalysis: From Small to Large Active-Site Models. In Quantum Biochemistry; John Wiley & Sons, Ltd: Weinheim, Germany, 2010; pp. 643–666. [Google Scholar]
- Garcia-Viloca, M.; Gao, J.; Karplus, M.; Truhlar, D.G. How enzymes work: Analysis by modern rate theory and computer simulations. Science 2004, 303, 186–195. [Google Scholar]
- Kamerlin, S.C.L.; Warshel, A. At the dawn of the 21st century: Is dynamics the missing link for understanding enzyme catalysis? Proteins: Struct. Funct. Bioinforma 2010, 78, 1339–1375. [Google Scholar]
- Glowacki, D.R.; Harvey, J.N.; Mulholland, A.J. Taking Ockham’s razor to enzyme dynamics and catalysis. Nat. Chem 2012, 4, 169–176. [Google Scholar]
- Hammes, G.G. Multiple conformational changes in enzyme catalysis. Biochemistry 2002, 41, 8221–8228. [Google Scholar]
- Benkovic, S.J.; Hammes-Schiffer, S. A perspective on enzyme catalysis. Science 2003, 301, 1196–1202. [Google Scholar]
- Henzler-Wildman, K.A.; Lei, M.; Thai, V.; Kerns, S.J.; Karplus, M.; Kern, D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature 2007, 450, 913–916. [Google Scholar]
- Borowski, T.; Bassan, A.; Siegbahn, P.E.M. Mechanism of dioxygen activation in 2-oxoglutarate-dependent enzymes: A hybrid DFT study. Chem. Eur. J 2004, 10, 1031–1041. [Google Scholar]
- De Visser, S.P.; Kumar, D.; Cohen, S.; Shacham, R.; Shaik, S. A predictive pattern of computed barriers for C–H hydroxylation by compound I of cytochrome P450. J. Am. Chem. Soc 2004, 126, 8362–8363. [Google Scholar]
- Bushnell, E.A.C.; Gherib, R.; Gauld, J.W. Insights into the catalytic mechanism of coral allene oxide synthase: A dispersion corrected density functional theory study. J. Phys. Chem. B 2013, 117, 6701–6710. [Google Scholar]
- Van Gunsteren, W.F.; Luque, F.; Timms, D.; Torda, A. Molecular mechanics in biology: From structure to function, taking account of solvation. Annu. Rev. Biophys. Biomol. Struct 1994, 23, 847–863. [Google Scholar]
- Krüger, P.; Straßburger, W.; Wollmer, A.; van Gunsteren, W.F. A comparison of the structure and dynamics of avian pancreatic polypeptide hormone in solution and in the crystal. Eur. Biophys. J 1985, 13, 77–88. [Google Scholar]
- Levy, Y.; Onuchic, J.N. Water mediation in protein folding and molecular recognition. Annu. Rev. Biophys. Biomol. Struct 2006, 35, 389–415. [Google Scholar]
- Huang, W.; Gherib, R.; Gauld, J.W. An active site water broadens substrate specificity in S-ribosylhomocysteinase (LuxS): A docking, MD, and QM/MM study. J. Phys. Chem. B 2012, 116, 8916–8929. [Google Scholar]
- Barillari, C.; Taylor, J.; Viner, R.; Essex, J.W. Classification of water molecules in protein binding sites. J. Am. Chem. Soc 2007, 129, 2577–2587. [Google Scholar]
- Storm, D.R.; Koshland, D.E. A source for the special catalytic power of enzymes: Orbital steering. Proc. Natl. Acad. Sci. USA 1970, 66, 445–452. [Google Scholar]
- Jonsson, T.; Glickman, M.H.; Sun, S.; Klinman, J.P. Experimental evidence for extensive tunneling of hydrogen in the lipoxygenase reaction: Implications for enzyme catalysis. J. Am. Chem. Soc 1996, 118, 10319–10320. [Google Scholar]
- Karplus, M.; Kuriyan, J. Molecular dynamics and protein function. Proc. Natl. Acad. Sci. USA 2005, 102, 6679–6685. [Google Scholar]
- Warren, G.L.; Andrews, C.W.; Capelli, A.M.; Clarke, B.; Lalonde, J.; Lambert, M.H.; Lindvall, M.; Nevins, N.; Semus, S.F.; Senger, S.; et al. A critical assessment of docking programs and scoring functions. J. Med. Chem 2006, 49, 5912–5931. [Google Scholar]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Mol. Biol 2002, 9, 646–652. [Google Scholar]
- Siegbahn, P.E.M.; Himo, F. The quantum chemical cluster approach for modeling enzyme reactions. Wiley Interdiscip. Rev. Comput. Mol. Sci 2011, 1, 323–336. [Google Scholar]
- Himo, F. Quantum chemical modeling of enzyme active sites and reaction mechanisms. Theor. Chem. Acc 2006, 116, 232–240. [Google Scholar]
- Siegbahn, P.E.M.; Blomberg, M.R.A. Transition-metal systems in biochemistry studied by high-accuracy quantum chemical methods. Chem. Rev 2000, 100, 421–438. [Google Scholar]
- Siegbahn, P.E.M.; Borowski, T. Modeling enzymatic reactions involving transition metals. Acc. Chem. Res 2006, 39, 729–738. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys 1993, 98, 5648. [Google Scholar]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [Google Scholar]
- Pérez, A.; Marchán, I.; Svozil, D.; Sponer, J.; Cheatham, T.E., III; Laughton, C.A.; Orozco, M. Refinement of the AMBER force field for nucleic acids: Improving the description of α/γ conformers. Biophys. J 2007, 92, 3817–3829. [Google Scholar]
- Meagher, K.L.; Redman, L.T.; Carlson, H.A. Development of polyphosphate parameters for use with the AMBER force field. J. Comput. Chem 2003, 24, 1016–1025. [Google Scholar]
- MacKerell, A.D.; Banavali, N.; Foloppe, N. Development and current status of the CHARMM force field for nucleic acids. Biopolymers 2000, 56, 257–265. [Google Scholar]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem 2010, 31, 671–690. [Google Scholar]
- Schmidt, J.M.; Brueschweiler, R.; Ernst, R.R.; Dunbrack, R.L., Jr.; Joseph, D.; Karplus, M. Molecular dynamics simulation of the proline conformational equilibrium and dynamics in antamanide using the CHARMM force field. J. Am. Chem. Soc 1993, 115, 8747–8756. [Google Scholar]
- Van Gunsteren, W.F.; Daura, X.; Mark, A.E. GROMOS Force Field. In Encyclopedia of Computational Chemistry; John Wiley & Sons, Ltd: Chichester, UK, 2002. [Google Scholar]
- Oostenbrink, C.; Soares, T.; Vegt, N.A.; van Gunsteren, W.F. Validation of the 53A6 GROMOS force field. Eur. Biophys. J 2005, 34, 273–284. [Google Scholar]
- Schmid, N.; Eichenberger, A.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; van Gunsteren, W.F. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J 2011, 40, 843–856. [Google Scholar]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar]
- Kahn, K.; Bruice, T.C. Parameterization of OPLS–AA force field for the conformational analysis of macrocyclic polyketides. J. Comput. Chem 2002, 23, 977–996. [Google Scholar]
- Kony, D.; Damm, W.; Stoll, S.; van Gunsteren, W.F. An improved OPLS–AA force field for carbohydrates. J. Comput. Chem 2002, 23, 1416–1429. [Google Scholar]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol 1976, 103, 227–249. [Google Scholar]
- Lin, H.; Truhlar, D.G. QM/MM: What have we learned, where are we, and where do we go from here? Theor. Chem. Acc 2007, 117, 185–199. [Google Scholar]
- Senn, H.M.; Thiel, W. QM/MM studies of enzymes. Curr. Opin. Chem. Biol 2007, 11, 182–187. [Google Scholar]
- Chung, L.W.; Hirao, H.; Li, X.; Morokuma, K. The ONIOM method: Its foundation and applications to metalloenzymes and photobiology. Wiley Interdiscip. Rev. Comput. Mol. Sci 2012, 2, 327–350. [Google Scholar]
- Plewczynski, D.; Łaźniewski, M.; Augustyniak, R.; Ginalski, K. Can we trust docking results? Evaluation of seven commonly used programs on PDBbind database. J. Comput. Chem 2011, 32, 742–755. [Google Scholar]
- Durrant, J.; McCammon, J.A. Molecular dynamics simulations and drug discovery. BMC Biol 2011, 9, 71. [Google Scholar]
- Ziegler, T.; Autschbach, J. Theoretical methods of potential use for studies of inorganic reaction mechanisms. Chem. Rev 2005, 105, 2695–2722. [Google Scholar]
- Van der Kamp, M.W.; Mulholland, A.J. Combined quantum mechanics/molecular mechanics (QM/MM) methods in computational enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar]
- Nobelprize.org. Available online: http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2013/ (accessed on 11 October 2013).
- Vogt, R.N.; Spies, H.S.C.; Steenkamp, D.J. The biosynthesis of ovothiol A (N1-methyl-4-mercaptohistidine). Eur. J. Biochem 2001, 268, 5229–5241. [Google Scholar]
- Braunshausen, A.; Seebeck, F.P. Identification and characterization of the first ovothiol biosynthetic enzyme. J. Am. Chem. Soc 2011, 133, 1757–1759. [Google Scholar]
- Bushnell, E.A.C.; Fortowsky, G.B.; Gauld, J.W. Model iron, oxo species and the oxidation of imidazole: Insights into the mechanism of OvoA and EgtB? Inorg. Chem 2012, 51, 13351–13356. [Google Scholar]
- Cances, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys 1997. [Google Scholar] [CrossRef]
- De Visser, S.P.; Straganz, G.D. Why do cysteine dioxygenase enzymes contain a 3-his ligand motif rather than a 2his/1Asp motif like most nonheme dioxygenases? J. Phys. Chem. A 2009, 113, 1835–1846. [Google Scholar]
- Fredrick, K.; Ibba, M. Protein synthesis errors rectified in retrospect. Nature 2009, 457, 157–158. [Google Scholar]
- Gromadski, K.B.; Rodnina, M.V. Kinetic determinants of high-fidelity tRNA discrimination on the ribosome. Mol. Cell 2004, 13, 191–200. [Google Scholar]
- Guth, E.C.; Francklyn, C.S. Kinetic discrimination of tRNA identity by the conserved motif 2 loop of a class II aminoacyl-tRNA synthetase. Mol. Cell 2007, 25, 531–542. [Google Scholar]
- Huang, W.; Bushnell, E.A.C.; Francklyn, C.S.; Gauld, J.W. The α-amino group of the threonine substrate as the general base during tRNA aminoacylation: A new version of substrate-assisted catalysis predicted by hybrid DFT. J. Phys. Chem. A 2011, 115, 13050–13060. [Google Scholar]
- Guth, E.; Connolly, S.H.; Bovee, M.; Francklyn, C.S. A substrate-assisted concerted mechanism for aminoacylation by a class II aminoacyl-tRNA synthetase. Biochemistry 2005, 44, 3785–3794. [Google Scholar]
- Liu, H.; Gauld, J.W. Substrate-assisted catalysis in the aminoacyl transfer mechanism of histidyl-tRNA synthetase: A density functional theory study. J. Phys. Chem. B 2008, 112, 16874–16882. [Google Scholar]
- Bushnell, E.A.C.; Huang, W.; Llano, J.; Gauld, J.W. Molecular dynamics investigation into substrate binding and identity of the catalytic base in the mechanism of threonyl-tRNA synthetase. J. Phys. Chem. B 2012, 116, 5205–5212. [Google Scholar]
- Minajigi, A.; Francklyn, C.S. RNA-assisted catalysis in a protein enzyme: The 2′-hydroxyl of tRNA (Thr) A76 promotes aminoacylation by threonyl-tRNA synthetase. Proc. Natl. Acad. Sci. USA 2008, 105, 17748–17753. [Google Scholar]
- Francklyn, C.S. DNA polymerases and aminoacyl-tRNA synthetases: Shared mechanisms for ensuring the fidelity of gene expression. Biochemistry 2008, 47, 11695–11703. [Google Scholar]
- Sethi, A.; Eargle, J.; Black, A.A.; Luthey-Schulten, Z. Dynamical networks in tRNA: Protein complexes. Proc. Natl. Acad. Sci. USA 2009, 106, 6620–6625. [Google Scholar]
- Jencks, W.P. Catalysis in Chemistry and Enzymology; Dover Publications: Mineola, NY, USA, 1987. [Google Scholar]
- Pei, D.; Zhu, J. Mechanism of action of S-ribosylhomocysteinase (LuxS). Curr. Opin. Chem. Biol 2004, 8, 492–497. [Google Scholar]
- Gopishetty, B.; Zhu, J.; Rajan, R.; Sobczak, A.J.; Wnuk, S.F.; Bell, C.E.; Pei, D. Probing the catalytic mechanism of S-ribosylhomocysteinase (LuxS) with catalytic intermediates and substrate analogues. J. Am. Chem. Soc 2009, 131, 1243–1250. [Google Scholar]
- Rajan, R.; Zhu, J.; Hu, X.; Pei, D.; Bell, C.E. Crystal structure of S-ribosylhomocysteinase (LuxS) in complex with a catalytic 2-ketone intermediate. Biochemistry 2005, 44, 3745–3753. [Google Scholar]
- Zhu, J.; Dizin, E.; Hu, X.; Wavreille, A.S.; Park, J.; Pei, D. S-Ribosylhomocysteinase (LuxS) is a mononuclear iron protein. Biochemistry 2003, 42, 4717–4726. [Google Scholar]
- Schauder, S.; Shokat, K.; Surette, M.G.; Bassler, B.L. The LuxS family of bacterial autoinducers: Biosynthesis of a novel quorum-sensing signal molecule. Mol. Microbiol 2001, 41, 463–476. [Google Scholar]
- Zhu, J.; Hu, X.; Dizin, E.; Pei, D. Catalytic mechanism of S-ribosylhomocysteinase (LuxS): Direct observation of ketone intermediates by 13C NMR spectroscopy. J. Am. Chem. Soc 2003, 125, 13379–13381. [Google Scholar]
- Lim, J.C.; You, Z.; Kim, G.; Levine, R.L. Methionine sulfoxide reductase A is a stereospecific methionine oxidase. Proc. Natl. Acad. Sci. USA 2011, 108, 10472–10477. [Google Scholar]
- Ezraty, B.; Aussel, L.; Barras, F. Methionine sulfoxide reductases in prokaryotes. BBA Proteins Proteomics 2005, 1703, 221–229. [Google Scholar]
- Weissbach, H.; Resnick, L.; Brot, N. Methionine sulfoxide reductases: History and cellular role in protecting against oxidative damage. BBA Proteins Proteomics 2005, 1703, 203–212. [Google Scholar]
- Moskovitz, J. Methionine sulfoxide reductases: Ubiquitous enzymes involved in antioxidant defense, protein regulation, and prevention of aging-associated diseases. BBA Proteins Proteomics 2005, 1703, 213–219. [Google Scholar]
- Ruan, H.; Tang, X.D.; Chen, M.L.; Joiner, M.A.; Sun, G.; Brot, N.; Weissbach, H.; Heinemann, S.H.; Iverson, L.; Wu, C.F.; et al. High-quality life extension by the enzyme peptide methionine sulfoxide reductase. Proc. Natl. Acad. Sci. USA 2002, 99, 2748–2753. [Google Scholar]
- Moskovitz, J.; Bar-Noy, S.; Williams, W.M.; Requena, J.; Berlett, B.S.; Stadtman, E.R. Methionine sulfoxide reductase (MsrA) is a regulator of antioxidant defense and lifespan in mammals. Proc. Natl. Acad. Sci. USA 2001, 98, 12920–12925. [Google Scholar]
- Boschi-Muller, S.; Olry, A.; Antoine, M.; Branlant, G. The enzymology and biochemistry of methionine sulfoxide reductases. BBA Proteins Proteomics 2005, 1703, 231–238. [Google Scholar]
- Dokainish, H.M.; Gauld, J.W. A molecular dynamics and quantum mechanics/molecular mechanics study of the catalytic reductase mechanism of methionine sulfoxide reductase A: Formation and reduction of a sulfenic acid. Biochemistry 2013, 52, 1814–1827. [Google Scholar]
- Antoine, M.; Gand, A.; Boschi-Muller, S.; Branlant, G. Characterization of the amino acids from Neisseria meningitidis MsrA involved in the chemical catalysis of the methionine sulfoxide reduction step. J. Biol. Chem 2006, 281, 39062–39070. [Google Scholar]
- Taylor, A.B.; Benglis, D.M.; Dhandayuthapani, S.; Hart, P.J. Structure of Mycobacterium tuberculosis methionine sulfoxide reductase A in complex with protein-bound methionine. J. Bacteriol 2003, 185, 4119–4126. [Google Scholar]
- Thiriot, E.; Monard, G.; Boschi-Muller, S.; Branlant, G.; Ruiz-López, M.F. Reduction mechanism in class A methionine sulfoxide reductases: A theoretical chemistry investigation. Theor. Chem. Acc 2011, 129, 93–103. [Google Scholar]
- Poole, L.B.; Karplus, P.A.; Claiborne, A. Protein sulfenic acids in redox signaling. Annu. Rev. Pharmacol. Toxicol 2004, 44, 325–347. [Google Scholar]



© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gherib, R.; Dokainish, H.M.; Gauld, J.W. Multi-Scale Computational Enzymology: Enhancing Our Understanding of Enzymatic Catalysis. Int. J. Mol. Sci. 2014, 15, 401-422. https://doi.org/10.3390/ijms15010401
Gherib R, Dokainish HM, Gauld JW. Multi-Scale Computational Enzymology: Enhancing Our Understanding of Enzymatic Catalysis. International Journal of Molecular Sciences. 2014; 15(1):401-422. https://doi.org/10.3390/ijms15010401
Chicago/Turabian StyleGherib, Rami, Hisham M. Dokainish, and James W. Gauld. 2014. "Multi-Scale Computational Enzymology: Enhancing Our Understanding of Enzymatic Catalysis" International Journal of Molecular Sciences 15, no. 1: 401-422. https://doi.org/10.3390/ijms15010401
APA StyleGherib, R., Dokainish, H. M., & Gauld, J. W. (2014). Multi-Scale Computational Enzymology: Enhancing Our Understanding of Enzymatic Catalysis. International Journal of Molecular Sciences, 15(1), 401-422. https://doi.org/10.3390/ijms15010401




