Recurrent Structural Motifs in Non-Homologous Protein Structures
Abstract
:1. Introduction
2. Results and Discussion
2.1. Protein Sets
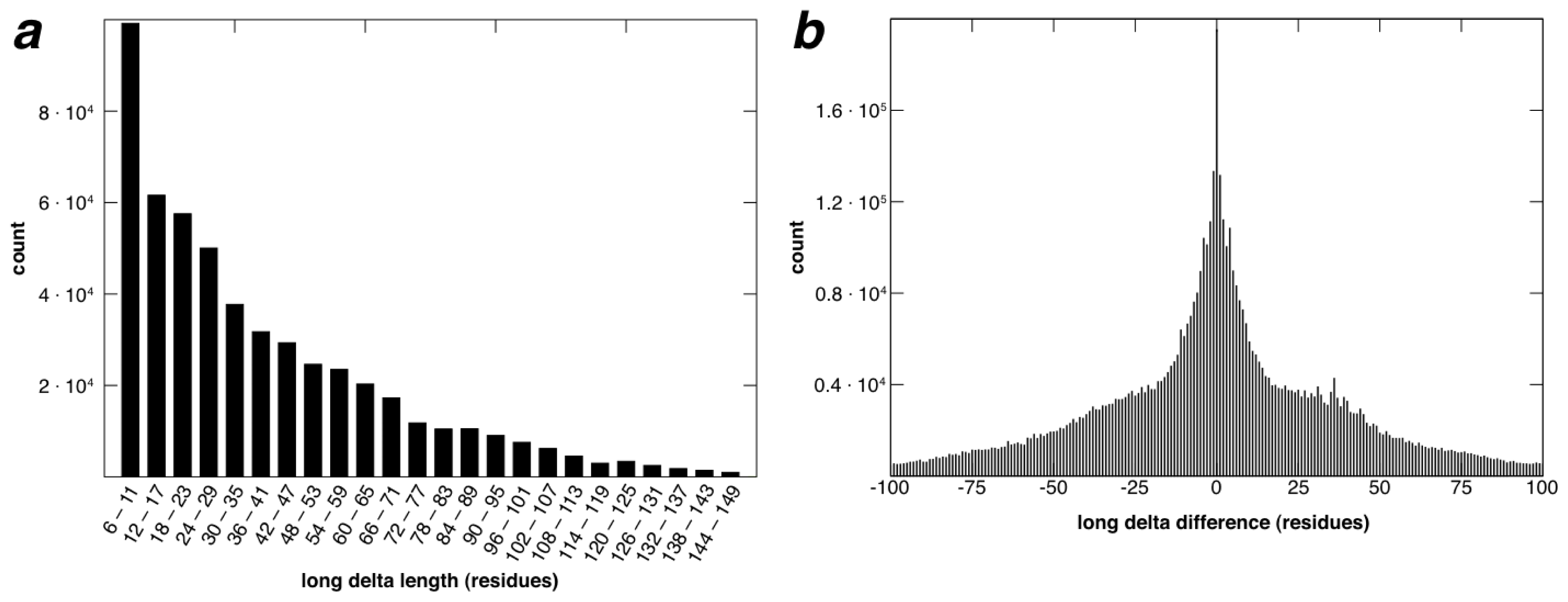
2.2. Identification of Non-Contiguous Recurrent Structural Motifs
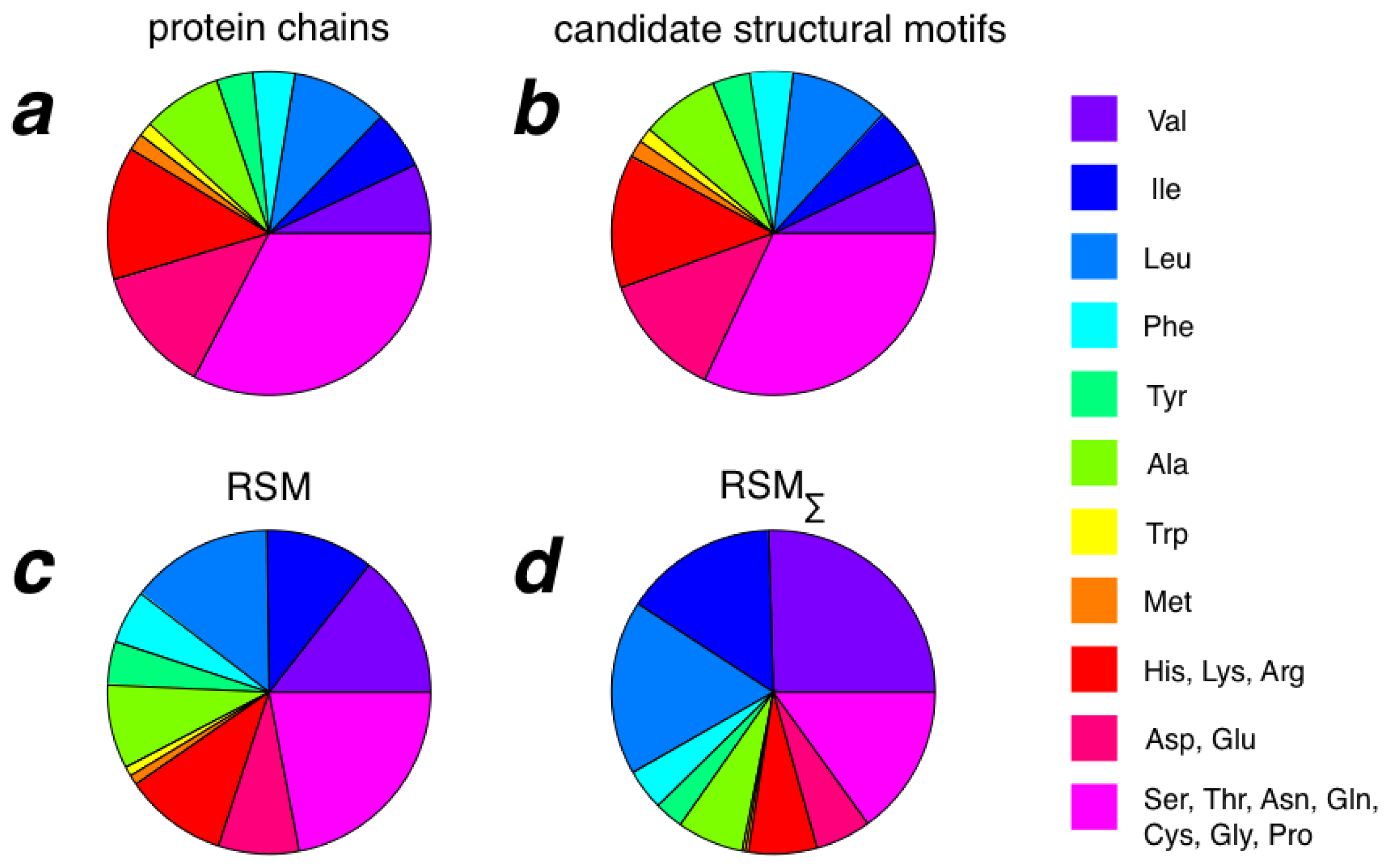
2.3. Amino Acid Composition of RSMs
2.4. Coverage
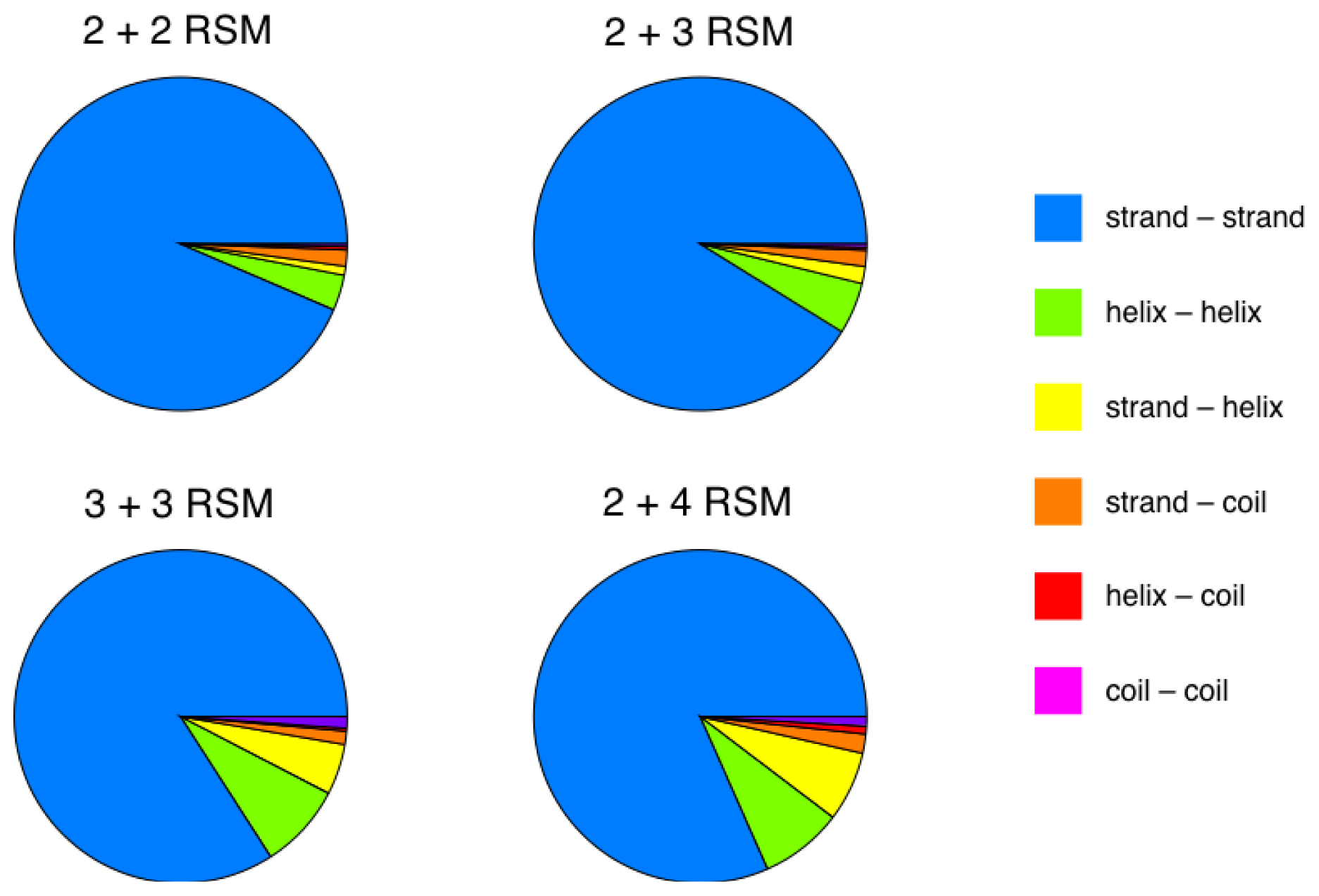
2.5. More Compact Candidate Structural Motifs Lead to Relatively More RSMs and Higher Recurrence
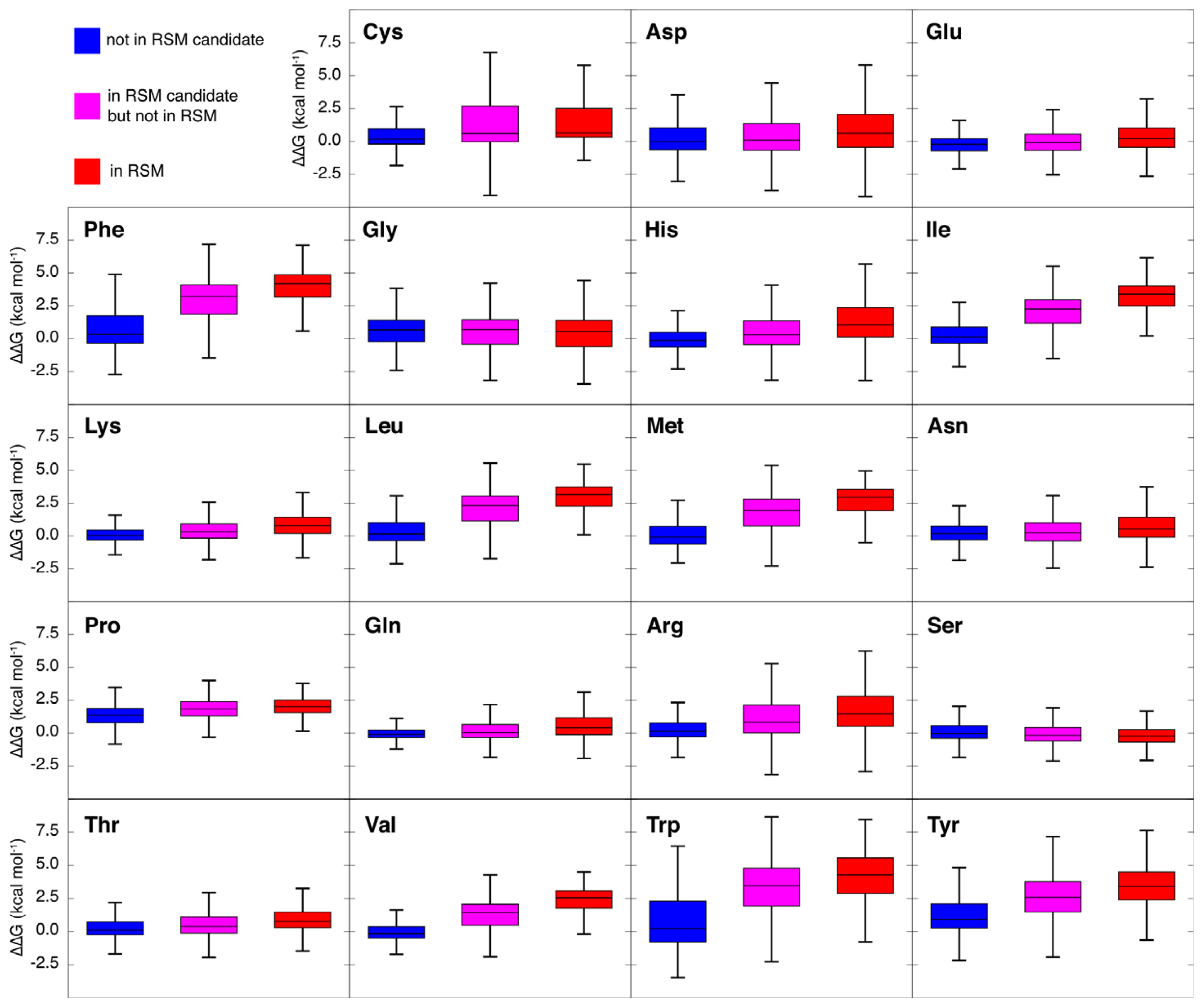
2.6. Computational Alanine Scanning
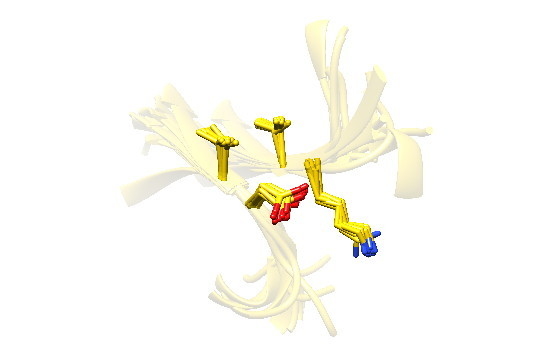
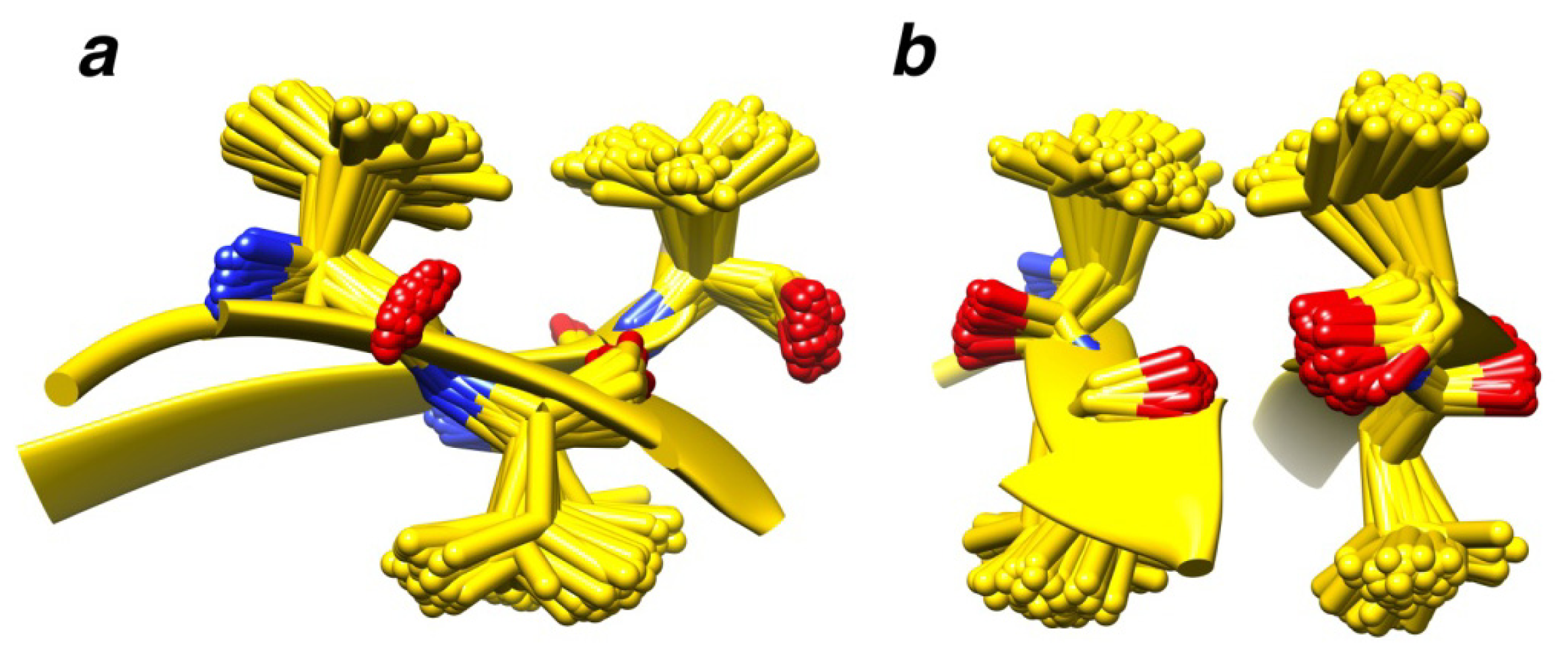
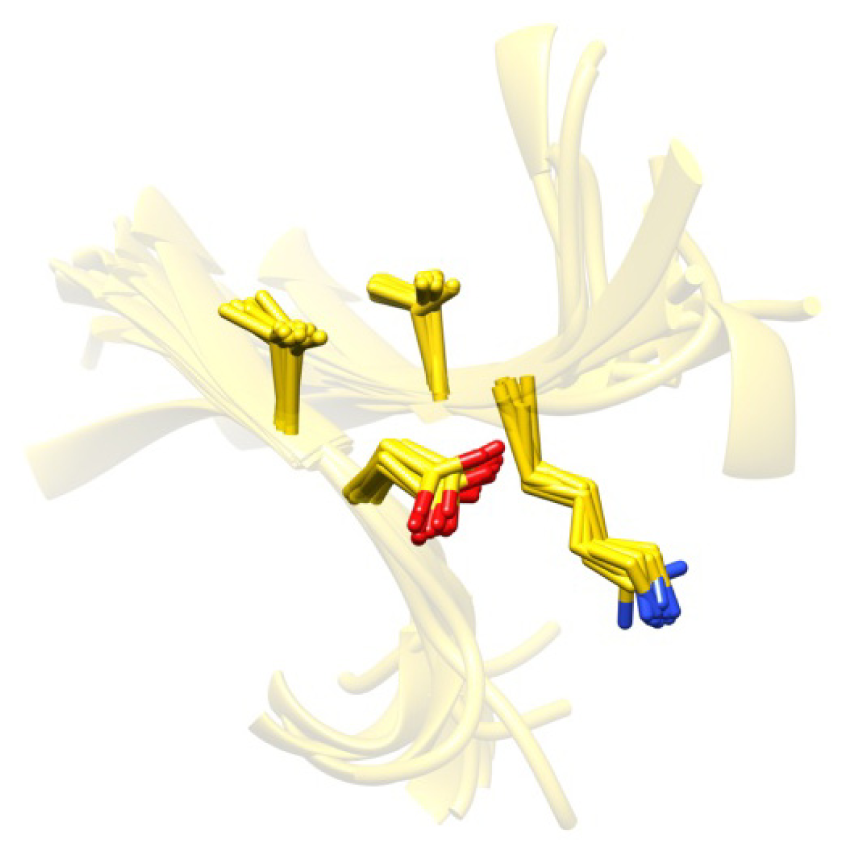
2.7. Examples
2.8. Side Chain Packing
3. Experimental Section
3.1. Selection of Protein Sets
3.2. Protein Chain Classification
3.3. Sequence Properties of Non-Contiguous Candidate Structural Motifs
3.4. Structure Properties of Non-Contiguous Candidate Structural Motifs
3.5. Identification of Recurrent Non-Contiguous Structural Motifs
3.6. Computational Alanine Scanning
4. Conclusions
Supplementary Information
ijms-14-07795-s001.pdfAcknowledgments
Conflict of Interest
References
- Montelione, G.T. The protein structure initiative: Achievements and visions for the future. F1000 Biol. Rep 2012, 4, 7. [Google Scholar]
- Nair, R.; Liu, J.; Soong, T.-T.; Acton, T.B.; Everett, J.K.; Kouranov, A.; Fiser, A.; Godzik, A.; Jaroszewski, L.; Orengo, C.; et al. Structural genomics is the largest contributor of novel structural leverage. J. Struct. Funct. Genomics 2009, 10, 181–191. [Google Scholar]
- Liu, J.; Montelione, G.T.; Rost, B. Novel leverage of structural genomics. Nat. Biotechnol 2007, 25, 849–851. [Google Scholar]
- Moult, J.; Fidelis, K.; Kryshtafovych, A.; Tramontano, A. Critical assessment of methods of protein structure prediction (CASP)—Round IX. Proteins 2011, 79, 1–5. [Google Scholar]
- Ben-David, M.; Noivirt-Brik, O.; Paz, A.; Prilusky, J.; Sussman, J.L.; Levy, Y. Assessment of CASP8 structure predictions for template free targets. Proteins 2009, 77, 50–65. [Google Scholar]
- Bowie, J.U.; Eisenberg, D. An evolutionary approach to folding small alpha-helical proteins that uses sequence information and an empirical guiding fitness function. Proc. Natl. Acad. Sci. USA 1994, 91, 4436–4440. [Google Scholar]
- Jones, T.A.; Thirup, S. Using known substructures in protein model building and crystallography. EMBO J 1986, 5, 819–822. [Google Scholar]
- Blundell, T.L.; Sibanda, B.L.; Sternberg, M.J.; Thornton, J.M. Knowledge-based prediction of protein structures and the design of novel molecules. Nature 1987, 326, 347–352. [Google Scholar]
- Kraulis, P.J.; Jones, T.A. Determination of three-dimensional protein structures from nuclear magnetic resonance data using fragments of known structures. Proteins 1987, 2, 188–201. [Google Scholar]
- Jones, T.A.; Zou, J.Y.; Cowan, S.W.; Kjeldgaard, M. Improved methods for building protein models in electron density maps and the location of errors in these models. Acta Crystallogr. A 1991, 47, 110–119. [Google Scholar]
- Kontaxis, G.; Delaglio, F.; Bax, A. Molecular fragment replacement approach to protein structure determination by chemical shift and dipolar homology database mining. Meth. Enzymol 2005, 394, 42–78. [Google Scholar]
- Cheng, H.; Kim, B.-H.; Grishin, N.V. MALISAM: A database of structurally analogous motifs in proteins. Nucleic Acids Res 2008, 36, D211–D217. [Google Scholar]
- Vanhee, P.; Verschueren, E.; Baeten, L.; Stricher, F.; Serrano, L.; Rousseau, F.; Schymkowitz, J. BriX: A database of protein building blocks for structural analysis, modeling and design. Nucleic Acids Res 2011, 39, D435–D442. [Google Scholar]
- Bradley, P.; Kim, P.S.; Berger, B. TRILOGY: Discovery of sequence-structure patterns across diverse proteins. Proc. Natl. Acad. Sci. USA 2002, 99, 8500–8505. [Google Scholar]
- Unger, R.; Harel, D.; Wherland, S.; Sussman, J.L. A 3D building blocks approach to analyzing and predicting structure of proteins. Proteins 1989, 5, 355–373. [Google Scholar]
- Bystroff, C.; Baker, D. Prediction of local structure in proteins using a library of sequence-structure motifs. J. Mol. Biol 1998, 281, 565–577. [Google Scholar]
- Kolodny, R.; Koehl, P.; Guibas, L.; Levitt, M. Small libraries of protein fragments model native protein structures accurately. J. Mol. Biol 2002, 323, 297–307. [Google Scholar]
- Simons, K.T.; Kooperberg, C.; Huang, E.; Baker, D. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J. Mol. Biol 1997, 268, 209–225. [Google Scholar]
- Leaver-Fay, A.; Tyka, M.; Lewis, S.M.; Lange, O.F.; Thompson, J.; Jacak, R.; Kaufman, K.; Renfrew, P.D.; Smith, C.A.; Sheffler, W.; et al. ROSETTA3: An object-oriented software suite for the simulation and design of macromolecules. Meth. Enzymol 2011, 487, 545–574. [Google Scholar]
- Han, K.F.; Bystroff, C.; Baker, D. Three-dimensional structures and contexts associated with recurrent amino acid sequence patterns. Protein Sci 1997, 6, 1587–1590. [Google Scholar]
- Das, R.; Qian, B.; Raman, S.; Vernon, R.; Thompson, J.; Bradley, P.; Khare, S.; Tyka, M.D.; Bhat, D.; Chivian, D.; et al. Structure prediction for CASP7 targets using extensive all-atom refinement with Rosetta@home. Proteins 2007, 69, 118–128. [Google Scholar]
- Jones, D.T. Predicting novel protein folds by using FRAGFOLD. Proteins 2001, (Suppl 5), 127–132. [Google Scholar]
- Fujitsuka, Y.; Chikenji, G.; Takada, S. SimFold energy function for de novo protein structure prediction: Consensus with Rosetta. Proteins 2006, 62, 381–398. [Google Scholar]
- Zhang, Y. I-TASSER server for protein 3D structure prediction. BMC Bioinformatics 2008, 9, 40. [Google Scholar]
- Roy, A.; Kucukural, A.; Zhang, Y. I-TASSER: A unified platform for automated protein structure and function prediction. Nat. Protoc 2010, 5, 725–738. [Google Scholar]
- Zhang, Y.; Skolnick, J. Automated structure prediction of weakly homologous proteins on a genomic scale. Proc. Natl. Acad. Sci. USA 2004, 101, 7594–7599. [Google Scholar]
- Wu, S.; Skolnick, J.; Zhang, Y. Ab initio modeling of small proteins by iterative TASSER simulations. BMC Biol 2007, 5, 17. [Google Scholar]
- Stark, A.; Sunyaev, S.; Russell, R.B. A model for statistical significance of local similarities in structure. J. Mol. Biol 2003, 326, 1307–1316. [Google Scholar]
- Porter, C.T.; Bartlett, G.J.; Thornton, J.M. The catalytic site atlas: A resource of catalytic sites and residues identified in enzymes using structural data. Nucleic Acids Res 2004, 32, D129–D133. [Google Scholar]
- Alva, V.; Remmert, M.; Biegert, A.; Lupas, A.N.; Söding, J. A galaxy of folds. Protein Sci 2010, 19, 124–130. [Google Scholar]
- Budowski-Tal, I.; Nov, Y.; Kolodny, R. FragBag, an accurate representation of protein structure, retrieves structural neighbors from the entire PDB quickly and accurately. Proc. Natl. Acad. Sci. USA 2010, 107, 3481–3486. [Google Scholar]
- Swindells, M.B.; Orengo, C.A.; Jones, D.T.; Pearl, L.H.; Thornton, J.M. Recurrence of a binding motif? Nature 1993, 362, 299. [Google Scholar]
- Torrance, J.W.; Macarthur, M.W.; Thornton, J.M. Evolution of binding sites for zinc and calcium ions playing structural roles. Proteins 2008, 71, 813–830. [Google Scholar]
- Fetrow, J.S.; Siew, N.; Skolnick, J. Structure-based functional motif identifies a potential disulfide oxidoreductase active site in the serine/threonine protein phosphatase-1 subfamily. FASEB J 1999, 13, 1866–1874. [Google Scholar]
- Huan, J.; Bandyopadhyay, D.; Prins, J.; Snoeyink, J.; Tropsha, A.; Wang, W. Distance-based identification of structure motifs in proteins using constrained frequent subgraph mining. Comput. Syst. Bioinformatics Conf. 2006, 227–238. [Google Scholar]
- Johansson, M.U.; Zoete, V.; Michielin, O.; Guex, N. Defining and searching for structural motifs using DeepView/Swiss-PDBViewer. BMC Bioinformatics 2012, 13, 173. [Google Scholar]
- Lupas, A.; van Dyke, M.; Stock, J. Predicting coiled coils from protein sequences. Science 1991, 252, 1162–1164. [Google Scholar]
- Murzin, A.G.; Brenner, S.E.; Hubbard, T.; Chothia, C. SCOP: A structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol 1995, 247, 536–540. [Google Scholar]
- Orengo, C.A.; Michie, A.D.; Jones, S.; Jones, D.T.; Swindells, M.B.; Thornton, J.M. CATH—A hierarchic classification of protein domain structures. Structure 1997, 5, 1093–1108. [Google Scholar]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res 1997, 25, 3389–3402. [Google Scholar]
- Altschul, S.F.; Wootton, J.C.; Gertz, E.M.; Agarwala, R.; Morgulis, A.; Schäffer, A.A.; Yu, Y.-K. Protein database searches using compositionally adjusted substitution matrices. FEBS J 2005, 272, 5101–5109. [Google Scholar]
- Chou, K.C.; Scheraga, H.A. Origin of the right-handed twist of beta-sheets of poly(LVal) chains. Proc. Natl. Acad. Sci. USA 1982, 79, 7047–7051. [Google Scholar]
- Di Costanzo, L.; Wade, H.; Geremia, S.; Randaccio, L.; Pavone, V.; DeGrado, W.F.; Lombardi, A. Toward the de novo design of a catalytically active helix bundle: A substrate-accessible carboxylate-bridged dinuclear metal center. J. Am. Chem. Soc 2001, 123, 12749–12757. [Google Scholar]
- Taylor, T.J.; Vaisman, I.I. Discrimination of thermophilic and mesophilic proteins. BMC Struct. Biol 2010, 10, S5. [Google Scholar]
- Prlic, A.; Bliven, S.; Rose, P.W.; Bluhm, W.F.; Bizon, C.; Godzik, A.; Bourne, P.E. Pre-calculated protein structure alignments at the RCSB PDB website. Bioinformatics 2010, 26, 2983–2985. [Google Scholar]
- Wang, G.; Dunbrack, R.L. PISCES: A protein sequence culling server. Bioinformatics 2003, 19, 1589–1591. [Google Scholar]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res 2000, 28, 235–242. [Google Scholar]
- Guex, N.; Peitsch, M.C. SWISS-MODEL and the Swiss-PDBViewer: An environment for comparative protein modeling. Electrophoresis 1997, 18, 2714–2723. [Google Scholar]
- Guex, N.; Peitsch, M.C.; Schwede, T. Automated comparative protein structure modeling with SWISS-MODEL and Swiss-PDBViewer: A historical perspective. Electrophoresis 2009, 30, S162–S173. [Google Scholar]
- Delaunay, B. Sur la sphère vide. Izv Akad Nauk SSSR 1934, 6, 793–800. [Google Scholar]
- Poupon, A. Voronoi and Voronoi-related tessellations in studies of protein structure and interaction. Curr. Opin. Struct. Biol 2004, 14, 233–241. [Google Scholar]
- Guerois, R.; Nielsen, J.E.; Serrano, L. Predicting changes in the stability of proteins and protein complexes: A study of more than 1000 mutations. J. Mol. Biol 2002, 320, 369–387. [Google Scholar]
- Schymkowitz, J.W.H.; Rousseau, F.; Martins, I.C.; Ferkinghoff-Borg, J.; Stricher, F.; Serrano, L. Prediction of water and metal binding sites and their affinities by using the Fold-X force field. Proc. Natl. Acad. Sci. USA 2005, 102, 10147–10152. [Google Scholar]





| Level | 2 + 2 RSM (0.4–0.8 Å) | 2 + 3 RSM (0.5–0.9 Å) | 3 + 3 RSM (0.6–1.0 Å) | 2 + 4 RSM (0.6–1.0 Å) | |
|---|---|---|---|---|---|
| RSMs entirely composed of secondary structure elements | 1 | 406,720 (127,807)/5.4 | 103,711 (68,911)/3.0 | 5,612 (4,802)/2.4 | 3,896 (3,362)/2.4 |
| 2 | 648,493 (210,897)/5.6 | 156,654 (104,859)/3.0 | 7,202 (6,149)/2.4 | 4,977 (4,299)/2.4 | |
| 3 | 890,876 (298,048)/5.7 | 211,128 (142,866)/3.0 | 8,487 (7,229)/2.4 | 5,958 (5,161)/2.4 | |
| 4 | 1,136,125 (389,668)/5.8 | 261,410 (178,977)/2.9 | 9,491 (8,095)/2.4 | 6,678 (5,792)/2.4 | |
| 5 | 1,364,736 (480,393)/5.8 | 303,198 (209,707)/2.9 | 10,245 (8,773)/2.4 | 7,206 (6,258)/2.3 | |
| RSMs containing coil regions | 1 | 8,931 (6,766)/4.8 | 2,304 (1,978)/3.0 | 155 (138)/2.4 | 143 (132)/2.3 |
| 2 | 14,602 (11,599)/4.9 | 3,169 (2,773)/3.0 | 189 (171)/2.4 | 168 (157)/2.3 | |
| 3 | 22,178 (18,236)/4.9 | 4,064 (3,622)/3.0 | 209 (191)/2.4 | 198 (186)/2.3 | |
| 4 | 32,815 (27,539)/4.8 | 4,922 (4,446)/3.0 | 222 (204)/2.4 | 210 (198)/2.3 | |
| 5 | 46,953 (39,806)/4.6 | 5,702 (5,196)/3.0 | 240 (222)/2.4 | 217 (205)/2.3 | |
| 2 + 2 RSM (0.4–0.8 Å) | 2 + 3 RSM (0.5–0.9 Å) | |
|---|---|---|
| RSMs entirely composed of secondary structure elements | 21,452/4.2 | 7,133/2.9 |
| 49,132/4.6 | 14,139/3.1 | |
| 92,774/4.9 | 24,247/3.1 | |
| 151,704/5.1 | 37,851/3.1 | |
| 229,068/5.2 | 56,275/3.1 | |
| RSMs containing coil regions | 1,505/4.0 | 487/2.8 |
| 2,655/4.4 | 780/2.8 | |
| 4,185/4.5 | 1,066/2.9 | |
| 6,028/4.6 | 1,437/2.9 | |
| 8,399/4.6 | 1,841/3.0 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Johansson, M.U.; Zoete, V.; Guex, N. Recurrent Structural Motifs in Non-Homologous Protein Structures. Int. J. Mol. Sci. 2013, 14, 7795-7814. https://doi.org/10.3390/ijms14047795
Johansson MU, Zoete V, Guex N. Recurrent Structural Motifs in Non-Homologous Protein Structures. International Journal of Molecular Sciences. 2013; 14(4):7795-7814. https://doi.org/10.3390/ijms14047795
Chicago/Turabian StyleJohansson, Maria U., Vincent Zoete, and Nicolas Guex. 2013. "Recurrent Structural Motifs in Non-Homologous Protein Structures" International Journal of Molecular Sciences 14, no. 4: 7795-7814. https://doi.org/10.3390/ijms14047795
APA StyleJohansson, M. U., Zoete, V., & Guex, N. (2013). Recurrent Structural Motifs in Non-Homologous Protein Structures. International Journal of Molecular Sciences, 14(4), 7795-7814. https://doi.org/10.3390/ijms14047795