2.1. Estimation of the Dynamic Viscosities
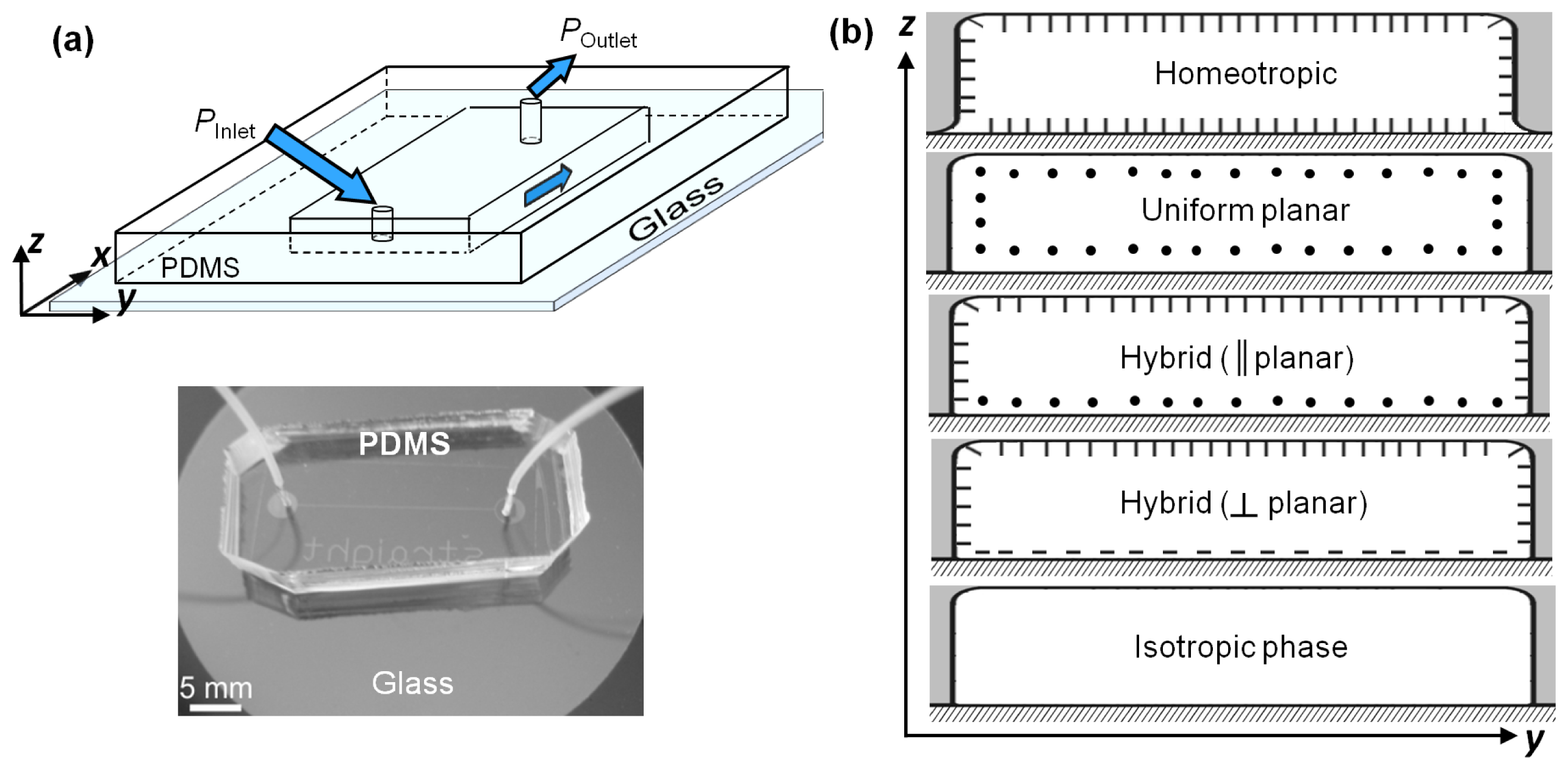
Estimation of the dynamic viscosity constitutes the first step towards characterizing the fluidic resistance of nematofluidic systems. The dynamic viscosities were measured under different boundary conditions (surface anchoring) over a range of driving pressures applied along the channel length. The inlet of the microchannel was connected to a pressure controller (discussed in Section 2.2), and the outlet was left at atmospheric pressure. For ensuring a reduced influence of the side walls, high aspect ratio (width/depth = w/d ~ 133) microchannels were considered for the viscosity measurements. The width, w was maintained at ~2 mm, whereas the channel depth, d, was fixed at ~15 μm. The nematic director in absence of any flow was determined by the surface-induced anchoring within the microchannels. Based on this initial director equilibrium with respect to the flow direction, v⃗, two limiting cases of the flow-director interactions emerge:
- a)
homeotropic anchoring: ↛ ⊥ v⃗ and ∇v⃗ || ↛, and
- b)
uniform planar anchoring: ↛ || v⃗.
Additionally, measurements were carried out for 5CB in isotropic phase (~35 °C).
Figure 1 plots the experimental estimation of the effective dynamic viscosity of 5CB as a function of the applied pressure difference Δ
P = Pinlet− Poutlet. The effective viscosity, η, was calculated by measuring the mass flow rate of 5CB at different pressure differences from the well-known relation:
Here,
w,
d, and
l ~ 4 cm denote the channel dimensions. ρ, Δ
P, and
ṁ signify 5CB density, applied pressure difference, and the measured mass flow rate, respectively. Two different values of 5CB density were considered: in nematic phase ρ = 1025 kg/m
3, and in isotropic phase ρ = 1013 kg/m
3[
17]. The prefactor
A in
Equation 1 depends upon the geometric dimensions of the channel [
16,
18], and was evaluated from the experiments: The flow rate of NLC 5CB was measured at a pressure difference of 200 mbar within a channel having no specific anchoring (degenerate anchoring) conditions. Using the average bulk viscosity of 5CB ~30 mPas at room temperature, the value of
A = 1.48 was experimentally determined for the given dimensions of the microchannel. The expansion of PDMS (either due to high pressures or due to elevated temperatures), and the pressure drop at the inlet tubing of the channel (~0.3 mbar at maximum flow rates), were neglected in determining the actual pressure at the inlet port. As is evident from
Equation 1, the relative change of the effective viscosity is affected only by the change in the mass flow rate, for a given microchannel under similar thermodynamic conditions.
The dynamic viscosity of the system was estimated from
Equation (1). For each value of the applied pressure, the mass of the NLC 5CB flowing out of the channel was measured over time. By varying the pressure at the channel inlet, we obtained the dependence of the mass flow rate on the pressure difference along the channel. Measurements were carried out for homeotropic, uniform planar and isotropic flow cases, and plotted in
Figure 1 (see inset). The effective viscosity for each of the cases is presented in
Figure 1. The measured viscosities of 5CB clearly varied with the magnitude of the driving pressure, and additionally, on the nature of the channel boundary conditions. At low driving pressures, the dynamic viscosity was observed to be significantly higher (up to ~5 times) for homeotropic conditions (
ηH), compared to the flow where the velocity and initial director were mutually parallel (
ηP). The measurements of 5CB flow in isotropic phase indicated lowest effective viscosity for the entire range of applied pressure difference. Consequently, for a similar difference of pressure between the inlet and the outlet ports, nematic 5CB flowed with the slowest speed in the homeotropic channel, whereas the flow in isotropic phase was the fastest. The difference between the effective viscosities of the homeotropic and uniform planar cases is particularly remarkable at applied pressures Δ
P < 100 mbar (
Figure 1): as the pressure increases the relative difference drops. This can be understood by considering the competing effects of the flow-induced viscous torque, and the surface-induced elastic torque, characterized by the non-dimensional number, Ericksen number,
Er. Typically,
Er >> 1 suggests a dominating influence of the viscous forces over its elastic counterpart. In the present experiment, this value varied between 0 <
Er < 250 for the homeotropic, and 0 <
Er < 160 for the uniform planar flows. At low driving pressures, and hence low viscous torques, the flow-induced distortion of the initial homeotropic alignment is marginal due to a dominating effect of the counter elastic torque from the surface-aligned director. Correspondingly, the anisotropic coupling between the flow and the nematic viscosity (which depends on the local director orientation) leads to a reduced transport of the nematic matrix. In contrast, flow under uniform planar conditions is more favorable, since the director orientation offers a minimum counter elastic torque. As the applied pressure is increased for the homeotropic channel, the viscous torque begins to overcome the elastic torque, and the director of the nematic 5CB aligns gradually along the flow direction. This results in an easier transport of the nematic matrix, and resulting in a lower effective viscosity [
13]. At high enough pressure differences in a homeotropic channel, the molecules are aligned almost along the flow direction, the effective viscosity thereby approaching values similar to that of the uniform planar case (see
Figure 1). Additionally, with increase in the applied pressure, the absolute value of the effective viscosity experiences a steeper drop for the homeotropic case (~125 mPas to 50 mPas), in contrast to the uniform planar case (~50 mPas to 18 mPas). Experiments carried out in hybrid channels with anchoring on the glass surface parallel to the flow direction (|| planar, see
Figure 8b) yielded effective viscosities similar to those of
ηP ≈
η|| over the range of pressure difference considered here. The experimental values for
η⊥ (hybrid
⊥ planar) were found to lie between
ηH and
ηP Interestingly, the variation of the viscosity within the planar microchannel shows an initial rise, before going down at higher applied pressures. This variation of
ηP at low inlet pressures (Δ
P ~ 25 mbar) can be attributed to the flow-induced director reorientation of the planar aligned molecules [
19]. Due to the interplay of the viscous and the elastic torques, the director reorients slightly away from the initial state (
↛ ||
v⃗ ) on starting the flow. Consequently, the effective viscosity has an additional contribution from the projection of the director component out of the plane containing the flow and director fields. The reorientation continues till the viscous torque vanishes at the critical Leslie angle [
19]. Thereafter, the viscosity reduces monotonically, as in the case of the homeotropic boundary conditions. By varying the applied pressure difference by ~200 mbar along the given microchannel, we could tune the relative change in the dynamic viscosity over the range 2 <
ηH/
ηP < 3.5. The overall behavior of the nematic microflow is in accordance to the expected shear thinning trend of the bulk 5CB [
20]. The present experiments additionally show that the shear thinning nature of 5CB holds true for each anchoring case, and also for the isotropic phase.
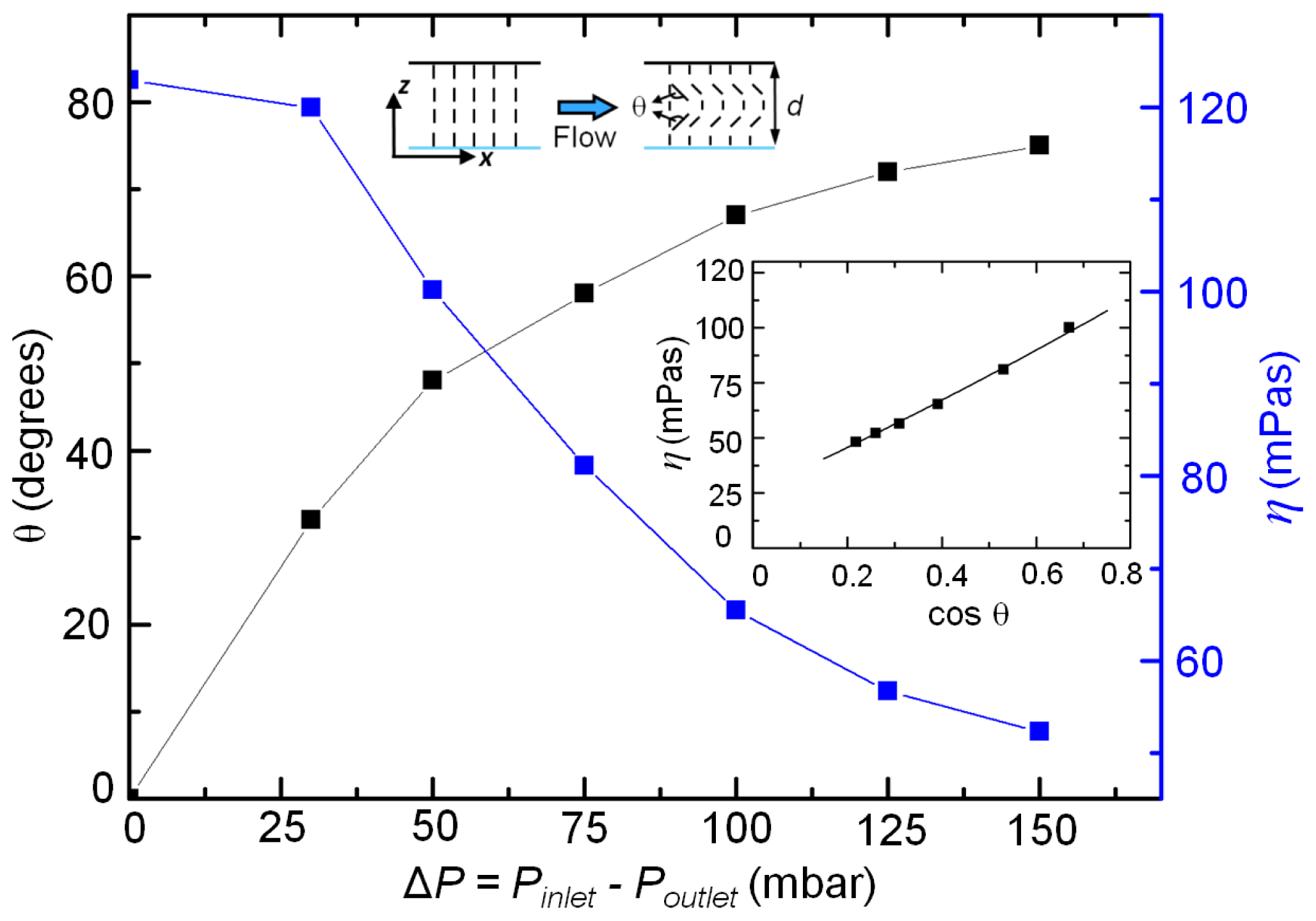
The variation of the dynamic viscosity is particularly prominent within microchannels having homeotropic anchoring. With increasing driving pressure, the nematic director distorts relative to the initial orientation. The average distortion of the nematic director, θ (see inset schematic,
Figure 2), was experimentally estimated from the optical birefringence measurements [
21]. We have used polarization optical microscopy to record the flow-induced birefringence (and its order). Within a microchannel of known depth, the birefringence was then used to calculate the average director distortion. As plotted in
Figure 2, the distortion angle θ (black squares) exhibits a non-linear rise with increasing driving pressure (and hence, flow speed), shown here for a 15 μm deep channel. The blue squares plot the corresponding decrease in the effective viscosity. The dependence of the nematic viscosity at any general value of the director distortion was obtained by plotting the former as a function of cosθ = ||
v⃗×
↛||/(||
v⃗|| ||
↛||) [
22]. The inset plot in
Figure 2 presents the variation of the effective viscosity with cos θ, which was fitted using a second degree polynomial as:
The values of the coefficients were found to be
p1 = 15.3,
p2 = 98.3, and
p3 = 25.4, all in the units of mPas. In the present configuration of the flow and director fields, the nematic director cannot withstand viscous torques, and consequently deform even with small driving pressures. Using the above relation, the effective viscosity in the limit of no flow situation (Δ
P → 0, θ → 0), is evaluated to be 139 mPas. This is within 15% of the reported 5CB viscosity, measured under homeotropic (
↛ ⊥
v⃗ and ∇
v⃗ ||
↛ ) condition [
17]. In the limit of flow alignment of the nematic director, θ → θ
Leslie ~78 degrees [
21], the effective viscosity is estimated to be 46 mPas. Thus, over the entire range of the angular distortion, the apparent viscosity drops by ~90 mPas in a homeotropic microchannel. The trend observed in our experiments agrees well that calculated using a friction model for shear flows of NLCs [
22]. However, the rate at which the viscosity drops (with the director deformation) is observed to be slower in our experiments, as is evident from the slope of the fitting function.
2.2. Estimation of the Fluidic Resistance
The fluidic resistance in a microchannel bears direct analogies with the electrical resistance of a current carrying wire [
18]. In the simplest case of an electrical circuit, the resistance is measured as the ratio
, where
Relec, Δ
V, and
I refer to the electrical resistance, applied voltage, and the current flow respectively. The electrical resistance,
Relec, takes into account the conductor geometry and the material resistivity, the latter obtained from the Drude model of electron scattering [
23].
In the parlance of microfluidics, the relevant transport occurs due to the driving pressure across the channel. Hence, the fluidic resistance in a channel, Rflow, is obtained as the ratio between the driving pressure difference and the volume flow rate:
where, ΔP is the applied pressure difference (analogous to the applied voltage, ΔV ), and
is the volume flow rate (analogous to the current flowing in an electrical circuit, I). In analogy to the electrical resistance, here
is dependent on the channel geometry, and η acts as the material resistivity. Correspondingly, the fluidic resistance per unit length of the channel is:
The analysis of fluid flows as electrical circuits allows us to apply equivalent rules to fluidic networks. For instance, the well known Kirchhoff’s current and voltage laws can be used to estimate the flow rates and pressure drops across different elements of a fluidic network. In case of nematofluidics, one has to take into account the apparent flow-induced viscosity, depending upon the existing boundary conditions. Consequently, the alignment of the nematic director relative to the flow (which can be tuned by the nature of surface anchoring) additionally influences the effective fluidic resistance in the nematofluidic circuits. Corresponding to the measurements in
Figure 1, the fluidic resistance per unit length of the homeotropic, and planar channels varied from 8.4 <
rH < 27, and 4 <
rP < 11 respectively, while it ranged over 2.5 <
riso < 6.3 for the flow in isotropic phase. The values are in the units of 10
15 Pas/m
4.
Influence of the Channel Depth
As derived in
Equation (5), the fluidic resistance in a channel scales with the channel dimensions as
. For an infinitely wide channel, the value of
A approaches a numerical constant. Thus, for a channel transporting a Newtonian fluid (constant
η), the hydrodynamic resistance is influenced due to the channel geometry only: for instance,
d →
d/2,
rflow → 8
rflow. However, in case of nematic microflows, the effective enhancement of the resistance should have an additional component arising due to the coupling between the flow and the director fields (
η =
f(ν)). Precisely, one has to take into account not only the effect of the flow speed, but also of the confinement, on the apparent viscosity term. Due to the large variation of the effective viscosity over a given range of applied pressure (see
Figure 2), homeotropic microchannels have been considered here for evaluating the influence of the channel depth.
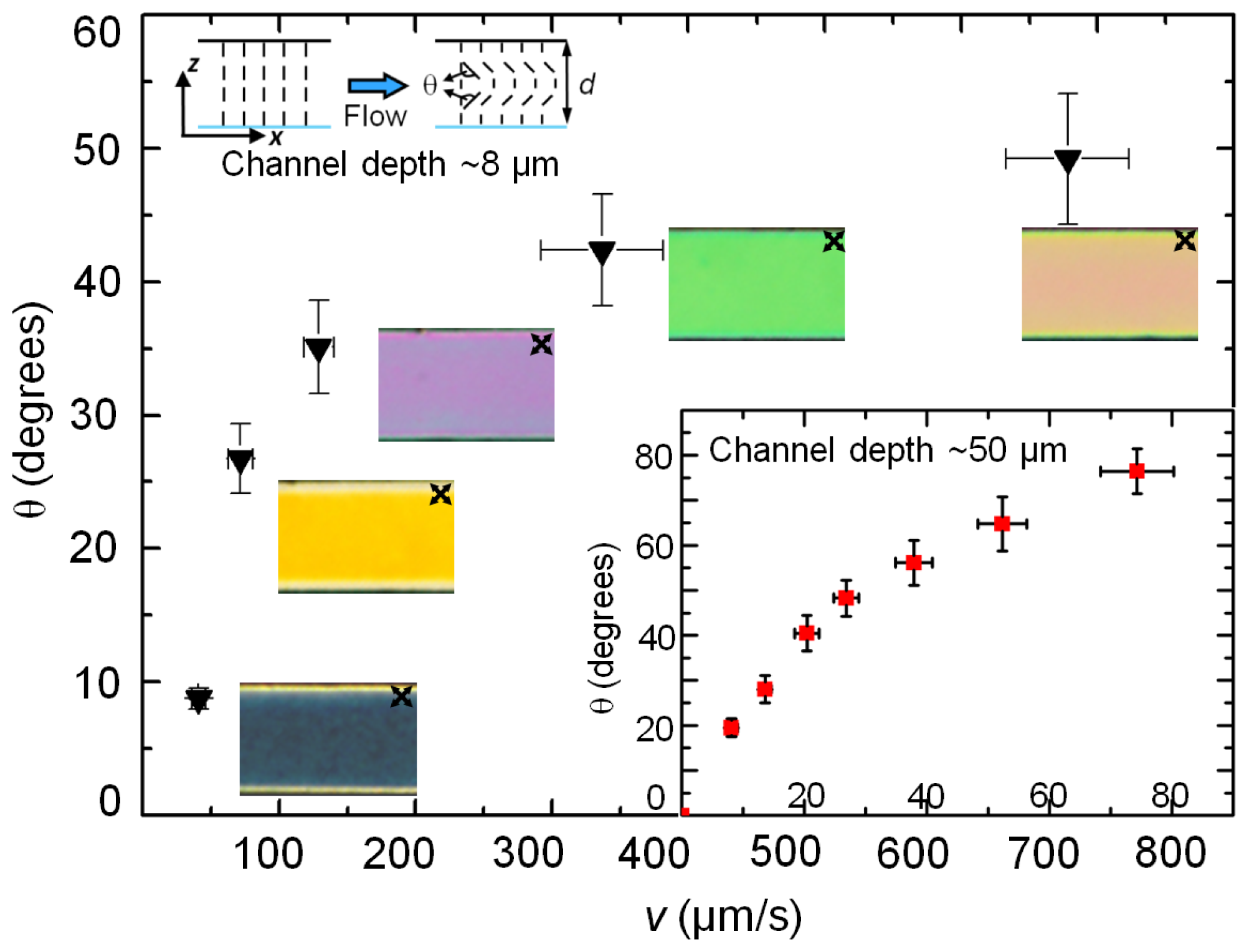
Figure 3 plots the flow-induced deformation of the nematic director in two different channels with depths,
d ~ 8 μm and 50 μm, both having width,
w = 100 μm. The flow speed was measured by tracking tracer particles, whereas the director distortion was estimated by quantifying the flow-induced birefringence within the homeotropic channels. From the initial homeotropic alignment, the nematic director begins to rotate along the flow direction. At low enough driving pressures, the viscous torque is countered by the surface-induced elastic torque, thereby hindering the director deformation. With increasing driving pressure, the average deformation angle, θ, increases until a saturation value (~78 degrees for 5CB at room temperature [
21]) is reached at which the viscous torque on the director vanishes. In
Figures 1 and
2, we have presented the corresponding reduction of the apparent viscosity.
The perturbation of the director field can be visually observed in white light microscopy by placing the sample between crossed polarizers. Because of the homeotropic anchoring conditions, the sample exhibits, at zero flow, apparently no birefringence along the
z direction. On increasing the flow speed
v (and thus increasing θ), the effective birefringence along
z increases and, for an appropriate sample thickness, one can expect a sequence of interference colors to appear [
21].
Figure 3 shows the polarized micrographs of the series of interference colors corresponding to different flow speeds as observed in an 8 μm deep microchannel. The director deformed over 7 < θ < 49 degrees as the flow speed was varied between ~10 to 700 μm/s. In contrast, the nematic director within the 50 μm deep channel attained the saturation angle at a significantly lower flow speed,
v ~ 80 μm/s (see
Figure 3, inset). It is thus easier to distort the static director field within a deeper channel – due to a weaker surface-induced elastic interaction—as compared to a shallow one, in which the strong confinement conditions assist to stabilize the homeotropic director orientation. For instance, to distort the director by ~40 degrees, one requires a flow speed of ~300 μm/s in a 8 μm deep channel, compared to ~20 μm/s in the 50 μm deep channel. Equivalently, as the characteristic length of the system (typically the channel depth) increases, the viscous torque overcomes the elastic torque at relatively lower flow speeds (and hence applied pressure difference). By introducing
ηθ (from
Equation (2)) in
Equation (5), we can generalize the expression for the flow resistance:
At a given flow speed, the ratio of the fluidic resistances in the homeotropic channels of similar widths but with different channel depths, d1 > d2 is thus given by:
The first term in
Equation (7),
signifies the relative change in the fluidic resistance due to the channel geometry, whereas the second term,
, arises solely due to the average deformation of the director. Since,
d1 >
d2, for a given flow speed (or applied pressure difference), θ
1 > θ
2. Using the measured values of the director deformation from
Figure 3: corresponding to
v ~ 40 μm/s, θ
1 ~ 56 degrees for
d1 = 50 μm, and θ
2 ~9 degrees for
d1 = 8 μm, the enhanced fluidic resistance of the shallower channel is
. This is about 60% more than that due to the usual hydrodynamic considerations.
2.4. Transition to Isotropic Phase
In Section 3.1, we have observed that 5CB in isotropic phase had the least effective viscosity over the entire range of applied pressure difference. In one of our previous works, we have demonstrated that the profile of a nematic microflow could be steered by applying a temperature gradient (between 25 °C and 32 °C) across the width of the channel [
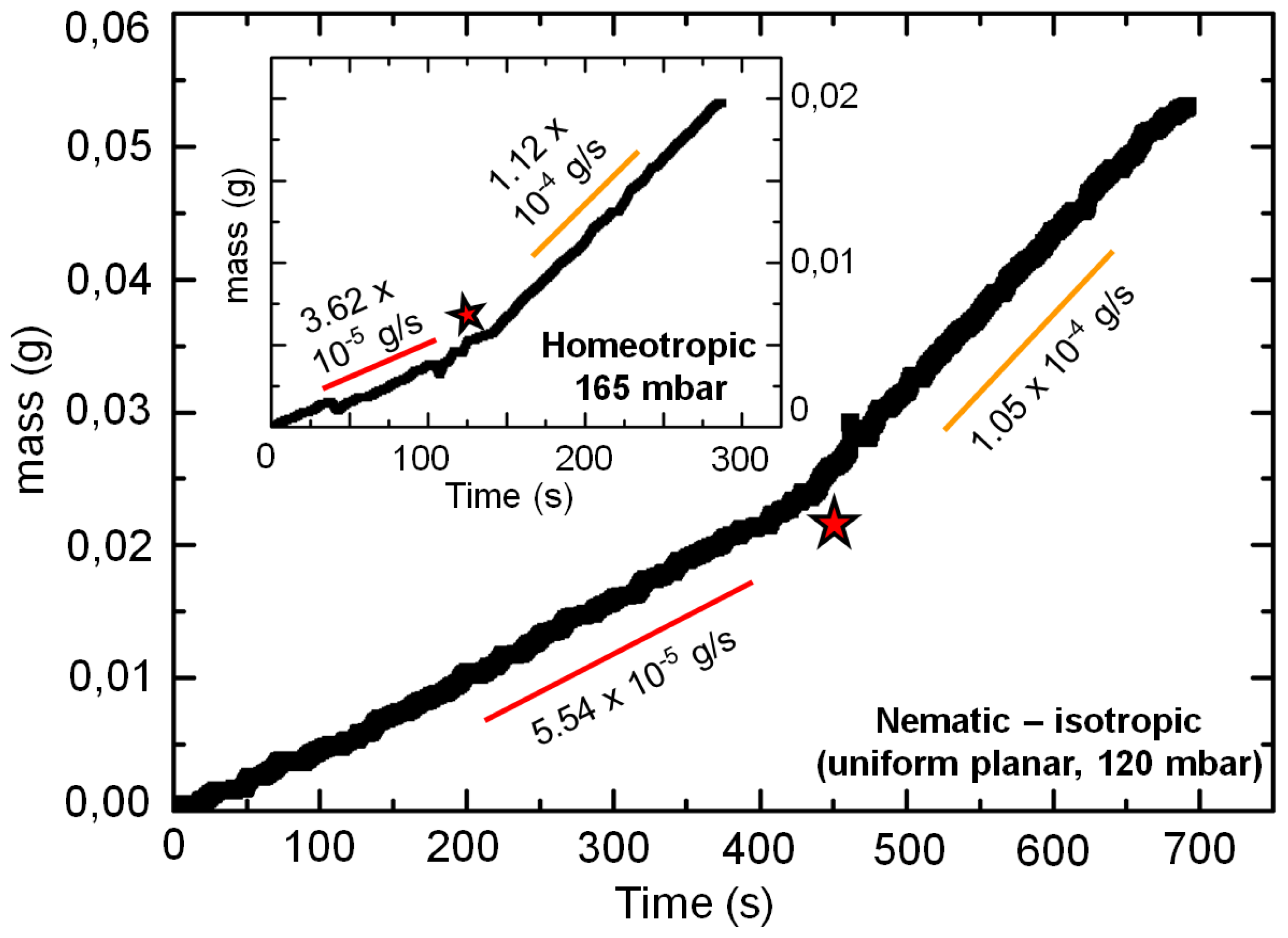
13]. Here, we carry out the experiments at an elevated temperature (~35 °C), so that the flowing nematic undergoes a transition to isotropic phase. The variation of the mass flow is plotted over time, as shown in
Figure 5. The measured mass flow, acquired from microchannels possessing two distinct anchoring conditions—uniform planar and homeotropic—both indicate an enhancement after transition to isotropic phase. At a given value of applied pressure, the mass flow rate enhanced by ~100% in planar case (at 120 mbar), and by ~200% in homeotropic case (165 mbar) upon transition from the nematic to the isotropic phase. Correspondingly, the effective viscosity approximately reduced from 25 mPas to 13 mPas in planar case, and from 53 mPas to 17 mPas in the homeotropic confinement. The temperature-induced reduction of the effective viscosity in the liquid crystalline material is significant considering that a usual isotropic fluid undergoes only a marginal drop for the corresponding temperature variation [
2].
The quantitative distinction, at the phase transition, between the two cases described above can be understood by analyzing the temperature-induced director alignment of 5CB. It is well established that the nematic liquid crystal molecules undergo thermal reorientation on variation of the temperature [
24]. For instance, with increasing temperature, the NLC molecules of a homeotropic sample gradually reorient parallel to the confining surfaces. This can be readily visualized using polarization optical microscopy when an LC cell, filled with 5CB, is gradually heated up to the nematic-isotropic phase transition temperature. In the present context, such an occurrence reduces the effective viscosity within the homeotropic confinement more drastically, in comparison to the uniform planar case. The temperature dependence of flow-alignment in NLCs, close to the transition temperature, was investigated experimentally by Gähwiller [
25], and the phenomenological relations were given by W. Helfrich [
26,
27]. The temperature-induced enhancement of the mass flow rate suggests a change in the flow profile. This is currently being investigated. On lowering the temperature, the flow-aligned nematic state is recovered. The degree of molecular order becomes larger again, and the effective viscosity is once again determined only by the relative orientation between the director and the flow fields.
2.5. Microfluidic Circuits via Composite Anchoring Templates
The characterizations of the nematic microflows presented here elucidate different possibilities to modulate fluidic resistance: surface anchoring, confinement, and temperature. In addition, electric field effects offer a promising approach to tune nematic flows [
28,
29]. The anisotropic coupling between the viscous and elastic interactions in a flowing NLC material is fundamental in modulating the flow properties. This is in contrast to isotropic fluids, wherein any variation is achieved generally through morphological patterning of the microfluidic architecture.
The discussed anisotropic attributes offer interesting avenues to tune the fluidic resistance in microchannels. For instance, spatially modulated flow fields can be created within microchannels by incorporating composite boundary conditions, as the ones shown in
Figure 6. Typically, one half of the glass substrate was treated for uniform planar anchoring, and the other half for homeotropic anchoring. After a brief exposure of the PDMS relief (with the imprinted microchannel) to plasma, it was surface-bonded to the pre-treated glass substrate. The fabricated channels were left overnight, during which PDMS reverted back to its native surface properties (favouring homeotropic anchoring) [
30]. The resulting anchoring on the microchannel walls is thus composite: one half homeotropic and the other hybrid || planar. As we have discussed before, microchannels possessing hybrid || planar surface anchoring has a significantly lower fluidic resistance compared to one having homeotropic anchoring.
Figure 6a presents an optical micrograph (
xy plane) of a NLC filled microfluidic device with composite anchoring conditions. As observed between crossed-polarizers, the left half of the channel is homeotropic, while the right half is functionalized to create hybrid || planar anchoring. Consequently, the fluidic resistance is higher on the left side of the channel as compared to the right side:
rH >
r||. In analogy to electrical circuits, this configuration presents a standard series connection of the resistors. The effective resistance per unit channel length is thus given by
reffective =
rH +
r||. Complementing the series connection,
Figure 6b shows the polarized micrograph (
xy plane) of a fluidic circuit having a combination of resistances in parallel: The upper half of the channel has hybrid || planar anchoring, while the lower half possesses homeotropic anchoring. For an applied pressure difference, the flow through the upper part was observed to be faster than that through the lower part. The equivalent resistance per unit length is given by
. It is rather straightforward to extend the series or the parallel configuration of the fluidic resistors by repeating each unit
i.e., repeating the nature of the surface anchoring, alternately.
Figure 6c presents a microfluidic node with three distinct anchoring conditions. Here, the three arms of the T-channel have three different fluidic resistances:
r⊥,
r||, and
rH respectively in the lower, right, and left arms, essentially creating a fluidic junction with flow guidance capabilities. In fact, one can fabricate a range of fluidic resistances by orienting the PDMS channels appropriately on a glass surface possessing uniform planar anchoring. One such example is shown in
Figure 6d. While the channels on the left half of the micrograph have all homeotropic anchoring, the ones on the right half have varying resistance. The resistance is lowest for the channel parallel to the direction of the flow (
r||), and gradually goes up,
rα <
rβ, as the angular separation of the channel path relative to the uniform alignment on the glass surface increases. It is worthwhile to note here that the flow of an isotropic fluid does not make any distinction between these distinct regions with specific fluidic resistances. Since the channel dimensions in each case remain fixed, the surface induced variation of the nematic resistance will have no bearing on isotropic fluid flows.
The composite anchoring templates within simple microfluidic confinements offer interesting applications including spatial modulation of flow profiles and speeds, guiding flow at a branched architecture, and separation of colloidal particles. Here we briefly demonstrate the application of an anchoring template in a T-junction as a nematofluidic valve. Using appropriate surface functionalization, the microchannel is divided symmetrically into homeotropic (left) and hybrid sections (
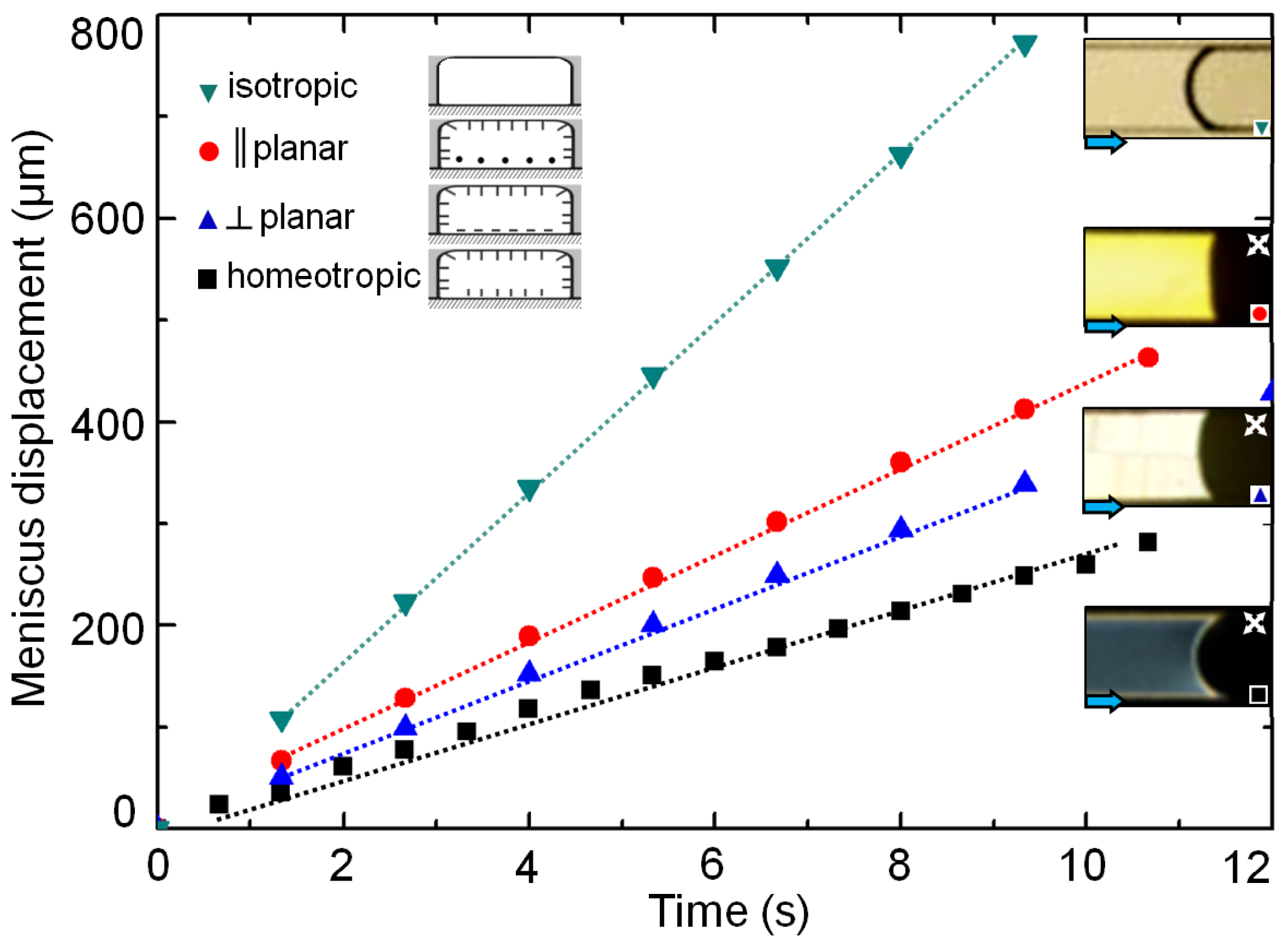
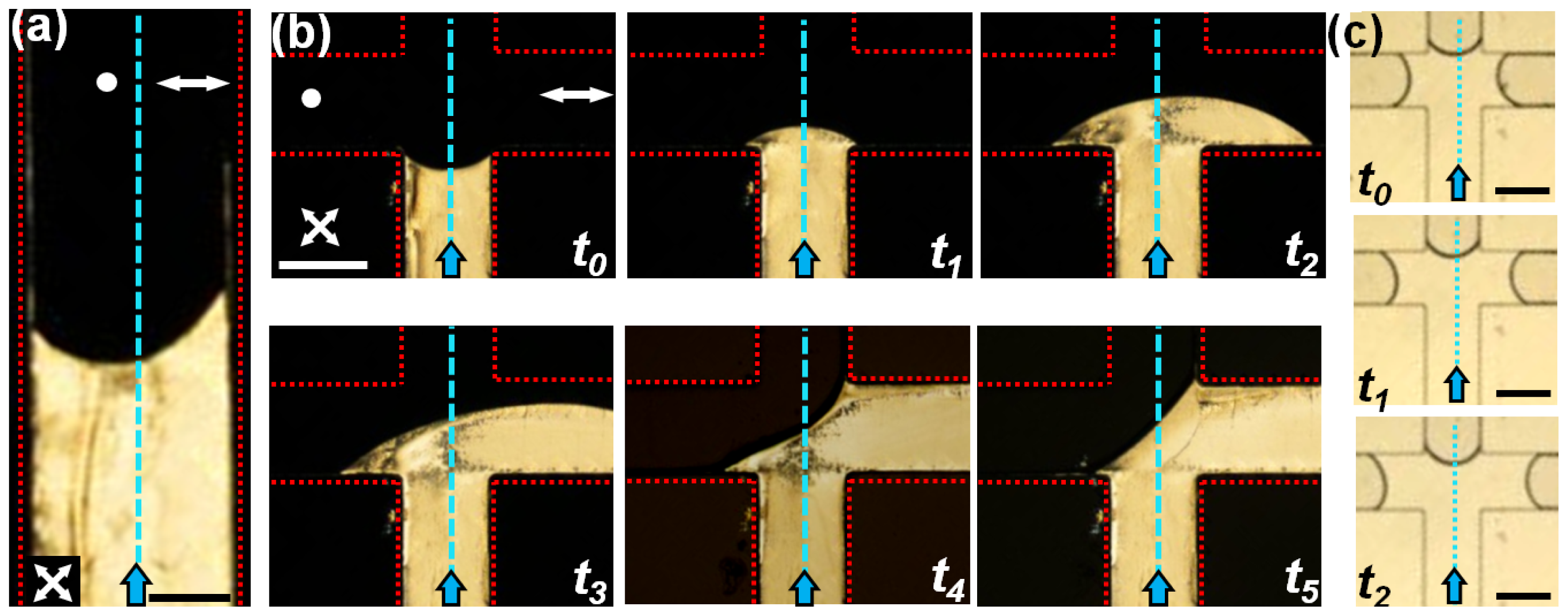
Figure 7) about the blue dotted lines. The channel is filled through the vertical arm of the T-channel using a constant gravitational head. Interestingly, the shape of the meniscus is asymmetric in the vertical arm (
Figure 7a) due to distinct anchoring conditions on either side of the channel (the red dotted lines indicate the channel walls).
Figure 7b shows a time sequence of polarized optical micrographs when the flow reaches the T-junction. As seen clearly, with increasing time, the nematic flow is guided preferentially along the right arm of the channel. Over time, the flow reaches a steady state and stabilizes completely at the right arm of the microchannel (
t5 of
Figure 7b). Flow can be however introduced to the left arm by increasing the outlet pressure of the right arm. The subsequent flow along the homeotropic arm is preceded by disruption of the stable interface between air and nematic 5CB, aligned diagonally at the junction (see
t5 of
Figure 7b). The stability of this interface under different pressure conditions is currently under investigation. In contrast to the nematic case, 5CB in isotropic phase does not exhibit preferential guidance along any arm of the T-junction. This is shown in
Figure 7c: both the arms of the channel have equal distribution of nematic volume at any given time.