Spontaneous Crystallization in Athermal Polymer Packings
Abstract
:1. Introduction
2. Methodology
2.1. System Studied/Monte Carlo Algorithm
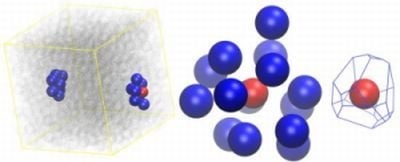
2.2. Analysis of Local Structure, Voronoi Cell and Characteristic Crystallographic Element Norm
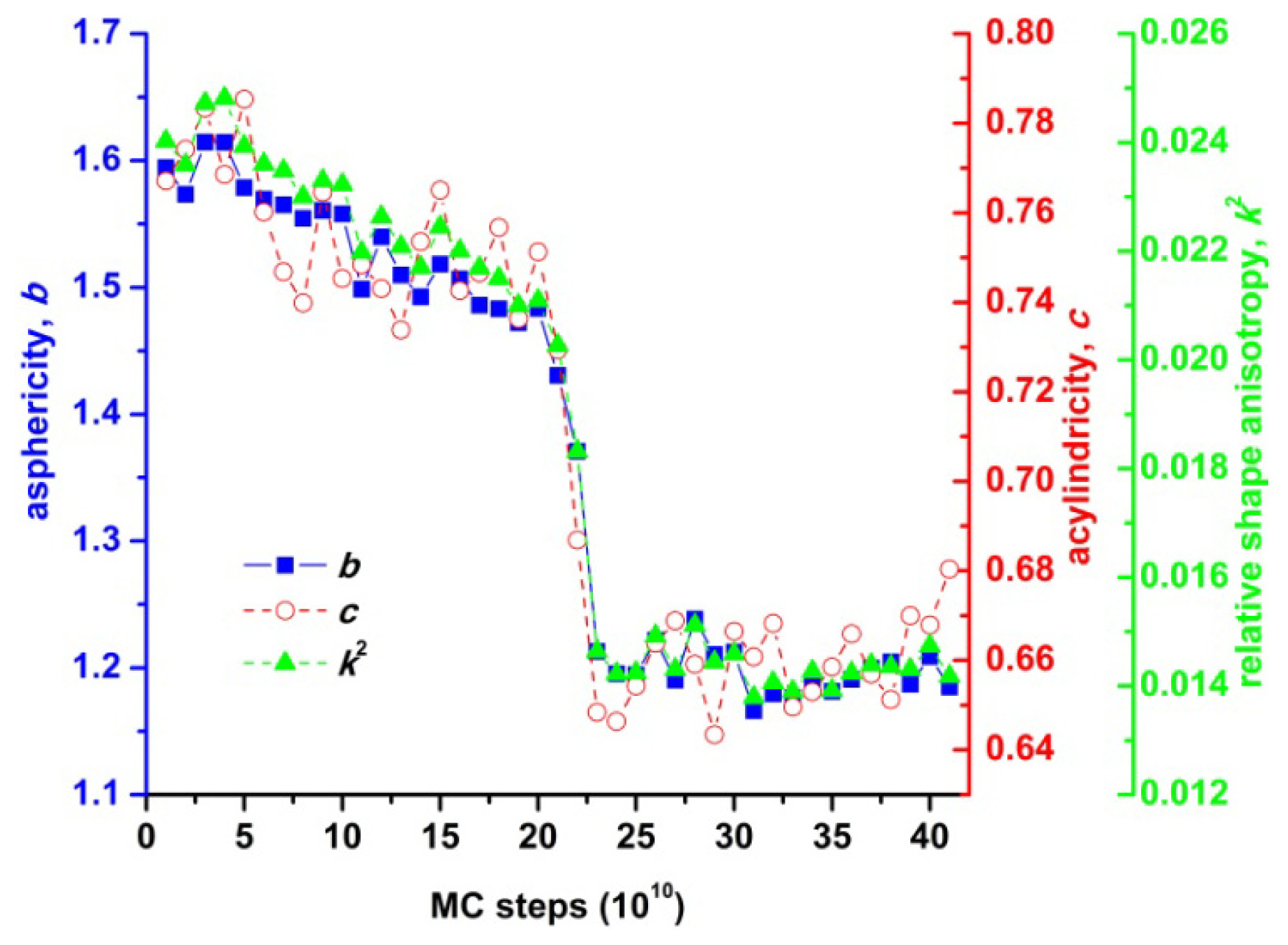
- asphericity:
- acylindricity:
- and relative shape anisotropy:
3. Results and Discussion
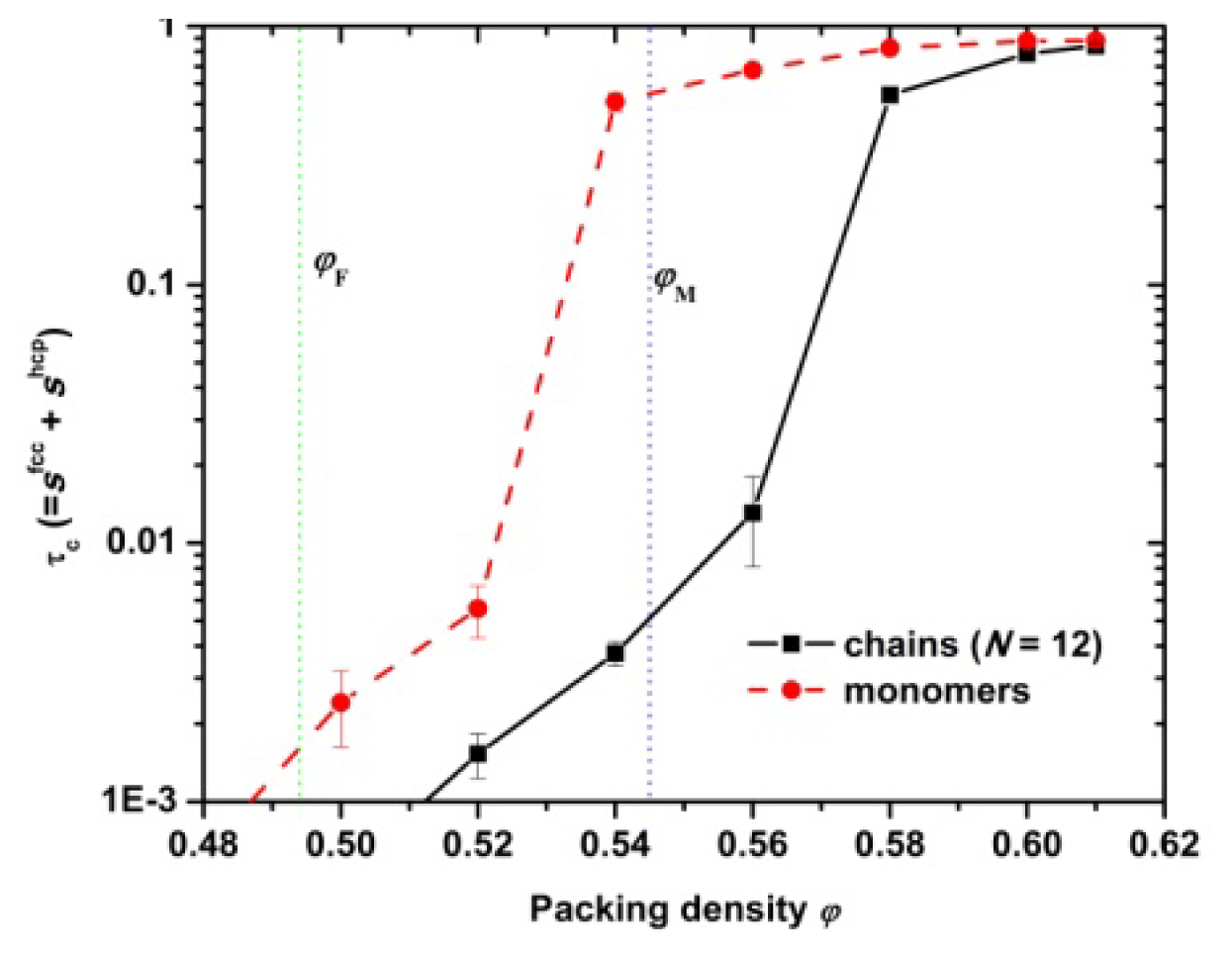
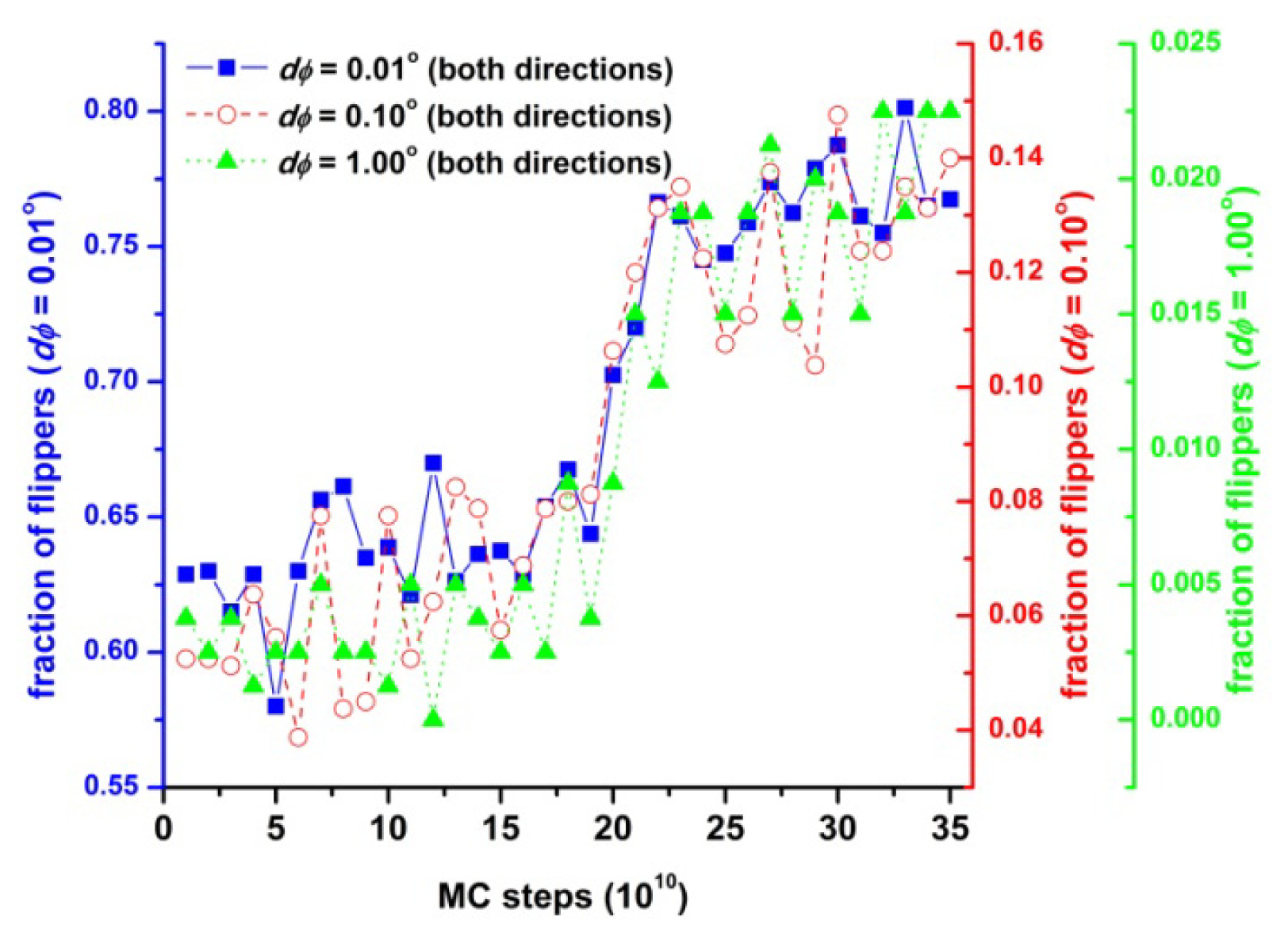
3.1. Phase Transition of Athermal Systems: Effect of Chain Connectivity
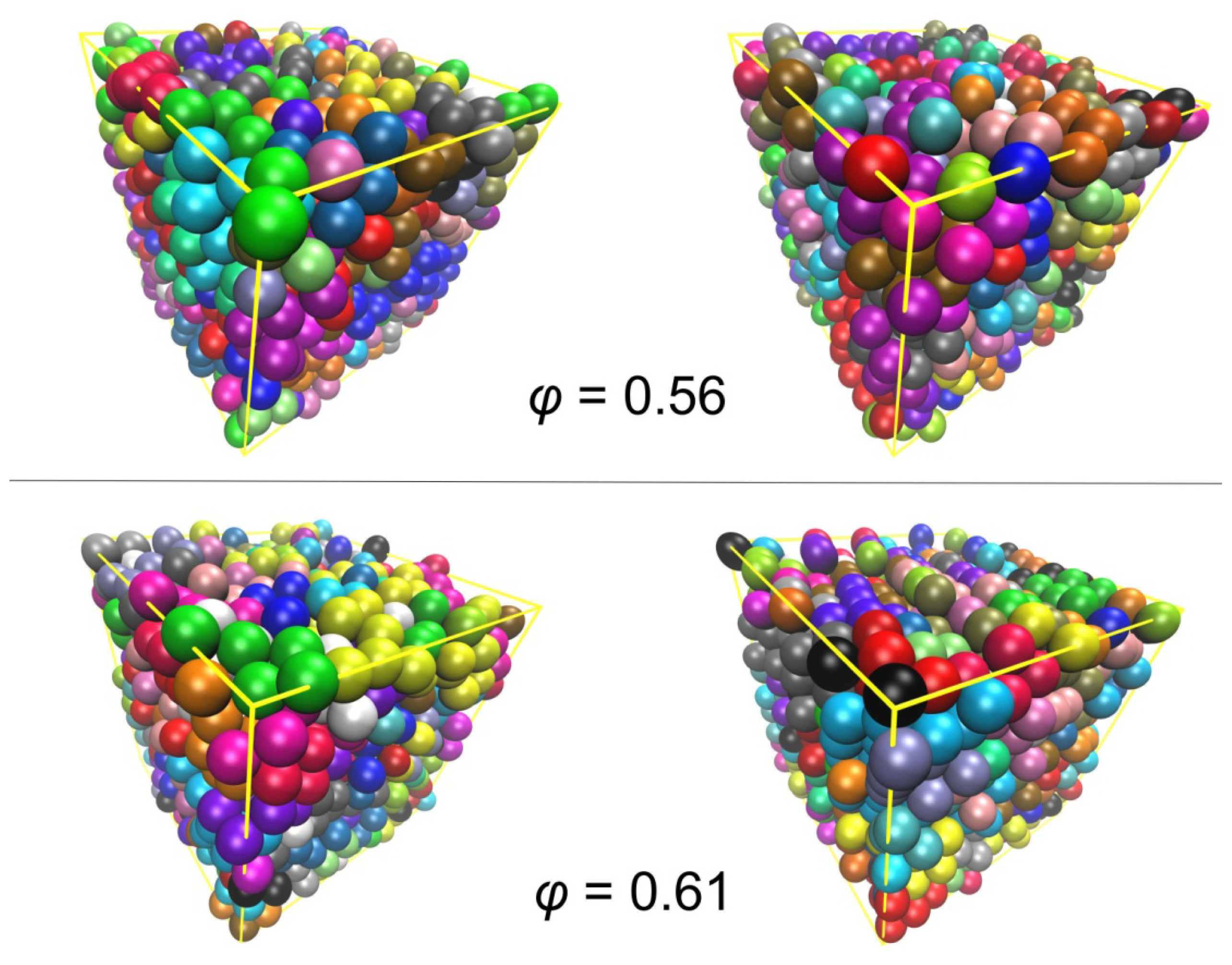
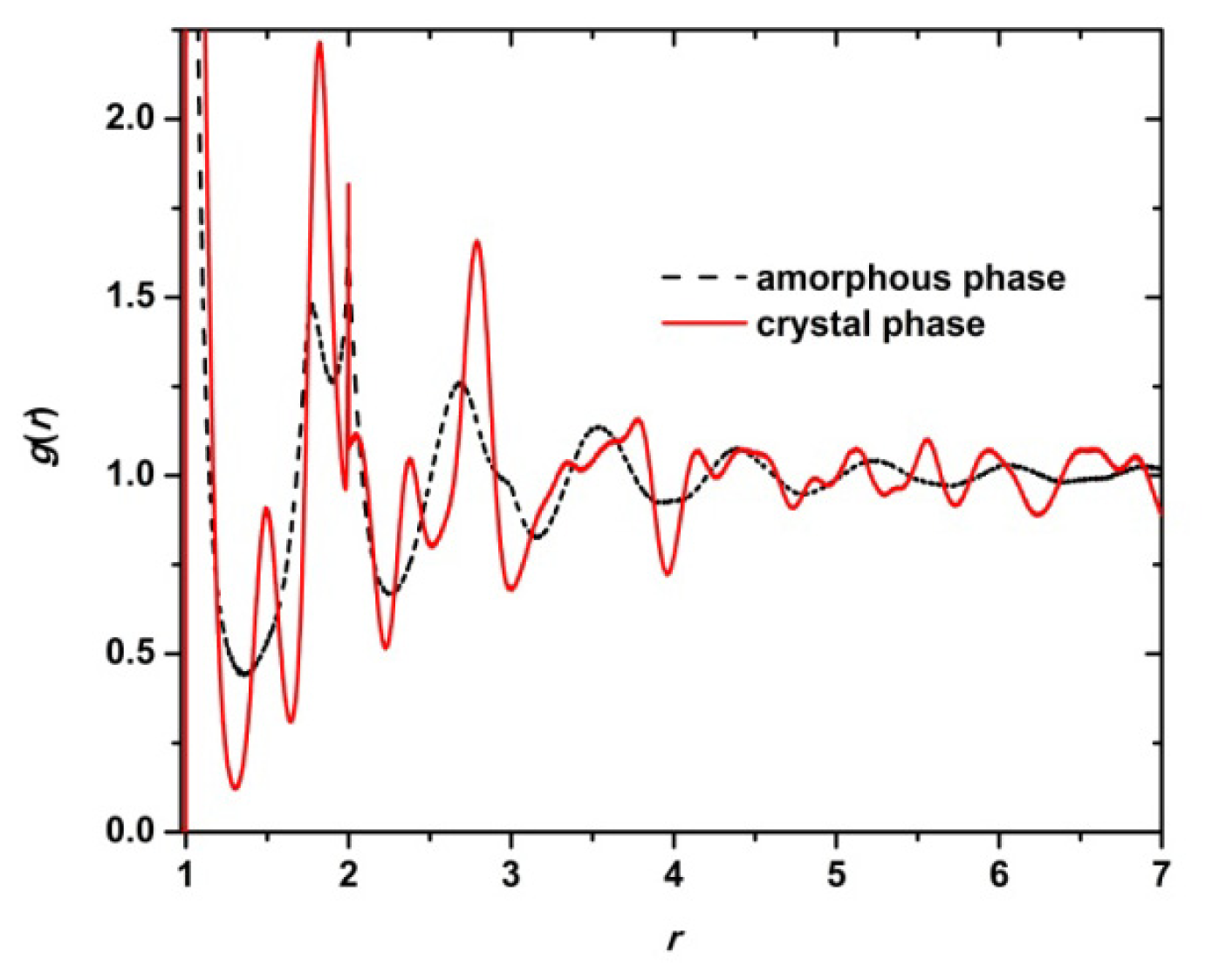
3.2. Crystal Morphologies in Ordered Packings of Athermal Chains
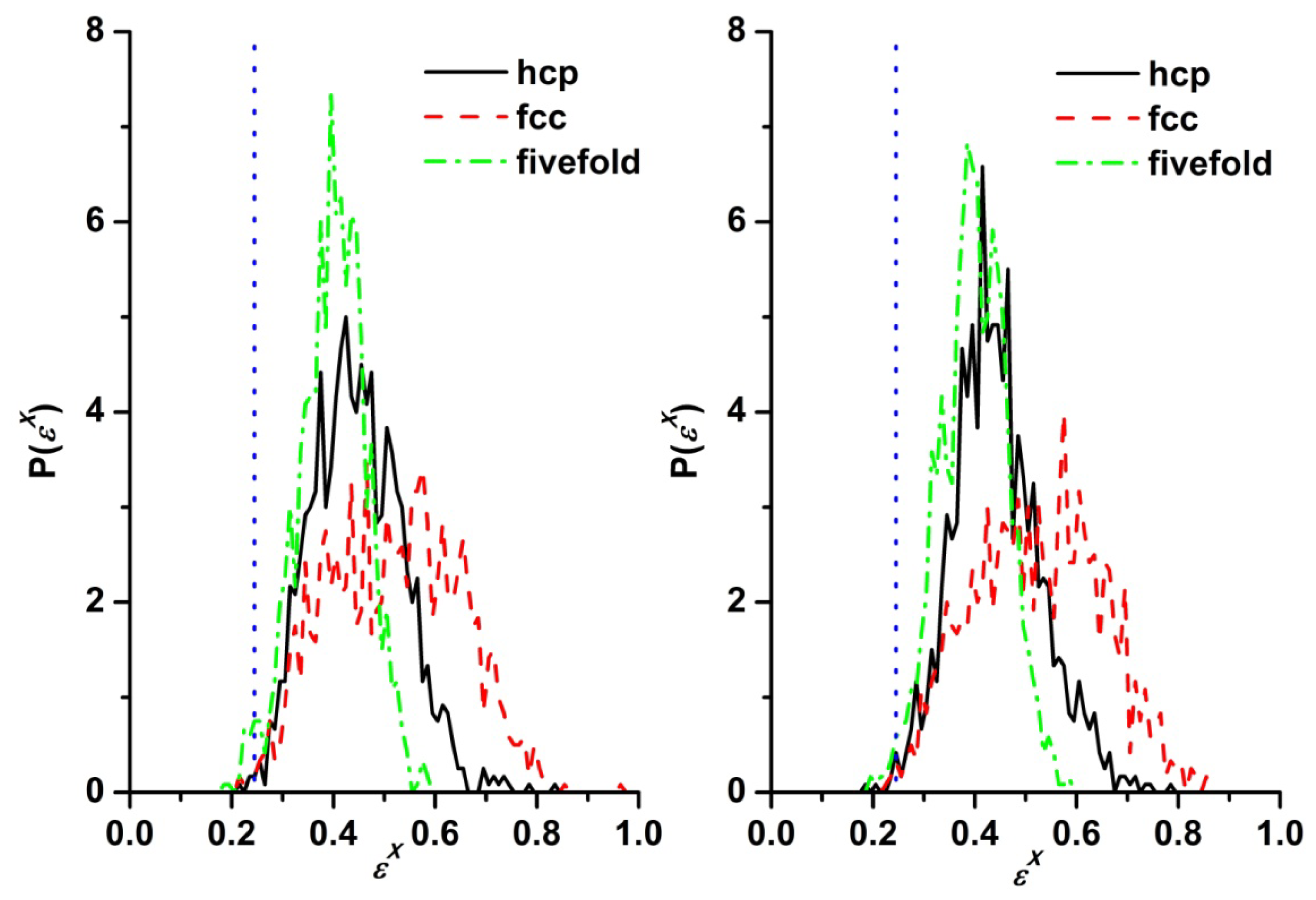
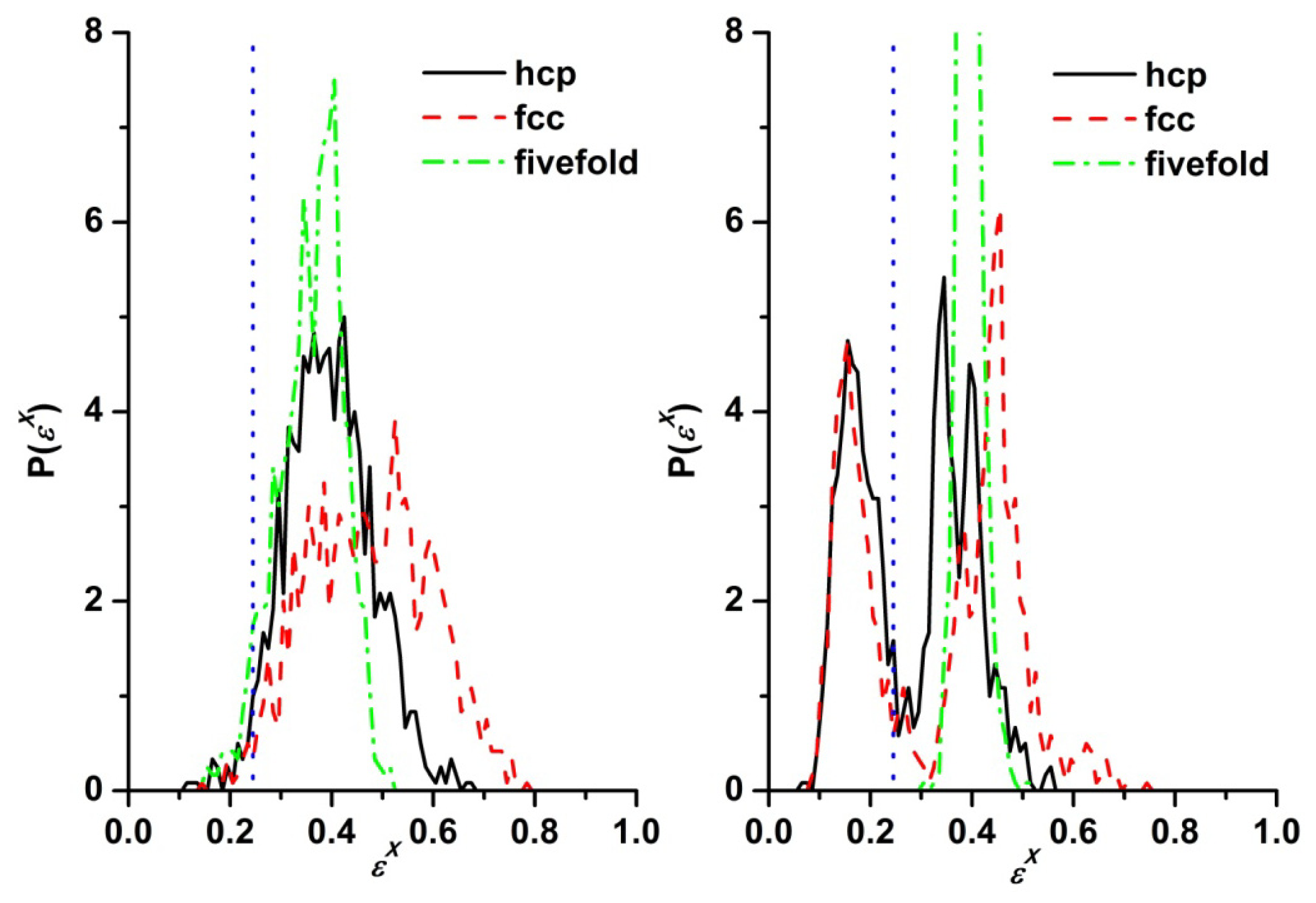
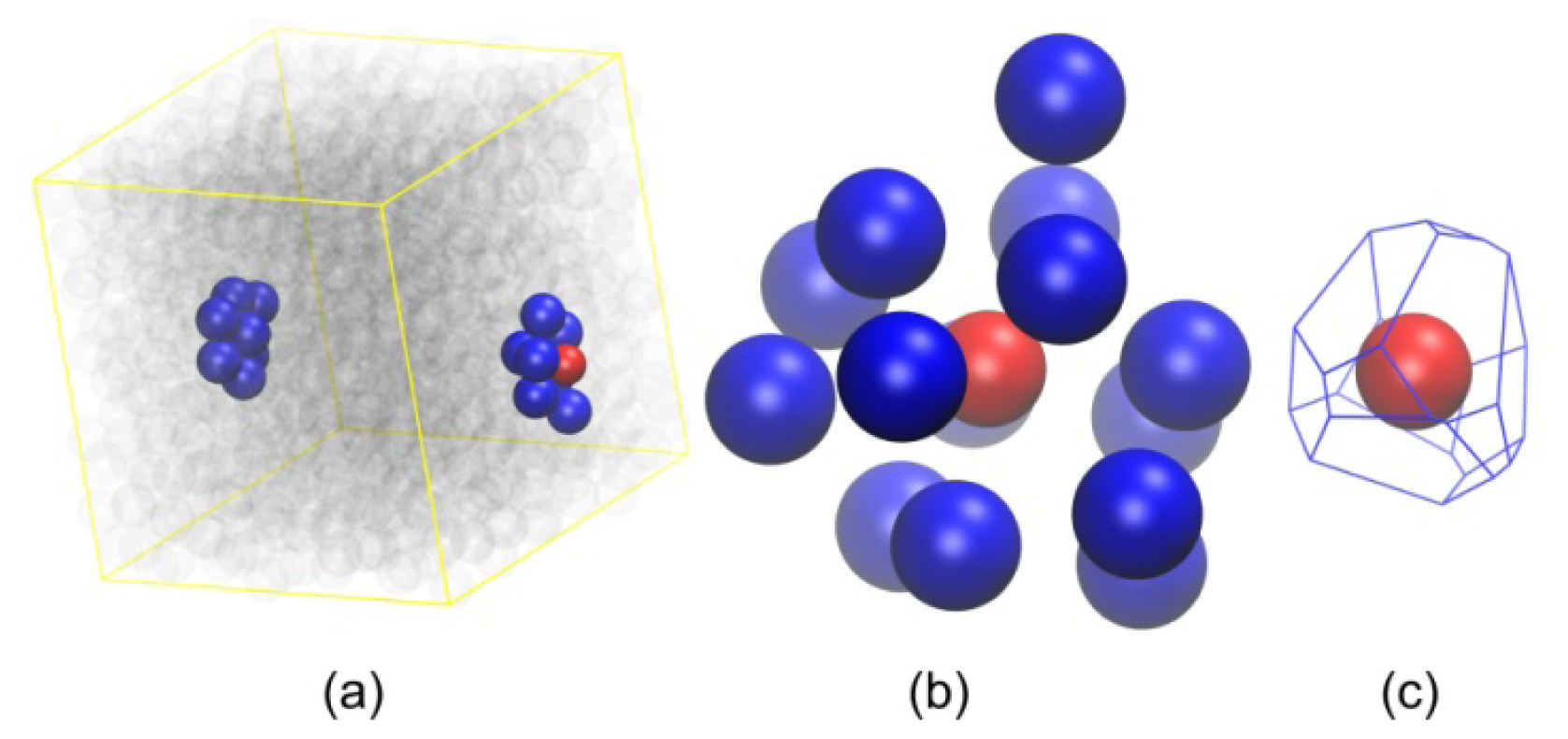
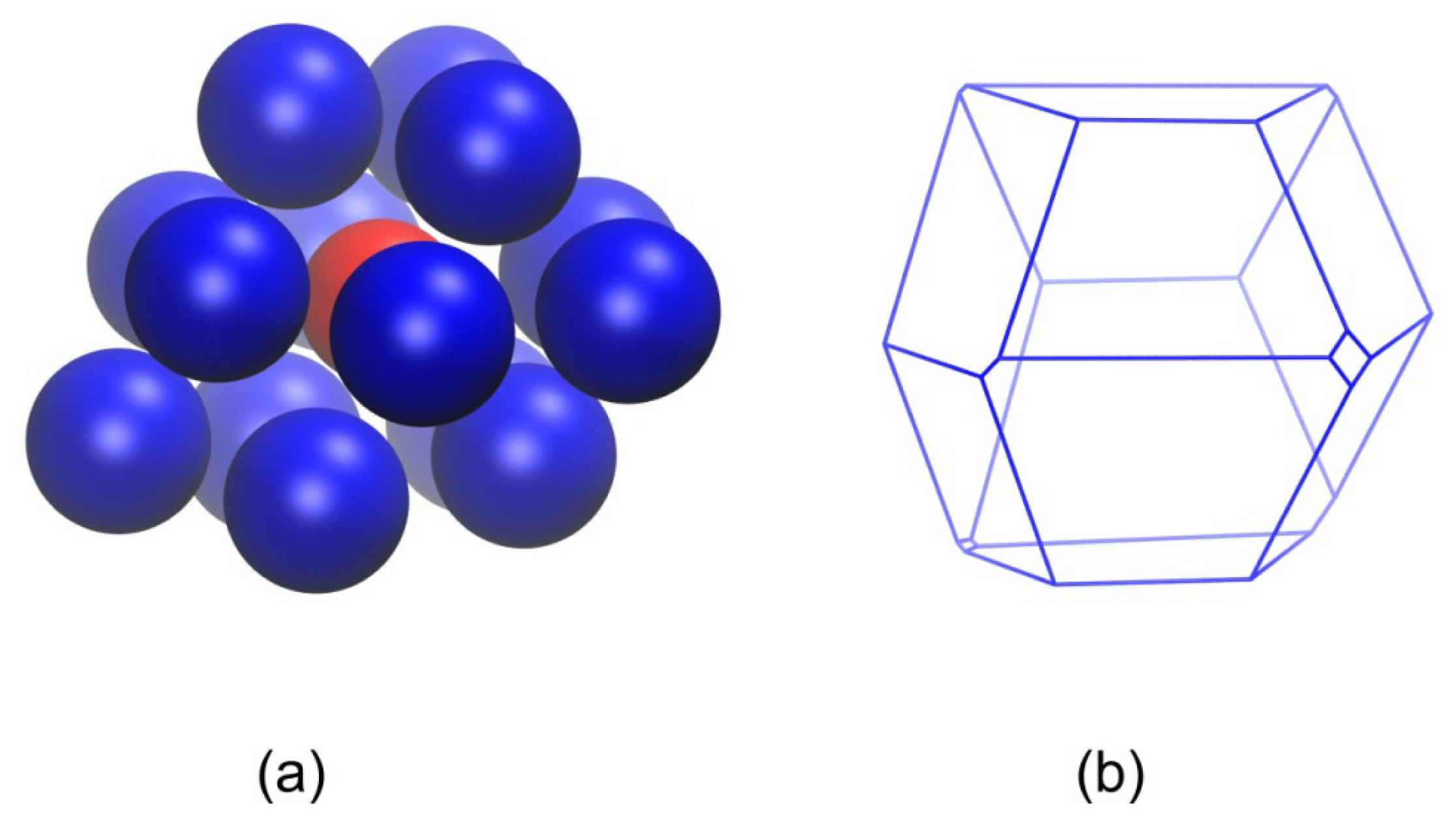
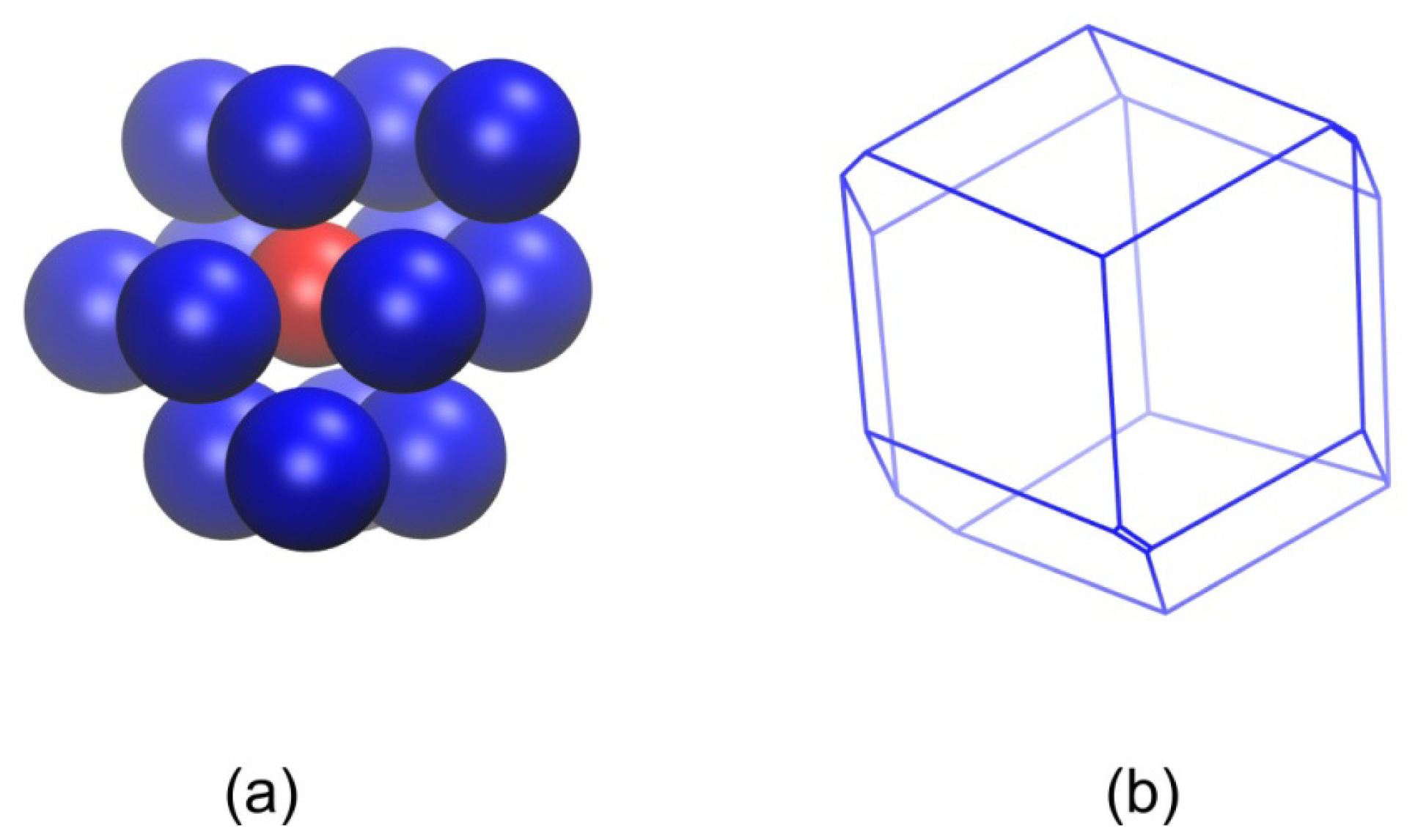
3.3. Evolution of the Voronoi Cell during Hard-Sphere Crystallization
3.4. Entropic Origins of Crystallization in Hard-Sphere Chain Packings
4. Conclusions
Acknowledgments
- Conflict of InterestThe authors declare no conflict of interest.
References
- Russo, J.; Tanaka, H. The microscopic pathway to crystallization in supercooled liquids. Sci. Rep 2012, 2, 505. [Google Scholar]
- Leocmach, A.; Tanaka, H. Roles of icosahedral and crystal-like order in the hard spheres glass transition. Nat. Commun 2012, 3, 974. [Google Scholar]
- Jones, M.R.; Macfarlane, R.J.; Lee, B.; Zhang, J.A.; Young, K.L.; Senesi, A.J.; Mirkin, C.A. DNA-nanoparticle superlattices formed from anisotropic building blocks. Nat. Mater 2010, 9, 913–917. [Google Scholar]
- Nykypanchuk, D.; Maye, M.M.; van der Lelie, D.; Gang, O. DNA-guided crystallization of colloidal nanoparticles. Nature 2008, 451, 549–552. [Google Scholar]
- Hegedus, J.; Elliott, S.R. Microscopic origin of the fast crystallization ability of ge-sb-te phase-change memory materials. Nat. Mater 2008, 7, 399–405. [Google Scholar]
- Gundlach, D.J.; Royer, J.E.; Park, S.K.; Subramanian, S.; Jurchescu, O.D.; Hamadani, B.H.; Moad, A.J.; Kline, R.J.; Teague, L.C.; Kirillov, O.; et al. Contact-induced crystallinity for high-performance soluble acene-based transistors and circuits. Nat. Mater 2008, 7, 216–221. [Google Scholar]
- Campoy-Quiles, M.; Ferenczi, T.; Agostinelli, T.; Etchegoin, P.G.; Kim, Y.; Anthopoulos, T.D.; Stavrinou, P.N.; Bradley, D.D.C.; Nelson, J. Morphology evolution via self-organization and lateral and vertical diffusion in polymer: Fullerene solar cell blends. Nat. Mater 2008, 7, 158–164. [Google Scholar]
- Hales, T.C. A proof of the Kepler conjecture. Ann. Math 2005, 162, 1065–1185. [Google Scholar]
- Hales, T.C.; Ferguson, S.P. A formulation of the Kepler conjecture. Discret. Comput. Geom 2006, 36, 21–69. [Google Scholar]
- Hales, T.C.; Harrison, J.; McLaughlin, S.; Nipkow, T.; Obua, S.; Zumkeller, R. A revision of the proof of the Kepler conjecture. Discret. Comput. Geom 2010, 44, 1–34. [Google Scholar]
- Bernal, J.D. Geometry of the structure of monatomic liquids. Nature 1960, 185, 68–70. [Google Scholar]
- Scott, G.D.; Knight, K.R.; Bernal, J.D.; Mason, J. Radial distribution of random close packing of equal spheres. Nature 1962, 194, 956–957. [Google Scholar]
- Bernal, J.D.; Finney, J.L. Random close-packed hard-sphere model. II. Geometry of random packing of hard spheres. Discuss. Faraday Soc 1967, 43, 62–69. [Google Scholar]
- Finney, J.L. Random packings and the structure of simple liquids. I. Geometry of random close packing. Proc. Roy. Soc. Lond. A 1970, 319, 479–493. [Google Scholar]
- Torquato, S.; Truskett, T.M.; Debenedetti, P.G. Is random close packing of spheres well defined? Phys. Rev. Lett 2000, 84, 2064–2067. [Google Scholar]
- Torquato, S.; Stillinger, F.H. Jammed hard-particle packings: From Kepler to Bernal and beyond. Rev. Mod. Phys 2010, 82, 2633–2672. [Google Scholar]
- Charbonneau, P.; Ikeda, A.; Parisi, G.; Zamponi, F. Glass transition and random close packing above three dimensions. Phys. Rev. Lett 2011, 107, 185702. [Google Scholar]
- Parisi, G.; Zamponi, F. Mean-field theory of hard sphere glasses and jamming. Rev. Mod. Phys 2010, 82, 789–845. [Google Scholar]
- O’Hern, C.S.; Silbert, L.E.; Liu, A.J.; Nagel, S.R. Jamming at zero temperature and zero applied stress: The epitome of disorder. Phys. Rev. E 2003, 68, 011306. [Google Scholar]
- Briscoe, C.; Song, C.; Wang, P.; Makse, H.A. Entropy of jammed matter. Phys. Rev. Lett 2008, 101, 188001. [Google Scholar]
- Brujic, J.; Song, C.M.; Wang, P.; Briscoe, C.; Marty, G.; Makse, H.A. Measuring the coordination number and entropy of a 3d jammed emulsion packing by confocal microscopy. Phys. Rev. Lett 2007, 98, 248001. [Google Scholar]
- Song, C.; Wang, P.; Makse, H.A. A phase diagram for jammed matter. Nature 2008, 453, 629–632. [Google Scholar]
- Stachurski, Z.H. Definition and properties of ideal amorphous solids. Phys. Rev. Lett 2003, 90, 155502. [Google Scholar]
- O’Hern, C.S.; Langer, S.A.; Liu, A.J.; Nagel, S.R. Random packings of frictionless particles. Phys. Rev. Lett 2002, 88, 075507. [Google Scholar]
- Trappe, V.; Prasad, V.; Cipelletti, L.; Segre, P.N.; Weitz, D.A. Jamming phase diagram for attractive particles. Nature 2001, 411, 772–775. [Google Scholar]
- Corwin, E.I.; Jaeger, H.M.; Nagel, S.R. Structural signature of jamming in granular media. Nature 2005, 435, 1075–1078. [Google Scholar]
- Xu, N.; Blawzdziewicz, J.; O’Hern, C.S. Random close packing revisited: Ways to pack frictionless disks. Phys. Rev. E 2005, 71, 061306. [Google Scholar]
- Kamien, R.D.; Liu, A.J. Why is random close packing reproducible? Phys. Rev. Lett 2007, 99, 155501. [Google Scholar]
- Goodrich, C.P.; Liu, A.J.; Nagel, S.R. Finite-size scaling at the jamming transition. Phys. Rev. Lett 2012, 109, 095704. [Google Scholar]
- Wang, K.; Song, C.M.; Wang, P.; Makse, H.A. Edwards Thermodynamics of the jamming transition for frictionless packings: Ergodicity test and role of angoricity and compactivity. Phys. Rev. E 2012, 86, 011305. [Google Scholar]
- Ikeda, A.; Berthier, L.; Sollich, P. Unified study of glass and jamming rheology in soft particle systems. Phys. Rev. Lett 2012, 109, 018301. [Google Scholar]
- Tighe, B.P. Relaxations and rheology near jamming. Phys. Rev. Lett 2011, 107, 158303. [Google Scholar]
- Lopatina, L.M.; Reichhardt, C.J.O.; Reichhardt, C. Jamming in granular polymers. Phys. Rev. E 2011, 84, 011303. [Google Scholar]
- Anikeenko, A.V.; Medvedev, N.N.; Aste, T. Structural and entropic insights into the nature of the random-close-packing limit. Phys. Rev. E 2008, 77, 031101. [Google Scholar] [Green Version]
- Jiao, Y.; Torquato, S. Maximally random jammed packings of platonic solids: Hyperuniform long-range correlations and isostaticity. Phys. Rev. E 2011, 84, 041309. [Google Scholar]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci 1949, 51, 627–659. [Google Scholar]
- Alder, B.J.; Wainwright, T.E. Phase transition for a hard sphere system. J. Chem. Phys 1957, 27, 1208–1209. [Google Scholar]
- Wood, W.W.; Jacobson, J.D. Preliminary results from a recalculation of the monte carlo equation of state of hard spheres. J. Chem. Phys 1957, 27, 1207–1208. [Google Scholar]
- Auer, S.; Frenkel, D. Suppression of crystal nucleation in polydisperse colloids due to increase of the surface free energy. Nature 2001, 413, 711–713. [Google Scholar]
- Auer, S.; Frenkel, D. Prediction of absolute crystal-nucleation rate in hard-sphere colloids. Nature 2001, 409, 1020–1023. [Google Scholar]
- Auer, S.; Frenkel, D. Line tension controls wall-induced crystal nucleation in hard-sphere colloids. Phys. Rev. Lett 2003, 91, 015703. [Google Scholar]
- Auer, S.; Frenkel, D. Numerical prediction of absolute crystallization rates in hard-sphere colloids. J. Chem. Phys 2004, 120, 3015–3029. [Google Scholar]
- Auer, S.; Frenkel, D. Quantitative prediction of crystal-nucleation rates for spherical colloids: A computational approach. Annu. Rev. Phys. Chem 2004, 55, 333–361. [Google Scholar]
- Blaak, R.; Auer, S.; Frenkel, D.; Lowen, H. Crystal nucleation of colloidal suspensions under shear. Phys. Rev. Lett 2004, 93, 068303. [Google Scholar]
- Bolhuis, P.G.; Frenkel, D.; Mau, S.C.; Huse, D.A. Entropy difference between crystal phases. Nature 1997, 388, 235–236. [Google Scholar]
- Cacciuto, A.; Auer, S.; Frenkel, D. Onset of heterogeneous crystal nucleation in colloidal suspensions. Nature 2004, 428, 404–406. [Google Scholar]
- Eldridge, M.D.; Madden, P.A.; Frenkel, D. Entropy-driven formation of a superlattice in a hard-sphere binary mixture. Nature 1993, 365, 35–37. [Google Scholar]
- Frenkel, D. Computation challenges in complex liquids: Entropy-driven phase-transitions. Futur. Gener. Comp. Syst 1994, 10, 207–212. [Google Scholar]
- Frenkel, D. Entropy-driven phase transitions. Phys. A (Amsterdam, Neth. ) 1999, 263, 26–38. [Google Scholar]
- Frenkel, D.; Lekkerkerker, H.N.W.; Stroobants, A. Thermodynamic stability of a smectic phase in a system of hard-rods. Nature 1988, 332, 822–823. [Google Scholar]
- Stroobants, A.; Lekkerkerker, H.N.W.; Frenkel, D. Evidence for one-dimensional, two-dimensional, and 3-dimensional order in a system of hard parallel spherocylinders. Phys. Rev. A 1987, 36, 2929–2945. [Google Scholar]
- Hoover, W.G.; Ree, F.H. Melting transition and communal entropy for hard spheres. J. Chem. Phys 1968, 49, 3609. [Google Scholar]
- Rintoul, M.D.; Torquato, S. Metastability and crystallization in hard-sphere systems. Phys. Rev. Lett 1996, 77, 4198–4201. [Google Scholar]
- Valeriani, C.; Sanz, E.; Pusey, P.N.; Poon, W.C.K.; Cates, M.E.; Zaccarelli, E. From compact to fractal crystalline clusters in concentrated systems of monodisperse hard spheres. Soft Matter 2012, 8, 4960–4970. [Google Scholar]
- Karayiannis, N.C.; Malshe, R.; de Pablo, J.J.; Laso, M. Fivefold symmetry as an inhibitor to hard-sphere crystallization. Phys. Rev. E 2011, 83, 061505. [Google Scholar]
- Karayiannis, N.C.; Malshe, R.; Kroger, M.; de Pablo, J.J.; Laso, M. Evolution of fivefold local symmetry during crystal nucleation and growth in dense hard-sphere packings. Soft Matter 2012, 8, 844–858. [Google Scholar]
- Pusey, P.N.; Zaccarelli, E.; Valeriani, C.; Sanz, E.; Poon, W.C.K.; Cates, M.E. Hard spheres: Crystallization and glass formation. Philos. Trans. R. Soc. A 2009, 367, 4993–5011. [Google Scholar]
- Zaccarelli, E.; Valeriani, C.; Sanz, E.; Poon, W.C.K.; Cates, M.E.; Pusey, P.N. Crystallization of hard-sphere glasses. Phys. Rev. Lett 2009, 103, 135704. [Google Scholar]
- Moriguchi, I.; Kawasaki, K.; Kawakatsu, T. Long-lived glassy states in dense nearly hard-sphere colloids. J. Phys. II 1995, 5, 143–157. [Google Scholar]
- Henderson, S.I.; Mortensen, T.C.; Underwood, S.M.; vanMegen, W. Effect of particle size distribution on crystallisation and the glass transition of hard sphere colloids. Phys. A (Amsterdam, Neth. ) 1996, 233, 102–116. [Google Scholar]
- Williams, S.R.; Royall, C.P.; Bryant, G. Crystallization of dense binary hard-sphere mixtures with marginal size ratio. Phys. Rev. Lett 2008, 100, 225502. [Google Scholar]
- Cheng, Z.D.; Chaikin, P.M.; Zhu, J.X.; Russel, W.B.; Meyer, W.V. Crystallization kinetics of hard spheres in microgravity in the coexistence regime: Interactions between growing crystallites. Phys. Rev. Lett 2002, 88, 015501. [Google Scholar]
- Zhu, J.X.; Li, M.; Rogers, R.; Meyer, W.; Ottewill, R.H.; Russell, W.B.; Chaikin, P.M. Crystallization of hard-sphere colloids in microgravity. Nature 1997, 387, 883–885. [Google Scholar]
- Panaitescu, A.; Reddy, K.A.; Kudrolli, A. Nucleation and crystal growth in sheared granular sphere packings. Phys. Rev. Lett 2012, 108, 108001. [Google Scholar]
- Besseling, T.H.; Hermes, M.; Fortini, A.; Dijkstra, M.; Imhof, A.; van Blaaderen, A. Oscillatory shear-induced 3d crystalline order in colloidal hard-sphere fluids. Soft Matter 2012, 8, 6931–6939. [Google Scholar]
- Veshnev, V.P.; Nurlygayanov, T.A. Crystallization of hard spheres near wall. Tech. Phys. Lett 2011, 37, 863–865. [Google Scholar]
- Beyer, R.; Iacopini, S.; Palberg, T.; Schope, H.J. Polymer induced changes of the crystallization scenario in suspensions of hard sphere like microgel particles. J. Chem. Phys 2012, 136, 234906. [Google Scholar]
- Edmond, K.V.; Nugent, C.R.; Weeks, E.R. Influence of confinement on dynamical heterogeneities in dense colloidal samples. Phys. Rev. E 2012, 85, 041401. [Google Scholar]
- Dorosz, S.; Schilling, T. On the influence of a patterned substrate on crystallization in suspensions of hard spheres. J. Chem. Phys 2012, 136, 044702. [Google Scholar]
- Bruce, A.D.; Wilding, N.B.; Ackland, G.J. Free energy of crystalline solids: A lattice-switch monte carlo method. Phys. Rev. Lett 1997, 79, 3002–3005. [Google Scholar]
- Woodcock, L.V. Entropy difference between the face-centred cubic and hexagonal close-packed crystal structures. Nature 1997, 385, 141–143. [Google Scholar]
- Ostwald, W. Studien über die Bildung and Umwandlung fester Körper. Z. Phys. Chem 1897, 22, 289–330. [Google Scholar]
- Pusey, P.N.; Vanmegen, W.; Bartlett, P.; Ackerson, B.J.; Rarity, J.G.; Underwood, S.M. Structure of crystals of hard colloidal spheres. Phys. Rev. Lett 1989, 63, 2753–2756. [Google Scholar]
- Anderson, V.J.; Lekkerkerker, H.N.W. Insights into phase transition kinetics from colloid science. Nature 2002, 416, 811–815. [Google Scholar]
- Dolbnya, I.P.; Petukhov, A.V.; Aarts, D.; Vroege, G.J.; Lekkerkerker, H.N.W. Coexistence of rhcp and fcc phases in hard-sphere colloidal crystals. Europhys. Lett 2005, 72, 962–968. [Google Scholar]
- O’Malley, B.; Snook, I. Crystal nucleation in the hard sphere system. Phys. Rev. Lett 2003, 90, 085702. [Google Scholar]
- Anikeenko, A.V.; Medvedev, N.N. Polytetrahedral nature of the dense disordered packings of hard spheres. Phys. Rev. Lett 2007, 98, 235504. [Google Scholar]
- Anikeenko, A.V.; Medvedev, N.N.; Bezrukov, A.; Stoyan, D. Observation of fivefold symmetry structures in computer models of dense packing of hard spheres. J. Non-Cryst. Solids 2007, 353, 3545–3549. [Google Scholar]
- Hoy, R.S.; Harwayne-Gidansky, J.; O’Hern, C.S. Structure of finite sphere packings via exact enumeration: Implications for colloidal crystal nucleation. Phys. Rev. E 2012, 85, 051403. [Google Scholar]
- Smith, K.C.; Alam, M.; Fisher, T.S. Athermal jamming of soft frictionless platonic solids. Phys. Rev. E 2010, 82, 051304. [Google Scholar]
- Torquato, S.; Jiao, Y. Organizing principles for dense packings of nonspherical hard particles: Not all shapes are created equal. Phys. Rev. E 2012, 86, 011102. [Google Scholar]
- Agarwal, U.; Escobedo, F.A. Mesophase behaviour of polyhedral particles. Nat. Mater 2011, 10, 230–235. [Google Scholar]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Predictive self-assembly of polyhedra into complex structures. Science 2012, 337, 453–457. [Google Scholar]
- De Graaf, J.; Manna, L. A roadmap for the assembly of polyhedral particles. Science 2012, 337, 417–418. [Google Scholar]
- Haji-Akbari, A.; Engel, M.; Glotzer, S.C. Degenerate quasicrystal of hard triangular bipyramids. Phys. Rev. Lett 2011, 107, 215702. [Google Scholar]
- Doppelbauer, G.; Noya, E.G.; Bianchi, E.; Kahl, G. Self-assembly scenarios of patchy colloidal particles. Soft Matter 2012, 8, 3768–3772. [Google Scholar]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M.; Kroger, M.; Mansfield, M.L. Universal scaling, entanglements, and knots of model chain molecules. Phys. Rev. Lett 2008, 101, 265702. [Google Scholar]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Contact network in nearly jammed disordered packings of hard-sphere chains. Phys. Rev. E 2009, 80, 011307. [Google Scholar]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The structure of random packings of freely jointed chains of tangent hard spheres. J. Chem. Phys 2009, 130, 164908. [Google Scholar]
- Karayiannis, N.C.; Kroger, M. Combined molecular algorithms for the generation, equilibration and topological analysis of entangled polymers: Methodology and performance. Int. J. Mol. Sci 2009, 10, 5054–5089. [Google Scholar]
- Karayiannis, N.C.; Laso, M. Monte carlo scheme for generation and relaxation of dense and nearly jammed random structures of freely jointed hard-sphere chains. Macromolecules 2008, 41, 1537–1551. [Google Scholar]
- Karayiannis, N.C.; Laso, M. Dense and nearly jammed random packings of freely jointed chains of tangent hard spheres. Phys. Rev. Lett 2008, 100, 050602. [Google Scholar]
- Laso, M.; Karayiannis, N.C. Flexible chain molecules in the marginal and concentrated regimes: Universal static scaling laws and cross-over predictions. J. Chem. Phys 2008, 128, 174901. [Google Scholar] [Green Version]
- Laso, M.; Karayiannis, N.C.; Foteinopoulou, K.; Mansfield, M.L.; Kroger, M. Random packing of model polymers: Local structure, topological hindrance and universal scaling. Soft Matter 2009, 5, 1762–1770. [Google Scholar]
- Brown, E.; Nasto, A.; Athanassiadis, A.G.; Jaeger, H.M. Strain stiffening in random packings of entangled granular chains. Phys. Rev. Lett 2012, 108, 108302. [Google Scholar]
- Hoy, R.S.; O’Hern, C.S. Minimal energy packings and collapse of sticky tangent hard-sphere polymers. Phys. Rev. Lett 2010, 105, 068001. [Google Scholar]
- Hoy, R.S.; O’Hern, C.S. Glassy dynamics of crystallite formation: The role of covalent bonds. Soft Matter 2012, 8, 1215–1225. [Google Scholar]
- Karayiannis, N.C.; Foteinopoulou, K.; Abrams, C.F.; Laso, M. Modeling of crystal nucleation and growth in athermal polymers: Self-assembly of layered nano-morphologies. Soft Matter 2010, 6, 2160–2173. [Google Scholar]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-driven crystallization in dense systems of athermal chain molecules. Phys. Rev. Lett 2009, 103, 045703. [Google Scholar]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The characteristic crystallographic element norm: A descriptor of local structure in atomistic and particulate systems. J. Chem. Phys 2009, 130, 074704. [Google Scholar]
- Siepmann, J.I.; Frenkel, D. Configurational bias Monte-Carlo—A new sampling scheme for flexible chains. Mol. Phys 1992, 75, 59–70. [Google Scholar]
- Depablo, J.J.; Laso, M.; Suter, U.W. Simulation of polyethylene above and below the melting-point. J. Chem. Phys 1992, 96, 2395–2403. [Google Scholar]
- Laso, M.; Depablo, J.J.; Suter, U.W. Simulation of phase-equilibria for chain molecules. J. Chem. Phys 1992, 97, 2817–2819. [Google Scholar]
- Pant, P.V.K.; Theodorou, D.N. Variable connectivity method for the atomistic monte-carlo simulation of polydisperse polymer melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar]
- Aleman, C.; Karayiannis, N.C.; Curco, D.; Foteinopoulou, K.; Laso, M. Computer simulations of amorphous polymers: From quantum mechanical calculations to mesoscopic models. J. Mol. Struct. THEOCHEM 2009, 898, 62–72. [Google Scholar]
- Foteinopoulou, K.; Karayiannis, N.C.; Laso, M.; Kroger, M. Structure, dimensions, and entanglement statistics of long linear polyethylene chains. J. Phys. Chem. B 2009, 113, 442–455. [Google Scholar]
- Gestoso, P.; Karayiannis, N.C. Molecular simulation of the effect of temperature and architecture on polyethylene barrier properties. J. Phys. Chem. B 2008, 112, 5646–5660. [Google Scholar]
- Karayiannis, N.C.; Giannousaki, A.E.; Mavrantzas, V.G. An advanced monte carlo method for the equilibration of model long-chain branched polymers with a well-defined molecular architecture: Detailed atomistic simulation of an h-shaped polyethylene melt. J. Chem. Phys 2003, 118, 2451–2454. [Google Scholar]
- Karayiannis, N.C.; Giannousaki, A.E.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic monte carlo simulation of strictly monodisperse long polyethylene melts through a generalized chain bridging algorithm. J. Chem. Phys 2002, 117, 5465–5479. [Google Scholar]
- Karayiannis, N.C.; Mavrantzas, V.G.; Theodorou, D.N. A novel monte carlo scheme for the rapid equilibration of atomistic model polymer systems of precisely defined molecular architecture. Phys. Rev. Lett 2002, 88, 105503. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar]
- Giacovazzo, C.; Monaco, H.L.; Artioli, G.; Viterbo, D.; Ferraris, G.; Gilli, G.; Zanotti, G.; Gatti, M. Fundamentals of Crystallography; Oxford Science: Oxford, UK, 2005. [Google Scholar]
- Borchard-Ott, W. Kristallographie; Springer Verlag: Berlin, Germany, 2002. [Google Scholar]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw 1996, 22, 469–483. [Google Scholar]
- Qhull. Available online: www.qhull.org accessed on 1 October 2012.
- Rapaport, D.C. Density-fluctuations and hydrogen-bonding in supercooled water. Mol. Phys 1983, 48, 23–31. [Google Scholar]
- Karayiannis, N.C.; Laso, M.; Kroger, M. Detailed atomistic molecular dynamics simulations of α-conotoxin AuIB in water. J. Phys. Chem. B 2009, 113, 5016–5024. [Google Scholar]
- Theodorou, D.N.; Suter, U.W. Shape of unperturbed linear-polymers—Polypropylene. Macromolecules 1985, 18, 1206–1214. [Google Scholar]
- Rubin, R.J.; Mazur, J. Spans of polymer-chains measured with respect to chain-fixed axes. Macromolecules 1977, 10, 139–149. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph 1996, 14, 33–38. [Google Scholar]





© 2013 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Spontaneous Crystallization in Athermal Polymer Packings. Int. J. Mol. Sci. 2013, 14, 332-358. https://doi.org/10.3390/ijms14010332
Karayiannis NC, Foteinopoulou K, Laso M. Spontaneous Crystallization in Athermal Polymer Packings. International Journal of Molecular Sciences. 2013; 14(1):332-358. https://doi.org/10.3390/ijms14010332
Chicago/Turabian StyleKarayiannis, Nikos Ch., Katerina Foteinopoulou, and Manuel Laso. 2013. "Spontaneous Crystallization in Athermal Polymer Packings" International Journal of Molecular Sciences 14, no. 1: 332-358. https://doi.org/10.3390/ijms14010332