CO2 Adsorption on Activated Carbon Honeycomb-Monoliths: A Comparison of Langmuir and Tóth Models
Abstract
:1. Introduction
2. Results and Discussion
2.1. Preparation and Characterization of Materials
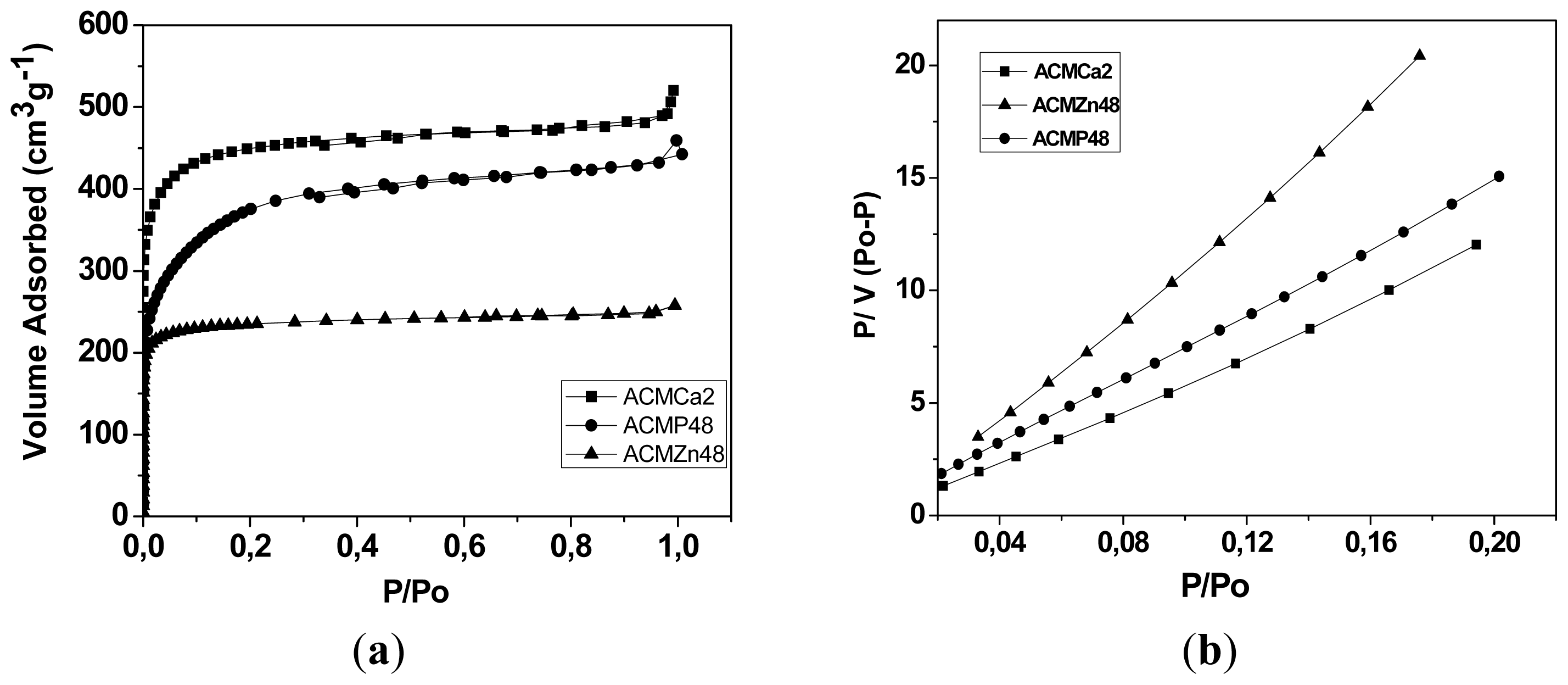
2.2. Adsorption Isotherms of CO2
3. Experimental Section
4. Conclusions
Acknowledgments
References
- Čejka, J; Centi, G; Perez-Pariente, J; Roth, W.J. Zeolite-based materials for novel catalytic applications: Opportunities, perspectives and open problems. Catal. Today 2012, 179, 2–15. [Google Scholar]
- Pinto, M.L; Pires, J. Porous and hybrid clay based materials for separation of hydrocarbons. Microporous Mesoporous Mater 2012, 151, 403–410. [Google Scholar]
- Dana, E; Sayari, A. Adsorption of heavy metals on amine-functionalized SBA-15 prepared by co-condensation: Applications to real water samples. Desalination 2012, 285, 62–67. [Google Scholar]
- Mohammad Abdollahi-Alibeik, M; Pouriayevali, M. Nanosized MCM-41 supported protic ionic liquid as an efficient novel catalytic system for Friedlander synthesis of quinolines. Catal. Commun 2012, 22, 13–18. [Google Scholar]
- Arulkumar, M; Thirumalai, K; Sathishkumar, P; Palvannan, T. Rapid removal of chromium from aqueous solution using novel prawn shell activated carbon. Chem. Eng. J 2012, (185–186), 178–186. [Google Scholar]
- Abid, H.R; Tian, H; Ang, H; Tade, M.O; Buckley, C.E; Wang, S. Nanosize Zr-metal organic framework (UiO-66) for hydrogen and carbon dioxide storage. Chem. Eng. J 2012, 187, 415–420. [Google Scholar]
- Krishna, R.M; van Baten, J. A comparison of the CO2 capture characteristics of zeolites and metal–organic frameworks. Sep. Purif. Technol 2012, 87, 120–126. [Google Scholar]
- Prabaharan, S.R.S; Vimala, R; Zainal, Z. Nanostructured mesoporous carbon as electrodes for supercapacitors. J. Power Sources 2006, 161, 730–736. [Google Scholar]
- Mi, H; Zhang, X; Yang, S; Ye, X; Luo, J. Polyaniline nanofibers as the electrode material for supercapacitors. Mater. Chem. Phys 2008, 112, 127–131. [Google Scholar]
- Rahmat, M; Hubert, P. Carbon nanotube–polymer interactions in nanocomposites: A review. Compos. Sci. Technol 2011, 72, 72–84. [Google Scholar]
- Moreno-Castilla, C; Pérez-Cadenas, A. Carbon-based honeycomb monoliths for environmental gas-phase applications. Materials 2010, 3, 1203–1227. [Google Scholar]
- Vargas, D.P; Giraldo, L; Silvestre-Albero, J; Moreno-Piraján, J.C. CO2 adsorption on binderless activated carbon monoliths. Adsorption 2011, 17, 497–504. [Google Scholar]
- Gadkaree, K.P. Carbon honeycomb structures for adsorption applications. Carbon 1998, 36, 981–989. [Google Scholar]
- Specchia, S; Tacchino, S; Specchia, V. Facing the catalytic combustion of CH4/H2 mixtures into monoliths. Chem. Eng. J 2011, 167, 622–633. [Google Scholar]
- Kumar, P.S; Ramalingam, S; Senthamarai, C; Niranjanaa, M; Vijayalakshmi, P; Sivanesan, S. Adsorption of dye from aqueous solution by cashew nut shell: Studies on equilibrium isotherm, kinetics and thermodynamics of interactions. Desalination 2010, 261, 52–60. [Google Scholar]
- Sekar, M; Sakthi, V; Rengaraj, S. Kinetics and equilibrium adsorption study of lead(II) onto activated carbon prepared from coconut shell. J. Colloid Interface Sci 2004, 279, 307–313. [Google Scholar]
- Moreno-Pirajána, J.C; Giraldo, L. Activated carbon obtained by pyrolysis of potato peel for the removal of heavy metal copper (II) from aqueous solutions. J. Anal. Appl. Pyrolysis 2011, 90, 42–47. [Google Scholar]
- Garnier, C; Finqueneisel, G; Zimny, T; Pokryszka, Z; Lafortune, S; Défossez, P.D.C; Gaucher, E.C. Selection of coals of different maturities for CO2 Storage by modelling of CH4 and CO2 adsorption isotherms. Int. J. Coal Geol 2011, 87, 80–86. [Google Scholar]
- Martín, M.J. Adsorción Física de Gases y Vapores por Carbones (in Spanish); Universidad de Alicante: Alicante, Espana, 1988; pp. 27–30. [Google Scholar]
- Lozano Castelló, D; Cazorla Amorós, D; Linares Solano, A; Quinn, D.F. Activated carbon monolith for methane storage influence of binder. Carbon 2002, 40, 2817–2825. [Google Scholar]
- Álvarez, P; Santamaría, R; Blanco, C; Granda, M. Thermal degradation of lignocellulosic materials treated with several acids. J. Anal. Appl. Pyrolysis 2005, 74, 337–343. [Google Scholar]
- Sing, K.S.W; Everett, D.H; Haul, R.A.W; Moscou, L; Pierotti, R.A; Rouquerol, J; Siemieniewska, T. Reporting physisorption data for gas/solid systems with Special Reference to the Determination of Surface Area and Porosity. Pure Appl. Chem 1985, 57, 603–619. [Google Scholar]
- Juárez-Galán, J.M; Silvestre-Albero, A; Silvestre-Albero, J; Rodríguez-Reinoso, F. Synthesis of activated carbon with highly developed “mesoporosity”. Microporous Mesoporous Mater 2009, 117, 519–521. [Google Scholar]
- Wang, H; Tewarson, R.P. A quasi-gauss-Newton method for solving non-linear algebraic equations. Comput. Math. Appl 1993, 25, 53–63. [Google Scholar]
- Kinniburgh, D.G. General purpose adsorption isotherms. Environ. Sci. Technol 1986, 20, 895–904. [Google Scholar]
- Chue, K.T; Kim, J.N; Yoo, Y.J; Cho, S.H; Yang, R.T. Comparison of activated carbon and zeolite 13X for CO2 recovery from flue gas by pressure swing adsorption. Ind. Eng. Chem. Res 1995, 34, 591–598. [Google Scholar]
- Choi, S; Drese, J.H; Jones, C.W. Adsorbent materials for carbon dioxide capture from large anthropogenic point sources. ChemSusChem 2009, 2, 796–854. [Google Scholar]
- Vargas, D.P; Giraldo, L; Silvestre-Albero, J; Moreno-Piraján, J.C. CO2 adsorption on binderless activated carbon monoliths. Adsorption 2011, 17, 497–504. [Google Scholar]
- Plaza, M.G; Pevida, C; Arenillas, A; Rubiera, F; Pis, J.J. CO2 capture by adsorption with nitrogen enriched carbons. Fuel 2007, 86, 2204–2212. [Google Scholar]
- Wahby, A; Ramos-Fernández, J.M; Martínez-Escandell, M; Sepúlveda-Escribano, A; Silvestre-Albero, J; Rodríguez-Reinoso, F. High-surface-area carbon molecular sieves for selective CO2 adsorption. ChemSusChem 2010, 3, 974–981. [Google Scholar]
- Águeda, V.I; Crittenden, B.D; Delgado, J.A; Tennison, S.R. Effect of channel geometry, degree of activation, relative humidity and temperature on the performance of binderless activated carbon monoliths in the removal of dichloromethane from air. Sep. Purif. Technol 2011, 78, 154–163. [Google Scholar]



| N2 adsorption 77 K | CO2 adsorption 273 K | ||||
|---|---|---|---|---|---|
| Sample | SBET (m2·g−1) | VOa (cm3·g−1) | Vmesob (cm3·g−1) | V0.99c (cm3·g−1) | Vnd (cm3·g−1) |
| ACMP32 | 1020 | 0.40 | 0.09 | 0.48 | 0.25 |
| ACMP36 | 1057 | 0.40 | 0.10 | 0.50 | 0.27 |
| ACMP40 | 1078 | 0.41 | 0.11 | 0.52 | 0.28 |
| ACMP48 | 1368 | 0.48 | 0.18 | 0.66 | 0.32 |
| ACMZn32 | 660 | 0.26 | 0.03 | 0.29 | 0.23 |
| ACMZn36 | 845 | 0.34 | 0.02 | 0.36 | 0.34 |
| ACMZn40 | 884 | 0.35 | 0.03 | 0.38 | 0.34 |
| ACMZn48 | 924 | 0.37 | 0.01 | 0.38 | 0.36 |
| ACMCa2 | 1700 | 0.64 | 0.10 | 0.74 | 0.43 |
| ACMCa3 | 1469 | 0.60 | 0.04 | 0.64 | 0.34 |
| ACMCa5 | 1445 | 0.57 | 0.06 | 0.63 | 0.36 |
| ACMCa7 | 926 | 0.37 | 0.05 | 0.42 | 0.23 |
| Sample | Langmuir | Tóth | |||||
|---|---|---|---|---|---|---|---|
| qmax (mmol·g−1) | KL (Bar−1) | R2 | qm (mmol·g−1) | αT (Bar−1) | n | R2 | |
| ACMP32 | 4.609 | 1.529 | 0.996 | 1.008 | 44.60 | 0.519 | 0.999 |
| ACMP36 | 4.757 | 1.464 | 0.996 | 1.068 | 44.17 | 0.556 | 0.999 |
| ACMP40 | 4.854 | 1.391 | 0.997 | 1.402 | 25.34 | 0.527 | 0.999 |
| ACMP48 | 5.122 | 0.992 | 0.998 | 1.592 | 21.70 | 0.457 | 0.999 |
| ACMZn32 | 3.786 | 2.068 | 0.998 | 2.398 | 8.417 | 0.687 | 0.999 |
| ACMZn36 | 5.606 | 1.928 | 0.998 | 3.608 | 7.658 | 0.677 | 0.999 |
| ACMZn40 | 5.687 | 1.829 | 0.998 | 3.523 | 7.967 | 0.658 | 0.999 |
| ACMZn48 | 5.939 | 1.390 | 0.998 | 3.211 | 8.332 | 0.593 | 1.000 |
| ACMCa2 | 7.550 | 2.638 | 0.996 | 1.116 | 185.4 | 0.570 | 0.999 |
| ACMCa3 | 3.807 | 2.770 | 0.996 | 1.762 | 32.26 | 0.707 | 0.999 |
| ACMCa5 | 5.709 | 2.870 | 0.997 | 2.498 | 24.68 | 0.663 | 0.999 |
| ACMCa7 | 3.643 | 2.930 | 0.998 | 1.535 | 27.24 | 0.659 | 0.999 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vargas, D.P.; Giraldo, L.; Moreno-Piraján, J.C. CO2 Adsorption on Activated Carbon Honeycomb-Monoliths: A Comparison of Langmuir and Tóth Models. Int. J. Mol. Sci. 2012, 13, 8388-8397. https://doi.org/10.3390/ijms13078388
Vargas DP, Giraldo L, Moreno-Piraján JC. CO2 Adsorption on Activated Carbon Honeycomb-Monoliths: A Comparison of Langmuir and Tóth Models. International Journal of Molecular Sciences. 2012; 13(7):8388-8397. https://doi.org/10.3390/ijms13078388
Chicago/Turabian StyleVargas, Diana P., Liliana Giraldo, and Juan C. Moreno-Piraján. 2012. "CO2 Adsorption on Activated Carbon Honeycomb-Monoliths: A Comparison of Langmuir and Tóth Models" International Journal of Molecular Sciences 13, no. 7: 8388-8397. https://doi.org/10.3390/ijms13078388