A Promising Tool to Achieve Chemical Accuracy for Density Functional Theory Calculations on Y-NO Homolysis Bond Dissociation Energies
Abstract
:1. Introduction
2. Methods
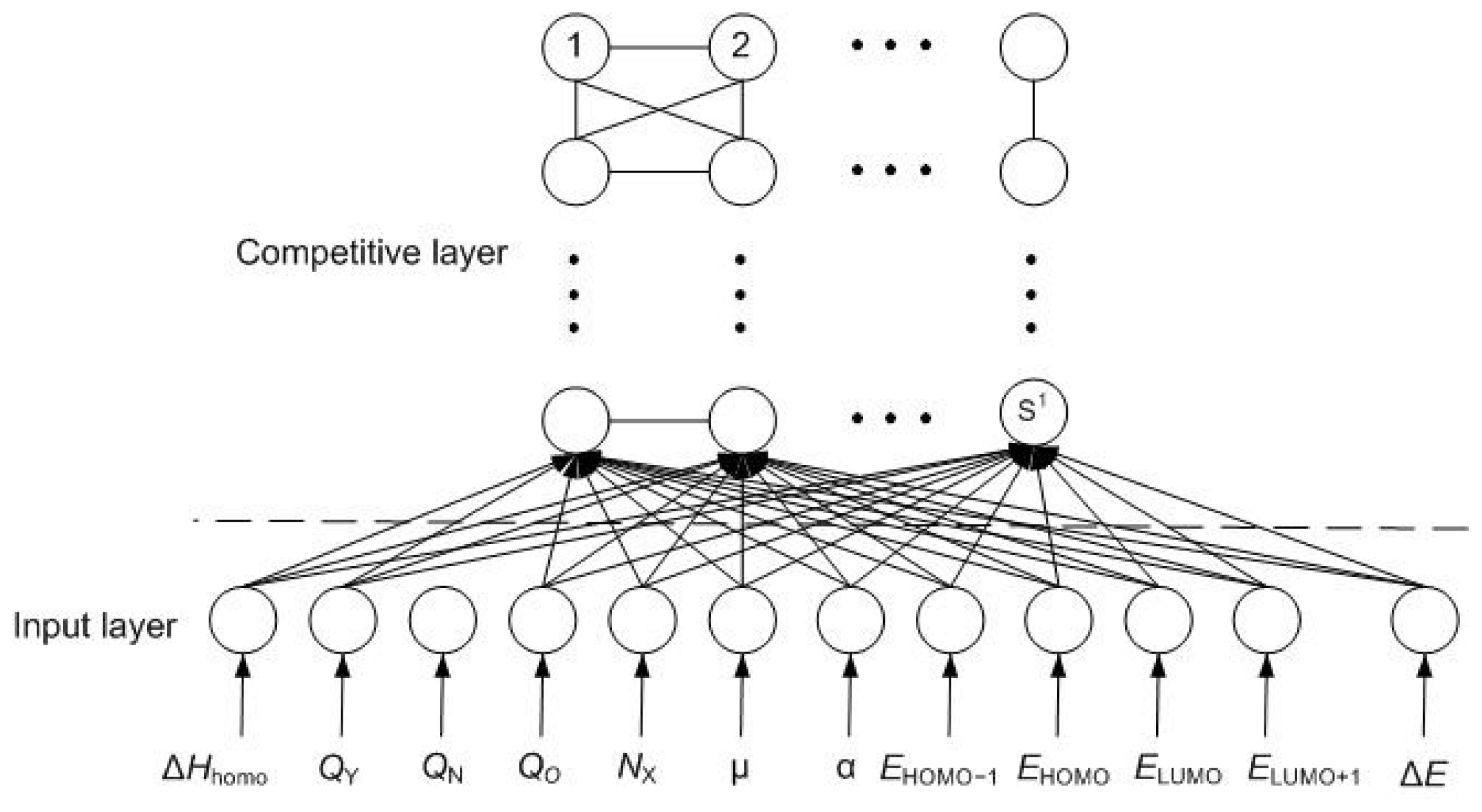
2.1. Self-Organizing Feature Mapping Neural Network
- Network initializationThe input layer and competitive layer are composed of R and S1 neurons, respectively. The initial values of each neuron in the competitive layer start from a small random number IWij1,1 (i = 1,2,…, S1, j = 1,2,…,R), where IWij1,1 represents the connection weight between the ith neuron in the competitive layer and the jth neuron in the input layer. Nc is set as the initial neighborhood, η as the initial learning rate, T as the maximum iterations, and N = 1 as the initial iteration.
- The winning neuron calculationA training sample p is selected randomly and the input of neurons in the competitive layer is calculated according to Equation (1)where ni1 and bi1 represent the output and the threshold value of the ith neuron in the competitive layer, respectively; pj stands for the value of the jth input variable of sample p.If the kth neuron in the competitive layer is the winning neuron, it should meet the requirements in Equation (2):
- Weight updateThe weights of the winning neuron k and all neurons in neighborhood Nc(t) will be updated according to Equation (3):
- Learning rate and neighborhood neurons updateOnce the weights of the winning neuron and the neighborhood neurons are updated, the learning rate and neighborhood neurons must be updated before the next iteration according to Equations 4,5:where the operator ⌈ ⌉ represents rounding up.
- IterationIf the learning process is not finished, another sample will be randomly chosen to continue the calculation, and the iteration returns to step (2), or if N < T, then N = N + 1, and iteration also returns to step (2). Otherwise, iteration concludes.
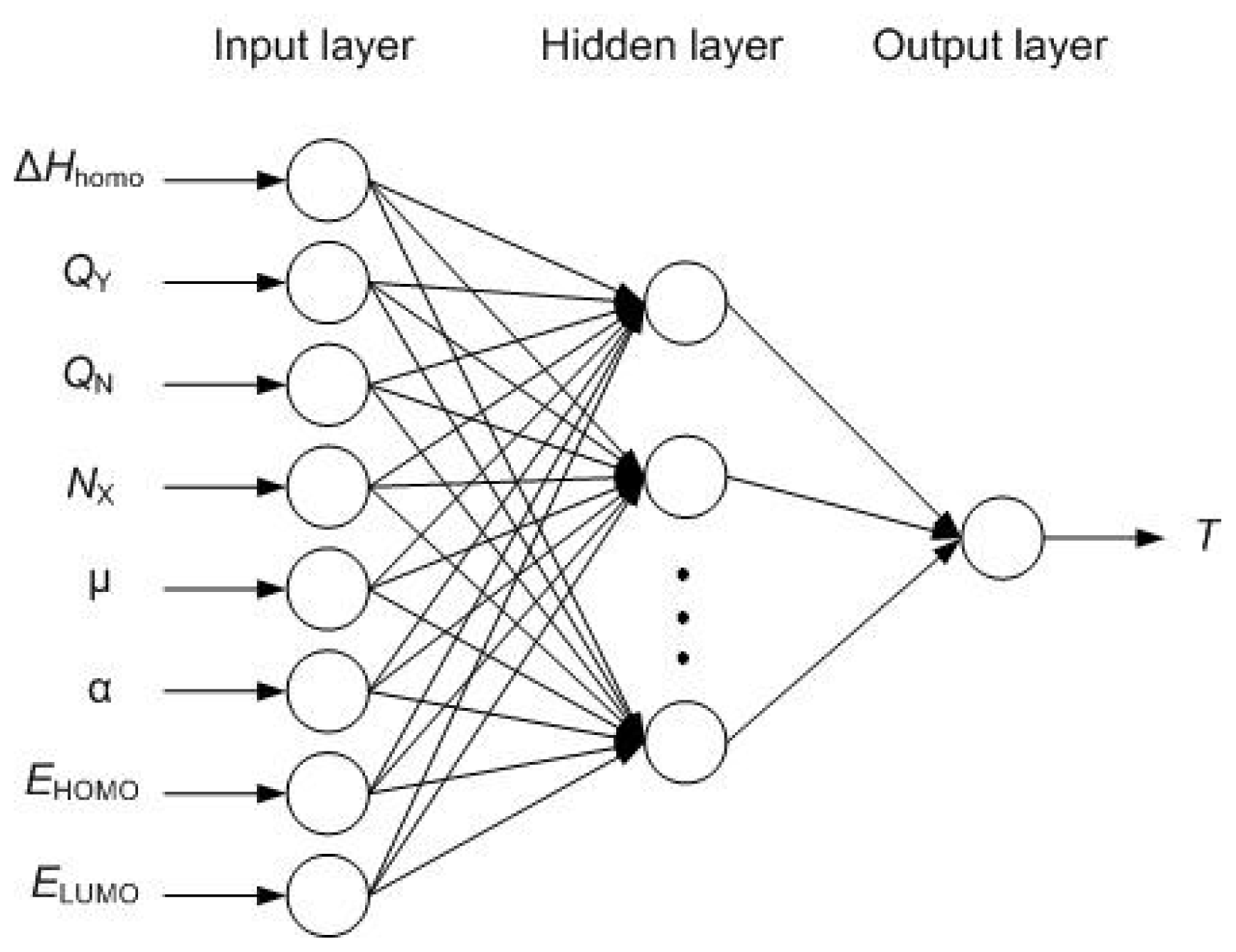
2.2. Radial Basis Function Neural Network
- Determining the RBF center of neurons in the hidden layerwhere pij represents the ith input variable of the jth training sample; tij represents the ith output variable of the jth training sample; M is the dimension of the input variables; N is the dimension of the output variables; and Q is the number of samples in training set.The corresponding RBF center of Q neurons in the hidden layer is:
- Determining the threshold value of neurons in the hidden layerThe corresponding threshold value of Q neurons in the hidden layer is:where b11 = b12 = ··· = b1Q = 0.8326/spread, spread is the expanding coefficient of RBF.
- Determining weights and threshold values between the hidden layer and the output layerOnce the RBF center and threshold value of neurons in the hidden layer is determined, the output of neurons in the hidden layer can be obtained by Equation (9):where pi = [pi1, pi2, ···, pim] is the ith vector of the training set. And the matrix A is set to A = [a1, a2, ··· aQ].
3. Calculations
3.1. Data Set
3.2. Molecular Descriptor Calculations
4. Results and Discussion
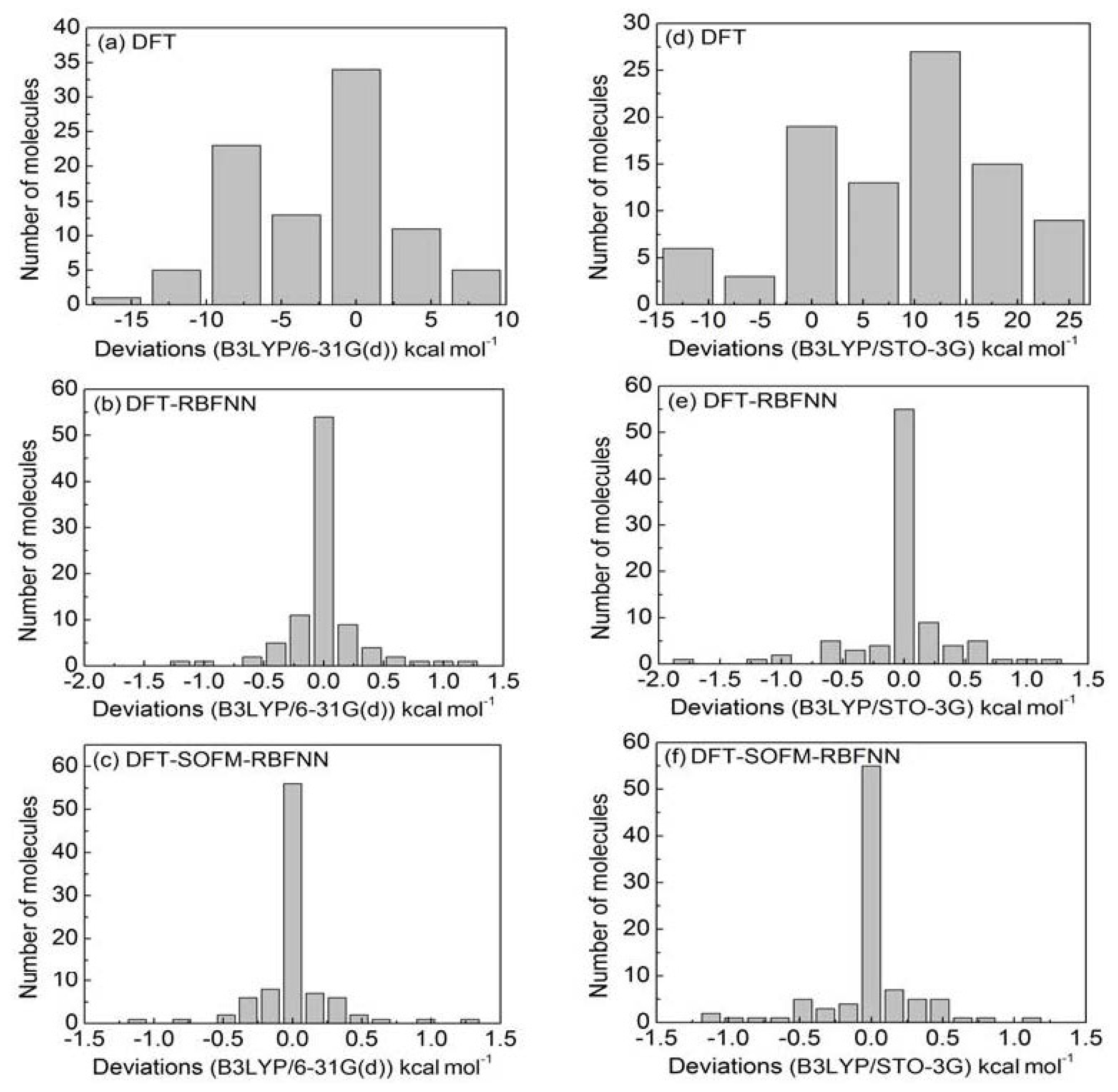
4.1. Calculating Y-NO Homolysis BDE with DFT Method
4.2. SOFMNN Calculation Results
4.3. RBFNN Calculation Results
5. Conclusions
Supplementary Materials
ijms-13-08051-s001.pdfAcknowledgements
References
- Sumowski, C.V.; Ochsenfeld, C. A convergence study of QM/MM isomerization energies with the selected size of the QM region for peptidic systems. J. Phys. Chem. A 2009, 113, 11734–11741. [Google Scholar]
- Hu, L.H.; Eliasson, J.; Heimda, J.; Ryde, U. Do quantum mechanical energies calculated for small models of protein-active sites converge? J. Phys. Chem. A 2009, 113, 11793–11800. [Google Scholar]
- Hu, L.H.; Soderhjelm, P.; Ryde, U. On the convergence of QM/MM energies. J. Chem. Theory. Comput 2011, 7, 761–777. [Google Scholar]
- Ku, J.; Lansac, Y.; Jang, Y.H. Time-dependent density functional theory study on benzothiadiazole-based low-band-gap fused-ring copolymers for organic solar cell applications. J. Phys. Chem. C 2011, 115, 21508–21516. [Google Scholar]
- Meng, S.; Kaxiras, E.; Nazeeruddin, M.K.; Grätzel, M. Dsign of dye acceptors for photovoltaics from first-principles calculations. J. Phys. Chem. C 2011, 115, 9276–9282. [Google Scholar]
- Rablen, P.R.; Lockman, J.W.; Jorgensen, W.L. Ab-initio study of hydrogen-bonded complexes of small organic-molecules with water. J. Phys. Chem. A 1998, 102, 3782–3797. [Google Scholar]
- Bond, D. Computational methods in organic thermochemistry. 1. Hydrocarbon enthalpies and free energies of formation. J. Org. Chem 2007, 72, 5555–5566. [Google Scholar]
- Riley, K.E.; Op’t Holt, B.T.; Merz, K.M., Jr. Critical assessment of the performance of density functional methods for several atomic and molecular properties. J. Chem. Theory Comput 2007, 3, 407–433. [Google Scholar]
- Hu, L.H.; Wang, X.J.; Wong, L.H.; Chen, G.H. Combined first-principles calculation and neural-network correction approach for heat of formation. J. Chem. Phys 2003, 119, 11501–11507. [Google Scholar]
- Wang, X.J.; Hu, L.H.; Wong, L.H.; Chen, G.H. A combined first-principles calculation and neural networks correction approach for evaluating Gibbs energy of formation. Mol. Simul 2004, 30, 9–15. [Google Scholar]
- Wang, X.J.; Wong, L.H.; Hu, L.H.; Chan, C.Y.; Su, Z.M.; Chen, G.H. Improving the accuracy of density-functional theory calculation: The statistical correction approach. J. Phys. Chem. A 2004, 108, 8514–8525. [Google Scholar]
- Zheng, X.; Hu, L.H.; Wang, X.J.; Chen, G.H. A generalized exchange-correlation functional: The Neural networks approach. Chem. Phys. Lett 2004, 390, 186–192. [Google Scholar]
- Li, H.; Shi, L.L.; Zhang, M.; Su, Z.M.; Wang, X.; Hu, L.; Chen, G.H. Improving the accuracy of density-functional theory calculation: The genetic algorithm and neural network approach. J. Chem. Phys 2007, 126, 144101–144108. [Google Scholar]
- Gao, T.; Sun, S.L.; Shi, L.L.; Li, H.; Li, H.Z.; Su, Z.M.; Lu, Y.H. An accurate density functional theory calculation for electronic excitation energies: The least-squares support vector machine. J. Chem. Phys 2009, 130, 184104–184107. [Google Scholar]
- Li, H.Z.; Tao, W.; Gao, T.; Li, H.; Lu, Y.H.; Su, Z.M. Improving the accuracy of density functional theory (DFT) calculation for homolysis bond dissociation energies of Y-NO bond: Generalized regression neural network based on grey relational analysis and principal component analysis. Int. J. Mol. Sci 2011, 12, 2242–2261. [Google Scholar]
- Wu, J.; Xu, X. The X1 method for accurate and efficient prediction of heats of formation. J. Chem. Phys 2007, 127, 214105–2141058. [Google Scholar]
- Balabin, R.M.; Lomakina, E.I. Neural network approach to quantum-chemistry data; Accurate prediction of density functional theory energies. J. Chem. Phys 2009, 131, 74104–74108. [Google Scholar]
- Wang, J.N.; Xu, H.L.; Sun, S.L.; Gao, T.; Li, H.Z.; Li, H.; Su, Z.M. An effective method for accurate prediction of the first hyperpolarizability of alkalides. J. Comput. Chem 2011, 33, 231–236. [Google Scholar]
- Rupp, M.; Tkatchenko, A.; Muller, K.R.; Lilienfeld, O.A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett 2012, 108, 058301:1–058301:5. [Google Scholar]
- Katritzky, A.R.; Lobanov, V.S.; Karelson, M. Physical Properties from Structure. Chem. Soc. Rev 1995, 24, 279–287. [Google Scholar]
- Butler, A.R.; Williams, D.L.H. The physiological role of nitric oxide. Chem. Soc. Rev 1993, 22, 233–241. [Google Scholar]
- Averill, B.A. Dissimilatory nitrite and nitric oxide reductases. Chem. Rev 1996, 96, 2951–2964. [Google Scholar]
- Palmer, R.M.J.; Ferrige, A.G.; Moncada, S. Nitric oxide release accounts for the biological activity of endothelium-derived relaxing factor. Nature 1987, 327, 524–526. [Google Scholar]
- Ignarro, L.J. Biosynthesis and metabolism of endothelium-derived nitric oxide. Annu. Rev. Pharmacol. Toxicol 1990, 30, 535–560. [Google Scholar]
- Feldman, P.L.; Griffith, O.W.; Stuehr, D.J. The surprising life of nitric oxide. Chem. Eng. News 1993, 71, 26–38. [Google Scholar]
- Fukuto, J.M.; Ignarro, L.J. In vivo aspects of nitric oxide (NO) chemistry: Does peroxynitrite (OONO) play a major role in cytotoxicity? Acc. Chem. Res 1997, 30, 149–152. [Google Scholar]
- Moncada, S.; Palmer, R.M.J.; Higgs, E.A. Nitric oxide: Physiology, pathophysiology, and pharmacology. Pharmacol. Rev 1991, 43, 109–142. [Google Scholar]
- Ignarro, L.J. Signal transduction mechanisms involving nitric oxide. Biochem. Pharmacol 1991, 41, 485–490. [Google Scholar]
- Gnewuch, C.T.; Sosnovsky, G.A. Critical appraisal of the evolution of N-nitrosoureas as anticancer drugs. Chem. Rev 1997, 97, 829–1014. [Google Scholar]
- Whited, C.A.; Warren, J.J.; Lavoie, K.D.; Weinert, E.E.; Agapie, T.; Winkler, J.R.; Gray, H.B. Gating NO release from nitric oxide synthase. J. Am. Chem. Soc 2012, 134, 27–30. [Google Scholar]
- Cheng, J.P.; Wang, K.; Yin, Z.; Zhu, X.; Lu, Y. NO affinity. The driving force of nitric oxide (NO) transfer in biomimetic N-nitrosoacetanilide and N-nitrososulfoanilide systems. Tetrahedron Lett 1998, 39, 7925–7928. [Google Scholar]
- Cheng, J.P.; Xian, M.; Wang, K.; Zhu, X.; Yin, Z.; Wang, P.G. Heterolytic and homolytic Y-NO bond energy scales of nitroso-containing compounds: Chemical origin of NO release and NO capture. J. Am. Chem. Soc 1998, 120, 10266–10267. [Google Scholar]
- Xian, M.; Zhu, X.Q.; Lu, J.; Wen, Z.; Cheng, J.P. The first O-NO bond energy scale in solution: Heterolytic and homolytic cleavage enthalpies of O-nitrosyl carboxylate. Compd. Org. Lett 2000, 2, 265–268. [Google Scholar]
- Zhu, X.Q.; He, J.Q.; Li, Q.; Xian, M.; Lu, J.; Cheng, J.P. N-NO bond dissociation energies of N-nitroso diphenylamine derivatives (or analogues) and their radical anions: Implications for the effect of reductive electron transfer on N-NO bond activation and for the mechanisms of NO transfer to nitranions. J. Org. Chem 2000, 65, 6729–6735. [Google Scholar]
- Lü, J.M.; Wittbrodt, J.M.; Wang, K.; Wen, Z.; Schlegel, H.B.; Wang, P.G.; Cheng, J.P. NO affinities of S-nitrosothiols: A direct experimental and computational investigation of RS-NO bond dissociation energies. J. Am. Chem. Soc 2001, 123, 2903–2904. [Google Scholar]
- Zhu, X.Q.; Hao, W.F.; Tang, H.; Wang, C.H.; Cheng, J.P. Determination of N-NO bond dissociation energies of N-methyl-N-nitrosobenzenesulfonamides in acetonitrile and application in the mechanism analyses on NO transfer. J. Am. Chem. Soc 2005, 127, 2696–2708. [Google Scholar]
- Zhu, X.Q.; Zhang, J.Y.; Cheng, J.P. Mechanism and driving force of NO transfer from S-nitrosothiol to cobalt(II) porphyrin: A detailed thermodynamic and kinetic study. Inorg. Chem 2006, 46, 592–600. [Google Scholar]
- Li, X.; Zhu, X.Q.; Wang, X.X.; Cheng, J.P. Determination of N-NO bond dissociation energies of N-nitrosoindoles and their radical anions in acetonitrile. Chem. J. Chin. Univ 2007, 28, 2295–2298. [Google Scholar]
- Li, X.; Zhu, X.Q.; Cheng, J.P. Determination of NO chemical affinities of benzyl nitrite in acetonitrile. Chem. J. Chin. Univ 2007, 29, 2327–2329. [Google Scholar]
- Li, X.; Cheng, J.P. Determination of S-NO bond dissociation energies of S-nitroso-N-acety-d,l-penicillamine dipeptides. Chem. J. Chin. Univ 2008, 29, 1569–1572. [Google Scholar]
- Li, X.; Deng, H.; Zhu, X.Q.; Wang, X.; Liang, H.; Cheng, J.P. Establishment of the C-NO Bond dissociation energy scale in solution and its application in analyzing the trend of NO transfer from C-nitroso compound to thiols. J. Org. Chem 2009, 74, 4472–4478. [Google Scholar]
- Teuvo, K. Self-organizing formation of topologically correct feature maps. Biol. Cybern 1982, 43, 59–69. [Google Scholar]
- Powell, M.J.D. Radial Basis Function for Multivariable Interpolation: A Review. Proceeding of the IMA Conference on Algorithms for the Approximation of Functions and Data, RMCS, Shrivenham, UK, July, 1985; Clarendon Press: Oxford, UK, 1987; pp. 143–167. [Google Scholar]
- Gaussian 03. Revision C.02; Gaussian, Inc: Pittsburgh, PA, USA, 2003.
- Fu, Y.; Mou, Y.; Lin, B.L.; Guo, Q.X. Structures of the X-Y-NO molecules and homolytic dissociation energies of the Y-NO bonds (Y = C, N, O, S). J. Phys. Chem. A 2002, 106, 12386–12392. [Google Scholar]

| No. | B3LYP/6-31G(d) | B3LYP/STO-3G | DFT-RBFNN | DFT-SOFM-RBFNN | ||
|---|---|---|---|---|---|---|
| 6-31G(d) | STO-3G | 6-31G(d) | STO-3G | |||
| 1 | −17.17 | −6.89 | −0.12 | −1.84 | −0.04 | −1.18 |
| 2 | −7.88 | 2.66 | 0.46 | 0.12 | 0.38 | 0.22 |
| 3 | −9.31 | 0.85 | −0.48 | −0.65 | −0.38 | −0.58 |
| 4 | −9.29 | 1.27 | −0.03 | −0.02 | −0.01 | −0.01 |
| 5 | −9.77 | 0.14 | 0.00 | −0.01 | 0.00 | 0.00 |
| 6a | −9.13 | 1.04 | −0.40 | −0.53 | −0.34 | −0.46 |
| 7 | −9.01 | 1.11 | 0.05 | −0.01 | 0.03 | 0.01 |
| 8 | −12.53 | 0.28 | −0.03 | 0.00 | −0.01 | 0.00 |
| 9 | −13.13 | −3.06 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | −10.9 | −0.51 | −0.01 | −0.01 | 0.00 | 0.00 |
| 11 | 2.16 | 12.31 | 0.07 | 0.02 | 0.04 | 0.01 |
| 12 | 2.70 | 13.23 | 0.58 | 0.81 | 0.55 | 0.68 |
| 13 | 1.72 | 12.17 | −0.34 | 0.42 | −0.34 | 0.23 |
| 14 | −0.39 | 10.26 | −0.10 | 0.03 | −0.06 | 0.01 |
| 15 | −1.56 | 10.1 | 0.00 | 0.01 | 0.00 | 0.01 |
| 16 | 1.69 | 11.63 | 0.00 | 0.01 | 0.00 | 0.00 |
| 17 | 2.00 | 12.39 | −0.20 | 0.25 | −0.23 | 0.13 |
| 18 | −8.37 | 2.73 | −0.16 | 0.05 | −0.06 | 0.03 |
| 19 | −7.30 | 4.12 | −0.28 | −0.02 | −0.21 | −0.01 |
| 20a | −6.93 | 4.16 | −0.22 | −0.47 | −0.21 | −0.41 |
| 21 | −7.68 | 3.96 | 0.29 | 0.01 | 0.27 | 0.00 |
| 22 | −10.58 | 0.56 | 0.00 | 0.00 | 0.00 | 0.00 |
| 23 | −2.11 | 8.33 | 0.01 | −0.93 | 0.06 | −0.75 |
| 24 | 3.45 | 12.33 | 0.35 | 0.67 | 0.19 | 0.45 |
| 25 | −8.07 | 3.05 | −0.53 | −0.21 | −0.51 | −0.18 |
| 26 | −7.90 | 3.23 | 0.28 | 0.18 | 0.29 | 0.17 |
| 27a | −8.60 | 2.58 | −0.42 | −0.01 | −0.38 | −0.01 |
| 28 | −8.22 | 4.07 | 0.01 | 0.00 | 0.00 | 0.00 |
| 29 | −4.97 | 6.77 | 0.00 | 0.00 | 0.00 | 0.00 |
| 30 | 1.87 | −11.2 | 0.00 | 0.02 | 0.00 | 0.01 |
| 31a | 1.97 | −11.27 | −0.05 | 0.00 | −0.04 | 0.00 |
| 32 | 0.33 | −12.53 | −0.01 | −0.03 | 0.00 | −0.02 |
| 33a | 1.91 | −6.79 | 0.04 | −0.03 | 0.03 | −0.03 |
| 34 | 0.74 | −11.6 | 0.00 | 0.00 | 0.00 | 0.00 |
| 35 | 1.92 | −10.83 | 0.18 | 0.01 | 0.15 | 0.01 |
| 36 | 0.62 | −14 | −0.18 | 0.00 | −0.15 | 0.00 |
| 37 | 1.16 | 10.52 | 0.00 | 0.00 | 0.00 | 0.00 |
| 38 | 0.76 | 11.2 | 0.14 | 0.12 | 0.10 | 0.10 |
| 39 | 0.29 | 11.06 | −0.05 | −0.09 | −0.07 | −0.08 |
| 40 | −0.36 | 10.68 | −0.06 | −0.39 | −0.05 | −0.36 |
| 41 | −0.41 | 11.52 | 0.00 | 0.00 | 0.00 | 0.00 |
| 42 | −0.04 | 11.72 | 0.02 | 0.40 | 0.01 | 0.37 |
| 43 | −0.26 | 10.28 | 0.04 | −0.05 | 0.04 | −0.03 |
| 44a | −1.14 | 11.08 | 1.01 | 0.95 | 0.92 | 0.84 |
| 45 | −0.97 | 9.89 | 0.00 | 0.00 | 0.00 | 0.00 |
| 46 | 0.03 | 12.03 | 0.00 | 0.00 | 0.00 | 0.00 |
| 47 | 0.87 | 10.84 | 0.02 | 0.04 | 0.01 | 0.02 |
| 48 | −1.67 | 8.65 | 0.00 | 0.00 | 0.00 | 0.00 |
| 49 | −3.41 | 8.59 | −0.01 | −0.03 | 0.00 | −0.02 |
| 50 | 7.47 | −0.71 | −0.01 | 0.01 | 0.01 | 0.01 |
| 51 | 5.60 | −0.55 | 0.00 | 0.00 | 0.00 | 0.00 |
| 52 | 7.03 | −1.38 | 0.03 | 0.00 | 0.01 | 0.00 |
| 53 | 6.33 | −2.14 | −0.01 | −0.01 | −0.01 | −0.01 |
| 54 | −2.62 | 15.71 | 0.00 | 0.00 | 0.00 | 0.00 |
| 55 | −2.88 | 15.23 | 0.12 | 0.28 | 0.08 | 0.25 |
| 56 | −3.88 | 14.1 | −0.12 | −0.28 | −0.08 | −0.25 |
| 57 | −3.89 | 13.76 | 0.00 | −0.01 | 0.00 | −0.01 |
| 58a | −7.57 | 9.35 | 0.00 | 0.00 | 0.00 | 0.00 |
| 59 | −4.88 | 12.76 | 1.26 | 1.19 | 1.20 | 1.14 |
| 60 | −7.33 | 9.84 | −1.20 | −1.15 | −1.16 | −1.12 |
| 61 | −6.90 | 10.9 | 0.17 | 0.26 | 0.20 | 0.28 |
| 62 | 6.39 | 18.5 | 0.00 | 0.00 | 0.00 | 0.00 |
| 63 | 4.12 | 17.94 | 0.00 | 0.38 | 0.00 | 0.35 |
| 64 | −9.96 | 16.41 | 0.00 | −0.37 | 0.00 | −0.34 |
| 65 | 4.19 | 15.06 | 0.00 | −0.01 | 0.00 | −0.01 |
| 66 | 0.55 | 14.42 | 0.00 | 0.00 | 0.00 | 0.00 |
| 67 | −3.51 | 19.3 | −0.60 | −0.52 | −0.47 | −0.43 |
| 68 | −2.46 | 21.15 | −0.93 | −0.93 | −0.85 | −0.90 |
| 69 | 0.27 | 22.96 | 0.51 | 0.57 | 0.44 | 0.54 |
| 70 | 0.05 | 22.7 | 0.07 | 0.50 | 0.04 | 0.47 |
| 71a | 2.43 | 22.6 | 0.19 | 0.18 | 0.16 | 0.14 |
| 72 | 0.20 | 19.63 | 0.01 | 0.00 | 0.00 | 0.00 |
| 73 | −0.88 | 20.53 | −0.16 | −0.52 | −0.09 | −0.48 |
| 74 | 7.91 | 19.5 | 0.02 | 0.03 | 0.01 | 0.02 |
| 75 | −0.36 | 22.56 | 0.38 | 0.39 | 0.39 | 0.40 |
| 76 | 2.96 | 21.38 | 0.00 | 0.00 | 0.00 | 0.00 |
| 77 | 1.69 | 22.06 | 0.83 | 0.53 | 0.61 | 0.43 |
| 78 | 2.77 | 21.23 | 0.00 | 0.01 | 0.00 | 0.01 |
| 79 | 2.52 | 20.27 | 0.21 | 0.00 | 0.13 | 0.00 |
| 80 | 0.84 | 19.65 | 0.01 | −0.01 | 0.00 | −0.01 |
| 81 | 1.17 | 21.22 | 0.00 | 0.00 | 0.00 | 0.00 |
| 82 | 0.68 | 20.49 | −0.21 | 0.00 | −0.13 | 0.00 |
| 83a | −2.03 | 16.73 | −0.27 | −0.57 | −0.26 | −0.56 |
| 84a | −0.24 | 18.15 | 0.27 | 0.57 | 0.26 | 0.56 |
| 85a | −7.63 | 2.33 | −0.04 | 0.02 | −0.03 | 0.02 |
| 86 | −4.58 | 6.59 | 0.00 | 0.00 | 0.00 | 0.00 |
| 87 | −7.16 | 5.16 | 0.48 | 0.16 | 0.36 | 0.12 |
| 88 | −8.00 | 2.5 | 0.02 | 0.10 | 0.01 | 0.07 |
| 89 | −3.70 | 11.26 | 0.00 | 0.00 | 0.00 | 0.00 |
| 90 | −10.85 | 0.62 | −0.49 | −0.26 | −0.37 | −0.18 |
| 91a | −8.77 | 5.98 | −0.16 | −0.17 | −0.13 | −0.13 |
| 92 | −8.61 | 1.34 | 0.00 | 0.00 | 0.00 | 0.00 |
| DFT | Training Steps | Clustering Analysis | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔHhomo | QY | QN | QO, | NX | μ | α | EHOMO-1 | EHOMO | ELUMO | ELUMO+1 | ΔE | ||
| B3LYP/6-31G(d) | 10 | 24 | 1 | 1 | 1 | 24 | 4 | 24 | 1 | 1 | 1 | 1 | 1 |
| 30 | 5 | 13 | 13 | 13 | 24 | 19 | 24 | 13 | 13 | 13 | 13 | 13 | |
| 50 | 4 | 12 | 6 | 12 | 1 | 21 | 1 | 12 | 12 | 12 | 12 | 12 | |
| 100 | 19 | 12 | 10 | 12 | 3 | 22 | 1 | 12 | 12 | 11 | 11 | 10 | |
| 200 | 16 | 1 | 8 | 1 | 11 | 19 | 24 | 1 | 1 | 2 | 2 | 8 | |
| 500 | 16 | 13 | 1 | 19 | 12 | 8 | 24 | 19 | 19 | 20 | 20 | 1 | |
| 1000 | 16 | 13 | 20 | 13 | 23 | 2 | 24 | 13 | 13 | 14 | 14 | 20 | |
| B3LYP/STO-3G | 10 | 2 | 1 | 1 | 1 | 24 | 1 | 24 | 1 | 1 | 1 | 1 | 1 |
| 30 | 23 | 1 | 7 | 1 | 24 | 5 | 24 | 1 | 1 | 1 | 2 | 7 | |
| 50 | 21 | 1 | 1 | 1 | 6 | 13 | 12 | 1 | 1 | 1 | 1 | 1 | |
| 100 | 21 | 7 | 19 | 7 | 24 | 3 | 12 | 7 | 7 | 14 | 19 | 19 | |
| 200 | 5 | 7 | 19 | 1 | 24 | 3 | 22 | 1 | 1 | 13 | 14 | 15 | |
| 500 | 4 | 16 | 19 | 21 | 24 | 8 | 12 | 21 | 21 | 20 | 19 | 13 | |
| 1000 | 10 | 13 | 15 | 19 | 24 | 2 | 12 | 19 | 19 | 20 | 15 | 21 | |
| No. | Structures | Expt. | B3LYP/6-31G(d) | DFT-SOFM-RBFNN 6-31G(d) | B3LYP/STO-3G | DFT-SOFM-RBFNN STO-3G |
|---|---|---|---|---|---|---|
| 1 | 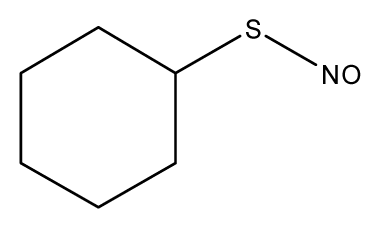 | 31.6 | 29.02 | 30.49 | 48.10 | 30.56 |
| 2 | 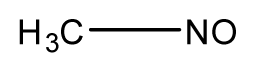 | 41.1 | 38.55 | 40.95 | 49.4 | 40.59 |
| 3 |  | 39.9 | 37.67 | 39.90 | 32.47 | 39.90 |
| 4 |  | 50.5 | 50.34 | 50.48 | 60.6 | 51.12 |
| 5 |  | 37.8 | 27.04 | 37.85 | 48.8 | 37.98 |
| 6 | 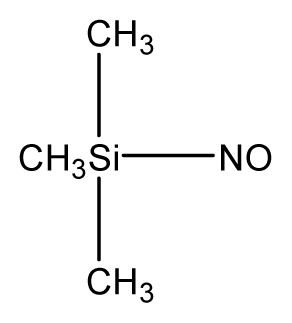 | 44.8 | 34.65 | 44.76 | 50.58 | 44.62 |
| NO. | DFT-SOFM-RBFNNa | M06-2X/6-311 + G(2d,p) | M06-2X/6-311 + G(2d,p) (PCM) | B3LYP/6-31G(d) |
|---|---|---|---|---|
| 39 | −0.1 | 3.6 | 2.4 | 0.29 |
| 59 | 1.2 | 1.5 | 0.8 | −4.9 |
| 76 | 0.0 | 4.2 | 4.2 | 3.0 |
| 91 | −0.1 | −2.2 | −4.1 | −8.7 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, H.Z.; Hu, L.H.; Tao, W.; Gao, T.; Li, H.; Lu, Y.H.; Su, Z.M. A Promising Tool to Achieve Chemical Accuracy for Density Functional Theory Calculations on Y-NO Homolysis Bond Dissociation Energies. Int. J. Mol. Sci. 2012, 13, 8051-8070. https://doi.org/10.3390/ijms13078051
Li HZ, Hu LH, Tao W, Gao T, Li H, Lu YH, Su ZM. A Promising Tool to Achieve Chemical Accuracy for Density Functional Theory Calculations on Y-NO Homolysis Bond Dissociation Energies. International Journal of Molecular Sciences. 2012; 13(7):8051-8070. https://doi.org/10.3390/ijms13078051
Chicago/Turabian StyleLi, Hong Zhi, Li Hong Hu, Wei Tao, Ting Gao, Hui Li, Ying Hua Lu, and Zhong Min Su. 2012. "A Promising Tool to Achieve Chemical Accuracy for Density Functional Theory Calculations on Y-NO Homolysis Bond Dissociation Energies" International Journal of Molecular Sciences 13, no. 7: 8051-8070. https://doi.org/10.3390/ijms13078051




