Artificial Intelligence Techniques to Optimize the EDC/NHS-Mediated Immobilization of Cellulase on Eudragit L-100
Abstract
:1. Introduction
2. Results and Discussion
2.1. ANN based Simulation and Prediction
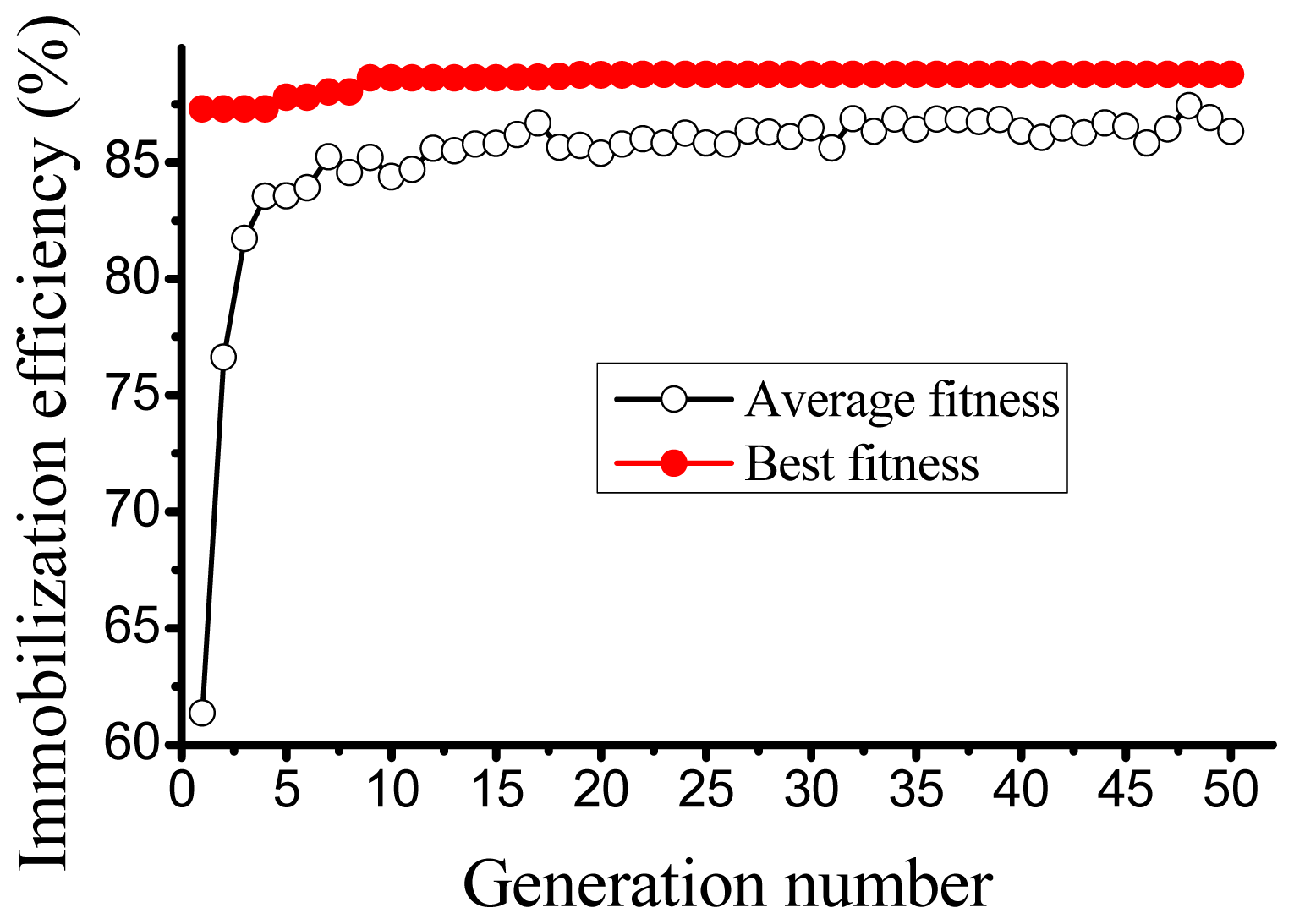
2.2. ANN based Optimization by GA
2.3. Reusability
3. Experimental Section
3.1. Materials
3.2. Immobilization of Cellulase on Eudragit L-100
3.3. Central Composite Design
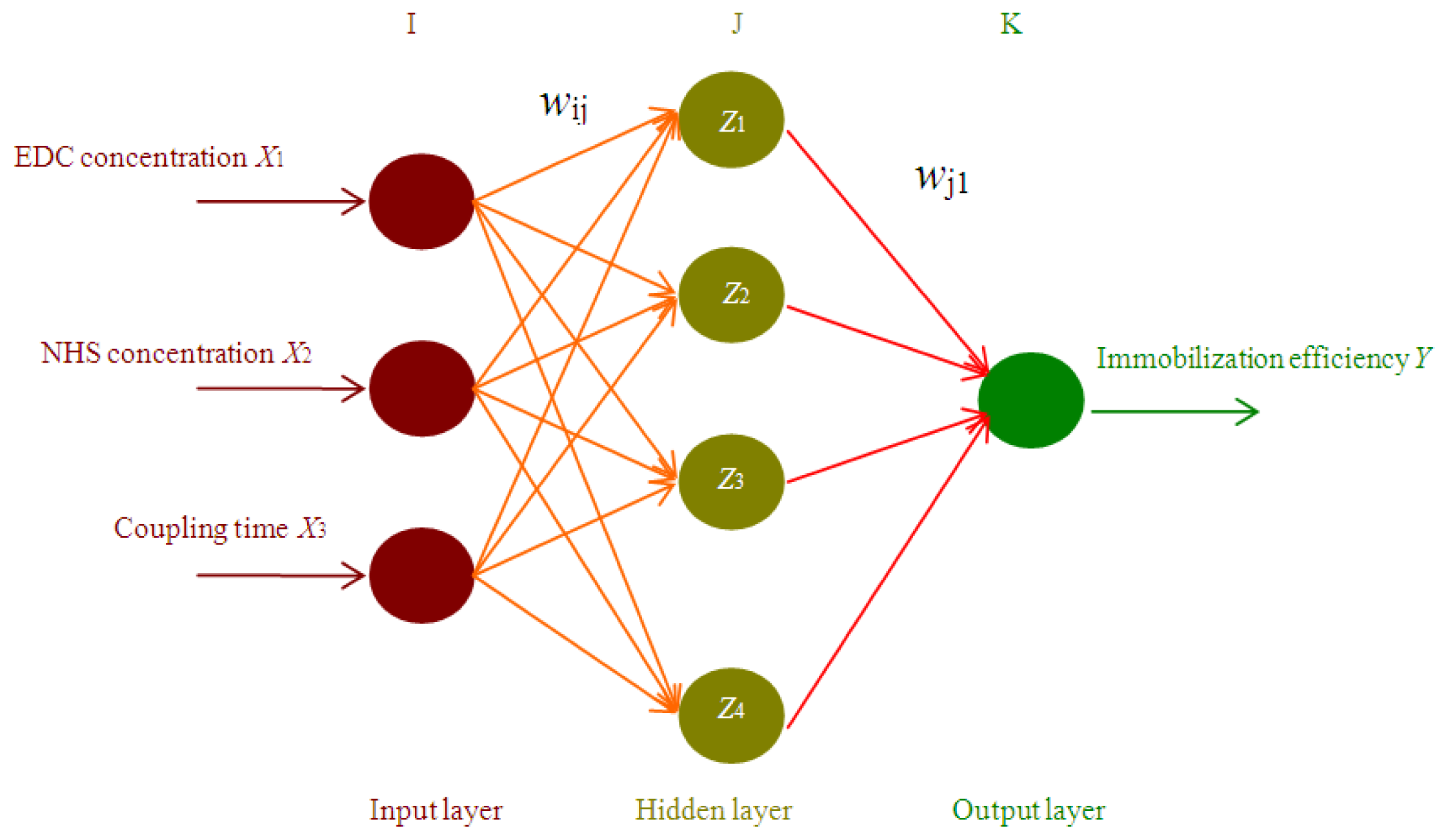
3.4. Artificial Neural Network
3.5. Genetic Algorithm
3.6. Determination of Immobilization Efficiency
3.7. HPLC Method
4. Conclusions
Acknowledgment
References
- Sheldon, R.A. Enzyme immobilization: The quest for optimum performance. Adv. Synth. Catal 2007, 349, 1289–1307. [Google Scholar]
- Tischer, W.; Wedekind, F. Immobilized enzymes: Methods and applications. Top. Curr. Chem 1999, 200, 95–126. [Google Scholar]
- Wang, Y.H.; Zhang, J.C.; Yin, J.M. Progress of enzyme immobilization and its potential application. Desalin. Water Treat 2009, 1, 151–171. [Google Scholar]
- Mateo, C.; Palomo, J.M.; Fernandez-Lorente, G.; Guisan, J.M.; Fernandez-Lafuente, R. Improvement of enzyme activity, stability and selectivity via immobilization techniques. Enzyme Microb. Technol 2007, 40, 1451–1463. [Google Scholar]
- Woodward, J. Immobilized cellulases for cellulose utilization. J. Biotechnol 1989, 11, 299–312. [Google Scholar]
- Galaev, I.; Mattiasson, B. Smart Polymers for Bioseparation and Bioprocessing, 1st ed; Taylor & Francis Inc.: New York, NY, USA, 2002. [Google Scholar]
- Roy, I.; Sharma, S.; Gupta, M.N. Smart biocatalysts: Design and applications. Adv. Biochem. Eng. Biotechnol 2004, 86, 159–189. [Google Scholar]
- Taniguchi, M.; Kobayashi, M.; Fujii, M. Properties of a reversible soluble insoluble cellulase and its application to repeated hydrolysis of crystalline cellulose. Biotechnol. Bioeng 1989, 34, 1092–1097. [Google Scholar]
- Zhang, Y.; Xu, J.L.; Yuan, Z.H.; Xu, H.J.; Yu, Q. Artificial neural network-genetic algorithm based optimization for the immobilization of cellulase on the smart polymer Eudragit L-100. Bioresour. Technol 2010, 101, 3153–3158. [Google Scholar]
- Zhang, Y.; Xu, J.L.; Li, D.; Yuan, Z.H. Preparation and properties of an immobilized cellulase on the reversibly soluble matrix Eudragit L-100. Biocatal. Biotransform 2010, 28, 313–319. [Google Scholar]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar]
- Bas, D.; Boyaci, I.H. Modeling and optimization I: Usability of response surface methodology. J. Food Eng 2007, 78, 836–845. [Google Scholar]
- Lakshminarayanan, A.K.; Balasubramanian, V. Comparison of RSM with ANN in predicting tensile strength of friction stir welded AA7039 aluminium alloy joints. T. Nonferr. Metal. Soc 2009, 19, 9–18. [Google Scholar]
- Zhang, Y.; Xu, J.L.; Yuan, Z.H.; Zhuang, X.S.; Lu, P.M. Kinetic model study on enzymatic hydrolysis of cellulose using artificial neural networks. Chin. J. Catal 2009, 30, 355–358. [Google Scholar]
- Guo, Y.; Xu, J.L.; Zhang, Y.; Xu, H.J.; Yuan, Z.H.; Li, D. Medium optimization for ethanol production with Clostridium autoethanogenum with carbon monoxide as sole carbon source. Bioresour. Technol 2010, 101, 8784–8789. [Google Scholar]
- Schubert, M.; Mourad, S.; Schwarze, F. Radial basis function neural networks for modeling growth rates of the basidiomycetes Physisporinus vitreus and Neolentinus lepideus. Appl. Microbiol. Biotechnol 2010, 85, 703–712. [Google Scholar]
- Marchitan, N.; Cojocaru, C.; Mereuta, A.; Duca, G.; Cretescu, I.; Gonta, M. Modeling and optimization of tartaric acid reactive extraction from aqueous solutions: A comparison between response surface methodology and artificial neural network. Sep. Purif. Technol 2010, 75, 273–285. [Google Scholar]
- Pal, M.P.; Vaidya, B.K.; Desai, K.M.; Joshi, R.M.; Nene, S.N.; Kulkarni, B.D. Media optimization for biosurfactant production by Rhodococcus erythropolis MTCC 2794: Artificial intelligence versus a statistical approach. J. Ind. Microbiol. Biotechnol 2009, 36, 747–756. [Google Scholar]
- Singh, A.; Majumder, A.; Goyal, A. Artificial intelligence based optimization of exocellular glucansucrase production from Leuconostoc dextranicum NRRL B-1146. Bioresour. Technol 2008, 99, 8201–8206. [Google Scholar]
- He, L.; Xu, Y.Q.; Zhang, X.H. Medium factor optimization and fermentation kinetics for phenazine-1-carboxylic acid production by Pseudomonas sp M18G. Biotechnol. Bioeng 2008, 100, 250–259. [Google Scholar]
- Chaibakhsh, N.; Rahman, M.B.A.; Vahabzadeh, F.; Abd-Aziz, S.; Basri, M.; Salleh, A.B. Optimization of operational conditions for adipate ester synthesis in a stirred tank reactor. Biotechnol. Bioprocess Eng 2010, 15, 846–853. [Google Scholar]
- Gurunathan, B.; Sahadevan, R. Design of experiments and artificial neural network linked genetic algorithm for modeling and optimization of l-asparaginase production by Aspergillus terreus MTCC 1782. Biotechnol. Bioprocess Eng 2011, 16, 50–58. [Google Scholar]
- Li, Y.; Du, X.L.; Yuan, Q.P.; Lv, X.H. Development and validation of a new PCR optimization method by combining experimental design and artificial neural network. Appl. Biochem. Biotechnol 2010, 160, 269–279. [Google Scholar]
- Sivapathasekaran, C.; Mukherjee, S.; Ray, A.; Gupta, A.; Sen, R. Artificial neural network modeling and genetic algorithm based medium optimization for the improved production of marine biosurfactant. Bioresour. Technol 2010, 101, 2884–2887. [Google Scholar]
- Rahman, M.B.A.; Chaibakhsh, N.; Basri, M.; Salleh, A.B.; Rahman, R.N.Z.R.A. Application of artificial neural network for yield prediction of lipase-catalyzed synthesis of dioctyl adipate. Appl. Biochem. Biotechnol 2009, 158, 722–735. [Google Scholar]
- Wang, J.L.; Wan, W. Application of desirability function based on neural network for optimizing biohydrogen production process. Int. J. Hydrog. Energy 2009, 34, 1253–1259. [Google Scholar]
- Izadifar, M.; Jahromi, M.Z. Application of genetic algorithm for optimization of vegetable oil hydrogenation process. J. Food Eng 2007, 78, 1–8. [Google Scholar]
- Almeida, J.S. Predictive non-linear modeling of complex data by artificial neural networks. Curr. Opin. Biotechnol 2002, 13, 72–76. [Google Scholar]
- Balkin, S.D.; Lin, D.K.J. A neural network approach to response surface methodology. Commun. Stat. Theory Methods 2000, 29, 2215–2227. [Google Scholar]
- Desai, K.M.; Survase, S.A.; Saudagar, P.S.; Lele, S.S.; Singhal, R.S. Comparison of artificial neural network (ANN) and response surface methodology (RSM) in fermentation media optimization: Case study of fermentative production of scleroglucan. Biochem. Eng. J 2008, 41, 266–273. [Google Scholar]
- Ghose, T.K. Measurements of cellulase activities. Pure Appl. Chem 1987, 2, 257–268. [Google Scholar]
- Carrillo, F.; Lis, M.J.; Colom, X.; Lopez-Mesas, M.; Valldeperas, J. Effect of alkali pretreatment on cellulase hydrolysis of wheat straw: Kinetic study. Process Biochem 2005, 40, 3360–3364. [Google Scholar]
- Sardar, M.; Roy, I.; Gupta, M.N. Simultaneous purification and immobilization of Aspergillus niger xylanase on the reversibly soluble polymer Eudragit™ L-100. Enzyme Microb. Technol 2000, 27, 672–679. [Google Scholar]
- Tompos, A.; Margitfalvi, J.L.; Tfirst, E.; Heberger, K. Predictive performance of “highly complex” artificial neural networks. Appl. Catal. A 2007, 324, 90–93. [Google Scholar]

| Trials | X1 | X2 | X3 | Immobilization efficiency (%) | |
|---|---|---|---|---|---|
| Experimental | ANN | ||||
| Data for ANN simulation (CCD) | |||||
| 1 | −1.00 | −1.00 | −1.00 | 76.29 ± 5.25 | 77.69 |
| 2 | +1.00 | −1.00 | −1.00 | 46.53 ± 3.14 | 46.85 |
| 3 | −1.00 | +1.00 | −1.00 | 45.64 ± 3.52 | 45.53 |
| 4 | +1.00 | +1.00 | −1.00 | 67.12 ± 4.94 | 68.28 |
| 5 | −1.00 | −1.00 | +1.00 | 59.45 ± 4.15 | 59.58 |
| 6 | +1.00 | −1.00 | +1.00 | 48.80 ± 3.88 | 49.40 |
| 7 | −1.00 | +1.00 | +1.00 | 61.89 ± 4.68 | 64.31 |
| 8 | +1.00 | +1.00 | +1.00 | 73.77 ± 5.01 | 74.10 |
| 9 | −1.68 | 0.00 | 0.00 | 54.74 ± 4.21 | 52.89 |
| 10 | +1.68 | 0.00 | 0.00 | 64.84 ± 4.52 | 63.87 |
| 11 | 0.00 | −1.68 | 0.00 | 45.73 ± 3.57 | 47.18 |
| 12 | 0.00 | +1.68 | 0.00 | 63.49 ± 4.36 | 62.75 |
| 13 | 0.00 | 0.00 | −1.68 | 55.12 ± 3.89 | 54.17 |
| 14 | 0.00 | 0.00 | +1.68 | 48.25 ± 3.31 | 48.00 |
| 15 | 0.00 | 0.00 | 0.00 | 77.01 ± 5.15 | 76.86 |
| 16 | 0.00 | 0.00 | 0.00 | 77.33 ± 5.07 | 76.86 |
| 17 | 0.00 | 0.00 | 0.00 | 77.22 ± 5.20 | 76.86 |
| Data for ANN simulation (CCD) | |||||
| 18 | 0.00 | 0.00 | 0.00 | 77.06 ± 5.19 | 76.86 |
| 19 | 0.00 | 0.00 | 0.00 | 77.30 ± 5.09 | 76.86 |
| 20 | 0.00 | 0.00 | 0.00 | 77.28 ± 5.08 | 76.86 |
| Data for ANN prediction (random) | |||||
| 21 | −1.68 | 0.00 | +1.00 | 76.22 ± 4.77 | 78.17 |
| 22 | −1.00 | +1.00 | 0.00 | 71.31 ± 3.98 | 69.38 |
| 23 | 0.00 | +1.68 | +1.68 | 57.59 ± 2.56 | 56.87 |
| DF | SS | MS | F-value | p-value | R2 | |
|---|---|---|---|---|---|---|
| Model | 1 | 2909.454 | 2909.454 | 2865.166 | 2.68E–21 | 0.9938 |
| Residual | 18 | 18.27823 | 1.015457 | |||
| Total | 19 | 2927.732 |
| Factors | Symbols | Ranges and levels | ||||
|---|---|---|---|---|---|---|
| −1.68 | −1.00 | 0 | 1.00 | 1.68 | ||
| EDC concentration | X1 | 0.06 | 0.20 | 0.40 | 0.60 | 0.74 |
| NHS concentration | X2 | 0.08 | 0.16 | 0.28 | 0.40 | 0.48 |
| Coupling time | X3 | 0.48 | 1.50 | 3.00 | 4.50 | 5.52 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, Y.; Xu, J.-L.; Yuan, Z.-H.; Qi, W.; Liu, Y.-Y.; He, M.-C. Artificial Intelligence Techniques to Optimize the EDC/NHS-Mediated Immobilization of Cellulase on Eudragit L-100. Int. J. Mol. Sci. 2012, 13, 7952-7962. https://doi.org/10.3390/ijms13077952
Zhang Y, Xu J-L, Yuan Z-H, Qi W, Liu Y-Y, He M-C. Artificial Intelligence Techniques to Optimize the EDC/NHS-Mediated Immobilization of Cellulase on Eudragit L-100. International Journal of Molecular Sciences. 2012; 13(7):7952-7962. https://doi.org/10.3390/ijms13077952
Chicago/Turabian StyleZhang, Yu, Jing-Liang Xu, Zhen-Hong Yuan, Wei Qi, Yun-Yun Liu, and Min-Chao He. 2012. "Artificial Intelligence Techniques to Optimize the EDC/NHS-Mediated Immobilization of Cellulase on Eudragit L-100" International Journal of Molecular Sciences 13, no. 7: 7952-7962. https://doi.org/10.3390/ijms13077952




