Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy
Abstract
:1. Introduction
2. Van der Waals Interactions
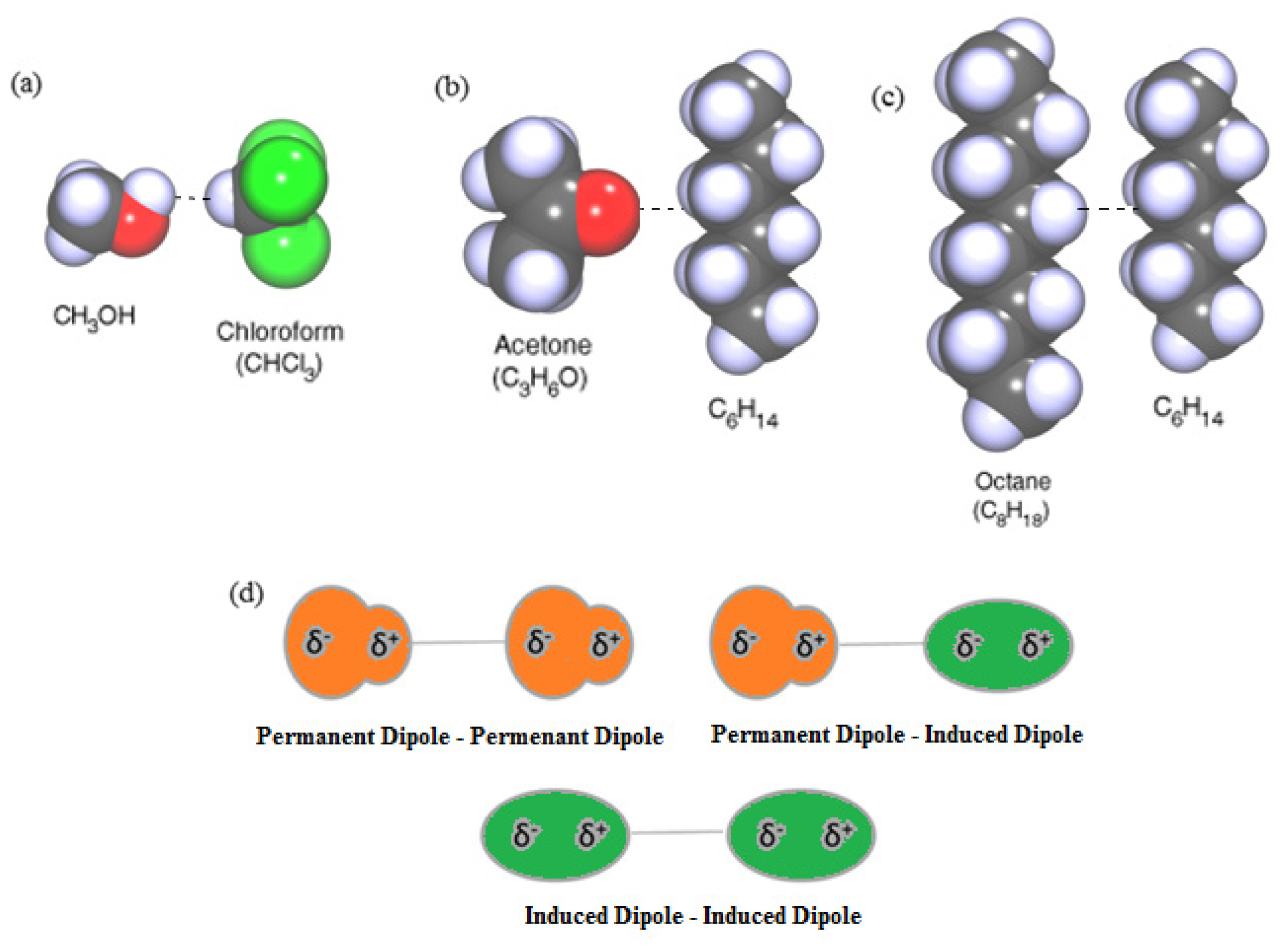
2.1. vdW Interactions between Molecules in Vacuum
2.2. vdW between Molecules in a Medium
- The vdW force is anisotropic, similarly to the polarizabilities of the majority of molecules, i.e., they have different values for different molecular directions (except for ideal spherical particles);
- The orienting effects of the anisotropic dispersion forces are usually less important than other forces such as dipole-dipole interactions;
- The vdW force is non-additive. The force between two molecules is affected by molecules nearby, which behave like a medium, and is important for large particles interacting with a surface;
- The vdW force is much reduced in a solvent medium.
3. Interactions between Surfaces and the Hamaker Constant
- The vdW force between two identical bodies in a medium is always attractive (A is positive), whereas the force between two different bodies may be attractive or repulsive. If ɛ3 and n3 are intermediate between ɛ1 and ɛ2 and n1 and n2, respectively, A is negative (repulsive). Hamaker noted this [78], which was supported by Derjaguin [88], while Visser [89] established the precise conditions necessary for repulsive vdW-London forces. Fowkes [90] was the first to indicate a few possible examples of such repulsions, and van Oss et al. [91] demonstrated the existence of many such systems;
- The vdW force between any two condensed bodies in vacuum or in air (ɛ3 = 1 and n3 = 1) is always attractive (A is always positive);
- If ɛ3 and n3 equal the dielectric constant and index of refraction of either of the two bodies, A vanishes;
- The polar term cannot be larger than (3/4) kBT;
- Since hν >> kBT, as for interactions in free space, the dispersion force contribution (ν > 0) is usually greater than the dipolar contribution (ν = 0);
- The vdW force is much reduced in a solvent medium.
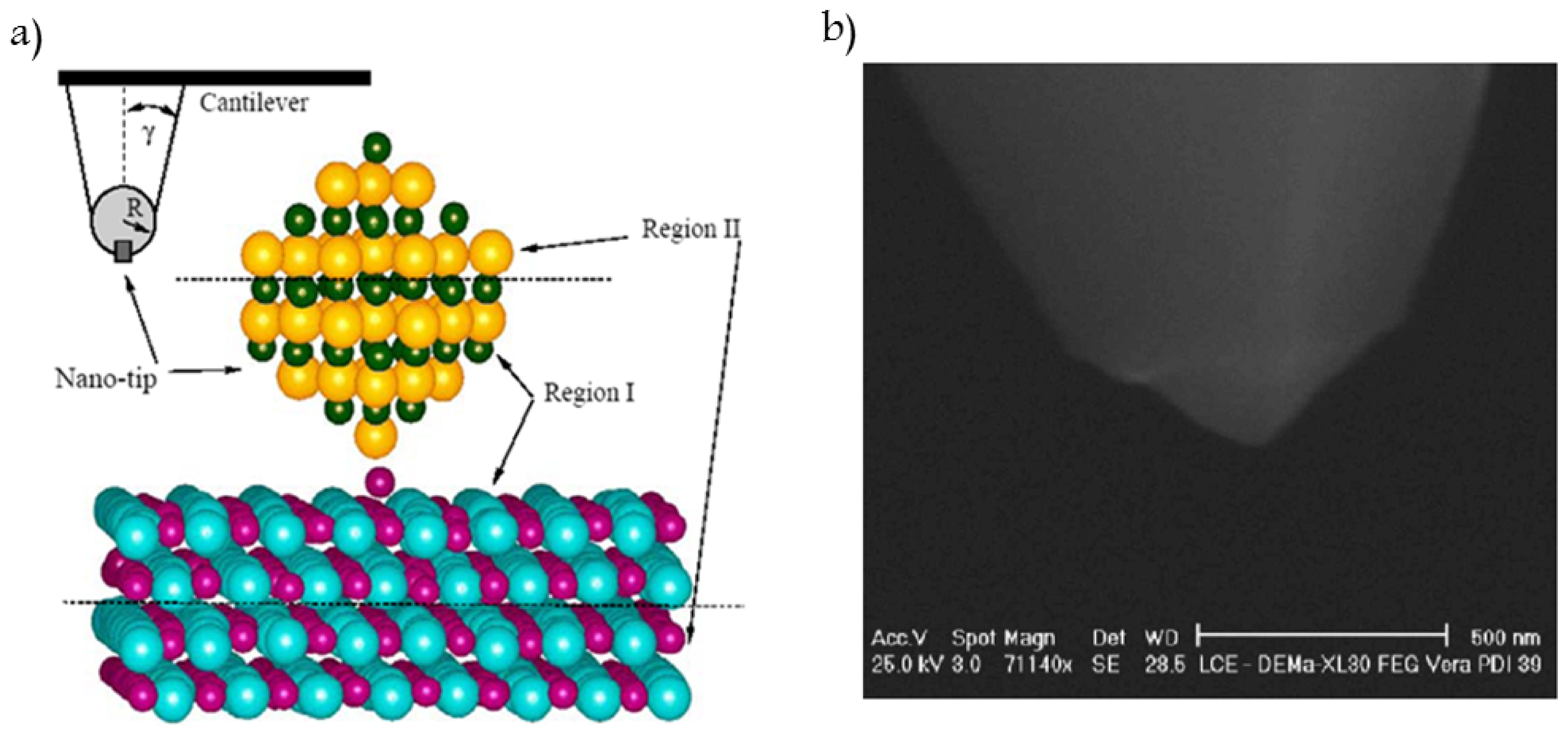
4. Introduction to Atomic Force Spectroscopy (AFS)
5. Measuring and Calculating van der Waals and Adhesion Forces
5.1. Interactions in Vacuum
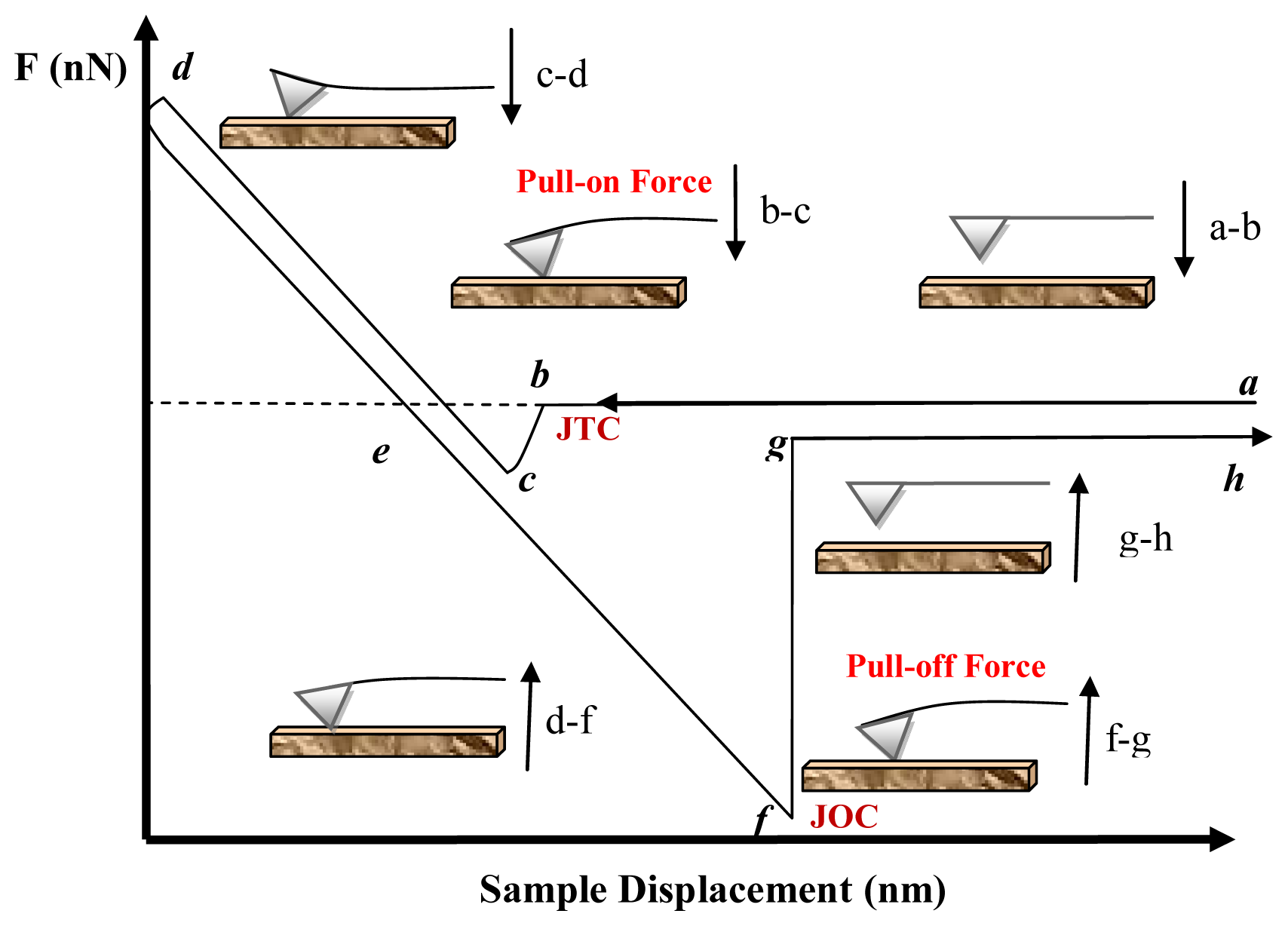
5.1.1. Attractive Forces (pull-on forces)
5.1.1.1. Electrostatic Forces (Fe)
- Surfaces are smooth, and the surface topography is not taken into account;
- The materials are conductive with charge uniformly distributed, only on the surface, and the electric field is normal to the surface;
- There is no charge between contacting objects.
5.1.1.1.1. Plane–Plane Model
5.1.1.1.2. Sphere–Plane Model
5.1.1.1.3. Uniformly Charged Line Models (Conical Tip Models)
5.1.1.1.4. The Asymptotic Model
5.1.1.1.5. The Hyperboloid Model (Hyperboloid Tip Model)
5.1.1.1.6. The Cylindrical Model
5.1.1.2. van der Waals Forces (Fvdw)
5.1.2. Adhesion Forces (Pull-Off Forces)
5.1.2.1. Electrostatic Forces (Fe)
5.1.2.2. Van der Waals Adhesiveness (FvdW )
5.1.3. Work of Adhesion and Surface Energy
5.1.3.1. Wettability
5.1.3.2. Work of Adhesion
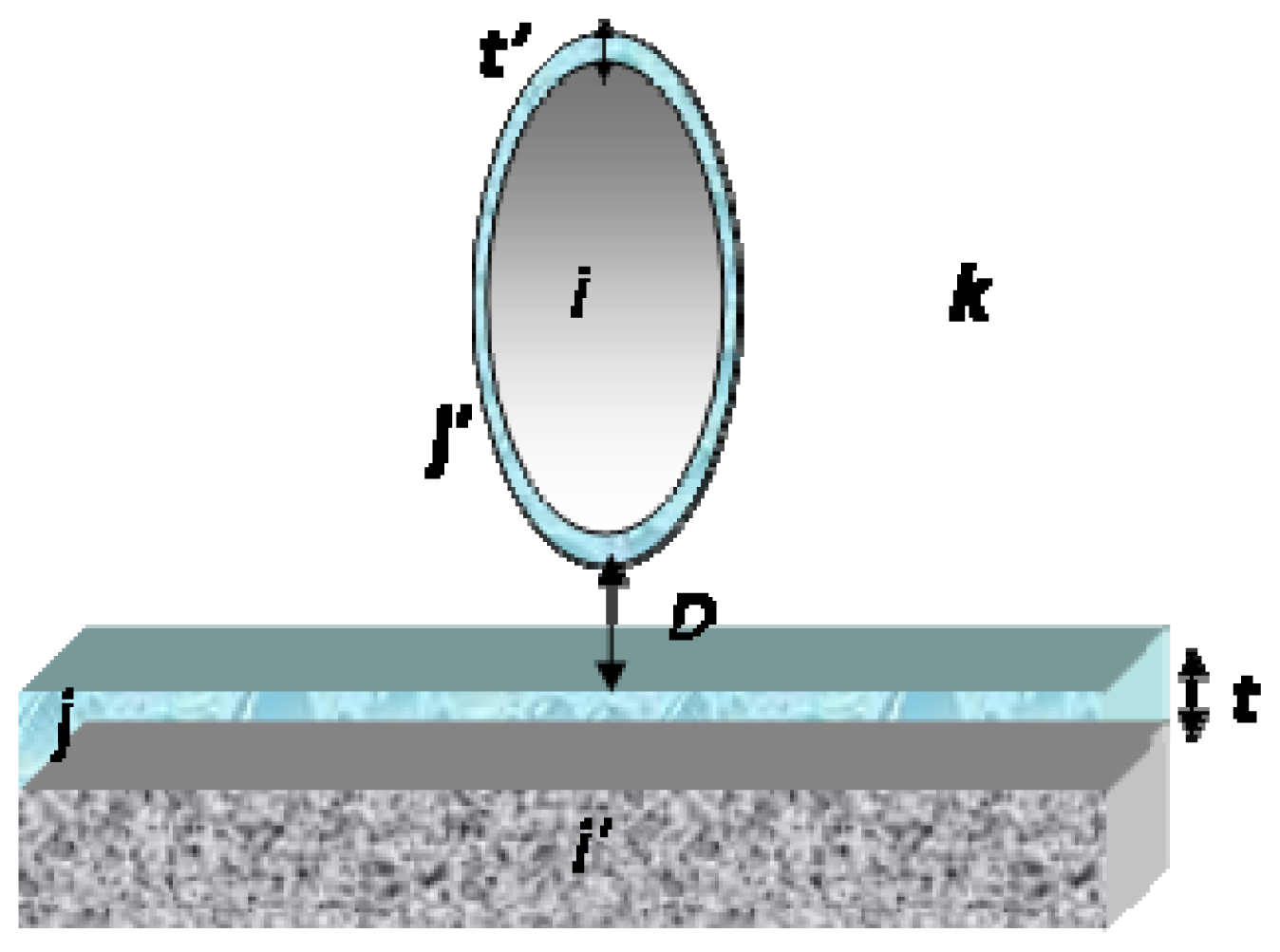
- unequal surfaces i and j in contact in vapor (V)
- equal surfaces i and j in contact in vapor
- equal surfaces i and i in contact under a liquid
5.1.3.3. Surface Tension
5.2. Interactions in Ambient Conditions
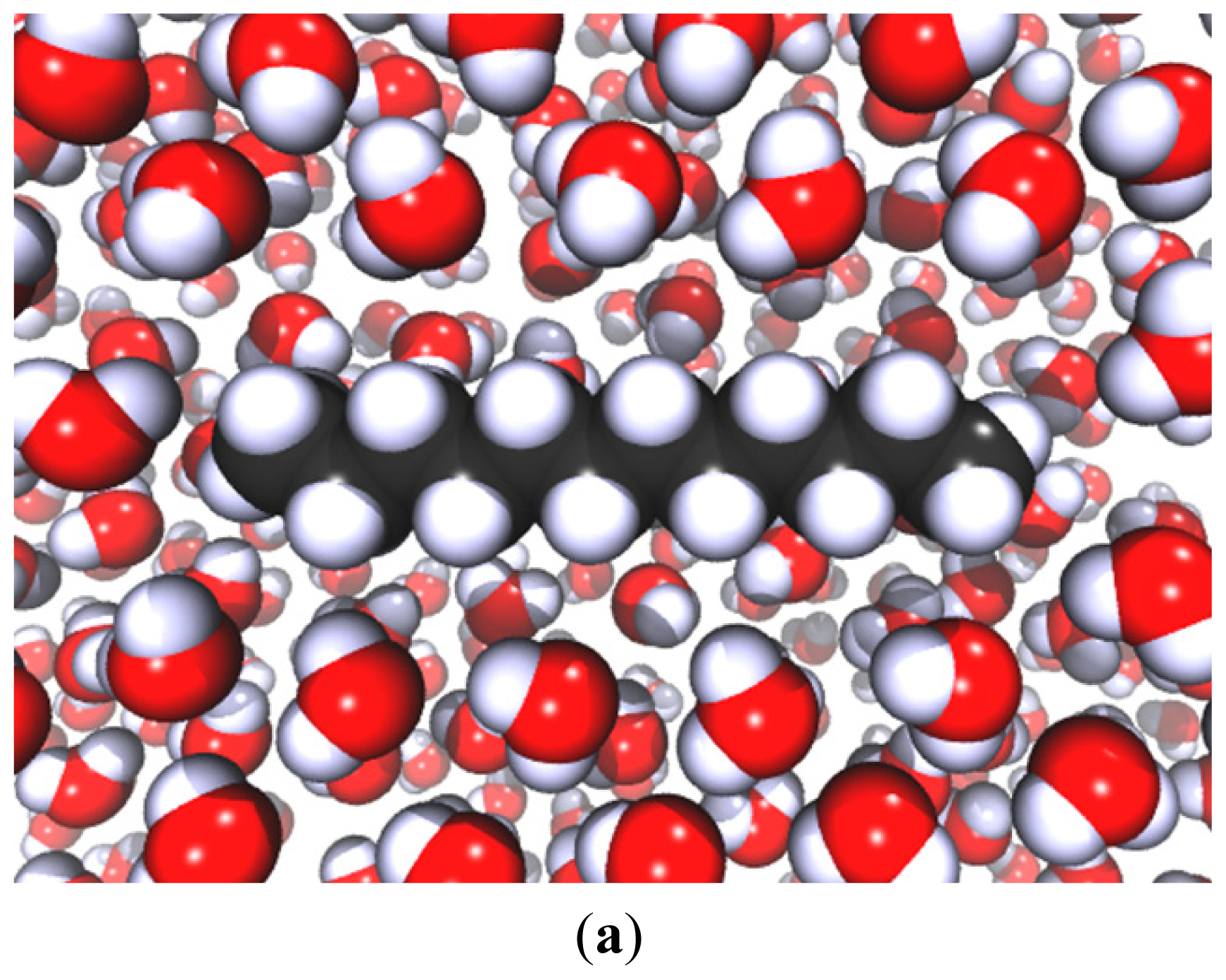
5.2.1. The Thin Water Film
5.2.2. Attractive Interactions (vdW) (Pull-On Forces)
5.2.3. Adhesion Forces (Pull-Off Forces)
5.2.3.1. Capillary Forces
5.2.3.2. Chemical Forces
5.2.3.3. Electric Forces
5.6.4. Total Adhesion Forces
5.3. Interactions in Solution
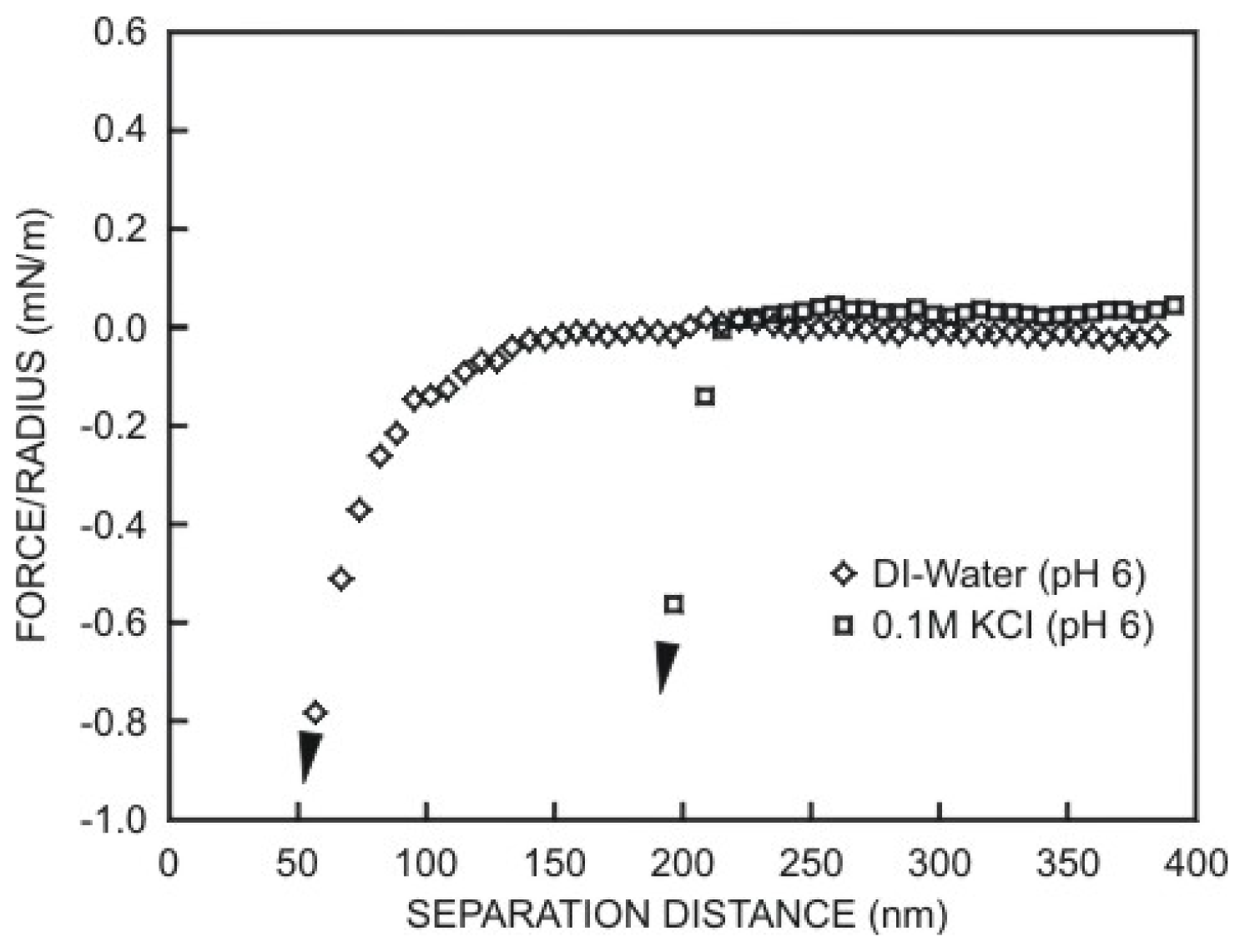
5.3.1. Screened vdW Forces in Electrolyte Solutions
5.3.2. The DLVO Theory: vdW and Double-Layer Forces Acting Together
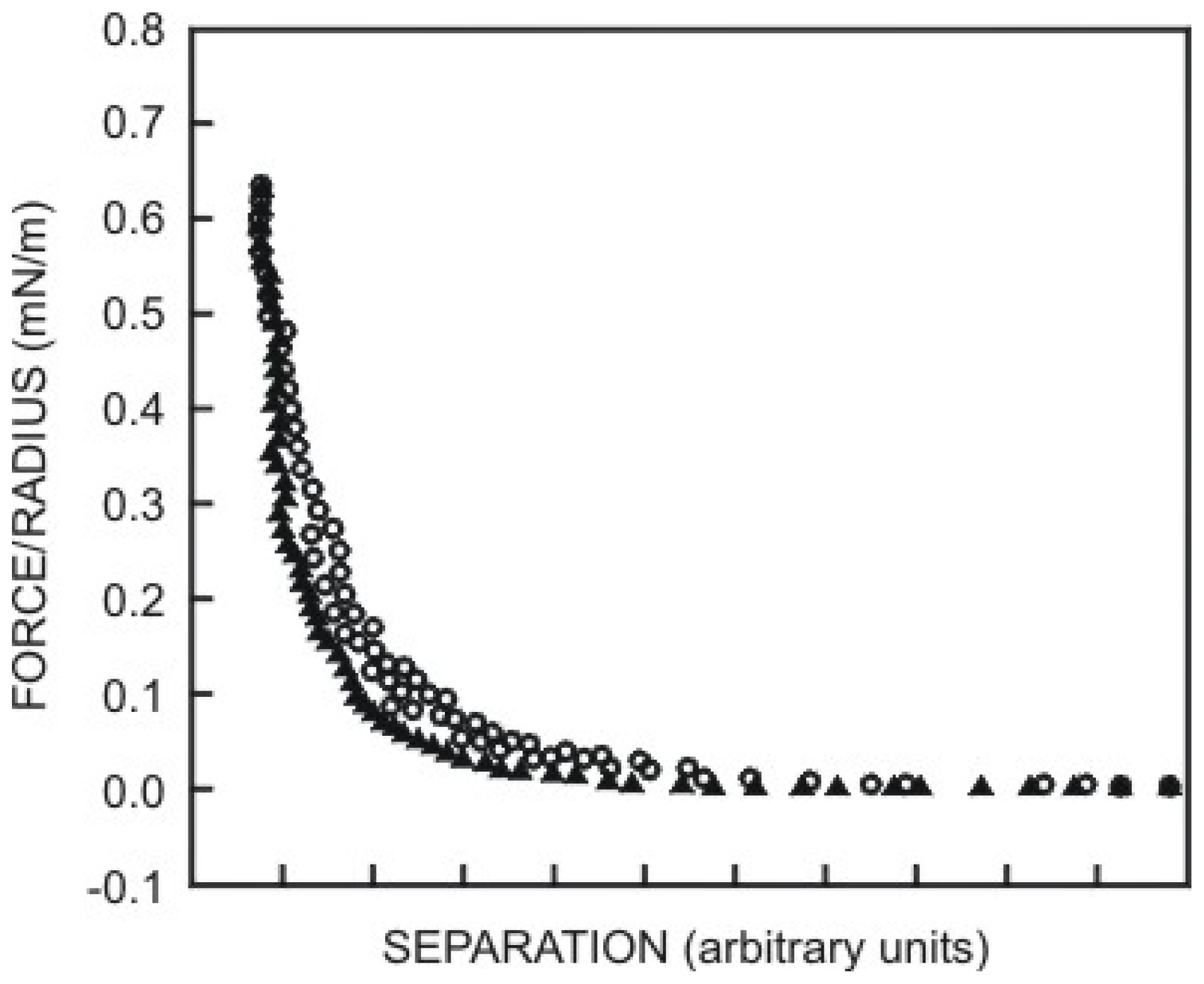
5.3.3. Non-DLVO Forces: vdW and Structural Forces Acting Together
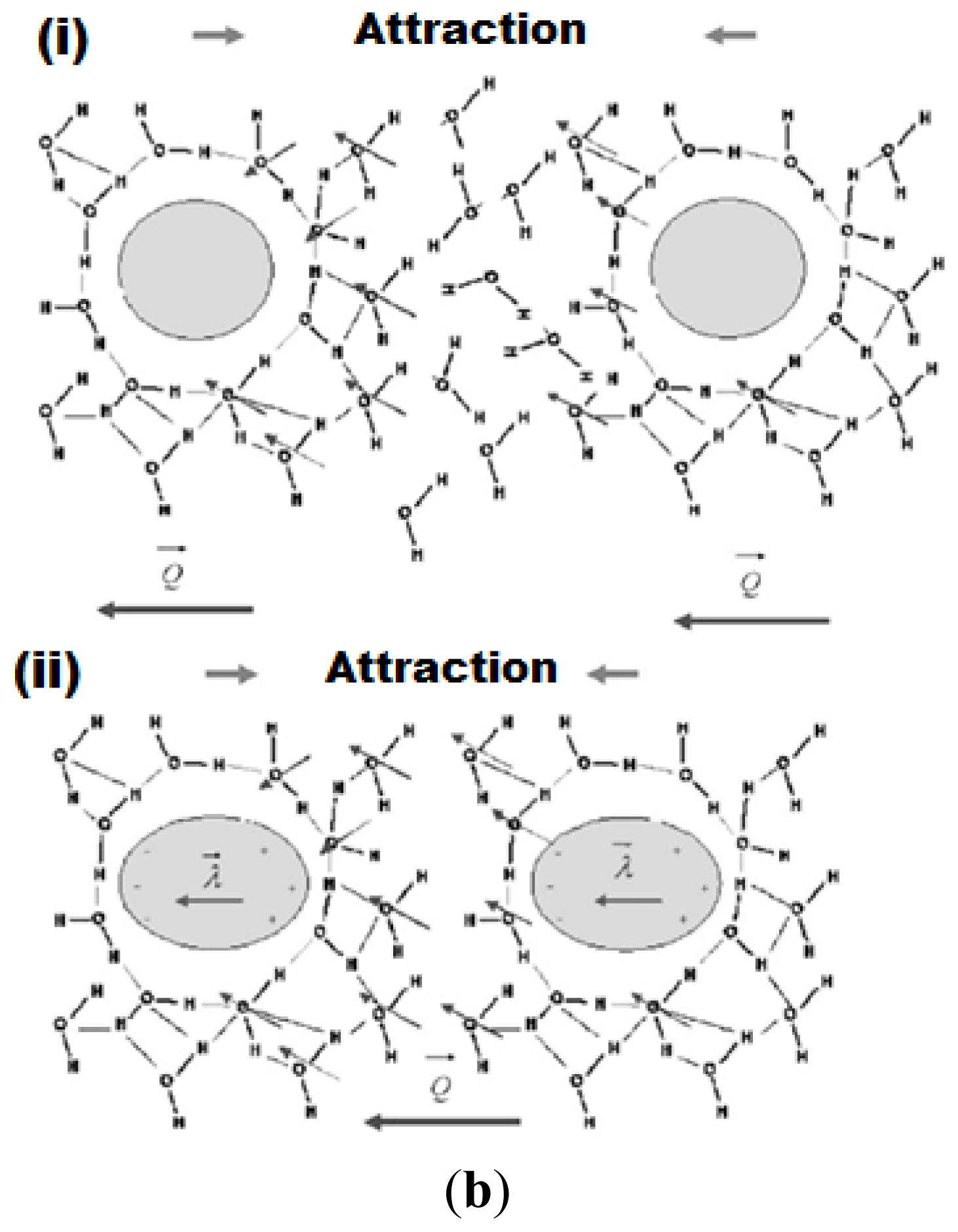
- Water Structure Theory: in the water-structuring models, the short-range repulsive interaction is attributed to an alignment of water dipoles in the vicinity of a hydrophilic surface, where the range of the surface force is determined by the orientation-correlation length of the solvent molecules [336]. Other researchers also suggested that the origin of the hydration force between silica surfaces may be related to the structuring of water molecules at the silica-water interface [337–339]. It is known that water can form strong H-bonds with the silanol groups. Derjaguin suggested that next to the silica surface there might be a layer of structured water up to 900 Å thick [340]. Attard and Batchelor [341] suggested that due to the strong orientation of water molecules near polar surfaces, there are fewer configurations available to maintain the bulk water structure and this represents lost entropy, which leads to a repulsive force.
- Image-charge model: the image-charge models take into account the discreteness of the surface charges, which induce orientation in the adjacent water dipoles [342].
- Dielectric-saturation model: this model assigns the hydration repulsion to a layer with lower dielectric constant, ɛ, in the vicinity of the interfaces [343]. Henderson and Lozadacassau [344] suggested that since the water molecules at the surface are strongly oriented, there should be a region of smaller dielectric constant at the solvent substrate interface when compared to the bulk.
- Excluded-volume model: it takes into account the finite size of the ions, leading to a lower counterion concentration near a charged surface, and to a weaker Debye screening of the electrostatic field, which results in a stronger repulsion between two charged surfaces at short separations [345].
- Gel-like layer model: the presence of a porous gel-like layer on silica was proposed by Lyklema [346] to explain the high surface charge and low potentials of the silica surface. Theoretical calculations to account for the observed charging characteristics of oxides have indicated that the gel layer maybe ~2–6 nm thick. Vigil et al. [347] used this explanation in the analysis of their experiments using silica surfaces and SFA.
- Layer of co-ions model: this relatively simple model [348] assumes that at sufficiently small thicknesses all co-ions are pressed out of the film so that it contains only counterions dissociated from the ionized surface groups. Under such conditions, the screening of the electric field of the film surface weakens, which considerably enhances the electrostatic repulsion in comparison with that predicted by DLVO theory. Such reduced screening of the electric field could exist only in a narrow range of film thicknesses, which practically coincides with the range where hydration is observed.
6. Conclusions
Acknowledgments
References
- Burnham, N.A.; Kulik, A.J. Surface Forces and Adhesion. In Handbook of Micro/Nanotribology; Bhushan, B., Ed.; CRC Press, LLC: Boca Raton, FL, USA, 1999. [Google Scholar]
- Myers, D. Surfaces, Interfaces, and Colloids: Principles and Applications, 2nd ed; Wiley-VCH: New York, NY, USA, 1999; p. 501. [Google Scholar]
- Varandas, A.J.C.; Brandao, J. A simple semi-empirical approach to the intermolecular potential of vanderwaals systems.1. Isotropic interactions—Application to the lowest triplet-state of the alkali dimers. Mol. Phys 1982, 45, 857–875. [Google Scholar]
- Van der Waals, J.D. Thermodynamische Theorie der Capillariteit in de Onderstelling van Continue Dichtheidsverandering; Verhandel Konink Akad Weten: Amsterdam, The Netherlands, 1893; Volume 1, p. 56. [Google Scholar]
- Kitchener, J.A.; Prosser, A.P. Direct measurement of the long-range van der waals forces. Proc. R. Soc. A 1957, 242, 403–409. [Google Scholar]
- Drelich, J.; Mittal, K.L. Atomic Force Microscopy in Adhesion Studies; Brill Academic Pub: Leiden, The Netherlands, 2005. [Google Scholar]
- Sun, L.; Li, X.; Hede, T.; Tu, Y.Q.; Leck, C.; Agren, H. Molecular dynamics simulations of the surface tension and structure of salt solutions and clusters. J. Phys. Chem. B 2012, 116, 3198–3204. [Google Scholar]
- Leite, F.L.; Borato, C.E.; da Silva, W.T.L.; Herrmann, P.S.P.; Oliveira, O.N., Jr; Mattoso, L.H.C. Atomic force spectroscopy on poly(O-ethoxyaniline) nanostructured films: Sensing nonspecific interactions. Microsc. Microanal. 2007, 13, 304–312. [Google Scholar]
- Bruch, L.W. Phys. Rev. B 2005, 72. [CrossRef]
- Nicolosi, V.; Nellist, P.D.; Sanvito, S.; Cosgriff, E.C.; Krishnamurthy, S.; Blau, W.J.; Green, M.L.H.; Vengust, D.; Dvorsek, D.; Mihailovic, D.; et al. Observation of van der waals driven self-assembly of mosi nanowires into a low-symmetry structure using aberration-corrected electron microscopy. Adv. Mater 2007, 19, 543–547. [Google Scholar]
- French, R.H.; Parsegian, V.A.; Podgornik, R.; Rajter, R.F.; Jagota, A.; Luo, J.; Asthagiri, D.; Chaudhury, M.K.; Chiang, Y.M.; Granick, S.; et al. Long range interactions in nanoscale science. Rev. Mod. Phys 2010, 82, 1887–1944. [Google Scholar]
- Leite, F.L.; Neto Mde, O.; Paterno, L.G.; Ballestero, M.R.M.; Polikarpov, I.; Mascarenhas, Y.P.; Herrmann, P.S.P.; Mattoso, L.H.C.; Oliveira, O.N., Jr. Nanoscale conformational ordering in polyanilines investigated by saxs and afm. J. Colloid Interface Sci. 2007, 316, 376–387. [Google Scholar]
- Xu, L.; Lio, A.; Hu, J.; Ogletree, D.F.; Salmeron, M. Wetting and capillary phenomena of water on mica. J. Phys. Chem. B 1998, 102, 540–548. [Google Scholar]
- Lubarsky, G.V.; Mitchell, S.A.; Davidson, M.R.; Bradley, R.H. Van der waals interaction in systems involving oxidised polystyrene surfaces. Colloids Surf. A: Physicochem. Eng. Asp 2006, 279, 188–195. [Google Scholar]
- Wang, C.X.; Chang, S.; Gong, X.Q.; Yang, F.; Li, C.H.; Chen, W.Z. Progress in the scoring functions of protein-protein docking. Acta Phys.Chim. Sin 2012, 28, 751–758. [Google Scholar]
- Chen, J.Z.; Zhang, D.L.; Zhang, Y.X.; Li, G.H. Computational studies of difference in binding modes of peptide and non-peptide inhibitors to mdm2/mdmx based on molecular dynamics simulations. Int. J. Mol. Sci 2012, 13, 2176–2195. [Google Scholar]
- Elbaum, M.; Lipson, S.G. How does a thin wetted film dry up? Phys. Rev. Lett. 1994, 72, 3562–3565. [Google Scholar]
- Elbaum, M.; Schick, M. Application of the theory of dispersion forces to the surface melting of ice. Phys. Rev. Lett. 1991, 66, 1713–1716. [Google Scholar]
- Hodges, C.S. Measuring forces with the AFM: Polymeric surfaces in liquids. Adv. Colloid Interface Sci 2002, 99, 13–75. [Google Scholar]
- Ninham, B.W.; Parsegian, V.A. Van der waals forces across triple-layer films. J. Chem. Phys 1970, 52, 4578–4587. [Google Scholar]
- Israelachvili, J.N. Adhesion forces between surfaces in liquids and condensable vapours. Surf. Sci. Rep 1992, 14, 109–159. [Google Scholar]
- Israelachvili, J.N.; Adams, G.E. Measurement of forces between two mica surfaces in aqueous electrolyte solutions in the range 0–100 nm. J. Chem. Soc., Faraday Trans 1978, 74, 975–1001. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces, 2nd ed; Academic Press: London, UK, 1995; p. 704. [Google Scholar]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic force microscope. Phys. Rev. Lett 1986, 56, 930–933. [Google Scholar]
- Hutter, J.L.; Bechhoefer, J. Measurement and manipulation of van-der-waals forces in atomic-force microscopy. J. Vac. Sci. Technol. B 1994, 12, 2251–2253. [Google Scholar]
- Meyer, E. Atomic force microscopy. Prog. Surf. Sci 1992, 41, 3–49. [Google Scholar]
- Frommer, J.E. Scanning probe microscopy of organics, an update. Thin Solid Films 1996, 273, 112–115. [Google Scholar]
- Butt, H.J. Measuring electrostatic, vanderwaals, and hydration forces in electrolyte-solutions with an atomic force microscope. Biophys. J 1991, 60, 1438–1444. [Google Scholar]
- Leite, F.L.; Herrmann, P.S.P. Application of atomic force spectroscopy (afs) to studies of adhesion phenomena: A review. J. Adhes. Sci. Technol 2005, 19, 365–405. [Google Scholar]
- Ducker, W.A.; Senden, T.J.; Pashley, R.M. Direct measurement of colloidal forces using an atomic force microscope. Nature 1991, 353, 239–241. [Google Scholar]
- Teschke, O.; Ceotto, G.; de Souza, E.F. Rupture force of adsorbed self-assembled surfactant layers—Effect of the dielectric exchange force. Chem. Phys. Lett 2001, 344, 429–433. [Google Scholar]
- Borkovec, M.; Papastavrou, G. Interactions between solid surfaces with adsorbed polyelectrolytes of opposite charge. Curr. Opin. Colloid Interface Sci 2008, 13, 429–437. [Google Scholar]
- Leite, F.L.; Paterno, L.G.; Borato, C.E.; Herrmann, P.S.P.; Oliveira, O.N.; Mattoso, L.H.C. Study on the adsorption of poly(O-ethoxyaniline) nanostructured films using atomic force microscopy. Polymer 2005, 46, 12503–12510. [Google Scholar]
- Sharp, T.G.; Oden, P.I.; Buseck, P.R. Lattice-scale imaging of mica and clay (001) surfaces by atomic force microscopy using net attractive forces. Surf. Sci 1993, 284, L405–L410. [Google Scholar]
- Sasaki, N.; Tsukada, M. Theory for the effect of the tip-surface interaction potential on atomic resolution in forced vibration system of noncontact afm. Appl. Surf. Sci 1999, 140, 339–343. [Google Scholar]
- Erts, D.; Lohmus, A.; Lohmus, R.; Olin, H.; Pokropivny, A.V.; Ryen, L.; Svensson, K. Force interactions and adhesion of gold contacts using a combined atomic force microscope and transmission electron microscope. Appl. Surf. Sci 2002, 188, 460–466. [Google Scholar]
- Persson, B.N.J. The atomic force microscope—Can it be used to study biological molecules. Chem. Phys. Lett 1987, 141, 366–368. [Google Scholar]
- Dagastine, R.R.; White, L.R. Forces between a rigid probe particle and a liquid interface—ii. The general case. J. Colloid Interface Sci 2002, 247, 310–320. [Google Scholar]
- Sokolov, I.Y.; Henderson, G.S.; Wicks, F.J. The contrast mechanism for true atomic resolution by afm in non-contact mode: Quasi-non-contact mode? Surf. Sci 1997, 381, L558–L562. [Google Scholar]
- Stone, A.J. The Theory of Intermolecular Forces; Clarendon Pres: Oxford, UK, 1996; Volume 32. [Google Scholar]
- Bhushan, B.; Israelachvili, J.N.; Landman, U. Nanotribology—Friction, wear and lubrication at the atomic-scale. Nature 1995, 374, 607–616. [Google Scholar]
- Kim, D.I.; Grobelny, J.; Pradeep, N.; Cook, R.F. Origin of adhesion in humid air. Langmuir 2008, 24, 1873–1877. [Google Scholar]
- Leckband, D.; Israelachvili, J. Intermolecular forces in biology. Q. Rev. Biophys 2001, 34, 105–267. [Google Scholar]
- Van der Waals, J.D. Thermodynamische theorie der capillariteit in de onderstelling van continue dichtheidsverandering; Verh. K. Akad. Wet: Amsterdam, The Netherlands, 1893. [Google Scholar]
- French, R.H. Origins and applications of london dispersion forces and hamaker constants in ceramics. J. Am. Ceram. Soc 2000, 83, 2117–2146. [Google Scholar]
- Garbassi, F.; Morra, M.; Occhiello, E. Polymer Surfaces from Physics to Technology; John Wiley & Sons: New York, NY, USA, 1994; p. 462. [Google Scholar]
- Tabor, D.; Winterto, R.H. Direct measurement of normal and retarded van der waals forces. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci 1969, 312, 435–450. [Google Scholar]
- Keesom, W.H. The second virial coefficient for rigid spherical molecules whose mutual attraction is equivalent to that of a quadruplet placed at its center. Proc. R. Acad. Sci 1915, 18, 636–646. [Google Scholar]
- Gerschel, A. Dipole-induced static and dynamic liquid structures. J. Chem. Soc., Faraday Trans. 2 Mol. Chem. Phys 1987, 83, 1765–1776. [Google Scholar]
- Debye, P. Die van der waalsschen kohäsionskräfte. Physikalische Zeitschrift 1920, 21, 178–187. [Google Scholar]
- London, F. Zur theorie und systematik der molekularkräfte. Zeitschrift für Physik A Hadrons Nuclei 1930, 63, 245–279. [Google Scholar]
- Feiler, A.A.; Bergstrom, L.; Rutland, M.W. Superlubricity using repulsive van der waals forces. Langmuir 2008, 24, 2274–2276. [Google Scholar]
- Duran-Vidal, S.; Simonin, J.P.; Turq, P. Electrolytes at Interfaces; Kluwer Academic Publishers: New York, NY, USA, 2002; Volume 1, p. 344. [Google Scholar]
- Debye, P. Molekularkräfte und ihre elektrische deutung. Physikalische Zeitschrift 1921, 22, 302–308. [Google Scholar]
- Keesom, W.M. Van der waals attractive force. Phys. Z 1921, 22, 129–141. [Google Scholar]
- Keesom, W.M. The quadrupole moments of the oxygen and nitrogen molecules. Proc. K. Ned. Akad. Wet 1920, 23, 939–942. [Google Scholar]
- London, F. Properties and applications of molecular forces. Zeitschrift für Physikalische Chemie (B) 1930, 11, 222–251. [Google Scholar]
- Jiang, X.P.; Toigo, F.; Cole, M.W. The dispersion force of physical adsorption.1. Local theory. Surf. Sci 1984, 145, 281–293. [Google Scholar]
- Jiang, X.P.; Toigo, F.; Cole, M.W. The dispersion force of physical adsorption.2. Nonlocal theory. Surf. Sci 1984, 148, 21–36. [Google Scholar]
- Hutson, J.M.; Fowler, P.W.; Zaremba, E. Quadrupolar contributions to the atom-surface vanderwaals interaction. Surf. Sci 1986, 175, L775–L781. [Google Scholar]
- Blaney, B.L.; Ewing, G.E. Vanderwaals molecules. Annu. Rev. Phys. Chem 1976, 27, 553–586. [Google Scholar]
- Ewing, G.E. Spectroscopy of vanderwaals molecules. Can. J. Phys 1976, 54, 487–504. [Google Scholar]
- Watanabe, A.; Welsh, H.L. Direct spectroscopic evidence of bound states of (h2)2 complexes at low temperatures. Phys. Rev. Lett 1964, 13, 810–812. [Google Scholar]
- Henderso, G; Ewing, G.E. Infrared-spectrum, structure and properties of n2-ar van der waals molecule. Mol. Phys. 1974, 27, 903–915. [Google Scholar]
- Power, E.A.; Thirunamachandran, T. Dispersion interactions between atoms involving electric quadrupole polarizabilities. Phys. Rev. A 1996, 53, 1567–1575. [Google Scholar]
- Marinescu, M.; Babb, J.F.; Dalgarno, A. Long-range potentials, including retardation, for the interaction of 2 alkali-metal atoms. Phys. Rev. A 1994, 50, 3096–3104. [Google Scholar]
- Au, C.K.E.; Feinberg, G. Higher-multipole contributions to retarded vanderwaals potential. Phys. Rev. A 1972, 6, 2433–2451. [Google Scholar]
- Mayer, J.E. Dispersion and polarizability and the van der waals potential in the alkali halides. J. Chem. Phys 1933, 1, 270–279. [Google Scholar]
- Margenau, H. The role of quadrupole forces in van der waals attractions. Phys. Rev 1931, 38, 747–756. [Google Scholar]
- Fontana, P.R.; Bernstein, R.B. Dipole-quadrupole + retardation effects in low-energy atom-atom scattering. J. Chem. Phys 1964, 41, 1431–1434. [Google Scholar]
- Jain, J.K.; Shanker, J.; Khandelwal, D.P. Evaluation of vanderwaals dipole-dipole and dipole-quadrupole energies in alkali-halides. Phys. Rev. B 1976, 13, 2692–2695. [Google Scholar]
- Porsev, S.G.; Derevianko, A. High-accuracy calculations of dipole, quadrupole, and octupole electric dynamic polarizabilities and van der waals coefficients c-6, c-8, and c-10 for alkaline-earth dimers. J. Exp. Theor. Phys 2006, 102, 195–205. [Google Scholar]
- Chang, T.Y. Moderately long-range interatomic forces. Rev. Mod. Phys 1967, 39, 911–941. [Google Scholar]
- Pauling, L.; Beach, J.Y. The van der waals interaction of hydrogen atoms. Phys. Rev 1935, 47, 686–692. [Google Scholar]
- McLachlan, A.D. Retarded dispersion forces in dielectrics at finite temperatures. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci 1963, 274, 80–90. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media, 2nd ed; Pergamon Press: Oxford, UK; p. 1963.
- Laven, J.; Vissers, J.P.C. The hamaker and the lifshitz approaches for the van der waals interaction between particles of composite materials dispersed in a medium. Colloids Surf. A: Physicochem. Eng. Asp 1999, 152, 345–355. [Google Scholar]
- Hamaker, H.C. The london—Van der waals attraction between spherical particles. Physica 1937, 4, 1058–1072. [Google Scholar]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Soviet Phys. JETP 1956, 2, 73–83. [Google Scholar]
- Shluger, A.L.; Livshits, A.I.; Foster, A.S.; Catlow, C.R.A. Theoretical modelling of non-contact atomic force microscopy on insulators. J. Phys-Condens. Mat 2000, 11, 295–322. [Google Scholar]
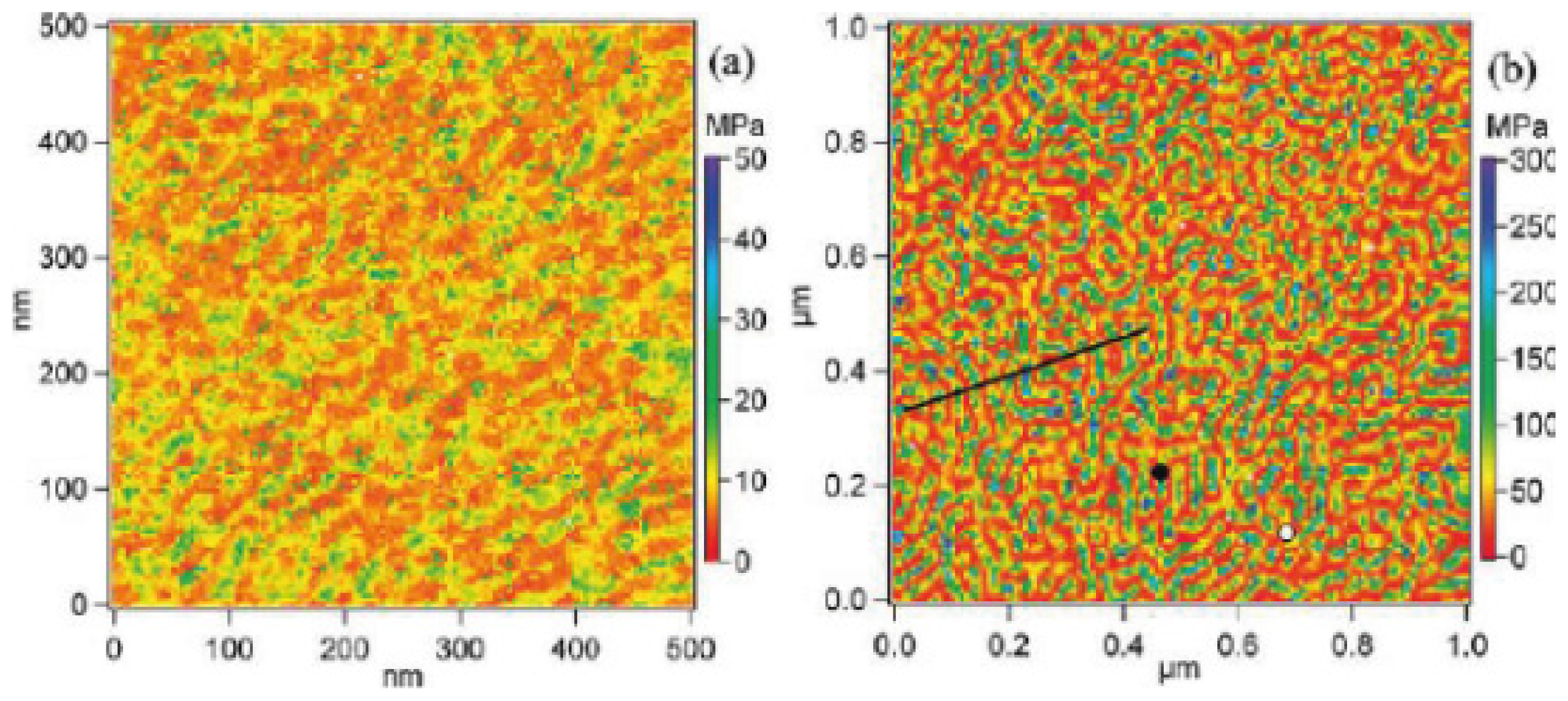
- Leite, F.L.; Riul, A.; Herrmann, P.S.P. Mapping of adhesion forces on soil minerals in air and water by atomic force spectroscopy (afs). J. Adhes. Sci. Technol 2003, 17, 2141–2156. [Google Scholar]
- Wang, H.Y.; Hu, M.; Liu, N.; Xia, M.F.; Ke, F.J.; Bai, Y.L. Multi-scale analysis of afm tip and surface interactions. Chem. Eng. Sci 2007, 62, 3589–3594. [Google Scholar]
- Bowen, W.R.; Jenner, F. The calculation of dispersion forces for engineering applications. Adv. Colloid Interface Sci 1995, 56, 201–243. [Google Scholar]
- Sokolov, I.Y. Pseudo-non-contact mode: Why it can give true atomic resolution. Appl. Surf. Sci 2003, 210, 37–42. [Google Scholar]
- London, F. The general theory of molecular forces. Trans. Faraday Soc 1937, 33, 8–26. [Google Scholar]
- Ackler, H.D.; French, R.H.; Chiang, Y.M. Comparisons of hamaker constants for ceramic systems with intervening vacuum or water: From force laws and physical properties. J. Colloid Interface Sci 1996, 179, 460–469. [Google Scholar]
- Hough, D.B.; White, L.R. The calculation of hamaker constants from lifshitz theory with applications to wetting phenomena. Adv. Colloid Interface Sci 1980, 14, 3–41. [Google Scholar]
- Derjaguin, B.V. A theory of the heterocoagulation, interaction and adhesion of dissimilar particles in solutions of electrolytes. Discuss. Faraday Soc 1954, 85–98. [Google Scholar]
- Visser, J. On hamaker constants: A comparison between hamaker constants and lifshitz-van der waals constants. Adv. Colloid Interface Sci 1972, 3, 331–363. [Google Scholar]
- Fowkes, F.M. Surfaces and Interfaces; Syracuse University Press: New York, NY, USA, 1967; Volume 1, p. 199. [Google Scholar]
- Van Oss, C.J.; Omenyi, S.N.; Neumann, A.W. Negative hamaker coefficients. Ii. Phase separation of polymer solutions. Colloid Polym. Sci 1979, 257, 737–744. [Google Scholar]
- Marra, J. Controlled deposition of lipid monolayers and bilayers onto mica and direct force measurements between galactolipid bilayers in aqueous-solutions. J. Colloid Interface Sci 1985, 107, 446–458. [Google Scholar]
- Cappella, B.; Dietler, G. Force-distance curves by atomic force microscopy. Surf. Sci. Rep 1999, 34, 1–104. [Google Scholar]
- Burnham, N.A.; Colton, R.J.; Pollock, H.M. Interpretation of force curves in force microscopy. Nanotechnology 1993, 4, 64–80. [Google Scholar]
- Meyer, E.; Heinzelmann, H.; Grutter, P.; Jung, T.; Hidber, H.R.; Rudin, H.; Guntherodt, H.J. Atomic force microscopy for the study of tribology and adhesion. Thin Solid Films 1989, 181, 527–544. [Google Scholar]
- Götzinger, M.; Peukert, W. Disperse forces of particle –surface interactions: Direct afm measurements and modeling. Powder Technol 2003, 130, 102–109. [Google Scholar]
- Das, S.; Sreeram, P.A.; Raychaudhuri, A.K. A method to quantitatively evaluate the hamaker constant using the jump-into-contact effect in atomic force microscopy. Nanotechnology 2007, 18. [Google Scholar] [CrossRef]
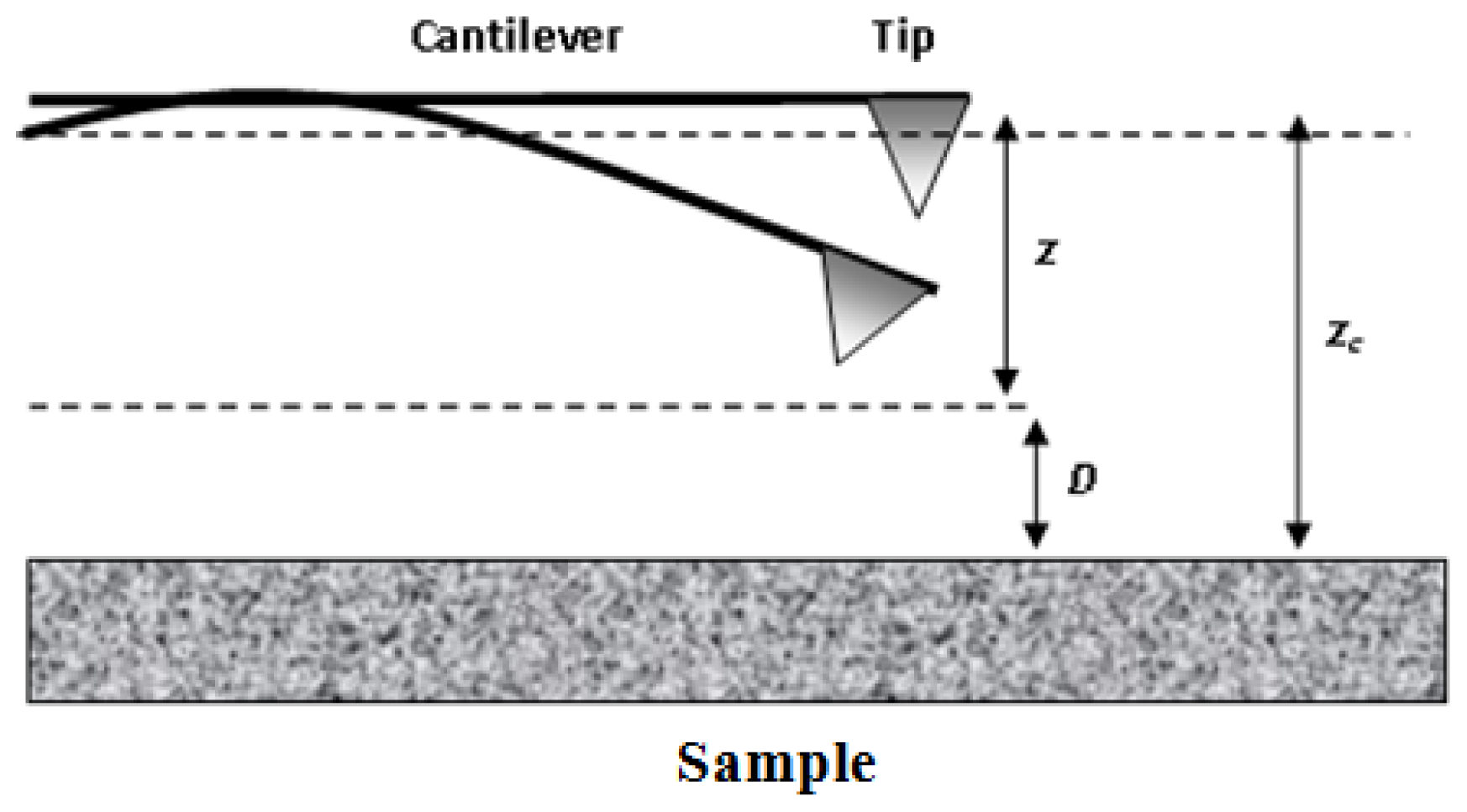
- Butt, H.J.; Cappella, B.; Kappl, M. Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep 2005, 59, 1–152. [Google Scholar]
- Bergstrom, L. Hamaker constants of inorganic materials. Adv. Colloid Interface Sci 1997, 70, 125–169. [Google Scholar]
- Eichenlaub, S.; Chan, C.; Beaudoin, S.P. Hamaker constants in integrated circuit metalization. J. Colloid Interface Sci 2002, 248, 389–397. [Google Scholar]
- Bergstrom, L.; Stemme, S.; Dahlfors, T.; Arwin, H.; Odberg, L. Spectroscopic ellipsometry characterisation and estimation of the hamaker constant of cellulose. Cellulose 1999, 6, 1–13. [Google Scholar]
- Drummond, C.J.; Chan, D.Y.C. Theoretical analysis of the soiling of “nonstick” organic materials. Langmuir 1996, 12, 3356–3359. [Google Scholar]
- Froberg, J.C.; Rojas, O.J.; Claesson, P.M. Surface forces and measuring techniques. Int. J. Miner. Process 1999, 56, 1–30. [Google Scholar]
- Gu, Y.A. Experimental determination of the hamaker constants for solid-water-oil-systems. J. Adhes. Sci. Technol 2001, 15, 1263–1283. [Google Scholar]
- Cooper, K.; Gupta, A.; Beaudoin, S. Substrate morphology and particle adhesion in reacting systems. J. Colloid Interface Sci 2000, 213–219. [Google Scholar]
- Hoh, J.H.; Engel, A. Friction effects on force measurements with an atomic-force microscope. Langmuir 1993, 9, 3310–3312. [Google Scholar]
- Reich, Z.; Kapon, R.; Nevo, R.; Pilpel, Y.; Zmora, S.; Scolnik, Y. Scanning force microscopy in the applied biological sciences. Biotechnol. Adv 2001, 19, 451–485. [Google Scholar]
- Heinz, W.F.; Hoh, J.H. Spatially resolved force spectroscopy of biological surfaces using the atomic force microscope. Trends Biotechnol 1999, 17, 143–150. [Google Scholar]
- Cleveland, J.P.; Manne, S.; Bocek, D.; Hansma, P.K. A nondestructive method for determining the spring constant of cantilevers for scanning force microscopy. Rev. Sci. Instrum 1993, 64, 403–405. [Google Scholar]
- Sader, J.E.; Larson, I.; Mulvaney, P.; White, L.R. Method for the calibration of atomic-force microscope cantilevers. Rev. Sci. Instrum 1995, 66, 3789–3798. [Google Scholar]
- Gibson, C.T.; Watson, G.S.; Myhra, S. Determination of the spring constants of probes for force microscopy/spectroscopy. Nanotechnology 1996, 7, 259–262. [Google Scholar]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys 1998, 84, 64–76. [Google Scholar]
- Sader, J.E. Parallel beam approximation for v-shaped atomic-force microscope cantilevers. Rev. Sci. Instrum 1995, 66, 4583–4587. [Google Scholar]
- Hutter, J.L.; Bechhoefer, J. Calibration of atomic-force microscope tips. Rev. Sci. Instrum 1993, 64, 1868–1873. [Google Scholar]
- Levy, R.; Maaloum, M. Measuring the spring constant of atomic force microscope cantilevers: Thermal fluctuations and other methods. Nanotechnology 2002, 13, 33–37. [Google Scholar]
- Burnham, N.A.; Colton, R.J. Measuring the nanomechanical properties and surface forces of materials using an atomic force microscope. J. Vac. Sci. Technol. A: Vac. Surf. Films 1989, 7, 2906–2913. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar]
- Baselt, D.R.; Baldeschwieler, J.D. Imaging spectroscopy with the atomico force microscope. J. Appl. Phys 1994, 76, 33–38. [Google Scholar]
- Wang, D.; Fujinami, S.; Liu, H.; Nakajima, K.; Nishi, T. Investingation of true surface morphology and nanomechanical properties of poly(styrene-b-ethilene-co-butylene-b-styrene) using nanomechanical mapping: Effects of composition. Macromolecules 2010, 43, 9049–9055. [Google Scholar]
- Willing, G.A.; Ibrahim, T.H.; Etzler, F.M.; Neuman, R.D. New approach to the study of particle-surface adhesion using atomic force microscopy. J. Colloid Interface Sci 2000, 226, 185–188. [Google Scholar]
- Zuo, F.; Angelopoulos, M.; Macdiarmid, A.G.; Epstein, A.J. Transport studies of protonated emeraldine polymer—A antigranulocytes polymeric metal system. Phys. Rev. B 1987, 36, 3475–3478. [Google Scholar]
- Leite, F.L.; Alves, W.F.; Mir, M.; Mascarenhas, Y.P.; Herrmann, P.S.P.; Mattoso, L.H.C.; Oliveira, O.N., Jr. Tem, xrd and afm study of poly(O-ethoxyaniline) films: New evidence for the formation of conducting islands. Appl. Phys. A: Mater. Sci. Process. 2008, 93, 537–542. [Google Scholar]
- Lux, F.; Hinrichsen, G.; Pohl, M.M. Tem evidence for the existence of conducting islands in highly conductive polyaniline. J. Polym. Sci. Pt. B Polym. Phys 1994, 32, 1957–1959. [Google Scholar]
- Knoll, A.; Magerle, R.; Krausch, G. Tapping mode atomic force microscopy on polymers: Where is the true sample surface? Macromolecules 2001, 34, 4159–4165. [Google Scholar]
- Chen, X.; Roberts, C.J.; Zhang, J.; Davies, M.C.; Tendler, S.J.B. Phase contrast and attraction-repulsion transition in tapping mode atomic force microscopy. Surf. Sci 2002, 519, L593–L598. [Google Scholar]
- Anczykowski, B.; Gotsmann, B.; Fuchs, H.; Cleveland, J.P.; Elings, V.B. How to measure energy dissipation in dynamic mode atomic force microscopy. Appl. Surf. Sci 1999, 140, 376–382. [Google Scholar]
- Yoshizawa, H.; Chen, Y.L.; Israelachvili, J. Fundamental mechanisms of interfacial friction.1. Relation between adhesion and friction. J. Phys. Chem 1993, 97, 4128–4140. [Google Scholar]
- Kitamura, S.; Iwatsuki, M. Observation of 7x7 reconstructed structure on the silicon (111) surface using ultrahigh-vacuum noncontact atomic-force microscopy. Jpn. J. Appl. Phys. Part 2 Lett 1995, 34, L145–L148. [Google Scholar]
- Sokolov, I.Y.; Henderson, G.S.; Wicks, F.J. Force spectroscopy in noncontact mode. Appl. Surf. Sci 1999, 140, 358–361. [Google Scholar]
- Giessibl, F.J. Atomic-resolution of the silicon (111)-(7x7) surface by atomic-force microscopy. Science 1995, 267, 68–71. [Google Scholar]
- Uchihashi, T.; Sugawara, Y.; Tsukamoto, T.; Ohta, M.; Morita, S.; Suzuki, M. Role of a covalent bonding interaction in noncontact-mode atomic-force microscopy on si(111)7x7. Phys. Rev. B 1997, 56, 9834–9840. [Google Scholar]
- van Honschoten, J.W.; Tas, N.R.; Elwenspoek, M. The profile of a capillary liquid bridge between solid surfaces. Am. J. Phys 2010, 78, 277–286. [Google Scholar]
- Men, Y.M.; Zhang, X.R.; Wang, W.C. Capillary liquid bridges in atomic force microscopy: Formation, rupture, and hysteresis. J. Chem. Phys 2009, 131, 184702:1–184702:8. [Google Scholar]
- Lambert, P.; Régnier, S. Microworld Modeling in Vacuum and Gaseous Environments; John Wiley & Sons, Inc: Hoboken, NJ, USA; p. 2010.
- Cappella, B.; Dietler, G. Force-distance curves by atomic force microscopy. Surf. Sci. Rep 1999, (3–5). [Google Scholar]
- Fearing, R.S. Survey of Sticking Effects for Micro Parts Handling. Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems: Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; 2, pp. 212–217.
- Hao, H.W.; Baro, A.M.; Saenz, J.J. Electrostatic and contact forces in force microscopy. J. Vac. Sci. Technol. B Microelectron. Process. Phenom 1991, 9, 1323–1328. [Google Scholar]
- Hudlet, S.; Saint Jean, M.; Guthmann, C.; Berger, J. Evaluation of the capacitive force between an atomic force microscopy tip and a metallic surface. Eur. Phys. J. B 1998, 2, 5–10. [Google Scholar]
- Patil, S.; Kulkarni, A.V.; Dharmadhikari, C.V. Study of the electrostatic force between a conducting tip in proximity with a metallic surface: Theory and experiment. J. Appl. Phys 2000, 88, 6940–6942. [Google Scholar]
- Patil, S.; Dharmadhikari, C.V. Investigation of the electrostatic forces in scanning probe microscopy at low bias voltages. Surf. Interface Anal 2002, 33, 155–158. [Google Scholar]
- Smythe, W.R. Static and Dynamic Electricity, 3rd ed; McGraw-Hill: New York, NY, USA, 1968; p. 623. [Google Scholar]
- Overbeek, J.T.G.; Sparnaay, M.J. Classical coagulation. London-vanderwaals attraction between macroscopic objects. Discuss. Faraday Soc 1954, 18, 12–24. [Google Scholar]
- Black, W.; Dejongh, J.G.V.; Overbeek, J.T.G.; Sparnaay, M.J. Measurements of retarded vanderwaals forces. Trans. Faraday Soc 1960, 56, 1597–1608. [Google Scholar]
- Ducker, W.A.; Senden, T.J.; Pashley, R.M. Measurement of forces in liquids using a force microscope. Langmuir 1992, 8, 1831–1836. [Google Scholar]
- Larson, I.; Drummond, C.J.; Chan, D.Y.C.; Grieser, F. Direct force measurements between TiO2 surfaces. J. Am. Chem. Soc 1993, 115, 11885–11890. [Google Scholar]
- Biggs, S.; Spinks, G. Atomic force microscopy investigation of the adhesion between a single polymer sphere and a flat surface. J. Adhes. Sci. Technol 1998, 12, 461–478. [Google Scholar]
- Butt, H.J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces; Wiley-VCH Verlag & Co. KGaA: Weinheim, Germany, 2003; p. 361. [Google Scholar]
- Lennard-Jones, J.E. Cohesion. Proc. Phys. Soc 1931, 43, 461–482. [Google Scholar]
- Stifter, T.; Marti, O.; Bhushan, B. Theoretical investigation of the distance dependence of capillary and van der waals forces in scanning force microscopy. Phys. Rev. B 2000, 62, 13667–13673. [Google Scholar]
- Derjaguin, B.V. Friction and adhesion. Iv. The theory of adhesion of small particles. Kolloid Zeits 1934, 69, 155–164. [Google Scholar]
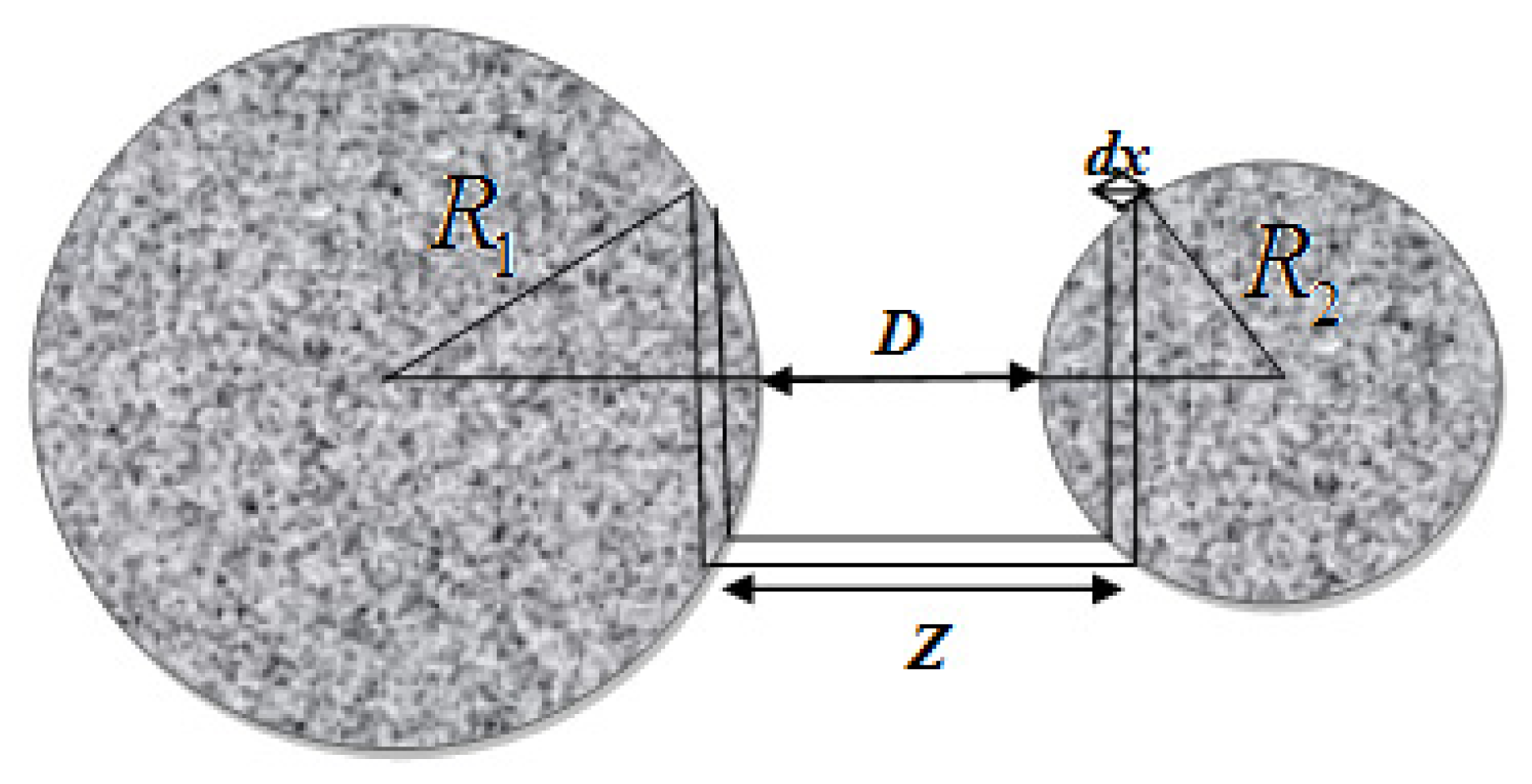
- Todd, B.A.; Eppell, S.J. Probing the limits of the derjaguin approximation with scanning force microscopy. Langmuir 2004, 20, 4892–4897. [Google Scholar]
- Hunter, R. Foundations of Colloid Science; Clarendon Press: Oxford, UK, 1989; Volume 2, p. 432. [Google Scholar]
- French, R.H.; Cannon, R.M.; Denoyer, L.K.; Chiang, Y.M. Full spectral calculation of nonretarded hamaker constants for ceramic systems from interband transition strengths. Solid State Ionics 1995, 75, 13–33. [Google Scholar]
- Hutter, J.L.; Bechhoefer, J. Manipulation of vanderwaals forces to improve image-resolution in atomic-force microscopy. J. Appl. Phys 1993, 73, 4123–4129. [Google Scholar]
- Burnham, N.A.; Dominguez, D.D.; Mowery, R.L.; Colton, R.J. Probing the surface forces of monolayer films with an atomic-force microscope. Phys. Rev. Lett 1990, 64, 1931–1934. [Google Scholar]
- Landman, U.; Luedtke, W.D.; Burnham, N.A.; Colton, R.J. Atomistic mechanisms and dynamics of adhesion, nanoindentation, and fracture. Science 1990, 248, 454–461. [Google Scholar]
- Goodman, F.O.; Garcia, N. Roles of the attractive and repulsive forces in atomic-force microscopy. Phys. Rev. B 1991, 43, 4728–4731. [Google Scholar]
- Kirsch, V.A. Calculation of the van der waals force between a spherical particle and an infinite cylinder. Adv. Colloid Interface Sci 2003, 104, 311–324. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press: New York, NY, USA, 1994; p. 1204. [Google Scholar]
- Casimir, H.B.G.; Polder, D. The influence of retardation on the london-vanderwaals forces. Phys. Rev 1948, 73, 360–372. [Google Scholar]
- Hartmann, U. Manifestation of zero-point quantum fluctuations in atomic force microscopy. Phys. Rev. B 1990, 42, 1541–1546. [Google Scholar]
- Wennerstrom, H.; Daicic, J.; Ninham, B.W. Temperature dependence of atom-atom interactions. Phys. Rev. A 1999, 60, 2581–2584. [Google Scholar]
- Ramos, S.M.M.; Charlaix, E.; Benyagoub, A.; Toulemonde, M. Wetting on nanorough surfaces. Phys. Rev. E 2003, 67, 6. [Google Scholar]
- Colak, A.; Wormeester, H.; Zandvliet, H.J.W.; Poelsema, B. Surface adhesion and its dependence on surface roughness and humidity measured with a flat tip. Appl. Surf. Sci 2012, 258, 6938–6942. [Google Scholar]
- Zhang, X.L.; Lu, Y.J.; Liu, E.Y.; Yi, G.W.; Jia, J.H. Adhesion and friction studies of microsphere-patterned surfaces in contact with atomic force microscopy colloidal probe. Colloids Surf. A: Physicochem. Eng. Asp 2012, 401, 90–96. [Google Scholar]
- Mizes, H.A.; Ott, M.; Eklund, E.; Hays, D.A. Small particle adhesion: Measurement and control. Colloids Surf. A: Physicochem. Eng. Asp 2000, 165, 11–23. [Google Scholar]
- Rimai, D.S.; DeMejo, L.P. Physical interactions affecting the adhesion of dry particles. Annu. Rev. Mater. Sci 1996, 26, 21–41. [Google Scholar]
- Hays, D.A. Toner Adhesion. In Proceedings of the Seventeenth Annual Meeting and the Symposium on Particle Adhesion; Adhesion Society: Orlando, FL, USA, 1994; pp. 91–93. [Google Scholar]
- Matsusaka, S. Control of particle tribocharging. KONA Powder Part. J 2011, 29, 27–38. [Google Scholar]
- Horn, R.G.; Smith, D.T. Contact electrification and adhesion between dissimilar materials. Science 1992, 256, 362–364. [Google Scholar]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and contact of elastic solids. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci 1971, 324, 301–313. [Google Scholar]
- Derjaguin, B.V.; Muller, V.M.; Toporov, Y.P. Effect of contact deformations on adhesion of particles. J. Colloid Interface Sci 1975, 53, 314–326. [Google Scholar]
- Harkins, W.D. Surface energy and the orientation of molecules in surfaces as revealed by surface energy relations. Zeitschrift für Physikalische Chemie 1928, 139, 647–691. [Google Scholar]
- Maugis, D.; Pollock, H.M. Surface forces, deformation and adherence at metal microcontacts. Acta Metall 1984, 32, 1323–1334. [Google Scholar]
- Skvarla, J. Hydrophobic interaction between macroscopic and microscopic surfaces. Unification using surface thermodynamics. Adv. Colloid Interface Sci 2001, 91, 335–390. [Google Scholar]
- Noy, A. Handbook of Molecular Force Spectroscopy, 1st ed; Springer Science: Amsterdam, The Netherlands, 2007; p. 300. [Google Scholar]
- Tabor, D. Surface forces and surface interactions. J. Colloid Interface Sci 1977, 58, 2–13. [Google Scholar]
- Muller, V.M.; Yushchenko, V.S.; Derjaguin, B.V. On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane. J. Colloid Interface Sci 1980, 77, 91–101. [Google Scholar]
- Maugis, D.J. Adhesion of spheres: The jkr-dmt transition using a dugdale model. J. Colloid Interface Sci 1992, 150, 243–269. [Google Scholar]
- Johnson, K.L.; Greenwood, J.A. An adhesion map for the contact of elastic spheres. J. Colloid Interface Sci 1997, 192, 326–333. [Google Scholar]
- Xu, D.W.; Liechti, K.M.; Ravi-Chandar, K. On the modified tabor parameter for the jkr-dmt transition in the presence of a liquid meniscus. J. Colloid Interface Sci 2007, 315, 772–785. [Google Scholar]
- Fogden, A.; White, L.R. Contact elasticity in the presence of capillary condensation. 1. The nonadhesive hertz problem. J. Colloid Interface Sci 1990, 138, 414–430. [Google Scholar]
- Maugis, D.; Gauthiermanuel, B. Jkr-dmt transition in the presence of a liquid meniscus. J. Adhes. Sci. Technol 1994, 8, 1311–1322. [Google Scholar]
- Johnson, K.L. Mechanics of adhesion. Tribol. Int 1998, 31, 413–418. [Google Scholar]
- Carpick, R.W.; Agrait, N.; Ogletree, D.F.; Salmeron, M. Variation of the interfacial shear strength and adhesion of a nanometer-sized contact. Langmuir 1996, 12, 3334–3340. [Google Scholar]
- Lantz, M.A.; Oshea, S.J.; Welland, M.E.; Johnson, K.L. Atomic-force-microscope study of contact area and friction on nbse2. Phys. Rev. B 1997, 55, 10776–10785. [Google Scholar]
- Carpick, R.W.; Ogletree, D.F.; Salmeron, M. A general equation for fitting contact area and friction vs load measurements. J. Colloid Interface Sci 1999, 211, 395–400. [Google Scholar]
- Shi, X.H.; Zhao, Y.P. Comparison of various adhesion contact theories and the influence of dimensionless load parameter. J. Adhes. Sci. Technol 2004, 18, 55–68. [Google Scholar]
- Patrick, D.L.; Flanagan, J.F.; Kohl, P.; Lynden-Bell, R.M. Atomistic molecular dynamics simulations of chemical force microscopy. J. Am. Chem. Soc 2003, 125, 6762–6773. [Google Scholar]
- Rabinovich, Y.I.; Adler, J.J.; Ata, A.; Singh, R.K.; Moudgil, B.M. Adhesion between nanoscale rough surfaces—i. Role of asperity geometry. J. Colloid Interface Sci 2000, 232, 10–16. [Google Scholar]
- Rabinovich, Y.I.; Adler, J.J.; Ata, A.; Singh, R.K.; Moudgil, B.M. Adhesion between nanoscale rough surfaces—ii. Measurement and comparison with theory. J. Colloid Interface Sci 2000, 232, 17–24. [Google Scholar]
- Beach, E.R.; Tormoen, G.W.; Drelich, J.; Han, R. Pull-off force measurements between rough surfaces by atomic force microscopy. J. Colloid Interface Sci 2002, 247, 84–99. [Google Scholar]
- Zhou, H.B.; Gotzinger, M.; Peukert, W. The influence of particle charge and roughness on particle-substrate adhesion. Powder Technol 2003, 135, 82–91. [Google Scholar]
- Atherton, A.; Born, G.V.R. Quantitative investigations of adhesiveness of circulating polymorphonuclear leukocytes to blood-vessel walls. J. Physiol.-Lond 1972, 222, 447–474. [Google Scholar]
- Li, Q.; Rudolph, V.; Weigl, B.; Earl, A. Interparticle van der waals force in powder flowability and compactibility. Int. J. Pharm 2004, 280, 77–93. [Google Scholar]
- Li, Q.; Rudolph, V.; Peukert, W. London-van der waals adhesiveness of rough particles. Powder Technol 2006, 161, 248–255. [Google Scholar]
- Schaefer, D.M.; Carpenter, M.; Reifenberger, R.; Demejo, L.P.; Rimai, D.S. Surface force interactions between micrometer-size polystyrene spheres and silicon substrates using atomic-force techniques. J. Adhes. Sci. Technol 1994, 8, 197–210. [Google Scholar]
- Schaefer, D.M.; Carpenter, M.; Gady, B.; Reifenberger, R.; Demejo, L.P.; Rimai, D.S. Surface-roughness and its influence on particle adhesion using atomic-force techniques. J. Adhes. Sci. Technol 1995, 9, 1049–1062. [Google Scholar]
- Thoreson, E.J.; Martin, J.; Burnham, N.A. The role of few-asperity contacts in adhesion. J. Colloid Interface Sci 2006, 298, 94–101. [Google Scholar]
- Eichenlaub, S.; Kumar, G.; Beaudoin, S. A modeling approach to describe the adhesion of rough, asymmetric particles to surfaces. J. Colloid Interface Sci 2006, 299, 656–664. [Google Scholar]
- Kumar, G.; Beaudoin, S. Undercut removal of micrometer-scale particles from surfaces. J. Electrochem. Soc 2006, 153, G175–G181. [Google Scholar]
- Cooper, K.; Gupta, A.; Beaudoin, S. Simulation of the adhesion of particles to surfaces. J. Colloid Interface Sci 2001, 234, 284–292. [Google Scholar]
- Kumar, G.; Smith, S.; Jaiswal, R.; Beaudoin, S. Scaling of van der waals and electrostatic adhesion interactions from the micro- to the nano-scale. J. Adhes. Sci. Technol 2008, 22, 407–428. [Google Scholar]
- Eichenlaub, S.; Gelb, A.; Beaudoin, S. Roughness models for particle adhesion. J. Colloid Interface Sci 2004, 280, 289–298. [Google Scholar]
- Lai, L.; Irene, E.A. Area evaluation of microscopically rough surfaces. J. Vac. Sci. Technol. B 1999, 17, 33–39. [Google Scholar]
- Liu, D.L.; Martin, J.; Burnham, N.A. Which fractal parameter contributes most to adhesion? J. Adhes. Sci. Technol 2010, 24, 2383–2396. [Google Scholar]
- Segeren, L.; Siebum, B.; Karssenberg, F.G.; Van den Berg, J.W.A.; Vancso, G.J. Microparticle adhesion studies by atomic force microscopy. J. Adhes. Sci. Technol 2002, 16, 793–828. [Google Scholar]
- Jaiswal, R.P.; Kumar, G.; Kilroy, C.M.; Beaudoin, S.P. Modeling and validation of the van der waals force during the adhesion of nanoscale objects to rough surfaces: A detailed description. Langmuir 2009, 25, 10612–10623. [Google Scholar]
- Liu, D.L.; Martin, J.; Burnham, N.A. Asme. Optimum Roughness for Minimum Adhesion. Proceedings of the STLE/ASME International Joint Tribology Conference 2008, Miami, FL, USA, 20–22 October 2008; pp. 593–595.
- Karan, S.; Mallik, B. Power spectral density analysis and photoconducting behavior in copper(ii) phthalocyanine nanostructured thin films. Phys. Chem. Chem. Phys 2008, 10, 6751–6761. [Google Scholar]
- Kosaka, P.M.; Kawano, Y.; Petri, D.F.S. Dewetting and surface properties of ultrathin films of cellulose esters. J. Colloid Interface Sci 2007, 316, 671–677. [Google Scholar]
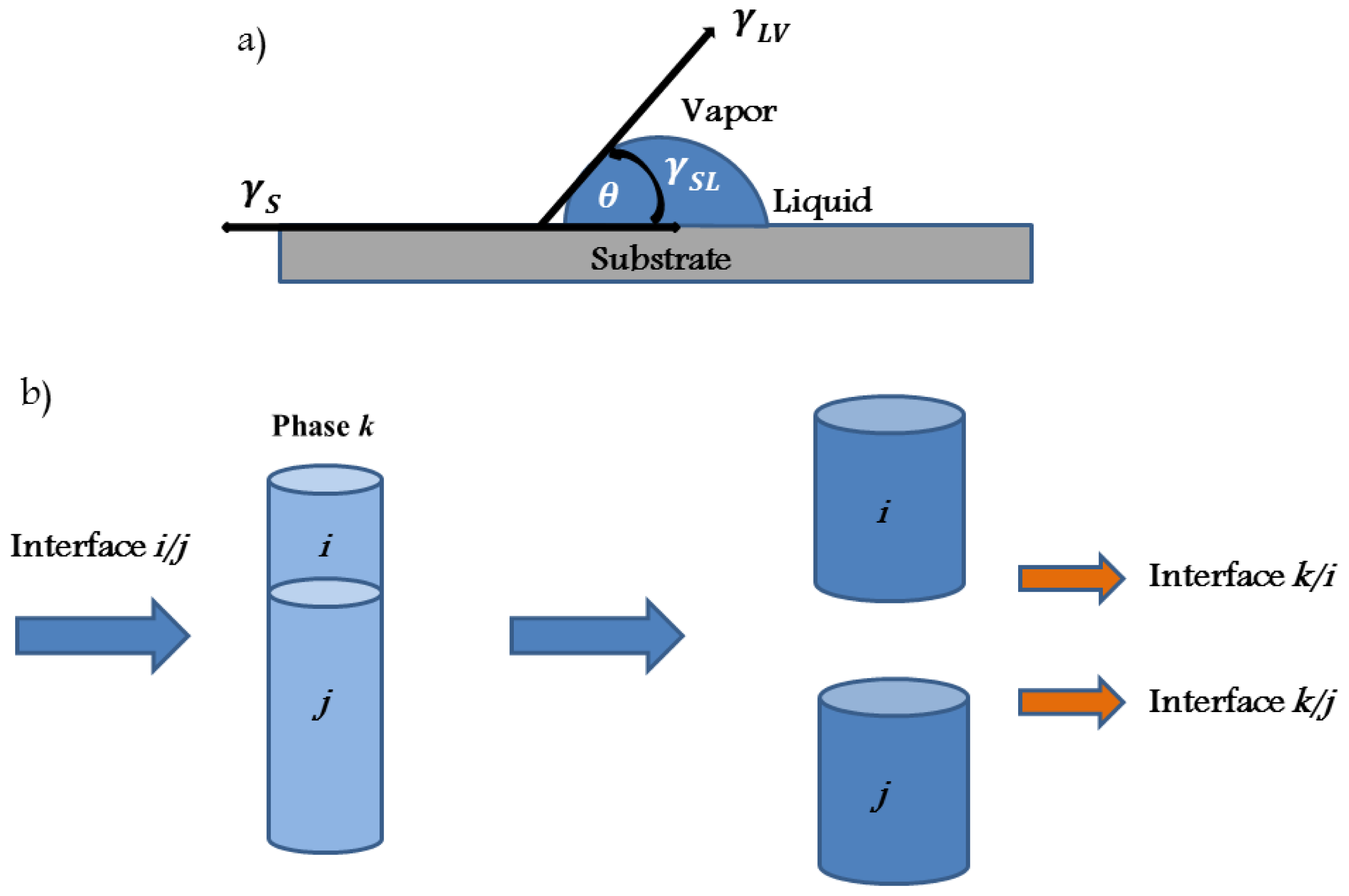
- Young, T. An essay on the cohesion of fluids. Philos. Trans. R. Soc 1805, 95, 65–87. [Google Scholar]
- Good, R.J. Physical significance of parameters γc, γs and Φ that govern spreading on adsorbed films. Society of the Chemical Industry Monographs 1966, 25, 328–350. [Google Scholar]
- Good, R.J. A thermodynamic analysis of formation of bilayer films. J. Colloid Interface Sci 1969, 31, 540–544. [Google Scholar]
- Dupre, A. Theorie Mechanique de la Chaleur; Gauthier-Villars: Paris, France, 1869. [Google Scholar]
- Fowkes, F.M. Additivity of intermolecular forces at interfaces .1. Determination of contribution to surface and interfacial tensions of dispersion forces in various liquids. J. Phys. Chem 1963, 67, 2538–2541. [Google Scholar]
- Clint, J.H.; Wicks, A.C. Adhesion under water: Surface energy considerations. Int. J. Adhes. Adhes 2001, 21, 267–273. [Google Scholar]
- Berg, J.C. Semi-Empiral Strategies for Predicting Adhesion. In Adhesion Science and Engineering: Surfaces, Chemistry and Applications; Dillard, D.A., Pocius, A.V., Eds.; Elsevier: Amsterdam, The Netherlands, 2002; Volume 2. [Google Scholar]
- Neumann, A.W. Contact angles and their temperature dependence: Thermodynamic status, measurement, interpretation and application. Adv. Colloid Interface Sci 1974, 4, 105–191. [Google Scholar]
- Kwok, D.Y.; Gietzelt, T.; Grundke, K.; Jacobasch, H.J.; Neumann, A.W. Contact angle measurements and contact angle interpretation. 1. Contact angle measurements by axisymmetric drop shape analysis and a goniometer sessile drop technique. Langmuir 1997, 13, 2880–2894. [Google Scholar]
- Kwok, D.Y.; Neumann, A.W. Contact angle interpretation in terms of solid surface tension. Colloids Surf. A: Physicochem. Eng. Asp 2000, 161, 31–48. [Google Scholar]
- Kwok, D.Y.; Neumann, A.W. Contact angle interpretation: Re-evaluation of existing contact angle data. Colloids Surf. A: Physicochem. Eng. Asp 2000, 161, 49–62. [Google Scholar]
- Jasper, J.J. The surface tension of pure liquid compounds. J. Phys. Chem. Ref. Data 1972, 1, 841–1010. [Google Scholar]
- Vanoss, C.J.; Good, R.J.; Chaudhury, M.K. Additive and nonadditive surface-tension components and the interpretation of contact angles. Langmuir 1988, 4, 884–891. [Google Scholar]
- Clint, J.H. Adhesion and components of solid surface energies. Curr. Opin. Colloid Interface Sci 2001, 6, 28–33. [Google Scholar]
- van Oss, C.J.; Good, R.J.; Chaudhury, M.K. Determination of the hydrophobic interaction energy —Application to separation processes. Sep. Sci. Technol 1987, 22, 1–24. [Google Scholar]
- Owens, D.K.; Wendt, R.C. Estimation of surface free energy of polymers. J. Appl. Polym. Sci 1969, 13. [Google Scholar] [CrossRef]
- Aveyard, R.; Saleem, S.M. Interfacial-tensions at alkane-aqueous electrolyte interfaces. J. Chem. Soc.-Faraday Trans. I 1976, 72, 1609–1617. [Google Scholar]
- Erbil, H.Y. Surfaces Chemistry of Solid and Liquid Interfaces; Blackwell Publishing Ltd: Oxford, UK, 2006; p. 352. [Google Scholar]
- Bodner, T.; Behrendt, A.; Prax, E.; Wiesbrock, F. Correlation of surface roughness and surface energy of silicon-based materials with their priming reactivity. Mon. Chem 2012, 143, 717–722. [Google Scholar]
- Miller, J.D.; Veeramasuneni, S.; Drelich, J.; Yalamanchili, M.R.; Yamauchi, G. Effect of roughness as determined by atomic force microscopy on the wetting properties of ptfe thin films. Polym. Eng. Sci 1996, 36, 1849–1855. [Google Scholar]
- Drelich, J.; Tormoen, G.W.; Beach, E.R. Determination of solid surface tension from particle-substrate pull-off forces measured with the atomic force microscope. J. Colloid Interface Sci 2004, 280, 484–497. [Google Scholar]
- Tormoen, G.W.; Drelich, J.; Beach, E.R. Analysis of atomic force microscope pull-off forces for gold surfaces portraying nanoscale roughness and specific chemical functionality. J. Adhes. Sci. Technol 2004, 18, 1–17. [Google Scholar]
- Correa, R.; Saramago, B. On the calculation of disjoining pressure isotherms for nonaqueous films. J. Colloid Interface Sci 2004, 270, 426–435. [Google Scholar]
- Halsey, G.D. Catalysis on non-uniform surfaces. J. Chem. Phys 1949, 17, 758–761. [Google Scholar]
- He, M.Y.; Blum, A.S.; Aston, D.E.; Buenviaje, C.; Overney, R.M.; Luginbuhl, R. Critical phenomena of water bridges in nanoasperity contacts. J. Chem. Phys 2001, 114, 1355–1360. [Google Scholar]
- de Gennes, P.G. Wetting: Statics and dynamics. Rev. Mod. Phys 1985, 57, 827–863. [Google Scholar]
- Heslot, F.; Fraysse, N.; Cazabat, A.M. Molecular layering in the spreading of wetting liquid drops. Nature 1989, 338, 640–642. [Google Scholar]
- Israelachvili, J.N. Solvation forces and liquid structure, as probed by direct force measurements. Acc. Chem. Res 1987, 20, 415–421. [Google Scholar]
- Hu, J.; Xiao, X.D.; Salmeron, M. Scanning polarization force microscopy—A technique for imaging liquids and weakly adsorbed layers. Appl. Phys. Lett 1995, 67, 476–478. [Google Scholar]
- Hu, J.; Xiao, X.D.; Ogletree, D.F.; Salmeron, M. Imaging the condensation and evaporation of molecularly thin-films of water with nanometer resolution. Science 1995, 268, 267–269. [Google Scholar]
- Herminghaus, S.; Fery, A.; Reim, D. Imaging of droplets of aqueous solutions by tapping-mode scanning force microscopy. Ultramicroscopy 1997, 69, 211–217. [Google Scholar]
- Gil, A.; Colchero, J.; Luna, M.; Gomez-Herrero, J.; Baro, A.M. Adsorption of water on solid surfaces studied by scanning force microscopy. Langmuir 2000, 16, 5086–5092. [Google Scholar]
- Forcada, M.L.; Jakas, M.M.; Grasmarti, A. On liquid-film thickness measurements with the atomic-force microscope. J. Chem. Phys 1991, 95, 706–708. [Google Scholar]
- Maeda, N.; Israelachvili, J.N.; Kohonen, M.M. Evaporation and instabilities of microscopic capillary bridges. Proc. Natl. Acad. Sci. USA 2003, 100, 803–808. [Google Scholar]
- Adamson, A.W. Physical Chemistry of Surfaces, 5th ed; Wiley & Sons: New York, NY, USA, 1976; p. 377. [Google Scholar]
- Wei, Z.; Zhao, Y.P. Growth of liquid bridge in afm. J. Phys. D-Appl. Phys 2007, 40, 4368–4375. [Google Scholar]
- Aveyard, R.; Clint, J.H.; Paunov, V.N.; Nees, D. Capillary condensation of vapours between two solid surfaces: Effects of line tension and surface forces. Phys. Chem. Chem. Phys 1999, 1, 155–163. [Google Scholar]
- Ata, A.; Rabinovich, Y.I.; Singh, R.K. Role of surface roughness in capillary adhesion. J. Adhes. Sci. Technol 2002, 16, 337–346. [Google Scholar]
- Binggeli, M.; Mate, C.M. Influence of capillary condensation of water on nanotribology studied by force microscopy. Appl. Phys. Lett 1994, 65, 415–417. [Google Scholar]
- Thundat, T.; Zheng, X.Y.; Chen, G.Y.; Warmack, R.J. Role of relative-humidity in atomic-force microscopy imaging. Surf. Sci 1993, 294, L939–L943. [Google Scholar]
- Hartholt, G.P.; Hoffmann, A.C.; Janssen, L. Visual observations of individual particle behaviour in gas and liquid fluidized beds. Powder Technol 1996, 88, 341–345. [Google Scholar]
- Obrien, W.J.; Hermann, J.J. Strength of liquid bridges between dissimilar materials. J. Adhes 1973, 5, 91–103. [Google Scholar]
- Miranda, P.B.; Xu, L.; Shen, Y.R.; Salmeron, M. Icelike water monolayer adsorbed on mica at room temperature. Phys. Rev. Lett 1998, 81, 5876–5879. [Google Scholar]
- Wiesendanger, R.; Guntherodt, H.J. Scanning Tunneling Microscopy II; Springer: New York, NY, USA, 1992. [Google Scholar]
- Utriainen, M.; Leijala, A.; Niinisto, L.; Matero, R. Chemical imaging of patterned inorganic thin-film structures by lateral force microscopy. Anal. Chem 1999, 71, 2452–2458. [Google Scholar]
- Jang, J.; Yang, M.; Schatz, G. Microscopic origin of the humidity dependence of the adhesion force in atomic force microscopy. J. Chem. Phys 2007, 126, 174705. [Google Scholar]
- Yang, G.L.; Vesenka, J.P.; Bustamante, C.J. Effects of tip-sample forces and humidity on the imaging of DNA with a scanning force microscope. Scanning 1996, 18, 344–350. [Google Scholar]
- Fujihira, M.; Aoki, D.; Okabe, Y.; Takano, H.; Hokari, H.; Frommer, J.; Nagatani, Y.; Sakai, F. Effect of capillary force on friction force microscopy: A scanning hydrophilicity microscope. Chem. Lett 1996, 499–500. [Google Scholar]
- Binggeli, M.; Mate, C.M. Influence of water-vapor on nanotribology studied by friction force microscopy. J. Vac. Sci. Technol. B 1995, 13, 1312–1315. [Google Scholar]
- Tanaka, M.; Komagata, M.; Tsukada, M.; Kamiya, H. Evaluation of the particle-particle interactions in a toner by colloid probe afm. Powder Technol 2008, 183, 273–281. [Google Scholar]
- Shen, Y.J.; Nakajima, M.; Ahmad, M.R.; Kojima, S.; Homma, M.; Fukuda, T. Effect of ambient humidity on the strength of the adhesion force of single yeast cell inside environmental-sem. Ultramicroscopy 2011, 111, 1176–1183. [Google Scholar]
- Shi, Q.; Wong, S.C.; Ye, W.; Hou, J.W.; Zhao, J.; Yin, J.H. Mechanism of adhesion between polymer fibers at nanoscale contacts. Langmuir 2012, 28, 4663–4671. [Google Scholar]
- Chen, S.C.; Lin, J.F. Detailed modeling of the adhesion force between an afm tip and a smooth flat surface under different humidity levels. J. Micromech. Microeng 2008, 18, 115006. [Google Scholar]
- Farshchi-Tabrizi, M.; Kappl, M.; Butt, H.J. Influence of humidity on adhesion: An atomic force microscope study. J. Adhes. Sci. Technol 2008, 22, 181–203. [Google Scholar]
- Yasuhisa, A. The effect of relative humidity on friction and pull-off forces measured on submicron-size asperity arrays. Wear 2000, 238, 12–19. [Google Scholar]
- Drelich, J.; Wang, Y.U. Charge heterogeneity of surfaces: Mapping and effects on surface forces. Adv. Colloid Interface Sci 2011, 165, 91–101. [Google Scholar]
- Yin, X.H.; Drelich, J. Surface charge microscopy: Novel technique for mapping charge-mosaic surfaces in electrolyte solutions. Langmuir 2008, 24, 8013–8020. [Google Scholar]
- Williams, C.C.; Hough, W.P.; Rishton, S.A. Scanning capacitance microscopy on a 25 nm scale. Appl. Phys. Lett 1989, 55, 203–205. [Google Scholar]
- Chang, M.N.; Chen, C.Y.; Wan, W.W.; Liang, J.H. The influence of the annealing sequence on p(+)/n junctions observed by scanning capacitance microscopy. Appl. Phys. Lett 2004, 84, 4705–4707. [Google Scholar]
- Williams, C.C.; Wickramasinghe, H.K. Scanning chemical-potential microscope—A new technique for atomic scale surface investigation. J. Vac. Sci. Technol. B 1991, 9, 537–540. [Google Scholar]
- Quirk, J.P. Comments on “diffuse double-layer models, long-range forces, and ordering of clay colloids”. Soil Sci. Soc. Am. J 2003, 67, 1960–1961. [Google Scholar]
- Liang, Y.; Hilal, N.; Langston, P.; Starov, V. Interaction forces between colloidal particles in liquid: Theory and experiment. Adv. Colloid Interface Sci 2007, 134–135, 151–166. [Google Scholar]
- Leneveu, D.M.; Rand, R.P.; Parsegian, V.A. Measurement of forces between lecithin bilayers. Nature 1976, 259, 601–603. [Google Scholar]
- Qiu, X.Y.; Rau, D.C.; Parsegian, V.A.; Fang, L.T.; Knobler, C.M.; Gelbart, W.M. Salt-dependent DNA-DNA spacings in intact bacteriophage lambda reflect relative importance of DNA self-repulsion and bending energies. Phys. Rev. Lett 2011, 106, 028102. [Google Scholar]
- Healy, T.W.; Homola, A.; James, R.O.; Hunter, R.J. Coagulation of amphoteric latex colloids—Reversibility and specific ion effects. Faraday Discuss 1978, 65, 156–163. [Google Scholar]
- de Souza, E.F.; Douglas, R.A.; Teschke, O. Atomic force microscopic imaging in liquids: Effects of the film compressed between the substrate and the tip. Langmuir 1997, 13, 6012–6017. [Google Scholar]
- Manhanty, J.; Ninham, B.W. Dispersion Forces; Academic Press: London, UK, 1976. [Google Scholar]
- Grasso, D.; Subramanian, K.; Butkus, M.; Strevett, K.; Bergendahl, J. A review of non-dlvo interactions in environmental colloidal systems. Rev. Environ. Sci. Biotechnol 2002, 1, 17–38. [Google Scholar]
- Pelin, I.M.; Piednoir, A.; Machon, D.; Farge, P.; Pirat, C.; Ramos, S.M.M. Adhesion forces between afm tips and superficial dentin surfaces. J. Colloid Interface Sci 2012, 376, 262–268. [Google Scholar]
- de Souza, E.F.; Ceotto, G.; Teschke, O. Dielectric constant measurements of interfacial aqueous solutions using atomic force microscopy. J. Mol. Catal. A-Chem 2001, 167, 235–243. [Google Scholar]
- Marra, J. Direct measurements of attractive van der waals and adhesion forces between uncharged lipid bilayers in aqueous solutions. J. Colloid Interface Sci 1985, 109, 11–20. [Google Scholar]
- Yaminsky, V.V.; Ninham, B.W.; Christenson, H.K.; Pashley, R.M. Adsorption forces between hydrophobic monolayers. Langmuir 1996, 12, 1936–1943. [Google Scholar]
- Bowen, W.R.; Williams, P.M. The osmotic pressure of electrostatically stabilized colloidal dispersions. J. Colloid Interface Sci 1996, 184, 241–250. [Google Scholar]
- Toikka, G.; Hayes, R.A.; Ralston, J. Surface forces between spherical zns particles in aqueous electrolyte. Langmuir 1996, 12, 3783–3788. [Google Scholar]
- Hamaker, H.C. A general theory of lyophobic colloids i. Recueil des Travaux Chimiques des Pays-Bas 1936, 55, 1015–1026. [Google Scholar]
- de Boer, J.H. The influence of van der waals forces and primary bonds on binding energy, strengh and orientation, with special reference to some artifical resins. Trans. Faraday Soc 1936, 32, 10–27. [Google Scholar]
- Derjaguin, B.V. A theory of interaction of particles in presence of electric double layers and the stability of lyophobe colloids and disperse systems. Acta Physico-Chimica URSS 1939, 10, 333–346. [Google Scholar]
- Derjaguin, B.V.; Landau, L. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solution of electrolytes. Acta Physico-Chimica URSS 1941, 14, 633–662. [Google Scholar]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948; p. 205. [Google Scholar]
- Christenson, H.K. Dlvo (derjaguin-landau-verwey-overbeek) theory and solvation forces between mica surfaces in polar and hydrogen-bonding liquids. J. Chem. Soc.-Faraday Trans. I 1984, 80, 1933–1946. [Google Scholar]
- Von Helmholtz, H.L.F. Studies of electric boundary layers. Annalen der Physik 1879, 7, 337–382. [Google Scholar]
- Conway, B.E. Encyclopedia of Surface and Colloid Science, 2nd ed; Taylor & Francis Group: New York, NY, USA, 2006; p. 8032. [Google Scholar]
- Gouy, G. Constitution of the electric charge at the surface of an electrolyte. J. Phys 1910, 9, 457–467. [Google Scholar]
- Chapman, D.L. A contribution to the theory of electrocapillarity. Philos. Mag 1913, 25, 475–481. [Google Scholar]
- Stern, O. Zur theorie der elektrolytischen doppelschicht. Elektrochem 1924, 30, 508–516. [Google Scholar]
- Debye, P.; Hückel, E. Zur theorie der electrolyte. Zeitschrift fur Physik A 1923, 24, 185–206. [Google Scholar]
- Luckham, P.F. Manipulating forces between surfaces: Applications in colloid science and biophysics. Adv. Colloid Interface Sci 2004, 111, 29–47. [Google Scholar]
- Parsegian, V.A.; Gingell, D. Electrostatic interaction across a salt solution between 2 bodies bearing unequal charges. Biophys. J 1972, 12, 1192–1204. [Google Scholar]
- Hogg, R.; Healy, T.W.; Fuerstenau, D.W. Mutual coagulation of colloidal dispersions. Trans. Faraday Soc 1966, 62, 1638–1651. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed; Elsevier: San Diego, CA, USA, 2011; p. 674. [Google Scholar]
- Hartley, P.G.; Larson, I.; Scales, P.J. Electrokinetic and direct force measurements between silica and mica surfaces in dilute electrolyte, solutions. Langmuir 1997, 13, 2207–2214. [Google Scholar]
- Bevan, M.A.; Prieve, D.C. Direct measurement of retarded van der waals attraction. Langmuir 1999, 15, 7925–7936. [Google Scholar]
- Prieve, D.C.; Luo, F.; Lanni, F. Brownian-motion of a hydrosol particle in a colloidal force-field. Faraday Discuss 1987, 83, 297–307. [Google Scholar]
- Teschke, O.; de Souza, E.F.; Ceotto, G. Double layer relaxation measurements using atomic force microscopy. Langmuir 1999, 15, 4935–4939. [Google Scholar]
- Milling, A.; Mulvaney, P.; Larson, I. Direct measurement of repulsive van der waals interactions using an atomic force microscope. J. Colloid Interface Sci 1996, 180, 460–465. [Google Scholar]
- Lee, S.W.; Sigmund, W.M. Afm study of repulsive van der waals forces between teflon af (tm) thin film and silica or alumina. Colloids Surf. A: Physicochem. Eng. Asp 2002, 204, 43–50. [Google Scholar]
- Borato, C.E.; Leite, F.L.; Oliveira, O.N., Jr; Mattoso, L.H.C. Efficient taste sensors made of bare metal electrodes. Sens. Lett. 2006, 4, 155–159. [Google Scholar]
- Senden, T.J.; Drummond, C.J. Surface-chemistry and tip sample interactions in atomic-force microscopy. Colloids Surf. A: Physicochem. Eng. Asp 1995, 94, 29–51. [Google Scholar]
- Ninham, B.W.; Kurihara, K.; Vinogradova, O.I. Hydrophobicity, specific ion adsorption and reactivity. Colloids Surf. A: Physicochem. Eng. Asp 1997, 123, 7–12. [Google Scholar]
- Derjaguin, B.V.; Voropayeva, T.N. Surface forces + stability of colloids + disperse systems. J. Colloid Sci 1964, 19, 113–135. [Google Scholar]
- Clunie, J.S.; Goodman, J.F.; Symons, P.C. Solvation forces in soap films. Nature 1967, 216, 1203–1204. [Google Scholar]
- Abraham, F.F. The interfacial density profile of a Lennard-Jones fluid in contact with a (100) Lennard-Jones wall and its relationship to idealized fluid-wall systems: A Monte-cCarlo simulation. J. Chem. Phys 1978, 68, 3713–3716. [Google Scholar]
- Vanmegen, W.; Snook, I. Solvent structure and solvation forces between solid bodies. J. Chem. Soc.-Faraday Trans. 2 1979, 75, 1095–1102. [Google Scholar]
- Horn, R.G.; Israelachvili, J.N. Direct measurement of structural forces between 2 surfaces in a non-polar liquid. J. Chem. Phys 1981, 75, 1400–1411. [Google Scholar]
- Evans, R.; Parry, A.O. Liquids at interfaces—What can a theorist contribute. J. Phys. Condes. Matter 1990, 2, SA15–32. [Google Scholar]
- Richetti, P.; Moreau, L.; Barois, P.; Kekicheff, P. Measurement of the interactions between two ordering surfaces under symmetric and asymmetric boundary conditions. Phys. Rev. E 1996, 54, 1749–1762. [Google Scholar]
- Kocevar, K.; Blinc, R.; Musevic, I. Atomic force microscope evidence for the existence of smecticlike surface layers in the isotropic phase of a nematic liquid crystal. Phys. Rev. E 2000, 62, R3055–R3058. [Google Scholar]
- Zemb, T.; Parsegian, V.A. Editorial overview: Hydration forces. Curr. Opin. Colloid Interface Sci 2011, 16, 515–516. [Google Scholar]
- Parsegian, V.A.; Zemb, T. Hydration forces: Observations, explanations, expectations, questions. Curr. Opin. Colloid Interface Sci 2011, 16, 618–624. [Google Scholar]
- Ninham, B.W. Surface forces - the last 30 a. Pure Appl. Chem 1981, 53, 2135–2147. [Google Scholar]
- Kaggwa, G.B.; Nalam, P.C.; Kilpatrick, J.I.; Spencer, N.D.; Jarvis, S.P. Impact of hydrophilic/hydrophobic surface chemistry on hydration forces in the absence of confinement. Langmuir 2012, 28, 6589–6594. [Google Scholar]
- Cevc, G. Hydration force and the interfacial structure of the polar surface. J. Chem. Soc. Faraday Trans 1991, 87, 2733–2739. [Google Scholar]
- Leikin, S.; Parsegian, V.A.; Rau, D.C.; Rand, R.P. Hydration forces. Annu. Rev. Phys. Chem 1993, 44, 369–395. [Google Scholar]
- Ho, R.Y.; Yuan, J.Y.; Shao, Z.F. Hydration force in the atomic force microscope: A computational study. Biophys. J 1998, 75, 1076–1083. [Google Scholar]
- Molina-Bolivar, J.A.; Ortega-Vinuesa, J.L. How proteins stabilize colloidal particles by means of hydration forces. Langmuir 1999, 15, 2644–2653. [Google Scholar]
- Pashley, R.M. Hydration forces between mica surfaces in electrolyte-solutions. Adv. Colloid Interface Sci 1982, 16, 57–62. [Google Scholar]
- Grabbe, A.; Horn, R.G. Double-layer and hydration forces measured between silica sheets subjected to various surface treatments. J. Colloid Interface Sci 1993, 157, 375–383. [Google Scholar]
- Yoon, R.H.; Vivek, S. Effects of short-chain alcohols and pyridine on the hydration forces between silica surfaces. J. Colloid Interface Sci 1998, 204, 179–186. [Google Scholar]
- Churaev, N.V.; Derjaguin, B.V. Inclusion of structural forces in the theory of stability of colloids and films. J. Colloid Interface Sci 1985, 103, 542–553. [Google Scholar]
- Rand, R.P.; Fuller, N.; Parsegian, V.A.; Rau, D.C. Variation in hydration forces between neutral phospholipid-bilayers - evidence for hydration attraction. Biochemistry 1988, 27, 7711–7722. [Google Scholar]
- Valle-Delgado, J.J.; Molina-Bolivar, J.A.; Galisteo-Gonzalez, F.; Galvez-Ruiz, M.J.; Feiler, A.; Rutland, M.W. Hydration forces between silica surfaces: Experimental data and predictions from different theories. J. Chem. Phys 2005, 123, 034708:1–034708:12. [Google Scholar]
- Valle-Delgado, J.J.; Molina-Bolivar, J.A.; Galisteo-Gonzalez, F.; Galvez-Ruiz, M.J.; Feiler, A.; Rutland, M. Interactions between bovine serum albumin layers adsorbed on different substrates measured with an atomic force microscope. Phys. Chem. Chem. Phys 2004, 6, 1482–1486. [Google Scholar]
- Valle-Delgado, J.J.; Molina-Bolivar, J.A.; Galisteo-Gonzalez, F.; Galvez-Ruiz, M.J.; Feiler, A.; Rutland, M.W. Existence of hydration forces in the interaction between apoferritin molecules adsorbed on silica surfaces. Langmuir 2005, 21, 9544–9554. [Google Scholar]
- Paunov, V.N.; Kaler, E.W.; Sandler, S.L.; Petsev, D.N. A model for hydration interactions between apoferritin molecules in solution. J. Colloid Interface Sci 2001, 240, 640–643. [Google Scholar]
- Besseling, N.A.M. Theory of hydration forces between surfaces. Langmuir 1997, 13, 2113–2122. [Google Scholar]
- Rabinovich, Y.I.; Derjaguin, B.V.; Churaev, N.V. Direct measurements of long-range surface forces in gas and liquid-media. Adv. Colloid Interface Sci 1982, 16, 63–78. [Google Scholar]
- Peschel, G.; Belouschek, P.; Muller, M.M.; Muller, M.R.; Konig, R. The interaction of solid-surfaces in aqueous systems. Colloid Polym. Sci 1982, 260, 444–451. [Google Scholar]
- Klier, K.; Zettlemoyer, A.C. Water at interfaces - molecular-structure and dynamics. J. Colloid Interface Sci 1977, 58, 216–229. [Google Scholar]
- Derjaguin, B.V. Effect of lyophile surfaces on properties of boundary liquid films. Discuss. Faraday Soc 1966, 42, 109–119. [Google Scholar]
- Attard, P.; Batchelor, M.T. A mechanism for the hydration force demonstrated in a model system. Chem. Phys. Lett 1988, 149, 206–211. [Google Scholar]
- Trokhymchuk, A.; Henderson, D.; Wasan, D.T. A molecular theory of the hydration force in an electrolyte solution. J. Colloid Interface Sci 1999, 210, 320–331. [Google Scholar]
- Basu, S.; Sharma, M.M. Effect of dielectric saturation on disjoining pressure in thin-films of aqueous-electrolytes. J. Colloid Interface Sci 1994, 165, 355–366. [Google Scholar]
- Henderson, D.; Lozadacassou, M. A simple theory for the force between spheres immersed in a fluid. J. Colloid Interface Sci 1986, 114, 180–183. [Google Scholar]
- Paunov, V.N.; Binks, B.P. Analytical expression for the electrostatic disjoining pressure taking into account the excluded volume of the hydrated ions between charged interfaces in electrolyte. Langmuir 1999, 15, 2015–2021. [Google Scholar]
- Lyklema, J. The structure of electrical double layer on porous surfaces. J. Electroanal. Chem 1968, 18, 341–348. [Google Scholar]
- Vigil, G.; Xu, Z.H.; Steinberg, S.; Israelachvili, J. Interactions of silica surfaces. J. Colloid Interface Sci 1994, 165, 367–385. [Google Scholar]
- Kralchevsky, P.A.; Danov, K.D.; Basheva, E.S. Hydration force due to the reduced screening of the electrostatic repulsion in few-nanometer-thick films. Curr. Opin. Colloid Interface Sci 2011, 16, 517–524. [Google Scholar]
- Norrish, K. The swelling of montmorillonite. Discuss. Faraday Soc 1954, 120–134. [Google Scholar]
- Pashley, R.M.; Israelachvili, J.N. A comparison of surface forces and interfacial properties of mica in purified surfactant solutions. Colloids Surf 1981, 2, 169–187. [Google Scholar]
- Pashley, R.M.; Israelachvili, J.N. Molecular layering of water in thin-films between mica surfaces and its relation to hydration forces. J. Colloid Interface Sci 1984, 101, 511–523. [Google Scholar]
- Israelachvili, J.N.; Pashley, R.M. Molecular layering of water at surfaces and origin of repulsive hydration forces. Nature 1983, 306, 249–250. [Google Scholar]
- Horn, R.G.; Smith, D.T.; Haller, W. Surface forces and viscosity of water measured between silica sheets. Chem. Phys. Lett 1989, 162, 404–408. [Google Scholar]
- Claesson, P.; Carmonaribeiro, A.M.; Kurihara, K. Dihexadecyl phosphate monolayers—Intralayer and interlayer interactions. J. Phys. Chem 1989, 93, 917–922. [Google Scholar]
- Chapel, J.P. Electrolyte species-dependent hydration forces between silica surfaces. Langmuir 1994, 10, 4237–4243. [Google Scholar]
- Allen, L.H.; Matijević, E. Stability of colloidal silica.I. Effect of simple electrolytes. J. Colloid Interface Sci 1969, 31, 287–296. [Google Scholar]
- Yotsumoto, H.; Yoon, R.H. Application of extended dlvo theory .1. Stability of rutile suspensions. J. Colloid Interface Sci 1993, 157, 426–433. [Google Scholar]
- Yotsumoto, H.; Yoon, R.H. Application of extended dlvo theory .2. Stability of silica suspensions. J. Colloid Interface Sci 1993, 157, 434–441. [Google Scholar]
- Depasse, J.; Watillon, A. Stability of amorphous colloidal silica. J. Colloid Interface Sci 1970, 33, 430–438. [Google Scholar]
- Persson, P.K.T.; Bergenstahl, B.A. Repulsive forces in lecithin glycol lamellar phases. Biophys. J 1985, 47, 743–746. [Google Scholar]
- Duan, J.M. Interfacial forces between silica surfaces measured by atomic force microscopy. J. Environ. Sci. -China 2009, 21, 30–34. [Google Scholar]
- Christenson, H.K.; Claesson, P.M. Cavitation and the interaction between macroscopic hydrophobic surfaces. Science 1988, 239, 390–392. [Google Scholar]
- Rabinovich, Y.I.; Derjaguin, B.V. Interaction of hydrophobized filaments in aqueous-electrolyte solutions. Colloids Surf 1988, 30, 243–251. [Google Scholar]
- Horinek, D.; Serr, A.; Bonthuis, D.J.; Bostrom, M.; Kunz, W.; Netz, R.R. Molecular hydrophobic attraction and ion-specific effects studied by molecular dynamics. Langmuir 2008, 24, 1271–1283. [Google Scholar]
- Christenson, H.K.; Claesson, P.M. Direct measurements of the force between hydrophobic surfaces in water. Adv. Colloid Interface Sci 2001, 91, 391–436. [Google Scholar]
- Derjaguin, B.V.; Churaev, N.V. Structural component of disjoining pressure. J. Colloid Interface Sci 1974, 49, 249–255. [Google Scholar]
- Ruckenstein, E.; Churaev, N. A possible hydrodynamic origin of the forces of hydrophobic attraction. J. Colloid Interface Sci 1991, 147, 535–538. [Google Scholar]
- Yushchenko, V.S.; Yaminsky, V.V.; Shchukin, E.D. Interaction between particles in a nonwetting liquid. J. Colloid Interface Sci 1983, 96, 307–314. [Google Scholar]
- Podgornik, R.; Parsegian, V.A. An electrostatic-surface stability interpretation of the hydrophobic force inferred to occur between mica plates in solutions of soluble surfactants. Chem. Phys 1991, 154, 477–483. [Google Scholar]
- Tsao, Y.H.; Evans, D.F.; Wennerstrom, H. Long-range attraction between a hydrophobic surface and a polar surface is stronger than that between 2 hydrophobic surfaces. Langmuir 1993, 9, 779–785. [Google Scholar]
- Berard, D.R.; Attard, P.; Patey, G.N. Cavitation of a lennard-jones fluid between hard walls, and the possible relevance to the attraction measured between hydrophobic surfaces. J. Chem. Phys 1993, 98, 7236–7244. [Google Scholar]
- Wood, J.; Sharma, R. How long is the long-range hydrophobic attraction? Langmuir 1995, 11, 4797–4802. [Google Scholar]
- Zhang, J.H.; Yoon, R.H.; Mao, M.; Ducker, W.A. Effects of degassing and ionic strength on afm force measurements in octadecyltrimethylammonium chloride solutions. Langmuir 2005, 21, 5831–5841. [Google Scholar]
- Podgornik, R. Forces between surfaces with surface-specific interactions in a dilute electrolyte. Chem. Phys. Lett 1989, 156, 71–75. [Google Scholar]
- Kekicheff, P.; Spalla, O. Long-range electrostatic attraction between similar, charge-neutral walls. Phys. Rev. Lett. 1995, 75, 1851–1854. [Google Scholar]
- Ishida, N.; Sakamoto, M.; Miyahara, M.; Higashitani, K. Attraction between hydrophobic surfaces with and without gas phase. Langmuir 2000, 16, 5681–5687. [Google Scholar]
- Stevens, H.; Considine, R.F.; Drummond, C.J.; Hayes, R.A.; Attard, P. Effects of degassing on the long-range attractive force between hydrophobic surfaces in water. Langmuir 2005, 21, 6399–6405. [Google Scholar]
- Teschke, O.; de Souza, E.F. Measurements of long-range attractive forces between hydrophobic surfaces and atomic force microscopy tips. Chem. Phys. Lett 2003, 375, 540–546. [Google Scholar]
- Chandler, D. Interfaces and the driving force of hydrophobic assembly. Nature 2005, 437, 640–647. [Google Scholar]
- Despa, F.; Berry, R.S. The origin of long-range attraction between hydrophobes in water. Biophys. J 2007, 92, 373–378. [Google Scholar]
- Parker, J.L.; Cho, D.L.; Claesson, P.M. Plasma modification of mica—forces between fluorocarbon surfaces in water and a nonpolar liquid. J. Phys. Chem 1989, 93, 6121–6125. [Google Scholar]
- Christenson, H.K.; Fang, J.F.; Ninham, B.W.; Parker, J.L. Effect of divalent electrolyte on the hydrophobic attraction. J. Phys. Chem 1990, 94, 8004–8006. [Google Scholar]
- Sirghi, L.; Nakagiri, N.; Sugimura, H.; Takai, O. Analysis of atomic force curve data for mapping of surface properties in water. Jpn. J. Appl. Phys 2001, 40, 1420–1424. [Google Scholar]
- Rabinovich, Y.I.; Yoon, R.H. Use of atomic-force microscope for the measurements of hydrophobic forces. Colloids Surf. A: Physicochem. Eng. Asp 1994, 93, 263–273. [Google Scholar]
- Rabinovich, Y.I.; Yoon, R.H. Use of atomic-force microscope for the measurements of hydrophobic forces between silanated silica plate and glass sphere. Langmuir 1994, 10, 1903–1909. [Google Scholar]
- Kokkoli, E.; Zukoski, C.F. Interactions between hydrophobic self-assembled monolayers. Effect of salt and the chemical potential of water on adhesion. Langmuir 1998, 14, 1189–1195. [Google Scholar]
- Freitas, A.M.; Sharma, M.M. Detachment of particles from surfaces: An afm study. J. Colloid Interface Sci 2001, 233, 73–82. [Google Scholar]
- Teschke, O.; de Souza, E.F. Hydrophobic surfaces probed by atomic force microscopy. Langmuir 2003, 19, 5357–5365. [Google Scholar]
- Teschke, O.; de Souza, E.F. Electrostatic response of hydrophobic surface measured by atomic force microscopy. Appl. Phys. Lett 2003, 82, 1126–1128. [Google Scholar]
- Yoon, R.H.; Ravishankar, S.A. Long-range hydrophobic forces between mica surfaces in dodecylammonium chloride solutions in the presence of dodecanol. J. Colloid Interface Sci 1996, 179, 391–402. [Google Scholar]


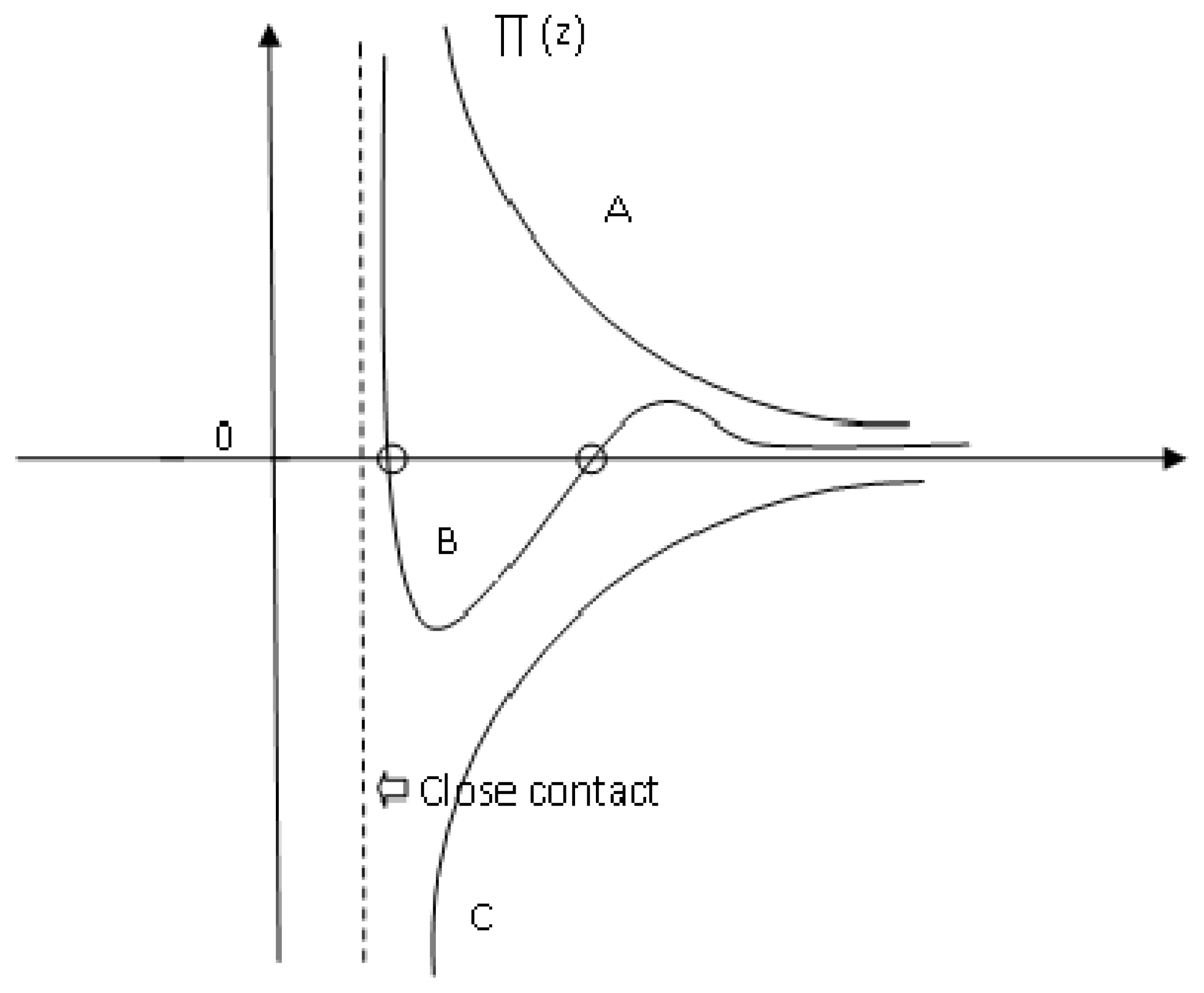
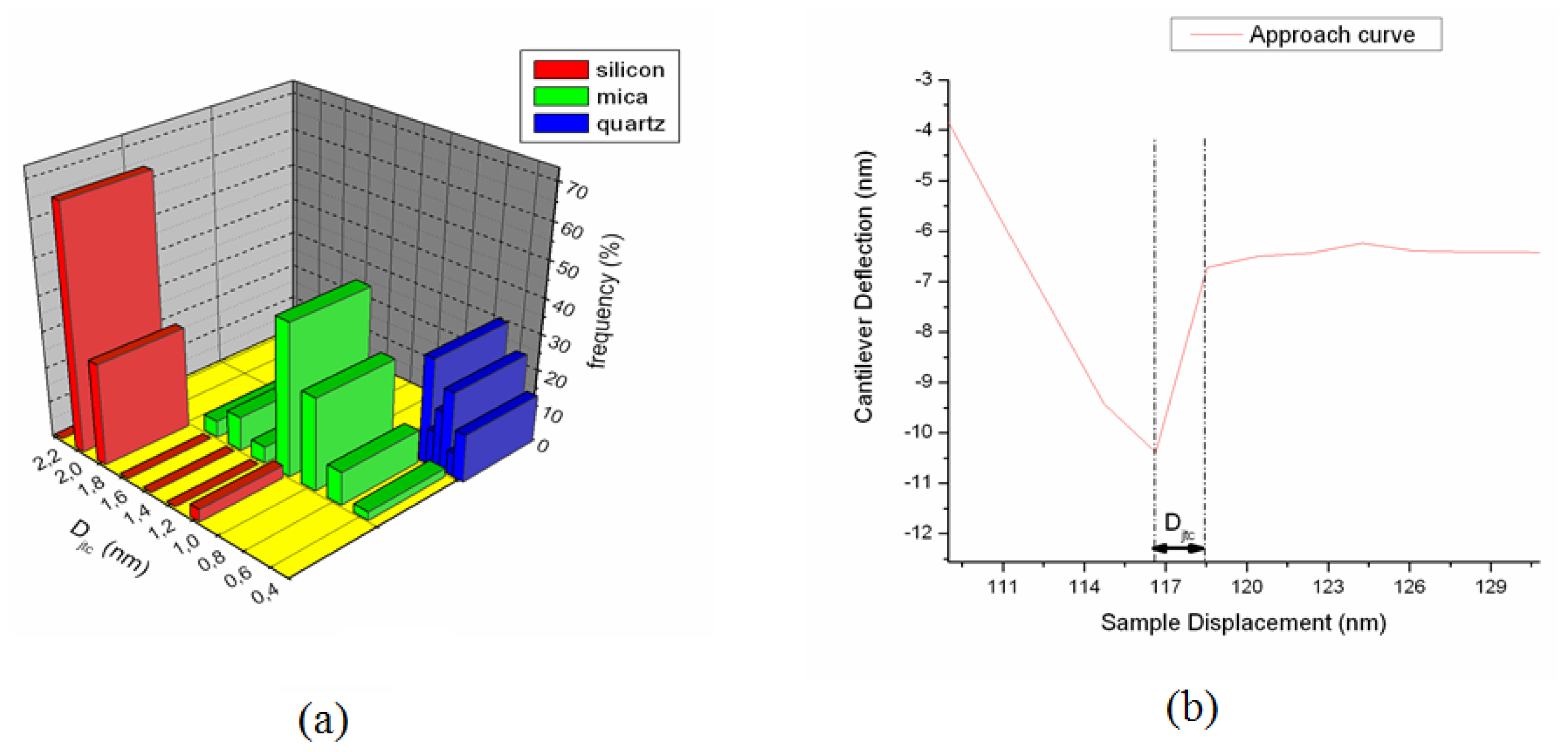
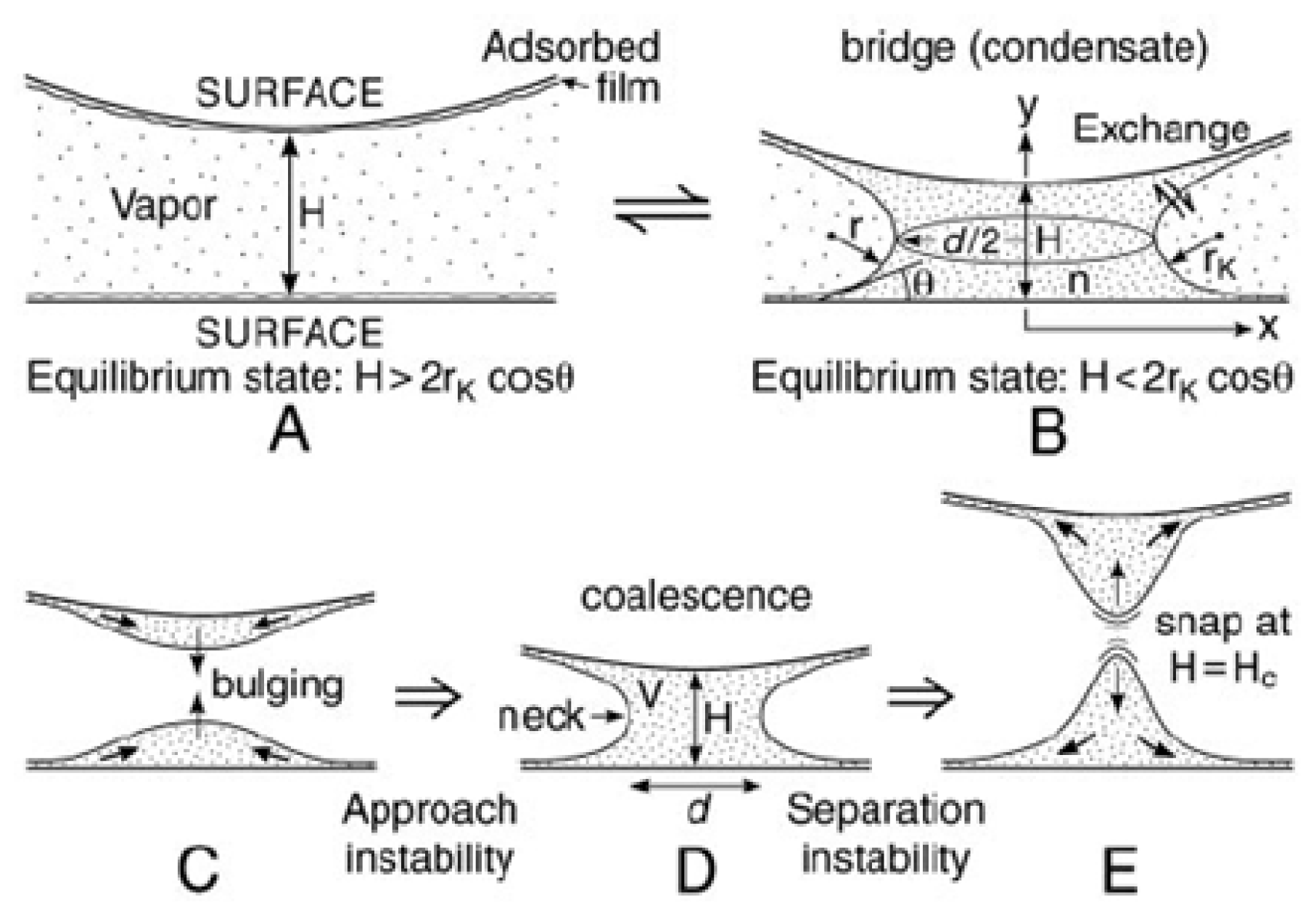
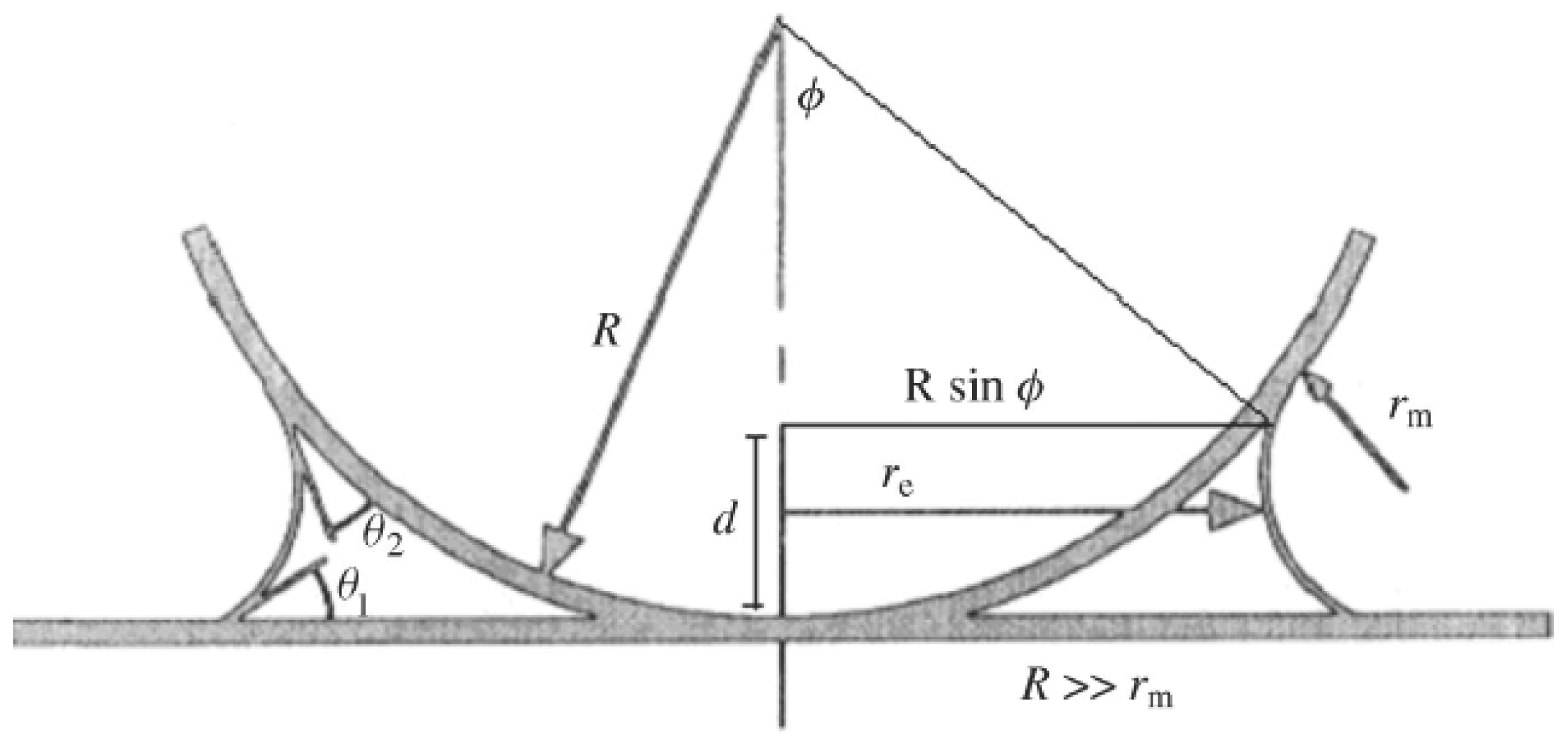





| Material (1) | Material (2) | Medium (3) | Calculated × 10−20 J | Experimental × 10−20 J |
|---|---|---|---|---|
| Si3N4 | Si3N4 | Air 1 | 16.70 | - |
| Si3N4 | Si3N4 | Water | 4.80–5.90 | 6.10 |
| Si3N4 | Mica | Water | 2.45 | 3.40 |
| SiO2 | SiO2 | Air | 6.50 | - |
| SiO2 | SiO2 | Water | 0.77–0.84 | 0.85–1.00 |
| SiO2 | Air | Water | −1.00 | −1.00 |
| SiO2 | Mica | Water | 1.20 | 1.20 |
| SiO2 | PTFE | Vacuum | 16.44 | 13.70 |
| Mica | Mica | Water | 2.00–2.20 | 2.20 |
| Mica | Mica | Air | 9.86 | - |
| Au | Au | Water | 40.00 | 25.00 |
| Silicon | Silicon | Air | 18.65 | - |
| Silicon | Silicon | Water | 9.75 | - |
| MgO | MgO | Air | 12.10 | - |
| MgO | MgO | Water | 2.21 | |
| Teflon | Teflon | Air | 2.75 | - |
| Teflon | Teflon | Water | 0.33 | |
| Polystyrene | Polystyrene | Air | 6.58 | - |
| Polystyrene | Polystyrene | Water | 0.95 | - |
| Poly(isoprene) | Poly(isoprene) | Air | 5.99 | - |
| Poly(isoprene) | Poly(isoprene) | Water | 0.743 | - |
| Ag | Ag | Air | 20.00–49.00 | 38.50 |
| C (diamondIIa) | C (diamondIIa) | Air | 29.60 | - |
| Cellulose | Cellulose | Air | 5.80 ± 0.20 | - |
| Cellulose | Cellulose | Water | 0.80 ± 0.05 | - |
| Hexadecane | Hexadecane | Air | 5.20 | - |
| Hexadecane | Hexadecane | Water | - | - |
| Cellulose | CaCO3 | Air | 7.40 ± 0.30 | - |
| Cellulose | CaCO3 | Water | 0.57 ± 0.10 | - |
| Cellulose | Si3N4 | Air | 9.50 ± 0.40 | - |
| Cellulose | Si3N4 | Water | 0.80 ± 0.20 | - |
| Cellulose | SiO2 | Air | 5.90 ± 0.30 | - |
| Cellulose | SiO2 | Water | 0.35 ± 0.03 | - |
| Cellulose | Mica | Air | 7.20 ± 0.30 | - |
| Cellulose | Mica | Water | 0.43 ± 0.08 | - |
| Cellulose | TiO2 | Air | 9.30 ± 0.40 | - |
| Cellulose | TiO2 | Water | 1.20 ± 0.20 | - |
| Octane | TPFP | Air | 4.50 | - |
| Octane | TPFP | Water | 29.00 | - |
| Octane | AF 2400 | Air | 4.00 | - |
| Octane | AF 2400 | Water | 31.00 | - |
| Octane | AF 1600 | Air | 4.10 | - |
| Octane | AF 1600 | Water | 32.00 | - |
| Octane | PTFE. LD | Air | 4.60 | - |
| Octane | PTFE. LD | Water | 40.00 | - |
| Octane | PTFE. HD | Air | 5.10 | - |
| Octane | PTFE. HD | Water | 42.00 | - |
| Octane | PDMS (liq) | Air | 4.05 | - |
| Octane | PDMS (liq) | Water | 38.00 | - |
| Octane | PDMS (s) | Air | 4.50 | - |
| Octane | PDMS (s) | Water | 40.00 | - |
| Octane | PE. LD | Air | 4.90 | - |
| Octane | PE. LD | Water | 43.00 | - |
| Octane | Rubber | Air | 5.05 | - |
| Octane | Rubber | Water | 50.00 | - |
| P-Xylene | TPFP | Air | 3.40 | - |
| P-Xylene | TPFP | Water | 22.00 | - |
| P-Xylene | AF 2400 | Air | 4.00 | - |
| P-Xylene | AF 2400 | Water | 27.00 | - |
| P-Xylene | AF 1600 | Air | 4.10 | - |
| P-Xylene | AF 1600 | Water | 30.00 | - |
| P-Xylene | PTFE. LD | Air | 4.70 | - |
| P-Xylene | PTFE. LD | Water | 31.00 | - |
| P-Xylene | PTFE. HD | Air | 5.07 | - |
| P-Xylene | PTFE. HD | Water | 34.00 | - |
| P-Xylene | PDMS (liq) | Air | 4.10 | - |
| P-Xylene | PDMS (liq) | Water | 42.00 | - |
| P-Xylene | PDMS (s) | Air | 4.50 | - |
| P-Xylene | PDMS (s) | Water | 45.00 | - |
| P-Xylene | PE. LD | Air | 5.00 | - |
| P-Xylene | PE. LD | Water | 51.00 | - |
| P-Xylene | Rubber | Air | 5.30 | - |
| P-Xylene | Rubber | Water | 60.00 | - |
| D-α-Pinene | TPFP | Air | 4.00 | - |
| D-α-Pinene | TPFP | Water | 21.00 | - |
| D-α-Pinene | AF 2400 | Air | 4.40 | - |
| D-α-Pinene | AF 2400 | Water | 30.00 | - |
| D-α-Pinene | AF 1600 | Air | 4.50 | - |
| D-α-Pinene | AF 1600 | Water | 32.00 | - |
| D-α-Pinene | PTFE. LD | Air | 5.10 | - |
| D-α-Pinene | PTFE. LD | Water | 41.00 | - |
| D-α-Pinene | PTFE. HD | Air | 5.60 | - |
| D-α-Pinene | PTFE. HD | Water | 51.00 | - |
| D-α-Pinene | PDMS (liq) | Air | 4.50 | - |
| D-α-Pinene | PDMS (liq) | Water | 40.00 | - |
| D-α-Pinene | PDMS (s) | Air | 5.00 | - |
| D-α-Pinene | PDMS (s) | Water | 48.00 | - |
| D-α-Pinene | PE. LD | Air | 5.40 | - |
| D-α-Pinene | PE. LD | Water | 59.00 | - |
| D-α-Pinene | Rubber | Air | 5.60 | - |
| D-α-Pinene | Rubber | Water | 61.00 | - |
| Olive oil | TPFP | Air | 4.10 | - |
| Olive oil | TPFP | Water | 21.00 | - |
| Olive oil | AF 2400 | Air | 4.50 | - |
| Olive oil | AF 2400 | Water | 30.00 | - |
| Olive oil | AF 1600 | Air | 4.80 | - |
| Olive oil | AF 1600 | Water | 35.00 | - |
| Olive oil | PTFE. LD | Air | 5.40 | - |
| Olive oil | PTFE. LD | Water | 50.00 | - |
| Olive oil | PTFE. HD | Air | 5.95 | - |
| Olive oil | PTFE. HD | Water | 60.00 | - |
| Olive oil | PDMS (liq) | Air | 4.80 | - |
| Olive oil | PDMS (liq) | Water | 40.00 | - |
| Olive oil | PDMS (s) | Air | 5.00 | - |
| Olive oil | PDMS (s) | Water | 48.00 | - |
| Olive oil | PE. LD | Air | 5.60 | - |
| Olive oil | PE. LD | Water | 59.00 | - |
| Olive oil | Rubber | Air | 5.90 | - |
| Olive oil | Rubber | Water | 69.00 | - |
| Sunfloweroil | TPFP | Air | 4.00 | - |
| Sunfloweroil | TPFP | Water | 20.00 | - |
| Sunfloweroil | AF 2400 | Air | 4.60 | - |
| Sunfloweroil | AF 2400 | Water | 30.00 | - |
| Sunfloweroil | AF 1600 | Air | 4.70 | - |
| Sunfloweroil | AF 1600 | Water | 35.00 | - |
| Sunfloweroil | PTFE. LD | Air | 5.20 | - |
| Sunfloweroil | PTFE. LD | Water | 44.00 | - |
| Sunfloweroil | PTFE. HD | Air | 5.90 | - |
| Sunfloweroil | PTFE. HD | Water | 57.00 | - |
| Sunfloweroil | PDMS (liq) | Air | 4.80 | - |
| Sunfloweroil | PDMS (liq) | Water | 40.00 | - |
| Sunfloweroil | PDMS (s) | Air | 5.00 | - |
| Sunfloweroil | PDMS (s) | Water | 49.00 | - |
| Sunfloweroil | PE. LD | Air | 5.70 | - |
| Sunfloweroil | PE. LD | Water | 60.00 | - |
| Sunfloweroil | Rubber | Air | 5.90 | - |
| Sunfloweroil | Rubber | Water | 64.00 | - |
| Tricosenoicacid | TPFP | Air | 4.30 | - |
| Tricosenoicacid | TPFP | Water | 19.00 | - |
| Tricosenoicacid | AF 2400 | Air | 4.90 | - |
| Tricosenoicacid | AF 2400 | Water | 30.00 | - |
| Tricosenoicacid | AF 1600 | Air | 5.00 | - |
| Tricosenoicacid | AF 1600 | Water | 39.00 | - |
| Tricosenoicacid | PTFE. LD | Air | 5.70 | - |
| Tricosenoicacid | PTFE. LD | Water | 58.00 | - |
| Tricosenoicacid | PTFE. HD | Air | 6.20 | - |
| Tricosenoicacid | PTFE. HD | Water | 70.00 | - |
| Tricosenoicacid | PDMS (liq) | Air | 5.00 | - |
| Tricosenoicacid | PDMS (liq) | Water | 40.05 | - |
| Tricosenoicacid | PDMS (s) | Air | 5.40 | - |
| Tricosenoicacid | PDMS (s) | Water | 50.00 | - |
| Tricosenoicacid | PE. LD | Air | 5.90 | - |
| Tricosenoicacid | PE. LD | Water | 69.00 | - |
| Tricosenoicacid | Rubber | Air | 6.10 | - |
| Tricosenoicacid | Rubber | Water | 74.00 | - |
| Cd-Arachidate | TPFP | Air | 4.00 | - |
| Cd-Arachidate | TPFP | Water | 19.00 | - |
| Cd-Arachidate | AF 2400 | Air | 4.30 | - |
| Cd-Arachidate | AF 2400 | Water | 27.00 | - |
| Cd-Arachidate | AF 1600 | Air | 4.30 | - |
| Cd-Arachidate | AF 1600 | Water | 30.00 | - |
| Cd-Arachidate | PTFE. LD | Air | 5.08 | - |
| Cd-Arachidate | PTFE. LD | Water | 37.00 | - |
| Cd-Arachidate | PTFE. HD | Air | 5.50 | - |
| Cd-Arachidate | PTFE. HD | Water | 46.00 | - |
| Cd-Arachidate | PDMS (liq) | Air | 4.70 | - |
| Cd-Arachidate | PDMS (liq) | Water | 42.00 | - |
| Cd-Arachidate | PDMS (s) | Air | 5.00 | - |
| Cd-Arachidate | PDMS (s) | Water | 50.00 | - |
| Cd-Arachidate | PE. LD | Air | 5.40 | - |
| Cd-Arachidate | PE. LD | Water | 62.00 | - |
| Cd-Arachidate | Rubber | Air | 5.70 | - |
| Cd-Arachidate | Rubber | Water | 70.00 | - |
| Cellulose | TPFP | Air | 4.90 | - |
| Cellulose | TPFP | Water | 18.00 | - |
| Cellulose | AF 2400 | Air | 5.20 | - |
| Cellulose | AF 2400 | Water | 37.00 | - |
| Cellulose | AF 1600 | Air | 5.50 | - |
| Cellulose | AF 1600 | Water | 39.00 | - |
| Cellulose | PTFE. LD | Air | 6.20 | - |
| Cellulose | PTFE. LD | Water | 60.00 | - |
| Cellulose | PTFE. HD | Air | 6.90 | - |
| Cellulose | PTFE. HD | Water | 83.00 | - |
| Cellulose | PDMS (liq) | Air | 5.70 | - |
| Cellulose | PDMS (liq) | Water | 40.00 | - |
| Cellulose | PDMS (s) | Air | 6.00 | - |
| Cellulose | PDMS (s) | Water | 51.00 | - |
| Cellulose | PE. LD | Air | 6.50 | - |
| Cellulose | PE. LD | Water | 78.00 | - |
| Cellulose | Rubber | Air | 6.70 | - |
| Cellulose | Rubber | Water | 82.00 | - |
| Hexadecane | TPFP | Air | 4.00 | - |
| Hexadecane | TPFP | Water | 22.00 | - |
| Hexadecane | AF 2400 | Air | 4.50 | - |
| Hexadecane | AF 2400 | Water | 32.00 | - |
| Hexadecane | AF 1600 | Air | 4.70 | - |
| Hexadecane | AF 1600 | Water | 34.00 | - |
| Hexadecane | PTFE. LD | Air | 5.10 | - |
| Hexadecane | PTFE. LD | Water | 42.00 | - |
| Hexadecane | PTFE. HD | Air | 5.60 | - |
| Hexadecane | PTFE. HD | Water | 55.00 | - |
| Hexadecane | PDMS (liq) | Air | 4.50 | - |
| Hexadecane | PDMS (liq) | Water | 38.00 | - |
| Hexadecane | PDMS (s) | Air | 5.00 | - |
| Hexadecane | PDMS (s) | Water | 31.00 | - |
| Hexadecane | PE. LD | Air | 5.10 | - |
| Hexadecane | PE. LD | Water | 53.00 | - |
| Hexadecane | Rubber | Air | 5.30 | - |
| Hexadecane | Rubber | Water | 59.00 | - |
| PVA | TPFP | Air | 4.60 | - |
| PVA | TPFP | Water | 18.00 | - |
| PVA | AF 2400 | Air | 5.10 | - |
| PVA | AF 2400 | Water | 33.00 | - |
| PVA | AF 1600 | Air | 5.40 | - |
| PVA | AF 1600 | Water | 40.00 | - |
| PVA | PTFE. LD | Air | 6.08 | - |
| PVA | PTFE. LD | Water | 60.00 | - |
| PVA | PTFE. HD | Air | 6.40 | - |
| PVA | PTFE. HD | Water | 78.00 | - |
| PVA | PDMS (liq) | Air | 5.50 | - |
| PVA | PDMS (liq) | Water | 40.05 | - |
| PVA | PDMS (s) | Air | 5.70 | - |
| PVA | PDMS (s) | Water | 71.00 | - |
| PVA | PE. LD | Air | 6.10 | - |
| PVA | PE. LD | Water | 77.00 | - |
| PVA | Rubber | Air | 6.30 | - |
| PVA | Rubber | Water | 80.00 | - |
| BSA | TPFP | Air | 5.00 | - |
| BSA | TPFP | Water | 16.00 | - |
| BSA | AF 2400 | Air | 5.50 | - |
| BSA | AF 2400 | Water | 29.00 | - |
| BSA | AF 1600 | Air | 5.80 | - |
| BSA | AF 1600 | Water | 40.00 | - |
| BSA | PTFE. LD | Air | 6.40 | - |
| BSA | PTFE. LD | Water | 61.00 | - |
| BSA | PTFE. HD | Air | 7.00 | - |
| BSA | PTFE. HD | Water | 80.05 | - |
| BSA | PDMS (liq) | Air | 5.60 | - |
| BSA | PDMS (liq) | Water | 42.00 | - |
| BSA | PDMS (s) | Air | 6.00 | - |
| BSA | PDMS (s) | Water | 60.00 | - |
| BSA | PE. LD | Air | 6.50 | - |
| BSA | PE. LD | Water | 80.00 | - |
| BSA | Rubber | Air | 7.00 | - |
| BSA | Rubber | Water | 82.00 | - |
| Nylon 6 | TPFP | Air | 4.50 | - |
| Nylon 6 | TPFP | Water | 17.00 | - |
| Nylon 6 | AF 2400 | Air | 5.00 | - |
| Nylon 6 | AF 2400 | Water | 23.00 | - |
| Nylon 6 | AF 1600 | Air | 5.10 | - |
| Nylon 6 | AF 1600 | Water | 37.00 | - |
| Nylon 6 | PTFE. LD | Air | 5.80 | - |
| Nylon 6 | PTFE. LD | Water | 50.00 | - |
| Nylon 6 | PTFE. HD | Air | 6.20 | - |
| Nylon 6 | PTFE. HD | Water | 64.00 | - |
| Nylon 6 | PDMS (liq) | Air | 5.20 | - |
| Nylon 6 | PDMS (liq) | Water | 40.00 | - |
| Nylon 6 | PDMS (s) | Air | 5.40 | - |
| Nylon 6 | PDMS (s) | Water | 53.00 | - |
| Nylon 6 | PE. LD | Air | 6.08 | - |
| Nylon 6 | PE. LD | Water | 79.00 | - |
| Nylon 6 | Rubber | Air | 6.30 | |
| Nylon 6 | Rubber | Water | 80.00 | - |
| Silver | Silver | Vacuum | 20.30 | 38.20 |
| Silver | Silver | Nitrogen | 20.30 | 37.90 |
| Copper | Copper | Vacuum | 24.82 | 27.20 |
| Copper | Copper | Nitrogen | 24.82 | 27.10 |
| PTFE | PTFE | Vacuum | 3.63 | - |
| PTFE | PTFE | Nitrogen | 3.63 | - |
| Silicon Dioxide | Silicon Dioxide | Vacuum | 6.55 | - |
| Silicon Dioxide | Silicon Dioxide | Nitrogen | 6.55 | 7.20 |
| Titanium Nitride | Titanium Nitride | Vacuum | 15.73 | - |
| Titanium Nitride | Titanium Nitride | Nitrogen | 15.73 | - |
| Parylene-n | Parylene-n | Vacuum | 11.10 | - |
| Parylene-n | Parylene-n | Nitrogen | 11.10 | - |
| Silver | Copper | Vacuum | 22.45 | 32.60 |
| Silver | Copper | Nitrogen | 22.45 | 32.40 |
| Silver | Silicon Dioxide | Vacuum | 11.12 | 12.92 |
| Silver | Silicon Dioxide | Nitrogen | 11.12 | 12.70 |
| Silver | PTFE | Vacuum | 8.34 | 13.70 |
| Silver | PTFE | Nitrogen | 8.34 | 13.60 |
| Silver | Parylene-n | Vacuum | 14.30 | 11.80 |
| Silver | Parylene-n | Nitrogen | 14.30 | 11.60 |
| Silver | Cross linked Parylene-n | Vacuum | 14.30 | 12.10 |
| Silver | Cross linked Parylene-n | Nitrogen | 14.30 | 12.00 |
| Silver | Titanium Nitride | Vacuum | 16.80 | 16.40 |
| Silver | Titanium Nitride | Nitrogen | 16.80 | 16.10 |
| Copper | Silicon Dioxide | Vacuum | 11.60 | 14.10 |
| Copper | Silicon Dioxide | Nitrogen | 11.60 | 13.90 |
| Copper | PTFE | Vacuum | 8.72 | 13.10 |
| Copper | PTFE | Nitrogen | 8.72 | 12.80 |
| Copper | Parylene-n | Vacuum | 15.00 | 9.80 |
| Copper | Parylene-n | Nitrogen | 15.00 | 10.10 |
| Copper | Cross linked Parylene-n | Vacuum | 15.00 | 11.00 |
| Copper | Cross linked Parylene-n | Nitrogen | 15.00 | 11.10 |
| Copper | Titanium Nitride | Vacuum | 17.59 | 12.30 |
| Copper | Titanium Nitride | Nitrogen | 17.59 | 12.50 |
| Silicon Dioxide | PTFE | Vacuum | 4.87 | - |
| Silicon Dioxide | PTFE | Nitrogen | 4.87 | 7.60 |
| Silicon Dioxide | Parylene-n | Vacuum | 8.55 | - |
| Silicon Dioxide | Parylene-n | Nitrogen | 8.55 | 6.80 |
| Silicon Dioxide | Cross linked Parylene-n | Vacuum | 8.55 | - |
| Silicon Dioxide | Cross linked Parylene-n | Nitrogen | 8.55 | 6.90 |
| Silicon Dioxide | Titanium Nitride | Vacuum | 10.10 | - |
| Silicon Dioxide | Titanium Nitride | Nitrogen | 10.10 | 8.80 |
| Pull-on force | ||
|---|---|---|
| Types of force | Topics or equations | Special features |
| van der Waals (a, v & s) | See Section2 | Ubiquitous force both in vacuum and in liquids, existing between all bodies. |
| Hydration (s) | See Section5 (Topic C) | Hydration repulsive force attributed to the energy required to remove the water of hydration from the surface, or the surface adsorbed species. |
| Solvation (s) | See Section5 (Topic C) | Solvation forces arise whenever liquid molecules are compelled to order in almost discrete layers between two surfaces. |
| Double-Layer (s) | See Section 5 (Topic C) | A force that exists only between charged molecules (ions) or surfaces, and depends on the electrolyte concentration. |
| Elastic (a, v & s) | Relation between the applied forces to the depth of indentation as the tip is pushed against the sample. | |
| Brush (a, v & s) | Polymer-brushing forces that result from the thermally driven motion of polymers grafted onto a solid surface in solution. | |
| Pull-off force | ||
| Adhesion (a, v & s) | See Section 5 (Topic A) | Adhesion between a sphere and a plane in the absence of contaminating adsorbates (typically in a vacuum). |
| Capillary (a) | See Section 5 (Topic B) | Capillary adhesion–very common under ambient conditions, under which many surfaces have a thin water layer. |
| Hydrophobic (s) | See Section 5 (Topic C) | The hydrophobic force has different origins depending on the system. For example, when two hydrophobic surfaces are in contact, a vapor cavity bridging is formed to cause strong adhesion. |
| Polymer Extension (a, v & s) | Polymers break or detach from one of the surfaces (tip and sample). | |
| Specific Binding (a, v & s) | Specific interactions (chemical force microscopy). Antibody-antigen interactions, receptor-ligand interactions and complementary binding. | |
| Geometry (D << R) | vdW Interactions | |
|---|---|---|
| Force | Energy | |
| Two atoms or small molecules | ||
| Atom-surface | ||
| Two spheres | ||
| Sphere-flat surface | ||
| Two flat plates | ||
| Two cylinders or fi1aments crossed at 90° | ||
| Cylinder near a flat surface | ||
| Two parallel cylinders or rods | ||
| Sample | Surface Energy γlit (mJ/m2) | Tip radius (μm) | Attractive force (nN) |
|---|---|---|---|
| Mica | 300, 375 | 2.5 ± 0.5 | 230 ± 30 |
| Graphite | 96, 123 | 2.5 ± 0.5 | 140 ± 90 |
| Al2O3 | 45 | 2.0 ± 0.5 | 85 ± 25 |
| CH3(CH2)16COOH | 21 | 2.0 ± 0.5 | 17 ± 11 |
| CF3(CH2)16COOH | 20 | 3.0 ± 0.5 | 5.0 ± 4.0 |
| PTFE | 18 | 2.5 ± 0.5 | 2.0 ± 2.0 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Leite, F.L.; Bueno, C.C.; Da Róz, A.L.; Ziemath, E.C.; Oliveira, O.N., Jr. Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy. Int. J. Mol. Sci. 2012, 13, 12773-12856. https://doi.org/10.3390/ijms131012773
Leite FL, Bueno CC, Da Róz AL, Ziemath EC, Oliveira ON Jr. Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy. International Journal of Molecular Sciences. 2012; 13(10):12773-12856. https://doi.org/10.3390/ijms131012773
Chicago/Turabian StyleLeite, Fabio L., Carolina C. Bueno, Alessandra L. Da Róz, Ervino C. Ziemath, and Osvaldo N. Oliveira, Jr. 2012. "Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy" International Journal of Molecular Sciences 13, no. 10: 12773-12856. https://doi.org/10.3390/ijms131012773
APA StyleLeite, F. L., Bueno, C. C., Da Róz, A. L., Ziemath, E. C., & Oliveira, O. N., Jr. (2012). Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy. International Journal of Molecular Sciences, 13(10), 12773-12856. https://doi.org/10.3390/ijms131012773




