On the Several Molecules and Nanostructures of Water
Abstract
:1. Introduction
2. Algebraic Chemistry
- Higher-Order Ionization Potentials: These are rewritten to highlight use of ‘population-generic’ information and ‘element-specific’ information.
- Ionization Potentials of Ions: These are developed here, starting from ‘population-generic information and ‘element-specific’ information.
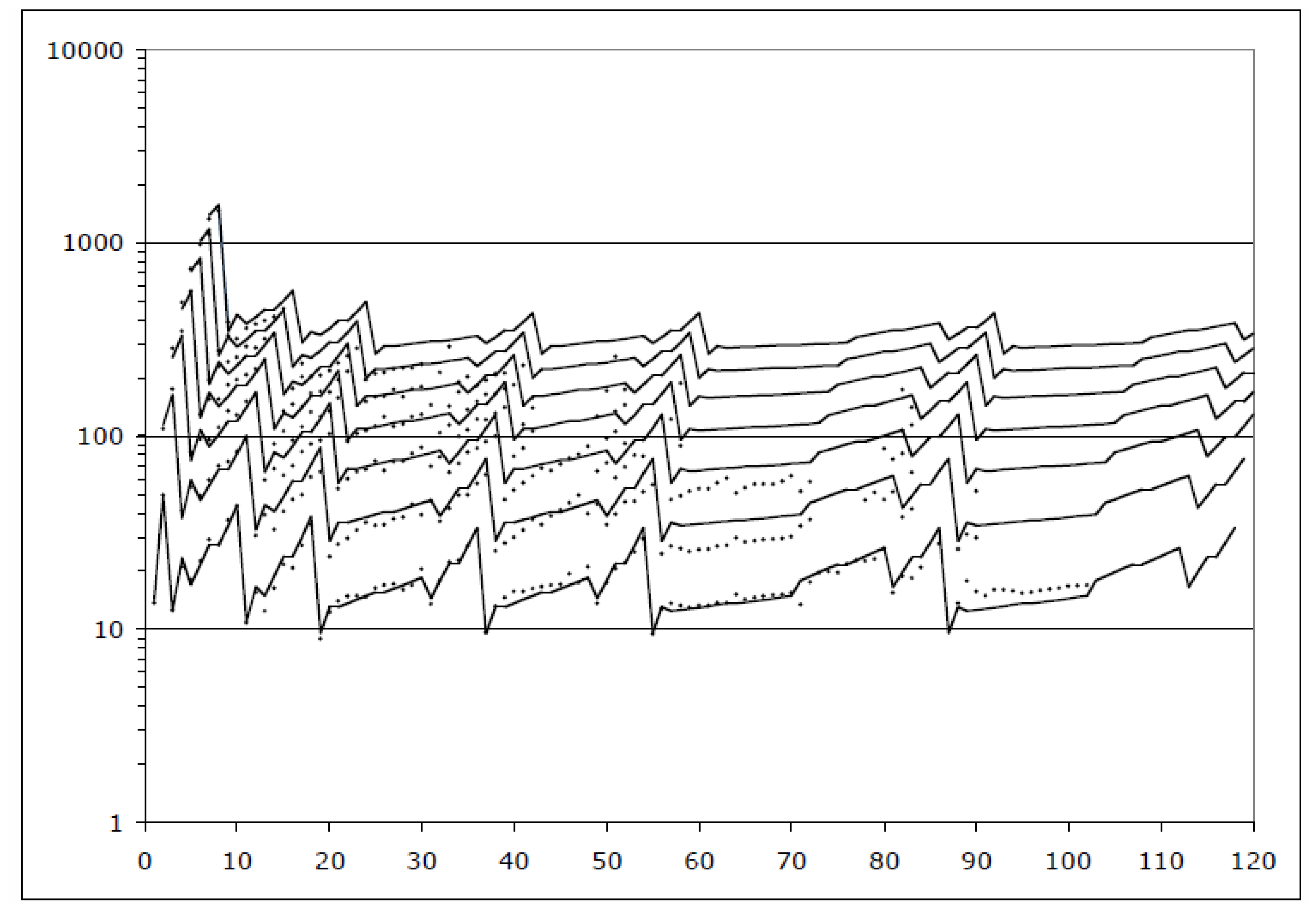
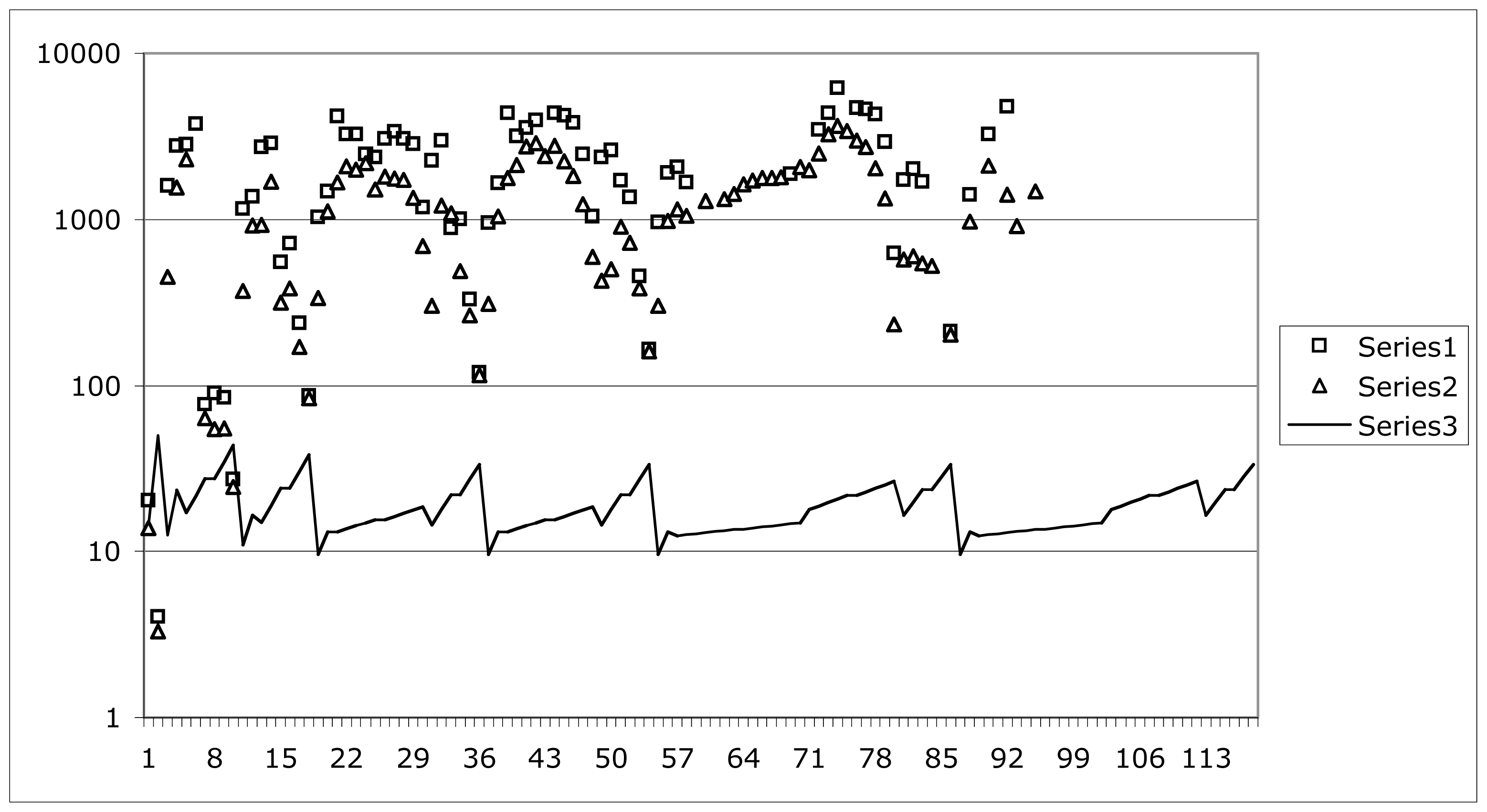
2.1. Patterns in Ionization Potentials
2.2. First-Order Ionization Potentials
2.3. Higher-Order Ionization Potentials
2.4. Ionization Potentials of Ions
3. Ordinary Water
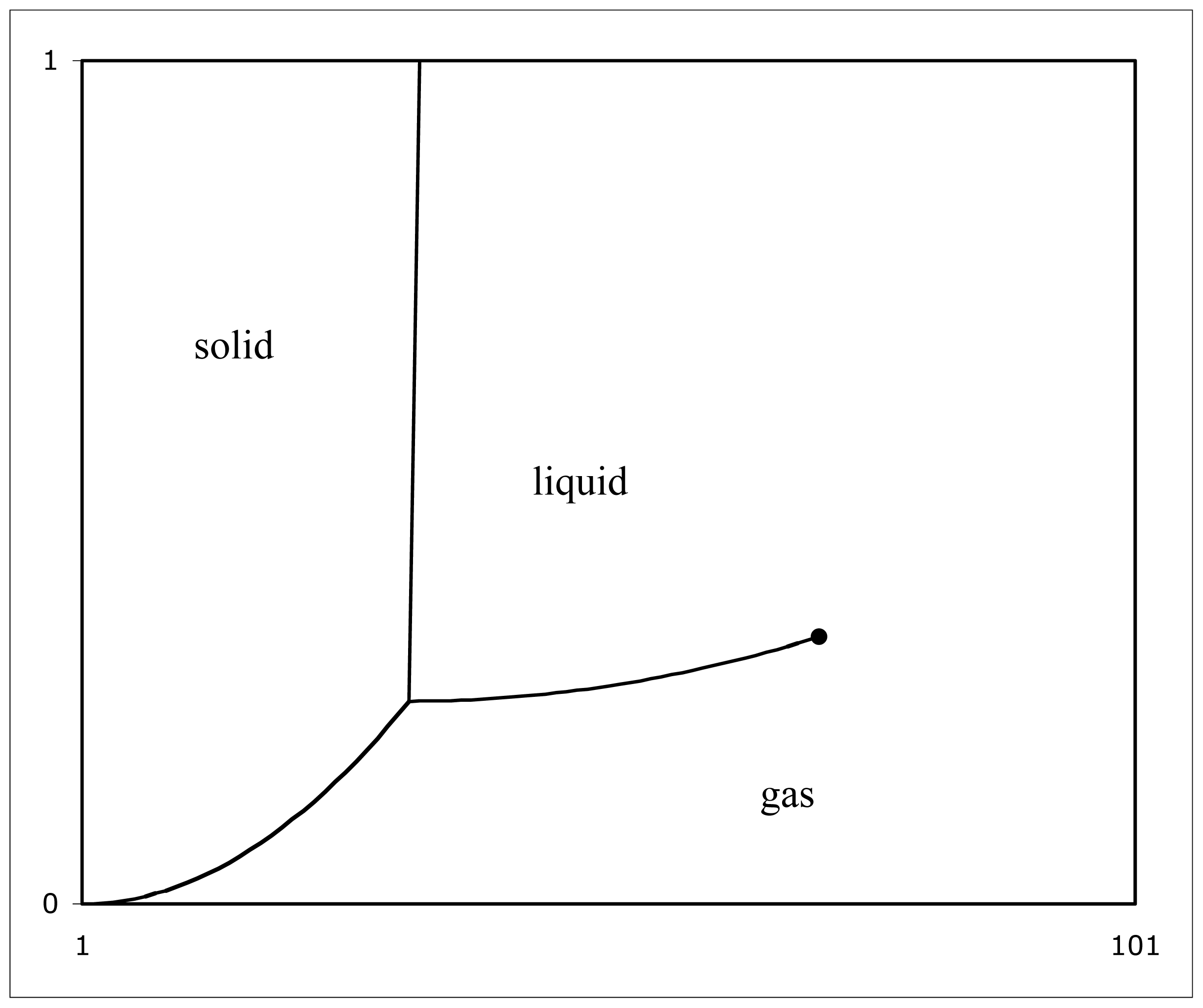
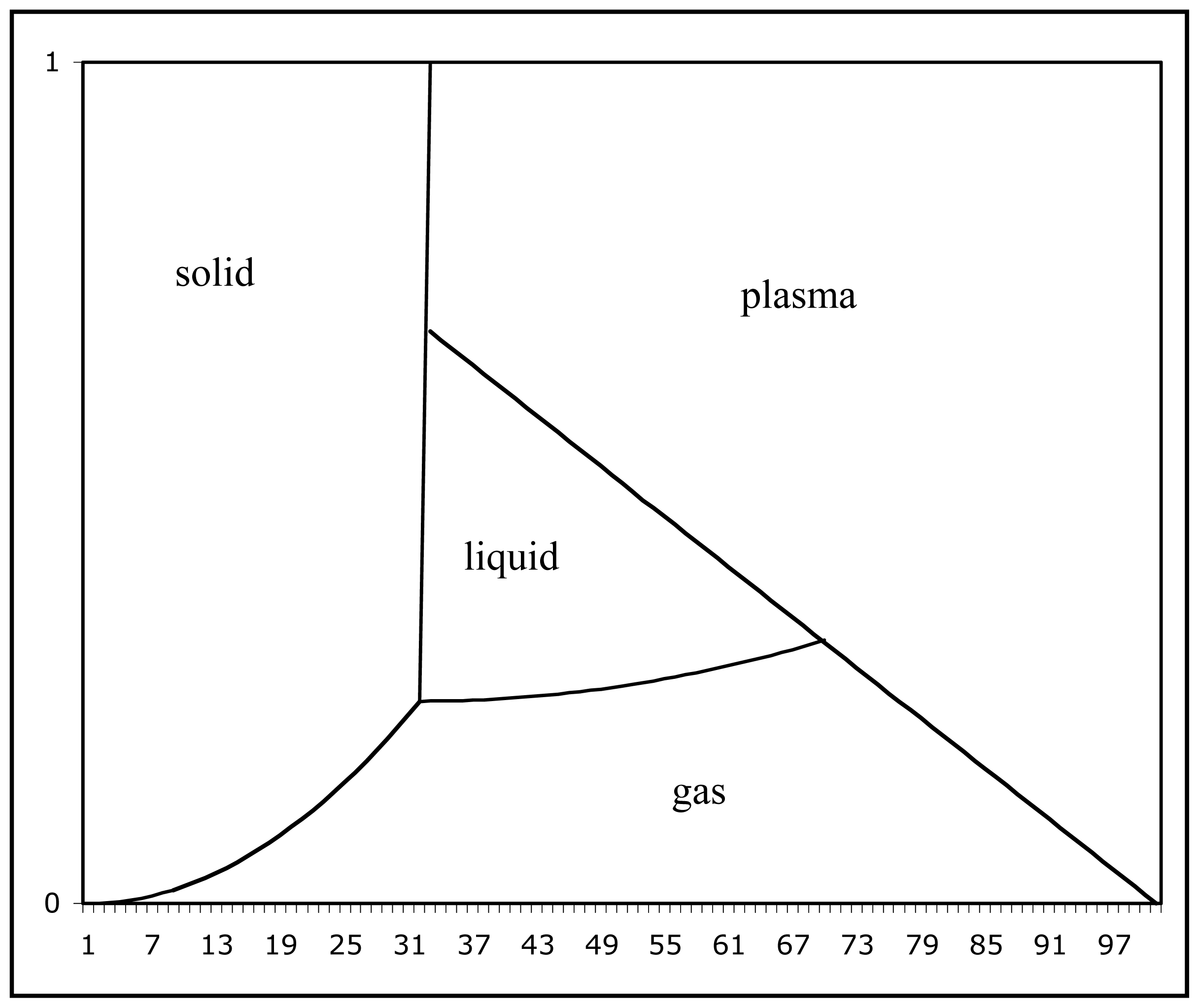
4. Physical States of Water
4.1. Macroscopic Physical States and Microscopic Ionization States
- The solid state involves ions and/or radicals existing in pairs that are in negative energy states;
- The liquid state involves neutral atoms and/or molecules, along with some ions existing in pairs that are mostly in negative energy states;
- The gas state involves neutral atoms and/or molecules, along with some ions existing in pairs that are mostly in positive energy states;
- The plasma state is composed significantly of ions existing in pairs that are in positive energy states.
4.2. Physical States and Ionization States
5. Isomers of Water
5.1. A Linear Isomer of Water
5.2. Isomers of Water Involving Proton Pairs
6. Water Containing Isotopes of Its Constituent Atoms
- Removal of electrons from the immediate environs of nuclei to be fused;
- Forcing of the naked nuclei into proximity sufficient for their attraction by nuclear forces to dominate their natural Coulomb repulsion.
6.1. Data on Isotopes of Hydrogen
6.2. Comments on Cold Fusion
The fact that neutrons are absent from, or at low concentration in, the environs of a purported CF experiment does not mean that there is no fusion occurring.
7. Conclusions
Acknowledgments
References
- Whitney, C.K. Closing in on chemical bonds by opening up relativity theory. Int. J. Mol. Sci 2009, 9, 272–298. [Google Scholar]
- Putz, M.V. Systematic formulations for electronegativity and hardness and their atomic scales within density functional softness theory. Int. J. Quantum Chem 2006, 106, 361–389. [Google Scholar]
- Eckman, C. Plasma orbital expansion of the electrons in water. Proc. NPA 2010, 7, 142–144. [Google Scholar]
- Santilli, R.M. A new gaseous and combustible form of water. Int. J. Hydrogen Energy 2010, in press. [Google Scholar]
- Whitney, C.K. The Algebraic Chemistry of Molecules and Reactons. In Quantum Frontiers of Atoms and Molecules; Putz, M.V., Ed.; Nova Science Publishers: New York, NY, USA, 2011; pp. 227–261. [Google Scholar]
- Scarborough, A.A. Origins of Universal Systems; Trafford Publishing: Victoria, Canada, 2008. [Google Scholar]
- Gordon, F. How Hot Is Cold Fusion? Power-Point Presentation to the Natural Philosophy Allaince, University of California at Long Beach, Long Beach, CA, USA, 23–26 June 2010.
- Tadahiko, M. Nuclear Transmutation: The Reality of Cold Fusion; English translation; Infinite Energy Press: Concord, NH, USA, 1998; p. 72. [Google Scholar]
Appendix 1 Basic data on first-order ionization potentials
| Element | Charge Z | Mass M | Raw Data IP | Scaled Data IP | Model IP | Model ΔIP |
|---|---|---|---|---|---|---|
| H | 1 | 1.008 | 13.610 | 13.718 | 14.250 | 0 |
| He | 2 | 4.003 | 24.606 | 49.244 | 49.875 | 35.625 |
| Li | 3 | 6.941 | 5.394 | 12.480 | 12.480 | −1.781 |
| Be | 4 | 9.012 | 9.326 | 21.011 | 23.327 | 9.077 |
| B | 5 | 10.811 | 8.309 | 17.966 | 17.055 | 2.805 |
| C | 6 | 14.007 | 11.266 | 22.551 | 21.570 | 7.320 |
| N | 7 | 14.007 | 14.544 | 29.101 | 27.281 | 13.031 |
| O | 8 | 15.999 | 13.631 | 27.260 | 27.281 | 13.031 |
| F | 9 | 18.998 | 17.438 | 36.810 | 34.504 | 20.254 |
| Ne | 10 | 20.180 | 21.587 | 43.562 | 43.641 | 29.391 |
| Na | 11 | 22.990 | 5.145 | 10.753 | 10.910 | −3.340 |
| Mg | 12 | 24.305 | 7.656 | 15.506 | 16.565 | 2.315 |
| Al | 13 | 26.982 | 5.996 | 12.444 | 14.923 | 0.673 |
| Si | 14 | 28.086 | 8.154 | 16.357 | 18.874 | 4.624 |
| P | 15 | 30.974 | 10.498 | 21.677 | 23.871 | 9.621 |
| S | 16 | 32.066 | 10.373 | 20.790 | 23.871 | 9.621 |
| CI | 17 | 35.453 | 12.977 | 27.063 | 30.192 | 15.942 |
| Ar | 18 | 39.948 | 15.778 | 35.017 | 38.186 | 23.936 |
| Element | Charge Z | Mass M | Raw Data IP | Scaled Data IP | Model IP | Model Δ IP |
|---|---|---|---|---|---|---|
| K | 19 | 39.098 | 4.346 | 8.944 | 9.546 | −4.704 |
| Ca | 20 | 40.078 | 6.120 | 12.265 | 13.057 | −1.193 |
| Sc | 21 | 44.956 | 6.546 | 14.013 | 13.057 | −1.193 |
| Ti | 22 | 47.867 | 6.826 | 14.851 | 13.638 | −0.612 |
| V | 23 | 50.942 | 6.743 | 14.934 | 14.244 | −0.006 |
| Cr | 24 | 51.996 | 6.774 | 14.676 | 14.877 | 0.627 |
| Mn | 25 | 54.938 | 7.438 | 16.345 | 15.539 | 1.289 |
| Fe | 26 | 55.845 | 7.873 | 16.911 | 15.539 | 1.289 |
| Co | 27 | 58.933 | 7.863 | 17.163 | 16.229 | 1.980 |
| Ni | 28 | 58.693 | 7.645 | 16.026 | 16.951 | 2.701 |
| Cu | 29 | 63.546 | 7.728 | 16.934 | 17.705 | 3.455 |
| Zn | 30 | 65.390 | 9.398 | 20.485 | 18.492 | 4.242 |
| Ga | 31 | 69.723 | 6.006 | 13.509 | 14.494 | 0.244 |
| Ge | 32 | 72.610 | 7.905 | 17.936 | 17.860 | 3.610 |
| As | 33 | 74.922 | 9.824 | 22.303 | 22.007 | 7.757 |
| Se | 34 | 78.960 | 9.761 | 22.669 | 22.007 | 7.757 |
| Br | 35 | 79.904 | 11.826 | 26.998 | 27.116 | 12.866 |
| Kr | 36 | 83.800 | 14.015 | 32.623 | 33.412 | 19.162 |
| Rb | 37 | 85.468 | 4.180 | 9.657 | 9.546 | −4.704 |
| Sr | 38 | 87.620 | 5.695 | 13.132 | 13.057 | −1.193 |
| Y | 39 | 88.906 | 6.390 | 14.567 | 13.057 | −1.193 |
| Zr | 40 | 91.224 | 6.846 | 15.614 | 13.638 | −0.612 |
| Nb | 41 | 92.906 | 6.888 | 15.608 | 14.244 | −0.006 |
| Mo | 42 | 95.940 | 7.106 | 16.232 | 14.877 | 0.627 |
| Tc | 43 | 98.000 | 7.282 | 16.597 | 15.539 | 1.289 |
| Ru | 44 | 101.070 | 7.376 | 16.942 | 15.539 | 1.289 |
| Rh | 45 | 102.906 | 7.469 | 17.080 | 16.230 | 1.980 |
| Pd | 46 | 106.420 | 8.351 | 19.319 | 16.951 | 2.701 |
| Ag | 47 | 107.868 | 7.583 | 17.403 | 17.705 | 3.455 |
| Cd | 48 | 112.411 | 9.004 | 21.087 | 18.492 | 4.242 |
| In | 49 | 114.818 | 5.788 | 13.563 | 14.494 | 0.244 |
| Sn | 50 | 118.710 | 7.355 | 17.462 | 17.860 | 3.610 |
| Sb | 51 | 121.760 | 8.651 | 20.655 | 22.007 | 7.757 |
| Te | 52 | 127.600 | 9.015 | 22.120 | 22.007 | 7.757 |
| I | 53 | 126.904 | 10.456 | 25.037 | 27.116 | 12.866 |
| Xe | 54 | 131.290 | 12.137 | 29.508 | 33.412 | 19.162 |
| Element | Charge Z | Mass M | Raw Data IP | Scaled Data IP | Model IP | Model Δ IP |
|---|---|---|---|---|---|---|
| Cs | 55 | 132.905 | 3.900 | 9.425 | 9.546 | −4.704 |
| Ba | 56 | 137.327 | 5.218 | 12.796 | 13.057 | −1.192 |
| La | 57 | 138.906 | 5.581 | 13.600 | 12.393 | −1.857 |
| Ce | 58 | 140.116 | 5.477 | 13.232 | 12.583 | −1.667 |
| Pr | 59 | 140.908 | 5.425 | 12.957 | 12.776 | −1.474 |
| Nd | 60 | 144.240 | 5.498 | 13.217 | 12.972 | −1.278 |
| Pm | 61 | 145.000 | 5.550 | 13.192 | 13.171 | −1.079 |
| Sm | 62 | 150.360 | 5.633 | 13.660 | 13.374 | −0.876 |
| Eu | 63 | 151.964 | 5.674 | 13.687 | 13.579 | −0.671 |
| Gd | 64 | 157.250 | 6.141 | 15.089 | 13.579 | −0.671 |
| Tb | 65 | 158.925 | 5.851 | 14.305 | 13.787 | −0.463 |
| Dy | 66 | 162.500 | 5.934 | 14.609 | 13.999 | −0.251 |
| Ho | 67 | 164.930 | 6.027 | 14.836 | 14.213 | −0.037 |
| Er | 68 | 167.260 | 6.110 | 15.029 | 14.431 | 0.181 |
| Tm | 69 | 168.934 | 6.183 | 15.137 | 14.653 | 0.403 |
| Yb | 70 | 170.040 | 6.255 | 15.463 | 14.878 | 0.627 |
| Lu | 71 | 174.967 | 5.436 | 13.395 | 17.860 | 3.610 |
| Hf | 72 | 178.490 | 7.054 | 17.487 | 18.755 | 4.505 |
| Ta | 73 | 180.948 | 7.894 | 19.568 | 19.696 | 5.446 |
| W | 74 | 183.840 | 7.988 | 19.844 | 20.684 | 6.434 |
| Re | 75 | 186.207 | 7.884 | 19.574 | 21.721 | 7.471 |
| Os | 76 | 190.230 | 8.714 | 21.811 | 21.721 | 7.471 |
| Ir | 77 | 192.217 | 9.129 | 22.788 | 22.811 | 8.560 |
| Pt | 78 | 195.076 | 9.025 | 22.571 | 23.955 | 9.705 |
| Au | 79 | 196.967 | 9.232 | 23.019 | 25.156 | 10.906 |
| Hg | 80 | 200.530 | 10.446 | 26.184 | 26.418 | 12.168 |
| Tl | 81 | 204.383 | 6.110 | 15.417 | 16.515 | 2.265 |
| Pb | 82 | 207.200 | 7.427 | 18.768 | 19.696 | 5.446 |
| Bi | 83 | 208.980 | 7.293 | 18.361 | 23.490 | 9.240 |
| Po | 84 | 209.000 | 8.423 | 20.958 | 23.490 | 9.240 |
| At | 85 | 210.000 | 28.015 | 13.765 | ||
| Rn | 86 | 222.000 | 10.757 | 27.769 | 33.412 | 19.164 |
| Element | Charge Z | Mass M | Raw Data IP | Scaled Data IP | Model IP | Model ΔIP |
|---|---|---|---|---|---|---|
| Fr | 87 | 223.000 | 9.546 | −4.704 | ||
| Ra | 88 | 226.000 | 5.280 | 13.560 | 13.057 | −1.193 |
| Ac | 89 | 227.000 | 6.950 | 17.727 | 12.393 | −1.857 |
| Th | 90 | 232.038 | 6.089 | 15.699 | 12.583 | −1.667 |
| Pa | 91 | 231.036 | 5.892 | 14.959 | 12.776 | −1.474 |
| U | 92 | 238.029 | 6.203 | 16.050 | 12.972 | −1.277 |
| Np | 93 | 237.000 | 6.276 | 15.994 | 13.171 | −1.079 |
| Pu | 94 | 244.000 | 6.068 | 15.752 | 13.374 | −0.876 |
| Am | 95 | 243.000 | 5.996 | 15.337 | 13.579 | −0.671 |
| Cm | 96 | 247.000 | 6.027 | 15.507 | 13.579 | −0.671 |
| Bk | 97 | 247.000 | 6.234 | 15.875 | 13.787 | −0.463 |
| Cf | 98 | 251.000 | 6.307 | 16.154 | 13.999 | −0.251 |
| Es | 99 | 252.000 | 6.421 | 16.345 | 14.213 | −0.037 |
| Fm | 100 | 257.000 | 6.504 | 16.716 | 14.431 | 0.181 |
| Md | 101 | 258.000 | 6.587 | 16.827 | 14.653 | 0.403 |
| No | 102 | 259.000 | 6.660 | 16.911 | 14.877 | 0.627 |
| Lf | 103 | 17.859 | 3.610 | |||
| Rf | 104 | 18.755 | 4.505 | |||
| Db | 105 | 19.696 | 5.446 | |||
| Sg | 106 | 20.684 | 6.434 | |||
| Bh | 107 | 21.721 | 7.471 | |||
| Hs | 108 | 21.721 | 7.471 | |||
| Mt | 109 | 22.811 | 8.561 | |||
| Ds | 110 | 23.955 | 9.705 | |||
| Rg | 111 | 25.156 | 10.906 | |||
| Cn | 112 | 26.418 | 12.168 | |||
| Uut | 113 | 16.515 | 2.265 | |||
| Uuq | 114 | 17.019 | 2.769 | |||
| Uup | 115 | 23.490 | 9.240 | |||
| Uuh | 116 | 23.490 | 9.240 | |||
| Uus | 117 | 28.015 | 13.765 | |||
| Uuo | 118 | 33.412 | 19.162 |
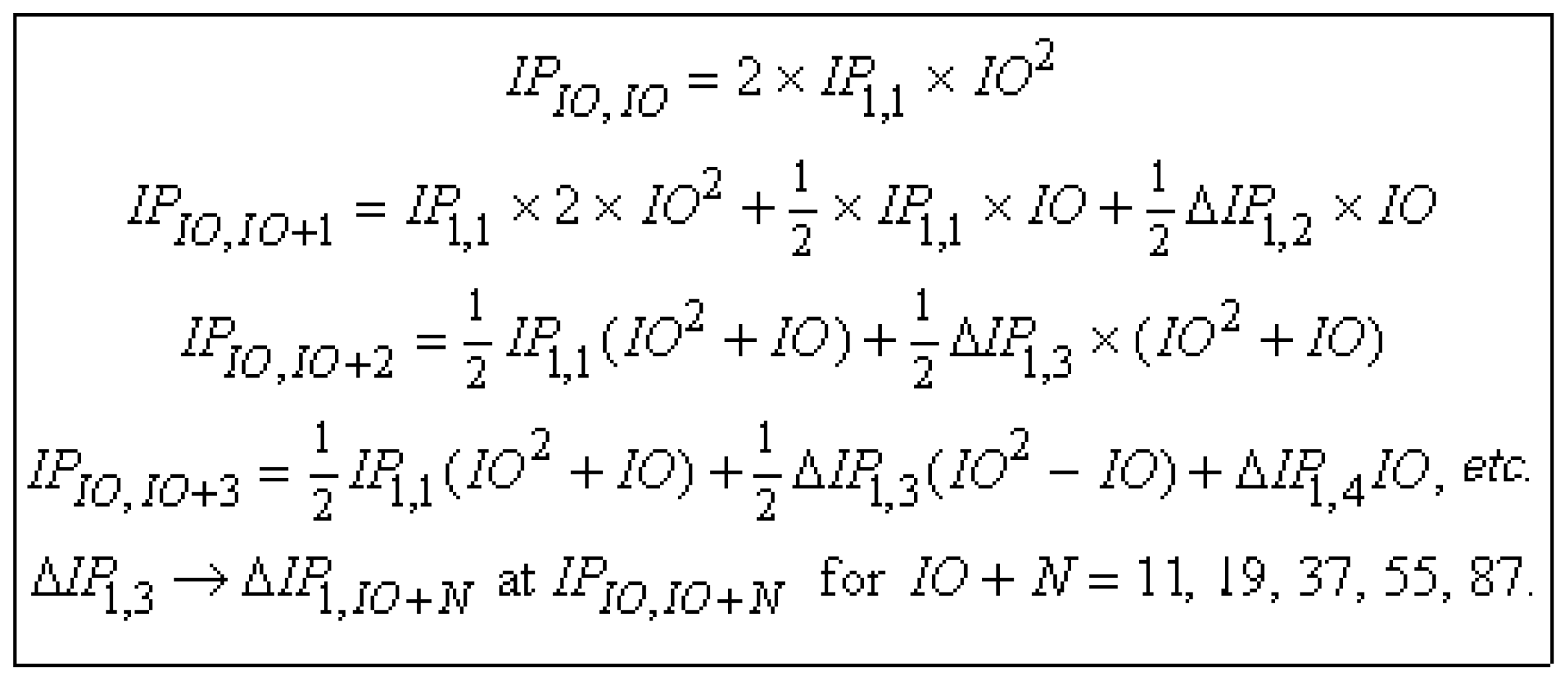
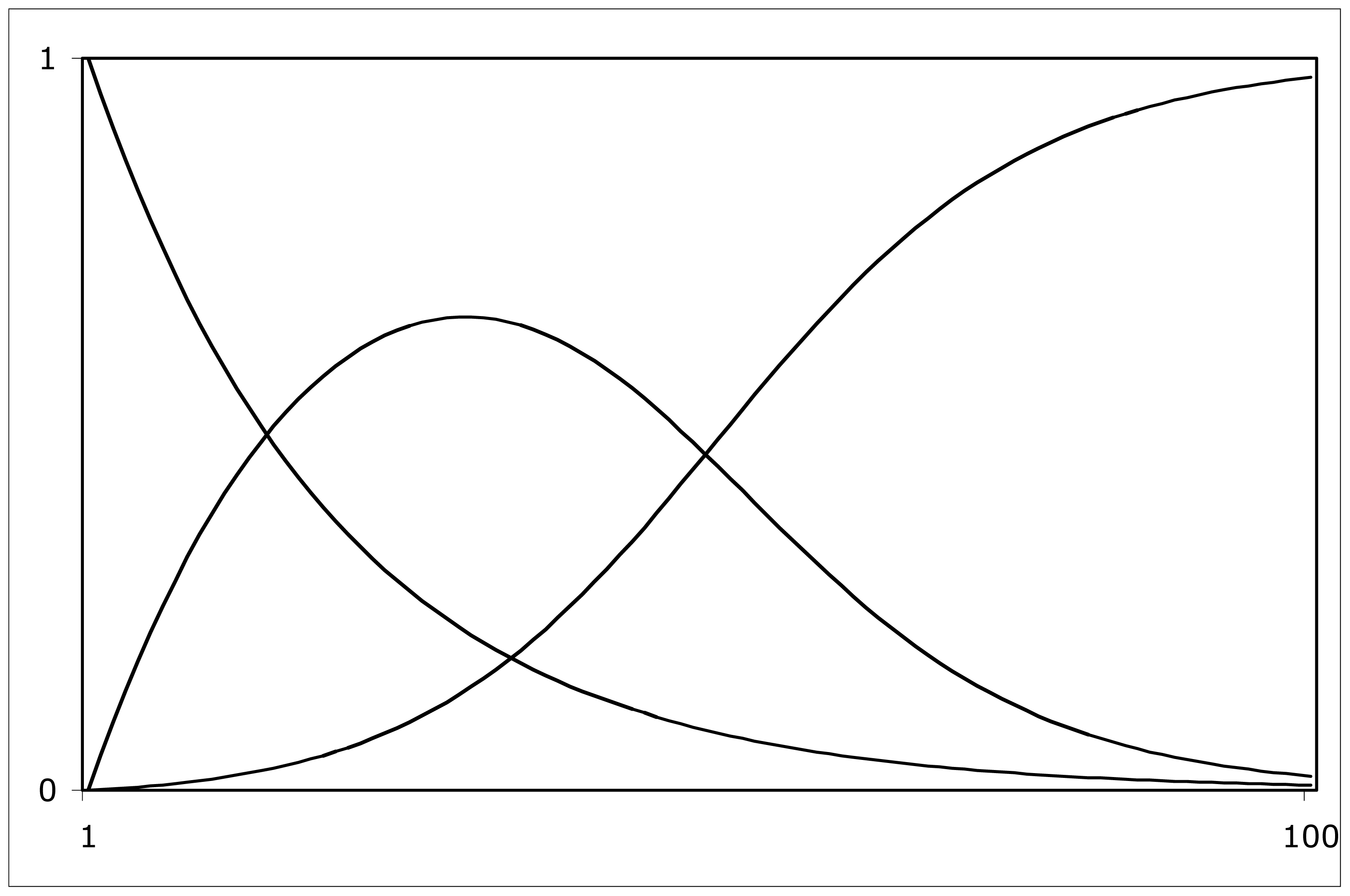
| period | L | N | l | fraction | l | fraction | l | fraction | l | fraction |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 0 | 1 | ||||||
| 2 | 8 | 2 | 0 | 1/2 | 1 | 3/4 | ||||
| 3 | 8 | 2 | 0 | 1/3 | 1 | 3/4 | ||||
| 4 | 18 | 3 | 0 | 1/4 | 2 | 5/18 | 1 | 2/3 | ||
| 5 | 18 | 3 | 0 | 1/4 | 2 | 5/18 | 1 | 2/3 | ||
| 6 | 32 | 4 | 0 | 1/4 | 3 | 7/48 | 2 | 5/16 | 1 | 9/16 |
| 7 | 32 | 4 | 0 | 1/4 | 3 | 7/48 | 2 | 5/16 | 1 | 9/16 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Whitney, C.K. On the Several Molecules and Nanostructures of Water. Int. J. Mol. Sci. 2012, 13, 1066-1094. https://doi.org/10.3390/ijms13011066
Whitney CK. On the Several Molecules and Nanostructures of Water. International Journal of Molecular Sciences. 2012; 13(1):1066-1094. https://doi.org/10.3390/ijms13011066
Chicago/Turabian StyleWhitney, Cynthia Kolb. 2012. "On the Several Molecules and Nanostructures of Water" International Journal of Molecular Sciences 13, no. 1: 1066-1094. https://doi.org/10.3390/ijms13011066




