Droplets Formation and Merging in Two-Phase Flow Microfluidics
Abstract
:1. Introduction
2. Dimensionless Numbers
3. Droplet Formation
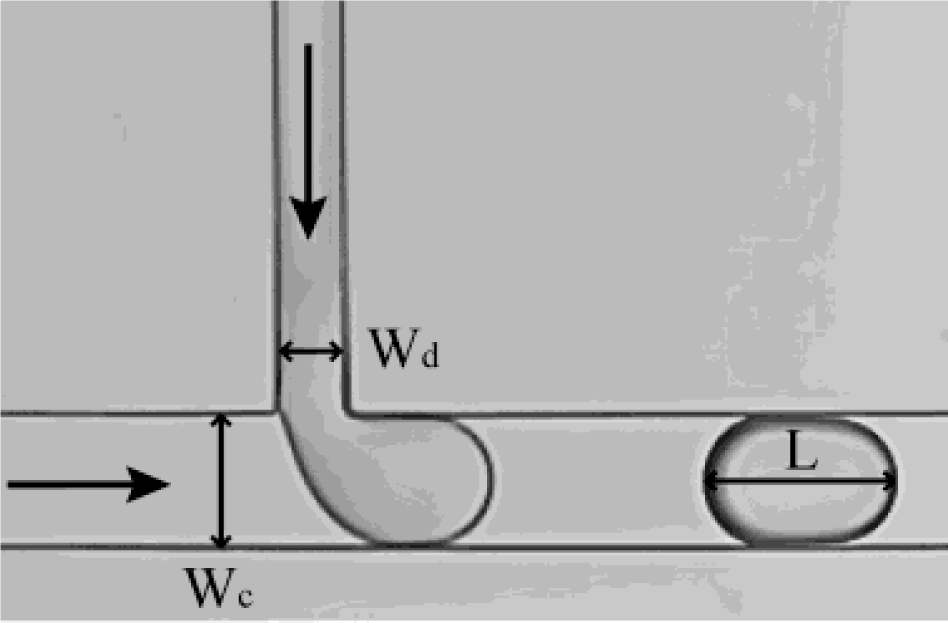
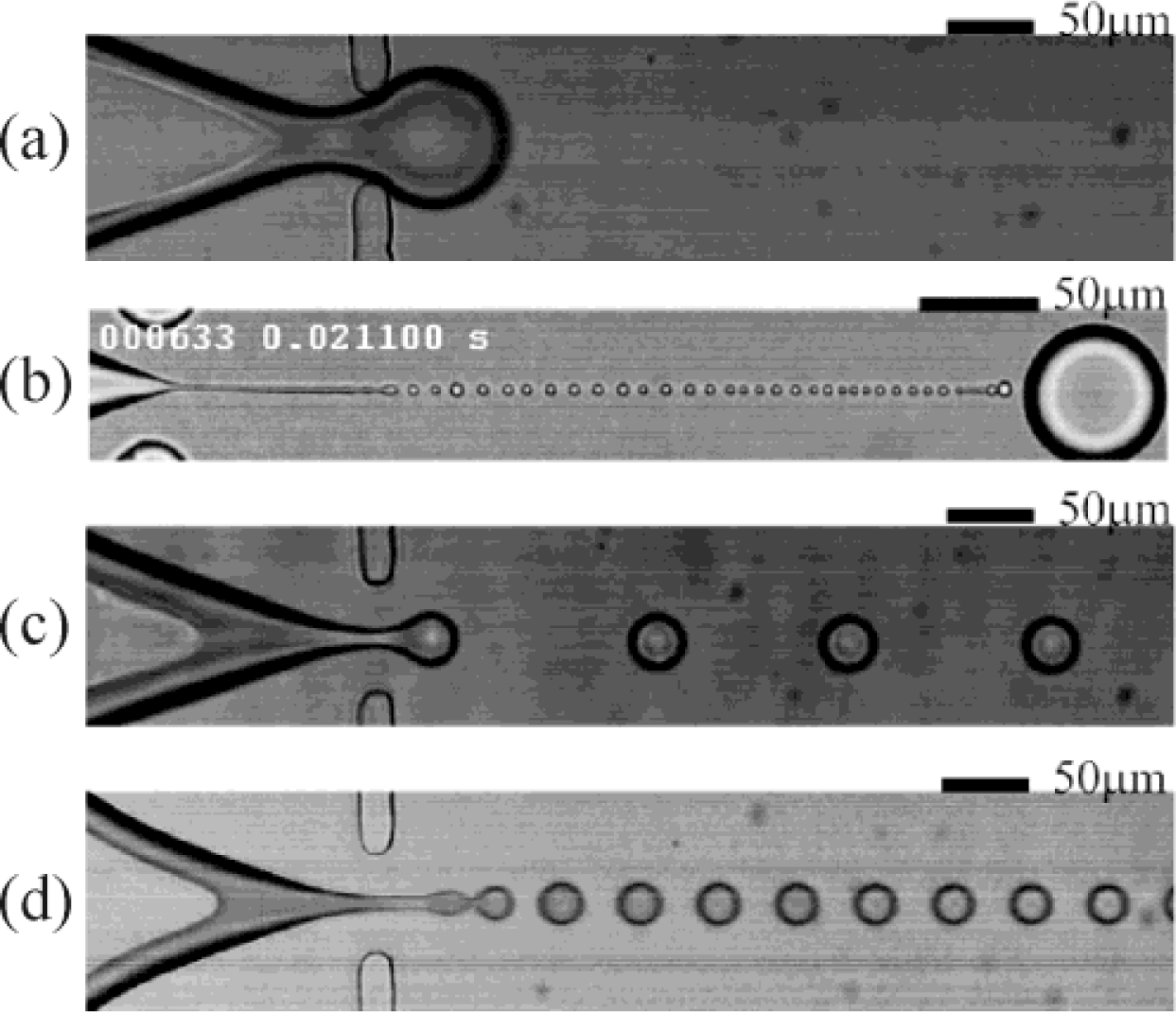
3.1. T-Junction Devices
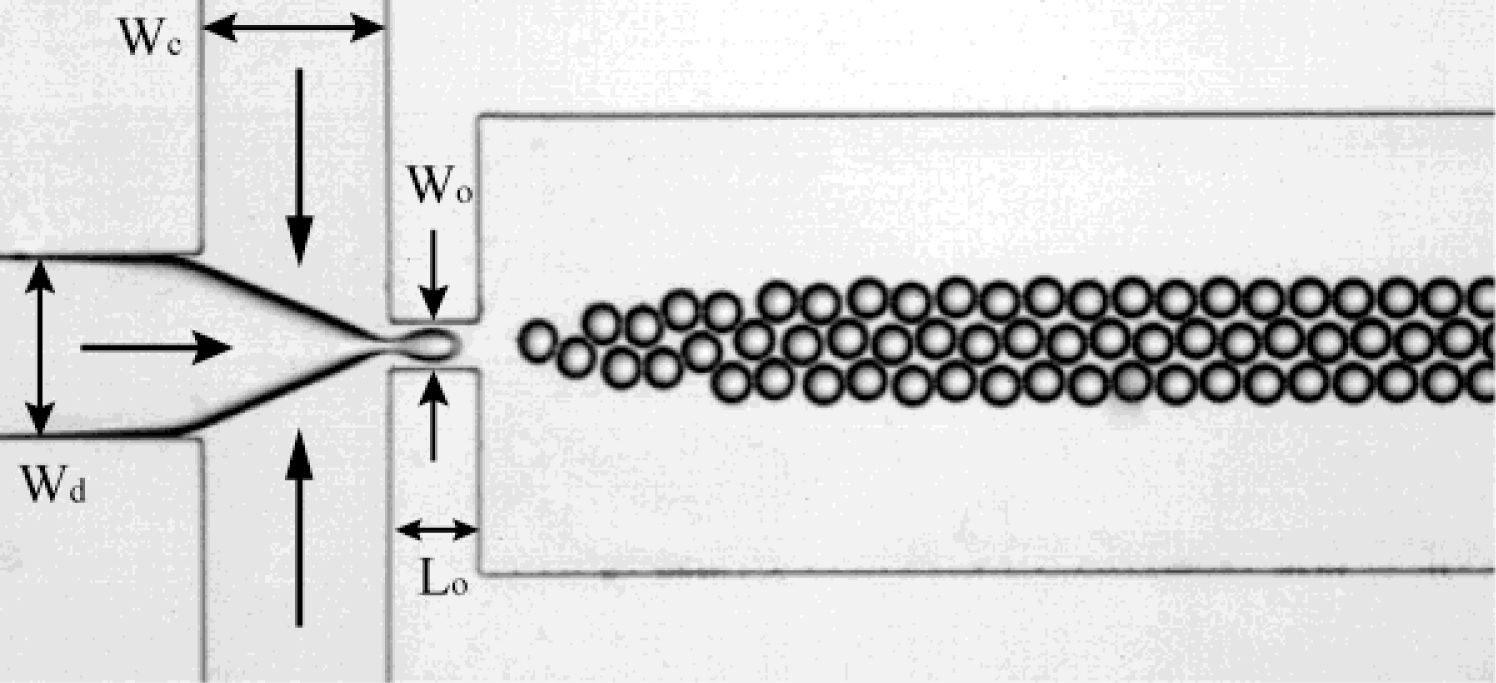
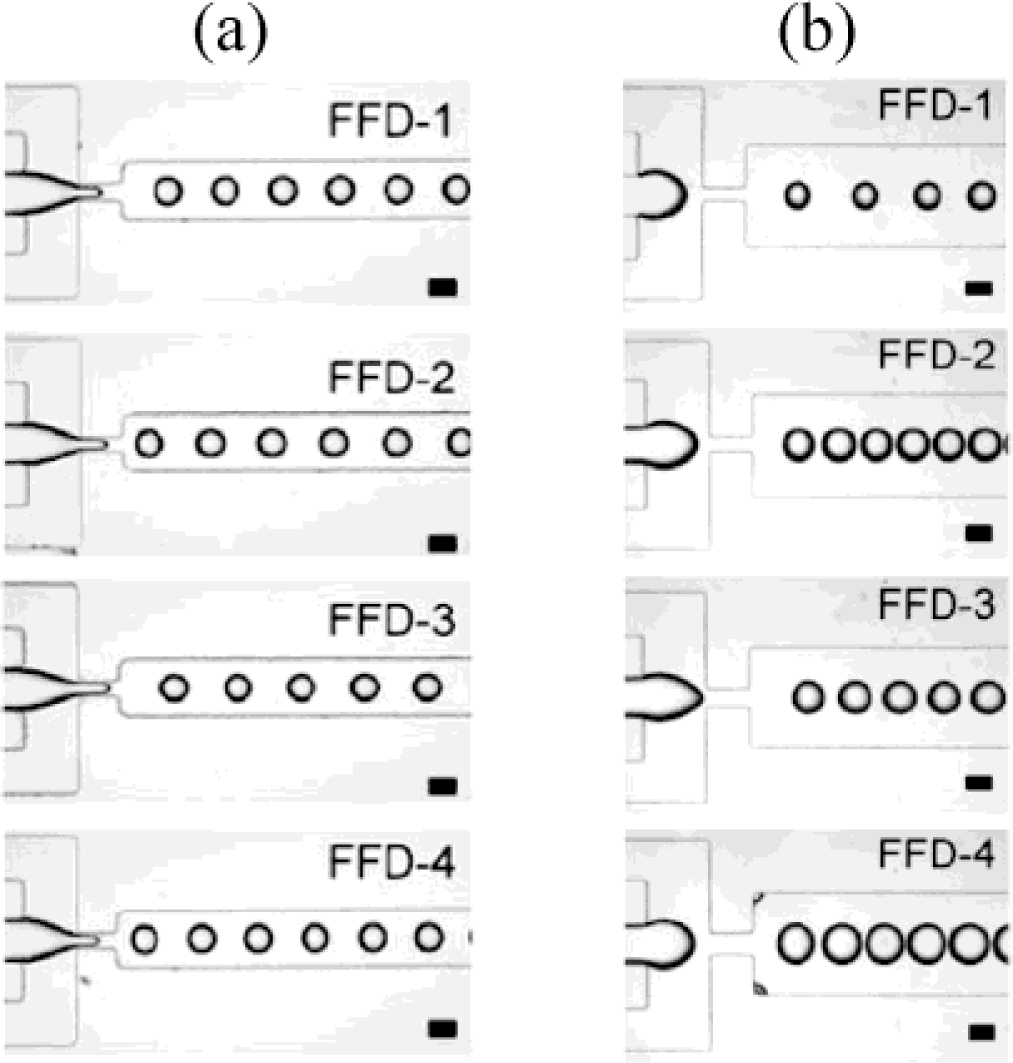
3.2. Flow Focusing Devices
3.3. Droplet Formation Assisted by Active Elements
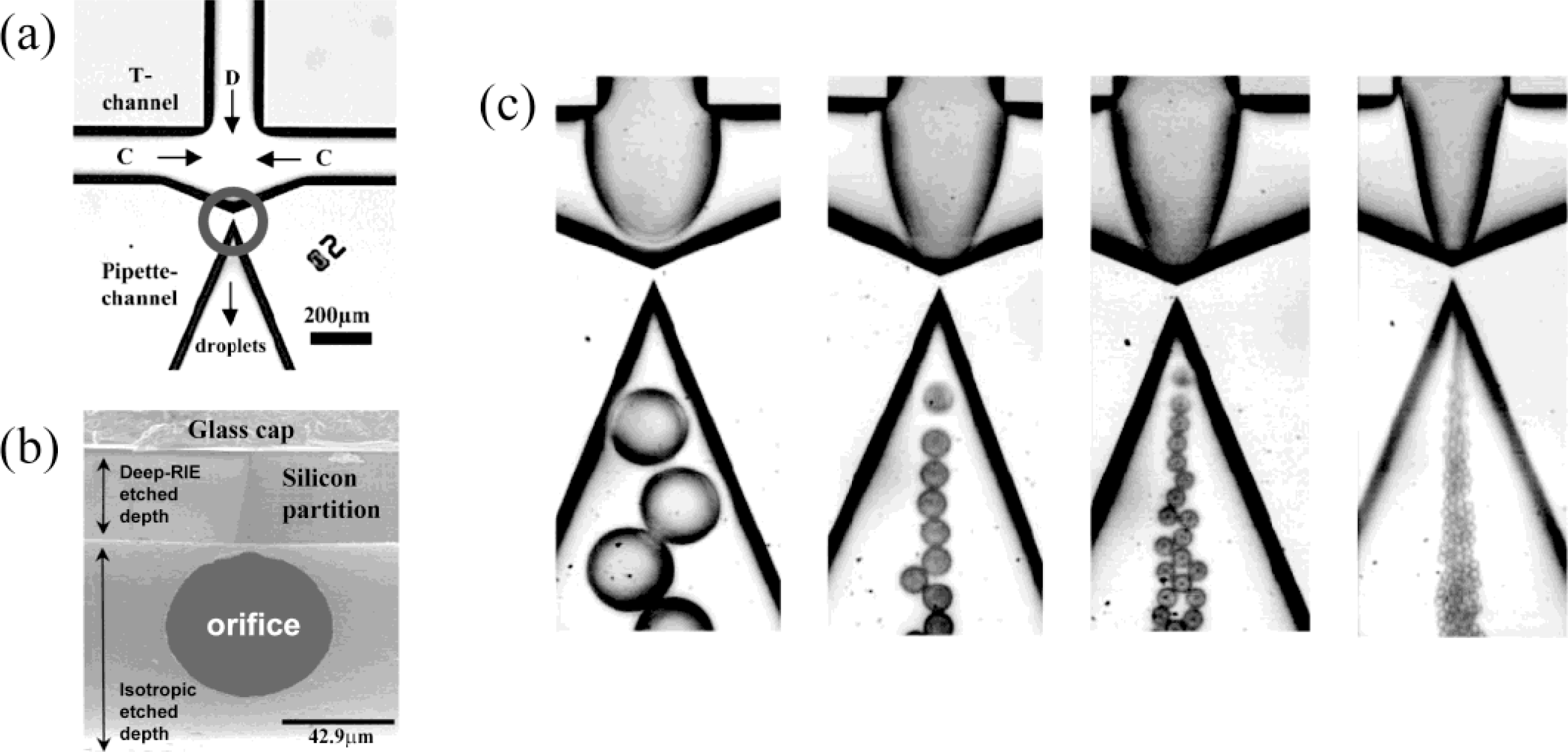
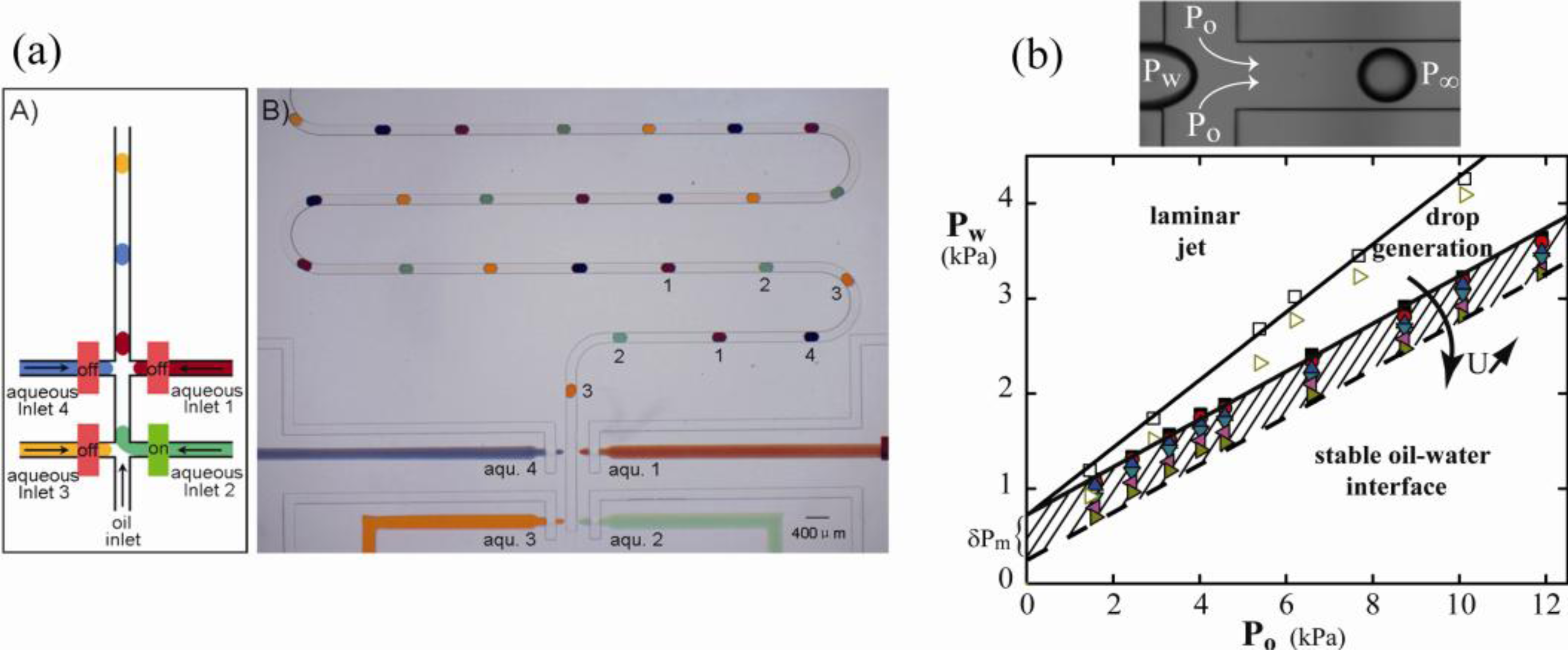
3.4. Droplet-on-Demand
4. Droplet Merging
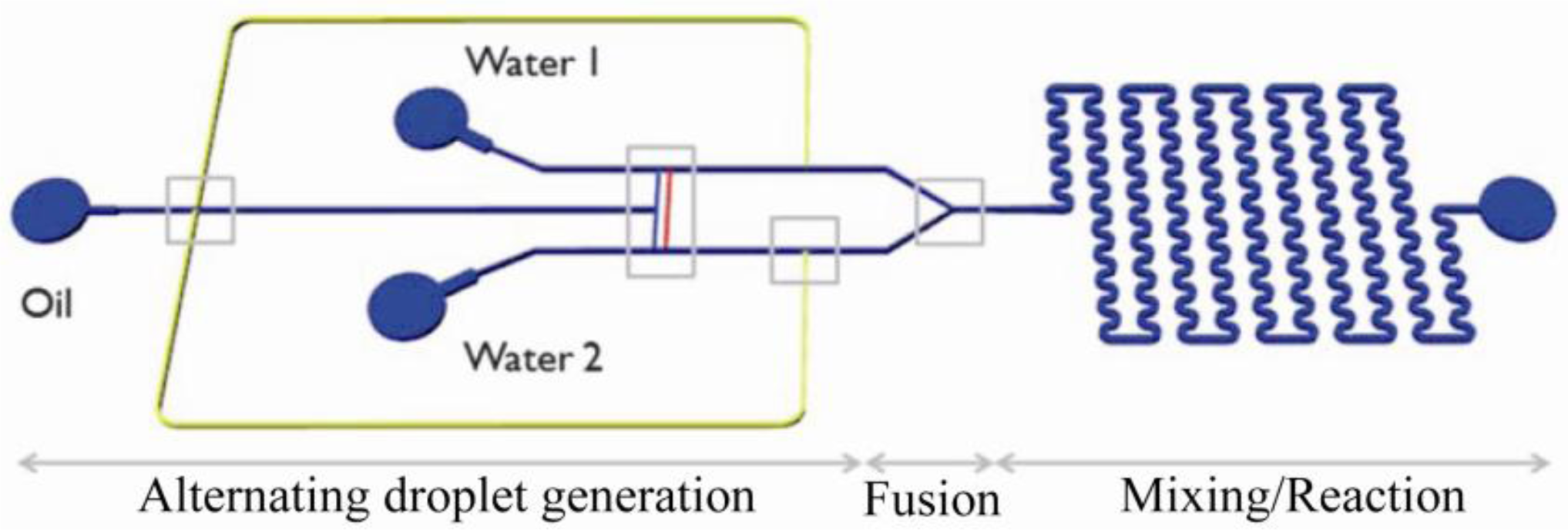
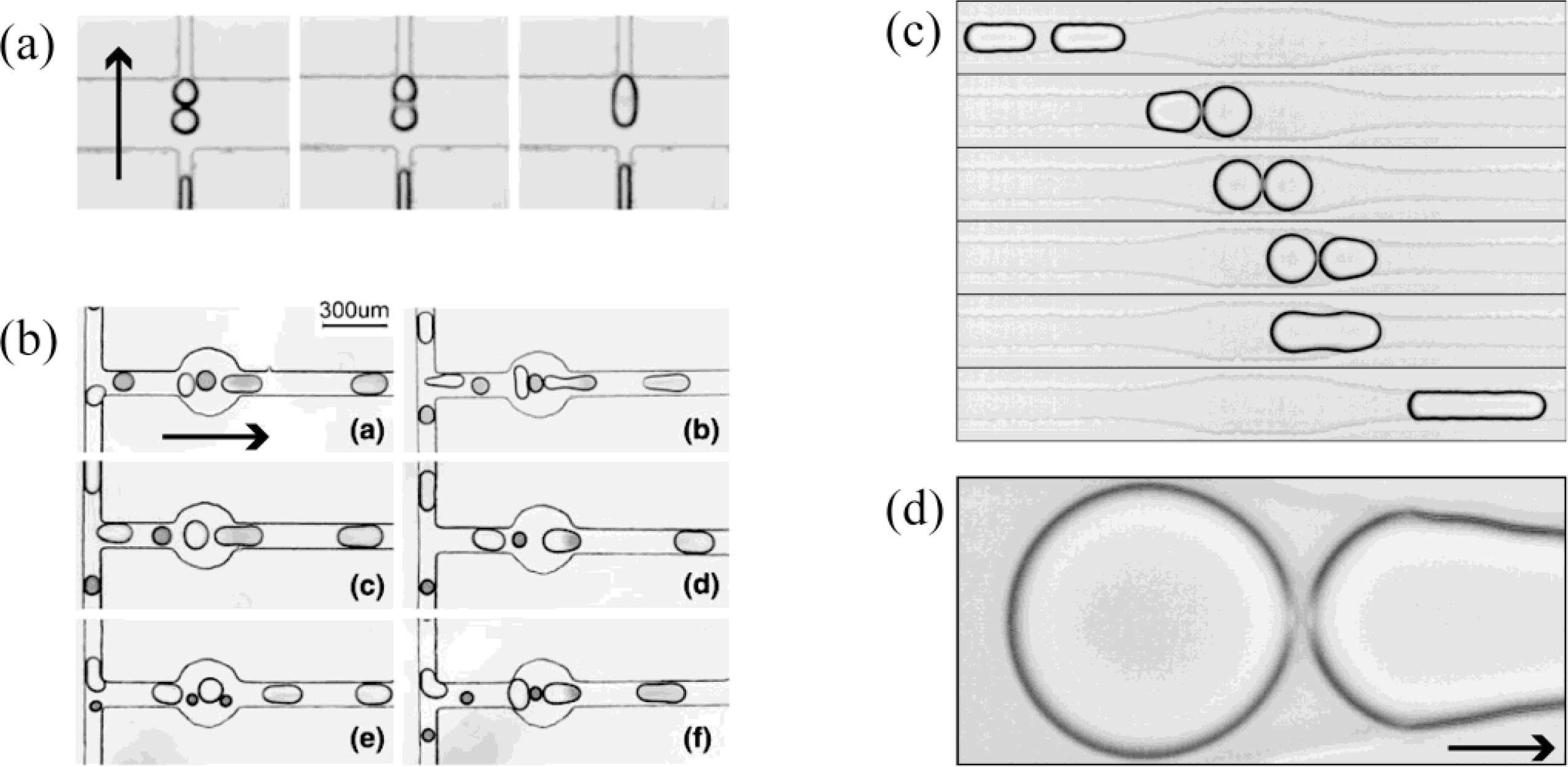
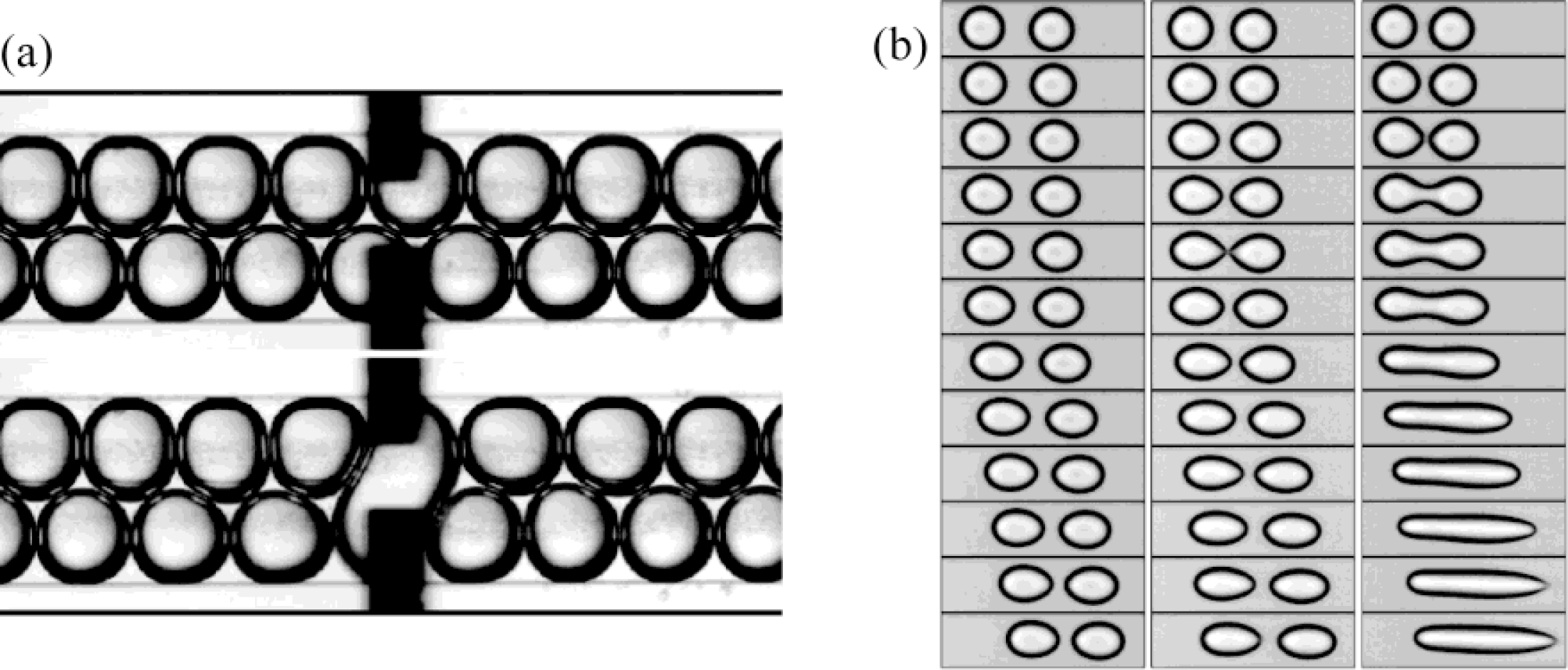
4.1. Passive Merging
4.2. Active Merging
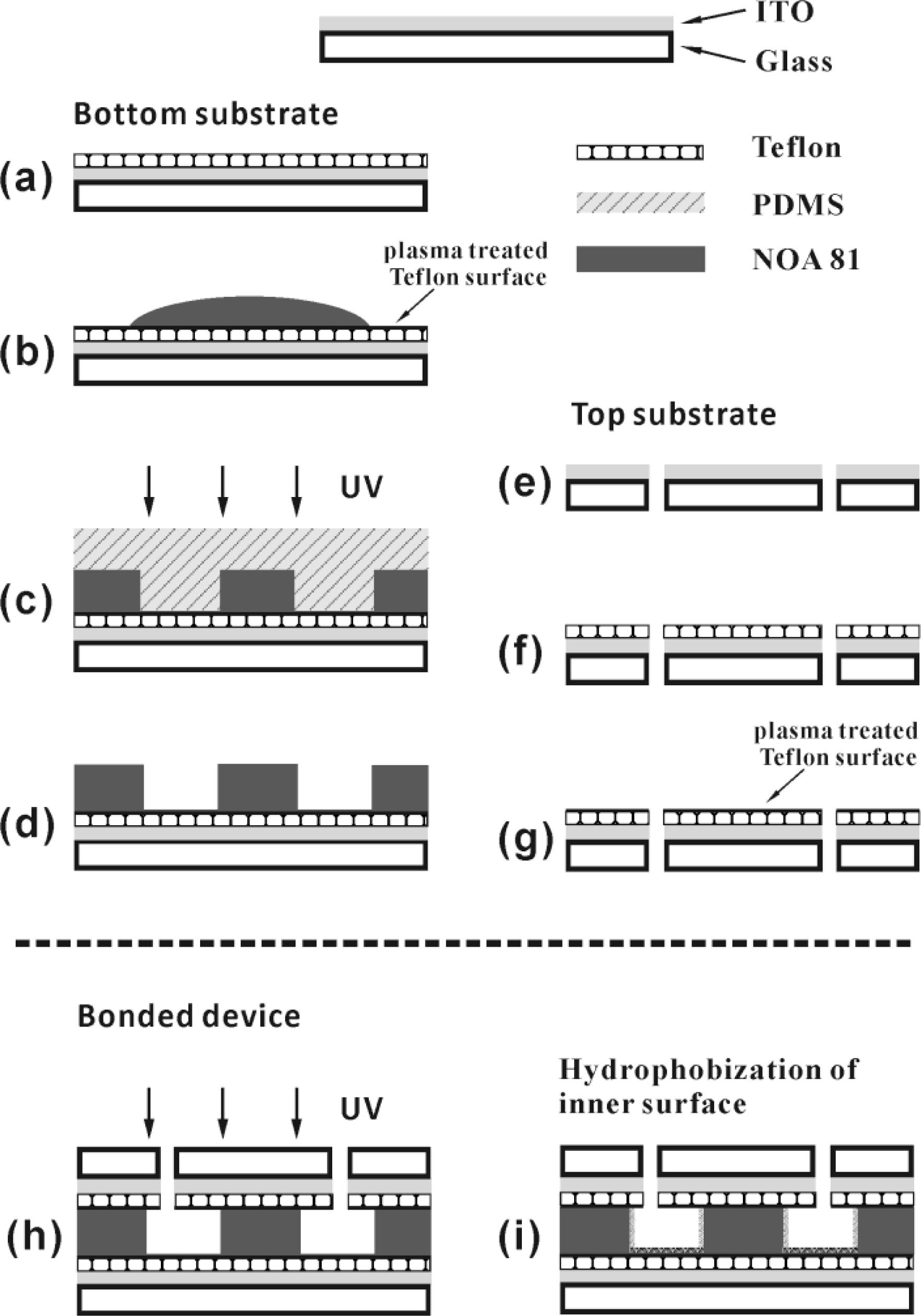
5. Microchannel Fabrication
6. Conclusions
Acknowledgments
References
- Stone, HA; Stroock, AD; Ajdari, A. Engineering flows in small devices: Microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech 2004, 36, 381–411. [Google Scholar]
- Song, H; Chen, DL; Ismagilov, RF. Reactions in droplets in microflulidic channels. Angew. Chem. Int. Ed. Engl 2006, 45, 7336–7356. [Google Scholar]
- Teh, SY; Lin, R; Hung, LH; Lee, AP. Droplet microfluidics. Lab Chip 2008, 8, 198–220. [Google Scholar]
- Mark, D; Haeberle, S; Roth, G; Von Stetten, F; Zengerle, R. Microfluidic lab-on-a-chip platforms: requirements, characteristics and applications. Chem. Soc. Rev 2010, 39, 1153–1182. [Google Scholar]
- Taylor, G. Dispersion of Soluble Matter in Solvent Flowing Slowly through a Tube. Proc. R. Soc. Lond. Ser. A 1953, 219, 186–203. [Google Scholar]
- Fuerstman, MJ; Garstecki, P; Whitesides, GM. Coding/decoding and reversibility of droplet trains in microfluidic networks. Science 2007, 315, 828–832. [Google Scholar]
- Prakash, M; Gershenfeld, N. Microfluidic bubble logic. Science 2007, 315, 832–835. [Google Scholar]
- Schindler, M; Ajdari, A. Droplet traffic in microfluidic networks: A simple model for understanding and designing. Phys Rev Lett 2008, 100, 044501:1–044501:4. [Google Scholar]
- Shui, L; Pennathur, S; Eijkel, JCT; van den Berg, A. Multiphase flow in lab on chip devices: A real tool for the future. Lab Chip 2008, 8, 1010–1014. [Google Scholar]
- Baroud, CN; Gallaire, F; Dangla, R. Dynamics of microfluidic droplets. Lab Chip 2010, 10, 2032–2045. [Google Scholar]
- Theberge, AB; Courtois, F; Schaerli, Y; Fischlechner, M; Abell, C; Hollfelder, F; Huck, WTS. Microdroplets in Microfluidics: An Evolving Platform for Discoveries in Chemistry and Biology. Angew. Chem. Int. Ed 2010, 49, 5846–5868. [Google Scholar]
- Fair, RB. Digital microfluidics: is a true lab-on-a-chip possible? Microfluid Nanofluid 2007, 3, 245–281. [Google Scholar]
- Jebrail, M; Wheeler, A. Let's get digital: digitizing chemical biology with microfluidics. Curr. Opin. Chem. Biol 2010, 14, 574–581. [Google Scholar]
- Fair, RB; Khlystov, A; Tailor, TD; Ivanov, V; Evans, RD; Griffin, PB; Srinivasan, V; Pamula, VK; Pollack, MG; Zhou, J. Chemical and biological applications of digital-microfluidic devices. IEEE Des. Test Comput 2007, 24, 10–24. [Google Scholar]
- Shui, L; Eijkel, JCT; van den Berg, A. Multiphase flow in microfluidic systems—Control and applications of droplets and interfaces. Adv. Colloid Interface 2007, 133, 35–49. [Google Scholar]
- Squires, TM; Quake, SR. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys 2005, 77, 977–1026. [Google Scholar]
- Utada, AS; Fernandez-Nieves, A; Stone, HA; Weitz, DA. Dripping to jetting transitions in coflowing liquid streams. Phys Rev Lett 2007, 99, 094502:1–094502:4. [Google Scholar]
- Stone, HA. Dynamics of Drop Deformation and Breakup in Viscous Fluids. Annu. Rev. Fluid Mech 1994, 26, 65–102. [Google Scholar]
- Guillot, P; Colin, A; Utada, AS; Ajdari, A. Stability of a jet in confined pressure-driven biphasic flows at low reynolds numbers. Phys Rev Lett 2007, 99, 104502:1–104502:4. [Google Scholar]
- Guillot, P; Colin, A; Ajdari, A. Stability of a jet in confined pressure-driven biphasic flows at low Reynolds number in various geometries. Phys Rev E 2008, 78, 016307:1–016307:13. [Google Scholar]
- Thoroddsen, ST; Tan, YK. Free-surface entrainment into a rimming flow containing surfactants. Phys. Fluids 2004, 16, 13–16. [Google Scholar]
- Serizawa, A; Feng, ZP; Kawara, Z. Two-phase flow in microchannels. Exp. Therm. Fluid Sci 2002, 26, 703–714. [Google Scholar]
- Christopher, GF; Anna, SL. Microfluidic methods for generating continuous droplet streams. J. Phys. D Appl. Phys 2007, 40, R319–R336. [Google Scholar]
- van der Graaf, S; Nisisako, T; Schroen, CGPH; van der Sman, RGM; Boom, RM. Lattice Boltzmann simulations of droplet formation in a T-shaped microchannel. Langmuir 2006, 22, 4144–4152. [Google Scholar]
- Gupta, A; Murshed, SMS; Kumar, R. Droplet formation and stability of flows in a microfluidic T-junction. Appl Phys Lett 2009, 94, 164107:1–164107:3. [Google Scholar]
- Dupin, MM; Halliday, I; Care, CM. Simulation of a microfluidic flow-focusing device. Phys Rev E 2006, 73. [Google Scholar]
- Wu, L; Tsutahara, M; Kim, LS; Ha, M. Three-dimensional lattice Boltzmann simulations of droplet formation in a cross-junction microchannel. Int. J. Multiphase Flow 2008, 34, 852–864. [Google Scholar]
- Thorsen, T; Roberts, RW; Arnold, FH; Quake, SR. Dynamic pattern formation in a vesicle-generating microfluidic device. Phys. Rev. Lett 2001, 86, 4163–4166. [Google Scholar]
- Garstecki, P; Fuerstman, MJ; Stone, HA; Whitesides, GM. Formation of droplets and bubbles in a microfluidic T-junction-scaling and mechanism of break-up. Lab Chip 2006, 6, 693–693. [Google Scholar]
- Christopher, GF; Noharuddin, NN; Taylor, JA; Anna, SL. Experimental observations of the squeezing-to-dripping transition in T-shaped microfluidic junctions. Phys Rev E 2008, 78, 036317:1–036317:12. [Google Scholar]
- Jullien, MC; Ching, MJTM; Cohen, C; Menetrier, L; Tabeling, P. Droplet breakup in microfluidic T-junctions at small capillary numbers. Phys Fluids 2009, 21, 072001:1–072001:6. [Google Scholar]
- Wang, K; Lu, YC; Tan, J; Yang, BD; Luo, GS. Generating gas/liquid/liquid three-phase microdispersed systems in double T-junctions microfluidic device. Microfluid Nanofluid 2010, 8, 813–821. [Google Scholar]
- Abate, AR; Poitzsch, A; Hwang, Y; Lee, J; Czerwinska, J; Weitz, DA. Impact of inlet channel geometry on microfluidic drop formation. Phys Rev E 2009, 80, 026310:1–026310:5. [Google Scholar]
- Steegmans, MLJ; Schroen, KGPH; Boom, RM. Characterization of Emulsification at Flat Microchannel Y Junctions. Langmuir 2009, 25, 3396–3401. [Google Scholar]
- Malsch, D; Gleichmann, N; Kielpinski, M; Mayer, G; Henkel, T; Mueller, D; van Steijn, V; Kleijn, CR; Kreutzer, MT. Dynamics of droplet formation at T-shaped nozzles with elastic feed lines. Microfluid Nanofluid 2010, 8, 497–507. [Google Scholar]
- Shui, LL; van den Berg, A; Eijkel, JCT. Interfacial tension controlled W/O and O/W 2-phase flows in microchannel. Lab Chip 2009, 9, 795–801. [Google Scholar]
- Steegmans, MLJ; Warmerdam, A; Schroen, KGPH; Boom, RM. Dynamic Interfacial Tension Measurements with Microfluidic Y-Junctions. Langmuir 2009, 25, 9751–9758. [Google Scholar]
- Song, H; Tice, JD; Ismagilov, RF. A microfluidic system for controlling reaction networks in time. Angew. Chem. Int. Ed 2003, 42, 768–772. [Google Scholar]
- Zheng, B; Tice, JD; Ismagilov, RF. Formation of droplets of in microfluidic channels alternating composition and applications to indexing of concentrations in droplet-based assays. Anal. Chem 2004, 76, 4977–4982. [Google Scholar]
- Wang, KL; Jones, TB; Raisanen, A. DEP actuated nanoliter droplet dispensing using feedback control. Lab Chip 2009, 9, 901–909. [Google Scholar]
- Nisisako, T; Torii, T. Microfluidic large-scale integration on a chip for mass production of monodisperse droplets and particles. Lab Chip 2008, 8, 287–293. [Google Scholar]
- Zeng, Y; Novak, R; Shuga, J; Smith, MT; Mathies, RA. High-Performance Single Cell Genetic Analysis Using Microfluidic Emulsion Generator Arrays. Anal. Chem 2010, 82, 3183–3190. [Google Scholar]
- Tice, JD; Lyon, AD; Ismagilov, RF. Effects of viscosity on droplet formation and mixing in microfluidic channels. Anal. Chim. Acta 2004, 507, 73–77. [Google Scholar]
- Baret, JC; Kleinschmidt, F; El Harrak, A; Griffiths, AD. Kinetic Aspects of Emulsion Stabilization by Surfactants: A Microfluidic Analysis. Langmuir 2009, 25, 6088–6093. [Google Scholar]
- De Menech, M; Garstecki, P; Jousse, F; Stone, HA. Transition from squeezing to dripping in a microfluidic T-shaped junction. J. Fluid Mech 2008, 595, 141–161. [Google Scholar]
- Shui, LL; Mugele, F; van den Berg, A; Eijkel, JCT. Geometry-controlled droplet generation in head-on microfluidic devices. Appl Phys Lett 2008, 93, 153113:1–153113:3. [Google Scholar]
- Shui, L. Two-Phase Flow in Micro and Nanofluidic Devices; University of Twente: Enschede, The Nerthland, 2009. [Google Scholar]
- Hung, LH; Choi, KM; Tseng, WY; Tan, YC; Shea, KJ; Lee, AP. Alternating droplet generation and controlled dynamic droplet fusion in microfluidic device for CdS nanoparticle synthesis. Lab Chip 2006, 6, 174–178. [Google Scholar]
- Barbier, V; Willaime, H; Tabeling, P; Jousse, F. Producing droplets in parallel microfluidic systems. Phys Rev E 2006, 74, 046306:1–046306:4. [Google Scholar]
- Frenz, L; Blouwolff, J; Griffiths, AD; Baret, JC. Microfluidic Production of Droplet Pairs. Langmuir 2008, 24, 12073–12076. [Google Scholar]
- Hong, J; Choi, M; Edel, JB; deMello, AJ. Passive self-synchronized two-droplet generation. Lab Chip 2010, 10, 2702–2709. [Google Scholar]
- Anna, SL; Bontoux, N; Stone, HA. Formation of dispersions using “flow focusing” in microchannels. Appl. Phys. Lett 2003, 82, 364–366. [Google Scholar]
- Dreyfus, R; Tabeling, P; Willaime, H. Ordered and disordered patterns in two-phase flows in microchannels. Phys Rev Lett 2003, 90, 144505:1–144505:4. [Google Scholar]
- Ward, T; Faivre, M; Abkarian, M; Stone, HA. Microfluidic flow focusing: Drop size and scaling in pressure versus flow-rate-driven pumping. Electrophoresis 2005, 26, 3716–3724. [Google Scholar]
- Collins, J; Lee, AP. Control of serial microfluidic droplet size gradient by step-wise ramping of flow rates. Microfluid Nanofluid 2007, 3, 19–25. [Google Scholar]
- Lee, W; Walker, LM; Anna, SL. Role of geometry and fluid properties in droplet and thread formation processes in planar flow focusing. Phys Fluids 2009, 21, 032103:1–032103:14. [Google Scholar]
- Cubaud, T; Mason, TG. Capillary threads and viscous droplets in square microchannels. Phys Fluids 2008, 20, 053302:1–053302:11. [Google Scholar]
- Nie, ZH; Seo, MS; Xu, SQ; Lewis, PC; Mok, M; Kumacheva, E; Whitesides, GM; Garstecki, P; Stone, HA. Emulsification in a microfluidic flow-focusing device: effect of the viscosities of the liquids. Microfluid Nanofluid 2008, 5, 585–594. [Google Scholar]
- Takeuchi, S; Garstecki, P; Weibel, DB; Whitesides, GM. An axisymmetric flow-focusing microfluidic device. Adv. Mater 2005, 17, 1067–1072. [Google Scholar]
- Huang, SH; Tan, WH; Tseng, FG; Takeuchi, S. A monolithically three-dimensional flow-focusing device for formation of single/double emulsions in closed/open microfluidic systems. J. Micromech. Microeng 2006, 16, 2336–2344. [Google Scholar]
- Yobas, L; Martens, S; Ong, WL; Ranganathan, N. High-performance flow-focusing geometry for spontaneous generation of monodispersed droplets. Lab Chip 2006, 6, 1073–1079. [Google Scholar]
- Funfschilling, D; Debas, H; Li, HZ; Mason, TG. Flow-field dynamics during droplet formation by dripping in hydrodynamic-focusing microfluidics. Phys Rev E 2009, 80, 015301:1–015301:4. [Google Scholar]
- Vansaarloos, W. Front Propagation into Unstable States—Marginal Stability as a Dynamical Mechanism for Velocity Selection. Phys. Rev. A 1988, 37, 211–229. [Google Scholar]
- Vansaarloos, W. Front Propagation into Unstable States 2. Linear Versus Nonlinear Marginal Stability and Rate of Convergence. Phys. Rev. A 1989, 39, 6367–6390. [Google Scholar]
- Li, W; Young, EWK; Seo, M; Nie, Z; Garstecki, P; Simmons, CA; Kumacheva, E. Simultaneous generation of droplets with different dimensions in parallel integrated microfluidic droplet generators. Soft Matter 2008, 4, 258–262. [Google Scholar]
- Hashimoto, M; Shevkoplyas, SS; Zasonska, B; Szymborski, T; Garstecki, P; Whitesides, GM. Formation of Bubbles and Droplets in Parallel, Coupled Flow-Focusing Geometries. Small 2008, 4, 1795–1805. [Google Scholar]
- Kim, H; Luo, DW; Link, D; Weitz, DA; Marquez, M; Cheng, ZD. Controlled production of emulsion drops using an electric field in a flow-focusing microfluidic device. Appl Phys Lett 2007, 91, 133106:1–133106:3. [Google Scholar]
- Gu, H; Malloggi, F; Vanapalli, SA; Mugele, F. Electrowetting-enhanced microfluidic device for drop generation. Appl Phys Lett 2008, 93, 183507:1–183507:3. [Google Scholar]
- Gu, H; Duits, MHG; Mugele, F. A hybrid microfluidic chip with electrowetting functionality using ultraviolet (UV)-curable polymer. Lab Chip 2010, 10, 1550–1556. [Google Scholar]
- He, P; Kim, H; Luo, DW; Marquez, M; Cheng, ZD. Low-frequency ac electro-flow-focusing microfluidic emulsification. Appl Phys Lett 2010, 96, 174103:1–174103:3. [Google Scholar]
- Mugele, F; Baret, JC. Electrowetting: From basics to applications. J. Phys.-Condens. Mat 2005, 17, R705–R774. [Google Scholar]
- Link, DR; Grasland-Mongrain, E; Duri, A; Sarrazin, F; Cheng, ZD; Cristobal, G; Marquez, M; Weitz, DA. Electric control of droplets in microfluidic devices. Angew. Chem. Int. Ed 2006, 45, 2556–2560. [Google Scholar]
- Hsiung, SK; Chen, CT; Lee, GB. Micro-droplet formation utilizing microfluidic flow focusing and controllable moving-wall chopping techniques. J. Micromech. Microeng 2006, 16, 2403–2410. [Google Scholar]
- Lee, CY; Lin, YH; Lee, GB. A droplet-based microfluidic system capable of droplet formation and manipulation. Microfluid Nanofluid 2009, 6, 599–610. [Google Scholar]
- Abate, AR; Romanowsky, MB; Agresti, JJ; Weitz, DA. Valve-based flow focusing for drop formation. Appl Phys Lett 2009, 94, 023503:1–023503:3. [Google Scholar]
- Baroud, CN; Delville, JP; Gallaire, F; Wunenburger, R. Thermocapillary valve for droplet production and sorting. Phys Rev E 2007, 75, 046302:1–046302:5. [Google Scholar]
- Nguyen, NT; Ting, TH; Yap, YF; Wong, TN; Chai, JCK; Ong, WL; Zhou, J; Tan, SH; Yobas, L. Thermally mediated droplet formation in microchannels. Appl Phys Lett 2007, 91, 084102:1–084102:3. [Google Scholar]
- Stan, CA; Tang, SKY; Whitesides, GM. Independent Control of Drop Size and Velocity in Microfluidic Flow-Focusing Generators Using Variable Temperature and Flow Rate. Anal. Chem 2009, 81, 2399–2402. [Google Scholar]
- Tan, SH; Nguyen, NT; Yobas, L; Kang, TG. Formation and manipulation of ferrofluid droplets at a microfluidic T-junction. J. Micromech. Microeng 2010, 20, 045004. [Google Scholar]
- Niu, XZ; Zhang, MY; Wu, JB; Wen, WJ; Sheng, P. Generation and manipulation of “smart” droplets. Soft Matter 2009, 5, 576–581. [Google Scholar]
- Murshed, SMS; Tan, SH; Nguyen, NT; Wong, TN; Yobas, L. Microdroplet formation of water and nanofluids in heat-induced microfluidic T-junction. Microfluid Nanofluid 2009, 6, 253–259. [Google Scholar]
- Zeng, SJ; Li, BW; Su, XO; Qin, JH; Lin, BC. Microvalve-actuated precise control of individual droplets in microfluidic devices. Lab Chip 2009, 9, 1340–1343. [Google Scholar]
- Malloggi, F; Vanapalli, SA; Gu, H; van den Ende, D; Mugele, F. Electrowetting-controlled droplet generation in a microfluidic flow-focusing device. J. Phys.-Condens. Matter 2007, 19, 462101. [Google Scholar]
- Willaime, H; Barbier, V; Kloul, L; Maine, S; Tabeling, P. Arnold tongues in a microfluidic drop emitter. Phys Rev Lett 2006, 96, 054501:1–054501:4. [Google Scholar]
- Galas, JC; Bartolo, D; Studer, V. Active connectors for microfluidic drops on demand. New J Phys 2009, 11, 075027:1–075027:11. [Google Scholar]
- Xu, J; Attinger, D. Drop on demand in a microfluidic chip. J Micromech Microeng 2008, 18. [Google Scholar] [CrossRef]
- Bransky, A; Korin, N; Khoury, M; Levenberg, S. A microfluidic droplet generator based on a piezoelectric actuator. Lab Chip 2009, 9, 516–520. [Google Scholar]
- Churski, K; Korczyk, P; Garstecki, P. High-throughput automated droplet microfluidic system for screening of reaction conditions. Lab Chip 2010, 10, 816–818. [Google Scholar]
- Malloggi, F; Gu, H; Banpurkar, AG; Vanapalli, SA; Mugele, F. Electrowetting—A versatile tool for controlling microdrop generation. Eur. Phys. J. E 2008, 26, 91–96. [Google Scholar]
- Tan, YC; Fisher, JS; Lee, AI; Cristini, V; Lee, AP. Design of microfluidic channel geometries for the control of droplet volume, chemical concentration, and sorting. Lab Chip 2004, 4, 292–298. [Google Scholar]
- Tan, YC; Ho, YL; Lee, AP. Droplet coalescence by geometrically mediated flow in microfluidic channels. Microfluid Nanofluid 2007, 3, 495–499. [Google Scholar]
- Liu, K; Ding, HJ; Chen, Y; Zhao, XZ. Droplet-based synthetic method using microflow focusing and droplet fusion. Microfluid Nanofluid 2007, 3, 239–243. [Google Scholar]
- Bremond, N; Thiam, AR; Bibette, J. Decompressing emulsion droplets favors coalescence. Phys Rev Lett 2008, 100, 024501:1–024501:4. [Google Scholar]
- Lin, BC; Su, YC. On-demand liquid-in-liquid droplet metering and fusion utilizing pneumatically actuated membrane valves. J Micromech Microeng 2008, 18. [Google Scholar] [CrossRef]
- Niu, X; Gulati, S; Edel, JB; deMello, AJ. Pillar-induced droplet merging in microfluidic circuits. Lab Chip 2008, 8, 1837–1841. [Google Scholar]
- Christopher, GF; Bergstein, J; End, NB; Poon, M; Nguyen, C; Anna, SL. Coalescence and splitting of confined droplets at microfluidic junctions. Lab Chip 2009, 9, 1102–1109. [Google Scholar]
- Chokkalingam, V; Weidenhof, B; Kramer, M; Herminghaus, S; Seemann, R; Maier, WF. Template-free Preparation of Mesoporous Silica Spheres through Optimized Microfluidics. ChemPhysChem 2010, 11, 2091–2095. [Google Scholar]
- Chokkalingam, V; Weidenhof, B; Kramer, M; Maier, WF; Herminghaus, S; Seemann, R. Optimized droplet-based microfluidics scheme for sol-gel reactions. Lab Chip 2010, 10, 1700–1705. [Google Scholar]
- Hudson, SD; Jamieson, AM; Burkhart, BE. The effect of surfactant on the efficiency of shear-induced drop coalescence. J. Colloid Interface Sci 2003, 265, 409–421. [Google Scholar]
- Mazutis, L; Baret, JC; Griffiths, AD. A fast and efficient microfluidic system for highly selective one-to-one droplet fusion. Lab Chip 2009, 9, 2665–2672. [Google Scholar]
- Sivasamy, J; Chim, YC; Wong, TN; Nguyen, NT; Yobas, L. Reliable addition of reagents into microfluidic droplets. Microfluid Nanofluid 2010, 8, 409–416. [Google Scholar]
- Bibette, J; Morse, DC; Witten, TA; Weitz, DA. Stability-Criteria for Emulsions. Phys. Rev. Lett 1992, 69, 2439–2442. [Google Scholar]
- Amarouchene, Y; Cristobal, G; Kellay, H. Noncoalescing drops. Phys Rev Lett 2001, 8720, 206104:1–206104:4. [Google Scholar]
- Cordero, ML; Burnham, DR; Baroud, CN; McGloin, D. Thermocapillary manipulation of droplets using holographic beam shaping: Microfluidic pin ball. Appl Phys Lett 2008, 93, 034107:1–034107:3. [Google Scholar]
- Priest, C; Herminghaus, S; Seemann, R. Controlled electrocoalescence in microfluidics: Targeting a single lamella. Appl Phys Lett 2006, 89, 134101:1–134101:3. [Google Scholar]
- Zagnoni, M; Baroud, CN; Cooper, JM. Electrically initiated upstream coalescence cascade of droplets in a microfluidic flow. Phys Rev E 2009, 80, 046303:1–046303:9. [Google Scholar]
- Zagnoni, M; Cooper, JM. On-chip electrocoalescence of microdroplets as a function of voltage, frequency and droplet size. Lab Chip 2009, 9, 2652–2658. [Google Scholar]
- Wang, W; Yang, C; Li, CM. Efficient On-Demand Compound Droplet Formation: From Microfluidics to Microdroplets as Miniaturized Laboratories. Small 2009, 5, 1149–1152. [Google Scholar]
- Thiam, AR; Bremond, N; Bibette, J. Breaking of an Emulsion under an ac Electric Field. Phys Rev Lett 2009, 102, 188304:1–188304:4. [Google Scholar]
- Niu, XZ; Gielen, F; deMello, AJ; Edel, JB. Electro-Coalescence of Digitally Controlled Droplets. Anal. Chem 2009, 81, 7321–7325. [Google Scholar]
- Lai, A; Bremond, N; Stone, HA. Separation-driven coalescence of droplets: An analytical criterion for the approach to contact. J. Fluid Mech 2009, 632, 97–107. [Google Scholar]
- Chabert, M; Dorfman, KD; Viovy, JL. Droplet fusion by alternating current (AC) field electrocoalescence in microchannels. Electrophoresis 2005, 26, 3706–3715. [Google Scholar]
- Herminghaus, S. Dynamical instability of thin liquid films between conducting media. Phys. Rev. Lett 1999, 83, 2359–2361. [Google Scholar]
- Mostowfi, F; Khristov, K; Czarnecki, J; Masliyah, J; Bhattacharjee, S. Electric field mediated breakdown of thin liquid films separating microscopic emulsion droplets. Appl Phys Lett 2007, 90, 184102:1–184102:3. [Google Scholar]
- Baygents, JC; Rivette, NJ; Stone, HA. Electrohydrodynamic deformation and interaction of drop pairs. J. Fluid Mech 1998, 368, 359–375. [Google Scholar]
- Davis, MH. Two Charged Spherical Conductors in a Uniform Electric Field: Forces and Field Strength. Q. J. Mech. Appl. Math 1964, 17, 499–511. [Google Scholar]
- Lewis, TJ. A model for bilayer membrane electroporation based on resultant electromechanical stress. IEEE Trans. Dielectr. Electr. Insul 2003, 10, 769–777. [Google Scholar]
- Tan, WH; Takeuchi, S. Timing controllable electrofusion device for aqueous droplet-based microreactors. Lab Chip 2006, 6, 757–763. [Google Scholar]
- Gu, H; Murade, CU; Duits, MHG; Mugele, F. A Microfluidic Platform for On-Demand Formation and Merging of Microdroplets using Electric Control. Biomicrofluidics 2011, 5, 011101:1–011101:6. [Google Scholar]
- Schwartz, JA; Vykoukal, JV; Gascoyne, PRC. Droplet-based chemistry on a programmable micro-chip. Lab Chip 2004, 4, 11–17. [Google Scholar]
- Singh, P; Aubry, N. Transport and deformation of droplets in a microdevice using dielectrophoresis. Electrophoresis 2007, 28, 644–657. [Google Scholar]
- Wang, W; Yang, C; Li, CM. On-demand microfluidic droplet trapping and fusion for on-chip static droplet assays. Lab Chip 2009, 9, 1504–1506. [Google Scholar]
- Lorenz, RM; Edgar, JS; Jeffries, GDM; Zhao, YQ; McGloin, D; Chiu, DT. Vortex-trap-induced fusion of femtoliter-volume aqueous droplets. Anal. Chem 2007, 79, 224–228. [Google Scholar]
- Verneuil, E; Cordero, ML; Gallaire, F; Baroud, CN. Laser-Induced Force on a Microfluidic Drop: Origin and Magnitude. Langmuir 2009, 25, 5127–5134. [Google Scholar]
- Manz, A; Harrison, DJ; Verpoorte, EMJ; Fettinger, JC; Paulus, A; Ludi, H; Widmer, HM. Planar Chips Technology for Miniaturization and Integration of Separation Techniques into Monitoring Systems - Capillary Electrophoresis on a Chip. J. Chromatogr 1992, 593, 253–258. [Google Scholar]
- Fan, ZH; Harrison, DJ. Micromachining of Capillary Electrophoresis Injectors and Separators on Glass Chips and Evaluation of Flow at Capillary Intersections. Anal. Chem 1994, 66, 177–184. [Google Scholar]
- Xia, YN; Whitesides, GM. Soft lithography. Annu. Rev. Mater. Sci 1998, 28, 153–184. [Google Scholar]
- Duffy, DC; McDonald, JC; Schueller, OJA; Whitesides, GM. Rapid prototyping of microfluidic systems in poly(dimethylsiloxane). Anal. Chem 1998, 70, 4974–4984. [Google Scholar]
- Qin, D; Xia, YN; Rogers, JA; Jackman, RJ; Zhao, XM; Whitesides, GM. Microfabrication, microstructures and microsystems. Microsyst. Technol. Chem. Life Sci 1998, 194, 1–20. [Google Scholar]
- Bohl, B; Steger, R; Zengerle, R; Koltay, P. Multi-layer SU-8 lift-off technology for microfluidic devices. J. Micromech. Microeng 2005, 15, 1125–1130. [Google Scholar]
- Belder, D; Ludwig, M. Surface modification in microchip electrophoresis. Electrophoresis 2003, 24, 3595–3606. [Google Scholar]
- Handique, K; Burke, DT; Mastrangelo, CH; Burns, MA. Nanoliter liquid metering in microchannels using hydrophobic patterns. Anal. Chem 2000, 72, 4100–4109. [Google Scholar]
- Rohr, T; Ogletree, DF; Svec, F; Frechet, JMJ. Surface functionalization of thermoplastic polymers for the fabrication of microfluidic devices by photoinitiated grafting. Adv. Funct. Mater 2003, 13, 264–270. [Google Scholar]
- Abate, AR; Lee, D; Do, T; Holtze, C; Weitz, DA. Glass coating for PDMS microfluidic channels by sol-gel methods. Lab Chip 2008, 8, 516–518. [Google Scholar]
- Hu, SW; Ren, XQ; Bachman, M; Sims, CE; Li, GP; Allbritton, NL. Surface-directed, graft polymerization within microfluidic channels. Anal. Chem 2004, 76, 1865–1870. [Google Scholar]
- Willis, PA; Hunt, BD; White, VE; Lee, MC; Ikeda, M; Bae, S; Pelletier, MJ; Grunthaner, FJ. Monolithic Teflon (R) membrane valves and pumps for harsh chemical and low-temperature use. Lab Chip 2007, 7, 1469–1474. [Google Scholar]
- Grover, WH; von Muhlen, MG; Manalis, SR. Teflon films for chemically-inert microfluidic valves and pumps. Lab Chip 2008, 8, 913–918. [Google Scholar]
- Song, YJ; Kumar, CSSR; Hormes, J. Fabrication of an SU-8 based microfluidic reactor on a PEEK substrate sealed by a ‘flexible semi-solid transfer’ (FST) process. J. Micromech. Microeng 2004, 14, 932–940. [Google Scholar]
- Cygan, ZT; Cabral, JT; Beers, KL; Amis, EJ. Microfluidic platform for the generation of organic-phase microreactors. Langmuir 2005, 21, 3629–3634. [Google Scholar]
- Kim, SH; Yang, Y; Kim, M; Nam, SW; Lee, KM; Lee, NY; Kim, YS; Park, S. Simple route to hydrophilic microfluidic chip fabrication using an ultraviolet (UV)-cured polymer. Adv. Funct. Mater 2007, 17, 3493–3498. [Google Scholar]
- Bartolo, D; Degre, G; Nghe, P; Studer, V. Microfluidic stickers. Lab Chip 2008, 8, 274–279. [Google Scholar]
- De Marco, C; Girardo, S; Mele, E; Cingolani, R; Pisignano, D. Ultraviolet-based bonding for perfluoropolyether low aspect-ratio microchannels and hybrid devices. Lab Chip 2008, 8, 1394–1397. [Google Scholar]
- Hung, LH; Lin, R; Lee, AP. Rapid microfabrication of solvent-resistant biocompatible microfluidic devices. Lab Chip 2008, 8, 983–987. [Google Scholar]
- Simms, R; Dubinsky, S; Yudin, A; Kumacheva, E. A method for fabricating microfluidic electrochemical reactors. Lab Chip 2009, 9, 2395–2397. [Google Scholar]
- Gates, BD; Xu, QB; Love, JC; Wolfe, DB; Whitesides, GM. Unconventional nanofabrication. Annu. Rev. Mater. Res 2004, 34, 339–372. [Google Scholar]
- Heckele, M; Schomburg, WK. Review on micro molding of thermoplastic polymers. J. Micromech. Microeng 2004, 14, R1–R14. [Google Scholar]
- Leech, PW; Wu, N; Zhu, Y. Application of dry film resist in the fabrication of microfluidic chips for droplet generation. J Micromech Microeng 2009, 19, 065019:1–065019:6. [Google Scholar]
- Greener, J; Li, W; Ren, J; Voicu, D; Pakharenko, V; Tang, T; Kumacheva, E. Rapid, cost-efficient fabrication of microfluidic reactors in thermoplastic polymers by combining photolithography and hot embossing. Lab Chip 2010, 10, 522–524. [Google Scholar]
- Tsao, CW; DeVoe, DL. Bonding of thermoplastic polymer microfluidics. Microfluid Nanofluid 2009, 6, 1–16. [Google Scholar]





© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gu, H.; Duits, M.H.G.; Mugele, F. Droplets Formation and Merging in Two-Phase Flow Microfluidics. Int. J. Mol. Sci. 2011, 12, 2572-2597. https://doi.org/10.3390/ijms12042572
Gu H, Duits MHG, Mugele F. Droplets Formation and Merging in Two-Phase Flow Microfluidics. International Journal of Molecular Sciences. 2011; 12(4):2572-2597. https://doi.org/10.3390/ijms12042572
Chicago/Turabian StyleGu, Hao, Michel H. G. Duits, and Frieder Mugele. 2011. "Droplets Formation and Merging in Two-Phase Flow Microfluidics" International Journal of Molecular Sciences 12, no. 4: 2572-2597. https://doi.org/10.3390/ijms12042572



