A Classification Study of Respiratory Syncytial Virus (RSV) Inhibitors by Variable Selection with Random Forest
Abstract
:1. Introduction
2. Results and Discussion
2.1. Self-organizing Map
2.2. Selected Descriptors Using VS-RF
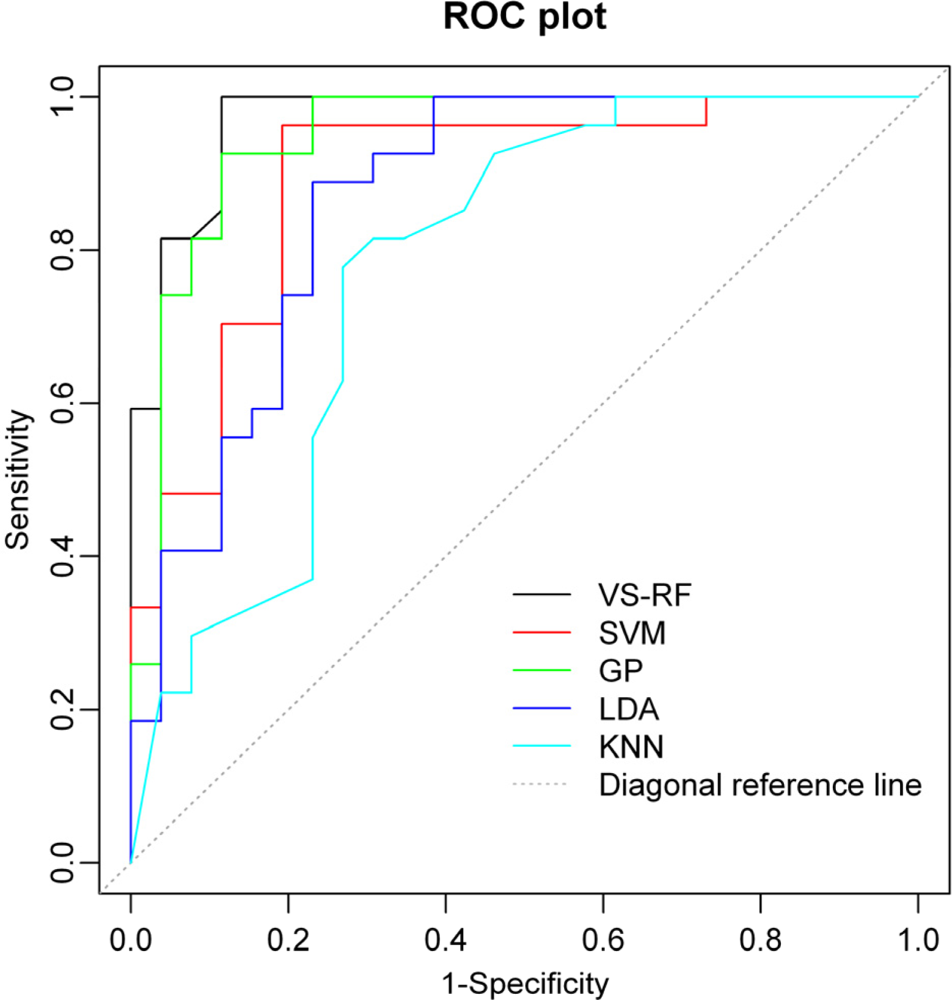
2.3. Performance of Different Statistical Methods
2.4. Comparison of Different Approaches
2.5. Interpretation of the Selected Descriptors
3. Material and Experimental Methods
3.1. Data Sets
3.2. Descriptors Calculation and Pre-processing
3.3. Split of the Training and Test Sets
3.4. Statistical Methods
3.5. Evaluation of the Statistical Performance
4. Conclusions
ijms-12-01259-s001.doc ijms-12-01259-s003.doc
Acknowledgments
References
- Chanock, R; Roizman, B; Myers, R. Recovery from infants with respiratory illness of a virus related to chimpanzee coryza agent (CCA). Am. J. Epidemiol 1957, 66, 281–290. [Google Scholar]
- Cianci, C; Genovesi, E; Lamb, L; Medina, I; Yang, Z; Zadjura, L; Yang, H; D’Arienzo, C; Sin, N; Yu, K. Oral efficacy of a respiratory syncytial virus inhibitor in rodent models of infection. Antimicrob. Agents Chemother 2004, 48, 2448–2454. [Google Scholar]
- Cianci, C; Yu, K; Combrink, K; Sin, N; Pearce, B; Wang, A; Civiello, R; Voss, S; Luo, G; Kadow, K. Orally active fusion inhibitor of respiratory syncytial virus. Antimicrob. Agents Chemother 2004, 48, 413–422. [Google Scholar]
- Greensill, J; McNamara, P; Dove, W; Flanagan, B; Smyth, R; Hart, C. Human metapneumovirus in severe respiratory syncytial virus bronchiolitis. Emerg. Infect. Dis 2003, 9, 372–375. [Google Scholar]
- Sigurs, N; Gustafsson, P; Bjarnason, R; Lundberg, F; Schmidt, S; Sigurbergsson, F; Kjellman, B. Severe respiratory syncytial virus bronchiolitis in infancy and asthma and allergy at age 13. Am. J. Respir. Crit. Care Med 2005, 171, 137–141. [Google Scholar]
- Hart, R. An outbreak of respiratory syncytial virus infection in an old people’s home. J. Infect 1984, 8, 259–261. [Google Scholar]
- Falsey, AR; Hennessey, PA; Formica, MA; Cox, C; Walsh, EE. Respiratory syncytial virus infection in elderly and high-risk adults. N. Engl. J. Med 2005, 352, 1749–1759. [Google Scholar]
- Ding, W-D; Mitsner, B; Krishnamurthy, G; Aulabaugh, A; Hess, CD; Zaccardi, J; Cutler, M; Feld, B; Gazumyan, A; Raifeld, Y; et al. Novel and specific respiratory syncytial virus inhibitors that target virus fusion. J. Med. Chem 1998, 41, 2671–2675. [Google Scholar]
- Sidwell, R; Barnard, D. Respiratory syncytial virus infections: Recent prospects for control. Antiviral Res 2006, 71, 379–390. [Google Scholar]
- Nikitenko, A; Raifeld, Y; Wang, T. The discovery of RFI-641 as a potent and selective inhibitor of the respiratory syncytial virus. Bioorg. Med. Chem. Lett 2001, 11, 1041–1044. [Google Scholar]
- Chapman, J; Abbott, E; Alber, D; Baxter, R; Bithell, S; Henderson, E; Carter, M; Chambers, P; Chubb, A; Cockerill, G. RSV604, a novel inhibitor of respiratory syncytial virus replication. Antimicrob. Agents Chemother 2007, 51, 3346–3353. [Google Scholar]
- Yu, K-L; Zhang, Y; Civiello, RL; Kadow, KF; Cianci, C; Krystal, M; Meanwell, NA. Fundamental structure-activity relationships associated with a new structural class of respiratory syncytial virus inhibitor. Bioorg. Med. Chem. Lett 2003, 13, 2141–2144. [Google Scholar]
- Yu, K-L; Zhang, Y; Civiello, RL; Trehan, AK; Pearce, BC; Yin, Z; Combrink, KD; Gulgeze, HB; Wang, XA; Kadow, KF; et al. Respiratory syncytial virus inhibitors. Part 2: Benzimidazol-2-one derivatives. Bioorg. Med. Chem. Lett 2004, 14, 1133–1137. [Google Scholar]
- Yu, K-L; Wang, XA; Civiello, RL; Trehan, AK; Pearce, BC; Yin, Z; Combrink, KD; Gulgeze, HB; Zhang, Y; Kadow, KF; et al. Respiratory syncytial virus fusion inhibitors. Part 3: Water-soluble benzimidazol-2-one derivatives with antiviral activity in vivo. Bioorg. Med. Chem. Lett 2006, 16, 1115–1122. [Google Scholar]
- Yu, K-L; Sin, N; Civiello, RL; Wang, XA; Combrink, KD; Gulgeze, HB; Venables, BL; Wright, JJK; Dalterio, RA; Zadjura, L; et al. Respiratory syncytial virus fusion inhibitors. Part 4: Optimization for oral bioavailability. Bioorg. Med. Chem. Lett 2007, 17, 895–901. [Google Scholar]
- Wang, XA; Cianci, CW; Yu, K-L; Combrink, KD; Thuring, JW; Zhang, Y; Civiello, RL; Kadow, KF; Roach, J; Li, Z; et al. Respiratory syncytial virus fusion inhibitors. Part 5: Optimization of benzimidazole substitution patterns towards derivatives with improved activity. Bioorg. Med. Chem. Lett 2007, 17, 4592–4598. [Google Scholar]
- Combrink, KD; Gulgeze, HB; Thuring, JW; Yu, K-L; Civiello, RL; Zhang, Y; Pearce, BC; Yin, Z; Langley, DR; Kadow, KF; et al. Respiratory syncytial virus fusion inhibitors. Part 6: An examination of the effect of structural variation of the benzimidazol-2-one heterocycle moiety. Bioorg. Med. Chem. Lett 2007, 17, 4784–4790. [Google Scholar]
- Sin, N; Venables, BL; Combrink, KD; Gulgeze, HB; Yu, K-L; Civiello, RL; Thuring, J; Wang, XA; Yang, Z; Zadjura, L; et al. Respiratory syncytial virus fusion inhibitors. Part 7: Structure-activity relationships associated with a series of isatin oximes that demonstrate antiviral activity in vivo. Bioorg. Med. Chem. Lett 2009, 19, 4857–4862. [Google Scholar]
- Roy, PP; Roy, K. QSAR studies of CYP2D6 inhibitor aryloxypropanolamines using 2D and 3D descriptors. Chem. Biol. Drug Des 2009, 73, 442–455. [Google Scholar]
- Hemmateenejad, B; Miri, R; Akhond, M; Shamsipur, M. QSAR study of the calcium channel antagonist activity of some recently synthesized dihydropyridine derivatives. An application of genetic algorithm for variable selection in MLR and PLS methods. Chemom. Intell. Lab. Syst 2002, 64, 91–99. [Google Scholar]
- Agrafiotis, D; Bandyopadhyay, D; Wegner, J; Van Vlijmen, H. Recent advances in chemoinformatics. J. Chem. Inf. Model 2007, 47, 1279–1293. [Google Scholar]
- Sun, X; Li, Y; Liu, X; Ding, J; Wang, Y; Shen, H; Chang, Y. Classification of bioaccumulative and non-bioaccumulative chemicals using statistical learning approaches. Mol. Divers 2008, 12, 157–169. [Google Scholar]
- Roy, K; Leonard, LT. Classical QSAR modeling of anti-HIV 2,3-diaryl-1,3-thiazolidin-4-ones. QSAR Comb. Sci 2005, 24, 579–592. [Google Scholar]
- Hong, H; Xie, Q; Ge, W; Qian, F; Fang, H; Shi, L; Su, Z; Perkins, R; Tong, W. Mold2, molecular descriptors from 2D structures for chemoinformatics and toxicoinformatics. J. Chem. Inf. Model 2008, 48, 1337–1344. [Google Scholar]
- Hao, M; Li, Y; Wang, Y; Zhang, S. Prediction of PKCθ inhibitory activity using the random forest algorithm. Int. J. Mol. Sci 2010, 11, 3413–3433. [Google Scholar]
- Wang, Y; Li, Y; Wang, B. An in silico method for screening nicotine derivatives as cytochrome P450 2A6 selective inhibitors based on kernel partial least squares. Int. J. Mol. Sci 2007, 8, 166–179. [Google Scholar]
- Wang, Z; Li, Y; Ai, C; Wang, Y. In silico prediction of estrogen receptor subtype binding affinity and selectivity using statistical methods and molecular docking with 2-arylnaphthalenes and 2-arylquinolines. Int. J. Mol. Sci 2010, 11, 3434–3458. [Google Scholar]
- Svetnik, V; Liaw, A; Tong, C; Culberson, JC; Sheridan, RP; Feuston, BP. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci 2003, 43, 1947–1958. [Google Scholar]
- Obrezanova, O; Segall, M. Gaussian processes for classification: QSAR modeling of ADMET and target activity. J. Chem. Inf. Model 2010, 50, 1053–1061. [Google Scholar]
- Zhou, P; Chen, X; Wu, Y; Shang, Z. Gaussian process: An alternative approach for QSAM modeling of peptides. Amino Acids 2010, 38, 199–212. [Google Scholar]
- Li, Y; Wang, Y; Ding, J; Wang, Y; Chang, Y; Zhang, S. In silico prediction of androgenic and nonandrogenic compounds using random forest. QSAR Comb. Sci 2009, 28, 396–405. [Google Scholar]
- Pontes, M; Galvãob, R; Araújo, M; Moreira, P; Neto, O; Joséa, G; Saldanha, T. The successive projections algorithm for spectral variable selection in classification problems. Chemom. Intell. Lab. Syst 2005, 78, 11–18. [Google Scholar]
- Bakken, G; Jurs, P. Classification of multidrug-resistance reversal agents using structure-based descriptors and linear discriminant analysis. J. Med. Chem 2000, 43, 4534–4541. [Google Scholar]
- Pourbasheer, E; Riahi, S; Ganjali, M; Norouzi, P. QSAR study on melanocortin-4 receptors by support vector machine. Eur. J. Med. Chem 2010, 45, 1087–1093. [Google Scholar]
- Doucet, JP; Barbault, F; Xia, HR; Panaye, A; Fan, B. Nonlinear SVM approaches to QSPR/QSAR studies and drug design. Curr. Comput. Aided Drug Des 2007, 3, 263–289. [Google Scholar]
- Díaz-Uriarte, R; Alvarez de Andrés, S. Gene selection and classification of microarray data using random forest. BMC bioinformatics 2006, 7(3). [Google Scholar]
- Vesanto, J; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Networks 2000, 11, 586–600. [Google Scholar]
- Zupan, J; Novič, M; Ruisánchez, I. Kohonen and counterpropagation artificial neural networks in analytical chemistry. Chemom. Intell. Lab. Syst 1997, 38, 1–23. [Google Scholar]
- Eriksson, L; Jaworska, J; Worth, A; Cronin, M; McDowell, R; Gramatica, P. Methods for reliability and uncertainty assessment and for applicability evaluations of classification-and regression-based QSARs. Environ. Health Perspect 2003, 111, 1361–1375. [Google Scholar]
- Kuhn, M. caret: Classification and Regression Training. CRAN: Wien, Austria, 2010; Available online: http://cran.r-project.org/web/packages/caret/index.html (accessed on 11 February 2011).
- Karatzoglou, A; Smola, A; Hornik, K. kernlab: Kernel-based Machine Learning Lab. CRAN: Wien, Austria, 2010; Available online: http://cran.r-project.org/web/packages/kernlab/index.html (accessed on 11 February 2011).
- Burden, F. Quantitative structure-activity relationship studies using gaussian processes. J. Chem. Inf. Comput. Sci 2001, 41, 830–835. [Google Scholar]
- Golbraikh, A; Tropsha, A. Beware of q2! J. Mol. Graph. Model 2002, 20, 269–276. [Google Scholar]
- Triballeau, N; Acher, F; Brabet, I; Pin, J-P; Bertrand, H-O. Virtual screening workflow development guided by the “receiver operating characteristic” curve approach. Application to high-throughput docking on metabotropic glutamate receptor subtype 4. J. Med. Chem 2005, 48, 2534–2547. [Google Scholar]
- Bradley, A. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit 1997, 30, 1145–1159. [Google Scholar]
- Lovasz, L; Pelikan, J. On the eigenvalues of trees. Periodica Mathematica Hungarica 1973, 3, 175–182. [Google Scholar]
- Helguera, AM; Rodriguez-Borges, JE; Garcia-Mera, X; Fernandez, F; Natalia, M; Cordeiro, DS. Probing the anticancer activity of nucleoside analogues: A QSAR model approach using an internally consistent training set. J. Med. Chem 2007, 50, 1537–1545. [Google Scholar]
- Randić, M; Wilkins, C. Graph theoretical approach to recognition of structural similarity in molecules. J. Chem. Inf. Comput. Sci 1979, 19, 31–37. [Google Scholar]
- Saíz-Urra, L; González, M; Teijeira, M. 2D-autocorrelation descriptors for predicting cytotoxicity of naphthoquinone ester derivatives against oral human epidermoid carcinoma. Bioorg. Med. Chem 2007, 15, 3565–3571. [Google Scholar]
- Caballero, J; Garriga, M; Fernández, M. 2D Autocorrelation modeling of the negative inotropic activity of calcium entry blockers using Bayesian-regularized genetic neural networks. Bioorg. Med. Chem 2006, 14, 3330–3340. [Google Scholar]
- Bauknecht, H; Zell, A; Bayer, H; Levi, P; Wagener, M; Sadowski, J; Gasteiger, J. Locating biologically active compounds in medium-sized heterogeneous datasets by topological autocorrelation vectors: Dopamine and benzodiazepine agonists. J. Chem. Inf. Comput. Sci 1996, 36, 1205–1213. [Google Scholar]
- Moreau, G; Broto, P. The autocorrelation of a topological structure: A new molecular descriptor. Nouv. J. Chim 1980, 4, 359–360. [Google Scholar]
- Wagener, M; Sadowski, J; Gasteiger, J. Autocorrelation of molecular surface properties for modeling corticosteroid binding globulin and cytosolic Ah receptor activity by neural networks. J. Am. Chem. Soc 1995, 117, 7769–7775. [Google Scholar]
- Moran, P. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar]
- Galvez, J; Garcia, R; Salabert, MT; Soler, R. Charge indexes. New topological descriptors. J. Chem. Inf. Comput. Sci 1994, 34, 520–525. [Google Scholar]
- ISIS Draw 2.3. MDL Information Systems, Inc.: San Leandro, CA, USA, 2010.
- Golbraikh, A; Tropsha, A. Predictive QSAR modeling based on diversity sampling of experimental datasets for the training and test set selection. J. Comput. Aided Mol. Des 2002, 16, 357–369. [Google Scholar]
- Kohonen, T. The self-organizing map. Proc. Inst. Electrical Electronics Eng 1990, 78, 1464–1480. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
- Polishchuk, PG; Muratov, EN; Artemenko, AG; Kolumbin, OG; Muratov, NN; Kuz’min, VE. Application of random forest approach to QSAR prediction of aquatic toxicity. J. Chem. Inf. Model 2009, 49, 2481–2488. [Google Scholar]
- Palmer, D; O’Boyle, N; Glen, R; Mitchell, J. Random forest models to predict aqueous solubility. J. Chem. Inf. Model 2007, 47, 150–158. [Google Scholar]
- Breiman, L; Cutler, A; Liaw, A; Wiener, M. randomForest: Breiman and Cutler’s Random Forests for Classification and Regression. CRAN: Wien, Austria, 2010; Available online: http://cran.r-project.org/web/packages/randomForest/index.html (accessed on 11 February 2011).
- Diaz-Uriarte, R. varSelRF: Variable Selection Using Random Forests. CRAN: Wien, Austria, 2010; Available online: http://cran.r-project.org/web/packages/varSelRF/index.html (accessed on 11 February 2011).
- Guyon, I; Weston, J; Barnhill, S; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn 2002, 46, 389–422. [Google Scholar]
- Riahi, S; Pourbasheer, E; Dinarvand, R; Ganjali, MR; Norouzi, P. Exploring QSARs for antiviral activity of 4-alkylamino-6-(2-hydroxyethyl)-2-methylthiopyrimidines by support vector machine. Chem. Biol. Drug Des 2008, 72, 205–216. [Google Scholar]
- Kriegl, JM; Arnhold, T; Beck, B; Fox, T. A support vector machine approach to classify human cytochrome P450 3A4 inhibitors. J. Comput. Aided Mol. Des 2005, 19, 189–201. [Google Scholar]
- Furey, T; Cristianini, N; Duffy, N; Bedarski, D; Schummer, M; Haussler, D. Support vector machine classification and validation of cancer tissue samples using microarray expression data. Bioinformatics 2000, 16, 906–914. [Google Scholar]
- Enot, D; Gautier, R; Marouille, J. Gaussian process: An efficient technique to solve quantitative structure-property relationship problems. SAR QSAR Environ. Res 2001, 12, 461–469. [Google Scholar]
- Tiño, P; Nabney, IT; Williams, BS; Lösel, J; Sun, Y. Nonlinear prediction of quantitative structure-activity relationships. J. Chem. Inf. Comput. Sci 2004, 44, 1647–1653. [Google Scholar]
- Schwaighofer, A; Schroeter, T; Mika, S; Laub, J; Ter Laak, A; Sülzle, D; Ganzer, U; Heinrich, N; Müller, K. Accurate solubility prediction with error bars for electrolytes: A machine learning approach. J. Chem. Inf. Model 2007, 47, 407–424. [Google Scholar]
- Schroeter, T; Schwaighofer, A; Mika, S; Ter Laak, A; Suelzle, D; Ganzer, U; Heinrich, N; Müller, K. Predicting lipophilicity of drug-discovery molecules using gaussian process models. Chem. Med. Chem 2007, 2, 1265–1267. [Google Scholar]
- Obrezanova, O; Csányi, G; Gola, JMR; Segall, MD. Gaussian processes: A method for automatic QSAR modeling of ADME properties. J. Chem. Inf. Model 2007, 47, 1847–1857. [Google Scholar]
- Chen, T; Morris, J; Martin, E. Gaussian process regression for multivariate spectroscopic calibration. Chemom. Intell. Lab. Syst 2007, 87, 59–71. [Google Scholar] [Green Version]
- MASS: Main Package of Venables and Ripley’s MASS. CRAN: Wien, Austria, 2010; Available online: http://cran.r-project.org/web/packages/MASS/index.html (accessed on 11 February 2011).
- Gunturi, SB; Narayanan, R. In silico ADME modeling 3: Computational models to predict human intestinal absorption using sphere exclusion and kNN QSAR methods. QSAR Comb. Sci 2007, 26, 653–668. [Google Scholar]

| Descriptor | Definition | Class |
|---|---|---|
| D299 | The largest eigenvalue | Eigenvalue-based indices |
| D347 | Molecular topological path index of order 07 | Walk and path counts |
| D490 | Moran topological structure autocorrelation length-4 weighted by atomic van der Waals volumes | 2D autocorrelation |
| D503 | Moran topological structure autocorrelation length-1 weighted by atomic polarizabilities | 2D autocorrelation |
| D513 | Molecular topological order-3 charge index | Topological charge indices |
| D528 | Mean molecular topological order-8 charge index | Topological charge indices |
| Model | High active inhibitors | Low active inhibitors | Q (%) | MCC | F | Qcv (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| TP | FN | SE (%) | TN | FP | SP (%) | |||||
| VS-RF | 27 | 0 | 100 | 23 | 3 | 88.46 | 94.34 | 0.89 | 0.96 | 81.6 |
| SVM | 23 | 4 | 85.19 | 21 | 5 | 80.77 | 83.02 | 0.66 | 0.84 | 79.1 |
| GP | 27 | 0 | 100 | 20 | 6 | 76.92 | 88.68 | 0.79 | 0.9 | 78 |
| LDA | 20 | 7 | 74.07 | 21 | 5 | 80.77 | 77.36 | 0.55 | 0.77 | 67.5 |
| kNN | 22 | 5 | 81.48 | 17 | 9 | 65.38 | 73.58 | 0.48 | 0.76 | 72.9 |
| High active inhibitors | Low active inhibitors | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | TP | FN | SE(%) | TN | FP | SP(%) | Q(%) | Qcv | Time cost (s) | |
| Training set | RF | 82 | 0 | 100 | 81 | 0 | 100 | 100 | 0.816 | 171.42 |
| VS-RF | 82 | 0 | 100 | 81 | 0 | 100 | 100 | 0.816 | 8.06 | |
| Test set | RF | 25 | 2 | 92.59 | 23 | 3 | 88.46 | 90.57 | - | - |
| VS-RF | 27 | 0 | 100 | 23 | 3 | 88.46 | 94.34 | - | - | |
| No. | Structure | pEC50 | Classb | Ref.a |
|---|---|---|---|---|
| 1 | 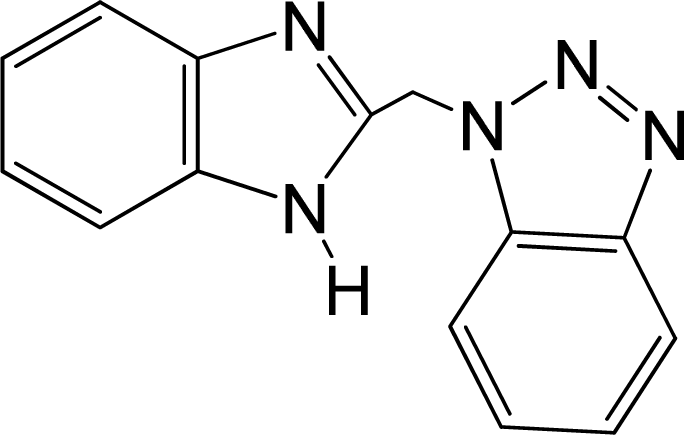 | 4.507 | L | 12 |
| 2 | 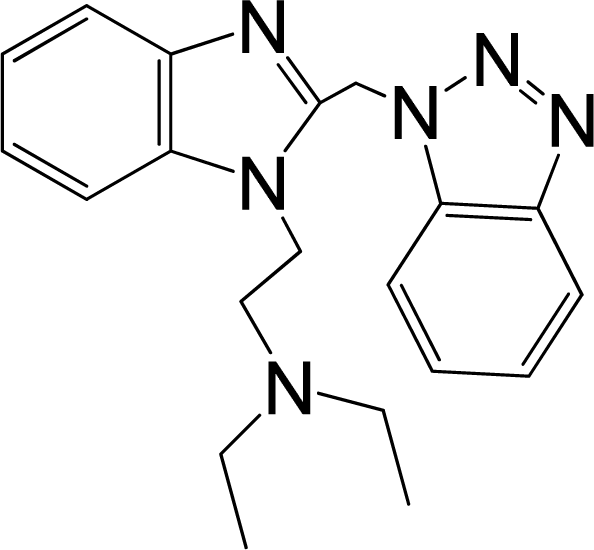 | 6.328 | L | 12 |
| 3 | 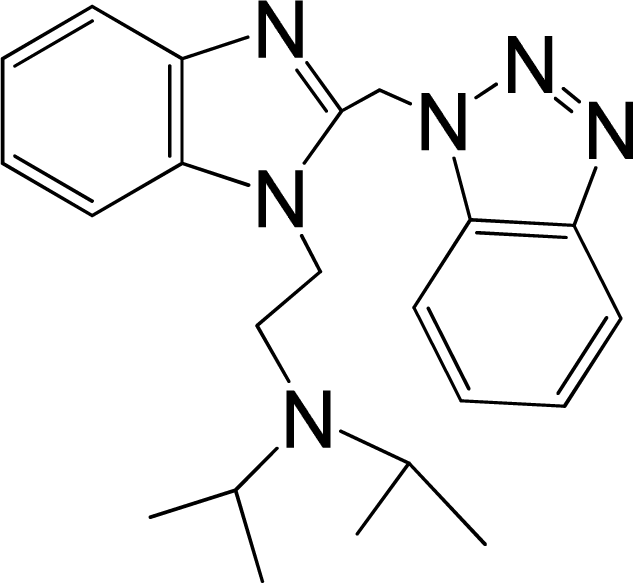 | 5.174 | L | 12 |
| 4* |  | 6.222 | L | 12 |
| 5 | 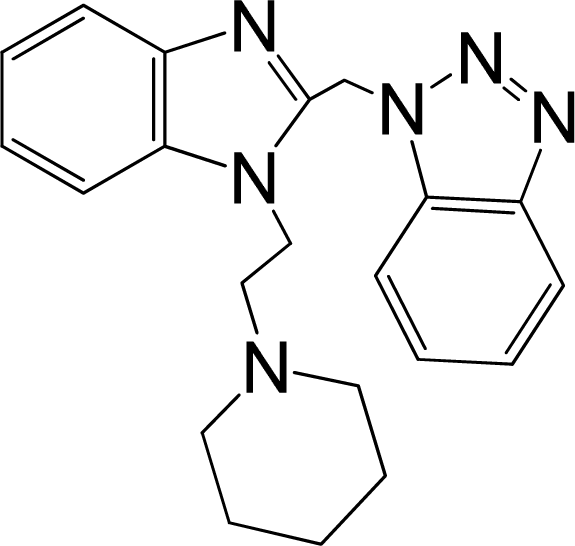 | 5.959 | L | 12 |
| 7 | 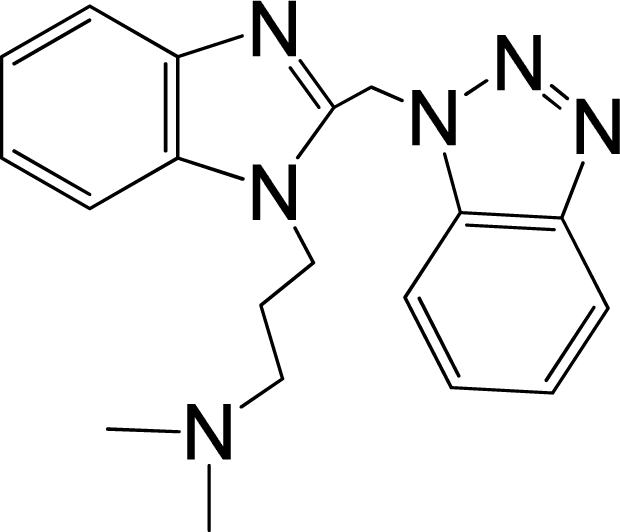 | 5.959 | L | 12 |
| 8* |  | 4.81 | L | 12 |
| 9 | 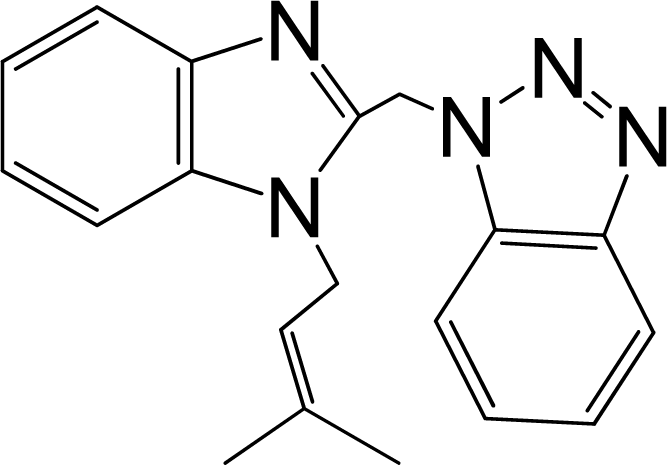 | 5.481 | L | 12 |
| 10 | 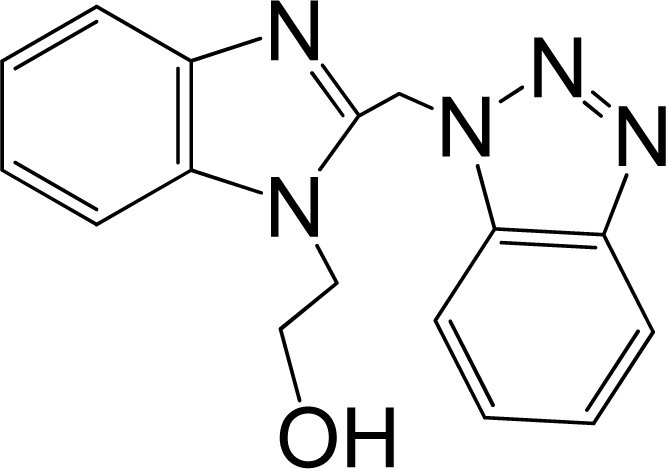 | 5.114 | L | 12 |
| 11 |  | 5.570 | L | 12 |
| 12* | 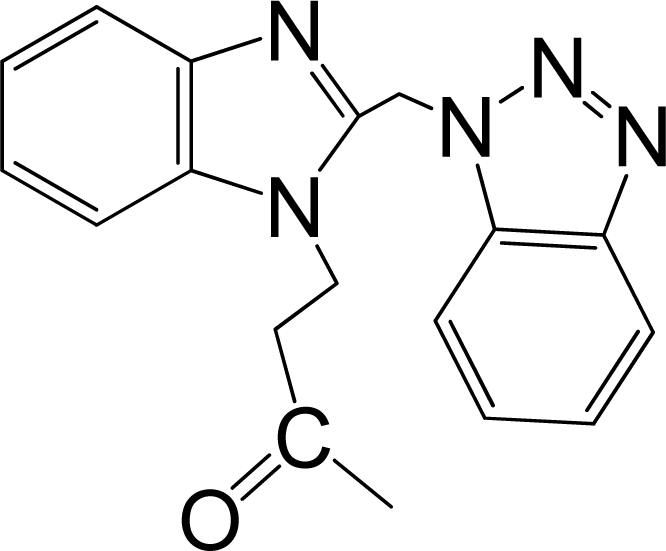 | 6.284 | L | 12 |
| 29 |  | 6.125 | L | 13 |
| 30 | 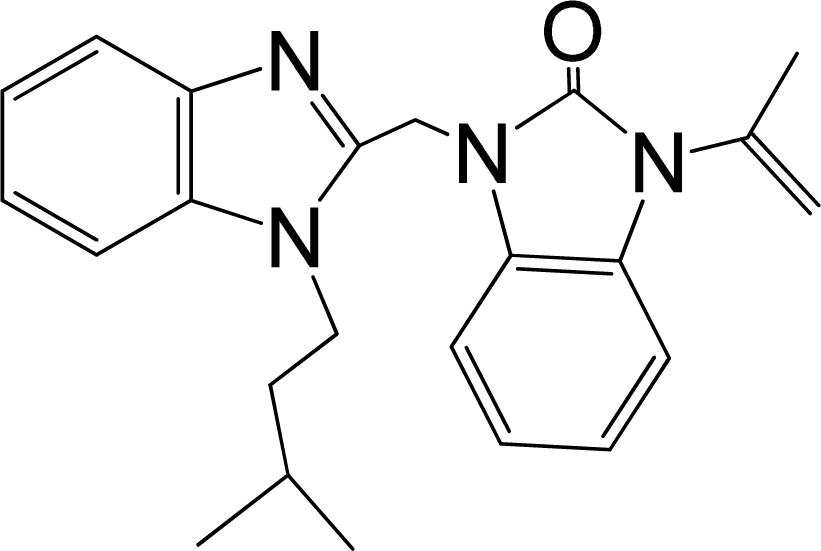 | 8.398 | H | 13 |
| 31 | 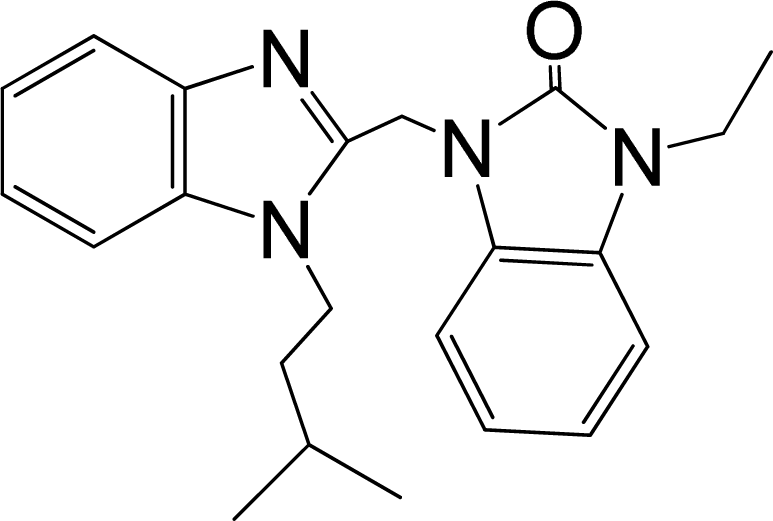 | 7.959 | H | 13 |
| 32* | 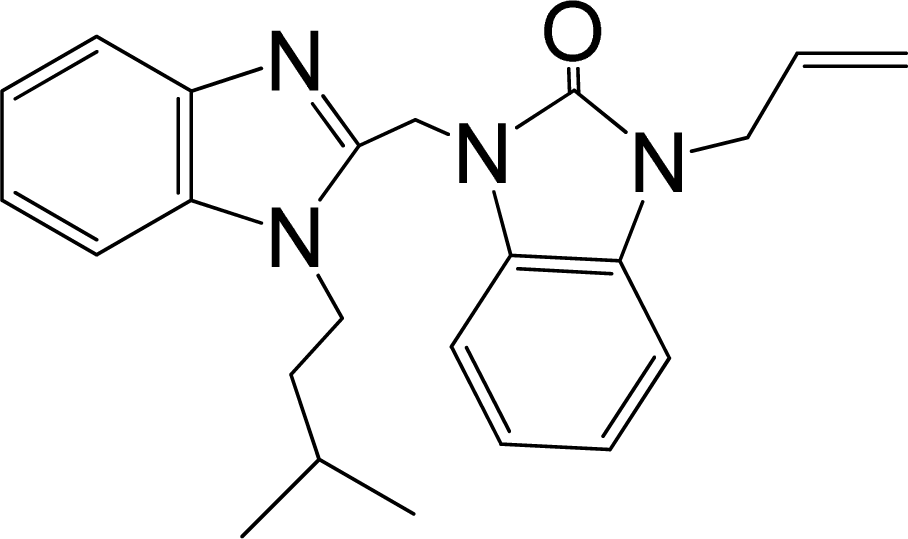 | 7.796 | H | 13 |
| 34 |  | 7.602 | H | 13 |
| 35 |  | 7.745 | H | 13 |
| 36 |  | 7.921 | H | 13 |
| 37 |  | 7.678 | H | 13 |
| 38 | 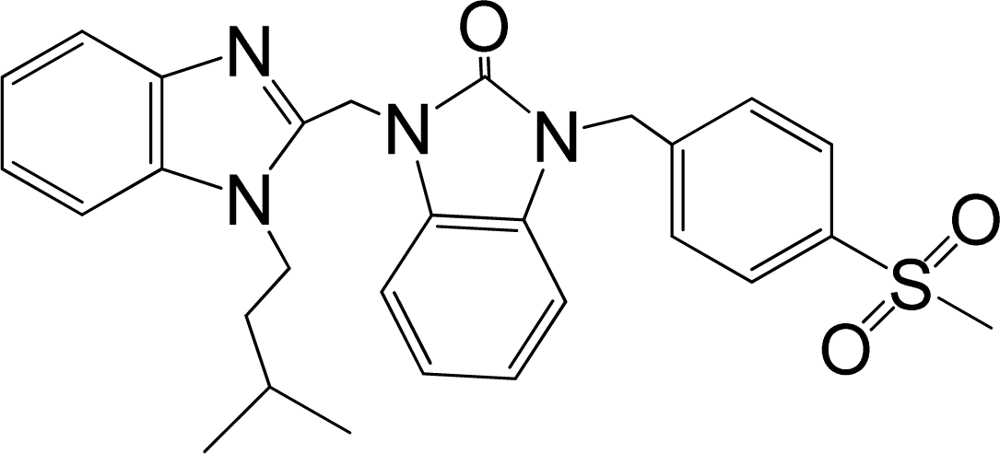 | 8.046 | H | 13 |
| 39* | 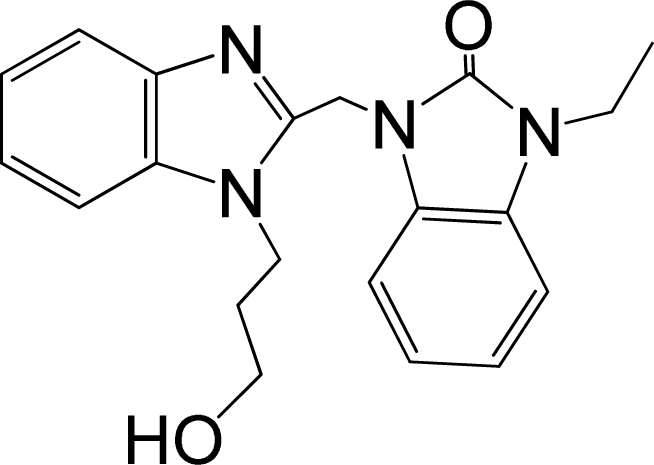 | 8.000 | H | 13 |
| 41 | 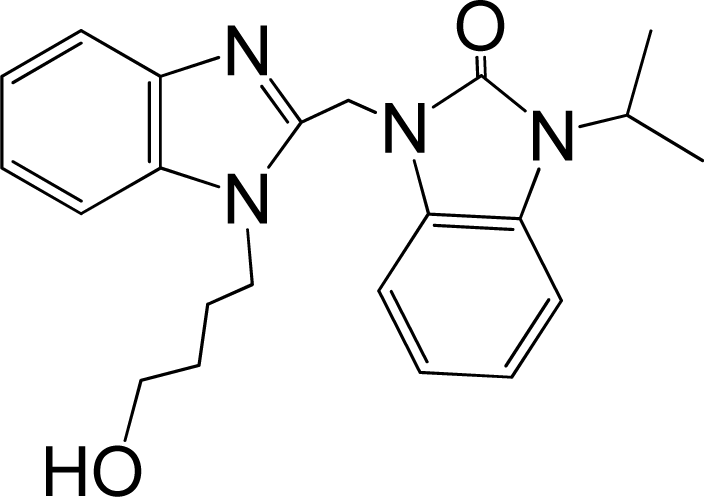 | 7.959 | H | 13 |
| 42* | 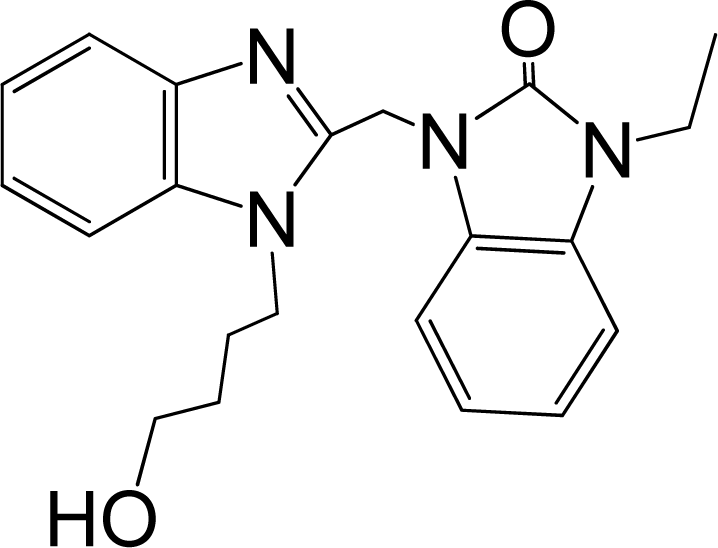 | 7.854 | H | 13 |
| 43 |  | 7.824 | H | 13 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hao, M.; Li, Y.; Wang, Y.; Zhang, S. A Classification Study of Respiratory Syncytial Virus (RSV) Inhibitors by Variable Selection with Random Forest. Int. J. Mol. Sci. 2011, 12, 1259-1280. https://doi.org/10.3390/ijms12021259
Hao M, Li Y, Wang Y, Zhang S. A Classification Study of Respiratory Syncytial Virus (RSV) Inhibitors by Variable Selection with Random Forest. International Journal of Molecular Sciences. 2011; 12(2):1259-1280. https://doi.org/10.3390/ijms12021259
Chicago/Turabian StyleHao, Ming, Yan Li, Yonghua Wang, and Shuwei Zhang. 2011. "A Classification Study of Respiratory Syncytial Virus (RSV) Inhibitors by Variable Selection with Random Forest" International Journal of Molecular Sciences 12, no. 2: 1259-1280. https://doi.org/10.3390/ijms12021259




