Symmetry-Adapted Rotator Functions for Molecules in Cylindrical Confinement
Abstract
:1. Introduction
2. Theoretical Formalism
2.1. Example #1
 (α, β, γ) are the Wigner
(α, β, γ) are the Wigner 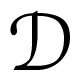 -functions. In the present case, cylindrical symmetry implies m = 0, for which the α-independent Wigner
-functions. In the present case, cylindrical symmetry implies m = 0, for which the α-independent Wigner 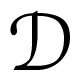 -functions reduce to
-functions reduce to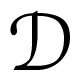 -functions are linear combinations of spherical harmonics [Equation (13)], and that the rotator functions
-functions are linear combinations of spherical harmonics [Equation (13)], and that the rotator functions 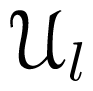 (β, γ) can be easily implemented:
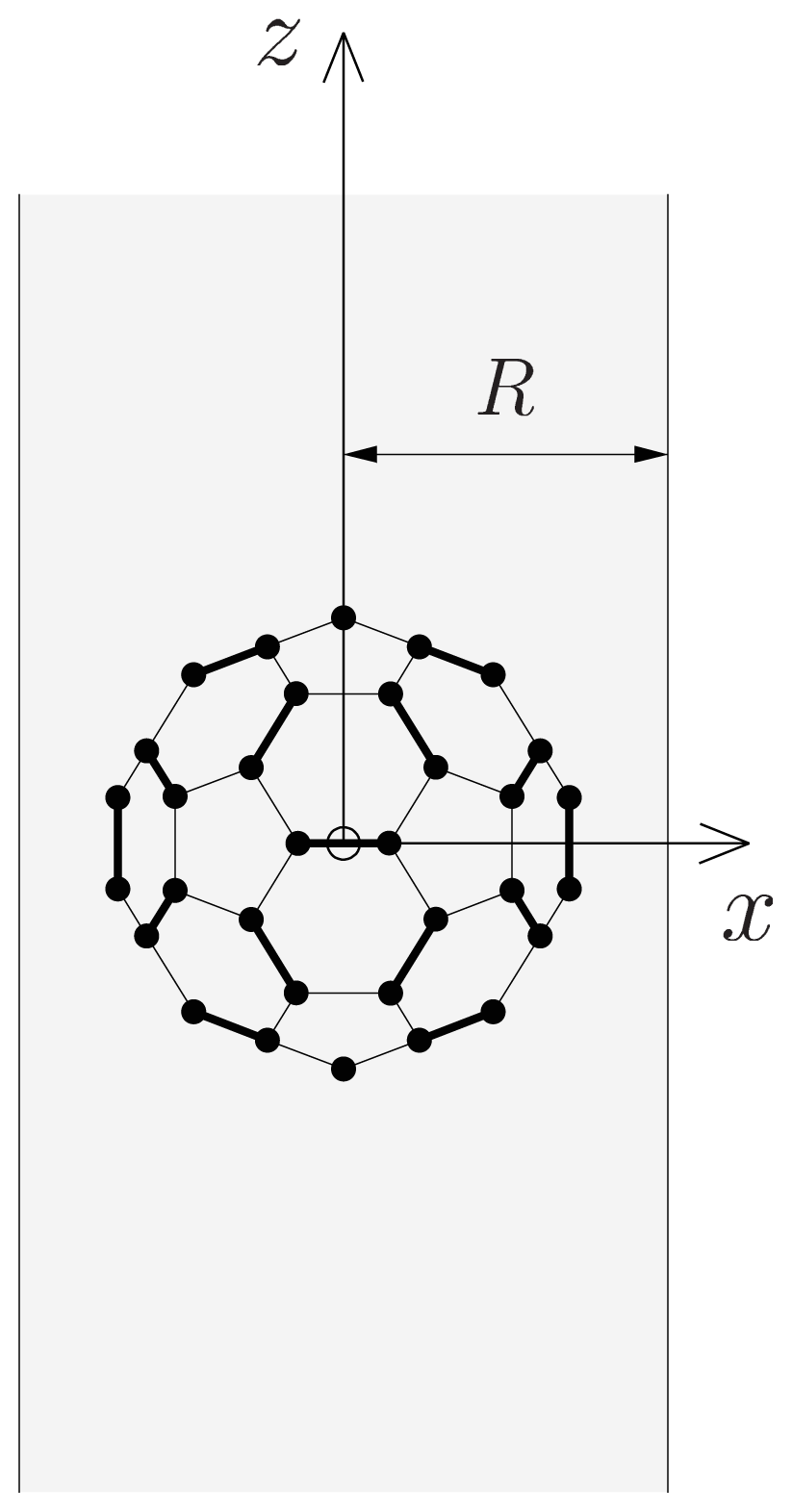
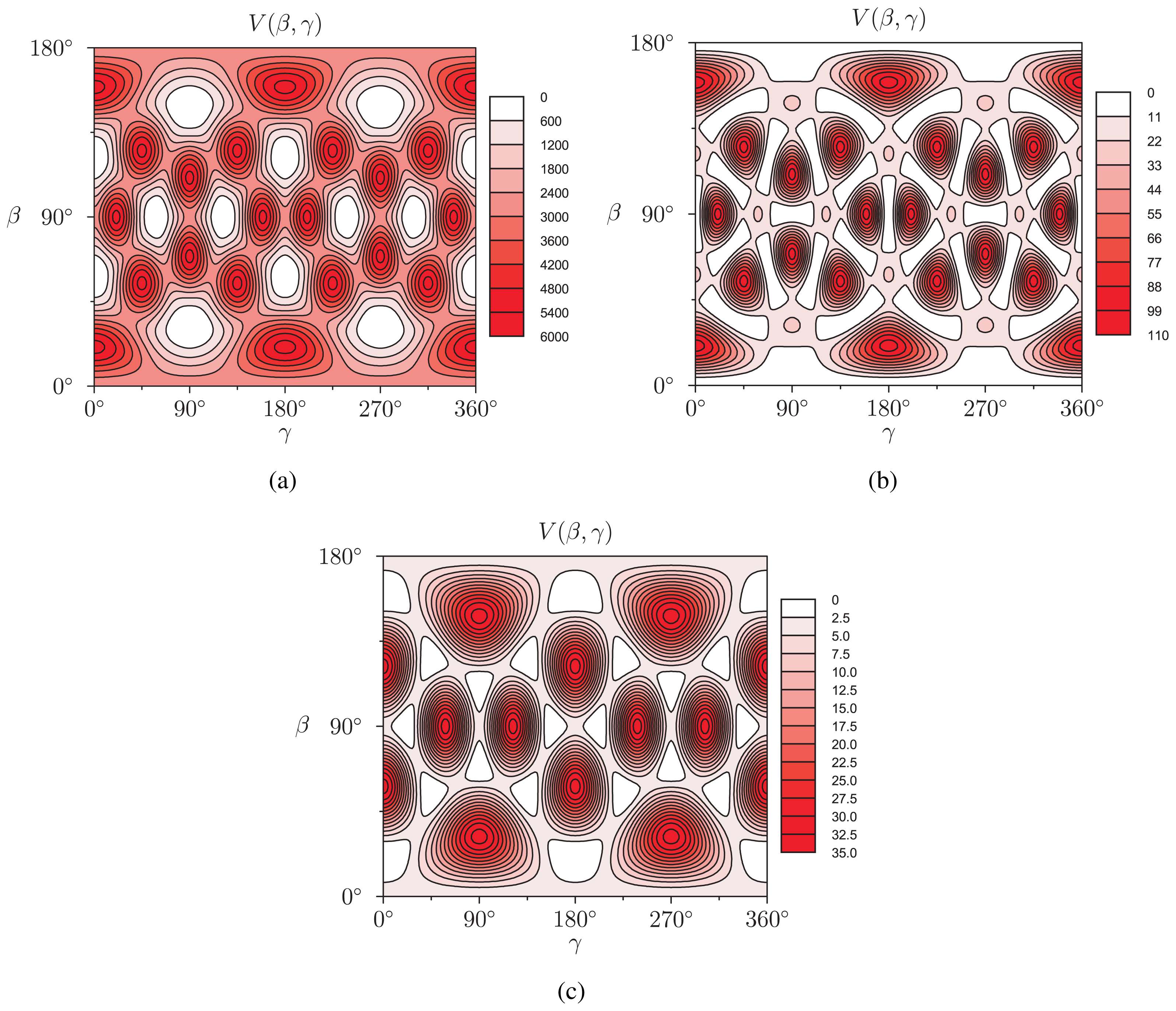
(β, γ) can be easily implemented: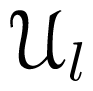 (β, γ) and to evaluate expression (18). In Figure 2, we show the results of V (β, γ) for R = 6.0 Å, R = 7.0 Å and R = 8.0 Å for a calculation up to l = 12. For R = 6.0 Å, there are 12 local minima, corresponding to the twelve equivalent molecular orientations where two opposing pentagons of the C60 molecule are perpendicular to the z-axis. The 20 maxima correspond to orientations where hexagons are perpendicular to the z-axis. (The “soccer-ball structure” indeed features 12 pentagons and 20 hexagons.) At R = 7.0 Å, there are 30 local minima: they correspond to the molecular configurations where opposing double bonds are perpendicular to the tube’s long axis (z-axis). The potential energy is maximal when a hexagon is perpendicular to the z-axis. Finally, at R = 8.0 Å, minima and maxima correspond to hexagons and pentagons perpendicular to the z-axis, respectively.
(β, γ) and to evaluate expression (18). In Figure 2, we show the results of V (β, γ) for R = 6.0 Å, R = 7.0 Å and R = 8.0 Å for a calculation up to l = 12. For R = 6.0 Å, there are 12 local minima, corresponding to the twelve equivalent molecular orientations where two opposing pentagons of the C60 molecule are perpendicular to the z-axis. The 20 maxima correspond to orientations where hexagons are perpendicular to the z-axis. (The “soccer-ball structure” indeed features 12 pentagons and 20 hexagons.) At R = 7.0 Å, there are 30 local minima: they correspond to the molecular configurations where opposing double bonds are perpendicular to the tube’s long axis (z-axis). The potential energy is maximal when a hexagon is perpendicular to the z-axis. Finally, at R = 8.0 Å, minima and maxima correspond to hexagons and pentagons perpendicular to the z-axis, respectively.2.2. Discussion
2.3. Extension to clusters with different types of interaction centers
2.4. General formulation for non-spherical clusters of interaction centers
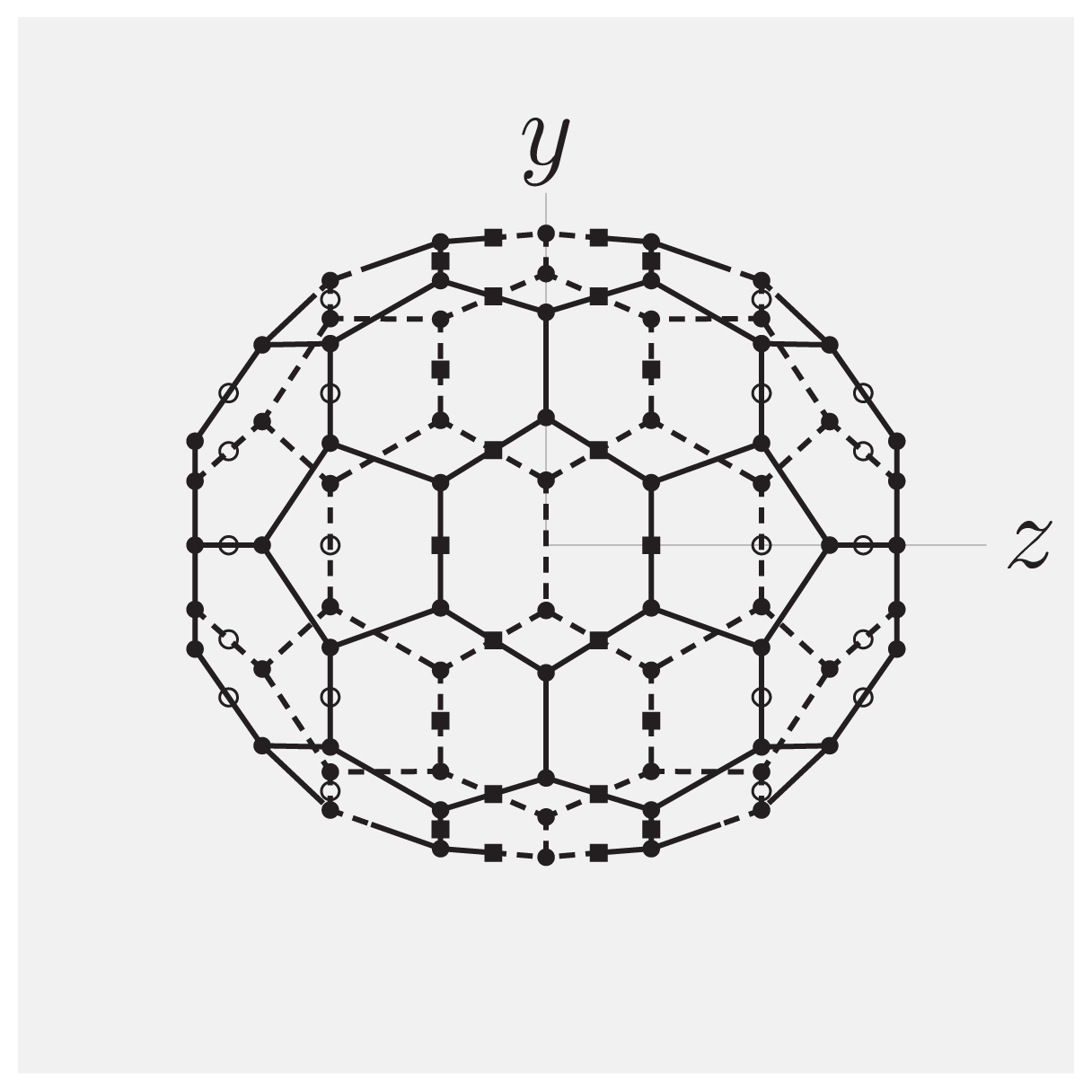
2.5. Example #2
3. Conclusions
 (λt; β, γ) are obtained via Equation (33), where the index λt groups ICs having the same radial coordinate rΛt ≡ rλt (layers of ICs). The SARFs are type- and layer-dependent. In some special cases, e.g., for spherical clusters like C60, type-independent SARFs can be constructed. The main consequence of the cylindrical site symmetry is the SARFs’ independence on the Euler angle α. The molecule-tube interaction energy (nanotube field) is conveniently obtained as an expansion into SARFs, Equation (34), where the expansion coefficients vlt (R) are obtained via numerical integrations [Equation (23)] involving the pair potentials vt(d). It turns out that a limited number of terms (typically up to l = 12) provides an excellent approximation to the exact expression [Equation (3)] with explicit coordinate transforms. For concrete examples, the SARFs expansion has proven to be computationally much more efficient: the calculations of a C60 molecule’s nanotube field take less than 1000 times the time for the direct calculation.
(λt; β, γ) are obtained via Equation (33), where the index λt groups ICs having the same radial coordinate rΛt ≡ rλt (layers of ICs). The SARFs are type- and layer-dependent. In some special cases, e.g., for spherical clusters like C60, type-independent SARFs can be constructed. The main consequence of the cylindrical site symmetry is the SARFs’ independence on the Euler angle α. The molecule-tube interaction energy (nanotube field) is conveniently obtained as an expansion into SARFs, Equation (34), where the expansion coefficients vlt (R) are obtained via numerical integrations [Equation (23)] involving the pair potentials vt(d). It turns out that a limited number of terms (typically up to l = 12) provides an excellent approximation to the exact expression [Equation (3)] with explicit coordinate transforms. For concrete examples, the SARFs expansion has proven to be computationally much more efficient: the calculations of a C60 molecule’s nanotube field take less than 1000 times the time for the direct calculation.References
- Lynden-Bell, RM; Michel, KH. Translation-rotation coupling, phase transitions, and elastic phenomena in orientationally disordered crystals. Rev. Mod. Phys 1994, 66, 721–762. [Google Scholar]
- James, HM; Keenan, TA. Theory of Phase Transitions in Solid Heavy Methane. J. Chem. Phys 1959, 31, 12–41. [Google Scholar]
- Yvinec, M; Pick, RM. Orientational disorder in plastic molecular crystals I. - Group theory and ODIC description. J. Phys (France) 1980, 41, 1045–1052. [Google Scholar]
- Michel, KH; Parlinski, K. Symmetry properties, normal modes, and free energy of orientationally disordered crystals. Phys. Rev B 1985, 31, 1823–1835. [Google Scholar]
- Smith, BW; Monthioux, M; Luzzi, DE. Encapsulated C60 in carbon nanotubes. Nature (London) 1998, 396, 323–324. [Google Scholar]
- Michel, KH; Verberck, B; Nikolaev, AV. Anisotropic Packing and One-Dimensional Fluctuations of C60 Molecules in Carbon Nanotubes. Phys Rev Lett 2005, 95, 185506-1–14. [Google Scholar]
- Michel, KH; Verberck, B; Nikolaev, AV. Nanotube field and one-dimensional fluctuations of C60 molecules in carbon nanotubes. Eur. Phys. J B 2005, 48, 113–124. [Google Scholar]
- Verberck, B; Michel, KH. Nanotube field of C60 molecules in carbon nanotubes: Atomistic versus continuous approach. Phys Rev B 2006, 74, 045421-1–14. [Google Scholar]
- Verberck, B; Michel, KH. Nanotube field and orientational properties of C70 molecules in carbon nanotubes. Phys Rev B 2007, 75, 045419-1–14. [Google Scholar]
- Verberck, B. Orientational properties of C70 and C80 fullerenes in carbon nanotubes. Phys Rev B 2011. accepted. [Google Scholar]
- Bradley, CJ; Cracknell, AP. The Mathematical Theory of Symmetry in Solids; Clarendon: Oxford, UK, 1972. [Google Scholar]
- Lamoen, D; Michel, KH. Crystal field and molecular structure in solid C60. Z. Phys. B: Condens Matter 1993, 92, 323–330. [Google Scholar]
- Copley, JRD; Michel, KH. Neutron and X-ray scattering cross sections of orientationally disordered solid C60. J. Phys.: Condens Matter 1993, 5, 4353–4370. [Google Scholar]
- Launois, P; Ravy, S; Moret, R. Tests of current models of intermolecular potentials against x-ray diffuse scattering in C60. Phys. Rev B 1997, 55, 2651–2665. [Google Scholar]
- Michel, KH; Copley, JRD. Orientational mode coupling, diffuse scattering, and the order-disorder phase transition in solid C60. Z. Phys. B: Condens Matter 1997, 103, 369–376. [Google Scholar]
- Sprik, M; Cheng, A; Klein, ML. Modeling the orientational ordering transition in solid fullerene C60. J. Phys. Chem 1992, 96, 2027–2029. [Google Scholar]
- Rols, S; Cambedouzou, J; Chorro, M; Schober, H; Agafonov, V; Launois, P; Davydov, V; Rakhmanina, AV; Kataura, H; Sauvajol, J-L. How Confinement Affects the Dynamics of C60 in Carbon Nanopeapods. Phys Rev Lett 2008, 101, 065507-1–4. [Google Scholar]
- Matsuda, K; Maniwa, Y; Kataura, H. Highly rotational C60 dynamics inside single-walled carbon nanotubes: NMR observations. Phys Rev B 2008, 77, 075421-1–6. [Google Scholar]
- Abou-Hamad, E; Kim, Y; Wågberg, T; Boesch, D; Aloni, S; Zettl, A; Rubio, A; Luzzi, DE; Goze-Bac, C. Molecular Dynamics and Phase Transition in One-Dimensional Crystal of C60 Encapsulated Single Wall Carbon Nanotubes. ACS Nano 2009, 12, 3878–3883. [Google Scholar]
- Zou, Y; Liu, B; Wang, L; Liu, D; Yu, S; Wang, P; Wang, T; Yao, M; Li, Q; Zou, B; Cui, T; Zou, G; Wågberg, T; Sundqvist, B; Mao, H-K. Rotational dynamics of confined C60 from nearinfrared Raman studies under high pressure. Proc. Natl. Acad. Sci USA 2009, 106, 22135–22138. [Google Scholar]
- Eaton, PE; Cole, TW, Jr. The cubane system. J. Am. Chem. Soc 1964, 86, 962–964. [Google Scholar]
- Pekker, S; Kováts, É; Oszlányi, G; Bényei, G; Klupp, G; Bortel, G; Jalsovszky, I; Jakab, E; Borondics, F; Kamarás, K; Bokor, M; Kriza, G; Tompa, K; Faigel, G. Rotorstator molecular crystals of fullerenes with cubane. Nature Mater 2005, 4, 764–767. [Google Scholar]
- Khlobystov, AN; Britz, DA; Briggs, GAD. Molecules in Carbon Nanotubes. Acc. Chem. Res 2005, 38, 901–909. [Google Scholar]
- Wang, J; Kuimova, MK; Poliakoff, M; Briggs, GAD; Khlobystov, AN. Encapsulation and IR Probing of Cube-Shaped Octasilasesquioxane H8Si8O12 in Carbon Nanotubes. Angew. Chem. Int. Ed 2006, 45, 5188–5191. [Google Scholar]
- Verberck, B; Vliegenthart, GA; Gompper, G. Orientational ordering in solid C60 fullerene-cubane. J Chem Phys 2009, 130, 154510-1–14. [Google Scholar]
- Liu, Z; Joung, S-J; Okazaki, T; Suenaga, K; Hagiwara, Y; Ohsuna, T; Kuroda, K; Iijima, S. Self-Assembled Double Ladder Structure Formed Inside Carbon Nanotubes by Encapsulation of H8Si8O12. ACS Nano 2009, 3, 1160–1166. [Google Scholar]
- Michel, KH; Copley, JRD; Neumann, DA. Microscopic theory of orientational disorder and the orientational phase transition in solid C60. Phys. Rev. Lett 1992, 68, 2929–2932. [Google Scholar]
- Verberck, B; Tarakina, NV. Tubular fullerenes inside carbon nanotubes: optimal molecular orientation versus tube radius. Eur J Phys B 2011. submitted. [Google Scholar]


| l | gl | n | |
|---|---|---|---|
| 0 | 16.9257 | 0 | 1 |
| 6 | 2.6365 | 0 | −0.2073 |
| 6 | 2 | −0.4750 | |
| 6 | 4 | 0.3878 | |
| 6 | 6 | 0.3202 | |
| 10 | 19.2982 | 0 | 0.3545 |
| 10 | 2 | −0.2880 | |
| 10 | 4 | −0.3572 | |
| 10 | 6 | −0.0565 | |
| 10 | 8 | −0.4251 | |
| 10 | 10 | 0.2069 | |
| 12 | 9.0051 | 0 | −0.4145 |
| 12 | 2 | −0.1179 | |
| 12 | 4 | −0.1830 | |
| 12 | 6 | 0.4635 | |
| 12 | 8 | −0.0738 | |
| 12 | 10 | −0.2924 | |
| 12 | 12 | −0.2469 | |
| R | v0(R) | v6(R) | v10(R) | v12(R) |
|---|---|---|---|---|
| 6.0 Å | −2201.02 | −833.92 | −53.79 | 7.87 |
| 7.0 Å | −2151.95 | −7.81 | −1.99 | 0.36 |
| 8.0 Å | −886.63 | 4.23 | −0.04 | 0.01 |
| R | g0v0(R) | g6v6(R) | g10v10(R) | g12v12(R) |
| 6.0 Å | −37253.82 | −2198.65 | −1038.13 | 62.97 |
| 7.0 Å | −36423.20 | −20.58 | −38.49 | 2.85 |
| 8.0 Å | −15006.86 | 11.14 | −0.71 | 0.09 |
| l | gl | n | |
|---|---|---|---|
| 0 | 2.2568 | 0 | 1 |
| 4 | 3.4473 | 0 | −0.7638 |
| 4 | 4 | −0.4564 | |
| 6 | 5.1143 | 0 | 0.3536 |
| 6 | 4 | −0.6614 | |
| 8 | 1.9797 | 0 | 0.7181 |
| 8 | 4 | 0.2700 | |
| 8 | 8 | 0.4114 | |
| 10 | 6.7237 | 0 | −0.4114 |
| 10 | 4 | 0.4146 | |
| 10 | 8 | 0.4934 | |
| 12 | 4.6866 | 0 | 0.0919 |
| 12 | 4 | −0.3625 | |
| 12 | 8 | 0.5977 | |
| 12 | 12 | −0.0849 | |
| R | v0(R) | v4(R) | v6(R) | v8(R) | v10(R) | v12(R) |
|---|---|---|---|---|---|---|
| 5.0 Å | −474.28 | 106.87 | −49.25 | 14.53 | −3.38 | 0.67 |
| 7.0 Å | −103.26 | −1.89 | 0.11 | 0.00 | 0.00 | 0.00 |
| R | g0v0(R) | g4v4(R) | g6v6(R) | g8v8(R) | g10v10(R) | g12v12(R) |
| 5.0 Å | −1070.37 | 368.41 | −251.86 | 28.76 | −22.71 | 3.14 |
| 7.0 Å | −233.04 | −6.53 | 0.55 | −0.01 | 0.00 | 0.00 |
© 2011 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Verberck, B. Symmetry-Adapted Rotator Functions for Molecules in Cylindrical Confinement. Int. J. Mol. Sci. 2011, 12, 317-333. https://doi.org/10.3390/ijms12010317
Verberck B. Symmetry-Adapted Rotator Functions for Molecules in Cylindrical Confinement. International Journal of Molecular Sciences. 2011; 12(1):317-333. https://doi.org/10.3390/ijms12010317
Chicago/Turabian StyleVerberck, Bart. 2011. "Symmetry-Adapted Rotator Functions for Molecules in Cylindrical Confinement" International Journal of Molecular Sciences 12, no. 1: 317-333. https://doi.org/10.3390/ijms12010317





