The Chemical Master Equation Approach to Nonequilibrium Steady-State of Open Biochemical Systems: Linear Single-Molecule Enzyme Kinetics and Nonlinear Biochemical Reaction Networks
Abstract
:1. Introduction
1.1. The Chemical Master Equation (CME)
1.2. Nonequilibrium Steady State (NESS)
- Equilibrium state with fluctuations which is well-understood according to Boltzmann’s law, and the theories of Gibbs, Einstein, and Onsager.
- Time-dependent, transient processes in which systems are changing with time. In the past, this type of problems is often called “nonequilibrium problems”. As all experimentalists and computational modellers know, time-dependent kinetic experiments are very difficult to perform, and time-dependent equations are very difficult to analyze.
- Nonequilibrium steady state: The system is no longer changing with time in a statistical sense, i.e., all the probability distributions are stationary; nevertheless, the system is not at equilibrium. The systems fluctuate, but the fluctuations do not obey Boltzmann’s law. Such a system only eixsts when it is driven by a sustained chemical energy input. Complex deterministic dynamics discussed in the past, such as chemical bistability and oscillations, are all macroscopic limit of such systems.
2. The Chemical Master Equation and Its Applications to Kinetics of Isolated Enzyme
2.1. Quasi-stationary approximation of the Michaelis-Menten enzyme kinetics
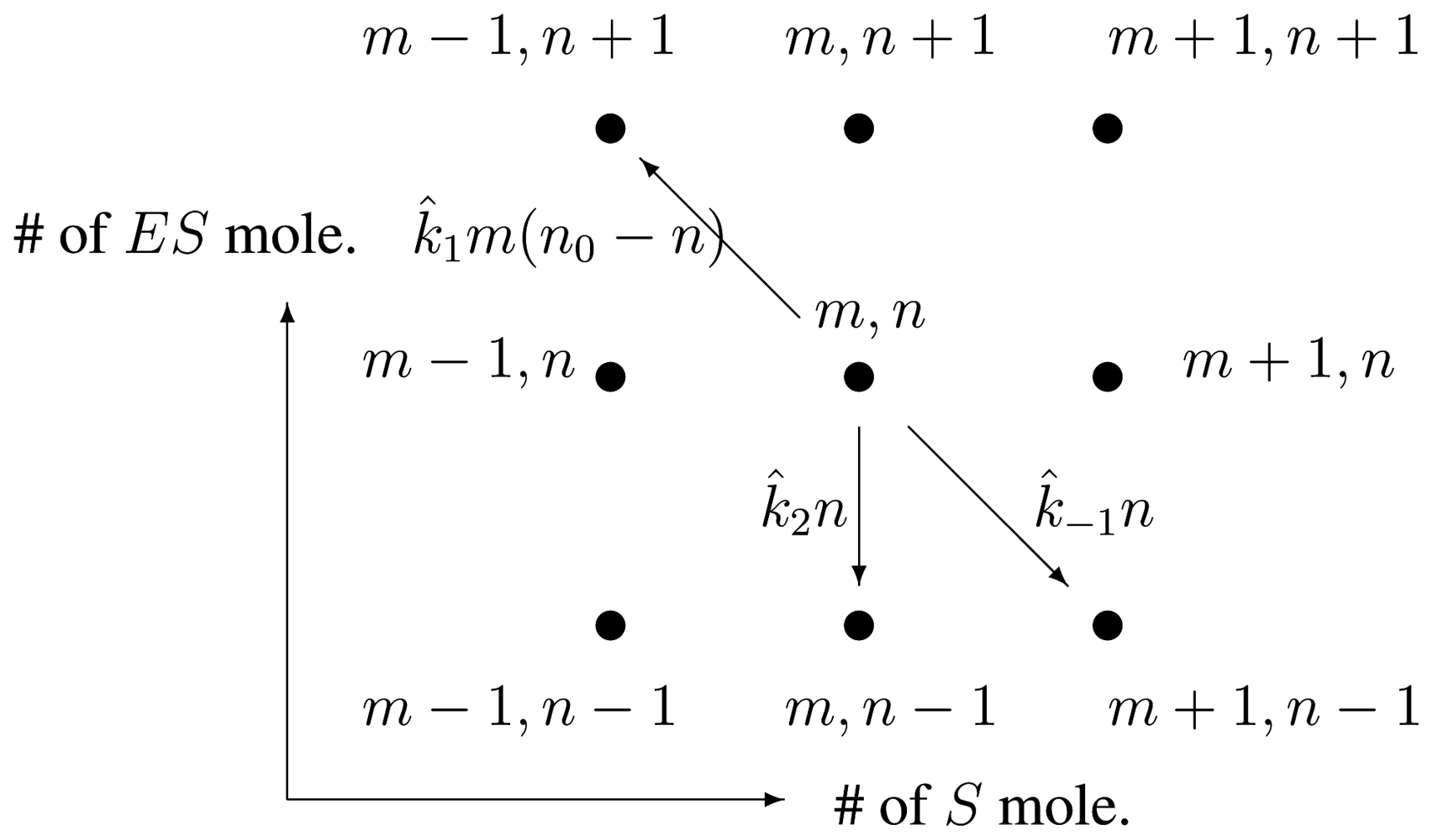
2.2. Single-Molecule Michaelis-Menten Enzyme Kinetics
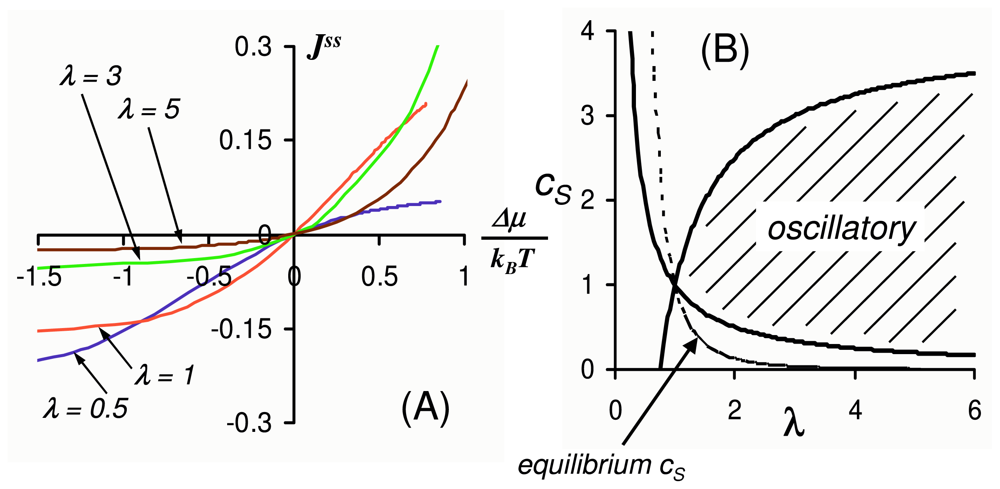
2.3. Driven Enzyme Kinetics
2.4. Far from Equilibrium and Enzyme Oscillations
3. The CME Approach to Nonlinear Biochemical Networks in Living Environment
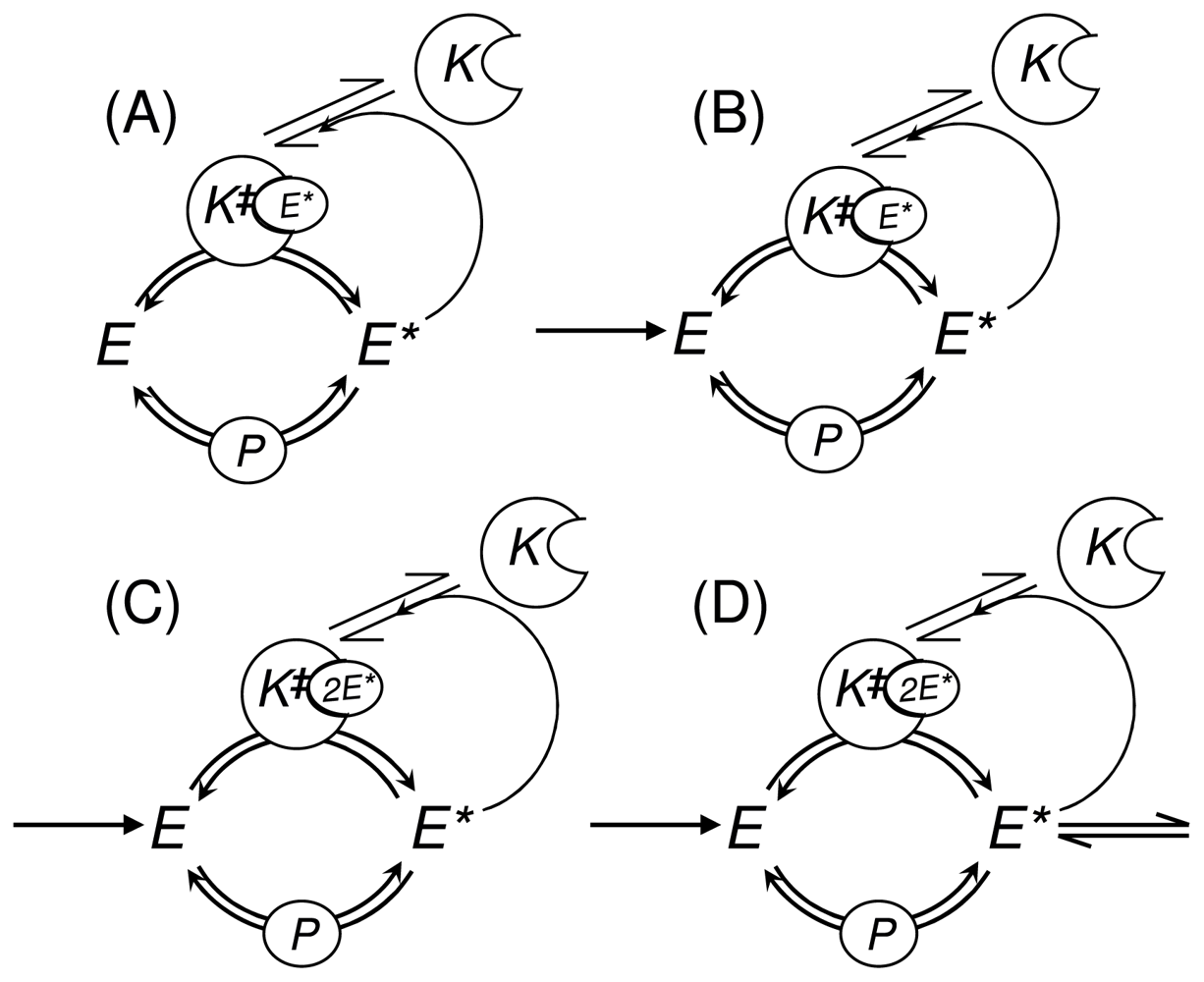
3.1. Phosphorylation-Dephosphorylation Cycle with Autocatalysis: A Positive Feedback Loop
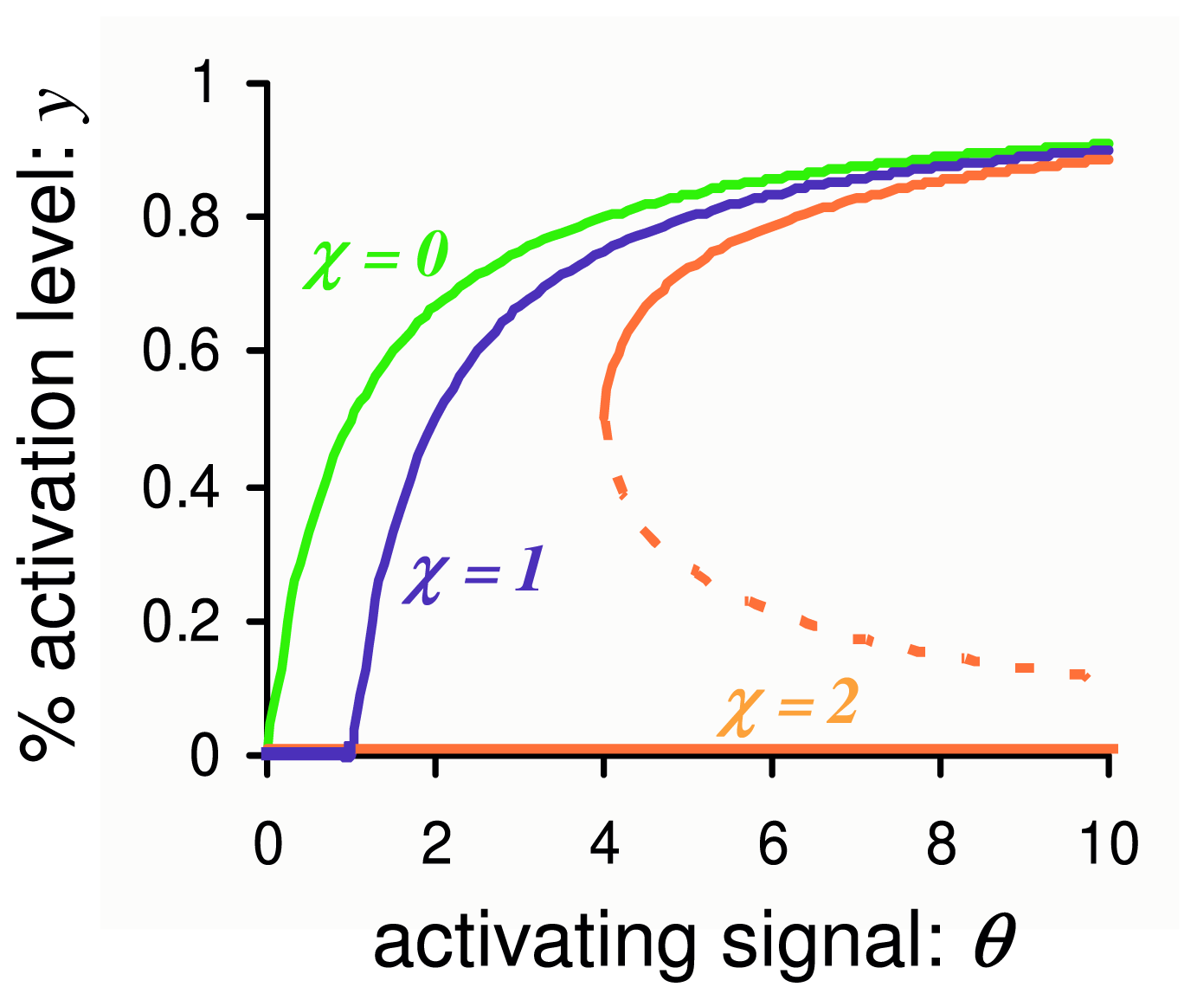
3.2. Stochastic Bistability in PdPC with First-Order Autocatalysis
3.2.1. Deterministic Kinetics of PdPC with First-Order Autocatalysis and Delayed Onset
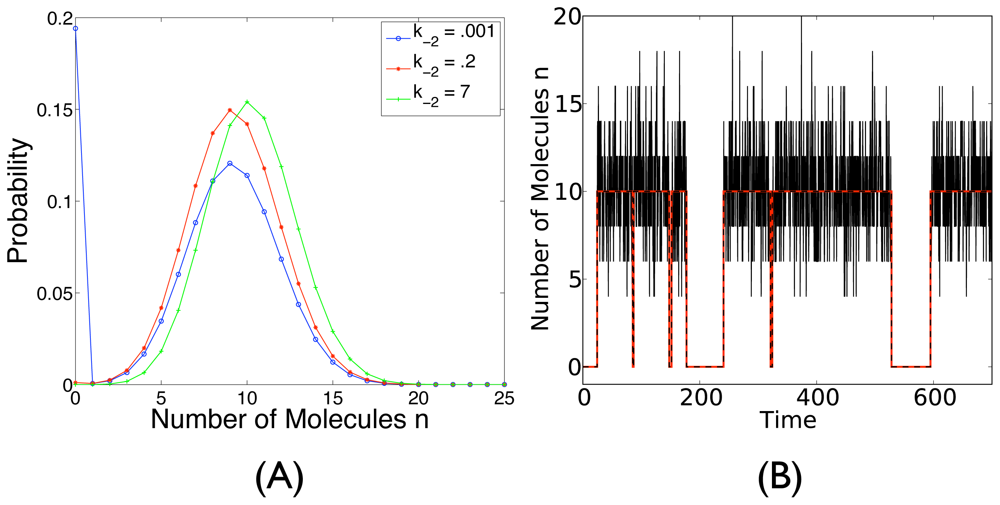
3.2.2. Stochastic Bistability and Bifurcation without Deterministic Counterpart
3.3. Keizer’s Paradox
3.4. Schlögl’s Nonlinear Bistability and PdPC with Second-Order Autocatalysis
3.5. Schnakenberg’s Oscillation
3.5.1. Sel’kov-Goldbeter-Lefever’s Glycolytic Oscillator
4. Conclusions
Acknowledgements
Appendix: The Chemical Master Equation for Systems of Biochemical Networks
A1. Michaelis-Menten model
A2. Keizer’s Model
A3. Schlögl Model
A3.1. Stationary Distribution: Steady State and Equilibrium
A4. Schnakenberg Model
References
- Gibbs, JW. The Scientific Papers of J. Willard Gibbs; Dover: New York, NY, USA, 1961. [Google Scholar]
- Tanford, C. Physical Chemisry of Macromolecules; John Wiley & Sons: New York, NY, USA, 1961. [Google Scholar]
- Dill, KA; Bromberg, S. Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Onsager, L; Machlup, S. Fluctuations and irreversible processes. Phys. Rev 1953, 91, 1505–1512. [Google Scholar]
- Machlup, S; Onsager, L. Fluctuations and irreversible process. II. Systems with kinetic energy. Phys. Rev 1953, 91, 1512–1515. [Google Scholar]
- Lund, EW. Guldberg and waage and the law of mass action. J. Chem. Ed 1965, 42, 548–550. [Google Scholar]
- Segel, I. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Qian, H; Beard, DA. Chemical biophysics: Quantitative analysis of cellular systems. In Cambridge Texts in Biomedical Engineering; Cambride Univ. Press: New York, NY, USA, 2008. [Google Scholar]
- Liang, J; Qian, H. Computational cellular dynamics based on the chemical master equation: A challange for understanding complexity. J. Comput. Sci. Tech 2010, 25, 154–168. [Google Scholar]
- Gillespie, DT. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem 2007, 58, 35–55. [Google Scholar]
- Ge, H; Qian, H. The physical origins of entropy production, free energy dissipation and their mathematical representations. Phys. Rev. E 2010, 81, 051133. [Google Scholar]
- Nicolis, G; Prigogine, I. Self-Organization in Non-Equilibrium Systems; JohnWiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Kurchan, J. Fluctuation theorem for stochastic dynamics. J. Phys. A: Math Gen 1998, 31, 3719–3729. [Google Scholar]
- Lebowitz, JL; Spohn, H. A gallavotti-cohen-type symmetry in the large deviation functional for stochastic dynamis. J. Stat. Phys 1999, 95, 333–365. [Google Scholar]
- Jiang, DQ; Qian, M; Qian, MP. Mathematical Theory of Nonequilibrium Steady States. In Lecture Notes in Mathematics; Springer: New York, NY, USA, 2004; Volume 1833. [Google Scholar]
- Qian, H. The mathematical theory of molecular motor movement and chemomechanical energy transduction. J. Mach. Chem 2000, 27, 219–234. [Google Scholar]
- Qian, H. Cycle kinetics, steady-state thermodynamics and motors — a paradigm for living matter physics. J. Phys.: Cond. Matt 2005, 17, S3783–S3794. [Google Scholar]
- Lewis, GN. A new principle of equilibrium. PNAS 1925, 11, 179–183. [Google Scholar]
- Qian, H. Open-system nonequilibrium steady state: Statistical thermodynamics, fluctuations, and chemical oscillations. J. Phys. Chem. B 2006, 110, 15063–15074. [Google Scholar]
- Qian, H. Phosphorylation energy hypothesis: Open chemical systems and their biological functions. Annu. Rev. Phys. Chem 2007, 58, 113–142. [Google Scholar]
- Kepler, TB; Elston, TC. Stochasticity in transcriptional regulation: Origins, consequences, and mathematical representations. Biophys. J 2001, 81, 3116–3136. [Google Scholar]
- Rao, CV; Arkin, AP. Stochastic chemical kinetics and the quasi-steady-state assumption: Application to the Gillespie algorithm. J. Chem. Phys 2003, 118, 4999–5010. [Google Scholar]
- Qian, H. Cooperativity and specificity in enzyme kinetics: a single-molecule time-based perspective. Biophys. J 2008, 95, 10–17. [Google Scholar]
- Gadgil, C; Lee, CH; Othmer, HG. A stochastic analysis of first-order reaction networks. Bull. Math. Biol 2005, 67, 901–946. [Google Scholar]
- Das, M; Green, F. Landauer formula without Landauer’s assumptions. J. Phys.: Condens. Matter 2003, 15, L687. [Google Scholar]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev 1931, 37, 405–426. [Google Scholar]
- Onsager, L. Reciprocal relations in irreversible processes. II. Phys. Rev 1931, 38, 2265–2279. [Google Scholar]
- Li, Y; Qian, H; Yi, Y. Oscillations and multiscale dynamics in a closed chemical reaction system: Second law of thermodynamics and temporal complexity. J. Chem. Phys 2008, 129, 154505. [Google Scholar]
- Li, Y; Qian, H; Yi, Y. Nonlinear oscillations and multiscale dynamics in a closed chemical reaction system. J. Dyn. Diff. Eqn 2010, 22, 491–507. [Google Scholar]
- Howard, J. Mechanics of Motor Proteins and the Cytoskele; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- Ferrell, JE; Xiong, W. Bistability in cell signaling: How to make continuous processes discontinuous, and reversible processes irreversible. Chaos 2001, 11, 227–236. [Google Scholar]
- Cooper, JA; Qian, H. A mechanism for Src kinase-dependent signaling by noncatalytic receptors. Biochemistry 2008, 47, 5681–5688. [Google Scholar]
- Zhu, H; Qian, H; Li, G. Delayed onset of positive feedback activation of Rab5 by Rabex-5 and Rabaptin-5 in endocytosis. PLoS ONE 2010, 5, e9226. [Google Scholar]
- Bishop, LM; Qian, H. Stochastic bistability and bifurcation in a mesoscopic signaling system with autocatalytic kinase. Biophys. J 2010, 98, 1–11. [Google Scholar]
- Paulsson, J. Models of stochastic gene expression. Phys. Life Rev 2005, 2, 157–175. [Google Scholar]
- Vellela, M; Qian, H. Stochastic dynamics and non-equilibrium thermodynamics of a bistable chemical system: the Schlogl model revisited. J. R. Soc. Interface 2009, 6, 925–940. [Google Scholar]
- Qian, H; Shi, PZ; Xing, J. Stochastic bifurcation, slow fluctuations, and bistability as an origin of biochemical complexity. Phys. Chem. Chem. Phys 2009, 11, 4861–4870. [Google Scholar]
- Epstein, IR; Pogman, JA. An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Qian, H. Entropy demystified: The “thermo”-dynamics of stochastically fluctuating systems. Meth. Enzym 2009, 467, 111–134. [Google Scholar]
- Gunawardena, J. Multisite protein phosphorylation makes a good threshold but can be a poor switch. Proc. Natl. Acad. Sci. USA 2005, 102, 14617–14622. [Google Scholar]
- Samoilov, M; Plyasunov, S; Arkin, AP. Stochastic amplification and signaling in enzymatic futile cycles through noise-induced bistability with oscillations. Proc. Natl. Acad. Sci. USA 2005, 102, 2310–2315. [Google Scholar]
- Keizer, J. Statistical Thermodynamics of Nonequilibrium Processes; Springer-Verlag: New York, NY, USA, 1987. [Google Scholar]
- Vellela, M; Qian, H. A quasistationary analysis of a stochastic chemical reaction: Keizer’s paradox. Bull. Math. Biol 2007, 69, 1727–1746. [Google Scholar]
- Hinch, R; Chapman, SJ. Exponentially slow transitions on a Markov chain: The frequency of calcium sparks. Eur. J. Appl. Math 2005, 16, 427–446. [Google Scholar]
- Ge, H; Qian, H. Nonequilibrium phase transition in mesoscoipic biochemical systems: From stochastic to nonlinear dynamics and beyond. J. R. Soc. Interf 2010. [Epub ahead of print]. [Google Scholar]
- Schlogl, F. Chemical reaction models for non-equilibrium phase transition. Z. Physik 1972, 253, 147–161. [Google Scholar]
- Qian, H; Reluga, T. Nonequilibrium thermodynamics and nonlinear kinetics in a cellular signaling switch. Phys. Rev. Lett 2005, 94, 028101. [Google Scholar]
- Keizer, J. Nonequilibrium thermodynamics and the stability of states far from equilibrium. Acc. Chem. Res 1979, 12, 243–249. [Google Scholar]
- Gardiner, CW. Handbook of Stochastic Methods for Physics, Chemistry, and the Natural Sciences, 2nd ed; Springer: New York, NY, USA, 1985. [Google Scholar]
- Matheson, I; Walls, DF; Gardiner, CW. Stochastic models of first-order nonequilibrium phase transitions in chemical reactions. J. Stat. Phys 1974, 12, 21–34. [Google Scholar]
- Ge, H; Qian, H. Thermodynamic limit of a nonequilibrium steady-state: Maxwell-type construction for a bistable biochemical system. Phys. Rev. Lett 2009, 103, 148103. [Google Scholar]
- Nicolis, G; Turner, JW. Stochastic analysis of a nonequilibrium phase transition: Some exact results. Phys. A 1977, 89, 326–338. [Google Scholar]
- Qian, H; Saffarian, S; Elson, EL. Concentration fluctuations in a mesoscopic oscillating chemical reaction system. Proc. Natl. Acad. Sci. USA 2002, 99, 10376–10381. [Google Scholar]
- Vellela, M; Qian, H. On Poincare-Hill cycle map of rotational random walk: Locating stochastic limit cycle in reversible Schnakenberg model. Proc. R. Soc. A 2010, 466, 771–788. [Google Scholar]
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (Studies in Nonlinearity); Perseus Books Group: New York, NY, USA, 2001. [Google Scholar]
- Hill, TL. Free Energy Transduction and Biochemical Cycle Kinetics; Spinger-Verlag: New York, NY, USA, 1989. [Google Scholar]
- Hill, TL; Chen, YD. Stochastics of cycle completions (fluxes) in biochemical kinetic diagrams. Proc. Natl. Acad. Sci. USA 1975, 72, 1291–1295. [Google Scholar]
- Sel’kov, EE. Self-oscillations in glycolysis. Eur. J. Biochem 1968, 4, 79–86. [Google Scholar]
- Goldbeter, A; Lefever, R. Dissipative structures for an allosteric model: Application to glycolytic oscillations. Biophys. J 1972, 12, 1302–1315. [Google Scholar]
- Keener, J; Sneyd, J. Mathematical Physiology; Springer: New York, NY, USA, 1998. [Google Scholar]
- Érdi, P; Tóth, J. Mathematical Models of Chemical Reactions: Theory and Applications of Deterministic and Stochastic Models; Manchester Univ. Press: Manchester, UK, 1989. [Google Scholar]
- Murray, JD. Mathematical Biology: An Introduction, 3rd ed; Springer: New York, NY, USA, 2002. [Google Scholar]
- Zheng, Q; Ross, J. Comparison of deterministic and stochastic kinetics for nonlinear systems. J. Chem. Phys 1991, 94, 3644–3648. [Google Scholar]
- Noyes, RM; Field, RJ. Oscillatory chemical reactions. Annu. Rev. Phys. Chem 1974, 25, 95–119. [Google Scholar]
- Xie, XS; Choi, PJ; Li, GW; Lee, NK; Lia, G. Single-molecule approach to molecular biology in living bacterial cells. Annu. Rev. Biophys 2008, 37, 417–444. [Google Scholar]
- Smolen, P; Baxter, DA; Byrne, JH. Modeling transcriptional control in gene networks – methods, recent results, and future directions. Bull. Math. Biol 2000, 62, 247–292. [Google Scholar]
- Turner, TE; Schnell, S; Burrage, K. Stochastic approaches for modeling in vivo reactions. Comput. Biol. Chem 2004, 28, 165–178. [Google Scholar]
- Paulsson, J; Berg, OG; Ehrenberg, M. Stochastic focusing: Fluctuation-enhanced sensitivity of intracellular regulation. Proc. Natl. Acad. Sci. USA 2000, 97, 7148–7153. [Google Scholar]
- Taylor, H; Karlin, S. An Introduction to Stochastic Modeling, 3rd ed; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Schnakenberg, J. Network theory of microscopic and macroscopic behaviour of Master equation systems. Rev. Mod. Phys 1976, 48, 571–585. [Google Scholar]
- Leontovich, MA. Basic equations of the kinetic gas theory from the point of view of the theory of random processes (in Russian). Zh. Teoret. Ehksper. Fiz 1935, 5, 211–231. [Google Scholar]
- McQuarrie, DA. Stochastic approach to chemical kinetics. J. Appl. Prob 1967, 4, 413–478. [Google Scholar]
- McQuarrie, DA. Stochastic Approach to Chemical Kinetics; Methuen: London, UK, 1968. [Google Scholar]
- Delbrück, M. Statistical fluctuations in autocatalytic reactions. J. Chem. Phys 1940, 8, 120–124. [Google Scholar]
- Heuett, WJ; Qian, H. Grand canonical Markov model: A stochastic theory for open nonequilibrium biochemical networks. J. Chem. Phys 2006, 124, 044110. [Google Scholar]
- Cao, Y; Liang, J. Optimal enumeration of state space of finitely buffered stochastic molecular networks and exact computation of steady state landscape probability. BMC Syst. Biol 2008, 2, 30. [Google Scholar]
- Van Kampen, N. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Kurtz, TG. Limit theorems and diffusion approximations for density dependent Markov chains. Math. Progr. Stud 1976, 5, 67–78. [Google Scholar]
- Kurtz, TG. Strong approximation theorems for density dependent Markov chains. Stochastic Process. Appl 1978, 6, 223–240. [Google Scholar]
- Hanggi, P; Grabert, H; Talkner, P; Thomas, H. Bistable systems: master equation versus Fokker-Planck modeling. Phys. Rev. A 1984, 29, 371–378. [Google Scholar]
- Baras, F; Mansour, M; Pearson, J. Microscopic simulation of chemical bistability in homogeneous systems. J. Chem. Phys 1996, 105, 8257. [Google Scholar]
- Luo, JL; van den Broeck, C; Nicolis, G. Stability criteria and fluctuations around nonequilibrium states. Z. Phys. B.: Cond. Matt 1984, 56, 165–170. [Google Scholar]
- Kurtz, TG. Limit theorems for sequences of jump Markov processes approximating ordinary differential equations. J. Appl. Prob 1971, 8, 344–356. [Google Scholar]
- Kurtz, TG. The relationship between stochastic and deterministic models for chemical reactions. J. Chem. Phys 1972, 57, 2976–2978. [Google Scholar]
- Sipos, T; Tóth, J; Érdi, J. Stochastic simulation of complex chemical reactions by digital computer, I. The model. React. Kinet. Catal. Lett 1974, 1, 113–117. [Google Scholar]
- Sipos, T; Tóth, J; Érdi, P. Stochastic simulation of complex chemical reactions by digital computer, II. Applications. React. Kinet. Catal. Lett 1974, 1, 209–213. [Google Scholar]
- McAdams, HH; Arkin, AP. It’s a noisy business! Genetic regulation at the nanomolar scale. Trends Genet 1999, 15, 65–69. [Google Scholar]
- Malek-Mansour, M; van den Broeck, C; Nicolis, G; Turner, JW. Asymptotic properties of Markovian master equations. Ann. Phys. (USA) 1981, 131, 283–313. [Google Scholar]
- Baras, F; Mansour, M. Particle simulations of chemical systems. Adv. Chem. Phys 1997, 100, 393–474. [Google Scholar]
- Ross, J. Thermodynamics and Fluctuations far from Equilibrium. In Springer Series in Chemical Physics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Zia, RKP; Schmittmann, B. Probability currents as principal characteristics in the statistical mechanics of non-equilibrium steady states. J. Stat. Mech.: Theor. Exp 2007, P07012. [Google Scholar]
- Tomita, K; Tomita, H. Irreversible circulation of fluctuation. Prog. Theor. Phys 1974, 51, 1731–1749. [Google Scholar]
- Wang, J; Xu, L; Wang, E. Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA 2008, 105, 12271–12276. [Google Scholar]
- Andrieux, D; Gaspard, P. Fluctuation theorem for currents and schnakenberg network theory. J. Stat. Phys 2007, 127, 107–131. [Google Scholar]
- Sevick, EM; Prabhakar, R; Williams, SR; Searles, DJ. Fluctuation theorems. Annu. Rev. Phys. Chem 2008, 59, 603–633. [Google Scholar]
- Han, B; Wang, J. Quantifying robustness and dissipation cost of yeast cell cycle network: the funneled energy landscape perspective. Biophys. J 2007, 92, 3755–3783. [Google Scholar]
- Han, B; Wang, J. Least dissipation cost as a design principle for robustness and function of cellular networks. Phys. Rev. E 2008, 77, 031922. [Google Scholar]
- Nasell, I. Extinction and quasi-stationarity in the Verhulst logistic model. J. Theor. Biol 2001, 211, 11–27. [Google Scholar]
- Luo, JL; Zhao, N; Hu, B. Effect of critical fluctuations to stochastic thermodynamic behavior of chemical reaction systems at steady state far from equilibrium. Phys. Chem. Chem. Phys 2002, 4, 4149–4154. [Google Scholar]
- Ao, P; Galas, D; Hood, L; Zhu, X. Cancer as robust intrinsic state of endogenous molecular-cellular network shaped by evolution. Med. Hypotheses 2008, 70, 678–84. [Google Scholar]
- Ao, P. Global view of bionetwork dynamics: adaptive landscape. J. Genet. Genomics 2009, 36, 63–73. [Google Scholar]
- Ge, H; Qian, H; Qian, M. Synchronized dynamics and nonequilibrium steady states in a yeast cell-cycle network. Math. Biosci 2008, 211, 132–152. [Google Scholar]
- Ge, H; Qian, M. Boolean network approach to negative feedback loops of the p53 pathways: Synchronized dynamics and stochastic limit cycles. J. Comput. Biol 2009, 16, 119–132. [Google Scholar]
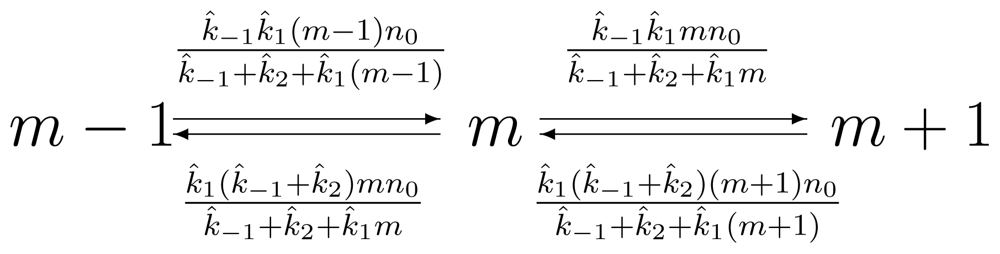
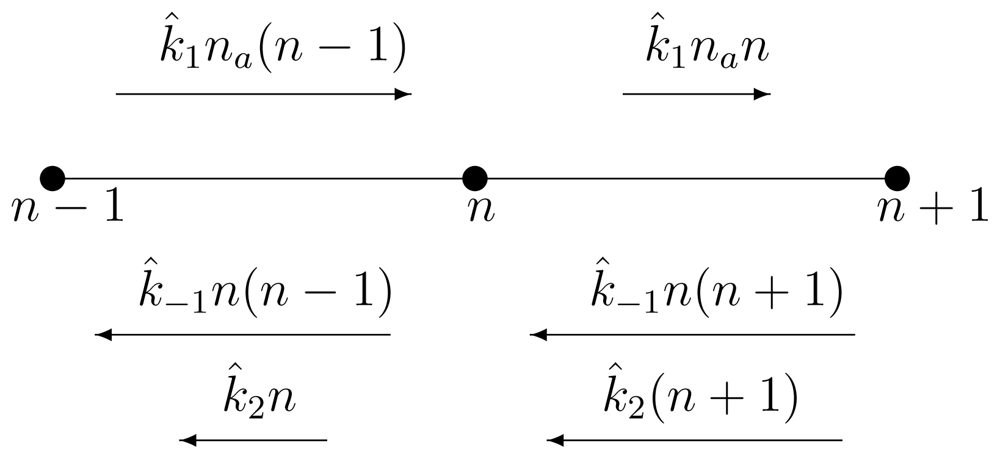


© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Qian, H.; Bishop, L.M. The Chemical Master Equation Approach to Nonequilibrium Steady-State of Open Biochemical Systems: Linear Single-Molecule Enzyme Kinetics and Nonlinear Biochemical Reaction Networks. Int. J. Mol. Sci. 2010, 11, 3472-3500. https://doi.org/10.3390/ijms11093472
Qian H, Bishop LM. The Chemical Master Equation Approach to Nonequilibrium Steady-State of Open Biochemical Systems: Linear Single-Molecule Enzyme Kinetics and Nonlinear Biochemical Reaction Networks. International Journal of Molecular Sciences. 2010; 11(9):3472-3500. https://doi.org/10.3390/ijms11093472
Chicago/Turabian StyleQian, Hong, and Lisa M. Bishop. 2010. "The Chemical Master Equation Approach to Nonequilibrium Steady-State of Open Biochemical Systems: Linear Single-Molecule Enzyme Kinetics and Nonlinear Biochemical Reaction Networks" International Journal of Molecular Sciences 11, no. 9: 3472-3500. https://doi.org/10.3390/ijms11093472
APA StyleQian, H., & Bishop, L. M. (2010). The Chemical Master Equation Approach to Nonequilibrium Steady-State of Open Biochemical Systems: Linear Single-Molecule Enzyme Kinetics and Nonlinear Biochemical Reaction Networks. International Journal of Molecular Sciences, 11(9), 3472-3500. https://doi.org/10.3390/ijms11093472



