1. Introduction
According to the Kyoto Protocol [
1] and the 2009 Copenhagen United Nations Climate Change Conference, climate change is a significant challenge, and actions must be taken to prevent any further increase in global temperature. Thus, renewable energy sources will play an increasingly important role in securing the European Union’s energy supply and providing sustainable development. Moreover, renewable energy sources also help to protect the environment. An increase in energy demand and atmospheric CO
2, as well as the high cost and limited availability of fossil fuels, have led to the partial replacement of fossil fuels with biomass [
2].
Knowledge of the chemical composition, thermal behavior and reactivity of biomass is essential for the effective design and operation of thermochemical conversion units. Thermoanalytical techniques, such as thermogravimetric analysis (TG) and derivative thermogravimetry (DTG), provide this information in a straightforward manner [
2–
4]. TG analyses are based on the volatilization rate of fuels, which is dependent on the heating rate applied to the sample and the type of fuel.
The intrinsic heterogeneity of biomass and the small amount of sample used in TG experiments makes it difficult to accurately determine the thermal properties of biomass; thus, to determine the characteristics of biomass with an acceptable, clearly defined level of uncertainty, a well-defined TG method must be developed. Many studies on the accuracy of TG experiments have been published [
5–
9], and various sampling methods have been proposed. Currently, TG methodologies are often based on small samples obtained from large batches; thus, careful reduction is necessary to prevent segregation and stratification problems [
8]. In general, a good sampling method should be able to achieve a representative sample without being affected by the aforementioned problems.
A new methodology for the sampling of solid biomass and determination of error associated with the measurement of thermal properties was presented [
10,
11] and validated. This method is independent of the origin, appearance and packaging of the batch used to acquire samples. In the present study, the error associated with the aforementioned methodology as well as the confidence intervals of moisture, volatile matter, fixed carbon and ash content were determined. Moisture content affects the heating value of biomass, and ash determines the level of fouling and corrosion [
12,
13]. Moreover, volatile compounds influence the behaviour of the flame. The overall uncertainty of the measurements was defined, allowing us to determine the minimum number of samples necessary to achieve an acceptable level of reliability. Because the fixed carbon content can be calculated as a function of moisture, volatile matter and ash content, the uncertainties of these properties affect the uncertainty in the concentration of fixed carbon [
11]. A comparative study on the mean values of the thermal properties and the corresponding uncertainties in TG experiments [
11] was conducted, and a relationship was not observed. Moreover, the confidence level and error associated with the measurement of thermal properties were not well correlated.
3. Results and Discussion
Moisture (
wb), volatile matter (
db), fixed carbon (
db) and ash content (
db) of the samples are presented in
Table 3, including the mean and variance of each variable. As shown in the table, brassica displayed a high ash content.
HIL, the heterogeneity invariant, was calculated according to the method described in Section 2.4.1. and is summarized in
Table 4. The maximum sampling error of a sample with a fixed mass was obtained from the
HIL, and the results indicated that the minimum sample size corresponded to a fixed sampling error. The minimum sample size and maximum sampling error associated with the determination of moisture, volatile matter, fixed carbon and ash content are provided in
Tables 5 and
6,
7 and
8,
9 and
10, and
11 and
12, respectively.
To show the utility of the results displayed in
Tables 5,
7,
9 and
11, the minimum sample mass required to achieve an accurate representation of the moisture content of hazelnut shells (Hs) was determined. A maximum sampling error of 0.05 was selected, and the corresponding non-dimensional sample size was 14.70, as shown in
Table 5. The minimum sampling size was subsequently multiplied by the average weight of Hs samples (21.29 × 10
−6 kg) to provide a minimum sample weight of 312.9 × 10
−6 kg.
To demonstrate the use of
Tables 6,
8,
10 and
12, an inverse calculation of the previous example was performed. The maximum sampling error of a sample with a mass of 312.9 × 10
−6 kg was determined by dividing the sample mass by the average weight of Hs samples (21.29 × 10
−6 kg), and a value of 14.7 was obtained. The maximum sampling error was calculated from the equation
. Using the methodology described in section 2.4.1,
Tables 5–
12 were generated with a confidence level of 95%.
According to the methodology described in Section 2.4.2, confidence intervals for the properties of each material were generated. As an example, the determination of the confidence intervals of the moisture content of hazelnut shells (Hs) is illustrated. According to the data shown in
Table 3, the mean moisture content of Hs is 10.873. Moreover, the results displayed in
Table 4 indicate that the
HIL of Hs is 4.79 × 10
−3. In this example, nine samples were tested; thus,
σ2(aS) ≈
(2/n)·
HIL·
aS2 = 0.126. According to the methodology described in Section 2.4.2., the confidence intervals of the moisture content of Hs are
. The confidence intervals of all of the materials and associated properties were calculated at a 95% confidence level, as shown in
Table 13. To compare the results of the present to those of previous studies, confidence intervals for the prompt analysis presented in the literature [
11] were calculated. The mean weights of the samples in TG analysis were approximately 1000-times less than those of the prompt analysis [
11]; thus, the confidence intervals of TG should be significantly wider (
). However, the accuracy of TG equipment compensates for a smaller sample weight, leading to confidence intervals that are approximately five-times greater than those of the prompt analysis.
Volatile matter and fixed carbon contents obtained from the TG and prompt analysis are not comparable because the results are dependent on the thermal history of the particles, which are completely different in the prompt and TG analysis. However, the moisture content of the materials should be comparable. Lignocellulosic biomass is mainly composed of cellulose, hemicellulose and lignin. At low heating rates, cellulose begins to decompose at temperatures greater than 300 ºC [
17], and hemicellulose begins to decompose at 220 ºC. However, lignin decomposes very slowly over a wide temperature range, beginning at 160 ºC [
18]. Because the moisture content was determined at temperatures below 378 K (
Table 2), it was assumed that water was not produced through pyrolysis; thus, the results of the present study should be comparable to those of the prompt analysis. As shown in
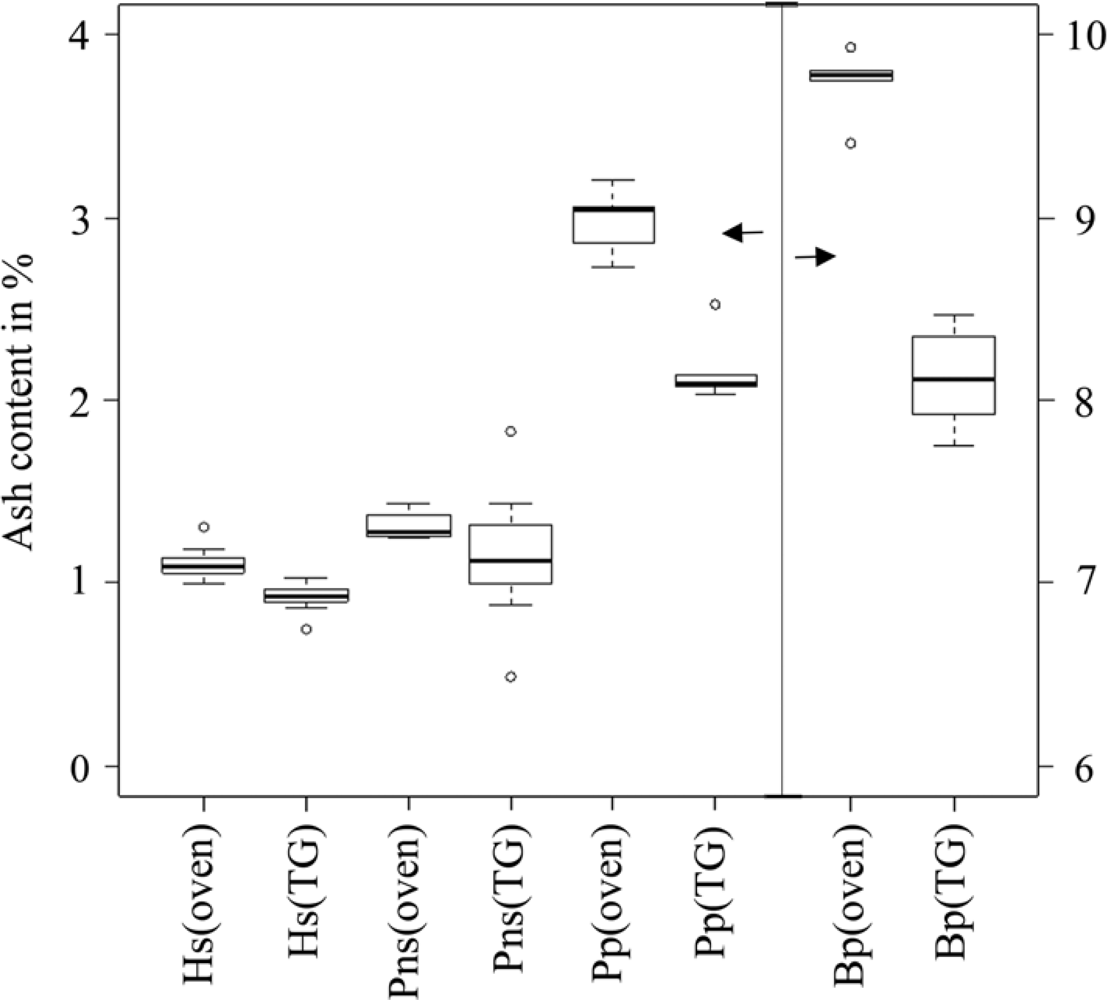
Table 13, the mean moisture content obtained in the TG analysis was lower than the mean moisture content of the prompt analysis. Moreover, the mean ash content obtained from TG analysis was lower than the mean ash content of the prompt analysis. A box-plot of ash content illustrating the median, outliers, smallest and largest observation, and lower and upper quartiles are shown in
Figure 1. The results indicated that the ash content obtained from the TG and prompt analyses were not comparable due to the methodology of the TG analysis. The ash content obtained from TG analysis was uniformly lower than that of the prompt analysis; thus, biomass heterogeneity was an unlikely cause for the discrepancy in the results. Due to the low sample weight (20 × 10
−6 kg), TG crucibles were loaded with tweezers. It is possible that big particles were favored in this process, and small particles and dust were effectively removed.
To verify the aforementioned hypothesis, the TG analysis was conducted on biomass with a small particle size (<0.3 × 10
−3 m). As shown in
Table 14, the ash content of fine particles was greater than the ash content of the original materials in the TG and prompt analyses. It is not possible to assure that the particle size distribution of the materials in the TG analysis is identical to that of the prompt analysis; therefore, the mean ash content of these methods is not comparable. A similar explanation is proposed for the determination of moisture content; however, handling particles smaller than 0.3 × 10
−3 m may affect the results. Thus, it was not feasible to validate this hypothesis. In general, these results indicate that the mean ash and moisture content obtained from the TG and prompt analysis are not comparable when the proposed methodology is applied.
Correlations between the moisture, volatile matter and ash content of the materials (fixed carbon was calculated from these properties) were observed at a confidence level of
α = 0.05. The ash and moisture content of Hs displayed a Pearson correlation coefficient of 0.69, and the moisture and volatile content of Pp displayed a correlation coefficient of 0.89. Thus, for all other properties and materials, the value of one variable cannot be explained by other variables because the properties are not linearly related. All three variables must be studied separately, and the analysis of one property cannot be used to infer the value of others. Based on the results of the prompt analysis, a similar conclusion was made [
11].
Although the properties of TG and prompt analysis are not related, a relationship between the maximum sampling error can be extrapolated from one analysis to the other. The maximum sampling error of the materials from the prompt analysis [
11] was extrapolated to the TG analysis, and the extrapolated error was greater than the maximum sampling error obtained from TG analysis. To illustrate this result, the error associated with the moisture content of hazelnut shells (Hs) was extrapolated. According to the literature results [
11],
HIL = 9.21 × 10
−5 and the maximum sampling error for a sample with an average weight of 21.7 × 10
−3 kg is 2.66 × 10
−2. By taking into account the relationship between the average weights of both analyses, the maximum sampling error of TG analysis was estimated:
This result does not agree with those shown in
Table 6 of the present paper, where
SEmax(TG) = 1.92 × 10
−1. The analysis was repeated for all of the materials and properties, and values of
SEmax(TG)/SEmax(prompt) varied vary from 1 to 16, while values of
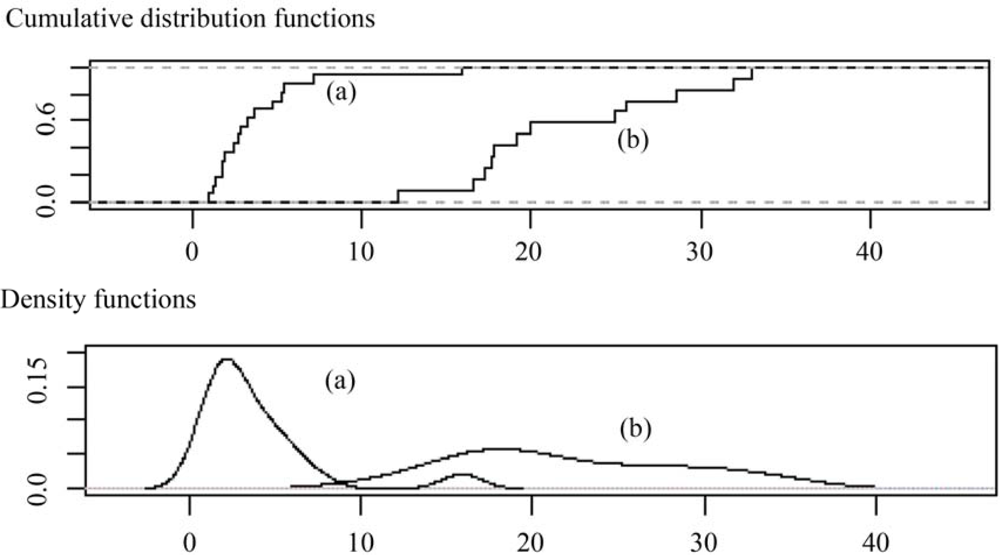
varied from 12 to 33. The empirical distribution and density functions of both quotients are shown in
Figure 2, and the results suggested that
SEmax(TG) cannot be estimated from
SEmax(prompt). SEmax(TG)/SEmax(prompt) reached a maximum value of 16 because atypical values were present in the density distribution function (
Figure 2 (a)). However, when atypical values were removed, the maximum quotient was equal to 7. The
HIL of the TG and prompt analysis are very different, which corroborates the lack of a relationship between the maximum sampling errors of the methods. As shown previously, the maximum sampling error of the TG analysis should be significantly greater (12–33 times) than that of the prompt analysis, but the accuracy of TG equipment compensates for the small sample weight, leading to maximum sampling errors that are approximately 1–7 times greater than
SEmax(prompt).To observe other relationships between
SEmax(TG) and
SEmax(prompt), a general correlation study was conducted on the sampling error associated with the volatile matter, fixed carbon and ash content and the corresponding
SEmax(prompt) [
11]. A significant correlation was observed, and a correlation coefficient of 0.63 and a p-value of 0.028 were obtained. Although the correlation is significant, the low value of the correlation coefficient suggests high levels of error will be encountered if
SEmax(TG) is estimated from
SEmax(prompt).