This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
The Particle Swarm Optimization (PSO) and Support Vector Machines (SVMs) approaches are used for predicting the thermodynamic parameters for the 1:1 inclusion complexation of chiral guests with β-cyclodextrin. A PSO is adopted for descriptor selection in the quantitative structure-property relationships (QSPR) of a dataset of 74 chiral guests due to its simplicity, speed, and consistency. The modified PSO is then combined with SVMs for its good approximating properties, to generate a QSPR model with the selected features. Linear, polynomial, and Gaussian radial basis functions are used as kernels in SVMs. All models have demonstrated an impressive performance with R2 higher than 0.8.
β-cyclodextrin (β-CD) is a cyclic oligosaccharide that naturally contains seven glucose residues linked by (1–4)-glycosidic bonds, with a hydrophilic outer surface and a relative hydrophobic central cavity, which can form complexes with appropriate guest molecules. It has received increasing attention in the pharmaceutical field for modifying drug physicochemical properties, such as solubility, stability and bio-availability, reducing their toxicity and side effects, and suppressing unpleasant taste or smell [1,2].
The high interest in the stability constants of CD-host complexes has initiated the search for proper models for predicting these association constants or the related free energies of complexation. The aim is not only to select convenient CDs for the complexation of a particular compound, but also to get some insight into the physico-chemical parameters influencing the affinity between host and guest molecules. The availability of a large amount of experimental data led to several interesting predictive models. The inclusion reactions of a series of benzene derivatives were used for a correlation model [3]. Diverse experimental information was used to develop a prediction model for the free energy of complexation using several molecular descriptors [4–7]. A CoMFA approach was applied to the binding constants of some organic compounds and various CDs [8]. An analysis of the complexation of 30 carboxylic acids and their anions was performed using a two-parameter correlation model [9]. Artificial neural networks were also used to correlate some molecular descriptors with complexation constants [10,11]. The free energies of a larger dataset of compounds complexed with all natural CDs were considered using a molecular-size based model [12,13]. Energies obtained from molecular docking of the guest molecule to the CDs’ cavities were used for systematic investigations of the interaction of organic substances with CDs [14–16]. A model correlating physico-chemical parameters directly with the solubility of the complexes was also presented [17]. A newer improved empirical model has been published just recently [18]. Most of these investigations considered the “natural” CDs, and generally, models were obtained with sufficient predictive power. The molecular descriptors are substantially different for various CDs, indicating differences in reaction mechanisms, or as a consequence of the varying flexibility of the ring system. Not much has been done up to now for the prediction of interaction energies with modified CDs, or considering different CD derivatives.
In this study, two novel approaches, Binary Particle Swarm Optimization (BPSO) [19] and Support Vector Machines (SVMs) [20] are used to predict the thermodynamic parameters for the 1:1 inclusion complexation of enantiomeric pairs of chiral guests with β-CD. SVMs represent a relatively new type of learning machine. They were designed to minimize the structural risk by minimizing an upper bound of the generalization error rather than the training error. Therefore, the over-fitting problem in machine learning is solved successfully. Another outstanding property of SVMs is that a solution obtained is always unique and globally optimal. In this paper, SVMs are investigated for a quantitative structure-property relationship (QSPR) study, to reduce the complexity of QSPR modeling and utilize the attractive properties of: not requiring the gradient information, consistent results, and fast convergence. The PSO was used to choose a set of important features.
Several factors such as number of atoms, van der Waals surface area, ionization potential, molecular weight, molar refractivity, atomic connectivity index, molecular flexibility, and angle bend energy, etc., influence thermodynamic properties. Only some of these factors strongly affect these thermodynamic properties and are controlled or set up in advance. The selection of these parameters is traditionally conducted by multiple linear regressions, partial least squares, and principle component analysis methods. Consequently, their assumptions must be verified and validated before the developed model can accurately be used. This results in a predictive model which may compromise the quality of the obtained products and/or efficiency of the modeling process.
With the increasing need for more accurate and practical evaluation QSPR models, techniques in artificial intelligence, particularly Artificial Neural Networks (ANNs), are receiving more attention in industry and academia today because they can be used to learn relationships between thermodynamic properties and their parameters. However, a number of parameters such as network topology, learning rate, and training methods have to be fine-tuned before they are deployed successfully. Furthermore, drawbacks like local optima, overfitting, and long learning time tend to occur.
Theoretically, the aforementioned shortcomings of ANNs have been countered by the development of Support Vector Machines. Unlike ANNs which minimize empirical risk, SVMs are designed to minimize the structural risk, by minimizing an upper bound of the generalization error, rather than the training error. Therefore, the overfitting problem in machine learning is solved successfully. Another outstanding property of SVMs is that the task of training SVMs is mapped to a uniquely solvable linearly constrained quadratic programming problem. This produces a solution that is always unique and globally optimal. They have been extended to solve regression problems as well.
In this paper, Support Vector Regression (SVR), which is based on Support Vector Machines, is investigated as an alternative technique for QSPR prediction. It has shown very good results for function approximation of Quantitative Structure-Activity Relationships (QSAR) [21]. The SVR retains much of the elegance of the SVMs, such as good generalization and global optimal properties, and has no normal distribution assumption requirement. The linear approximation is a fundamental concept of SVR. Its extension to a nonlinear case is achieved by using the mechanism of inner-product kernel to avoid the problem of dimensionality. To speed up its regression, the use of a proper kernel is calculated in advance. Even though this kernel computation requires large memory space, various problem optimizations have already been proposed [22,23].
Since SVM can build a very reliable QSPR model based on the training data, it is incorporated in our feature selection process. The Pearson correlation coefficient (R) is then treated as the objective function for a formulated optimization problem. Our previous paper [21] presented a similar approach by attempting to optimize R for predictive QSPR model building with a combined Feed-Forward Neural Network and a Particle Swarm Optimization. The PSO also showed good performance and was suitable for use with the found model, where no explicit relation between inputs and outputs was available. With attractive properties of no requirements for gradient information, consistent results, fast convergence, and successful applications in [24–28], PSO is then selected as an optimizer in this work.
Therefore, the purpose of this study was to develop a procedure that can determine key features for predicting complexation thermodynamic parameters of β-CD complexes with enantiomeric pairs of a chiral guest.
Methodology
The proposed methodology consists of two parts: feature selection and QSPR modeling. First, a machine learning technique called Support Vector Machines (SVMs) is used to capture characteristics of QSPR and their factors, because of the SVMs’ superior properties of generalization and global optima. They are next incorporated in an optimization problem so that a relatively new, effective, and efficient optimization algorithm, Particle Swarm Optimization (PSO), is applied to find key parameters. The cooperation between both techniques can produce a very good predictive QSPR model.
Support Vector Machines Based QSPR Model
SVMs represent a relatively new type of learning machine. They are an approximate implementation of the method of structural risk minimization, which attempts to minimize the generalization error, which occurs when the machines are tested with unseen data. The generalization error rate is bounded by the sum of a pair of competing terms, the training error rate and the confidence interval, which depends on the Vapnik-Chervonenkis (VC) dimension. Hence, the VC dimension and the training error (empirical risk) are both minimized at the same time. To realize this in SVMs, a structure is imposed on the set of hyperplanes, by trying to obtain the weight vector w having the minimum Euclidean norm. Coupled with dual transformations, the optimization model yields a global optimum. These key properties really separate the SVM from other learning machine algorithms.
In regression problems, the problem of approximating the following set of data {(x1, y1),..., (xl, yl)} ⊂ ℜn × ℜ with a linear function f (x) = 〈w, x〉 + b, where w ∈ ℜn,b ∈ ℜ, and 〈.,.〉 represents dot product, is taken into consideration. The xi is the set of descriptors, and yi is the output, which is the thermodynamic value. The ɛ-insensitive loss function proposed by Vapnik [20] is commonly incorporated with SVMs (ɛ-SVR) to create sparseness in the support vectors and to embed the robustness of the Huber’s loss function. This means that f(x) is allowed to vary at most ɛ deviation from the target, and is as flat as possible, simultaneously. If the deviations are larger than the ɛ specified, this implies a bad fit and this function is proportionally penalized with constant C. This constant C determines the tradeoff between the training errors and model complexity. The flatness test of f(x) is accomplished by searching for the smallest w. Hence, a formulation of ɛ-SVR is described by:
min:
12‖w‖2+C∑i=1l(ξi+ξi*)subject to:
yi−〈w,xi〉−b≤ɛ+ξi〈w,xi〉+b−yi≤ɛ+ξi*ξi,ξi*≥0
Everything above ɛ is captured in slack variables ξi and everything below -ɛ is captured in slack variables
ξi*. This ɛ-insensitive loss function,|ξ|ɛis defined as:
|ξ|ɛ={0;if|f(x)−y|<ɛ|f(x)−y|−ɛ;otherwise
Using the Lagrangian multipliers and the Karush-Kuhn-Tucker (KKT) conditions, the following dual problem is obtained:
maxα−12∑i=1l∑j=1l(αi−αi*)(αj−αj*)〈xi,xj〉−ɛ∑i=1l(αi+αi*)+∑i=1lyi(αi−αi*)subject to:
∑i=1l(αi−αi*)=0and:
αi,αi*∈[0,C],i=1,…,1.
Transforming into dual form yields a quadratic programming problem with linear constraints and a positive definite Hessian matrix. This leads to a global optimum. A nonlinear form is usually required to adequately model data. Hence, a nonlinear mapping, ϕ, is used to map data from an input space into a higher dimensional intermediate space, where linear regression is performed. Consequently, complications result in the complexity of ϕ and the problem of dimensionality in Equation (3). To alleviate these difficulties, the inner-product kernel is then introduced as follows:
K(xi,xj)=〈ϕ(xi),ϕ(xj)〉.
The dimensionality of the intermediate space is thus hidden from the remaining computations. Some of the most widely used kernels, such as linear, polynomial, and Gaussian radial basis functions (RBF), were tested in this study. The kernel function is employed in the optimization models above by replacing 〈.,.〉 with K(.,.). This adds the capability to approximate both linear and nonlinear functions.
In summary, the main advantages of SVR are implicit mapping by using kernels in handling nonlinear data, convexity of quadratic optimization, and generalization properties. In addition, distribution of the data is not necessarily assumed in advance, which makes it very promising for real-world problems.
Particle Swarm Optimization
PSO was introduced by Kennedy and Eberhart [19] to imitate social behavior of animals such as birds flocking in searching for food. Each particle flies in hyperspace searching for the best solution by adjusting position and velocity based on its own flying experience (pbest) and its companions’ experience (gbest). The inertia weight w was later introduced to improve the PSO optimizer. It is very attractive because the requirements of gradient information are not needed. Hence, it is unaffected by discontinuities of the objective function. The equations used consist of flexible and well-balanced mechanisms to enhance the global and local exploration abilities. These allow a thorough search and simultaneously avoid premature convergence. In addition, PSO uses probabilistic rules for a particle’s movements. Therefore, it is quite robust for local optima. The standard PSO consists of the following steps [19,29]:
Initialize a population of I particles with random positions and velocities in D dimensions.
Evaluate the desired optimization function in D variables for each particle.
Compare the evaluation with the particle’s previous best value, pbest[i]. If the current value is better than pbest[i], then pbest[i] = current value and the pbest location, pbestx[i][d], is set to the current location in d-dimensional space.
Compare the evaluation with the swarm’s previous best value, (pbest[gbest]). If the current value is better than pbest[gbest]), then gbest = current particle’s array index.
Change the velocity and position of the particle according to the following equations, respectively:
V[i][d]=V[i][d]+c1*rand()*(pbestx[i][d]− presentx[i][d])+c2*rand()*(pbestx[gbest][d]− persentx[i][d])presentx[i][d]= presentx[i][d]+ V[i][d]
Loop to step 2 until a stopping criterion, a sufficiently good evaluation function value, or a maximum number of iterations, is met.
In feature selection, the input presented to the regression modeling is in the form of a table where the rows represent chemical compounds and the columns are the molecular descriptors. Each compound contains a value for each corresponding factor. How accurately a QSPR model can predict the biological activity of the compounds depends on their values in a subset of the selected features. Hence, the selection of each column or feature is treated as a binary number. A numerical value of zero is used to represent that the corresponding descriptor is not selected for QSPR modeling. Otherwise, a numerical value of one is assigned. This binary problem calls for some modification of the original PSO. Thus presentx[i][d], which represents the value stored by the ith particle in the dth dimension, can only take on a binary value, instead of a real valued number. This indicates whether the dth feature is selected or not. Note that the D dimensions above are equal to the total number of descriptors. After the update step (Equation (5)), presentx[i][d] is discretized to a binary value by using probabilistic selection or roulette wheel selection. The fractional values of presentx[i][d] are treated as probability thresholds to determine subset membership. Each dimension or feature of the particle is assigned a slice of a roulette wheel whose size is proportional to presentx[i][d]. The subset is assembled by spinning the wheel and selecting the features to which the wheel’s marker points. This process is repeated k times, which are the predefined number of selected features. The chosen descriptors are then set to 1 and the remaining parameters are set to 0. The actual probabilities, pid, are computed as follows:
pid=xida∑d=1Dxidawhere xid is the fractional coordinates presentx[i][d] after the update step (Equation (5)), and a is a scaling factor or selection pressure and is set to 2. This binary PSO (BPSO) still presents the same advantages as the original PSO. The near-optimal solutions are found much faster, compared with the performance of a random search or an exhaustive search. This allows BPSO to perform feature selection efficiently in datasets with large numbers of descriptors. The objective function evaluated by the BPSO is the Pearson correlation coefficient that measures the quality of QSPR model with the selected features:
R=N∑n=1Nyiy^i−∑n=1Nyi∑n=1Ny^i[N∑n=1Nyi2−(∑n=1Nyi)2][N∑n=1Ny^i2−(∑n=1Ny^i)2]where N is the number of training compounds for regression and yi and ŷi are the measured and the predicted activities of the ith compound, respectively.
Chiral Guest Dataset and Descriptor Generation
The complex stability constant (ln K), the standard free energy (ΔG°), the enthalpy (ΔH°) and the entropy change (TΔS°) for the 1:1 inclusion complexation of enantiomer pairs of 74 selected chiral compounds with β-CD were taken from the experiments of Rekharsky and Inoue [30]. The values are given in Table 1. The guest structures were constructed by using the HyperChem program and fully geometrically optimized at the HF/3–21G level by the Gaussian03 program [31]. Two hundred structural properties were calculated by the Molecular Operating Environment (MOE) program package [32]. Descriptors are categorized by class: 2D descriptors (2D) are calculated from purely atomic and connectivity properties, internal 3D descriptors (i3D) use 3D coordinate information about each molecule, and external 3D descriptors (x3D) use absolute 3D atomic coordinate information, but also require an absolute frame of reference (such as, the molecules docked into the same receptor). The chiral guest dataset consisted of 56 compounds for training the models and 18 compounds for testing the quality of models.
QSPR Models
The PSO was adopted for major descriptor selection in QSPR of the chiral guest dataset. Swarm parameters are 50 particles and 100 iterations. The iterative PSO attempts to select the key features that maximize the Pearson correlation coefficient (R), resulting in a QSPR model developed by SVMs. The linear approximation is a fundamental concept of SVMs. Some of the most widely used kernels, such as linear, polynomial, and Gaussian radial basis functions (RBF) were tested in this study. This adds the capability to approximate both linear and nonlinear functions. Both PSO and SVMs were implemented in MATLAB 7.0.4 running on a Pentium IV (2.4 GHz) computer. The correlation coefficient for all PSO-SVM models are the average values from 10 calculations.
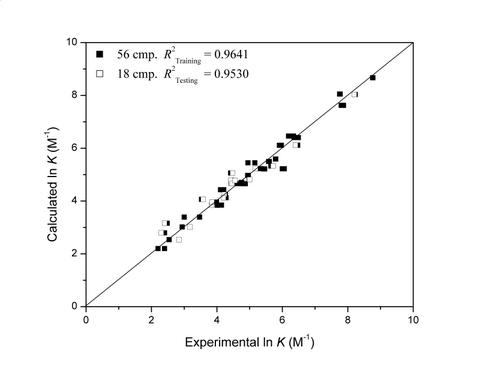
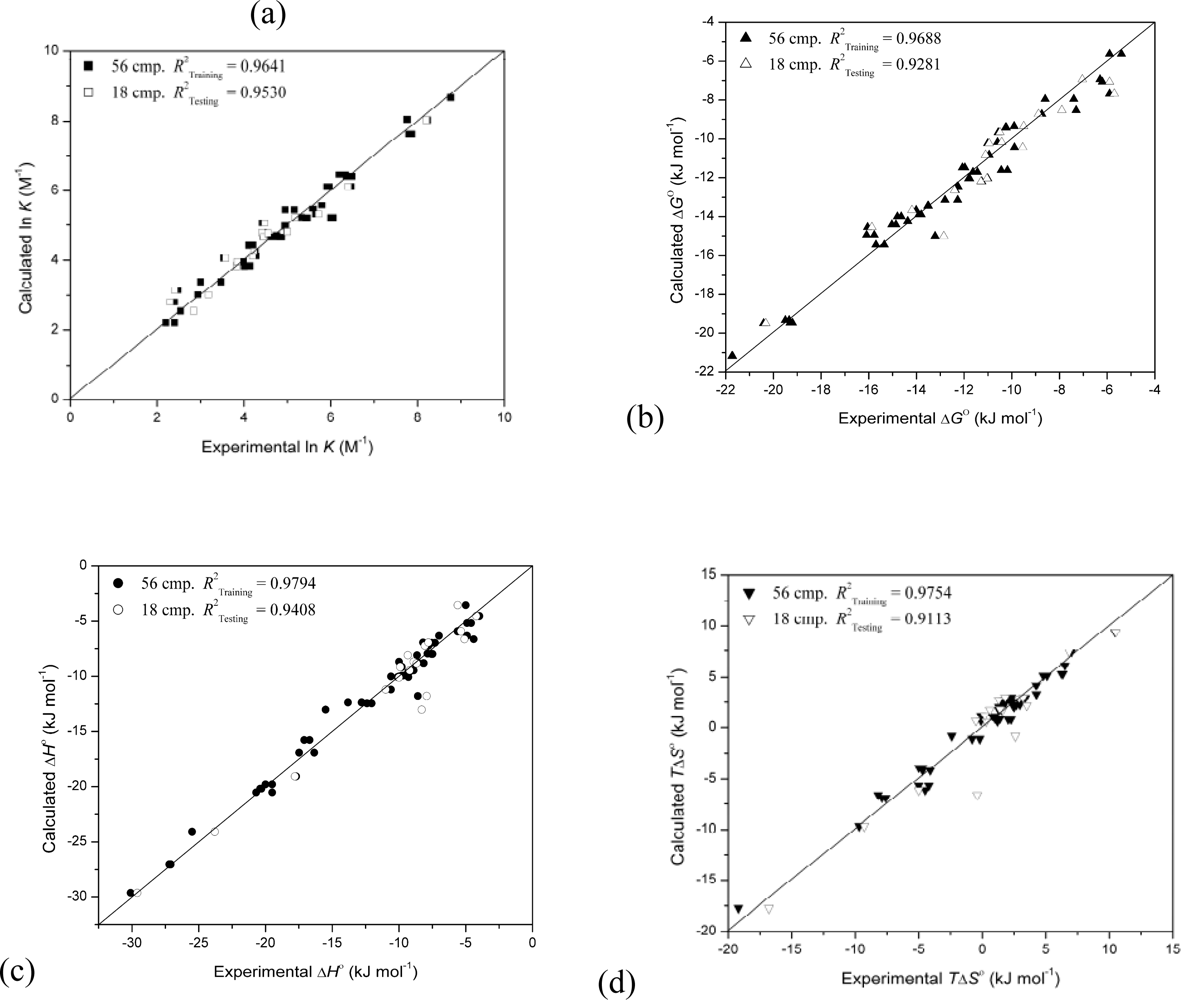
Results and Discussion
Table 2 shows that the PSO-SVMs with three different kernels give very good results. All models have demonstrated an impressive performance with R2 for training set (R2Training) higher than 0.8. The nonlinear kernels give better results than the linear function for the training chiral guest dataset. The polynomial kernel, with R2Training between 0.9991 and 0.9994, has better calibration correlation coefficients than the Gaussian RBF kernel, whereas the Gaussian RBF gives much better predictions than those obtained with the polynomial SVM. These agree with our previous work [33], in which K and ΔH° of the given enantiomer pair dataset were predicted best with a Gaussian RBF kernel.
The numbers of descriptors in the QSPR models of these thermodynamic properties are further investigated by using the Gaussian RBF kernel, which gives the best outcome for the chiral guest dataset. The statistics for all PSO-SVM models are given in Table 3. Models with four features also provide satisfactory predictive abilities when compared to the eight feature models. The best prediction performances of the individual models are presented in Table 4.
Table 5 presents the selected descriptors in the best prediction QSPR models. All models were developed with four 2D descriptors, which use the atoms and connection information of the molecule for the calculation. This illustrates that the molecular size and shape factors are important for the thermodynamic properties of 74 chiral compounds in 1:1 inclusion complex with β-CD. The plots of the best QSPR models with 4 features for ln K, ΔG°, ΔH° and TΔS° by PSO-SVM integration against the experimental values are shown in Figure 1.
Even though PSO-SVM methods are not able to explain the values of descriptors in the models, the maximum outlier from the QSPR models can point out the error of the experimental data. In ΔH° and TΔS° predictions by four features, PSO-SVM models indicate that cmp. 32 is the maximum outlier. Considering the values in Table 1, experimental results show that ΔH° of cmp. 31 (1R, 3S-camphoric acid) and cmp. 32 (1S, 3R-camphoric acid) are −15.5 and −8.3 kJ mol−1, and TΔS° are −8.3 and 0.4 kJ mol−1, respectively. The experimental results have different values for this enantiomeric pair, whereas the PSO-SVM models have identical results: ΔH° = −13.02 kJ mol−1and TΔS° = −6.63 kJ mol−1.
Conclusions
This work demonstrated that the combination of PSO and SVMs can be applied to effectively and efficiently select major features in QSPR modeling of the thermodynamic parameters of 1:1 inclusion complexation of enantiomeric pairs of chiral guests with β-CD. This responds to the needs of drug designers for prediction of the thermodynamic parameters of new compounds in complexation with β-CD. The method was based on a discrete binary modification of PSO. The fitness function was the Pearson correlation which was curve fitted by SVMs. The modified PSO appeared to be an effective and efficient algorithm, which robustly finds near-optimal and consistent results with short computer code and simple mathematical operators, while converging rather quickly. The SVMs showed excellent performance in predicting ln K, ΔG°, ΔH° and TΔS°, by considering major selected features. The combination of the adopted methods showed satisfactory results with the large dataset.
This work is financially supported by Thailand Research Fund (grant number RSA5080001). We are appreciative to Paul V. Neilson for carefully reading through the manuscript.
ReferencesSzejtliJIntroduction and general overview of cyclodextrin chemistryChem. Rev19989817431754LipkowitzKBApplications of computational chemistry to the study of cyclodextrinsChem. Rev19989818291874EstradaEPerdomo-LopezITorres-LabandeiraJJCombination of 2D-, 3D-connectivity and quantum chemical descriptors in QSPR. Complexation of α- and β-cyclodextrin with benzene derivativesJ. Chem. Inf. Comput. Sci20014115611568KleinCTPolheimDViernsteinHWolschannPPredicting the free energies of complexation between cyclodextrins and guest molecules: linear versus nonlinear modelsPharm. Res200017358365KleinCTPolheimDViernsteinHWolschannPA method for predicting the free energies of complexation between β-cyclodextrin and guest moleculesJ. Incl. Phenom. Macroc. Chem200036409423KatritzkyARFaraDCYangHKarelsonMSuzukiTSolovevVPVarnekAQuantitative structure-property relationship modeling of β-cyclodextrin complexation free energiesJ. Chem. Inf. Comput. Sci200444529541SuzukiTA nonlinear group contribution method for predicting the free energies of inclusion complexation of organic molecules with α- and β-cyclodextrinsJ Chem Inf Comput Sci20014112661273SuzukiTIshidaMFabianWMFClassical QSAR and comparative molecular field analyses of the host-guest interaction of organic molecules with cyclodextrinsJ. Comput. -Aided Mol. Des200014669678JimenezVAldereteJBThe role of charge transfer interactions in the inclusion complexation of anionic guests with α-cyclodextrinsTetrahedron20056154495456LeiLWen-GuangLQing-XiangGAssociation constant prediction for the inclusion of α-cyclodextrin with benzene derivatives by an artificial neural networkJ. Incl. Phenom. Macroc. Chem199934291298LoukasYLQuantitative structure-binding relationships QSBR, and artificial neural networks, improved predictions in drug, cyclodextrin inclusion complexesJ. Pharm. Sci2001226207211BodorNBuchwaldPTheoretical Insights into the formation; structure; and energetics of some cyclodextrin complexesJ. Incl. Phenom. Macroc. Chem200244914BuchwaldPComplexation Thermodynamic of cyclodextrins in the framework of a molecular size-based model for nonassociative organic liquids that includes a modified hydration-shell hydrogen-bond model for waterJ. Phys. Chem. B200210668646870FaucciMTMelaniFMuraPComputer-aided molecular modeling techniques for predicting the stability of drug-cyclodextrin inclusion complexes in aqueous solutionChem. Phys. Lett2002358383390HyunmyungKKarpjooJHyungwooPSeunhoJPreference prediction for the stable inclusion complexes between cyclodextrins and monocyclic insoluble chemicals based on Monte Carlo docking simulationsJ. Incl. Phenom. Macroc. Chem200654165170YoungjinCKumWCKarpjooJSeungRPSeunhoJComputational prediction for the slopes of AL-type phase solubility curves of organic compounds complexed with α-; β-; or γ-cyclodextrins based on Monte Carlo docking simulationsJ Incl Phenom Macroc Chem200655103108ZhaoLOrtonEVemuriNMPredicting solubility in multiple nonpolar drugs-cyclodextrin systemJ. Pharm. Sci20029123012306ChariRQureshiFMoscheraJTarantinoRKaloniaDDevelopment of improved empirical models for estimating the binding constant of a β-cyclodextrin inclusion complexPharm. Res200926161171KennedyJEberhartRParticle swarm optimizationProceedings of IEEE International Conference on Neural NetworksPerth, Australia1995Institute of Electrical and Electronics EngineersPiscataway, NJ, USA1995419421948VapnikVThe Nature of Statistical Learning TheorySpringerNew York, NY, USA1995LawtrakulLPrakasvudhisarnCCorrelation studies of HEPT derivatives using swarm intelligence and support vector machinesMonatsh. Chem200513616811691JoachimsTMaking large-scale support vector machine learning practicalAdvances in Kernel Methods: Support Vector LearningSchölkopfBBurgesCJCSmolaAJMIT PressCambridge, Massachusetts, USA1999169184PlattJFast training of support vector machines using sequential minimal optimizationAdvances in Kernel Methods: Support Vector LearningSchölkopfBBurgesCJCSmolaAJMIT PressCambridge, Massachusetts, USA1999185208SutterJMDixonSLJursPCAutomated descriptor selection for quantitative structure-activity relationships using generalized simulated annealingJ. Chem. Inf. Comput. Sci1995357784SoSSKarplusMEvolutionary optimization in quantitative structure – activity relationship: an application of genetic neural networksJ. Med. Chem19963915211530YasriAHartsoughDToward an optimal procedure for variable selection and QSAR model buildingJ. Chem. Inf. Comput. Sci20014112181227HasegawaKMiyashitaYFunatsuKGA strategy for variable selection in QSAR studies: GA-based PLS analysis of calcium channel antagonistsJ. Chem. Inf. Comput. Sci199737306310AgrafiotisDKCedeñoWFeature selection for structure – activity correlation using particle swarmsJ. Med. Chem20024510981107EberhartRCShiYParticle swarm optimization: developments, applications and resourcesProceedings of the 2001 Congress on Evolutionary ComputationSeoul, South Korea2001Institute of Electrical and Electronics EngineersPiscataway, NJ, USA200118186RekharskyMVInoueYChiral recognition thermodynamic of β-cyclodextrin: The thermodynamic origin of enantioselectivity and the enthalpy entropy compensation effectJ. Am. Chem. Soc200012244184435FrischMJTrucksGWSchlegelHBScuseriaGERobbMACheesemanJRMontgomeryJAJrVrevenTKudinKNBurantJCMillamJMIyengarSSTomasiJBaroneVMennucciBCossiMScalmaniGRegaNPeterssonGANakatsujiHHadaMEharaMToyotaKFukudaRHasegawaJIshidaMNakajimaTHondaYKitaoONakaiHKleneMLiXKnoxJEHratchianHPCrossJBBakkenVAdamoCJaramilloJGompertsRStratmannREYazyevOAustinAJCammiRPomelliCOchterskiJWAyalaPYMorokumaKVothGASalvadorPDannenbergJJZakrzewskiVGDapprichSDanielsADStrainMCFarkasOMalickDKRabuckADRaghavachariKForesmanJBOrtizJVCuiQBaboulAGCliffordSCioslowskiJStefanovBBLiuGLiashenkoAPiskorzPKomaromiIMartinRLFoxDJKeithTAl-LahamMAPengCYNanayakkaraAChallacombeMGillPMWJohnsonBChenWWongMWGonzalezCPopleJAGaussian 03Gaussian, IncWallingford, CT, USA2004Molecular Operating Environment (MOE)Chemical Computing Group, Inc.Montreal, Quebec, Canada2005Available online: http://www.chemcomp.com (accessed Jul. 31, 2008).LawtrakulLWolschannPPrakasvudhisarnCPredicting complexation thermodynamic of β-cyclodextrin with enantiomeric pairs of chiral guests by using swarm intelligence and support vector machinesProceedings of the 14th International Cyclodextrins SymposiumKyoto, Japan2008The Society of Cyclodextrins, JapanTokyo, Japan2008421424Figure and Tables
Plots of calculated thermodynamic parameters by PSO-SVM with Gaussian RBF kernel models with 4 features, versus the experimental values: (a) complex stability constant (ln K), (b) standard free energy (ΔG°), (c) enthalpy (ΔH°) and (d) entropy change (TΔS°).
Experimental Thermodynamic parameters: ln K (M−1), ΔG° (kJ mol−1), ΔH° (kJ mol−1) and TΔS° (kJ mol−1) of 74 chiral compounds in 1:1 inclusion complexation with β-CD taken from Ref. [30] and the values from the best prediction QSPR models with four features.
cmp
guest
Experimental
Calculationb
ln K
ΔG°
ΔH°
TΔS°
ln K
ΔG°
ΔH°
TΔS°
1
N-acetyl-D-phenylalanine
4.11
−10.18
−8.14
2.04
4.43
−11.61
−8.82
0.78
2
N-acetyl-L-phenylalanine
4.21
−10.44
−8.17
2.27
4.43
−11.61
−8.82
0.78
3
N-acetyl-D-tryptophan
2.54
−6.30
−25.50
−19.20
2.54
−6.94
−24.09
−17.72
4a
N-acetyl-L-tryptophan
2.84
−7.04
−23.80
−16.80
2.54
−6.94
−24.09
−17.72
5
N-acetyl-D-tyrosine
4.83
−11.97
−16.70
−4.70
4.65
−11.48
−15.77
−3.92
6
N-acetyl-L-tyrosine
4.87
−12.07
−17.10
−5.00
4.65
−11.48
−15.77
−3.92
7
(1R,2S)-2-amino-1,2-diphenylethanol
4.01
−9.90
−10.00
−0.10
3.84
−9.35
−10.11
0.65
8a
(1S,2R)-2-amino-1,2-diphenylethanol
3.83
−9.50
−10.00
−0.50
3.84
−9.35
−10.11
0.65
9
(R)-benzyl glycidyl ether
5.46
−13.52
−9.20
4.30
5.21
−13.45
−9.58
4.22
10
(S)-benzyl glycidyl ether
5.43
−13.50
−9.30
4.20
5.21
−13.45
−9.58
4.22
11
2,3-O-benzylidene-D-threitol
4.76
−11.81
−7.56
4.25
4.70
−12.05
−7.98
3.30
12
2,3-O-benzylidene-L-threitol
4.74
−11.76
−7.49
4.27
4.70
−12.05
−7.98
3.30
13a
(2R,3R)-3-benzyloxy-1,2,4-butanetriol
4.42
−10.95
−8.07
2.90
4.79
−10.23
−7.23
2.90
14
(2S,3S)-3-benzyloxy-1,2,4-butanetriol
4.44
−11.01
−7.79
3.20
4.79
−10.23
−7.23
2.90
15
O-benzyl-D-serine
4.26
−10.57
−8.90
1.70
4.25
−9.67
−9.46
2.74
16a
O-benzyl-L-serine
4.23
−10.50
−9.20
1.30
4.25
−9.67
−9.46
2.74
17
N-t-Boc-D-alanine
5.97
−14.80
−9.70
5.10
6.11
−14.00
−9.94
5.16
18
N-t-Boc-L-alanine
5.91
−14.64
−9.80
4.80
6.11
−14.00
−9.94
5.16
19
N-t-Boc-D-alanine methyl ester
6.49
−16.09
−13.82
2.30
6.40
−14.95
−12.37
2.43
20
N-t-Boc-L-alanine methyl ester
6.36
−15.77
−12.80
3.00
6.40
−14.95
−12.37
2.43
21a
N-t-Boc-D-serine
5.72
−14.19
−11.00
3.20
5.33
−13.67
−11.20
2.95
22
N-t-Boc-L-serine
5.65
−14.01
−10.60
3.40
5.33
−13.67
−11.20
2.95
23
(R)-3-bromo-8-camphorsulfonic acid
8.23
−20.41
−30.10
−9.70
8.03
−19.49
−29.63
−9.67
24a
(S)-3-bromo-8-camphorsulfonic acid
8.20
−20.32
−29.60
−9.30
8.03
−19.49
−29.63
−9.67
25
(R)-3-bromo-2-methyl-1 propanol
4.96
−12.29
−9.30
3.00
4.97
−12.47
−10.07
2.65
26
(S)-3-bromo-2-methyl-1 propanol
4.94
−12.25
−10.10
2.20
4.97
−12.47
−10.07
2.65
27
(R)-3-bromo-2-methylpropionic acid methyl ester
5.58
−13.80
−12.05
1.80
5.50
−13.90
−12.45
2.40
28
(S)-3-bromo-2-methylpropionic acid methyl ester
5.60
−13.90
−12.40
1.50
5.50
−13.90
−12.45
2.40
29a
(R)-camphanic acid
5.18
−12.85
−17.80
−5.00
5.23
−15.01
−19.07
−6.17
30
(S)-camphanic acid
5.33
−13.22
−17.70
−4.50
5.23
−15.01
−19.07
−6.17
31
(1R,3S)-camphoric acid
2.94
−7.30
−15.50
−8.20
3.02
−8.52
−13.02
−6.63
32a
(1S,3R)-camphoric acid
3.18
−7.90
−8.30
−0.40
3.02
−8.52
−13.02
−6.63
33
(R)-camphorquinone-3-oxime
7.87
−19.50
−27.10
−7.60
7.62
−19.33
−27.04
−6.91
34
(S)-camphorquinone-3-oxime
7.80
−19.34
−27.20
−7.90
7.62
−19.33
−27.04
−6.91
35
(R)-10-camphorsulfonic acid
6.34
−15.70
−20.70
−5.00
6.46
−15.44
−20.53
−5.74
36
(S)-10-camphorsulfonic acid
6.19
−15.35
−19.50
−4.20
6.46
−15.44
−20.53
−5.74
37a
N-Cbz-D-alanine
5.00
−12.40
−8.90
3.50
4.81
−12.64
−8.69
2.17
38
N-Cbz-L-alanine
4.99
−12.37
−10.00
2.40
4.81
−12.64
−8.69
2.17
39
(1R,2R)-trans-1,2-cyclohexanediol
4.44
−11.01
−3.98
7.03
4.66
−12.04
−4.54
7.43
40a
(1S,2S)-trans-1,2-cyclohexanediol
4.45
−11.04
−4.21
6.83
4.66
−12.04
−4.54
7.43
41
(R)-1-cyclohexylethylamine
5.80
−14.37
−7.85
6.50
5.59
−14.24
−7.94
6.15
42
(S)-1-cyclohexylethylamine
5.79
−14.36
−7.87
6.50
5.59
−14.24
−7.94
6.15
43
O,O'-dibenzoyl-D-tartaric acid
3.47
−8.60
−7.00
1.60
3.39
−7.95
−6.32
2.02
44
O,O'-dibenzoyl-L-tartaric acid
3.00
−7.40
−4.90
2.50
3.39
−7.95
−6.32
2.02
45a
Gly-D-Phe
3.85
−9.54
−7.93
1.60
3.96
−10.44
−11.79
1.74
46
Gly-L-Phe
3.99
−9.89
−8.59
1.30
3.96
−10.44
−11.79
1.74
47
(R)-hexahydromandelic acid
6.47
−16.05
−5.61
10.44
6.11
−14.54
−5.92
9.37
48a
(S)-hexahydromandelic acid
6.40
−15.87
−5.36
10.51
6.11
−14.54
−5.92
9.37
49
(1R,2R,5R)-2-hydroxy-3-pipanone
7.77
−19.30
−19.50
−0.20
8.05
−19.47
−19.79
−1.12
50
(1S,2S,5S)-2-hydroxy-3-pipanone
7.75
−19.20
−20.00
−0.80
8.05
−19.47
−19.79
−1.12
51
(R)-mandelic acid
2.40
−5.90
−4.90
1.00
2.20
−5.63
−5.17
1.11
52
(S)-mandelic acid
2.20
−5.40
−4.60
0.80
2.20
−5.63
−5.17
1.11
53a
(R)-mandelic acid methyl ester
4.20
−10.42
−7.80
2.60
4.13
−10.17
−6.94
−0.86
54
(S)-mandelic acid methyl ester
4.28
−10.60
−8.20
−2.40
4.13
−10.17
−6.94
−0.86
55
(R)-α-methoxyphenylacetic acid
2.40
−5.90
−4.40
1.50
2.79
−7.68
−6.63
1.75
56a
(S)-α-methoxyphenylacetic acid
2.30
−5.70
−5.10
0.60
2.79
−7.68
−6.63
1.75
57
(R)-α-methoxy-α-trifluoromethylphenylacetic acid
5.16
−12.80
−17.48
−4.70
5.45
−13.14
−16.92
−4.19
58
(S)-α-methoxy-α-trifluoromethylphenylacetic acid
4.95
−12.27
−16.35
−4.10
5.45
−13.14
−16.92
−4.19
59
D-phenylalanine amide
4.62
−11.44
−10.00
1.40
4.66
−11.71
−10.01
0.87
60
L-phenylalanine amide
4.69
−11.63
−10.60
1.00
4.66
−11.71
−10.01
0.87
61a
D-phenylalanine methyl ester
2.40
−5.90
−5.60
0.30
3.16
−7.07
−3.56
0.58
62
L-phenylalanine methyl ester
2.48
−6.20
−5.00
1.20
3.16
−7.07
−3.56
0.58
63
(R)-2-phenylbutyric acid
4.54
−11.26
−9.79
1.50
4.77
−12.20
−9.15
1.81
64a
(S)-2-phenylbutyric acid
4.55
−11.29
−9.91
1.40
4.77
−12.20
−9.15
1.81
65
(R)-3-phenylbutyric acid
6.00
−14.86
−8.62
6.24
5.22
−14.41
−8.72
5.34
66
(S)-3-phenylbutyric acid
6.06
−15.03
−8.68
6.35
5.22
−14.41
−8.72
5.34
67
(R)-1-phenyl-1,2-ethanediol
4.13
−10.23
−7.54
2.69
3.85
−9.42
−6.96
2.24
68
(S)-1-phenyl-1,2-ethanediol
4.14
−10.26
−7.30
2.96
3.85
−9.42
−6.96
2.24
69a
(R)-phenyllactic acid
4.48
−11.10
−9.34
1.80
5.06
−10.83
−8.09
2.99
70
(S)-phenyllactic acid
4.42
−10.95
−8.65
2.30
5.06
−10.83
−8.09
2.99
71
(R)-2-phenylpropionic acid
3.53
−8.74
−8.81
−0.10
4.06
−8.72
−8.84
1.18
72a
(S)-2-phenylpropionic acid
3.58
−8.88
−8.69
0.20
4.06
−8.72
−8.84
1.18
73
(1R,2R,3S,5R)-pinanediol
8.77
−21.74
−20.40
1.30
8.67
−21.18
−20.19
2.03
74
(1S,2S,3R,5S)-pinanediol
8.76
−21.71
−20.30
1.40
8.67
−21.18
−20.19
2.03
Compounds in test set;
The descriptors in the QSPR models are provided in Table 4.
The average predictive ability of PSO-SVMs QSPR models with 8 descriptors.
SVMs
ln K
ΔG°
ΔH°
TΔS°
R2Training
R2Testing
R2Training
R2Testing
R2Training
R2Testing
R2Training
R2Testing
Linear
0.8201
0.6666
0.8239
0.6349
0.9048
0.8455
0.8220
0.8257
Polynomial
0.9993
0.7358
0.9994
0.8213
0.9992
0.8432
0.9991
0.8251
Gaussian RBF
0.9983
0.9762
0.9987
0.9713
0.9983
0.9350
0.9986
0.8853
The average predictive ability of PSO-SVM with Gaussian RBF kernel models.
Number of descriptors
ln K
ΔG°
ΔH°
TΔS°
R2Training
R2Testing
R2Training
R2Testing
R2Training
R2Testing
R2Training
R2Testing
8
0.9983
0.9762
0.9987
0.9713
0.9983
0.9350
0.9986
0.8853
7
0.9977
0.9534
0.9981
0.9778
0.9978
0.9325
0.9981
0.8936
6
0.9963
0.9629
0.9967
0.9039
0.9966
0.9271
0.9967
0.8868
5
0.9869
0.9292
0.9872
0.9507
0.9932
0.9142
0.9919
0.8812
4
0.9534
0.9020
0.9496
0.8498
0.9820
0.8563
0.9572
0.8707
Descriptors in the best predictive ability of PSO-SVM with Gaussian RBF kernel models.
Number of descriptors
R2Training
R2Testing
Descriptors in the model
I
II
III
IV
V
VI
VII
VIII
ln K
8
0.9982
0.9903
2
20
31
76
80
143
164
185
7
0.9982
0.9922
2
12
90
94
122
144
164
6
0.9968
0.9879
3
20
30
94
140
167
5
0.9929
0.9829
3
20
27
59
134
4
0.9641
0.9530
12
79
114
134
ΔG°
8
0.9985
0.9924
3
11
28
79
94
112
136
144
7
0.9978
0.9928
2
9
111
123
129
133
140
6
0.9969
0.9894
3
12
94
124
133
140
5
0.9935
0.9849
3
20
27
59
134
4
0.9688
0.9281
20
72
94
122
ΔH°
8
0.9987
0.9510
28
54
76
83
124
173
181
186
7
0.9977
0.9385
20
79
91
140
143
153
187
6
0.9965
0.9417
2
21
27
112
154
176
5
0.9943
0.9374
16
36
79
91
122
4
0.9794
0.9408
20
21
30
36
TΔS°
8
0.9986
0.8949
3
23
36
44
94
112
114
159
7
0.9982
0.9371
9
20
33
100
122
158
199
6
0.9952
0.8991
9
12
93
94
154
164
5
0.9868
0.9079
6
30
39
76
90
4
0.9754
0.9113
8
76
114
129
The selected descriptors in four feature QSPR models.